【小初高学习】2018数学高考(文)二轮复习检测：题型练6大题专项 立体几何综合问题 Word版含解

2018年高考数学（文）二轮复习讲练测总分 _______ 时间 _______ 班级 _______ 学号 _______ 得分_______一、选择题（12*5=60分）1．“直线1y kx =+与圆()2221x y -+=相切”是“43k =-”的（ ） A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件 【答案】C2．【2018届安徽省六安市第一中学高三上学期第五次月考】设m R ∈，则“0m = ”是“直线()()1:1110l m x m y ++--=与直线()()2:12140l m x m y -+++=垂直”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 【答案】A【解析】由直线12l l 与垂直可得()()()()111210m m m m +-+-+=，解得01m m ==或．所以“0m = ”是“直线()()1:1110l m x m y ++--=与直线()()2:12140l m x m y -+++=垂直”的充分不必要条件．选A ．3．已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线为y =，则该双曲线的离心率等于【答案】C4．已知双曲线C ： 2219x y a -= (a>0)与双曲线221412x y -=有相同的离心率，则实数a 的值为( ) A. 1 B. 2 C. 3 D. 4 【答案】C 92a a+=，解得a ＝3. 5．已知圆22:20M x y ay +-=（0a >）截直线0x y +=所得弦长是22a 的值为26 D. 3 【答案】B【解析】圆M ： ()222x y a a +-= ，圆心为()0,a ，半径为a ，圆心到直线0x y +=2a =，半，根据圆的弦长公式可知2221242a a a +=⇒=， 0,2a a >∴=，选B. 6．已知点M 是抛物线2:2(0)C y px p =>上一点， F 为C 的焦点， MF 的中点坐标是()2,2，则p 的值为（ ） A. 1 B. 2 C. 3 D. 4 【答案】D【解析】,02p F ⎛⎫⎪⎝⎭，又中点()2,2，所以4,42p M ⎛⎫- ⎪⎝⎭，所以16242p p ⎛⎫=-⎪⎝⎭，得4p =.故选D. 7．【2018届辽宁省丹东市五校协作体高三上学期联考】已知双曲线22221x y a b -=（0,0a b >>）的一条渐近线被圆22650x y x +-+=截得的弦长为2，则该双曲线的离心率为A. 235262【答案】D点睛：双曲线几何性质是高考考查的热点，其中离心率是双曲线的重要性质，求双曲线的离心率时，将提供的双曲线的几何关系转化为关于双曲线基本量,,a b c 的方程或不等式，利用222b c a ＝－和e=ca转化为关于e 的方程或不等式，通过解方程或不等式求得离心率的值或取值范围．8．设斜率为22的直线l 与椭圆22221x y a b+=（0a b >>）交于不同的两点，且这两个交点在x 轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为（ ）1213【答案】C【解析】由题意， 222b ac =，得)222ac a c =-2220e e +=，所以22e =，故选C.9．【2018届吉林省普通中学高三第二次调研】已知F 为抛物线2y x =的焦点，点,A B 在该抛物线上且位于x 轴的两侧，而且·6OAOB =（O 为坐标原点），若ABO ∆与AFO ∆的面积分别为1S 和2S ，则124S S +最小值是A.2 B. 6 C. 132D. 43【答案】B故选B.点睛：圆锥曲线中最值与范围问题的常见求法(1)几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决；(2)代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立目标函数，再求这个函数的最值．在利用代数法解决最值与范围问题时常从以下几个方面考虑：①利用判别式来构造不等关系，从而确定参数的取值范围；②利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；③利用基本不等式求出参数的取值范围；④利用函数的值域的求法，确定参数的取值范围．10．已知双曲线22221(00)x ya ba b-=>>，的左右焦点分别为12,F F，以2OF为直径作圆C，再以1CF为直径作圆E ，两圆的交点恰好在已知的双曲线上，则该双曲线的离心率为（ ）【答案】D【解析】11．【2018届湖北省襄阳市高三1月调研】设双曲线22221(00)x y a b a b-=>>，的左、右焦点分别为F 1、F 2，离心率为e ，过F 2的直线与双曲线的右支交于A 、B 两点，若△F 1AB 是以A 为直角顶点的等腰直角三角形，则2e =（ ）A. 3+522-122+422- 【答案】B【解析】设2AF x =，则12AF x a =+，所以22BF a =，也就是14BF a =，故2224164242cos 4c a a a a π=+-⨯⨯⨯，因此2425c a ⎛⎫=- ⎪⎝⎭B ．12．【2018届湖南省长郡中学高三月考（五）】已知1F ， 2F 是椭圆和双曲线的公共焦点， p 是它们的一个公共点，且123F PF π∠=，设椭圆和双曲线的离心率分别为1e ， 2e ，则1e ， 2e 的关系为（ ）A. 1213e e =B. 2212143e e += C. 2211134e e += D. 221134e e +=【答案】C二、填空题（4*5=20分）13.【2018届天津市第一中学高三上学期第二次月考】圆心在直线4y x =-，且与直线10x y +-=相切于点()32P -，的圆的标准方程为__________.【答案】()()22148x y -++= 【解析】∵圆心在直线y=﹣4x 上，设圆心C 为（a ，﹣4a ），圆与直线x+y ﹣1=0相切于点P （3，﹣2）， 则k PC =423a a--=1，∴a=1．即圆心为（1，﹣4）．，∴圆的标准方程为（x ﹣1）2+（y+4）=8．故答案为：（x ﹣1）2+（y+4）=8．14．【2018届吉林省实验中学高三上学期第五次月考（一模）】若双曲线2212516x y -= 的左、右焦点分别为12,F F ，点P 在双曲线上，且13PF =，则2PF 等于__________. 【答案】13 【解析】1222210,31013PF PF a PF PF -==∴-=∴= 或7- （舍）.15．【2018届内蒙古集宁第一中学高三上学期第二次月考】已知双曲线Ｓ与椭圆221934x y +=的焦点相同,如果34y x =是双曲线Ｓ的一条渐近线,那么双曲线Ｓ的方程为_______________. 【答案】221916y x -=∴双曲线Ｓ的方程为221916y x -=. 故答案为221916y x -=16．【2018届甘肃省张掖市高三第一次检测】已知抛物线22,,y x A B =是抛物线上的两点，线段AB 的垂直平分线与x 轴相交于点()00P x ，则0x 的取值范围是__________．（用区间表示） 【答案】()1,+∞【解析】设,A B 的坐标分别为()11,x y 和()22,x y ，线段AB 的垂直平分线与x 轴相交点()0,0,P x AB ∴不平行于y 轴，即12x x ≠，又PA PB =，即()()2222101202x x y x x y -+=-+，得()()2212120212,,x x x x x y y A B -+-=-是抛物线上的两点， 2211222,2y x y x ∴==，代入上式，得12012121,0,0,2x x x x x x x +=+≥≥≠， 120x x ∴+>，即01x >，故答案为()1,+∞.三、解答题（共6道小题，共70分）17. 【2018届甘肃省张掖市高三第一次检测】设直线l 的方程为()25x m y =++，该直线交抛物线2:4C y x =于,P Q 两个不同的点.（1）若点()5,2A -为线段PQ 的中点，求直线l 的方程； （2）证明：以线段PQ 为直径的圆M 恒过点()1,2B . 【答案】（1）30x y +-=（2）见解析18．【2018届湖南省长郡中学高三月考试题（五）】已知O 为坐标原点， ()11,M x y ， ()22,N x y 是椭圆22193x y +=上的点，且121230x x y y +=，设动点P 满足3OP OM ON =+． （Ⅰ）求动点P 的轨迹C 的方程；（Ⅱ）若直线():0l y x m m =+≠与曲线C 交于,A B 两点，求三角形OAB 面积的最大值．【答案】（Ⅰ）22390x y +=；（Ⅱ）153【解析】试题分析：(Ⅰ)设点(),P x y ， ()11,M x y ， ()22,N x y ，结合3OP OM ON =+整理变形可得动点P 的轨迹C 的方程为22390x y +=．(Ⅱ)联立直线与椭圆方程可得22463900x mx m ++-=，理由弦长公式有()2121AB k x=+-=O 到直线:0AB x y m -+=的距离d =，据此可得面积函数：ABCS ∆=≤22360332m m -+=OAB 面积的最大值为试题解析：∴()223644390m m ∆=-⨯⨯- ()2121200m =->，又∵0m ≠，得20120m <<，3432mx x +=-， 2343904m x x -=， ∴12AB x =-=2229390324180442m m m ⎛⎫-⨯-⨯=-⎪⎝⎭，∵点O 到直线:0AB x y m -+=的距离d =，∴122ABCm S ∆==≤22360332m m -+=260m =时等号成立，满足（*）∴三角形OAB 面积的最大值为19．【2018届甘肃省张掖市高三第一次检测】已知椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ，上顶点为M ，若直线1MF 的斜率为1，且与椭圆的另一个交点为2,N F MN ∆的周长为42（1）求椭圆的标准方程；（2）过点1F 的直线l （直线l 的斜率不为1）与椭圆交于,P Q 两点，点P 在点Q 的上方，若1123F NQ F MP S S ∆∆= ，求直线l 的斜率.【答案】（1）2212x y +=；（2）11.因为1123F NQ F MP S S ∆∆=，即111111121sin sin 232NF QF QF N MF PF PF M ⎛⎫∠=⋅∠ ⎪⎝⎭，【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式，属于难题.用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在x 轴上，还是在y 轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程()222210x y a b a b +=>>或22221x y b a+= ()0a b >>；③找关系：根据已知条件，建立关于a 、b 、c 的方程组；④得方程：解方程组，将解代入所设方程，即为所求.20．【2018届吉林省普通中学高三第二次调研】设椭圆22122:1(0)x y C a b a b+=>>的左焦点为F ，右顶点为A ，离2，已知A 是抛物线22:2(0)C y px p =>的焦点. （1）求椭圆1C 的方程和抛物线2C 的方程;（2）若抛物线2C 的准线l 上两点,P Q 关于x 轴对称，直线AP 与椭圆相交于点B （B 异于点A ），直线BQ 与x 轴相交于点D ，若APD ∆的面积为3，求直线AP 的方程. 【答案】（1）2221x y += ， 24y x =（2）见解析（2）设直线AP 方程为()10x my m =+≠，与直线l 的方程1x =-联立 可得点221,,1,P Q m m ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭， 联立AP 跟椭圆方程2221{ 1x y x my +==+消去x ，整理得()22220m y my ++=，解得12220,2my y m -==+，可得22222,22m m B m m ⎛⎫-+- ⎪++⎝⎭∵21,Q m ⎛⎫- ⎪⎝⎭∴22222212212BQm m m m k m mm --++==--+++，则直线BQ 方程()2211m y x m m +-=-+，令0y =，解得2211m x m -=+，即221,01m D m ⎛⎫- ⎪+⎝⎭∴有2211222121m 3APDm Sm ⎛⎫-=-= ⎪+⎝⎭，整理得260m -+=,解得2m m ==±∴直线AP 的方程为：10,10,220,220x x x x -=--=+-=-= .21．【2018届江苏省泰州中学高三12月月考】已知椭圆的中心为坐标原点O ，椭圆短轴长为2，动点()2M t ，（0t >）在椭圆的准线上. （1）求椭圆的标准方程；（2）求以OM 为直径且被直线3450x y --=截得的弦长为2的圆的方程；（3）设F 是椭圆的右焦点，过点F 作OM 的垂线与以OM 为直径的圆交于点N ，求证：线段ON 的长为定值，并求出这个定值.【答案】(1) 2212x y += (2) 圆的方程为()()22125x y -+-=2点睛：圆中涉及直线与圆的位置关系时，可考虑平面几何得性质，特别是半弦长，弦心距，半径构成的直角三角形，可以迅速解决问题，要注意使用.22．已知椭圆C ： 22221x y a b += (a>b>0)过点(1， 32)，且离心率e ＝12.(Ⅰ)求椭圆C 的标准方程；(Ⅱ)若直线l ：y ＝kx ＋m 与椭圆C 相交于A ，B 两点(A ，B 不是左右顶点)，椭圆的右顶点为D ，且满足DA ·DB ＝0，试判断直线l 是否过定点，若过定点，求出该定点的坐标；若不过定点，请说明理由．【答案】(1) 22143x y += (2) 直线过定点(27，0) 【解析】试题分析：（Ⅰ）由e ＝12可得12c a =，利用222a b c =+，把点(1， 32)代入椭圆方程，即可得出椭圆C 的标准方程；（Ⅱ）设A(x 1，y 1)，B(x 2，y 2)，联立22{ 143y kx mx y =++=，得到根与系数的关系，利用0DA DB ⋅=，得到k AD ·k BD ＝－1，即可得出结论.试题解析：(Ⅰ)由题意椭圆的离心率e ＝12. ∴12c a = ∴a ＝2c(Ⅱ)设A(x 1，y 1)，B(x 2，y 2)，由22{ 143y kx mx y =++=得(3＋4k 2)x 2＋8mkx ＋4(m 2－3)＝0， Δ＝64m 2k 2－16(3＋4k 2)(m 2－3)>0,3＋4k 2－m 2>0，则x 1＋x 2＝2834mkk -+，x 1·x 2＝()224334m k-+ ∴y 1·y 2＝(kx 1＋m)·(kx 2＋m)＝k 2x 1x 2＋mk(x 1＋x 2)＋m 2＝()2223434m k k -+∵0DA DB ⋅= ∴k AD ·k BD ＝－1又∵椭圆的右顶点D(2,0)， ∴1212122y yx x ⋅=---，则y 1y 2＋x 1x 2－2(x 1＋x 2)＋4＝0 ()()222222344316++40343434m k mmkk k k --+=+++，7m 2＋16mk ＋4k 2＝0，解得m 1＝－2k ，m 2＝27k -，且满足3＋4k 2－m 2>0 当m ＝－2k 时，l ：y ＝k(x －2)，直线过定点(2,0)与已知矛盾；当m＝27k-时，l：y＝k(x27-)，直线过定点(27，0)．综上可知，直线l过定点，定点坐标为(27，0).点睛：本题考查了椭圆的标准方程的求法，及直线过定点的证明，此题关键是联立直线与椭圆方程消去y得到关于x的一元二次方程，然后借助韦达定理，将向量的数量积等于零表示出来，得到方程，进而求出定点.。

第一单元 高考中档大题突破
解答题: 立体几何
基本考点——空间平行、垂直关系及体积、表面积的计算
．直线、平面平行的判定及其性质
()线面平行的判定定理：⊄α，⊂α，∥⇒∥α.
()线面平行的性质定理：∥α，⊂β，α∩β＝⇒∥.
()面面平行的判定定理：⊂β，⊂β，∩＝，∥α，∥α⇒α∥β.
()面面平行的性质定理：α∥β，α∩γ＝，β∩γ＝⇒∥.
．直线、平面垂直的判定及其性质
()线面垂直的判定定理：⊂α，⊂α，∩＝，⊥，⊥⇒⊥α.
()线面垂直的性质定理：⊥α，⊥α⇒∥.
()面面垂直的判定定理：⊂β，⊥α⇒α⊥β.
()面面垂直的性质定理：α⊥β，α∩β＝，⊂α，⊥⇒⊥β.
.(·全国卷Ⅰ)如图，在四棱锥－中，∥，且∠＝∠＝°.
()证明：平面⊥平面；
()若＝＝＝，∠＝°，且四棱锥－的体积为，求该四棱锥的侧面积．
()证明：由已知∠＝∠＝°，
得⊥，⊥.
由于∥，故⊥，从而⊥平面.
又⊂平面，
所以平面⊥平面.
()解：如图，在平面内作⊥，垂足为.
由()知，⊥平面，故⊥，⊥，
可得⊥平面.
设＝，则由已知可得＝，＝.
故四棱锥－的体积
－＝··＝.
由题设得＝，故＝.
从而结合已知可得＝＝＝＝，＝＝，＝＝.
可得四棱锥－的侧面积为
·＋·＋·＋°＝＋. .(·全国卷Ⅱ)如图，四棱锥－中，侧面为等边三角形且垂直于底面，＝＝，∠＝∠＝°.。

2018年高考真题解答题专项训练：立体几何（文科）学生版1．（2018年浙江卷）如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．2．（2018年天津卷）如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB=2，AD=BAD=90°．（（（求证：AD（BC（（（（求异面直线BC与MD所成角的余弦值；（Ⅲ）求直线CD与平面ABD所成角的正弦值．3．（2018年北京卷）如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面P AD，平面ABCD，P A，PD，P A=PD，E，F分别为AD，PB的中点.，，）求证：PE，BC，，，）求证：平面P AB，平面PCD，，，）求证：EF，平面PCD.4．（2018年新课标1卷）如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA，（1）证明：平面ACD⊥平面ABC，DA，求三棱锥Q−ABP的（2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=23体积．5．（2018年新课标3卷）如图，矩形ABCD所在平面与半圆弧CD所在平面垂直，M是CD 上异于C，D的点，（1）证明：平面AMD⊥平面BMC，（2）在线段AM上是否存在点P，使得MC∥平面PBD？说明理由，6．（2018年新课标2卷）如图，在三棱锥P−ABC中，AB=BC=2√2，PA=PB=PC= AC=4，O为AC的中点．（1）证明：PO⊥平面ABC，（2）若点M在棱BC上，且MC=2MB，求点C到平面POM的距离．参考答案1．（Ⅰ）见解析；（Ⅱ）√3913.【来源】2018年全国普通高等学校招生统一考试数学（浙江卷）【解析】分析:方法一：（Ⅰ）通过计算，根据勾股定理得AB 1⊥A 1B 1,AB 1⊥B 1C 1,再根据线面垂直的判定定理得结论，（Ⅱ，找出直线AC 1与平面ABB 1所成的角，再在直角三角形中求解.方法二：（Ⅰ）根据条件建立空间直角坐标系，写出各点的坐标，根据向量之积为0得出AB 1⊥A 1B 1,AB 1⊥A 1C 1,再根据线面垂直的判定定理得结论，（Ⅱ）根据方程组解出平面ABB 1的一个法向量，然后利用AC 1⃑⃑⃑⃑⃑⃑⃑ 与平面ABB 1法向量的夹角的余弦公式及线面角与向量夹角的互余关系求解. 详解：方法一：（Ⅰ）由AB =2,AA 1=4,BB 1=2,AA 1⊥AB,BB 1⊥AB 得AB 1=A 1B 1=2√2，所以A 1B 12+AB 12=AA 12.故AB 1⊥A 1B 1.由BC =2，BB 1=2,CC 1=1, BB 1⊥BC,CC 1⊥BC 得B 1C 1=√5， 由AB =BC =2,∠ABC =120°得AC =2√3，由CC 1⊥AC ，得AC 1=√13，所以AB 12+B 1C 12=AC 12，故AB 1⊥B 1C 1.因此AB 1⊥平面A 1B 1C 1.，Ⅱ）如图，过点C 1作C 1D ⊥A 1B 1，交直线A 1B 1于点D ，连结AD .由AB 1⊥平面A 1B 1C 1得平面A 1B 1C 1⊥平面ABB 1， 由C 1D ⊥A 1B 1得C 1D ⊥平面ABB 1，所以∠C 1AD 是AC 1与平面ABB 1所成的角.学科.网由B 1C 1=√5,A 1B 1=2√2,A 1C 1=√21得cos∠C 1A 1B 1=√6√7sin∠C 1A 1B 1=√7，所以C 1D =√3，故sin∠C 1AD =C 1D AC 1=√3913. 因此，直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二：，Ⅰ）如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系O -xyz .由题意知各点坐标如下：A(0,−√3,0),B(1,0,0),A 1(0,−√3,4),B 1(1,0,2),C 1(0,√3,1),因此AB 1⃑⃑⃑⃑⃑⃑⃑ =(1,√3,2),A 1B 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(1,√3,−2),A 1C 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(0,2√3,−3), 由AB 1⃑⃑⃑⃑⃑⃑⃑ ⋅A 1B 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =0得AB 1⊥A 1B 1. 由AB 1⃑⃑⃑⃑⃑⃑⃑ ⋅A 1C 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.（Ⅱ）设直线AC 1与平面ABB 1所成的角为θ.由（Ⅰ）可知AC 1⃑⃑⃑⃑⃑⃑⃑ =(0,2√3,1),AB ⃑⃑⃑⃑⃑ =(1,√3,0),BB 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2), 设平面ABB 1的法向量n =(x,y,z).由{n ⋅AB ⃑⃑⃑⃑⃑ =0,n ⋅BB 1⃑⃑⃑⃑⃑⃑⃑ =0,即{x +√3y =0,2z =0, 可取n =(−√3,1,0). 所以sinθ=|cos⟨AC 1⃑⃑⃑⃑⃑⃑⃑ ,n⟩|=|AC 1⃑⃑⃑⃑⃑⃑⃑⃑⋅n||AC 1⃑⃑⃑⃑⃑⃑⃑⃑ |⋅|n|=√3913. 因此，直线AC 1与平面ABB 1所成的角的正弦值是√3913.点睛：利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.2．(Ⅰ)证明见解析；(Ⅱ)26；(Ⅲ)4． 【来源】2018年全国普通高等学校招生统一考试文科数学（天津卷） 【解析】分析：（Ⅰ（由面面垂直的性质定理可得AD ⊥平面ABC （则AD ⊥BC （（Ⅱ）取棱AC 的中点N ，连接MN ，ND ．由几何关系可知∠DMN （或其补角）为异面直线BC 与MD所成的角．计算可得1226MNcos DMN DM ∠==．则异面直线BC 与MD 所成角（Ⅲ）连接CM ．由题意可知CM ⊥平面ABD ．则∠CDM 为直线CD 与平面ABD 所成的角．计算可得4CM sin CDM CD ∠==．即直线CD 与平面ABD所成角的正弦值为4． 详解：（Ⅰ）证明：由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD =AB ，AD ⊥AB ，可得AD ⊥平面ABC ，故AD ⊥BC ．（Ⅱ）取棱AC 的中点N ，连接MN ，ND ．又因为M 为棱AB 的中点，故MN ∥BC ．所以∠DMN （或其补角）为异面直线BC 与MD 所成的角．在Rt △DAM 中，AM =1，故DM因为AD ⊥平面ABC ，故AD ⊥AC ． 在Rt △DAN 中，AN =1，故DN．在等腰三角形DMN 中，MN =1，可得12cos MNDMN DM ∠==所以，异面直线BC 与MD所成角的余弦值为26． （Ⅲ）连接CM ．因为△ABC 为等边三角形，M 为边AB 的中点，故CM ⊥AB ，CM又因为平面ABC ⊥平面ABD ，而CM ⊂平面ABC ，故CM ⊥平面ABD ．所以，∠CDM为直线CD 与平面ABD 所成的角．在Rt △CAD 中，CD ．在Rt △CMD 中， sin CM CDM CD ∠==所以，直线CD 与平面ABD 所成角的正弦值为4． 点睛：本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力． 3．，Ⅰ，见解析 ，Ⅱ，见解析 ，Ⅲ，见解析【来源】2018年全国普通高等学校招生统一考试文科数学（北京卷）【解析】分析：（1）欲证PE ⊥BC ，只需证明PE ⊥AD 即可；（2）先证PD ⊥平面PAB ，再证平面P AB ，平面PCD ；（3）取PC 中点G ，连接FG,DG ，证明EF//DG ，则EF//平面PCD . 详解：（Ⅰ），PA =PD ，且E 为AD 的中点，∴PE ⊥AD . ∵底面ABCD 为矩形，∴BC ∥AD ， ，PE ⊥BC .（Ⅱ）∵底面ABCD 为矩形，∴AB ⊥AD . ，平面PAD ⊥平面ABCD ，，AB ⊥平面PAD . ，AB ⊥PD .又PA ⊥PD ,，PD ⊥平面PAB ，，平面PAB ⊥平面PCD . （Ⅲ）如图，取PC 中点G ，连接FG,GD .BC.，F,G分别为PB和PC的中点，∴FG∥BC，且FG=12∵四边形ABCD为矩形，且E为AD的中点，BC，，ED∥BC,DE=12，ED∥FG，且ED=FG，∴四边形EFGD为平行四边形，，EF∥GD.又EF⊄平面PCD，GD⊂平面PCD，，EF∥平面PCD.点睛，证明面面关系的核心是证明线面关系，证明线面关系的核心是证明线线关系.证明线线平行的方法：（1，线面平行的性质定理，，2，三角形中位线法，，3，平行四边形法. 证明线线垂直的常用方法，，1）等腰三角形三线合一；（2，勾股定理逆定理；（3，线面垂直的性质定理；，4，菱形对角线互相垂直.4．(1)见解析.(2)1.【来源】2018年全国普通高等学校招生统一考试文科数学（新课标I卷）【解析】分析：(1)首先根据题的条件，可以得到∠BAC=90，即BA⊥AC，再结合已知条件BA，AD，利用线面垂直的判定定理证得AB⊥平面ACD，又因为AB⊂平面ABC，根据面面垂直的判定定理，证得平面ACD⊥平面ABC，(2)根据已知条件，求得相关的线段的长度，根据第一问的相关垂直的条件，求得三棱锥的高，之后借助于三棱锥的体积公式求得三棱锥的体积.详解：（1）由已知可得，∠BAC=90°，BA⊥AC，又BA，AD，且AC∩AD=A，所以AB⊥平面ACD，又AB⊂平面ABC，所以平面ACD⊥平面ABC，，2）由已知可得，DC=CM=AB=3，DA=3√2，又BP=DQ=23DA，所以BP=2√2，作QE，AC，垂足为E，则QE=∥13DC，由已知及（1）可得DC⊥平面ABC，所以QE⊥平面ABC，QE=1，因此，三棱锥Q−ABP的体积为V Q−ABP=13×QE×S△ABP=13×1×12×3×2√2sin45°=1，点睛：该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的判定以及三棱锥的体积的求解，在解题的过程中，需要清楚题中的有关垂直的直线的位置，结合线面垂直的判定定理证得线面垂直，之后应用面面垂直的判定定理证得面面垂直，需要明确线线垂直、线面垂直和面面垂直的关系，在求三棱锥的体积的时候，注意应用体积公式求解即可. 5．（1）证明见解析（2）存在，理由见解析【来源】2018年全国卷Ⅲ文数高考试题文档版【解析】分析：（1）先证AD⊥CM,再证CM⊥MD，进而完成证明。

专题1 空间点、直线、平面之间的位置关系专题[基础达标](30分钟60分)一、选择题(每小题5分，共30分)1.如图，在长方体ABCD-A1B1C1D1中，E，F分别为B1O和C1O的中点，长方体的各棱中与EF平行的有()A.一条B.两条C.三条D.四条D【解析】与EF平行的棱为BC，B1C1，AD，A1D1，共四条.2a和平面α，β，α∩β=l，a⊄α，a⊄β，且a在α，β内的射影分别为直线b和c，则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面D【解析】依题意，直线b和c的位置关系可能是相交、平行或异面.3.E，F，G，H是三棱锥A-BCD棱AB，AD，CD，CB上的点，延长EF，HG交于点P，则点P() A.一定在直线AC上B.一定在直线BD上C.只在平面BCD内D.只在平面ABD内B【解析】∵EF⊂平面ABD，HG⊂平面BCD，∴EF∩HG=P∈平面ABD∩平面BCD=BD，∴点P一定在直线BD上.4.长方体ABCD-A1B1C1D1中，既与AB共面也与CC1共面的棱有()A.3条B.4条C.5条D.6条C【解析】如图，用列举法知符合要求的棱为BC，CD，C1D1，BB1，AA1.5a，b是互不垂直的两条异面直线，则下列命题成立的是()A.存在唯一直线l，使得l⊥a，且l⊥bB.存在唯一直线l，使得l∥a，且l⊥bC.存在唯一平面α，使得a⊂α，且b∥αD.存在唯一平面α，使得a⊂α，且b⊥αC【解析】A项，存在无数条直线l，故错误；B，D项，因为a，b互不垂直，故错误.6在四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB和△PAD都是等边三角形，则异面直线CD与PB所成角的大小为()A.90°B.75°C.60°D.45°A【解析】如图，过点B作直线BE∥CD，交DA的延长线于点E，连接PE.∴∠PBE(或其补角)是异面直线CD与PB所成角.∵△PAB和△PAD都是等边三角形，∴∠PAD=60°，DA=PA=AB=PB=AE，∠PAE=120°.设PA=AB=PB=AE=a，则PE=√3a.又∠ABC=∠BAD=90°，∴∠BAE=90°，∴BE=√2a.∴在△PBE中，PB2+BE2=PE2，∴∠PBE=90°，∴异面直线CD与PB所成角的大小为90°.二、填空题(每小题5分，共10分)7.在正四棱椎V-ABCD中，底面正方形ABCD的边长为1，侧棱长为2，则异面直线VA与BD所成角的大小为.π【解析】如图，设AC∩BD=O，连接VO.因为四棱锥V-ABCD是正四棱锥，2所以VO⊥平面ABCD，故BD⊥VO.又四边形ABCD是正方形，所以BD⊥AC，因为VO∩AC=O，所以BD⊥平面VAC，所以BD⊥VA，即异面直线VA与BD所成角的大小为π.28.如果三个平面两两相交有三条交线，则三条交线的位置关系是.互相平行或者交于一点【解析】由图1知三条交线平行，由图2知三条交线交于一点.三、解答题(共20分)9.(10分)在正方体ABCD-A1B1C1D1中，E，F分别是AD，AA1的中点.(1)求直线AB1和CC1所成的角的大小；(2)求直线AB1和EF所成的角的大小.【解析】(1)如图，连接DC1，∵DC1∥AB1，∴直线DC1和CC1所成的锐角∠CC1D就是直线AB1和CC1所成的角.∵∠CC1D=45°，∴直线AB1和CC1所成的角是45°.(2)如图，连接A1D，A1C1，∵EF∥A1D，AB1∥DC1，∴∠A1DC1是直线AB1和EF所成的角.∵△A1DC1是等边三角形，∴∠A1DC1=60°，∴直线AB1和EF所成的角是60°.10.(10分)正方体ABCD-A1B1C1D1中，对角线A1C与平面BDC1交于点O，AC，BD交于点M，判断点C1，O，M是否共线，并说明理由.【解析】如图所示，由A1A∥C1C确定平面AA1C1C，因为A1C⊂平面AA1C1C，O∈A1C，所以O∈平面AA1C1C.又因为平面BC1D∩直线A1C=O，所以O∈平面BC1D，所以O在平面AA1C1C与平面BC1D的交线上.因为AC∩BD=M，所以M∈平面BC1D.又因为M∈平面AA1C1C，平面BC1D∩平面AA1C1C=C1M，所以O∈C1M，即O，C1，M三点共线.[高考冲关](15分钟20分)1.(5分ABCD-A1B1C1D1中，P，Q，R分别是AB，AD，B1C1的中点，那么正方体中过点P，Q，R的截面图形是() A.三角形B.四边形C.五边形D.六边形D【解析】如图所示，作RG∥PQ交C1D1于点G，连接QP并延长，与CB的延长线交于点M，且QP的反向延长线与CD的延长线交于点N，连接MR交BB1于点E，连接PE，则PE，RE为截面与正方体的交线，同理连接NG，交DD1于点F，连接QF，则QF，FG为截面与正方体的交线，故截面为六边形PQFGRE.2.(5分)如图是正方体的平面展开图，在这个正方体中，下列命题正确的序号有.①BM与ED平行；②CN与BE是异面直线；③CN与BM成60°角；④DM与BN垂直.③④【解析】由已知中正方体的平面展开图，得到正方体的直观图如图所示.由正方体的几何特征可得：①BM与ED是垂直的，所以①错误.②CN是BE是平行线，所以②错误.③BM∥AN，且三角形ACN为正三角形，所以CN与BM成60°角，所以③正确.由DM⊥CN，DM⊥BC，所以DM⊥平面BCNE，DM⊥BN，所以④正确.3.(5分ABCD中，AD⊥AB，AD⊥DC，若AD与BC成60°角，且AD=√3，则BC=.2√3【解析】将该四面体放入长方体中，如图，有AD CE，所以在直角三角形CBE中，CE=√3，∠BCE=60°，所以斜边BC=√3=2√3.cos60°4.(5分在正三棱柱ABC-A 1B 1C 1中，D 是AC 的中点，AA 1∶AB=√2∶1，则异面直线AB 1与BD 所成的角为 .60° 【解析】如图，取A 1C 1的中点D 1，连接B 1D 1.因为D 是AC 的中点，所以B 1D 1∥BD ，所以∠AB 1D 1即为异面直线AB 1与BD 所成的角.连接AD 1，设AB=a ，则AA 1=√2a ，所以AB 1=√3a ，B 1D 1=√32a ，AD 1=32a.所以在△AB 1D 1中，由余弦定理得cos ∠AB 1D 1=AB 12+B 1D 12-AD 122AB 1·B 1D 1=12，所以∠AB 1D 1=60°，即异面直线AB 1与BD所成的角为60°.专题2 空间几何体的表面积与体积专题[基础达标] (30分钟 45分) 一、选择题(每小题5分，共35分)1剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15D 【解析】如图，剩余部分几何体是由正方体截去一角所得，设正方体棱长为1，则截去部分与剩余部分的体积比为V A -A 'B 'D '1-VA -A 'B 'D '=13×12×1×1×11-13×12×1×1×1=15.2.已知某几何体的三视图如图所示，正(主)视图和侧(左)视图是边长为1的正方形，俯视图是腰长为1的等腰直角三角形，则该几何体的体积是( )A .2B .1C .12D .13C 【解析】根据几何体的三视图，得该几何体是如图所示的直三棱柱，且该三棱柱的底面是腰长为1的等腰直角三角形，高为1，则该三棱柱的体积为V=Sh=12×1×1×1=12.3 ( )A .3πB .4πC .2π+4D.3π+4D【解析】由三视图可得该几何体是底面直径和高都是2的半个圆柱，其表面积为2π+π+2×2=3π+4.4.某几何体的三视图如图所示，则该几何体的体积为()A.12+πB.6+πC.12-πD.6-πC【解析】由三视图可知该几何体是组合体，是一个底面边长为2的正方形、高为3的长方体中挖去一个圆柱，该圆柱的底面是长方体下底面正方形的内切圆、高为1，所以该几何体的体积是2×2×3-π=12-π.5()A.1+√3B.2+√3C.1+2√2D.2√2B【解析】由题图知该几何体为如图所示的三棱锥，则其表面积为2×12×√2×√2+2×12×√2×√32×√2=2+√3.6据图中所给的数据，那么该棱锥外接球的体积是()A .4π3 B .8π3C .8√23π D .16√23π C 【解析】由三视图可得该几何体是四棱锥，底面是边长为√2的正方形，一条长度为2的侧棱垂直于底面，其外接球的球心在长度为2√2的侧棱的中点，所以外接球的半径R=√2，则该球的体积为43πR 3=8√23π.7图中的四边形都是边长为4的正方形，其中正(主)视图、侧(左)视图中的两条虚线互相垂直，则该几何体的表面积是( )A .92B .16√2+80C .80D .16√2+92B 【解析】由三视图可知，该几何体是一个正方体挖去一个四棱锥所得，正方体的边长为4，故每个侧面的面积为4×4=16，棱锥侧面的高为2√2，故每个侧面的面积为12×4×2√2=4√2，故该几何体的表面积S=5×16+4×4√2=16√2+80. 二、填空题(每小题5分，共10分)8.正四棱锥P-ABCD 的五个顶点在同一球面上，若正四棱锥的底面边长是4，侧棱长为2√6，则此球的表面积为 .36π 【解析】设该正四棱锥外接球的半径为R ，底面中心为O ，则正四棱锥的高PO=4，OA=2√2，则(2√2)2+(4-R )2=R 2，解得R=3，故此球的表面积为4πR 2=36π.9(单位：m)，则该几何体的体积为 m 3.8π3【解析】由三视图知该几何体由三部分组成，两边是底面半径为r=1，高为1的圆锥，中间部分是底面半径为r=1，高为2的圆柱，则其体积为V=13×πr 2×1×2+πr 2×2=8π3.[高考冲关] (15分钟 25分)1.(5分)已知三棱锥的三视图如图所示，其正(主)视图是直角边长为2的等腰直角三角形，侧(左)视图也为直角三角形，俯视图是边长为2的等边三角形，则它的外接球的表面积为( )A .48πB .28π3C .16πD .6πB 【解析】由三视图可得该三棱锥的底面是边长为2的正三角形，有一条长度为2的侧棱垂直于底面，底面正三角形的中心为O ，OP 垂直于底面，且OP=1(点P 为其外接球的球心)，则该球的半径R=√1+(2√33)2=√73，所以它的外接球的表面积为4πR 2=4π×73=28π3.2.(5分积为( )A .√32 B .12 C .32D .√32+1B 【解析】该几何体为四棱锥.其底面为梯形，梯形的上底为1，下底为2，高为1；四棱锥的高为1，故V=13×12×(1+2)×1×1=12.3.(5分√2的正方形硬纸，沿各边中点垂直折起四个小三角形，做成一个纸巢，将体积为4π3的球放在纸巢上方，则球的最高点与纸巢底面的距离为( )A .√62+32 B .32C .√22+32D .√32+32D 【解析】由题得，纸巢的底面是边长为1的正方形，故经过4个顶点所得的截面圆的直径为1，又由已知可得球的半径为1，故球心到截面圆的距离为√1-(12)2=√32，而垂直折起的4个小直角三角形的高为12，故球的最高点与纸巢底面的距离为√32+1+12=√32+32. 4.(5分)已知三棱锥S-ABC 的所有顶点都在球O 的球面上，SA ⊥平面ABC ，SA=2√3，AB=1，AC=2，∠BAC=60°，则球O 的表面积为 ( )A .4πB .12πC .16πD .64πC 【解析】由题意可得△ABC 中，AB ⊥BC ，BC=√3，又SA ⊥平面ABC ，则BC ⊥平面SAB ，BC ⊥SB ，则该三棱锥S-ABC 的外接球的球心O 在SC 的中点，半径R=12|SC|=2，则球O 的表面积为4πR 2=16π.5.(5分面积为 .222+6√41 【解析】由三视图可得该几何体是三棱柱ABC-A 1B 1C 1截去一个三棱锥P-A 1B 1C 1后的几何体(如图)，AB=8，AC=6，BC=10，AP=4，BB 1=CC 1=10，则侧面APB 1B 的面积是56，侧面APC 1C 的面积是42，侧面BCC 1B 1的面积是100，底面ABC 的面积是24，在△PB 1C 1中，PB 1=B 1C 1=10，PC 1=6√2，该三角形面积为6√41，所以该几何体的表面积是56+42+100+24+6√41=222+6√41.专题3 空间几何体的结构、三视图与直观图专题[基础达标](30分钟55分)一、选择题(每小题5分，共30分)1.如图，在下列几何体中是棱柱的有()A.1个B.2个C.3个D.4个C【解析】由棱柱的概念和题图可知，①③④为棱柱.2.连接正方体相邻各面的中心(所谓中心是指各面所在正方形的两条对角线的交点)，所得的一个几何体是() A.四面体B.六面体C.八面体D.十面体C【解析】如图，正方体ABCD-A1B1C1D1，O1，O2，O3，O4，O5，O6分别是各表面的中心.由点O1，O2，O3，O4，O5，O6组成了一个八面体.3面的面积是()A.8B.10C.6√2D.8√2B【解析】将三视图还原成几何体的直观图，如图所示.由三视图可知，四面体的四个面都是直角三角形，面积分别为6，8，10，6√2，故面积最大的是10.4.将正方体(如图1所示)截去两个三棱锥，得到图2所示的几何体，则该几何体的侧(左)视图为()B【解析】由侧(左)视图的规则可得该几何体的侧(左)视图如B项所示.5根据图中标出的尺寸，可得这个几何体最长的棱长是()A.2B.√5C.2√2D.2√3C【解析】根据几何体的三视图，得该几何体为底面是等腰三角形，且侧面SBC 垂直于底面ABC的三棱锥，如图所示.三棱锥的高SD=2，底面三角形边长BC=2，高AD=2，故该三棱锥的最长棱是SA=√SD2+AD2=√22+22=2√2.6.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正(主)视图的面积不可能等于 ( )A .1B .√2C .√2-12D .√2+12C 【解析】由题意知，正(主)视图的最大面积是对角面的面积，为√2，最小面积为1，而√2-12<1，故该正方体的正(主)视图的面积不可能为√2-12. 二、填空题(每小题5分，共15分)7(主)视图与俯视图如图所示，则它的侧(左)视图的面积为 .34【解析】由题意可得该三棱锥的底面三角形的边长均为1，三棱锥高为√3，故它的侧(左)视图的面积为12×√32×√3=34.8.如图，△A'B'C'是水平放置的△ABC 的直观图，则在△ABC 的三边及中线AD 中，最长的线段是 .AC 【解析】△ABC 是角B 为直角顶点的直角三角形，AD 是直角边BC 上的中线，所以最长的线段为AC.9.用一个平面去截几何体，如果截面是三角形，那么这个几何体可能是 (填序号).①棱柱 ②棱锥 ③棱台 ④圆柱 ⑤圆锥 ⑥圆台 ⑦球.①②③⑤ 【解析】通过画图，易知①②③⑤都能被截得到三角形的截面，而④⑥⑦不论如何去截，都得不到截面是三角形.三、解答题(共10分)10.(10分)某几何体的三视图如图所示，画出该几何体的直观图.【解析】该几何体类似棱台，先画底面矩形和中心轴，然后上底面矩形，连线即成.画法：如图，先画轴，依次画x'，y'，z'轴，三轴相交于点O'，使∠x'O'y'=45°，∠x'O'z'=90°.在z'轴上取O'O″=8 cm，再画x″，y″轴.在坐标系x'O'y'中作直观图ABCD，使得AD=20 cm，AB=8 cm；在坐标系x″O″y″中作直观图A'B'C'D'，使得A'D'=12 cm，A'B'=4 cm.连接AA'，BB'，CC'，DD'，即得到所求直观图.[高考冲关](15分钟25分)1.(5分ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形) ()A .③④⑤B .④⑤⑥C .①②③D .①②⑥C 【解析】该四面体的正(主)视图是①，侧(左)视图是②，俯视图是③.2.(5分中，面积最大的侧面的面积为( )A .√22B .√52C .√62D .3B 【解析】由三视图可知，该几何体的直观图如图所示，平面AED ⊥平面BCDE ，四棱锥A-BCDE 的高为1，四边形BCDE 是边长为1的正方形，则S △AED =12×1×1=12，S △ABC =S △ABE =12×1×√2=√22，S △ACD =12×1×√5=√52.3.(5分)一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的侧面积是 .3√154【解析】由题意知，球心是底面三角形的中心，球的半径，就是三棱锥的高.由已知球的半径为1，设底面三角形的边长为a ，有23×√32a=1，得a=√3，三棱锥侧面的高h=√12+(12)2=√52，则该正三棱锥的侧面积S=3×12×√3×√52=3√154.4.(5分)如图，在六面体PABCQ中，QA=QB=QC=AB=CB=CA=√2PA=√2PB=√2PC=2，设O1为正三棱锥P-ABC外接球的球心，O2为正四面体Q-ABC内切球的球心，则O1O2等于.0【解析】将该六面体放入一棱长为√2正方体中，如图.正三棱锥P-ABC外接球的球心O1为正方体的体对角线PQ的中点，正四面体Q-ABC的内切球的球心O2也为PQ的中点，所以O1O2=0.5.(5分)已知某四棱锥，底面是边长为2的正方形，且俯视图如图所示，关于该四棱锥的下列结论中：①四棱锥中至少有两组侧面互相垂直；②四棱锥的侧面中可能存在三个直角三角形；③四棱锥中不可能存在四组互相垂直的侧面；④四棱锥的四个侧面不可能都是等腰三角形.所有正确结论的序号是.①②③【解析】由俯视图可知，四棱锥的顶点在底面上的射影落在正方形的一边上，如图所示，则可知平面PBC⊥平面PAB，平面PAD⊥平面PAB，故①正确；当PA⊥PB时，四棱锥的侧面中存在三个直角三角形，故②正确；显然△PCD 不能是直角三角形，故四棱锥中不可能存在四组互相垂直的侧面，故③正确；当PA=PB=AB时，四棱锥的四个侧面都是等腰三角形，故④错误.专题4 空间角与距离的求解专题[基础达标] (35分钟 65分) 一、选择题(每小题5分，共25分)1.一条直线与平面α成60°角，则这条直线与平面内的直线所成角的取值范围是( )A .[0°，90°]B .(0°，45°]C .[60°，180°]D .[60°，90°]D 【解析】由线面角的定义可得答案.2.正三棱柱ABC-A 1B 1C 1中，D 是AB 的中点，CD 等于√3，则顶点A 1到平面CDC 1的距离为( )A .12 B .1 C .√32D .√2B 【解析】由题意可得该正三棱柱的底面边长为2，且AD ⊥平面CDC 1，AA 1∥平面CDC 1，所以顶点A 1到平面CDC 1的距离等于顶点A 到平面CDC 1的距离，即为AD=1.3a 的正方体ABCD-A 1B 1C 1D 1中，M 是AA 1的中点，则点A 1到平面BDM 的距离是 ( )A .√66aB .√306a C .√34aD .√63aA 【解析】以D 为原点建立如图所示的空间直角坐标系，正方体的棱长为a ，则A 1(a ，0，a )，A (a ，0，0)，M (a ，0，12a)，B (a ，a ，0)，D (0，0，0).设n =(x ，y ，z )为平面BDM 的法向量，则n ·BM ⃗⃗⃗⃗⃗⃗ =0，且n ·DM⃗⃗⃗⃗⃗⃗ =0.而BM ⃗⃗⃗⃗⃗⃗ =(0，-a ，12a)，DM ⃗⃗⃗⃗⃗⃗ =(a ，0，12a)，得{-y +12z =0，x +12z =0，所以{y =12z ，x =-12z ，令z=2，则n =(-1，1，2)，DA ⃗⃗⃗⃗⃗ 1=(a ，0，a ).则A 1到平面BDM 的距离d=|DA 1⃗⃗⃗⃗⃗⃗⃗⃗·n ||n |=√66a.4.在长方体ABCD-A 1B 1C 1D 1中，B 1C 和C 1D 与底面所成的角分别为60°和45°，则异面直线B 1C 和C 1D 所成角的余弦值为( )A .√64 B .√63 C .√26D .√36A 【解析】设BC=1，则由∠CB 1C 1=60°可得CC 1=√3，B 1C=2.由∠DC 1D 1=45°可得D 1C 1=√3，DC 1=√6.连接AB 1，AC ，则DC 1∥AB 1，所以异面直线B 1C 和C 1D 所成角即为∠AB 1C.在△AB 1C 中，因为AB 1=√6，B 1C=2，AC=2，由余弦定理可得cos ∠AB 1C=2√6×2=√64.5ABCD-A 1B 1C 1D 1中，AB=BC=1，BB 1=√2.设点A 关于直线BD 1的对称点为P ，则点P 与点C 1之间的距离为 ( )A .1B .√2C .√33D .√32A 【解析】如图所示，将长方体中平面ABC 1D 1取出，过点A 作AM ⊥BD 1，交BD 1于点M ，延长AM 到点P ，使MP=AM ，则点P 是点A 关于直线BD 1的对称点，过点P 作PE ⊥BC 1，垂足为E ，连接PB ，PC 1，依题意AB=1，AD 1=√3，BD 1=2，∠ABD 1=60°，∠BAM=30°，∠PBE=30°，PE=12，BE=√32，所以PE 垂直平分BC 1，所以PC 1=PB=1.二、填空题(每小题5分，共15分)6.在正三棱柱ABC-A 1B 1C 1中，AB=1，点D 在棱BB 1上，若BD=1，则AD 与平面AA 1C 1C 所成角的正切值为 .√155【解析】由题意可得点D 到平面AA 1C 1C 的距离为√32，且|AD|=√2，所以直线AD 与平面AA 1C 1C 所成角θ的正弦值sin θ=√32√2=√64，则cos θ=√104，tan θ=√6√10=√155. 7.△BCD 为正三角形，A 为△BCD 所在平面外一点，且AB=AC=AD ，若△ABC 的面积与△BCD 的面积之比为2∶3，则面ABC 与面BCD 所成的二面角的度数为 .60° 【解析】设面ABC 与面BCD 所成角为θ，则由题意可得cos θ=13S△BCD S △ABC=12，所以θ=60°.8.已知Rt △ABC 的直角顶点C 在平面α内，斜边AB ∥α，AB=2√6，AC ，BC 分别和平面α成45°和30°角，则AB 到平面α的距离为 .2 【解析】设AB 到平面α的距离为h ，则BC=2h ，AC=√2h ，则(2h )2+(√2h )2=24，解得h=2，即AB 到平面α的距离为2. 三、解答题(共25分)9.(12分PAC ⊥平面ABC ，△ABC 是以AC 为斜边的等腰直角三角形，E ，F ，O 分别为PA ，PB ，AC 的中点，AC=16，PA=PC=10. (1)设G 是OC 的中点，证明：FG ∥平面BOE ；(2)证明：在△ABO 内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ，OB 的距离.【解析】(1)如图，连接OP ，易知OB ，OC ，OP 两两垂直，以点O 为坐标原点，分别以OB ，OC ，OP 所在直线为x 轴，y 轴，z 轴，建立空间直角坐标系Oxyz ，则O (0，0，0)，A (0，-8，0)，B (8，0，0)，C (0，8，0)，P (0，0，6)，E (0，-4，3)，F (4，0，3).由题意，得G (0，4，0)，因为OB ⃗⃗⃗⃗⃗ =(8，0，0)，OE ⃗⃗⃗⃗⃗ =(0，-4，3)， 所以平面BOE 的一个法向量为n =(0，3，4). 由FG ⃗⃗⃗⃗⃗ =(-4，4，-3)，得n ·FG ⃗⃗⃗⃗⃗ =0，即n ⊥FG ⃗⃗⃗⃗⃗ . 又直线FG 不在平面BOE 内，所以FG ∥平面BOE. (2)设点M 的坐标为(x 0，y 0，0)，则FM ⃗⃗⃗⃗⃗⃗ =(x 0-4，y 0，-3). 若FM ⊥平面BOE ，则FM ⃗⃗⃗⃗⃗⃗ ∥n .因此x 0=4，y 0=-94，即点M 的坐标是(4，-94，0).在平面直角坐标系xOy 中，△AOB 的内部区域可表示为不等式组{x >0，y <0，x -y <8.经检验，点M 的坐标满足上述不等式组，所以在△AOB 内存在一点M ， 使FM ⊥平面BOE.由点M 的坐标得点M 到OA ，OB 的距离分别为4，94.10.(13分ABCD-A 1B 1C 1D 1中，AD=A 1A=12AB=2，点E 是棱AB 上一点，且AEEB =λ. (1)证明：D 1E ⊥A 1D ；(2)若二面角D 1-EC-D 的余弦值为√63，求CE 与平面D 1ED 所成的角.【解析】(1)以D 为原点，DA 所在直线为x 轴，DC 所在直线为y 轴，DD 1所在直线为z 轴建立空间直角坐标系，则D (0，0，0)，A (2，0，0)，B (2，4，0)，C (0，4，0)，A 1(2，0，2)，B 1(2，4，2)，C 1(0，4，2)，D 1(0，0，2).因为AEEB =λ，所以E (2，4λ1+λ，0)，于是D 1E ⃗⃗⃗⃗⃗⃗⃗ =(2，4λ1+λ，-2)，A 1D⃗⃗⃗⃗⃗⃗⃗⃗ =(-2，0，-2) 所以D 1E ⃗⃗⃗⃗⃗⃗⃗ ·A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(2，4λ1+λ，-2)·(-2，0，-2)=0，故D 1E ⊥A 1D. (或用几何法先证出A 1D ⊥平面D 1AE ，然后证出A 1D ⊥D 1E )(2)因为D 1D ⊥平面ABCD ，所以平面DEC 的一个法向量为n 1=(0，0，2). 又CE ⃗⃗⃗⃗⃗ =(2，4λ1+λ-4，0)，CD 1⃗⃗⃗⃗⃗⃗⃗ =(0，-4，2)，设平面D 1CE 的法向量为n 2=(x ，y ，z )，则n 2·CE⃗⃗⃗⃗⃗ =2x+y (4λ1+λ-4)=0，n 2·CD 1⃗⃗⃗⃗⃗⃗⃗ =-4y+2z=0，得向量n 2的一个解是(2-2λ1+λ，1，2).因为二面角D 1-EC-D 的余弦值为√63，则n 1·n2|n 1|·|n 2|=√63， 解得λ=1.所以E (2，2，0)，故DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(0，0，2)，DE ⃗⃗⃗⃗⃗ =(2，2，0)，CE ⃗⃗⃗⃗⃗ =(2，-2，0)， 因此CE ⃗⃗⃗⃗⃗ ·DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =0，CE ⃗⃗⃗⃗⃗ ·DE ⃗⃗⃗⃗⃗ =0，故CE ⊥平面D 1ED. 即CE 与平面D 1ED 所成角为π2.[高考冲关] (30分钟 50分)1.(5分ABCD-A 1B 1C 1D 1中，AA 1=2AB ，则CD 与平面BDC 1所成角的正弦值等于 ( )A .23B .√33C .√23D .13A 【解析】如图，连接AC 交BD 于点O ，连接C 1O ，过点C 作CH ⊥C 1O 于点H ，连接DH.由BD ⊥AC ，BD ⊥AA 1，AC ∩AA 1=A ，得BD ⊥平面ACC 1A 1.又CH ⊂平面ACC 1A 1，则CH ⊥BD.又CH ⊥C 1O ，且BD ∩C 1O=O ，则CH ⊥平面BDC 1.所以∠HDC 为CD 与平面BDC 1所成的角.设AA 1=2AB=2，则OC=AC2=√22，C 1O=√OC 2+CC 12=√(√22)2+22=3√22.由等面积法，得C 1O ·CH=OC ·CC 1，即3√22·CH=√22×2，则CH=23，故sin ∠HDC=CHDC =23，即CD 与平面BDC 1所成角的正弦值为23.2.(5分P-ABC 的各顶点都在以O 为球心的球面上，且PA ，PB ，PC 两两垂直，若PA=PB=PC=2，则球心O 到平面ABC 的距离为 .√33【解析】由条件知三棱锥P-ABC 可看作正方体的一部分，点P ，A ，B ，C分别为该正方体的顶点，它的外接球就是该正方体的外接球，正方体的体对角线就是外接球的直径，又体对角线长为2√3，故球的半径R=√3.设点P 到平面ABC 的距离为h ，因为V P-ABC =V A-PBC ，即13h ·S △ABC =13PA ·S △PBC ，可得h=2√33，所以球心O 到平面ABC 的距离为R-h=√33.3.(12分1，在直角梯形ABCD 中，AD ∥BC ，∠BAD=π2，AB=BC=1，AD=2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2. (1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 夹角的余弦值.【解析】(1)在图1中，因为AB=BC=1，AD=2，E 是AD 的中点， ∠BAD=π2，所以BE ⊥AC.即在图2中，BE ⊥OA 1，BE ⊥OC ， 从而BE ⊥平面A 1OC ， 又CD ∥BE ， 所以CD ⊥平面A 1OC.(2)由已知，平面A 1BE ⊥平面BCDE ， 又由(1)知，BE ⊥OA 1，BE ⊥OC ， 所以∠A 1OC 为二面角A 1-BE-C 的平面角， 所以∠A 1OC=π2.如图，以O 为原点，建立空间直角坐标系，因为A 1B=A 1E=BC=ED=1，BC ∥ED ， 所以B (√22，0，0)，E (-√22，0，0)，A 10，0，√22，C (0，√22，0)， 得BC⃗⃗⃗⃗⃗ =(-√22，√22，0)，A 1C ⃗⃗⃗⃗⃗⃗⃗ =(0，√22，-√22)， CD ⃗⃗⃗⃗⃗ =BE ⃗⃗⃗⃗⃗ =(-√2，0，0).设平面A 1BC 的法向量n 1=(x 1，y 1，z 1)，平面A 1CD 的法向量n 2=(x 2，y 2，z 2)，平面A 1BC 与平面A 1CD 夹角为θ，则{n 1·BC ⃗⃗⃗⃗⃗ =0，n 1·A 1C ⃗⃗⃗⃗⃗⃗⃗ =0，得{-x 1+y 1=0，y 1-z 1=0，取n 1=(1，1，1)；{n 2·CD ⃗⃗⃗⃗⃗ =0，n 2·A 1C ⃗⃗⃗⃗⃗⃗⃗ =0，得{x 2=0，y 2-z 2=0，取n 2=(0，1，1)，从而cos θ=|cos <n 1，n 2>|=√3×√2=√63， 即平面A 1BC 与平面A 1CD 夹角的余弦值为√63.4.(13分A-OCB 中，AO ⊥底面BOC ，且∠BAO=∠CAO=π6，AB=4，点D 为线段AB 的中点，记二面角B-AO-C 的大小为θ.(1)求三棱锥A-OCB 体积V 的最大值； (2)当θ=2π3时，求二面角C-OD-B 的余弦值.【解析】(1)由条件，∠BOC 即为二面角B-AO-C 的平面角，即为θ，V=13×12×BO×OC×sin θ×AO=4√33sin θ≤4√33，所以当θ=π2时，V 取得最大值4√33. (2)如图，以O 为原点，平面OBC 内垂直于OB 的直线为x 轴，OB ，OA 所在的直线分别为y 轴，z 轴建立空间直角坐标系Oxyz ，则A (0，0，2√3)，B (0，2，0)，D (0，1，√3)，C (√3，-1，0).设n 1=(x ，y ，z )为平面COD 的法向量， 由{n 1·OD ⃗⃗⃗⃗⃗⃗ =0，n 1·OC ⃗⃗⃗⃗⃗ =0，得{y +√3z =0，√3x -y =0，取z=√32，则n 1=(-√32，-32，√32)，取平面AOB 的一个法向量为n 2=(1，0，0)， 设二面角C-OD-B 的大小为α，cos α=n 1·n 2|n 1||n 2|=-√32√152=-√55，综上，二面角C-OD-B 的余弦值为-√55.5.(15分)如图，将长为4，宽为1的长方形折叠成长方体ABCD-A 1B 1C 1D 1的四个侧面，记底面上一边AB=t (0<t<2)，连接A 1B ，A 1C ，A 1D.(1)当长方体ABCD-A 1B 1C 1D 1的体积最大时，求二面角B-A 1C-D 的值.(2)线段A 1C 上是否存在一点P ，使得A 1C ⊥平面BPD ?若存在，求出P 点的位置；若不存在，请说明理由.【解析】(1)根据题意，以A 为原点O ，AB 为x 轴，AD 为y 轴，AA 1为z 轴，建立如图所示的空间直角坐标系.长方体体积V=t (2-t )×1=t (2-t )≤(t+2-t 2)2=1，当且仅当t=2-t ，即t=1时，体积V 有最大值1，所以当长方体ABCD-A 1B 1C 1D 1的体积最大时，底面四边形ABCD 为正方形，则A 1(0，0，1)，B (1，0，0)，C (1，1，0)，A 1B ⃗⃗⃗⃗⃗⃗⃗ =(1，0，-1)，BC ⃗⃗⃗⃗⃗ =(0，1，0)， 设平面A 1BC 的法向量m =(x ，y ，z )，则{x -z =0，y =0，取x=z=1，得m =(1，0，1)，同理，可得平面A 1CD 的法向量n =(0，1，1)， 所以cos <m ，n >=m ·n|m |·|n |=12，又二面角B-A 1C-D 为钝角，故二面角B-A 1C-D 的值是120°.(2)根据题意有B (t ，0，0)，C (t ，2-t ，0)，D (0，2-t ，0)，A 1C ⃗⃗⃗⃗⃗⃗⃗ =(t ，2-t ，-1)， 若线段A 1C 上存在一点P 满足要求，不妨设A 1P ⃗⃗⃗⃗⃗⃗⃗ =λA 1C ⃗⃗⃗⃗⃗⃗⃗ (λ>0)，可得P (λt ，λ(2-t )，1-λ)，BP ⃗⃗⃗⃗⃗ =(λt-t ，λ(2-t )，1-λ)，BD⃗⃗⃗⃗⃗⃗ =(-t ，2-t ，0)， 由A 1C ⊥平面BPD ，得{t (λt -t )+λ(2-t )2-(1-λ)=0，-t 2+(2-t )2=0， 解得t=1，λ=23， 即只有当底面四边形是正方形时才有符合要求的点P ，位置是线段A 1C 上A 1P ∶PC=2∶1处.专题5 空间直角坐标系、空间向量及其运算专题一、选择题(每小题5分，共25分)1a =(λ+1，0，2)，b =(6，2μ-1，2λ)，若a ∥b ，则λ与μ的值可以是( )A .2，12B .-13，12C .-3，2D .2，2 A 【解析】由a ∥b 可得{λ+16=22λ，2μ-1=0，解得{λ=2，μ=12或{λ=-3，μ=12.2a =(2，1，-3)，b =(-1，2，3)，c =(7，6，λ)，若a ，b ，c 三向量共面，则λ= ( )A .9B .-9C .-3D .3B 【解析】由题意设c =x a +y b ，即(7，6，λ)=x (2，1，-3)+y (-1，2，3)，所以{2x -y =7，x +2y =6，-3x +3y =λ，解得λ=-9. 3.在空间直角坐标系中，A (1，2，3)，B (-2，-1，6)，C (3，2，1)，D (4，3，0)，则直线AB 与CD 的位置关系是 ( )A .垂直B .平行C .异面D .相交但不垂直B 【解析】由题意，得AB ⃗⃗⃗⃗⃗ =(-3，-3，3)，CD ⃗⃗⃗⃗⃗ =(1，1，-1)，则AB ⃗⃗⃗⃗⃗ =-3CD ⃗⃗⃗⃗⃗ ，故AB 与CD ⃗⃗⃗⃗⃗ 共线，又AB⃗⃗⃗⃗⃗ 与CD ⃗⃗⃗⃗⃗ 没有公共点，则AB ∥CD. 4.已知长方体ABCD-A 1B 1C 1D 1，下列向量的数量积一定不为0的是( )A.AD 1⃗⃗⃗⃗⃗⃗⃗ ·B 1C ⃗⃗⃗⃗⃗⃗⃗B.BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗C.AB ⃗⃗⃗⃗⃗ ·AD 1⃗⃗⃗⃗⃗⃗⃗D.BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗D 【解析】选项A ，当四边形ADD 1A 1为正方形时，有AD 1⊥A 1D ，而A 1D ∥B 1C ，可得AD 1⊥B 1C ，此时有AD 1⃗⃗⃗⃗⃗⃗⃗ ·B 1C ⃗⃗⃗⃗⃗⃗⃗ =0；选项B ，当四边形ABCD 为正方形时，有AC ⊥BD ，可得AC ⊥平面BB 1D 1D ，故有AC ⊥BD 1，此时有BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =0；选项C ，由长方体的性质可得AB ⊥平面ADD 1A 1，可得AB ⊥AD 1，此时必有AB ⃗⃗⃗⃗⃗ ·AD 1⃗⃗⃗⃗⃗⃗⃗ =0；选项D ，由长方体的性质可得BC ⊥平面CDD 1C 1，可得BC ⊥CD 1，△BCD 1为直角三角形，∠BCD 1为直角，故BC 与BD 1不可能垂直，即BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ ≠0.5.在边长为1的正方体ABCD-A 1B 1C 1D 1中，F 是BD 的中点，点G 在棱CD 上，且CG=14CD ，H 是C 1G 的中点，则|FH ⃗⃗⃗⃗⃗ |为( )A .6564 B .√658C .4164D .√418D 【解析】如图，以D 点为原点建立空间直角坐标系，则F (12，12，0)，C 1(0，1，1)，G (0，34，0).因为H 是C 1G 的中点，所以H (0，78，12)，所以FH ⃗⃗⃗⃗⃗ =-12，38，12，则|FH ⃗⃗⃗⃗⃗ |=√418.二、填空题(每小题5分，共15分)6.已知向量a =(-4，2，4)，b =(-6，3，-2)，则a ·b = ；|a |= . 22 6 【解析】a ·b =(-4)×(-6)+2×3+4×(-2)=22，|a |=√(-4)2+22+42=6.7a =(1，2，x )，b =(2，y ，-1)，若|a |=√5，且a ⊥b ，则x+y= .-1 【解析】由|a |=√5得√x 2+5=√5，解得x=0，即a =(1，2，0)，又a ⊥b ，则a ·b =0，即2+2y=0，解得y=-1，从而x+y=-1.8.已知空间四点A (-2，3，1)，B (2，-5，3)，C (10，0，10)，D (8，4，a )，如果四边形ABCD 为梯形，则实数a 的值为 .9 【解析】因为AB ⃗⃗⃗⃗⃗ =(4，-8，2)，BC ⃗⃗⃗⃗⃗ =(8，5，7)，DC ⃗⃗⃗⃗⃗ =(2，-4，10-a )，AD ⃗⃗⃗⃗⃗ =(10，1，a-1)，四边形ABCD 为梯形，则AB ⃗⃗⃗⃗⃗ ∥DC ⃗⃗⃗⃗⃗ ，解得a=9，此时BC ⃗⃗⃗⃗⃗ 与AD ⃗⃗⃗⃗⃗ 不平行. 三、解答题(共20分)9.(10分A (-2，0，2)，B (-1，1，2)，C (-3，0，4)，设a =AB ⃗⃗⃗⃗⃗ ，b =AC ⃗⃗⃗⃗⃗ . (1)求a 和b 夹角的余弦值. (2)设|c |=3，c ∥BC⃗⃗⃗⃗⃗ ，求c 的坐标. 【解析】(1)因为AB ⃗⃗⃗⃗⃗ =(1，1，0)，AC ⃗⃗⃗⃗⃗ =(-1，0，2)， 所以a ·b =-1+0+0=-1，|a |=√2，|b |=√5. 所以cos <a ，b >=a ·b|a ||b |=√2×√5=-√1010.(2)BC⃗⃗⃗⃗⃗ =(-2，-1，2).设c =(x ，y ，z )， 因为|c |=3，c ∥BC⃗⃗⃗⃗⃗ ， 所以√x 2+y 2+z 2=3，存在实数λ使得c =λBC⃗⃗⃗⃗⃗ ，即{x =-2λ，y =-λ，z =2λ，解得{x =-2，y =-1，z =2，λ=1或{x =2，y =1，z =-2，λ=-1， 所以c =(-2，-1，2)或(2，1，-2).10.(10分)如图，在四棱锥P-ABCD 中，M ，N 分别是AB ，PC 的中点，若ABCD 是平行四边形.求证：MN ∥平面PAD.【解析】取DP 的中点E ，连接AE ，EN ，则EN ⃗⃗⃗⃗⃗⃗ =12DC ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ =AM ⃗⃗⃗⃗⃗⃗ ，所以MN ⃗⃗⃗⃗⃗⃗⃗ =AE ⃗⃗⃗⃗⃗ =12AP ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ ，所以MN ⃗⃗⃗⃗⃗⃗⃗ ，AD ⃗⃗⃗⃗⃗ ，AP ⃗⃗⃗⃗⃗ 共面，且MN 不在平面PAD 上， 所以MN ∥平面PAD.[高考冲关] (25分钟 45分)1.(5分)一个四面体的顶点在空间直角坐标系Oxyz 中的坐标分别是(0，0，0)，(0，1，1)，(1，0，1)，(1，1，0)，该四面体的体积为( ) A .13B .√64C .1D .2√3A 【解析】在空间直角坐标系中作出四面体的四个顶点，可知该四面体是棱长为√2的正四面体，所以体积为13×2√33×12×√2×√2×√32=13.2.(5分)设P (2，3，4)在三个坐标平面上的射影分别为P 1，P 2，P 3，则向量：①(6，-3，-4)；②(4，-3，-4)；③(0，-3，4)；④(2，-6，4).其中与平面P 1P 2P 3平行的向量有 ( )A .1个B .2个C .3个D .4个C 【解析】由题意可知，P 1，P 2，P 3的坐标分别为(2，3，0)，(2，0，4)，(0，3，4)，可以求得平面P 1P 2P 3的一个法向量为(6，4，3)，①不与该法向量垂直，所以不与平面P 1P 2P 3平行，②③④与该法向量垂直，且不在平面P 1P 2P 3内，所以与平面P 1P 2P 3平行.3.(5分)已知空间四边形ABCD 中，AB ⃗⃗⃗⃗⃗ =a -2c ，CD ⃗⃗⃗⃗⃗ =5a +6b -8c ，对角线AC ，BD 的中点分别为E ，F ，则EF ⃗⃗⃗⃗⃗ = . 3a +3b -5c 【解析】EF⃗⃗⃗⃗⃗ =(EA⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ +BF ⃗⃗⃗⃗⃗ )+(EC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ )2=AB ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ 2=a -2c+5a+6b -8c2=3a +3b -5c .4.(10分)已知空间四边形ABCD ，E ，F ，G ，H ，M ，N 分别是AB ，BC ，CD ，DA ，AC ，BD 的中点，求证：EG ，FH ，MN 交于一点且互相平分.【解析】设P 1，P 2，P 3分别为EG ，FH ，MN 的中点，又设AB ⃗⃗⃗⃗⃗ =a ，AC ⃗⃗⃗⃗⃗ =b ，AD ⃗⃗⃗⃗⃗ =c ， 则AP 1⃗⃗⃗⃗⃗⃗⃗ =AE ⃗⃗⃗⃗⃗ +EP 1⃗⃗⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +12EG ⃗⃗⃗⃗⃗ =12AB ⃗⃗⃗⃗⃗ +12(AG ⃗⃗⃗⃗⃗ −AE ⃗⃗⃗⃗⃗ )=14(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )=14(a +b +c ).同理可得AP 2⃗⃗⃗⃗⃗⃗⃗ =14(a +b +c )，AP 3⃗⃗⃗⃗⃗⃗⃗ =14(a +b +c )，故P 1，P 2，P 3三点重合.从而原命题得证.5.(10分BC=2，原点O 是BC 的中点，点A 的坐标是(√32，12，0)，点D 在平面yOz 上，且∠BDC=90°，∠DCB=30°.(1)求向量OD⃗⃗⃗⃗⃗⃗ 的坐标； (2)设向量AD ⃗⃗⃗⃗⃗ 和BC⃗⃗⃗⃗⃗ 的夹角为θ，求cos θ的值.【解析】(1)如图所示，过点D 作DE ⊥BC ，垂足为点E.在Rt △BDC 中，由∠BDC=90°，∠DCB=30°，BC=2，得BD=1，CD=√3. 所以DE=CD ·sin 30°=√32，OE=OB-BD ·cos 60°=1-12=12. 所以D 点坐标为(0，-12，√32)， 即向量OD⃗⃗⃗⃗⃗⃗ 的坐标为(0，-12，√32). (2)依题意知，OA ⃗⃗⃗⃗⃗ =(√32，12，0)，OB ⃗⃗⃗⃗⃗ =(0，-1，0)，OC ⃗⃗⃗⃗⃗ =(0，1，0). 所以AD ⃗⃗⃗⃗⃗ =OD ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(-√32，-1，√32)，BC⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ −OB ⃗⃗⃗⃗⃗ =(0，2，0).则cos θ=(-√32)×0+(-1)×2+√32×0√(-√32)+(-1)2+(√32)·√02+22+02=-√10=-√105. 6.(10分)已知正三棱柱ABC-A 1B 1C 1的侧棱长为2，底面边长为1，M 是BC 的中点.在直线CC 1上是否存在一点N ，使得MN ⊥AB 1?若存在，请你求出它的位置；若不存在，请说明理由.【解析】在直线CC 1上存在一点N ，使得MN ⊥AB 1. 如图，建立空间直角坐标系，有 A (0，0，0)，B (√32，12，0)，M√34，34，0，N (0，1，z )，B 1(√32，12，2)，则AB 1⃗⃗⃗⃗⃗⃗⃗ =(√32，12，2)，MN⃗⃗⃗⃗⃗⃗⃗ =(-√34，14，z). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ⊥MN⃗⃗⃗⃗⃗⃗⃗ ， 有AB 1⃗⃗⃗⃗⃗⃗⃗ ·MN⃗⃗⃗⃗⃗⃗⃗ =(√32，12，2)·(-√34，14，z)=-38+18+2z=0， 解得z=18，N (0，1，18)，即CN=18时，AB 1⊥MN.专题6 热点专题突破四 立体几何的综合问题1在多面体ABCDEF 中，四边形ABCD 为矩形，△ADE ，△BCF 均为等边三角形，EF ∥AB ，EF=AD=12AB ，N 为线段PC 的中点. (1)求证：AF ∥平面BDN ；(2)求直线BN 与平面ABF 所成角的正弦值.【解析】(1)连接AC 交BD 于点M ，连接MN ，∵四边形ABCD 是矩形，∴M 是AC 的中点，∵N 是CF 的中点，∴MN ∥AF ，又AF ⊄平面BDN ，MN ⊂平面BDN ，∴AF ∥平面BDN.(2)取BC 的中点P ，AD 的中点Q ，连接PQ ，过点F 作FO ⊥PQ 交PQ 于点O ， ∵BC ⊥FP ，BC ⊥PQ ，PQ ∩FP=P ，∴BC ⊥平面EFPQ ， ∵FO ⊂平面EFPQ ，∴BC ⊥FO ，又FO ⊥PQ ，PQ ∩BC=P ，∴FO ⊥平面ABCD.如图，以O 为坐标原点，x 轴⊥AB ，y 轴⊥BC 建立空间直角坐标系，连接FP ，FM ，设EF=AD=12AB=a ，∵△ADE ，△FBC 是等边三角形， ∴FP=FM=√32a ，∴OP=12(AB-EF )=12a ，∴OF=√22a ，∴A (12a ，-32a ，0)，B (12a ，12a ，0)，C (-12a ，12a ，0)， F (0，0，√22a)，N (-14a ，14a ，√24a). ∴AB ⃗⃗⃗⃗⃗ =(0，2a ，0)，AF ⃗⃗⃗⃗⃗ =(-12a ，32a ，√22a)，BN⃗⃗⃗⃗⃗⃗ =-34a ，-14a ，√24a . 设平面ABF 的法向量为n =(x ，y ，z )， 则{n ·AB ⃗⃗⃗⃗⃗ =0，n ·AF ⃗⃗⃗⃗⃗ =0，∴{2ay =0，-12ax +32ay +√22az =0，令z=√2，得n =(2，0，√2)， ∴cos <n ·BN ⃗⃗⃗⃗⃗⃗ >=n ·BN ⃗⃗⃗⃗⃗⃗|n ||BN ⃗⃗⃗⃗⃗⃗ |=-√23，∴直线BN 与平面ABF 所成角的正弦值为√23.2ABCD-A 1B 1C 1D 1经平面AEFG 所截后得到的图形，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°. (1)求证：BD ⊥平面ADG ；(2)求平面AEFG 与平面ABCD 所成锐二面角的余弦值.【解析】(1)在△BAD 中，∵AB=2AD=2，∠BAD=60°， ∴由余弦定理可得BD=√3，∴AB 2=AD 2+BD 2，∴AD ⊥BD. 又在直平行六面体中，GD ⊥平面ABCD ， 又BD ⊂平面ABCD ，∴GD ⊥BD. 又AD ∩GD=D ，∴BD ⊥平面ADG.(2)以D 为坐标原点，建立如图所示的空间直角坐标系Dxyz.∵∠BAE=∠GAD=45°，AB=2AD=2，则有A (1，0，0)，B (0，√3，0)，G (0，0，1)，E (0，√3，2)，C (-1，√3，0)， ∴AE ⃗⃗⃗⃗⃗ =(-1，√3，2)，AG ⃗⃗⃗⃗⃗ =(-1，0，1). 设平面AEFG 的法向量为n =(x ，y ，z )， ∴{n ·AE ⃗⃗⃗⃗⃗ =-x +√3y +2z =0，n ·AG ⃗⃗⃗⃗⃗ =-x +z =0，令x=1，得y=-√33，z=1，n =(1，-√33，1).而平面ABCD 的一个法向量为DG ⃗⃗⃗⃗⃗ =(0，0，1)，∴cos <DG ⃗⃗⃗⃗⃗ ，n >=DG ⃗⃗⃗⃗⃗⃗·n |DG ⃗⃗⃗⃗⃗⃗ ||n |=√217. 故平面AEFG 与平面ABCD 所成锐二面角的余弦值为√217. 3.如图，平面ABCD ⊥平面ABE ，四边形ABCD 是边长为2的正方形，且点B 在平面ACE 上的射影F 恰好落在边CE 上. (1)求证：AE ⊥平面BCE ；(2)当二面角B-AC-E 的余弦值为√33时，求∠BAE 的大小.【解析】(1)∵BF ⊥平面ACE ，AE ⊂平面ACE ，∴BF ⊥AE ， 又∵四边形ABCD 是边长为2的正方形， ∴BC ⊥AB ，∵平面ABCD ⊥平面ABE ，且平面ABCD ∩平面ABE=AB ，BC ⊂平面ABCD ， ∴BC ⊥平面ABE ，∴BC ⊥AE ， 又∵BC ∩BF=B ，∴AE ⊥平面BCE.(2)以A 为原点，垂直于平面ABCD 的直线AG 为x 轴，AB 所在直线为y 轴，AD 所在直线为z 轴，如图所示建立空间直角坐标系Axyz.设E (a ，b ，0)，则AE ⃗⃗⃗⃗⃗ =(a ，b ，0)，AC ⃗⃗⃗⃗⃗ =(0，2，2)，BE ⃗⃗⃗⃗⃗ =(a ，b-2，0)， 设平面AEC 的法向量为n =(x ，y ，z )，∴{AE⃗⃗⃗⃗⃗ ·n =0，AC⃗⃗⃗⃗⃗ ·n =0，。

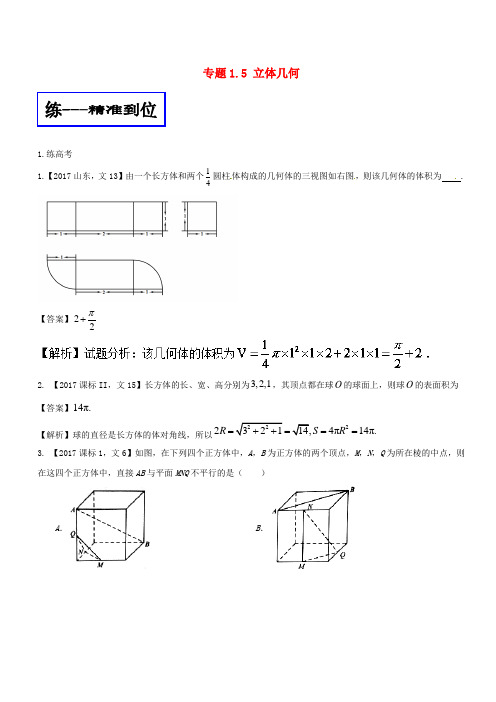
专题1.5 立体几何1.练高考1.【2017山东，文13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图，则该几何体的体积为.【答案】22π+2. 【2017课标II，文15】长方体的长、宽、高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为【答案】14π.【解析】球的直径是长方体的体对角线，所以224π14π.R S R====3. 【2017课标1，文6】如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是（）A ．B ．C ．D ．【答案】A【解析】4. 【2017课标1，文18】如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠= ．（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠= ，且四棱锥P-ABCD 的体积为83，求该四棱锥的侧面积． 【答案】（1）证明见解析； （2）326+．【解析】5. 【2017山东，文18】（本小题满分12分）由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD ,（Ⅰ）证明：1AO ∥平面B 1CD 1;（Ⅱ）设M 是OD 的中点,证明：平面A 1EM ⊥平面B 1CD 1.【答案】①证明见解析.②证明见解析.【解析】试题分析：（Ⅰ）取11B D 中点F ,证明1//AO CF ,（Ⅱ）证明11B D ⊥面1A EM .所以1,A E BD ⊥因为11//,B D BD所以11111,,EM B D A E B D ⊥⊥ 又1,A E EM ⊂平面1A EM，1A E EM E = .所以11B D ⊥平面1,A EM 又11B D ⊂平面11B CD , 所以平面1A EM ⊥平面11B CD .6. 【2017天津，文17】如图，在四棱锥P ABCD -中，AD ⊥平面PDC ，AD BC ∥，PD PB ⊥，1AD =，3BC =，4CD =，2PD =.（I ）求异面直线AP 与BC 所成角的余弦值；（II ）求证：PD ⊥平面PBC ；（Ⅲ）求直线AB 与平面PBC 所成角的正弦值.【答案】(ⅠⅡ . 【解析】。

2018年高考数学（文）二轮复习讲练测总分 _______ 时间 _______ 班级 _______ 学号 _______ 得分_______一、选择题（12*5=60分）1．如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（）A. MN∥PDB. MN∥PAC. MN∥ADD. 以上均有可能【答案】B则四棱锥侧面中最大侧面的面积是（）A.4D. 4【答案】D【解析】3．设,αβ是两个不同的平面， l 是一条直线，以下命题正确的是（ ） A. 若,l ααβ⊥⊥，则l β⊂ B. 若,//l ααβ⊥，则l β⊥ C. 若//,//l ααβ，则l β⊂ D. 若//,l ααβ⊥，则l β⊥ 【答案】B【解析】若l ⊥α,α⊥β,则l ⊂β或l ∥β，故A 错误；若l ⊥α,α∥β，由平面平行的性质，我们可得l ⊥β，故B 正确； 若l ∥α,α∥β,则l ⊂β或l ∥β，故C 错误； 若l ∥α,α⊥β,则l ⊥β或l ∥β，故D 错误； 故选：C.4．在正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ＝4，则点A 1到平面AB 1D 1的距离是( ) A. 1 B. 43 C. 169D. 2 【答案】B【解析】设点A 1到平面AB 1D 1的距离为h ，因为V A1－AB1D1＝V A －A1B1D1，所以13S △AB1D1h ＝13S △A1B1D1×AA 1，所以h ＝111111122443A B D AB D SAA S⨯⨯⨯⨯==故选B.点睛：点面距离往往转化为对应棱锥的高，通过等体积法求高得点面距离.5．【2018届吉林省实验中学高三上学期第五次月考（一模）】四棱锥P­ABCD的三视图如图所示，四棱锥P­ABCD的五个顶点都在一个球面上， E，F分别是棱AB，CD的中点，直线EF被球面所截得的线段长为2，则该球的表面积为（）A. 12πB. 24πC. 36πD. 48π【答案】A6．祖暅原理：“幂势既同，则积不容异”．“幂”是截面积，“势”是几何体的高，意思是两个同高的几何体，如在等高处截面的面积恒相等，则体积相等．已知某不规则几何体与如图所示的几何体满足“幂势同”，则该不规则几何体的体积为( )A. 165B.325C. 3D. 6【答案】B7．已知△ABC的三个顶点在以O为球心的球面上，且AB＝2，AC＝4，BC＝2，三棱锥O－ABC的体积为，则球O 的表面积为( )A. 22πB.C. 24πD. 36π【答案】D【解析】△ABC中，AB＝2，AC＝4，BC＝5BC中点O′就是△ABC的外接圆的圆8．已知在四棱锥P－ABCD中，ABCD是矩形，PA⊥平面ABCD，则在四棱锥P－ABCD的任意两个顶点的连线中，互相垂直的异面直线共有( )A. 3对B. 4对C. 5对D. 6对【答案】C【解析】因为ABCD是矩形，PA⊥平面ABCD，所以PA⊥BC，PA⊥CD，AB⊥PD，BD⊥PA，AD⊥PB.共5对．9．如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中，给出下面四个结论中错误的是（）A. 平面//EFGH平面ABCDB. 直线BE,CF相交于一点C. EF//平面BGDD. //PA平面BGD【答案】C【解析】把图形还原为一个四棱锥,如图所示,根据三角形中位线的性质，可得//,//EH AB GH BC,平面//EFGH平面ABCD，A正确；在△PAD中,根据三角形的中位线定理可得EF∥AD，又∵AD∥BC，∴EF∥BC，因此四边形EFBC是梯形，故直线BE与直线CF相交于一点，所以B是正确的；连接AC，设AC中点为M，则M也是BD的中点，因为MG∥PA，且直线MG在平面BDG上，所以有PA∥平面BDG，所以D是正确的；∵EF∥BC，∵EF⊄平面PBC，BC⊂平面PBC，∴直线EF∥平面PBC，再结合图形可得：直线EF与平面BDG不平行，因此C是错误的.故选C10．在四棱锥P－ABCD中，四条侧棱长均为2，底面ABCD为正方形，E为PC的中点．若异面直线PA与BE所成的角为45°，则该四棱锥的体积是( )343D.33【答案】D11．在直三棱柱ABC－A1B1C1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α.有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE.其中正确的命题有( ) A. ①② B. ②③C.①③D. ①②③【答案】C【解析】直线AA1∥平面α，平面α∩平面AA1B1B＝EH，所以AA1∥EH.同理AA1∥GF，所以EH∥GF，又ABC－A1B1C1是直三棱柱，易知EH＝GF＝AA1，所以四边形EFGH是平行四边形，故①正确；若平面α∥平面BCC1B1，由平面α∩平面A1B1C1＝GH，平面BCC1B1∩平面A1B1C1＝B1C1，知GH∥B1C1，而GH∥B1C1不一定成立，故②错误；由AA1⊥平面BCFE，结合AA1∥EH知EH⊥平面BCFE，又EH⊂平面α，所以平面α⊥平面BCFE，故③正确.答案 C.12．如图，在△ABC中，AB＝BC6，∠ABC＝90°，点D为AC的中点，将△ABD沿BD折起到△PBD的位置，使PC ＝PD，连接PC，得到三棱锥P－BCD，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是( )A. 7πB. 5πC. 3πD. π【答案】A二、填空题（4*5=20分）13. 【2018届西藏拉萨市高三第一次模拟考试（期末）】中国古代数学瑰宝《九章算术》中有这样一道题：“今有堑堵（底面为直角三角形的直棱柱）下广二丈，袤一十八丈六尺，高二丈五尺，问积几何？”其意思为：“今有底面为直角三角形的直棱柱，底面的直角边长宽为2丈，长为18丈6尺，高为2丈5尺，问它的体积是多少？”已知1丈为10尺，则题中的堑堵的外接球的表面积为__________平方尺．【答案】35621π【解析】根据题意可将此堑堵补成一个长方体，且长、宽、高分别为186尺，20尺，25尺，则外接球的直径为35621235621435621ππ=⎝⎭.14．如图，三棱柱ABC－A1B1C12，且顶点A1在底面ABC上的射影O为△ABC的中心，则三棱锥A1－ABC的体积为________．【答案】1 3【解析】如图，由题意可知，底面三角形ABC为正三角形，15．已知m ，n 是两条不同的直线，α，β是两个不同的平面．给出下列命题： (1)若m ⊂α，m ⊥β，则α⊥β；(2)若m ⊂α，α∩β＝n ，α⊥β，则m ⊥n ；(3)若m ∥α，m ⊂β，α∩β＝n ，则m ∥n. 其中真命题是________(填序号)． 【答案】(1)(3)【解析】(2)中，m ∥n ，m 与n 相交都有可能．16．将正方形ABCD 沿对角线BD 折成直二面角A BD C --， AC BD O ⋂=有如下四个结论：①AC BD ⊥；②ACD 是等边三角形；③AB 与CD 所成的角为90︒，④取BC 中点E ，则AEO ∠为二面角A BC D --的平面角．其中正确结论是__________．（写出所有正确结论的序号） 【答案】①②④如上图所示，由题意可得： AB AC =，则AE BC ⊥, 由,,BE EC BO OD BC CD ==⊥可得OE BC ⊥，据此可知： AEO ∠为二面角A BC D --的平面角， 说法④正确. 故答案为：①②④.三、解答题（共6道小题，共70分）17. 如图，正方体ABCD －A 1B 1C 1D 1中，点E 是A 1D 1的中点，点F 是CE 的中点． (Ⅰ)求证：平面ACE⊥平面BDD 1B 1； (Ⅱ)求证：AE∥平面BDF.【答案】(1)见解析(2)见解析点睛：垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行，需转化为证明线线平行.(2)证明线面垂直，需转化为证明线线垂直.(3)证明线线垂直，需转化为证明线面垂直.=，点F为CE的中点.18．如图所示，平面ABCD⊥平面BCE，四边形ABCD为矩形，BC CEAE平面BDF.(1)证明：//⊥？若存在，确定点P的位置，并加以证(2)点M为CD上任意一点，在线段AE上是否存在点P，使得PM BE明；若不存在，请说明理由.【答案】（1）见解析；（2）中点【解析】试题分析：OF AE，再由线面平行的判定定理可证；（1）连接AB交BD于O，连接OF，利用ABCD是矩形得到//∵P为AE的中点，H为BE的中点，∴PH∥AB，又AB∥CD，∴PH∥CD，∴P，H，C，D四点共面．∵平面ABCD∥平面BCE，CD⊥BC∴CD⊥平面BCE，又BE⊂平面BCE，∴CD⊥BE∵BC=CE，H为BE的中点，∴CH⊥BE，∴BE⊥平面DPHC，又PM⊂平面DPHC，∴BE⊥PM即PM⊥BE.19．如图,在直三棱柱ABCA1B1C1中,D是BC的中点．(1)求证:A1B∥平面ADC1;(2)若AB⊥AC,AB＝AC＝1,AA1＝2,求几何体ABD-A1B1C1的体积．【答案】（1）详见解析（2）5 620．【2018届西藏拉萨市高三第一次模拟考试（期末）】如图，四棱锥P ABCD -底面为等腰梯形， //AD BC 且24BC AD ==，点E 为PC 中点．（1）证明： //DE 平面PAB ；（2）若PA ⊥平面ABCD ， 60ABC ∠=︒，直线PB 与平面ABCD 所成角的正切值为32，求四棱锥P ABCD -的体积V ．【答案】(1)见解析；（2）33即在PAB ∆中，有32PA AB =，则3PA =. 所以，四棱锥P ABCD -的体积13ABCD V S PA =⋅梯形 ()243133332+=⨯=． 21．如图1，在梯形ABCD 中，AD∥BC，AD⊥DC，BC ＝2AD ，四边形ABEF 是矩形，将矩形ABEF 沿AB 折起到四边形ABE 1F 1的位置，使平面ABE 1F 1⊥平面ABCD ，M 为AF 1的中点，如图2. (1)求证：BE 1⊥DC； (2)求证：DM∥平面BCE 1；(3)判断直线CD 与ME 1的位置关系，并说明理由．【答案】(1)见解析；(2)见解析.（3）相交，理由详见解析所以平面ADM∥平面BCE1.因为DM⊂平面ADM，所以DM∥平面BCE1.(3)解直线CD与ME1相交，理由如下：取BC的中点P，CE1的中点Q，连接AP，PQ，QM，22．如图：设一正方形纸片ABCD边长为2分米，切去阴影部分所示的四个全等的等腰三角形，剩余为一个正方形和，O为正四棱锥四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥（粘接损耗不计），图中AH PQ底面中心．（Ⅰ）若正四棱锥的棱长都相等，求这个正四棱锥的体积Ｖ；（Ⅱ）设等腰三角形APQ的底角为x，试把正四棱锥的侧面积S表示为x的函数，并求S的范围．【答案】（1）3403立方分米（2）02S<<平方分米。

高考大题专攻练7.立体几何(A组)大题集训练,练就慧眼和规范,占领高考制胜点!1.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.(1)求证:AB⊥平面ADE.(2)求凸多面体ABCDE的体积.【解析】(1)因为AE⊥平面CDE,CD⊂平面CDE,所以AE⊥CD,又在正方形ABCD中,CD⊥AD,且AE∩AD=A,所以CD⊥平面ADE,又在正方形ABCD中,AB∥CD,所以AB⊥平面ADE.(2)连接BD,设B到平面CDE的距离为h,因为AB∥CD,CD⊂平面CDE,所以AB∥平面CDE,又AE⊥平面CDE,所以h=AE=1,又S△CDE=CD×DE=×2×=,所以V B-CDE=××1=,又V B-ADE=×S△ADE×AB=××1××2=,所以凸多面体ABCDE的体积V=V B-CDE+V B-ADE=.2.如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,AC,BD,点E,F分别在线段SB,SC 上,连接AF,AE,EC.(1)证明:BD⊥AF.(2)若三棱锥B-AEC的体积是四棱锥S-ABCD体积的,求点E到平面ABCD的距离.【解析】(1)因为四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,二面角S-AB-C的大小为90°,所以SA⊥AD,又SA⊥AB,AB∩AD=A,所以SA⊥平面ABCD,又BD⊂平面ABCD,所以SA⊥BD,在直角梯形ABCD中,∠BAD=∠ADC=90°,AD=2CD=1,AB=SD=2,所以tan∠ABD=tan∠CAD=,又∠DAC+∠BAC=90°,所以∠ABD+∠BAC=90°,即AC⊥BD,又AC∩SA=A,所以BD⊥平面SAC,因为AF⊂平面SAC,所以BD⊥AF.(2)设点E到平面ABCD的距离为h,因为V B-AEC=V E-ABC,且=,所以===, 解得h=,所以点E到平面ABCD的距离为.。

2018年高考数学（文）二轮复习讲练测【高考改编☆回顾基础】1【空间几何体的直观图和面积计算】由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为________．【答案】12【解析】该几何体为一个三棱柱和一个三棱锥的组合体，其直观图如图所示，各个面中有两个全等的梯形，其面积之和为2×2＋42×2＝12.【三视图与空间几何体的体积】【2017·全国卷Ⅱ改编】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为________．【答案】63π 【解析】3. 【空间几何体的体积】【2017课标3，改编】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 . 【答案】3π4【解析】【命题预测☆看准方向】1.空间几何体的三视图成为近几年高考的必考点,单独考查三视图的逐渐减少,主要考查由三视图求原几何体的面积、体积,主要以选择题、填空题的形式考查.2.对柱体、锥体、台体表面积、体积及球与多面体的切接问题中的有关几何体的表面积、体积的考查又是高考的一个热点,难度不大,主要以选择题、填空题的形式考查.3.2018年应注意抓住考查的主要题目类型进行训练,重点有三个:一是三视图中的几何体的形状及面积、体积;二是求柱体、锥体、台体及球的表面积、体积;三是求球与多面体的相切、接问题中的有关几何体的表面积、体积.【典例分析☆提升能力】【例1】17世纪日本数学家们对于数学关于体积方法的问题还不了解，他们将体积公式“V＝kD 3”中的常数k 称为“立圆术”或“玉积率”，创用了求“玉积率”的独特方法“会玉术”，其中，D 为直径，类似地，对于等边圆柱(轴截面是正方形的圆柱叫做等边圆柱)、正方体也有类似的体积公式V ＝kD 3，其中，在等边圆柱中，D 表示底面圆的直径；在正方体中，D 表示棱长．假设运用此“会玉术”，求得的球、等边圆柱、正方体的“玉积率”分别为k 1，k 2，k 3，那么，k 1∶k 2∶k 3＝( ) A.4π∶6π∶1 B. 6π∶4π∶2 C. 1∶3∶12π D. 1∶32∶6π【答案】D【解析】球中， 33331144,33266D V R D k D k ππππ⎛⎫====∴= ⎪⎝⎭；等边圆柱中， 23322,244D V D D k D k πππ⎛⎫=⋅==∴= ⎪⎝⎭；正方体中， 3333,1V D k D k ==∴=；所以12336::::11::642k k k πππ==.故选D. 【趁热打铁】将一个底面半径为1，高为2的圆锥形工件切割成一个圆柱体，能切割出的圆柱的最大体积为( )A. π27B.8π27C.π3D.2π9【答案】B【解析】【例2】【2018届河南省郑州市第一次模拟】刍薨（chuhong），中国古代算术中的一种几何形体，《九章算术》中记载“刍薨者，下有褒有广，而上有褒无广.刍，草也.薨，屋盖也.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱，刍薨字面意思为茅草屋顶”，如图，为一刍薨的三视图，其中正视图为等腰梯形，侧视图为等腰三角形，则搭建它（无底面，不考虑厚度）需要的茅草面积至少为（）A. 24B. 325C. 64D. 326【答案】B【趁热打铁】【2018届湖北省稳派教育高三上第二次联考】已知一个几何体的三视图如图所示，则该几何体的体积为（ ）A.8163π+ B. 1683π+ C. 126π+ D. 443π+ 【答案】A【解析】由三视图可得，该几何体为右侧的一个半圆锥和左侧的一个三棱锥拼接而成。

立体几何专题一、选择题(本大题共12题,每小题5分,共60分)1.棱锥侧面是有公共顶点的三角形,能围成一个棱锥侧面的正三角形的个数的最大值是( )A. 3B. 4C. 5D. 62. 在三棱锥S ABC -的三条侧棱,,SA SB SC 上分别任取点',','A B C ，则有（ ） A ．几何体'''S A B C -一定是三棱锥，几何体'''ABC A B C -一定是三棱台 B ．几何体'''S A B C -一定是棱锥，几何体'''ABC A B C -不一定是棱台 C ．几何体'''S A B C -不一定是棱锥，几何体'''ABC A B C -一定是棱台D ．几何体'''S A B C -不一定是三棱锥，几何体'''ABC A B C -也不一定是三棱台 3.4. 用斜二侧法将四边形ABCD 画成四边形''''A B C D ， 在：（1）若//AB CD ，则''//''A B C D ； （2）若AB CD =，则''''A B C D =； （3）若AB CD >，则''''A B C D >； （4）P 为AB 中点，则'P 必为''A B 中点． 中，正确的是（ ） A ．（1）和（2） B ．（1）和（3） C ．（1）和（4） D ．（1）、（2）和（4）5. 已知直线21,l l 与平面α. 则下列结论正确的是（ ）A ．若A l l =⊂αα 21,，则21,l l 为异面直线B ．若α//,//121l l l ，则α//2l .C ．若,,121α⊥⊥l l l 则.//2αlD ．若,,21αα⊥⊥l l ，则21//l l . 6. 四棱锥的8条棱所在直线中，互为异面的直线共有（ ）．A ．4对B ．8对C ．12对D ．16对7. 图示最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截得的图形可能是( )8. 四棱柱1111ABCD A BC D -底面为平行四边形，对角线1AC 与平面1A BD 相交于P ．则P 是△1A BD 的（ ）A ．重心B ．内心C ．外心D ．垂心9. 空间四边形ABCD 的各边与两条对角线的长都是1，点P 在边AB 上移动，点Q 在CD 上移动，则点P 与Q 的最短距离为 ( ) A .12 B. 2 C .34 D .210.11. 如图，水平地面上有一个大球，现用如下方法测量球的大小：用一个锐角为450的三角板，斜边紧靠球面，一条直角边紧靠地面，并使三角板与地面垂直，P 为三角板与球的切点，如果测得PA=5cm,则球的表面积为 （ ）2.100A cm π.B 2.200D c m π12. 如图所示，正四面体ABCD 中，E 在棱AB 上，F 在棱CD 上，使)0(>==λλFDCFEB AE ，设λλλαβλ,)(+=a f 表示EF 与AC 所成的角，λβ表示EF 与BD 所成的角，则（ ） A.),0()(∞+在λf 上单调递增 B.),0()(∞+在λf 上单调递减 C.)1,0()(在λf 上单调递增， 而在),1(∞+上单调递减D.),0()(∞+在λf 上为常数二、填空题(本大题共4小题,每小题4分,共16分) 13. 在正方体ABCD —A 1B 1C 1D 1中，O 1为上底中心，异面直线AB 1与BC 1所成的角为 . 14.点P 是棱长为a 的正方体1111D C B A ABCD -棱11B A 上的动点,则四棱锥11D ABC P -的体积为 . 15.16. 在正四棱柱1111D C B A ABCD -中，如果底边正方形ABCD 的边长为2=AB ，侧棱21=AA ，则下列四个命题：E ADFC B①1AA 与1BC 成ο45角； ② 1AA 与1BC 的距离为2 ； ③ 二面角C AB C --1的正切值为为2； ④ ⊥D B 1平面AC D 1.则正确命题的序号为 .三、解答题(本大题共6小题, 共74分, 解答应写出文字说明、证明过程或演算步骤) 17.（本小题满分12分）把一个圆锥截成圆台，已知圆台的上、下底半径的比是1︰4，圆台的母线长是9cm ，求圆锥的母线长．18.（本小题满分12分）19.（本小题满分12分）ABCD 为空间四边形,点M 、E 、F 分别为△BAC 、△ACD 及△ADB 的重心. （1）求证：面MEF ∥面BCD ； （2）求S △MEF 与S △BCD 面积的比值.20.（本小题满分12分）如图所示，直角梯形O 2BAO 1内有一个内切半圆O ，把这个平面图形绕O 1O 2旋转一周得到圆台内有一个内切球，已知圆台全面积与球面积的比是k(k>1),求它们的体积比.21.（本小题满分12分）BC 已知P A ⊥平面ABCD ，ABCD 为矩形，P A ＝AD ，M 、N 分别是AB 、PC 的中点，求证：（Ⅰ）MN ∥平面P AD ； （Ⅱ）平面PMC ⊥平面PDC .22.（本小题满分14分）如图，在直三棱柱ABC —A 1B 1C 1中，AA 1=2， AC=BC=1，∠ACB=90°，点E 是AB 的中点， 点F 在侧棱BB 1上，且EF ⊥CA 1.（Ⅰ）求二面角C —A 1F —E 的大小. （Ⅱ）求点E 到平面CA 1F 的距离.1数学参考答案与解析1．C 解析：正三角形的每一个内角为600，六个这样的正三角形为侧面不能围成棱锥(顶点出发的几个内角的和应小于3600).所以最大值应有5个,故应选C.2.B 解析：由棱锥与棱台的概念可得几何体'''S A B C -一定是棱锥，几何体'''ABC A B C -不一定是棱台.故应选B.3.4.C 解析：斜二侧画法中, 若//AB CD ，则''//''A B C D ；P 为AB 中点，则'P 必为''A B 中点．正确的是（1）和（4）.故应选C.5.D 解析：A 错,21,l l 也可能相交; B 错,2l 也可以能在α内;C 错, 2l 也可以能在α内; D 正确,垂直于同一条直线的两条直线平行. 综上所述,正确结论应选D.6.B 解析：每一条侧棱均与底面的2条边成异面直线,即有两对异面直线,四条侧棱共有8对互为异面的直线.7.D 解析：截面(2)(3)的外轮廓是整个的矩形，所以是错的.故排除A 、B;截面（4）圆锥的轮廓是抛物线而不是三角形，所以是错的.故选D.8.A 解析：如图所示,连接AC 、AB 1 ,可得面1A BD 与平面1A AC 交线为1A P ,1A P 所在直线为1A BD ∆ 的中线,同理可得DP 所在直线也为1A BD ∆的中线, 即点P 为1A BD ∆的重心.故应选A.9.B 解析：P 与Q 的最短距离就是异面直线AB与 DC 的距离,分别取AB 与DC 的中点,可得PQ 即 为所求,2=, 故应选B . 10.PDABC A 1B 11D 111.B 解析：如图所示,5,1)R R +=∴== 224100(3.S R cm ππ∴==+球12.D 解析：作EG ∥AC,交BC 于G,连GF,则,,EFG GEF ∠=∠=λλβαEGF ∠-=+πβαλλ，∴EGF ∠为常数.故选D.13.60°解析：如图所示, 连结AD 1，则AD 1∥BC 1 ∴∠D 1AB 1是异面直线AB 1与BC 1所成的角 ∵△D 1AB 1是正三角形,∴∠D 1AB 1=60°. 即AB 1与BC 1所成的角是60°.14.313a 解析：本题考查了正方体模型下动点条 件下锥体体积的探究.点P到面11ABC D,其底面11ABC D 的2,则其体积2311323V a a =⋅=.15.16.②③解析：①如图,连结BC 1,则BC C 1∠就是AA 1,与BC 1成的角,,22tan 1=∠BC C 则BCC 1∠不是450; ②如图,正四棱柱中,AB 就是AA 1与BC 1的距离为2; ③二面角C 1-AB-C 的平面角就是1tan 2C BC ∠=; ④因为四棱柱不是正方体,则B 1D 与平面D 1AC 不垂直. 综上所述,正确命题的序号为②③.17.解析：如图，圆锥是由直角三角形POA 绕PO 旋转而成，A BCDA 1B 1C 1D 1D则''//O A OA 知：'''O A PA OA PA=， 即1'4PA AA PA-=，'9AA =， ∴ 12PA =．即圆锥的母线长是12cm. 12分18.19.解析:（1）证明：连结AM 、AE 及AF ,分别延长使之交BC 、CD 、 DA 于G 、H 、P 三点.∵E 、F 、M 分别为三角形的重心,∴AG AM =AH AE =AP AF =32. ∴连结ME 、EF 、FM 及连结GH 、HP 、PG 后 有ME ∥GH ,EF ∥PH ,即ME ∥面BCD ,EF ∥面BCD .故面EFM ∥面BCD . 6分（2）由GH ME =32,PH EF =32知ME =32GH ,EF =32PH 而GH =21BD ,PH =21BC ,故ME =31BD ,EF =31BC , 即BD ME =BC EF =31.则BCD MEF S S ∆∆=91. 12分20.解析:设r A O =1,)(2r R R B O >=,,则圆台母线AB=BM+AM=R+r,球O 的直径 Rr r R r R O O 2)()(2221=--+=,),(2)(22222Rr r R r R r R S ++=+++=∴ππππ圆台全Rr S π4=球 6分 .222k RrRrr R S S =++=∴球圆台全故.2)(34)(23122322k Rr r Rr R Rr r Rr R Rr V V =++=++⋅=ππ球圆台 12分21. 证明：（Ⅰ）取PD 的中点为Q ，连结AQ 、QN ，∵PN ＝NC ，∴QN //=21DC .∵四边形ABCD 为矩形，∴QN //=AM .∴MN ∥AQ .又∵AQ ⊂平面P AD ，∴MN ∥平面P AD . 6分 （Ⅱ）∵P A ⊥平面ABCD ，∴∠P AD ＝90°. ∵P A =AD ，∴△P AD 为等腰直角三角形. ∵Q 为PD 中点，∴AQ ⊥PD .∵CD ⊥AD ，CD ⊥P A ，∴CD ⊥平面P AD ， ∴CD ⊥AQ ，∴AQ ⊥平面PDC .由（1）MN ∥AQ ，∴MN ⊥平面PDC . 又∵MN ⊂平面PMC ，∴平面PMC ⊥平面PDC . 12分 22.解析：（Ⅰ）过E 作EG ⊥FA 1，垂足为G ，连结CG 在直三棱柱ABC —A 1B 1C 1中，面A 1B ⊥面ABC 又AC=BC ，E 为AB 中点 ∴CE ⊥AB ∴CE ⊥面A 1B ， ∴CG ⊥A 1F ∴∠CGE 为二面角C —A 1F —E 的平面角 而∵CE ⊥面A 1B ∴CE ⊥EF EF ⊥CA 1 ∴EF ⊥面A 1CE ∴EF ⊥A 1E ∴△A 1AE ∽△EBF∴41222221=⨯=⋅=BE AA AE BF在Rt △A 1AE 中，A 1E=223)22(22221=+=+AE A A在Rt △EBF 中，EF=43)41()22(2222=+=+BF BE22494322349112211=⨯=⋅=∴=+=∴F A EF E A EG EF E A F A 又CE=221t a n==∠∴EG CE CGE ︒=∠∴45CGE即二面角C —A 1F —E 的大小为45° 7分（Ⅱ）设顶点E 到平面A 1CF 的距离为d ，由（1）CG=1，CE ⊥面A 1B ，A 1F ⊥EF ，EF A C CF A E V V 11--=2149121314322322312131213111=∴⋅⨯⨯⨯=⨯⨯⨯∴⋅⋅⋅⨯=⋅⋅∴d d d F A CG EF E A CE即点E 到平面CA 1F 的距离为21. 14分。