天津市南开区南大附中2018年高中数学必修5解三角形综合复习卷含答案

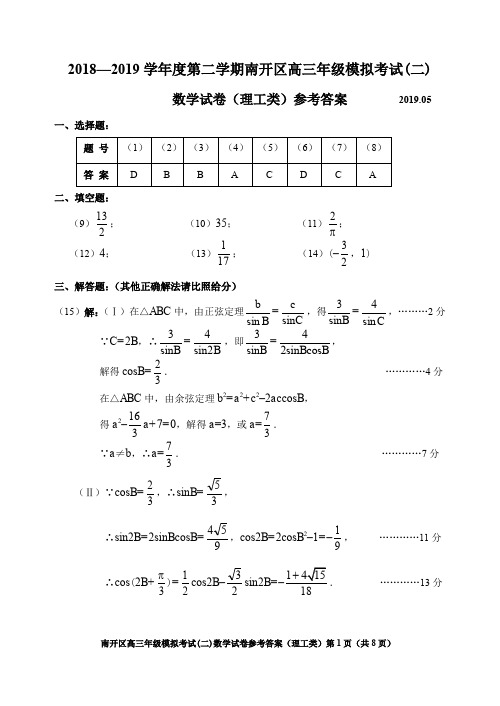
专题03解三角形考点一、利用正弦定理、余弦定理解三角形考点二、判断三角形的形状考点三、解三角形的实际应用1、根据正弦定理、余弦定理求边或角2、求三角形的周长或面积3、解三角形中求取值范围或最值问题4、解三角形的综合应用利用正弦定理和余弦定理解三角形1．（22-23高一下·天津·期中）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．若1a =，2b =，c =C =（）A ．120︒B ．90︒C ．60︒D ．45︒2．（22-23高一下·天津·期中）在ABC 中，内角A ，B ，C 所对的边为a ，b ，c ，若4a =，b =π6A =，则角B 的大小为（）A ．π3B ．π3或2π3C ．2π3D ．π63．（22-23高一下·天津·期中）已知ABC ，内角、、A B C 的对边分别是,,,60a b c a b B ===︒，则A 等于（）A ．45︒B ．30︒C ．45︒或135︒D ．30︒或150︒4．（22-23高一下·天津·期中）在ABC 中，75,45AB A B === ，则AC =（）A B ．2CD ．3【答案】B【分析】根据三角形内角和先求出角C ，再根据正弦定理即得．【详解】因为180A B C ++= ，所以60C = ，5．（22-23高一下·天津·期中）若ABC 2BC =，60C =︒，则边AB 的长度等于（）A B C ．2D ．36．（22-23高一下·天津南开·期中）在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若()42cos 1,sin 5a c B C =+=，则sin B =（）A ．1825B ．2425-C ．1825-D ．24257．（22-23高一下·天津·期中）ABC 的内角A B C ，，的对边分别为a ，b ，c ，若ABC 的面积为2224a b c +-，则C =A ．π2B ．π3C ．π4D ．π68．（22-23高一下·天津·期中）在ABC 中，a 3b =，6A π=，则此三角形（）A ．无解B ．一解C ．两解D ．解的个数不确定判断三角形的形状9．（19-20高一下·天津东丽·期末）已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，下列四个命题中正确的是（）A ．若4,30a b A === ，则B 只有一解B ．若2220a b c +->，则△ABC 一定是锐角三角形C ．若b cos C ＋c cos B ＝b ，则△ABC 一定是等腰三角形D ．若a cos A ＝b cos B ，则△ABC 一定是等腰三角形10．（22-23高一下·天津·期中）在ABC 中，内角A 、B 、C 的对边分别为a ，b ，c ，且cos a c B =，则ABC 的形状是（）A ．等腰三角形B ．直角三角形C ．等边三角形D ．等腰直角三角形【答案】B，再由诱导公式及两角和的正弦公式判断即11．（22-23高一下·天津·期中）在ABC 中，已知()sin 2sin cos A A C C =+，那么ABC 一定是（）A ．等腰直角三角形B ．直角三角形C ．等腰三角形D ．等边三角形12．（22-23高一下·天津·期中）在ABC 中，内角,,A B C 满足2sin cos sin B C A =，则ABC 的形状为（）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．正三角形【答案】B【分析】根据()sin sin A B C =+得到()sin 0B C -=，求出B C =，得到三角形形状.【详解】()2sin cos sin sin sin cos cos sin B C A B C B C B C ==+=+，故sin cos cos sin 0B C B C -=，即()sin 0B C -=，因为(),0,πB C ∈，所以B C =，故ABC 为等腰三角形.故选：B13．（22-23高一下·天津·期中）在 ABC 中，如果满足cos cos b A a B =，则 ABC 一定是（）A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰或直角三角形14．（22-23高一下·天津·期中）设在ABC ∆中,角,A B C ，所对的边分别为,a b c ，,若cos cos sin b C c B a A +=,则ABC ∆的形状为（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定15．（22-23高一下·天津·期中）在ABC 中，已知||||AB AC AB AC +=-，且sin 2sin cos A B C =，则ABC 是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形16．（2021·甘肃天水·模拟预测）在ABC 中，若21sin cos C b C B c B -=-，则ABC 的形状是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形B解三角形的实际应用17．（22-23高一下·天津·期中）一艘轮船按照北偏东40︒方向，以18海里/时的速度直线航行，一座灯塔原来在轮船的南偏东20︒方向上，经过20分钟的航行，轮船与灯塔的距离为与轮船原来的距离为A．6海里B．12海里C．6海里或12海里D．由题意得：18AC=则2 cos ACCAB∠=即灯塔与轮船原来的距离为本题正确选项：A【点睛】本题考查解三角形的实际应用问题，关键是能够利用余弦定理构造方程，解方程求得结果18．（22-23高一下·天津·期中）一艘轮船沿北偏东28o方向，以18海里/时的速度沿直线航行，一座灯塔原来在轮船的南偏东32o方向上，经过10灯塔与轮船原来的距离为海里.19．（20-21高一下·天津宁河·阶段练习）一艘轮船按照北偏东40°方向，以18海里/时的速度直线航行，一座灯塔原来在轮船的南偏东20°方向上，经过20分钟的航行，轮船与灯塔的距离为则灯塔与轮船原来的距离为海里．【答案】6【分析】由题意画出图形，求出相关量，然后利用余弦定理求解即可.【详解】记轮船的初始位置为A，灯塔位置为B，20分钟后轮船的位置为C，如图所示：由题意得：11863AC =⨯=，1804020120CAB ∠=--= 63BC =，在ABC 中，由余弦定理得：22cos 2AC AB BC CAB AC AB +-∠=⋅()2226631262AB AB+-==-⨯⋅，所以解得6AB =或12AB =-20．（22-23高一下·天津南开·期中）2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86（单位：米），三角高程测量法是珠穆朗玛峰高程测量方法之一.如图是三角高程测量法的一个示意图，现有A ，B ，C 三点，且A ，B ，C 在同一水平面上的投影,,A B C '''满足45,60A C B A B C ''''''∠=∠= ，由点C 测得点B 的仰角为15 ，BB '与CC '的差为100，由点B 测得点A 的仰角为45 ，则A ，C 两点到水平面ABC '''的高度差AA CC ''-为米.已知BB '与CC '的差为100，则又15BCD ∠=，则tan15CD =则3131010100(2B C CD ''=-==+根据正弦定理和余弦定理求边或角21．（22-23高一下·天津·期中）在ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ．已知3a =c =2π3A =．(1)求C 的值；(2)求b 的值．22．（22-23高一下·天津河西·期中）在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知2cos c b b A -=.(1)若a =3b =，求边c 的长；(2)若π2C =，求角B 的大小．23．（22-23高一下·天津·期中）在ABC 中，角A 、B 、C 的对边分别为a ，b ，c.已知12,cos 4a b c A ===-.(1)求c 的值；(2)求sin B 的值；(3)求sin(2)A B -的值.24．（22-23高一下·天津·期中）在非等腰ABC 中，a ，b ，c 分别是三个内角A ，B ，C 的对边，且3a =，4c =，2C A =.(1)求cos A 的值；(2)求ABC 的周长；(3)求πcos 26A ⎛⎫+ ⎪⎝⎭的值.25．（22-23高一下·天津·期中）在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c.已知sin cos 6b A a B π⎛⎫=- ⎪⎝⎭.（1）求角B 的大小；（2）设a =2，c =3，求b 和()sin 2A B -的值.26．（22-23高一下·天津和平·期中）ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，向量()m a =u r与()cos ,sin n A B =r平行.(1)求A ；(2)若a =2b =，求sin C 的值.27．（22-23高一下·天津滨海新·期中）在ABC 中，角,,A B C 所对的边分别为,,a b c .已知45,6,cos 5a b B ===-.(1)求A 的值；(2)求()sin 2B A +的值.28．（22-23高一下·天津·期中）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .已知sin A C =，150B =︒，ABC(1)求a 的值；(2)求sin A 的值；(3)求sin 26A π⎛⎫+ ⎪的值.29．（22-23高一下·天津·期中）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，且222sin sin sin cos cos A A B B C +=-.(1)求角C 的大小；(2)若sin 2sin A B =，c =ABC 的面积.30．（22-23高一下·天津·期中）在ABC 中，角A ，B ，C 所对的分别为a ，b ，c ．向量),m b =，()sin ,cos n A B = ，且m n ∥．(1)求B 的值；(2)若2a =，b ，求ABC 的面积31．（2021·广西·二模）已知ABC 的内角A 、B 、C 的对边分别为、b 、，且c b c a=--.(1)求角A 的大小；(2)若a =，且ABC S = ABC 的周长.32．（22-23高一下·天津河北·期中）已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，向量()m a =u r，()cos ,sin n A B =r ，且//m n .(1)求角A ；(2)若a =2b =，求边c及ABC 的面积；(3)在（2）的条件下，求()sin 2B A -的值.33．（22-23高一下·天津和平·期中）ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin 0A A =，4c =，a =(1)求A ，b ；(2)设D 为BC 边上一点，且AD AC ⊥，求ABD △的面积.34．（22-23高一下·天津滨海新·期中）在ABC 中，角,,A B C 所对的边分别为,,a b c ，已知2cos cos b c a A B=+.(1)求角B 的大小；(2)若4,b a c =+=ABC 的面积.35．（22-23高一下·天津滨海新·期中）已知ABC 内角A ，B ，C 的对边分别为a ，b ，c ，且2cos cos cos c A a B b A =+．(1)求角A ；(2)若ABC 的外接圆半径R =4b =，求ABC 的面积；(3)若a =3BA AC ⋅=- ，A ∠的平分线交边BC 于点T ，求AT 的长．求取值范围或最值问题36．（22-23高一下·天津·期中）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知cos2cos2cos212sin sin A B C A B +-=-.(1)求角C 的大小；(2)若ABC 为锐角三角形，求sin sin sin A B C ++的取值范围.37．（21-22高一下·湖北·期中）已知ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且()2cos cos a b C c B-=(1)求角C(2)若2a =，3b =，CD 为角C 的平分线，求CD 的长；(3)若cos cos 4a B b A +=，求锐角ABC 面积的取值范围.=38．（2020·全国·模拟预测）在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且()223sin sin 222C B bc b c b c a +=++.(1)求角A 的大小；(2)若c a >，求a b m c +=的取值范围.39．（21-22高一下·江苏无锡·期中）从①222sin sin sin sin sin 0B A C B C -+-=②sin cos b A B =，这两个条件中任选一个，补充在下面问题中，并加以解答（注：若选择多个条件，按第一个解答计分）.在ABC 中，,,a b c 分别是角,,A B C 的对边，若__________.(1)求角A 的大小：(2)若D 是BC 的中点，AD =ABC 面积的最大值.(3)若O 为ABC 的外接圆圆心，且cos cos 2sin sin B C AB AC mAO C B+= ，求实数m 的值.【详解】（1）解：选条件①时，222sin sin sin sin sin 0B A C B C -+-=，根据正弦定理：222b a c bc -+=，40．（20-21高一下·山东济南·期中）如图所示，某市有一块空地OAB ，其中2km OA =，60OAM ∠=︒，90AOB ∠=︒．当地政府计划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖OMN ，其中M ，N ，都在边AB 上，且30MON ∠=︒，挖出的泥土堆放在OAM △地带上形成假山，剩下的OBN △地带开设儿童游乐场．为安全起见，需在OAN 的周围安装防护网．设=AOM θ∠．（1）当1km AM =时，求此时防护网的总长度；（2）若15θ=︒，问此时人工湖用地OMN 的面积是堆假山用地OAM △的面积的多少倍？（3）为节省投入资金，人工湖OMN 的面积要尽可能小，问如何设计施工方案，可使OMN 的面积最小？最小面积是多少？（2）15θ=︒时，在三角形sin 60sin15OM AM =︒︒在三角形OMN 中，由正弦定理得，sin 30sin 75MN OM =︒︒所以sin 60sin 75MN AM =sin 60sin 301sin 302︒⋅︒=︒以O 为顶点时，所以OMN OAM S MN S AM=△△即人工湖用地OMN （3）在三角形OAN 18060ONA ∠=︒-由正弦定理得，(2sin 60sin 90ON =︒︒在三角形OAM 中，由正弦定理得sin OM。

一、选择题1．已知曲线1:sin C y x =，曲线2:sin 23C y x π⎛⎫=-⎪⎝⎭，则下列结论正确的是（ ） A ．把曲线1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移3π个单位长度，得到曲线2C B ．把曲线1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移6π个单位长度，得到曲线2C C ．把曲线1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移3π个单位长度，得到曲线2C D ．把曲线1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移6π个单位长度，得到曲线2C 2．已知曲线C 1：y ＝2sin x ，C 2：2sin(2)3y x π=+，则错误的是（ ）A ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平行移动6π个单位长度，得到曲线C 2 B ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平行移动56π个单位长度，得到曲线C 2 C ．把C 1向左平行移动3π个单位长度，再把得到的曲线上各点的横坐标缩短到原来的12倍，纵坐标不变，得到曲线C 2 D ．把C 1向左平行移动6π个单位长度，再把得到的曲线上各点的横坐标缩短到原来的12倍，纵坐标不变，得到曲线C 23．函数()sin()(0)f x x ωϕω=+>的一段图象如图所示，则ω=（ ）A ．14B ．2π C ．4π D ．124．已知函数()()2sin 3,0,2f x x x x π=∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭，则()f x 的单调递增区间是（ ） A ．06,π⎡⎤⎢⎥⎣⎦B ．0,4⎡⎤⎢⎥⎣⎦πC ．0,3π⎡⎤⎢⎥⎣⎦D ．0,2π⎡⎤⎢⎥⎣⎦5．已知角θ终边经过点)2,P a ，若6πθ=-，则a =（ ）A 6B ．63C ．63-D ．6-6．cos75cos15sin75sin15︒⋅︒+︒⋅︒的值是（ ） A ．0B ．12C 3D ．17．把函数sin y x =的图象上所有的点向左平行移动6π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数解析式是（ ） A ．sin 23y x π⎛⎫=- ⎪⎝⎭B ．sin 26x y π⎛⎫=+⎪⎝⎭C ．sin 26y x π⎛⎫=-⎪⎝⎭D ．sin 26y x π⎛⎫=+⎪⎝⎭8．将函数()f x 的图象向左平移02πϕϕ⎛⎫<<⎪⎝⎭个单位后得到函数()sin 2g x x =的图象，若对满足()()122f x g x -=的1x ，2x ，有12min3x x π-=，则ϕ=（ ） A ．512π B ．3π C ．4π D ．6π 9．()()sin f x A x =+ωϕ0,0,2A πωϕ⎛⎫>>< ⎪⎝⎭的部分图象如图所示，若将函数()f x的图象向右平移2π个单位长度，得到函数()g x 的图象，则（ ）A ．()12sin 212g x x π⎛⎫=- ⎪⎝⎭ B ．()12sin 212g x x π⎛⎫=+⎪⎝⎭ C ．()2sin 212g x x π⎛⎫=- ⎪⎝⎭D ．()2sin 212g x x π⎛⎫=+⎪⎝⎭10．sin 20cos10cos160sin10-=（ ） A ．3 B ．12C ．12-D ．3211．已知函数()()()cos >0,0<<f x x ωθωθπ=+的最小正周期为π，且()()0f x f x -+=，若tan 2α=，则()f α等于（ ）A ．45-B ．45C ．35D ．3512．已知2cos 432θπ⎛⎫= ⎪⎝⎭-，则sin θ=（ ） A ．79 B ．19C ．－19D ．－79二、填空题13．设()sin 2cos2f x a x b x =+，0ab ≠，若()6f x f π⎛⎫≤ ⎪⎝⎭对任意x ∈R 成立，则下列命题中正确的命题是______.（填序号） ①11012f π⎛⎫=⎪⎝⎭；②7105f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭；③()f x 不具有奇偶性；④()f x 的单调增区间是()2,63k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z ；⑤可能存在经过点(),a b 的直线与函数的图象不相交. 14．将函数sin(2)y x ϕ=+的图像向左平移12π个单位后所得函数图像关于原点中心对称，则sin 2ϕ=_________．15．设α、β都是锐角，且()3cos ,sin 55ααβ=+=，则cos β=____________. 16．已知tan 2α=，则cos2=α__． 17．若0,2x π⎛⎫∀∈ ⎪⎝⎭，sin cos m x x ≥+恒成立，则m 的取值范围为_______________. 18．已知sin θ＋cos θ＝15，则tan θ＋cos sin θθ的值是____________________. 19．若6x π=是函数()3sin 2cos2f x x a x =+的一条对称轴，则函数()f x 的最大值是___________.20．已知7sin cos 5αα+=-，22sin cos 5αα-=-，则cos2=α_______.三、解答题21．已知函数()2sin cos ,3f x x x x R π⎛⎫⎪⎝=-∈⎭. （1）求函数()f x 的最小正周期； （2）当,34x ππ⎡⎤∈-⎢⎥⎣⎦，求函数()f x 的最大值与最小值，并指出相应的x 值.22．已知函数1()sin 2cos 244f x x x =+ （1）求()f x 的最小正周期； （2）求()f x 在区间50,12π⎡⎤⎢⎥⎣⎦上的值域.23．已知()()()()1122,,,A x f x B x f x 是函数()()2sin f x x ωϕ=+0,02πωϕ⎛⎫>-<< ⎪⎝⎭图象上的任意两点，且角ϕ的终边经过点(1,P ，当()()124f x f x -=时，12x x -的最小值为3π． （1）求函数()f x 的解析式; （2）当0,6x π⎡⎤∈⎢⎥⎣⎦时，不等式()()2mf x m f x +≥恒成立，求实数m 的取值范围．24．已知函数()()2cos cos sin f x x x x x =+-． （1）求函数()f x 的单调递增区间； （2）若当0,2x π⎡⎤∈⎢⎥⎣⎦时，关于()f x m ≥的不等式 _______，求实数m 的取值范围． 请选择①和②中的一个条件，补全问题（2），并求解．其中，①有解；②恒成立． 注意：如果选择①和②两个条件解答，以解答过程中书写在前面的情况计分． 25．（1）在面积为16的扇形中，半径多少时扇形的周长最小；（2. 26．已知函数π()2sin 6f x x ⎛⎫=+ ⎪⎝⎭. （1）求()f x 的单调递减区间；（2）设π()()6g x f x f x ⎛⎫=- ⎪⎝⎭. 当[0,]x m ∈时，()g x 的取值范围为0,2⎡⎣，求m 的最大值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】根据三角函数的伸缩变换与平移变换原则，可直接得出结果. 【详解】因为sin 2sin 236y x x ππ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 所以将sin y x =图象上各点的横坐标缩短为原来的12，纵坐标不变，可得sin 2y x =的图象，再将sin 2y x =的图象向右平移6π个单位，即可得到sin 23y x π⎛⎫=- ⎪⎝⎭的图象. 故选：D.2．D解析：D 【分析】利用函数()sin +y A x ωϕ=的图象变换规律对各个选项进行检验即可.【详解】A. 1C 上各点横坐标缩短到原来的12倍，得到2sin 2y x =，再向左平移6π个单位长度，得到2sin 2+=2sin 2+63y x x ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，正确； B. 1C 上各点的横坐标缩短到原来的12倍，得到2sin 2y x =，再向右平移56π个单位长度，得到5552sin 2=2sin 2=2sin 222sin 26333y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=---+=+⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，正确； C. 1C 向左平移3π个单位长度，得到2sin +3y x π⎛⎫= ⎪⎝⎭，再把各点横坐标缩短到原来的12倍，得到2sin 2+3y x π⎛⎫= ⎪⎝⎭，正确； D. 1C 向左平移6π个单位长度，得到2sin +6y x π⎛⎫= ⎪⎝⎭，再把各点横坐标缩短到原来的12倍，得到2sin 2+6y x π⎛⎫= ⎪⎝⎭，错误. 故选：D3．B解析：B 【分析】根据函数的图象，求得函数的最小正周期，结合三角函数周期的公式，即可求解. 【详解】由题意，函数()sin()(0)f x x ωϕω=+>的一段图象， 可得2114T=-=，所以4T =，又由24w π=，解得2w π=. 故选：B.4．A解析：A 【分析】根据三角恒等变换公式化简()f x ，结合x 的范围，可得选项. 【详解】因为()()2sin ,0,2f x x x x π=+∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭，所以()()222sin sin cos +3cos f x x xx x x x +==222cos +12cos 2+22sin 2+26x x x x x π⎛⎫=+=+=+ ⎪⎝⎭，因为0,2x π⎡⎤∈⎢⎥⎣⎦，所以72+,666x πππ∈⎡⎤⎢⎥⎣⎦，所以由2+662x πππ≤≤，解得06x π≤≤， 所以()f x 的单调递增区间是06,π⎡⎤⎢⎥⎣⎦，故选：A.5．C解析：C 【分析】根据三角函数的定义，列出方程，即可求解. 【详解】由题意，角θ终边经过点)P a ，可得OP =，又由6πθ=-，根据三角函数的定义，可得cos()6π-=且0a <，解得a =. 故选：C.6．B解析：B 【分析】由两角和的余弦公式化简计算． 【详解】原式＝1cos(7515)cos 602︒-︒=︒=． 故选：B ．7．D解析：D 【分析】根据三角函数的图象变换规律可得解析式． 【详解】函数sin y x =的图象上所有的点向左平行移动6π个单位长度，得sin 6y x π⎛⎫=+ ⎪⎝⎭，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），可得sin 26y x π⎛⎫=+ ⎪⎝⎭. 故选：D ．8．D解析：D 【分析】利用三角函数的最值，取自变量1x 、2x 的特值，然后判断选项即可. 【详解】因为函数()sin 2g x x =的周期为π，由题意可得：()()sin 2x f x ϕ=-⎡⎤⎣⎦， 若()()122f x g x -=，两个函数的最大值与最小值的差等于2，有12min3x x π-=，所以不妨取24x π=，则1712x π=，即()()sin 2x f x ϕ=-⎡⎤⎣⎦在1712x π=取得最小值， 所以77121s 12in 2f ϕππ⎛⎫=-=- ⎪⎡⎤⎛⎫⎪⎢⎝⎥⎭⎣⎦⎭⎝，此时5+,6k k Z πϕπ=∈，又02πϕ<<，所以此时不符合题意，取24x π=，则112x π=-，即()()sin 2x f x ϕ=-⎡⎤⎣⎦在112x π=-取得最小值， 所以12sin 21ϕπ⎡⎤⎛⎫-=- ⎪⎢⎥⎝⎭⎣⎦-，此时,6k k Z πϕπ=-∈，当0k =时，6π=ϕ满足题意，故选：D ． 【点睛】本题考查三角函数的图象的平移，三角函数性质之最值，关键在于取出2x ，得出1x ，再利用正弦函数取得最小值的点，求得ϕ的值，属于中档题．9．A解析：A 【分析】根据图象易得2A =，最小正周期T 2433ππ⎛⎫=-- ⎪⎝⎭，进而求得ω，再由图象过点2,23π⎛⎫⎪⎝⎭求得函数()f x ，然后再根据平移变换得到()g x 即可. 【详解】由图象可知2A =，最小正周期2T 4433πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦， ∴212T πω==，1()2sin 2f x x ϕ⎛⎫=+ ⎪⎝⎭， 又22sin 233f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭， ∴232k ππϕπ+=+，26k πϕπ=+，∵||2ϕπ<，∴6π=ϕ，1()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，将其图象向右平移2π个单位长度得 11()2sin 2sin 226212g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，故选：A 10．B解析：B 【分析】利用诱导公式cos160cos 20=-，再利用两角和的正弦公式即可求解. 【详解】sin 20cos10cos160sin10-()sin 20cos10cos 18020sin10=-- sin 20cos10cos 20sin10=+()sin 2010=+sin30=12=故选：B11．A解析：A 【分析】利用三角函数的周期性和奇偶性得到()cos 2sin 22f x x x π⎛⎫=+=- ⎪⎝⎭，进而求出()f α【详解】 由2ππω=，得2ω=，又()()0f x f x -+=，()()()cos cos 2f x x x ωθθ=+=+为奇函数，()2k k Z πθπ∴=+∈，，又0θπ<<，得2πθ=，()cos 2sin 22f x x x π⎛⎫∴=+=- ⎪⎝⎭，又由tan 2α=，可得()2222sin cos 2tan 4sin 2sin cos tan 15f αααααααα-=-==-=-++故选：A 【点睛】关键点睛：解题关键在于通过三角函数性质得到()cos 2sin 22f x x x π⎛⎫=+=- ⎪⎝⎭，难度属于基础题12．C解析：C 【分析】根据题中条件，由诱导公式，以及二倍角公式，即可求出结果. 【详解】 因为2cos 432θπ⎛⎫=⎪⎝⎭-， 所以241sin cos 2cos 12124299ππθθθ⎛⎫⎛⎫=-=--=⨯-=- ⎪ ⎪⎝⎭⎝⎭. 故选：C二、填空题13．①③【分析】由题可知直线与函数的图象的一条对称轴可求得可化简函数的解析式为计算出的值可判断①的正误；计算可判断②的正误；利用特殊值法可判断③的正误；取利用正弦函数的单调性可判断④的正误；假设命题⑤正解析：①③ 【分析】 由题可知，直线6x π=与函数()f x 的图象的一条对称轴，可求得3ab ，可化简函数()f x 的解析式为()2sin 26f x b x π⎛⎫=+ ⎪⎝⎭.计算出1112f π⎛⎫⎪⎝⎭的值，可判断①的正误；计算710f π⎛⎫⎪⎝⎭、5f π⎛⎫⎪⎝⎭，可判断②的正误；利用特殊值法可判断③的正误；取0b >，利用正弦函数的单调性可判断④的正误；假设命题⑤正确，求出直线的方程，结合函数()f x 的最值可判断⑤的正误.【详解】 由题可知，直线6x π=与函数()f x 的图象的一条对称轴，可得162f b π⎛⎫=+=⎪⎝⎭，整理可得2230a b -+=，即()20a -=，a ∴=.()sin 2cos 22sin 26f x x b x b x π⎛⎫∴=+=+ ⎪⎝⎭.对于命题①，11112sin 2012126f b πππ⎛⎫⎛⎫=⨯+=⎪ ⎪⎝⎭⎝⎭，①正确；对于命题②，7747172sin 22sin 2sin 101063030f b b b ππππππ⎛⎫⎛⎫⎛⎫=⨯+==+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭17172sin 2sin 3030b b ππ=-=，172sin 22sin 55630f b b ππππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭，所以，7105f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，②不正确；对于命题③，2sin 66f b b ππ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭，2sin 262f b b ππ⎛⎫== ⎪⎝⎭，则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭且66f f ππ⎛⎫⎛⎫-≠- ⎪ ⎪⎝⎭⎝⎭，所以，函数()f x 不具有奇偶性，③正确； 对于命题④，当()2,63x k k k ππππ⎡⎤∈++∈⎢⎥⎣⎦Z 时，则()3222262k x k k Z πππππ+≤+≤+∈， 当0b >时，函数()f x 在区间()2,63k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z 上单调递减，④错误； 对于命题⑤，假设经过点(),a b 的直线与函数()f x 的图象不相交，则该直线与x 轴平行，此时该直线的方程为y b =，则2b b >，由于0b ≠，矛盾，⑤错误.故答案为：①③. 【点睛】关键点点睛：本题考查正弦型函数()()sin f x A x =+ωϕ的单调性、奇偶性、三角函数值的计算，解题的关键就是从()6f x f π⎛⎫≤⎪⎝⎭分析得出直线6x π=与函数()f x 的图象的一条对称轴，进而借助辅助角公式化简得出a 、b 的倍数关系.14．【分析】先根据函数平移变换得平移后的解析式为再根据其图象关于原点中心对称得进而计算得【详解】解：根据题意得函数的图像向左平移个单位后得到的函数解析式为：由函数图象关于原点中心对称故即所以故答案为：【解析： 【分析】先根据函数平移变换得平移后的解析式为sin 26y x πϕ⎛⎫=++ ⎪⎝⎭，再根据其图象关于原点中心对称得,6k k Z πϕπ=-+∈，进而计算得sin 2ϕ=.【详解】解：根据题意得函数sin(2)y x ϕ=+的图像向左平移12π个单位后得到的函数解析式为：sin 26y x πϕ⎛⎫=++ ⎪⎝⎭，由函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭图象关于原点中心对称， 故,6k k Z πϕπ+=∈，即,6k k Z πϕπ=-+∈所以sin 2sin 2sin 33k ππϕπ⎛⎫⎛⎫=-+=-= ⎪ ⎪⎝⎭⎝⎭.故答案为： 【点睛】三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母x 而言. 函数()sin ,y A x x R ωϕ=+∈是奇函数()k k Z ϕπ⇔=∈ ； 函数()sin ,y A x x R ωϕ=+∈是偶函数2()k k Z πϕπ⇔=+∈； 函数()cos ,y A x x R ωϕ=+∈是奇函数2()k k Z πϕπ⇔=+∈；函数()cos ,y A x x R ωϕ=+∈是偶函数()k k Z ϕπ⇔=∈.15．【分析】由α是锐角求出的值再由β是锐角得出的值将角转化成利用两角和差的余弦公式化简计算并验证即可【详解】因为α是锐角所以因为β是锐角所以又所以所以当时此时即与矛盾舍去当时符合要求故答案为：【点睛】本【分析】由α是锐角，cos α=求出sin α的值，再由β是锐角，()3sin 5αβ+=得出()cos αβ+的值，将β角转化成()αβα+-，利用两角和差的余弦公式化简计算，并验证即可. 【详解】因为α是锐角，cos α=，所以sin 5α==， 因为β是锐角，所以0αβ<+<π，又()3sin 5αβ+=，所以()4cos 5αβ+==±， 所以()()()cos cos cos cos sin sin βαβααβααβα=+-=+++当()4cos 5αβ+=时， 43cos +55555β=⨯⨯=，此时cos sin βα=，即2παβ+=，与()3sin 5αβ+=矛盾，舍去，当()4cos 5αβ+=-时， 43cos 55β=-=.【点睛】本题主要考查了两角和与差的正余弦公式以及同角三角函数基本关系，属于中档题，熟练掌无公式并应用是解题的关键.16．【分析】利用余弦的倍角公式和三角函数的基本关系式即可求解【详解】由又由故答案为： 解析：35【分析】利用余弦的倍角公式和三角函数的基本关系式，即可求解. 【详解】由tan 2α=，又由22222222cos sin cos 2cos sin cos sin 1tan 1431tan 145ααααααααα--===-++-=-==+. 故答案为：35． 17．【分析】根据三角函数的性质求得的最大值进而可求出结果【详解】因为由可得所以则因为恒成立所以只需故答案为：解析：)+∞【分析】根据三角函数的性质，求得sin cos x x +的最大值，进而可求出结果. 【详解】因为sin cos 4x x x π⎛⎫+=+ ⎪⎝⎭，由0,2x π⎛⎫∈ ⎪⎝⎭可得3,444x πππ⎛⎫+∈ ⎪⎝⎭，所以sin 42x π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦，则(sin cos 4x x x π⎛⎫+=+∈ ⎪⎝⎭，因为0,2x π⎛⎫∀∈ ⎪⎝⎭，sin cos m x x ≥+恒成立，所以只需m ≥故答案为：)+∞.18．【分析】先通过已知求出再化简tanθ＋即得解【详解】由sinθ＋cosθ＝得tanθ＋故答案为：【点睛】关键点睛：解答本题的关键是把sinθ＋cosθ＝两边平方得到 解析：2512-【分析】先通过已知求出12sin cos 25θθ=-，再化简tan θ＋cos sin θθ即得解. 【详解】 由sin θ＋cos θ＝15得1121+2sin cos ,sin cos 2525θθθθ=∴=-. tan θ＋cos sin θθsin cos 125cos sin sin cos 12θθθθθθ=+==-.故答案为：2512- 【点睛】关键点睛：解答本题的关键是把sin θ＋cos θ＝15两边平方得到12sin cos 25θθ=-. 19．【分析】利用对称关系得代入即可求解值再结合辅助角公式化简可求最值【详解】由对称轴关系得令得求得从而当时取到最大值故答案为：解析：【分析】利用对称关系，得()03f f π⎛⎫=⎪⎝⎭，代入即可求解a 值，再结合辅助角公式化简可求()f x 最值【详解】由对称轴关系得66f x f x ππ⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭，令6x π=得()03f f π⎛⎫= ⎪⎝⎭，求得a =从而()3sin 2226f x x x x π⎛⎫=+=+ ⎪⎝⎭，当22,62x k k Z πππ+=+∈时，()f x 取到最大值故答案为：20．【分析】联立方程组求得的值结合余弦的倍角公式即可求解【详解】由题意知：联立方程组求得所以故答案为： 解析：725【分析】联立方程组，求得sin ,cos αα的值，结合余弦的倍角公式，即可求解. 【详解】由题意知：7sin cos 5αα+=-，22sin cos 5αα-=-，联立方程组，求得34sin ,cos 55αα=-=-，所以2247cos 22cos 12()1525αα=-=⨯--=. 故答案为：725. 三、解答题21．（1）π；（2）当(),12x f x π=-取得最大值为22+-；当4x π=时，()f x 取得最小值为12. 【分析】（1）由两角差的正弦公式、二倍角公式化函数为一个角的一个三角函数形式（一次的），然后由正弦函数性质求得最小正周期； （2）求出23x π-的范围，利用正弦函数性质可得最值．【详解】 （1）根据题意得：()2sin cos 2sin cos cos sin cos333f x x x x x x πππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭2sin cos x x x=1cos 211sin 2sin 22sin 2222232x x x x x π+⎛⎫==-=--⎪⎝⎭ 所以最小正周期22T ππ== （2）因为,34x ππ⎡⎤∈-⎢⎥⎣⎦ 所以2,36x πππ⎡⎤-∈-⎢⎥⎣⎦当232x ππ-=-时，即12x π=-()min f x = 当236x ππ-=时，即4x π=()min 11222f x =-=所以当(),12x f x π=-取得最大值为22+-当4x π=时，()f x 取得最小值为12． 【点睛】方法点睛：本题考查两角差的正弦公式，二倍角公式，考查正弦函数的性质．此类问题的解题方法是：利用二倍角公式降幂，利用诱导公式、两角和与差的正弦（余弦）公式展开与合并，最终把函数化为()sin()f x A x m ωϕ=++形式，然后结合正弦函数性质求解． 22．（1）π；（2）10,2⎡⎤⎢⎥⎣⎦.【分析】（1）利用辅助角公式化简1()sin 226f x x π⎛⎫=+ ⎪⎝⎭，再利用周期公式即可求解； （2）由50,12x π⎡⎤∈⎢⎥⎣⎦，求出26x π+的范围，再利用正弦函数的性质即可求解. 【详解】（1）因为1111()2cos 2sin 2cos 2sin 24422226f x x x x x x π⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭所以()f x 的最小正周期为22T ππ==， （2）因为5012x π≤≤， 所以5026x π≤≤，所以266x πππ≤+≤所以0sin 216x π⎛⎫≤+≤ ⎪⎝⎭， 所以110sin 2262x π⎛⎫≤+≤ ⎪⎝⎭，所以()f x 在区间50,12π⎡⎤⎢⎥⎣⎦上的值域为10,2⎡⎤⎢⎥⎣⎦. 23．（1）()2sin 33f x x π⎛⎫=- ⎪⎝⎭；（2）13m ≥.【分析】（1）由ϕ的终边上的点可求出ϕ，再由题可得23T π=，即可求出ω，得出解析式；（2）根据0,6x π⎡⎤∈⎢⎥⎣⎦可得()1f x ≤≤，不等式化为()212m f x ≥-+，求出()212f x -+的最大值即可.【详解】（1）角ϕ的终边经过点(1,P ，∴tan ϕ= 又02πϕ-<<，∴3πϕ=-.∵当()()124f x f x -=时，12x x -的最小值为3π， ∴23T π=，即223ππω=，∴3ω=， ∴()2sin 33f x x π⎛⎫=- ⎪⎝⎭. （2）当0,6x π⎡⎤∈⎢⎥⎣⎦时，3,336x πππ⎡⎤-∈-⎢⎥⎣⎦，∴()1f x ≤≤，于是()20f x +>，于是()()2mf x m f x +≥即为()()()2122f x m f x f x ≥=-++，由()1f x ≤≤，得()212f x -+的最大值为13.∴实数m 的取值范围是13m ≥. 【点睛】本题考查正弦型函数的性质，解题的关键是由当()()124f x f x -=时，12x x -的最小值为3π得出23T π=，以便求出解析式，第二问得出()1f x ≤≤，将不等式化为()212m f x ≥-+.24．（1）[,],36k k k Z ππππ-++∈；（2）若选择①，2m ≤． 若选择②，1m ≤-．【分析】(1)先结合二倍角公式及辅助角公式对已知函数进行化简，然后结合正弦函数的单调性可求; (2）若选择①，由()f x m ≥有解，即max ()m f x ≤，结合正弦函数的性质可求; 若选择②，由()f x m ≥恒成立，即min ()m f x ≤，结合正弦函数的性质可求. 【详解】（1）因为()()2cos cos sin f x x x x x =+-22cos s n cos i x x x x =+-2cos2x x =+2sin(2).6x π=+令222,262k x k k Z πππππ-+≤+≤+∈，解得36k x k k Z ππ-+π≤≤+π,∈. 所以函数()f x 的单调递增区间,,.36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦（2）若选择①，由题意可知，不等式()f x m ≥有解，即max ()m f x ≤，因为0,2x π⎡⎤∈⎢⎥⎣⎦，所以72666x πππ≤+≤， 故当262x ππ+=，即6x π=时，()f x 取得最大值，且最大值为()26f π=，所以2m ≤.若选择②，由()f x m ≥恒成立，即min ()m f x ≤, 因为0,2x π⎡⎤∈⎢⎥⎣⎦，所以72666x πππ≤+≤, 故当7266x ππ+=，即2x π=时,()f x 取得最小值，且最小值为()12f π=-，所以1m ≤- 【点睛】关键点点睛：考查了二倍角公式辅助角公式在三角函数化简中的应用，还考查了正弦函数性质的综合应用，其中，考查了存在性命题与全称命题的理解，理解含量词命题转化成适当的不等式是解题关键，属于中档试题. 25．（1）4，16；（2）5. 【分析】（1）设扇形的半径为r ，弧长为l ，根据面积为16，可得32l r=，列出周长表达式，利用基本不等式即可求得答案；（2）利用基本不等式，即可求得所求乘积的最大值. 【详解】（1）设扇形的半径为r ，弧长为l ， 所以面积1162S l r =⋅=，即32l r=，且08r <<，则周长322216c l r r r =+=+≥=，当且仅当322r r =即4r =时等号成立，所以当半径4r =时，周长有最小值16. （2）由题意得(10)0x x -≥，解得010x ≤≤，1052x x+-≤=，当且仅当(10)x x =-，即5x =时等号成立，5. 26．（1）42,2()33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦；（2）56π. 【分析】 （1）令322262πππk πx k π+≤+≤+，()k Z ∈，解不等式即可求解；（2）先求出并化简()2sin 23g x x π⎛⎫=-+ ⎪⎝⎭()g x 的值域可得出sin 23π⎡⎤⎛⎫-∈⎢⎥ ⎪⎝⎭⎣⎦x ，结合正弦函数的图象可知42233m πππ≤-≤，即可求出m 的最大值. 【详解】 （1）令322262πππk πx k π+≤+≤+，k Z ∈. 所以42233ππk πx k π+≤≤+，()k Z ∈. 所以函数()f x 的单调递减区间42,2()33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.（2）()()4sin sin 66g x f x f x x x ππ⎛⎫⎛⎫=-=+ ⎪ ⎪⎝⎭⎝⎭14cos sin 2x x x ⎫=+⎪⎝⎭22cos sin x x x =+cos2)sin 2x x =-+2sin 23x π⎛⎫=-+ ⎪⎝⎭因为0x m ≤≤， 所以22333x m πππ-≤-≤-.因为()g x 的取值范围为0,2⎡⎣，所以sin 23x π⎛⎫- ⎪⎝⎭的取值范围为2⎡⎤-⎢⎥⎣⎦所以42233m πππ≤-≤. 解得：55126m ππ≤≤. 所以m 的最大值为56π.【点睛】关键点点睛：本题的关键点是要熟记正弦函数的图象，灵活运用三角恒等变换将()g x 化为一名一角，能结合正弦函数的图象得出42233m πππ≤-≤.。

天津南开中学2018年高三数学文测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知是定义在上且以3为周期的奇函数，当时，，则函数在区间上的零点个数是 ( )A．3 B．5 C．7D．9参考答案：D略2. 设满足约束条件，则的取值范围是（）A． B． C． D．参考答案：D3. 若抛物线上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为（）A． B． C．1 D．2参考答案：D略4. 下列说法正确的是( )(A) 命题“使得”的否定是：“”(B) “”是“”的必要不充分条件(C) 命题p：“ ”，则p是真命题(D) “”是“在上为增函数”的充要条件参考答案：D略5. 已知函数的图像向左平移个单位长度，横坐标伸长为原来的2倍得函数的图像，则下列区间为的单调递增区间的是A．B．C．D．参考答案：A6. 椭圆两个焦点分别是F1，F2，点P是椭圆上任意一点，则的取值范围是（）A．[﹣1，1] B．[﹣1，0] C．[0，1] D．[﹣1，2]参考答案：C【考点】椭圆的简单性质．【专题】转化思想；向量法；圆锥曲线的定义、性质与方程．【分析】设P（x，y），，，则=x2+y2﹣i=即可．【解答】解：由椭圆方程得F1（﹣1，0）F2（1，0），设P（x，y），∴，，则=x2+y2﹣1=∈[0，1]故选：C【点评】本题考查了椭圆与向量，转化思想是关键，属于中档题．7.从0，1，2，3，4，5，6，7，8，9十个数字中，选出一个偶数和三个奇数，组成一个没有重复数字的四位数，这样的四位数共有（）.A.1440个B.1480个C.1140个D.1200个参考答案：答案：C8. （5分）如图在等腰直角△ABC中，点O是斜边BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若，则mn的最大值为（）A． B． 1 C． 2 D． 3参考答案：B【考点】：向量在几何中的应用；基本不等式在最值问题中的应用．【专题】：计算题．【分析】：利用三角形的直角建立坐标系，求出各个点的坐标，有条件求出M和N坐标，则由截距式直线方程求出MN的直线方程，根据点O（1，1）在直线上，求出m和n的关系式，利用基本不等式求出mn的最大值，注意成立时条件是否成立．解：以AC、AB为x、y轴建立直角坐标系，设等腰直角△ABC的腰长为2，则O点坐标为（1，1），B（0，2）、C（2，0），∵，∴，∴、，∴直线MN的方程为，∵直线MN过点O（1，1），∴=1，即m+n=2∵（m＞0，n＞0），∴，∴当且仅当m=n=1时取等号，且mn的最大值为1．故选B．【点评】：本题的考查了利用向量的坐标运算求最值问题，需要根据图形的特征建立坐标系，转化为几何问题，根据条件求出两数的和，再由基本不等式求出它们的积的最大值，注意验证三个条件：一正二定三相等，考查了转化思想．9. 已知函数满足，且是偶函数，当时，，若在区间内，函数有4个零点，则实数的取值范围是(A) (B) (C) (D)参考答案：C由得，，所以函数为周期为2的周期函数，又因为函数为偶函数，有，所以有，所以函数关于对称，令，得函数，令函数，做出函数和函数的图象，如图：当直线必须过点时有4个交点，此时直线的斜率为，要使函数有四个零点，则直线的斜率，选C.10. 平面向量与的夹角为60°，=（2，0），||=1，则|+2|=（）A．B．C．12 D．参考答案：【考点】平面向量数量积的运算．【分析】原式利用二次根式性质化简，再利用完全平方公式展开，利用平面向量的数量积运算法则计算即可得到结果．【解答】解：∵平面向量与的夹角为60°，=（2，0），||=1，∴|+2|=====2，故选：B．二、填空题:本大题共7小题,每小题4分,共28分11. 高三毕业时，甲，乙，丙等五位同学站成一排合影留念，已知甲，乙相邻，则甲丙相邻的概率为参考答案：12. 执行如图所示的程序框图,若输入m=5则输出k的值为参考答案：本题考查程序框图.13. 已知p：﹣2≤x≤1，q：（x﹣a）（x﹣a﹣4）＞0，若p是q成立的充分不必要条件，则实数a的取值范围是．参考答案：（﹣∞，﹣6）∪（1，+∞）【考点】必要条件、充分条件与充要条件的判断．【分析】先求出q下的不等式，得到q：x＜a，或x＞a+4，而若p是q成立的充分不必要条件，即由p能得到q，而由q得不到p，所以a＞1，或a+4＜﹣2，这样便得到了a的取值范围．【解答】解：q：x＜a，或x＞a+4；∴若p是q成立的充分不必要条件，则：a＞1，或a+4＜﹣2；∴a＞1，或a＜﹣6；∴实数a的取值范围是（﹣∞，﹣6）∪（1，+∞）．故答案为：（﹣∞，﹣6）∪（1，+∞）．14. 已知函数y=a x+b（b＞0）的图象经过点P（1，3），如图所示，则+的最小值为．参考答案：【考点】基本不等式．【专题】不等式的解法及应用．【分析】函数y=a x+b（b＞0）的图象经过点P（1，3），可得3=a+b，a＞1，b＞0．即（a ﹣1）+b=2．再利用“乘1法”与基本不等式的性质即可得出．【解答】解：∵函数y=a x+b（b＞0）的图象经过点P（1，3），∴3=a+b，a＞1，b＞0．∴（a﹣1）+b=2．∴+===，当且仅当a﹣1=2b=时取等号．故答案为：．【点评】本题考查了函数的图象与性质、“乘1法”与基本不等式的性质，属于基础题．15. 如果函数在区间上有且仅有一条平行于轴的对称轴，则的取值范围是．参考答案：略16. 函数f（x）=的定义域为．参考答案：{x|x}【考点】函数的定义域及其求法．【分析】利用被开方数非负，得到不等式，求解即可得到函数的定义域．【解答】解：要使函数有意义，则：1﹣2x≥0，解得：x．函数的定义域为：{x|x}．故答案为：：{x|x}．17. （坐标系与参数方程选做题）如图，为圆O的直径，为圆O上一点，和过的切线互相垂直，垂足为，过的切线交过的切线于，交圆O于，若，，则= .参考答案：三、解答题：本大题共5小题，共72分。

2018年天津市南开中学高三模拟考试数学（文）第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 复数等于（）A. B. C. D.【答案】C【解析】【分析】化简分式，分子、分母分别平方，再按照复数的除法运算法则化简可得结果.【详解】，故选：C【点睛】本题主要考查了复数代数形式的运算，是基础题．2. 命题：“”的否定形式是（）A. B.C. D.【答案】C【解析】【分析】含有全称量词的命题就称为全称命题，含有存在量词的命题称为特称命题．一般形式为：全称命题：，；特称命题，．【详解】命题“”的否定形式是特称命题；“”，故选C.【点睛】通常像“所有”、“任意”、“每一个”等表示全体的量词在逻辑中称为全称量词，通常用符号“”表示“对任意”；“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为存在量词，通常用符号“”表示“存在”．3. 执行如图所示的程序框图，若输入的值为1，则输出的值为（）A. 1B. 2C. 3D. 4【答案】B【解析】试题分析：程序执行的数据变化如下：成立，输出考点：程序框图4. 已知，则下列关系正确的是（）A. B. C. D.【答案】A【解析】【分析】利用对数的运算法则，化简，推导出的范围，然后推出与的范围并比较大小，从而可得答案．【详解】∵，，，因为，即，∴，故选A.【点睛】本题考查对数函数的单调性的应用，对数值大小的比较，着重考查对数函数的单调性，属于基础题.5. 在长为的线段上任取一点.现作一矩形，邻边长分别等于线段的长，则该矩形面积大于的概率为（）A. B. C. D.【答案】C【解析】试题分析：设AC=x，则BC=12-x（0＜x＜12）矩形的面积S=x（12-x）＞20∴x2-12x+20＜0∴2＜x＜10由几何概率的求解公式可得，矩形面积大于20cm2的概率考点：几何概型视频6. 已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（）A. B. C. D.【答案】D【解析】试题分析：双曲线的一条渐近线是，则①，抛物线的准线是，因此，即②，由①②联立解得，所以双曲线方程为．故选D．考点：双曲线的标准方程．视频7. 设，若函数在区间上有三个零点，则实数的取值范围是（）A. B. C. D.【答案】D 【解析】试题分析：当时,,设直线与的切点为,因,故,则代入可得,所以，解之得,结合图象可知,当,即,所以当,即当时,函数与直线有三个交点,故应选D.考点：函数的图象和零点．【易错点晴】本题考查的是函数的图象与零点的综合运用问题.解答时可依据题设条件将问题进行合理有效的转化与化归,画出函数的图象,结合图象不难看出, 函数在区间上有三个零点等价于函数与直线有三个交点.然后以导数为工具,求出切点的坐标,,数形结合求出参数的取值范围是.8. 已知函数，将图象向右平移个单位长度得到函数的图象，若对任意，都有成立，则的值为（ ）A.B. 1C.D. 2【答案】D【解析】【分析】利用辅助角公式化简的解析式，再利用正弦型函数的图象变换规律，正弦函数的图象的对称性，求得的值．【详解】，（其中，），将图象向右平移个单位长度得到函数的图象，得到，∴，，解得，故选D.【点睛】本题主要考查辅助角公式，的图象变换规律，正弦函数的图象的对称性，属于中档题．第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9. 已知集合，则__________．【答案】.【解析】【分析】由，，根据集合确定出，根据定义求出与的交集即可．【详解】∵集合中，，，∴，3，9，即，∴，故答案为.【点睛】本题主要考查了交集及其运算，熟练掌握集合的定义及交集的定义是解本题的关键.10. 若变量满足约束条件，则的取值范围是__________．【答案】.【解析】【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，通过平移求出的取值范围.【详解】作出不等式组对应的平面区域如图所示阴影部分；由得，即直线的截距最大，也最大；平移直线，可得直线经过点时，截距最大，此时最大，即；经过点A时，截距最小，由，得，即，此时最小，为；即的取值范围是，故答案为．【点睛】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.11. 某几何体的三视图如图，其正视图中的曲线部分为半个圆弧，则该几何体的体积为__________．【答案】.【解析】【分析】由三视图知该几何体是左边为横放的直三棱柱，右边是横放的半圆柱，结合图中数据求出它的体积．【详解】由三视图知，该几何体是由左右两部分组成的，左边的是横放的直三棱柱，高为3，底面是边长为2的等腰直角三角形，右边是一个半圆柱，高为3，底面半径为1；∴该几何体的体积为（）．故答案为.【点睛】本题考查了利用三视图求几何体的体积问题，由三视图正确恢复原几何体是解题的关键，是基础题．12. 设函数是定义在上的以5为周期的奇函数，若，则的取值范围是__________．【答案】.【解析】【分析】根据函数是以5为周期的奇函数，得，结合函数为奇函数，得由此结合建立关于的不等式，解之可得的取值范围．【详解】∵函数以5为周期，∴，又∵，函数是奇函数，∴，因此，解之得或，故答案为．【点睛】本题主要考查了函数的奇偶性和周期性，以及不等式的解法等知识，熟练运用函数的性质是关键，属于基础题．13. 如图，已知正六边形的边长为，点为的中点，则__________．【答案】.【解析】【分析】根据题意，建立直角坐标系，进而可得、、、、、的坐标，由中点坐标公式可得的坐标，由向量的坐标公式可得向量，的坐标，进而由数量积的坐标计算公式计算可得答案【详解】根据题意，如图建立直角坐标系，则，则，，，，，，又由点为的中点，则，则有，，则，故答案为.【点睛】本题考查向量数量积的坐标计算，关键是建立直角坐标系，求出点的坐标，属于基础题. 14. 若二次函数的值域为，则的最小值为__________．【答案】.【解析】【分析】由题意可知，，，从而求出，将所求式子中的4代换成，利用裂项法进行整理，进而利用均值不等式求出最小值．【详解】∵二次函数（）的值域为，∴，，∴，，，∴，当且仅当时取等号，故答案为．【点睛】本题主要考查了基本不等式.基本不等式求最值应注意的问题(1)使用基本不等式求最值，其失误的真正原因是对其前提“一正、二定、三相等”的忽视．要利用基本不等式求最值，这三个条件缺一不可．(2)在运用基本不等式时，要特别注意“拆”“拼”“凑”等技巧，使其满足基本不等式中“正”“定”“等”的条件．三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15. 在中，角的对边分别为.已知的面积为，周长为，且.（1）求及的值；（2）求的值.【答案】（1）；.（2）.【解析】【分析】（1）由已知及三角形面积公式可求，进而可求，利用余弦定理即可得解的值；（2）利用同角三角函数基本关系式可求，利用二倍角公式可求，的值，进而利用两角差的余弦函数公式即可得解．【详解】（1）∴∴∴..（2）由（1）得，，∴∴，【点睛】本题主要考查了三角形面积公式，余弦定理，同角三角函数基本关系式，二倍角公式，两角差的余弦函数公式在解三角形中的应用，考查了计算能力和转化思想，属于基础题.16. 某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数)分成六段：后得到如图的频率分布直方图.（1）求图中实数的值.（2）若该校高一年级共有学生640人，试估计该校髙一年级期中考试数学成绩不低于60分的人数；（3）若从数学成绩在与两个分数段内的学生中随机选取两名学生，求这两名学生的数学成绩之差的绝对值不大于10的概率.【答案】（1）.（2）544人.（3）.【解析】试题分析：（1）根据图中所有小矩形的面积之和等于1建立关于a的等式，解之即可求出所求；（2）根据频率分布直方图，成绩不低于60分的频率，然后根据频数=频率×总数可求出所求；（3）成绩在[40，50）分数段内的人数，以及成绩在[90，100]分数段内的人数，列出所有的基本事件，以及两名学生的数学成绩之差的绝对值不大于10的基本事件，最后利用古典概型的概率公式解之即可．试题解析：(1)由于图中所有小矩形的面积之和等于1，所以10×(0.005+0.01+0.02+a+0.025+0.01)=1.解得a=0.03(2)根据频率分布直方图,成绩不低于60分的频率为1−10×(0.005+0.01)=0.85由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为640×0.85=544人(3)成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B，成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,则所有的基本事件有：(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.…(9分)如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内，那么这两名学生的数学成绩之差的绝对值一定大于10.记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有：(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.所以所求概率为P(M)=.点睛：古典概型中基本事件数的探求方法(1)列举法.(2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法.(3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法：适用于限制条件较多且元素数目较多的题目.17. 如图，在四棱锥中，底面是菱形，，平面，，点分别为和中点.（1）求证：直线平面；（2）求证：面；（3）求与平面所成角的正弦值.【答案】（1）见解析.（2）见解析.（3）.【解析】【分析】（1）利用中点和平行四边形性质得出，利用直线平面的平行问题求解证明即可；（2）根据几何图形得出，直线平面的垂直得出，再运用判定定理求解证明即可；（3）运用直线平面所成角的定义得出夹角，转化为直角三角形中求解即可．【详解】（1）证明：作交于．∵点为中点，∴，∵，∴，∴为平行四边形，∴，∵平面，平面，∴直线平面．（2）∵底面是菱形，∴，∵平面，平面，∴∵，∴平面；（3）连接，，∵点，分别为和中点，∴，∵平面，∴平面，根据直线与平面所成角的定义可得：为与平面所成角或补角，中，，，，，∴，∴与平面所成角的正弦值为．【点睛】本题考查了空间直线平面的平行，垂直，空间夹角问题，关键是熟练掌握定理，定义，把空间问题转化为平面问题求解，直线，直线，平面之间的转化问题．18. 设数列的首项，前项和满足关系式.（1）求证：数列是等比数列；（2）设数列的公比为，作数列，使，求数列的通项公式；（3）数列满足条件（2），求和：.【答案】（1）见解析.（2）.（3）.【解析】【分析】（1）利用，求得数列的递推式，整理得，进而可推断出时，数列成等比数列，然后分别求得和，验证亦符合，进而可推断出是一个首项为1，公比为的等比数列；（2）把的解析式代入，进而可知，判断出是一个首项为1，公差为1的等差数列．进而根据等差数列的通项公式求得答案；（3）由是等差数列．进而可推断出和也是首项分别为1和2，公差均为2的等差数列，进而用分组法可求得结果．【详解】（1）因为①②，得，所以.又由，得.又因为，所以.所以是一个首项为1，公比为的等比数列.（2）由，得.所以是一个首项为1，公差为1的等差数列.于是.（3）由，可知和是首项分别为1和2，公差均为2的等差数列，于是，所以.【点睛】本题主要考查了等比关系的确定，考查了学生综合分析问题的能力，考查了利用分组求和法求数列的和.19. 已知函数.（1）求函数的单调区间；（2）若函数存在极小值点，且，求实数的取值范围.【答案】（1）当时，函数的单调递减区间为；当时，函数的单调递增区间为，单调递减区间为.（2）.【解析】试题分析：（Ⅰ）求出，分两种情况分别令得增区间，得减区间；（Ⅱ）函数存在极小值点，所以在上存在两个零点，，设为函数的极小值点，由，得，所以可得结果.试题解析：（Ⅰ）因为函数，所以其定义域为.所以.当时，，函数在区间上单调递减.当时，.当时，，函数在区间上单调递减.当时，，函数在区间上单调递增.综上可知，当时，函数的单调递减区间为；当时，函数的单调递增区间为，单调递减区间为.（Ⅱ）因为，所以（）.因为函数存在极小值点，所以在上存在两个零点，，且.即方程的两个根为，，且，所以，解得.则.当或时，，当时，，所以函数的单调递减区间为与，单调递增区间为.所以为函数的极小值点.由，得.由于等价于.由，得，所以.因为，所以有，即.因为，所以.解得.所以实数的取值范围为.20. 已知椭圆的两个焦点分别为和，过点的直线与椭圆相交与两点，且.（1）求椭圆的离心率；（2）求直线的斜率；（3）设点与点关于坐标原点对称，直线上有一点在的外接圆上，且，求椭圆方程.【答案】（1）.（2）.（3）.【解析】【分析】（1）由，，得，得到的关系式，由此能求出离心率；（2）将椭圆的方程为写为，设直线的方程为，设，，联立方程组，由此利用根的判别式、韦达定理，结合已知条件能求出直线的斜率；（3）求出，，取，得，推导出外接圆的方程，与直线的方程联立解出，得，再由，解得，由此能求出椭圆方程．【详解】（1）由且，得，从而整理，得，故离心率.（2）由（1）得，所以椭圆的方程可写为设直线的方程为，即.由已知设，则它们的坐标满足方程组消去整理，得.依题意，，得.而①②由题设知，点为线段的中点，所以③联立①③解得将代入②中，解得.（3）由（2）可知.不妨取，得，由已知得.线段的垂直平分线的方程为，直线与轴的交点是外接圆的圆心，因此外接圆的方程为.直线的方程为，于是点的坐标满足方程组，由，解得由解得故椭圆方程为.【点睛】本题考查椭圆的离心率、直线的斜率、椭圆方程的求法，考查椭圆、直线方程、圆、根的判别式、韦达定理、两点间距离公式等基础知识，考查函数与方程思想，考查运算求解能力，是中档题.。

高一下单元综合测试 数学 第四章 三角函数（满分150，时间120分钟）一、选择题（每小题5分，共60分）1.把－411π表示成θ+2k π（k ∈Z ）的形式，使|θ|最小的θ值是 A.－43π B.－4π C. 4πD.4π3 答案：A 2.函数y =cos （x －3π2）·sin （x －6π5）是 A.周期为π的非奇非偶函数B.周期为2π的非奇非偶函数C.周期为π的奇函数D.周期为π的偶函数答案：D3.在［0，2π］上满足sin x ≥21的x 的取值范围是 A.［0，6π］B.［6π，6π5］ C.［6π，3π2］D.［6π5，π］ 答案：B4.若α、β∈（0，2π）且tan α=34，tan β=71，则α－β的值是A.3πB.4πC.6πD.8π答案：B5.设a =sin13°+cos13°，b =sin17°+cos17°，c =26，则a 、b 、c 的大小关系是 A.a <c<bB.a <b <cC.b <c<aD.b <a <c答案：A6.要得到函数y =cos （2x －4π）的图象，只需将y =sin2x 的图象 A.向左平移8π个单位 B.向右平移8π个单位C.向左平移4π个单位D.向右平移4π个单位答案：A 7.函数y =x2sin 1－tan x 的最小正周期是 A.2πB.πC.23π D.2π答案：A8.函数y =|sin x |－2sin x 的值域是A.［－3，－1］B.［－1，3］C.［0，3］D.［－3，0］ 答案：B9.在△ABC 中，cos2A >cos2B 是B >A 的 A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 答案：C10.函数f （x ）在［－1，1］上满足f （－x ）=－f （x ），且是减函数，α、β是锐角三角形的两个内角，且α≠β，则下列不等式中正确的是A.f （cos α）>f （cos β）B.f （sin α）>f （sin β）C.f （cos α）<f （sin β）D.f （sin α）<f （cos β） 答案：D11.已知函数y =f （x ）的图象，如图1所示，则函数y =f （2π－x ）sin x 在［0，π］的大致图象为yA2B yC图2答案：A 12.对于函数f （x ）=⎩⎨⎧>≥,sin cos ,cos ,cos sin ,sin 时当时当x x x x x x 给出下列四个命题：①该函数的值域为［－1，1］； ②当且仅当x =2k π+2π（k ∈Z ）时，该函数取得最大值1； ③该函数是以π为最小正周期的周期函数； ④当且仅当2k π+π<x <2k π+23π（k ∈Z ）时，f （x ）<0.上述命题中正确的是 A.① B.② C.③ D.④ 答案：D二、填空题（每小题4分，共16分）13.若f （x ）是奇函数，且当x >0时，f （x ）=x 2+sin x ，则当x ∈R 时，f （x ）=__________. 答案：|x |x +sin x 14.函数y =sin42πx +sin 42πx-的单调递增区间为______________.答案：［－π+2k π，2k π］（k ∈Z ） 15.已知cos （α+β）=31，cos （α－β）=21，则log 5（tan α·tan β）=____________. 答案：－116.在△ABC 中，如果4sin A +2cos B =1，2sin B +4cos A =33，则C 的大小是____________. 答案：6π或65π三、解答题（本大题共6小题，满分74分）17.（12分）求函数f （x ）=sin x +sin2x －cos x ，x ∈［0，π］的最大值和最小值. 解：设sin x －cos x =t ，则t =2sin （x －4π）∈［－1，2］. sin2x =－(sin x －cos x )2+1=1－t 2， 则原函数可化为y =－t 2+t +1=－(t －21)2+45，t ∈［－1，2］. ∴当t =21时，y max =45； 当t =－1时，y min =－1.18.（12分）若sin θ、sin2x 、cos θ成等差数列，sin θ、sin x 、cos θ成等比数列，求cos2x 的值.解：依题意，得⎪⎩⎪⎨⎧=+=②①.cos sin sin ,cos sin 2sin 22θθθθx x①2－②×2，得4sin 22x －2sin 2x =1.即4cos 22x －cos2x －2=0，∴cos2x =8331±. 又cos2x =1－2sin 2x =1－2sin θcos θ，且sin 2x =sin θcos θ≥0， ∴1－sin2θ∈［0，1］，即cos2x ∈［0，1］，∴cos2x =8331+. 19.（12分）已知函数f （x ）=2sin （x +2θ）cos （x +2θ）+23cos 2（x +2θ）－3. （1）化简f （x ）的解析式；（2）若0≤θ≤π，求θ，使f （x ）为偶函数；（3）在（2）成立的条件下，求满足f （x ）=1，x ∈［－π，π］的x 的集合. 解：（1）f （x ）=sin （2x +θ）+3［2cos 2（x +2θ）－1］ =sin （2x +θ）+3cos （2x +θ） =2cos （2x +θ－6π）［或f （x ）=2sin （2x +θ+3π）］. （2）∵f （x ）为偶函数，∴f （－x ）=f （x ）. 即2cos （－2x +θ－6π）=2cos （2x +θ－6π）观察易见，当θ=6π时，上式成立. （3）由f （x ）=1，得2cos2x =1， ∴cos2x =21. ∵x ∈［－π，π］， ∴x =±65π或x =±6π， ∴所求x 的集合是⎭⎬⎫⎩⎨⎧--65π,6π,6π,65.20.（12分）定义在（－∞，3］上的单调减函数f （x ）满足f （a 2－sin x ）≤f （a +1+cos 2x ）对一切实数x 均成立，求实数a 的取值范围.解：由题意可知⎪⎩⎪⎨⎧++≥-≤-.cos 1sin ,3sin 222x a x a x a 即有⎪⎩⎪⎨⎧+--=+≥--+≤.45)21(sin sin cos 1,sin 32222x x x a a x a 上述不等式组对一切实数x 均成立.当且仅当⎪⎪⎪⎩⎪⎪⎪⎨⎧-≤+≥≤≤≤-⇒⎪⎪⎩⎪⎪⎨⎧≥--≤≤.2101,2101,1,224511222a a a a a a a a 或 ∴－21012-≤≤a . 即所求实数a 的取值范围为［－2101,2-］. 21.（12分）已知tan α、tan β是方程x 2+px +q =0的两个根.求sin 2（α+β）+p sin （α+β）cos （α+β）+q cos 2（α+β）的值.解：由根与系数的关系，得⎩⎨⎧=⋅-=+.tan tan ,tan tan q p βαβα（1）当q =1时，由tan α·tan β=1得tan α=βtan 1=cot β=tan （2π－β）. ∴α=2π－β+k π（k ∈Z ），∴α+β=2π+k π（k ∈Z ）. ∴cos （α+β）=0，sin 2（α+β）=1， ∴原式=1.（2）当q ≠1时，cos （α+β）≠0，∴tan （α+β）=qp--=-+1tan tan 1tan tan βαβα. ∴原式=)(cos )(sin )(cos )cos()tan()(sin 2222βαβαβαβαβαβα+++++++++q p=1)(tan )tan()(tan 22++++++βαβαβαqp =1)1(1)1(22+--+--⋅+--qp q qpp q p =q .综上所述，原式=q .22.（14分）设函数f （x ）=sin 2x +（2a －1）sin x +a 2+41，其中x ∈［2π3,6π5］，31≤a ≤1，求f （x ）的最大值与最小值（一般用a 表示），并写出对应的a 的取值范围及对应的x 值.解：设t =sin x ，因为x ∈［2π3,6π5］，得－1≤t ≤21， 于是y =f （x ）=g （t ）=t 2+（2a －1）t +a 2+41=(t －221a -)2+a .所以y =g （t ）的对称轴方程为t =221a-.因为31≤a ≤1，得－21≤221a -=t ≤61，显然 ［－21，61］［－1，21］，所以y min =g ⎪⎭⎫⎝⎛-221a =a . 此时31≤a ≤1，x =π－arcsin 221a -. 下面求最大值：∵2211+-=－41， （1）当－21≤221a -<－41，即43<a ≤1时， y max =g （21）=a 2+a ，此时t =sin x =21x =6π5.（2）当221a -=－41，即a =43时，y max =g （21）=g （－1）=1621，此时t =sin x =21或t =sin x =－1，即x =6π5或x =2π3.（3）当－41<221a -≤61，即31≤a <43时，y max =g （－1）=a 2－2a +49，此时t =sin x =－1，即x =23π. 综上可知：y min =a ⎪⎭⎫⎝⎛≤≤131a ，对应的x =π－arcsin 221a -；y max =⎪⎪⎪⎩⎪⎪⎪⎨⎧=<≤+-====≤<+).2π3,4331(45)1(),2π3π65,43(1621),π65,143(22x a a x x a x a a a 或。

八年级数学三角形认识与三角形有关的线段知识点+例题+练习题1.关于三角形的概念及其按角的分类:定义：由上的三条线段所组成的图形叫做三角形。

2.三角形的分类：①三角形按内角的大小分为三类：、、。

②三角形按边分为两类：和。

3.关于三角形三条边的关系（判断三条线段能否构成三角形的方法、比较线段的长短）根据公理“两点之间，线段最短”可得：三角形任意两边之和；三角形任意两边之差。

4.与三角形有关的线段．．：三角形的角平分线、中线和高：三角形的角平分线：三角形的一个角的平分线与对边相交形成的线段；三角形的中线：连接三角形的一个顶点与对边中点的线段，三角形任意一条中线将三角形分成相等的两个部分；三角形的高：过三角形的一个顶点做对边的垂线，这条叫做三角形的高。

注意：①三角形的角平分线、中线和高都是；②任意一个三角形都有三条角平分线，三条中线和三条高；③任意一个三角形的三条角平分线、三条中线都在三角形的。

但三角形的高却有不同的位置：锐角三角形的三条高都在三角形的；直角三角形有一条高在三角形的内部，另两条高恰好是它两条直角边；钝角三角形一条高在三角形的内部，另两条高在三角形的。

④一个三角形中，三条中线交于一点，叫；三条角平分线交于一点，叫；三条高所在的直线交于一点，叫. 【例1】三条线段a，b，c分别满足下列条件，其中能构成三角形的是（）A.a+b=4，a+b+c=9B.a：b：c=1：2：3C.a：b：c=2：3：4D.a：b：c=2：2：4【例2】如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）【例3】已知a、b、c为△ABC的三边，化简：|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|=______.【例4】如图，A，B，C分别是线段A1B，B1C，C1A中点，若△ABC的面积是1，则△A1B1C1面积为_______.例4题图第5题图【例5】如图，一个面积为50cm2的正方形与另一个小正方形并排放在一下起，则△ABC面积为. 【例6】如图：(1)在△ABC中，BC边上的高是________；(2)在△AEC中，AE边上的高是________；(3)若AB=CD=2cm，AE=3cm，求△AEC的面积及CE的长.【例7】已知△ABC的面积是60，请完成下列问题：（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积_______△ACD的面积（填“＞”“＜”或“=”）（2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD=DB得：S△ADO=S△BDO，同理：S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=x，S△AEO=y.由题意得：S△ABE =S△ABC=30，S△ADC =S△ABC=30，可列方程组为：，解得_______，通过解这个方程组可得四边形ADOE的面积为_______.（3）如图3，AD：DB=1：3，CE：AE=1：2，请你计算四边形ADOE的面积，并说明理由.一、选择题：1、已知三角形的三边长分别是4、5、x ，则不可能是（ ）A.3B.5C.7D.9 2、下列说法不正确的是（ ）A.三角形的中线在三角形的内部B.三角形的角平分线在三角形的内部C.三角形的高在三角形的内部D.三角形必有一高线在三角形的内部 3、三角形一边上的中线把原三角形分成两个（ ） A.形状相同的三角形 B.面积相等的三角形 C.直角三角形 D.周长相等的三角形4、四根长度分别为3cm 、4cm 、7cm 、10cm 的木条，以其中三根的长为边长钉成一个三角形框架，那么这个框架的周长可能是（ ）A.14cmB.17cmC.20cmD.21cm 5、三条线段a=5，b=3，c 的值为整数，由a 、b 、c 为边可组成三角形（ ） A.1个 B.3个 C.5个 D.无数个 6、图中能表示△ABC 的BC 边上的高的是()7、若△ABC 的边长都是整数，周长为11，且有一边长为4，则这个三角形的最大边长为（ ） A.7 B.6 C.5 D.48、如图，在△ABC 中，已知点D 、E 、F 分别是BC 、AD 、BE 上的中点，且△ABC 的面积为8cm 2，则△BCF 的面积为（ ）A.0.5cm 2B.1cm 2C.2cm 2D.4cm 29、如果一个三角形的三边长分别为1、k 、4.则化简|2k ﹣5|﹣2)6( k 的结果是（ ）A.3k ﹣11B.k+1C.1D.11﹣3k10、如图，在长方形网格中，每个小长方形的长为2，宽为1，A 、B 两点在网格格点上，若点C 也在网格格点上，以A 、B 、C 为顶点的三角形面积为1，则满足条件的点C 个数是（ ）A.5B.6C.7D.8 二、填空题:11、木工师傅在做完门框后，为防止变形常常像图中那样钉上两条斜拉的木板条（即图中AB 、CD 两个木条），这样做根据的数学道理是 .第11题图 第15题图 第16题图 12、已知等腰三角形两条边长6和3，则此这个三角形的周长是_______.13、若三角形的周长是60cm ，且三条边的比为3：4：5，则三边长分别为 . 14、如果将长度为a ﹣2，a+5和a+2的三根线段首尾顺次相接可以得到一个三角形，那么a 的取值范围是__________.15、如图，D ，E ，F 分别是△ABC 的边AB ，BC ，AC 上的中点，连接AE ，BF ，CD 交于点G ，AG:GE=2:1，△ABC 的面积为6，设△BDG 的面积为S 1，△CGF 的面积为S 2，则S 1＋S 2=________.16、如图，已知在长方形ABCD 中，AB=10cm ，BC=8cm ，点E 是CD 中点，动点P 从A 点出发，以每秒2cm 的速度沿A →B →C →E 运动，最终到达点E ，若点P 运动的时间为x 秒，那么当x=_______s 时，△APE 的面积等于32cm.三、作图题:17、如图，在方格纸内将△ABC 水平向右平移4个单位，再向下后平移1得到△A ′B ′C ′. （1）画出平移后的△A ′B ′C ′；（2）画出AB 边上的高线CD （利用三角板画图）；（3）画出△ABC 中AB 边上的中线CE ；（4）图中AC 与A ′C ′的关系是： ； （5）△BCE 的面积为 .（6）若△A ″BC 的面积与△ABC 面积相同，则A ″（A ″在格点上）的位置（除A 点外）共有 个.四、解答题: 18、如图，在△ABC 中，AD 是BC 边上的中线，△ADC 的周长比△ABD 的周长多5cm ，AB 与AC 的和为11cm ，求AC 的长.19、如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 面积是28cm 2，AB=20cm ，AC=8cm ，求DE 的长.20、如图，AD 是△ABC 的中线，BE 是△ABD 的中线. （1）在△BED 中作BD 边上的高.（2）若△ABC 的面积为20，BD=5，则点E 到BC 边的距离为多少？一、选择题：1、下列长度的三条线段能组成三角形的是( )A.1，2，3B.20，15，8C.4，5，9D.5，15，8 2、下列图形中有稳定性的是( )A.正方形B.长方形C.直角三角形D.平行四边形 3、AD 是△ABC 的中线，设△ABD 的面积为S 1，△ACD 的面积为S 2，那么( ) A.S 1＞S 2 B.S 1=S 2 C.S 1＜S 2 D.S 1≠S 24、满足下列条件：①a=2，b=3，c=4；②a=3，b=5，c=2；③a ：b ：c=1：2：3；④a=m+1，b=n+2，c=2m （m ＞2）的三条线段a 、b 、c ，能组成三角形的有( )A.①②B.③④C.①④D.①③ 5、下列说法错误的是( )A.三角形的中线、高、角平分线都是线段B.任意三角形内角和都是180°C.三角形按角可分为锐角三角形、直角三角形和等腰三角形D.直角三角形两锐角互余6、以下是四位同学在钝角三角形ABC 中画BC 边上的高，其中画法正确的是( )7、如图，为估计池塘岸边A 、B 两点的距离，小方在池塘的一侧选取一点O ，测得OA=15米，OB=10米，A 、B 间的距离不可能是( )A.5米B.10米C.15米D.20米第7题图 第9题图8、已知三角形两边长分别为7、11，那么第三边的长可以是( )A.2B.3C.4D.5 9、如图，共有三角形的个数是（ ）A.3B.4C.5D.610、如图，CD ⊥AB ，垂足为D ，AC ⊥BC ，垂足为C.图中线段的长能表示点到直线（或线段）距离的线段有（ ）A.1条B.3条C.5条D.7条二、填空题:11、电工师傅在安好电线杆后，为了防止电线杆倾倒，常常按图所示引两条拉线，这样做的数学道理是_______.12、若一个三角形的两边长分别为2厘米和8厘米，且第三边的长为偶数，则这个三角形的周长为厘米.13、如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线.若CD=3，则△ABD的面积为______.14、一个三角形3条边长分别为xcm、（x+1）cm、（x+2）cm，它的周长不超过39cm，则x的取值范围是.15、如图，△ABC的两条中线AM、BN相交于点O，已知△BOM的面积为2，则四边形MCNO的面积为.16、若三角形三边长为3、2a-1、8，则a的取值范围是 .三、作图题:17、如图，在△ABC中，ÐBAC是钝角，完成下列画图.(1)ÐBAC的平分线AD (2)AC边上的中线BE；(3)AC边上的高BF；四、解答题:18、如果一个三角形的三边长为连续奇数，且周长小于18，求这个三角形的三边长.19、如图, AD为△ABC的中线，BE为△ABD的中线.（1）∠ABE=15°，∠BAD=36°，求∠BED的度数；（2）作出△BED中DE边上的高，垂足为H；（3）若△ABC面积为20,过点C作CF//AD交BA的延长线于点F，求△BCF的面积。

2018年天津市南开中学高三模拟考试数学（理）第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则（）A. B. C. D.【答案】B【解析】分析：分别求出不等式和的解集，求得集合，再求出集合的交集即可.详解：，，则，故选B.点睛：该题考查的是有关集合的运算问题，在解题的过程中，注意正确求解对应的不等式，属于基础题目.2. 若实数满足不等式组，则的最小值为（）A. 2B. 3C.D. 14【答案】A【解析】作出不等式组表示的可行域，则在点处取到最小值，，所以最小值为2，故选A.3. 执行如图所示的程序框图，如果输出的，那么判断框中填入的条件可以是（）A. B. C. D.【答案】C【解析】分析：首先从框图中观察各变量和各语句的作用，再根据流程图，可得到该程序所要解决的问题，逐步执行，求出满足条件的，并确定循环的条件，据此即可得到答案.详解：根据题中所给的框图，执行过程中会出现：，；，；，；观察选项，没有合适的条件，继续执行；根据上边的规律可以得到，再执行三次，得到，从而可以从选项中选出合适，故选C.点睛：该题考查的是有关程序框图的问题，在解题的过程中，注意对执行框中的内容认真分析，虚拟执行，判断条件，得到结果.4. 已知，则的大小关系为（）A. B. C. D.【答案】A【解析】分析：利用指数函数与对数函数的单调性即可得出结果.详解：因为，，，所以，故选A.点睛：该题考查的是有关指数幂和对数值的比较大小的问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围，借助于中介值来完成任务.5. 已知等比数列的前项和为，且，，则（）A. B. C. D.【答案】D【解析】分析：设出等比数列的公比为，利用等比数列的性质，根据已知等式求出的值，进而求出的值，表示出与，即可求出结果.详解：设等比数列的公比为，所以，所以，解得，，，所以，故选D.点睛：该题考查的是有关等比数列的问题，涉及到的知识点有等比数列项之间的关系，等比数列的通项公式和等比数列的求和公式的应用，在解题的过程中，注意认真运算.6. 中，“”是“为直角三角形”的（）A. 充分不必要条件B. 必要不充分条件C. 充分且必要条件D. 既不充分也不必要条件【答案】B【解析】分析：利用正弦定理以及二倍角公式，化简已知表达式，然后确定三角形的形状，即可推出两者的关系，得到选项.详解：由正弦定理可知，化为，所以，因为是三角形内角，所以或，即或，即或，所以中，“”是“为直角三角形”的必要不充分条件，故选B.点睛：该题考查的是有关充分条件和必要条件的判断，涉及到的知识点有正弦定理，诱导公式，三角形形状的判断问题，在解题的过程中，需要对题的条件认真分析，理解透彻，从而求得最后的结果.7. 过双曲线的左焦点，作圆的切线交双曲线右支于点，切点为，的中点在第一象限，则以下结论正确的是（）A. B.C. D.【答案】A【解析】试题分析：连结，则，在直角三角形中，，连结为线段的中点，为坐标原点，，故选A．考点：1、双曲线和圆的标准方程；2、双曲线的定义和简单几何性质．【思路点睛】本题主要通过双曲线和圆的标准方程考查双曲线的定义和几何性质，属于难题．本题的难点在于怎样巧妙将双曲线的定义运用于解题过程，在解题过程中一定要注意两点：一是圆的半径正是双曲线的实半轴，从而利用切线性质得出；二是利用中位线得出后再巧妙地利用双曲线的定义得到．8. 设，，且为偶函数，为奇函数，若存在实数，当时，不等式成立，则的最小值为（）A. B. C. D.【答案】A【解析】分析：由及的奇偶性求得，进而可把表示出来，分离出参数后，求函数的最值，问题即可解决.详解：由，即，得，又分别为偶函数、奇函数，所以，联立两个式子，可以解得，，即，即，即，因为存在实数，当时，不等式成立，，所以，所以的最小值为，故选A.点睛：该题考查的是有关恒成立问题对应的参数的取值范围问题，涉及到的知识点有奇偶函数的定义、函数解析式的求解、分离参数，恒成立问题向最值靠拢，利用函数的单调性得到最值，从而求得结果.第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9. 随机抽取100名年龄在年龄段的市民进行问卷调査，由此得到样本的频率分布直方图如图所示，从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人，则在年龄段抽取的人数为__________．【答案】2.【解析】分析：根据频率分布直方图，求出样本中不小于40岁的人的频率与频数，再求用分层抽样方法抽取的人数.详解：根据频率分布直方图，得样本中不小于40岁的人的频率是，所以不小于40岁的人的频数是；从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人，在年龄段抽取的人数为，故答案为2.10. 已知，则的展开式中常数项为__________．【答案】.【解析】n＝，二项式的展开式的通项为，令＝0，则r＝3，展开式中常数项为(－2)3＝－8×4＝－32.故答案为：-32.点睛：求二项展开式有关问题的常见类型及解题策略：(1)求展开式中的特定项.可依据条件写出第项，再由特定项的特点求出值即可.(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第项，由特定项得出值，最后求出其参数.11. 一个几何体的三视图如图所示（单位：)，则该几何体的体积为__________.【答案】.【解析】分析：首先根据题中所给的三视图，将几何体还原，分析得到其为一个圆柱和一个圆锥的组合体，所以其体积为圆柱和圆锥的体积之和，结合图中所给的数据，利用体积公式求得结果.详解：根据题中所给的几何体的三视图，将几何体还原，可以得到几何体是一个圆柱和圆锥的组合体，利用相关数据可知圆柱的体积为，圆锥的体积为，所以该几何体的体积为，故答案是.点睛：该题考查的是有关根据几何体的三视图求其体积的问题，在解题的过程中，还原几何体是解题的关键，之后利用图中的相关数据，结合体积公式求得结果，注意组合体的体积在求解的时候将其分割，计算即可.12. 已知抛物线的参数方程为(为参数），其中，焦点为，准线为，过抛物线上一点作的垂线，垂足为.若，点的横坐标为3，则__________．【答案】2.详解：抛物线的参数方程为（为参数），其中，焦点为，准线为，消去参数可得，化简可得，表示顶点在原点、开口向右、对称轴是轴的抛物线，故焦点，准线的方程为，则由抛物线的定义可得，再由，可得为等边三角形，设点的坐标为，则点，把点的坐标代入抛物线的方程可得，即，再由，可得，即，解得或（舍去），故答案是2.点睛：该题考查的是有关抛物线方程的求解问题，在解题的过程中，涉及到的知识点有抛物线的定义，有关三角形的边的关系，对应的等量关系式的建立，最后求得结果.13. 平行四边形中，，是平行四边形内一点，且，若，则的最大值为__________．【答案】2.【解析】分析：根据，利用，利用向量的平方和向量模的平方是相等的，利用基本不等式得出的最大值.详解：因为，所以，又，即，所以，当且仅当，即时，取得最大值2，故答案是2.点睛：该题考查的是求式子的最值的问题，涉及到的知识点有向量的平方和向量模的平方是相等的，向量数量积的定义式，利用基本不等式求最值，在解题的过程中，注意式子的正确使用.14. 用五种不同的颜色给三棱柱六个顶点涂色，要求每个点涂一种颜色，且每条棱的两个端点涂不同颜色，则不同的涂色方法有__________种.(用数字作答）【答案】1920.【解析】分析：分两步来进行，先涂，再涂，然后分若5种颜色都用上、若5种颜色只用4种、若5种颜色只用3种这三种情况，分别求得结果，再相加，即可得结果.详解：分两步来进行，先涂，再涂.第一类：若5种颜色都用上，先涂，方法有种，再涂中的两个点，方法有种，最后剩余的一个点只有2种涂法，故此时方法共有种；第二类：若5种颜色只用4种，首先选出4种颜色，方法有种；先涂，方法有种，再涂中的一个点，方法有3种，最后剩余的两个点只有3种涂法，故此时方法共有种；第三类：若5种颜色只用3种，首先选出3种颜色，方法有种；先涂，方法有种，再涂，方法有2种，故此时方法共有种；综上可得，不同涂色方案共有种，故答案是1920.点睛：该题考查的是有关排列组合的综合题，在解题的过程中，涉及到的知识点有分步计数乘法原理和分类计数加法原理，要认真分析题的条件，列式求得结果.解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15. 已知函数的图象经过点.（1）求的值，并求函数的单调递增区间；（2）若当时，不等式恒成立，求实数的取值范围.【答案】(1)；的单调递增区间为.(2).【解析】分析：（1）利用倍角公式和辅助角公式可以求得，然后再利用正弦函数的单调性即可得出单调区间；（2）由，可得，可得的取值范围是，根据不等式恒成立，即，从而求得结果.详解：（1）因为经过点，所以，，因为的单调递增区间为所以所以所以的单调递增区间为.（2）由（1）知，因为，所以，当，即时，，因为恒成立即，所以所.点睛：该题考查的是有关三角函数的恒等变换以及恒成立问题，涉及到的知识点有倍角公式、辅助角公式、正弦函数的单调性、三角函数在闭区间上的最值等，在解题的过程中，注意正确使用公式，再者就是将恒成立问题转化为最值来处理即可.16. 现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.（1）求这4个人中恰有2人去参加甲游戏的概率；（2）用分别表示这4个人中去参加甲、乙游戏的人数，记，求随机变量的分布列与数学期望. 【答案】(1).(2)分布列见解析；.【解析】分析：依题意，这4个人中，每个人去参加甲游戏的槪率为，去参加乙游戏的概率为.设“这4个人中恰有人去参加甲游戏”为事件，则 ,(1)这4个人中恰有2人去参加甲游戏的槪率为；(2)的所有可能取值为0, 2, 4，由于与互斥，与互斥，求出相应的概率，可得的分布列与数学期望. 详解：（1）依题意，这4个人中，每个人去参加甲游戏的槪率为，去参加乙游戏的概率为.设“这4个人中恰有人去参加甲游戏”为事件，则 ,这4个人中恰有2人去参加甲游戏的槪率.（2）的所有可能取值为0, 2, 4.由于与互斥，与互斥，所以，，所以的分布列是所以随机变量的数学期望.点睛：该题考查的是有关概率的问题，涉及到的知识点有古典概型及其概率计算公式，离散型随机变量的分布列及其期望，在解题的过程中，需要认真审题，正确使用公式计算结果.17. 如图所示，四边形是边长为3的正方形，平面，，，与平面所成角为.（1）求证：平面；（2）求二面角的余弦值；（3）设点是线段上的一个动点，试确定点的位置，使得平面，并证明你的结论.【答案】(1)证明见解析.(2).(3)；证明见解析.【解析】试题分析：（1）由正方形性质得，由平面得，再根据线面垂直判定定理得平面（2）利用空间向量求二面角：先根据条件建立空间直角坐标系，设立各点坐标，利用方程组解各面法向量，根据向量数量积求向量夹角，最后根据二面角与向量夹角关系求二面角（3）设点坐标，根据平面得，列方程解得点坐标，再确定位置试题解析：（Ⅰ）证明：∵平面，平面，∴，又∵是正方形，∴，∵，∴平面．（Ⅱ）∵，，两两垂直，所以建立如图空间直角坐标系，∵与平面所成角为，即，∴，由，可知：，．则，，，，，∴，，设平面的法向量为，则，即，令，则．因为平面，所以为平面的法向量，∴，所以．因为二面角为锐角，故二面角的余弦值为．（Ⅲ）依题意得，设，则，∵平面，∴，即，解得：，∴点的坐标为，此时，∴点是线段靠近点的三等分点．点睛：利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.18. 已知数列是首项的等差数列，设.（1）求证：是等比数列；（2）记，求数列的前项和；（3）在（2）的条件下，记，若对任意正整数，不等式恒成立，求整数的最大值.【答案】(1)证明见解析.(2) .(3)11.【解析】分析：(1)运用等差数列的通项公式，可得公差，进而得到，再由对数的运算性质和等比数列的定义，即可得证；(2)利用裂项相消法求和即可；(3)根据题意，求得，设，判断其为单调递增，求得最小值，再由恒成立思想可得的范围，进而得到最大值.详解：（1）由及，得，所以.因为，所以，即.则，所以数列是首项，公比的等比数列.（2）由（1），得，所以（3）因为，则问题转化为对任意正整数使不等式恒成立.设，则.所以，故的最小值是/.由，得整数可取最大值为11.点睛：该题考查的是有关数列的问题，涉及到的知识点有用定义证明等比数列，对数的运算，裂项相消法求和，恒成立问题求有关参数的取值范围和最值问题，在解题的过程中，注意对公式的正确使用以及对问题的正确理解.19. 在平面直角坐标系中，椭圆的离心率为,直线被椭圆截得的线段长为. （1）求椭圆的方程；（2）过原点的直线与椭圆交于两点（不是椭圆的顶点），点在椭圆上，且，直线与轴轴分别交于两点.①设直线斜率分别为，证明存在常数使得，并求出的值；②求面积的最大值.【答案】(1).(2) ①证明见解析，；②.【解析】试题分析：（1）首先由题意得到，即.将代入可得，由，可得.得解.（2）（ⅰ）注意从确定的表达式入手，探求使成立的.设，则，得到，根据直线BD的方程为，令，得，即.得到.由，作出结论.（ⅱ）直线BD的方程，从确定的面积表达式入手，应用基本不等式得解. 试题解析：（1）由题意知，可得.椭圆C的方程可化简为.将代入可得，因此，可得.因此，所以椭圆C的方程为.（2）（ⅰ）设，则，因为直线AB的斜率，又，所以直线AD的斜率，设直线AD的方程为，由题意知，由，可得.所以，因此，由题意知，所以，所以直线BD的方程为，令，得，即.可得.所以，即.因此存在常数使得结论成立.（ⅱ）直线BD的方程，令，得，即，由（ⅰ）知，可得的面积，因为，当且仅当时等号成立，此时S取得最大值，所以的面积的最大值为.考点：椭圆的几何性质，直线与椭圆的位置关系，三角形面积，基本不等式的应用.视频20. 已知，其中常数.（1）当时，求函数的极值；（2）若函数有两个零点，求证：；（3）求证：.【答案】(1)有极小值，没有极大值.(2)证明见解析.(3)证明见解析.【解析】试题分析：先写出函数的定义域，（1）由，求出的导数，再求出的单调性，即可求得极值；（2）先证明：当恒成立时，有成立，若，则显然成立；若，运用参数分离，构造新函数通过求导数及单调性，结合函数零点存在定理，即可得证；（3）讨论当当时，恒成立，可设设，求出导数，单调区间及最大值，运用不等式的性质，即可得证.试题解析：函数的定义域为，（1）当时，，，而在上单调递增，又，当时，，则在上单调递减；当时，，则在上单调递增，所以有极小值，没有极大值.（2）先证明：当恒成立时，有成立.若，则显然成立；若，由得，令，则，令，由得在上单调递增，又∵，所以在上为负，在上为正，∴ 在上递减，在上递增∴，从而.因而函数若有两个零点，则，所以，由得，则，∴在上单调递增，∴，∴在上单调递增∴，则∴由得，则∴，综上得.（3）由（2）知当时，恒成立，所以，即，设，则，当时，，所以在上单调递增；当时，，所以在上单调递减；所以的最大值为，即，因而，所以，即点睛:导数是研究函数的单调性、极值(最值)最有效的工具对导数的应用的考查主要从以下几个角度进行：（1）考查导数的几何意义，往往与解析几何、微积分相联系；（2）利用导数求函数的单调区间，判断单调性；已知单调性求参数；（3）利用导数求函数的最值(极值)，解决生活中的优化问题；（4）考查数形结合思想的应用．。

天津市南开中学2018届高三下学期第四次月考数学（文）试题第Ⅰ卷一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.在复平面内，复数ii 3113+-对应的点的坐标为（ ）A ．)53,54( B ．)53,1(- C ．)54,53( D ．)1,53(2.已知命题12,0:>>∀xx p ,则p ⌝为（ ）A.12,0≤≤∃x x B ．12,0≤>∀xxC ．12,0≤≤∀xx D ．12,0≤>∃xx3.函数xx x f 1)2ln()(-=的零点一定位于区间（ ） A ．)2,1( B ．)3,2( C ．)4,3( D ．)5,4(运行结果为720，那么判断框中应填入（ ） 4.执行如图所示的程序框图，如果A ．?6<k B ．?7<k C ．?6>k D ．?7>k5.如图，AB 是⊙O 的直径，AC 是弦，BAC ∠的平分线AD 交⊙O 于点D ，E ，ABDF ⊥AC DE ⊥，交AC 的延长线于点于点F ，且8=AE ，10=AB . 在上述条件下，给出下列四个结论：①BD DE =；②CDE BDF ∆≅∆；③2=CE ；④BF AF DE⋅=2，则所有正确结论的序号是（ ）A ．①②③B ．②③④C ．①③④D ．①②④6.函数)22,0)(sin(2)(πϕπωϕω<<->+=x x f 的部分图象如图所示，则)(x f 的单调递增区间为（ ）A ．)](3,6[Z k k k ∈+-ππππ B ．)](125,12[Z k k k ∈+-ππππ C ．)](1211,125[Z k k k ∈++ππππ D ．)](65,3[Z k k k ∈++ππππ7.已知)(x f 是定义在),0(+∞上的函数，对任意两个不相等的正数21,x x ，都有0)()(2112<-x f x x f x ，记3l og)3(l og ,6si n)6(si n ,2)2(2.02.0ππππf c f b f a ===，则A ．a b c <<B ．b a c <<C ．c a b <<D ．a c b <<8.已知函数)0(1)(>--=m x mx x f ，若关于x 的不等式0)(≥x f 的解集中的整数恰有3个，则实数m 的取值范围为（ ）A ．]1,0(B ．)43,32[ C ．)23,34[ D ．)2,32[第Ⅱ卷二、填空题（每题5分，满分30分，将答案填在答题纸上）9.已知集合{}02≤-=x x x A ，{})1lg()(x x f x B -==，则=B A _______.10.某高中学校共有学生1800名，各年级男女学生人数如下表.已知在全校学生中随机抽取1名，抽到高二女生的概率是16.0.现用分层抽样的方法，在全校抽取45名学生，则应在高三抽取的学生人数为_____.11.某三棱锥的三视图如图所示，该三棱锥的体积是______.x y282=的准线上，则双曲线的方程为______.14.如图，等腰三角形ABC ，120,2=∠==BAC AC AB .F E ,分别为边AC AB ,上的动点，且满足AC n AF AB m AE ==,，其中1),1,0(,=+∈n m n m ，N M ,分别是BC EF ,的中点，的最小值为______.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）15.（本小题满分13分）某旅行社租用两种型号的客车安排900名客人旅行，B A ,两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B 型车不多于A 型车7辆，则如何安排才能使租金最少，最少租金为多少？16.（本小题满分13分）在ABC ∆中，内角C B A ,,所对的边分别是c b a ,,，已知42cos ,22,4-===A c a .（1）求b 和C sin 的值； （2）求)62cos(π+A 的值.17.（本小题满分13分）如图，梯形ABEF 中，，，∥BF AB EF AB ⊥M O ,分别是FC AB ,的中点，矩形ABCD 所在的平面与ABEF 所在的平面互相垂直，且1,2===EF AD AB .（1）证明：⊥AF 平面CBF ； （2）证明：∥OM 平面DAF ；（3）若二面角F BC D --为60，求直线EM 与平面CBF 所成角的大小.18.（本小题满分13分）在等比数列{}n a 中，21=a ，5423,,a a a a +成等差数列. （1）求数列{}n a 的通项公式； （2）若数列{}n b 满足)(221*∈=+⋅⋅⋅++N n a nb b b n n ，{}n b 的前n 项和为n S ，求使06≥+-nn naS 成立的正整数n 的最大值.19.（本小题满分14分） 已知椭圆)0(12222>>=+b a by ax 的左顶点为A ，右焦点为2F ，过点2F 作垂直于x 轴的直线交该椭圆于N M ,两点，直线M A 1的斜率为21.（1）求椭圆的离心率；（2）若MN A 1∆的外接圆在M 处的切线与椭圆交于另一点D ，且MD F 2∆的面积为712，求该椭圆方程.20.（本小题满分14分） 设函数bx axx x f --=221ln )(.（1）当2,3==b a 时，求函数)(x f 的单调区间； （2）令)30(21)()(2≤<+++=x xa bx axx f x F ，其图象上任意一点),(00y x P 处切线的斜率81≤k 恒成立，求实数a 的取值范围；（3）当0==b a 时，令mx x G xx f x H =-=)(,1)()(，若)(x H 与)(x G 的图象有两个交点),(),,(2211y x B y x A ，求证：2212e x x >.天津市南开中学2018届高三下学期第四次月考数学（文）试题参考答案一、选择题 ADBC BBDB 二、填空题9.]1,1-（ 10.14 11.12 12.3 13.16222=-yx14.21三、解答题15.解：设租用A 型车x 辆，租用B 型车y 辆.所用租金z 元，则x ，y 满足⎪⎪⎩⎪⎪⎨⎧∈∈≥+≤-≤+N y N x y x x y y x ,9006036721，化简得⎪⎪⎩⎪⎪⎨⎧∈∈≥+≤-≤+N y N x y x x y y x ,7553721， 作出可行域如图所示目标函数y x z 24001600+=，变形为240032z x y +-=，当240032z x y +-=经过可行域上的A 点时，截距2400z 最小，即z 最小，16.解：（1）由余弦定理，A bc c b a cos 2222-+=，∴b b b b 284222281622++=⨯⨯-+=，∴0822=-+b b ，∴2=b 或4-（舍），∴2=b .414)42(1cos1sin 22=--=-=A A ,由正弦定理Cc Aa sin sin =，∴47441422sin sin =⨯==aA c C .（2）6sin2sin 6cos2cos )62cos(πππA A A -=+A A A cos sin 221)1cos2(232⨯--=42414)11622(23⨯--⨯=1672)43(23+-⨯=8337-=.17.证明：（1）⎪⎪⎭⎪⎪⎬⎫⊥=⊂⊥⇒ABEF ABCD AB ABEF ABCD ABCD BC AB BC ABCD平面平面平面平面，平面，矩形 ⎭⎬⎫⊂⊥⇒ABEF BF ABEF BC 平面平面 CBF AF F BF AF BF AF BFBC 平面⊥⇒⎪⎭⎪⎬⎫=⊥⊥⇒ . （2）取DF 中点N ，连接AN MN ,，为平行四边形四边形∥∥∥ANMD AD MN ABCD AB C A CD MN ⇒⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫===2121DAF OM DAF AN DAF OM DMAN 平面∥平面平面∥⇒⎪⎭⎪⎬⎫⊂⊄⇒.（3）的平面角为二面角F -BC -D ABF BCF B BC AB ∠⇒⎭⎬⎫⊥⊥⎪⎭⎪⎬⎫==∠=∠⇒⎭⎬⎫=⊥=∠⇒1602,60EF ABF BFE EF AB AB BF AF ABF ，∥为等边三角形BEF ∆⇒.由（1）知⇒⎪⎭⎪⎬⎫⊂=⊥⇒⎭⎬⎫⊂⊥ABEF EH BF ABEF CBF ABEF CBF CBF CB ABEF CB 平面平面平面平面平面平面平面所成角与平面为内射影在平面为平面CBF EM EMH CBF EM MH CBF EH ∠⇒⇒⊥，EMH RT ∆中，212121===AD BC MH ，23=EH ，∴3tan =∠EMH，∴ 60=∠EMH ，∴EM 与平面CBF 成60角.18.解：（1）设数列{}n a 的公比为q ，∴5342)(a a a a +=+，∴4121311)(2q a q a q a q a +=+，∴)1()1(2222q q q q +=+，∴2=q ，∴n n n n qa a 222111=⋅==--. （2）n n a nb b b =+⋅⋅⋅++221①，112112--=-+⋅⋅⋅++n n a n b b b )2(≥n ②，①-②得，111222---=-=-=n n nn n n a a nb ，∴)2(21≥⋅=-n n b n n .①中令1=n ，∴211==a b 不符合上式.∴⎩⎨⎧≥⋅==-2,2,1,21n n n b n n . ∴当2≥n 时，12223222-⋅+⋅⋅⋅+⋅+⋅+=n n n S ③，nn n S 223224232⋅+⋅⋅⋅+⋅+⋅+=④，③-④得nn n n S 22222132⋅-+⋅⋅⋅+++=--nn n 212)12(21⋅---=-nn n 222⋅--=，∴22)1(+-=nn n S .当1=n 时，211==b S ，符合上式，∴22)1(+-=n n n S )(*∈N n .826222)1(6+-=+⋅-+-=+-nn n nn n n naS ,∴082≥+-n，即82≤n，∴3≤n ，∴n 的最大值为3.19.解：（1）),(122222a b c M b y ax c x ⇒⎪⎩⎪⎨⎧=+=，∴a c a c a a c a c a a b-=+-=+=)(21222， ∴c a 2=，∴21=e .（2）22222234c c c c a b =-=-=，∴c b 3=，∴椭圆方程为1342222=+cy cx，)23,(c c M ，)0,2(c A -，设外接圆圆心)0,(t T ，由TM TA =得22249)()2(c c t c t +-=+，整理得2436c tc -=，∴8c t -=，∴)0,8(c T -，∴34823=+=c c c DM，∴切线斜率43-=k ，∴切线方程为)(4323c x c y --=-，即0943=-+c y x ，代入椭圆方程消y 得01118722=+-c cx x ，0161174182222>=⨯⨯-=∆c c c ，1425,711c y c x D D ==，∴75)231415()711()()(2222c c c c c y y x x CD D c D c =-+-=-+-=，2F 点到CD 的距离c cc d 56593=-=，由d MD S 21=得273567521712c c c =⨯⨯=，∴42=c，所以椭圆方程为1121622=+yx.20.解：（1）x x x x f 223ln )(2--=，定义域),0(+∞，xx x xx x x xx f )1)(13()123(231)(2+--=-+-=--='，令0)(>'x f ，解得310<<x ，令0)(<'x f ，解得31>x ，∴)(x f 的单增区间为)31,0(，单减区间为),31(+∞.（2）xa x x F +=ln )(，221)(xa x xa xx F -=-='，∴]3,0(,81)(0200∈≤-='=x x a x x F k ，即a x x 88200≤-，令16)4(8)(202000+--=-=x x x x g ，∴)(0x g 在]3,0(上单调递增，∴15924)93)(0=-=≤g x g ，∴158≥a ，∴815≥a .（3）mx x G xx x H =-=)(,1ln )(，定义域),0(+∞，∴1111ln mx x x =-①，2221ln mxx x =-②，①+②得)(11ln ln 212121x x m x x x x +=--+，即)(ln 21212121x x m x x x x x x +=+-，③②-①得)(11ln ln 122112x x m x x x x -=-+-，即)(ln12211212x x m x x x x x x -=-+，④由③④得121221212121ln)(2ln x x x x x x x x x x x x -+=+-，不妨设210x x <<，记112>=x x t ，令)1(1)1(2ln )(>+--=t t t t t F ，∴0)1()1()(2>+-='t t t t F ，∴)(t F 在),1(+∞上单调递增，∴0)1()(=>F t F ，∴1)1(2ln +->t t t ，即211212)(2lnx x x x x x +->，∴2ln)(2ln 121221212121>-+=+-x x x x x x x x x x x x ，∴212121212121212121214ln24ln 4ln )(2ln x x x x x x x x x x x x x x x x x x x x -=-=-<+-，∴24ln22121>-x x x x ，即12ln2121>-x x x x ，令xx x 2ln )(-=ϕ，∴021)(2>+='xxx ϕ，∴)(x ϕ在),0(+∞上单调递增.又1212ln 2122)2ln(<-+=-eee ，∴>>-12ln2121x x x x ee 22)2ln(-，即)2()(21e x x ϕϕ>，∴e x x 221>，∴2212e x x >.。

中考数学专题三角形综合测试题一、选择题（每小题3分，共30分）1.一直角三角形的两条直角边分别为3和4，下列说法中不正确的是 （ ） A.斜边长为5 B.三角形周长为12 C.第三边长为25 D.三角形面积为6 2．如图，AB ∥CD ，AE 交CD 于C ，∠A=34°，∠DEC=90°，则∠D 的度数为 （ ）A.17°B.34°C.56°D.124°3.计算sin 245°+cos30°•tan60°，其结果是（ ） A.2 B.1 C.25 D.45 4．如图，在Rt△ABC 中，∠ACB=90°，BC=1，AB=2，则下列结论正确的是（ ）A.sin A =B.1tan 2A =C.cos B =D.tan B =5．如图，在△ABC 中，∠ACB=90°，BE 平分∠ABC，ED⊥AB 于D ．如果∠A=30°，AE=6cm ，那么CE 等于 （ ） A.cm B.2cm C.3cm D.8cm6．如图，点F 在正方形ABCD 内，满足∠AFB=90°，AF=6，BF=8，则图中阴影部分面积为 （ ）A.48B.60C.76D.807.等腰三角形底边长为10cm ，周长为36cm ，那么它的底角的余弦是（ ） A.135 B.1312 C.1310 D.125 8．如果一个三角形的一个内角是另一个内角的3倍，那么我们称这个三角形是“智慧三角形”，下列各组数据中，能作为一个智慧三角形三边长的是( ) A.1，2，3 B.1，1，2 C.1，2，3 D.1，1，39．如图，在一笔直的海岸线l 上有A ，B 两个观测站，AB=2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为（ ）A.4kmB.（4﹣）kmC.2kmD.（2+）kmBCA10．小明去爬山，在山脚看山顶仰为30°，小明在坡比为5︰12的山坡上走1300米，此时小明看山顶的角度为60°，则山高为（ ） A.（600﹣250) 米 B.（600﹣250）米 C.（350+350）米 D.500米二、填空题（每小题4分，共32分） 11．已知α为锐角，且23)10sin(=︒-α，则α=_______． 12.已知在Rt △ABC 中，∠C=90°，AC=6，BC=8，D 为AB 中点，则CD=______．13．已知在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 的对的边分别为a ，b ，c ，其中22=a ，62=b ，小明得到下面4个结论：①24=c ；②33tan =A ；③1cos sin =+B A ；④∠B =30°，正确的结论是_______（填序号）.14．如图，在Rt △ABC 中，∠B=90°，∠ACB=60°，斜边AC 的垂直平分线DE 分别交AB ，AC 于D ，E 两点，若BD=2，则AC 的长为______.15．如图，△ABC 中，∠A=30°，23tan =B ，AC=32，则AB 的长为______. 16.某厂家新开发的一种电动车如图，它的大灯A 射出的光线AB,AC 与地面MN 所夹的锐角分别为8︒和10︒，大灯A 离地面的距离为1m 则该车大灯照亮地面的宽度BC 是 米.（不考虑其他因素））（参考数据：sin 8°≈254，tan8°≈71，sin10°≈509tan10°≈285）第16题图17．一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH 的边长为2米，∠B＝90°，BC ＝6米，AC=12米. 当正方形DEFH 运动到什么位置，即当AE ＝______米时，有DC 2＝A E 2＋BC 2.18.如图，在小山的东侧A 点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，20分钟后到达C 处，此时热气球上的人测得小山西侧B 点的俯角为30°，则小山东西两侧A ，B 两点间的距离为_______米．三、解答题（共58分）19．（10分）如图，在Rt△ABC 中，∠C=90°，AD 平分∠CAB，CD=3，BD=32，求AB 及∠B.20．（10分）如图，在△ABC 中，AD 是BC 边上的高，AE 是BC 边上的中线，∠C=45°，sinB=，AD=1．（1）求BC 的长；（2）求tan∠DAE 的值．21．（12分）如图，MN 表示一段笔直的高架道路，线段AB 表示高架道路旁的一排居民楼．已知点A 到MN 的距离为15米，BA 的延长线与MN 相交于点D ，且∠BDN ＝30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．(1)过点A 作MN 的垂线，垂足为点H ．如果汽车沿着从M 到N 的方向在MN 上行驶，当汽车到达点P 处时，噪音开始影响这一排的居民楼，那么此时汽车与点H 的距离为多少米？ (2)降低噪音的一种方法是在高架道路旁安装隔音板．当汽车行驶到点Q 时，它与这一排居DCBA民楼的距离QC 为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？(精确到1米) (参考数据：3≈1.7)22．（12分）如图，已知斜坡AB 长60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D 处挖去部分坡体（用阴影表示）修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE ．（请将下面2小题的结果都精确到0.1米，参考数据：≈1.732）．（1）若修建的斜坡BE 的坡角（即∠BEF）不大于45°，则平台DE 的长最多为_____米； （2）一座建筑物GH 距离坡角A 点27米远（即AG=27米），小明在D 点测得建筑物顶部H 的仰角（即∠HDM）为30°．点B 、C 、A 、G 、H 在同一个平面内，点C 、A 、G 在同一条直线上，且HG⊥CG，问建筑物GH 高为多少米？23．（14分）如图，我南海某海域A 处有一艘捕鱼船在作业时突遇特大风浪，船长马上向我国渔政搜救中心发出求救信号，此时一艘渔政船正巡航到捕鱼船正西方向的B 处，该渔政船收到渔政求救中心指令后前去救援，但两船之间有大片暗礁，无法直线到达，于是决定马上调整方向，先向北偏东60 º方向以每小时30海里的速度航行半小时到达C 处，同时捕鱼船低速航行到A 点的正北1.5海里D 处，渔政船航行到点C 处时测得点D 在南偏东53 º方向上．(1)求CD 两点的距离；(2)渔政船决定再次调整航向前去救援，若两船航速不变，并且在点E 处相会合，求∠ECD 的正弦值 (参考数据：5453sin ≈︒，5353cos ≈︒，3453tan ≈︒).第23题图三角形（二）综合测试题参考答案一、1.C 2.C 3.A 4.D 5.C 6.C 7.A 8.C 9.D 10.B9．解析：过点B 作BE ⊥AD 交AC 于点E ，则BE =AB =2，AE根据题意可知，∠CBD=67.5°，所以∠BCE=22.5°，所以CE=BE=2，，在Rt△ACD 中，sin∠CAD=22=AC CD ,所以CD =(2km.E第9题图 第10题图10．解析：如图，根据题意可得，BE=500米，AE=1200米，设EC=x 米，则DF=x 3, 所以CD=500+x 3，AC=1200+x ，在Rt△ACD 中，AC=3CD ，即1200+x=()x 35003+，解得3250600-=x .∴DF=x 3=7503600-， CD= DF+CF=2503600-，故应选B.二、11．70 12．5 13．①② 14．38 15．5 16．57 17．31418．2600 三、19．解：过D 点作DE⊥AB 于E 点，因为AD 平分∠CAB，所以DE=DC=3.在Rt△BED 中，sinB=21，∴∠B=30°，在Rt△ABC 中，23AB BC cosB ==，所以AB=6．第19题图20．解：（1）在△ABC 中，∵AD 是BC 边上的高， ∴∠ADB=∠ADC=90°．在△ADC 中，∵∠ADC=90°，∠C=45°，AD=1，∴DC=AD=1． 在△ADB 中，∵∠ADB=90°，sinB=，AD=1，∴AB==3，∴BD==2，∴BC=BD+DC=2+1；（2）∵AE 是BC 边上的中线，∴CE=BC=+， ∴DE=CE ﹣CD=﹣，∴tan∠DAE==﹣．21．解：（1）如图，连接PA ．由题意知，AP=39m ．在直角△APH 中，PH=22221539-=-AH AP =36（米）.（2）由题意知，隔音板的长度是PQ 的长度．在Rt△ADH 中，DH=31530tan =︒AH（米）．在Rt△CDQ 中，DQ=7830sin =︒CQ（米）． 则PQ=PH+HQ=PH+DQ-DH=36+78-153≈114-15×1.7=88.5≈89（米）． 答：高架道路旁安装的隔音板至少需要89米．第21题图22．解：（1）11.0；（2）过点D 作DP⊥AC，垂足为P ．在Rt△DPA 中，DP=AD=×30=15，PA=AD•cos30°=×30=15．在矩形DPGM 中，MG=DP=15，DM=PG=15+27，在Rt△DMH 中， HM=DM•tan30°=×（15+27）=15+9．GH=HM+MG=15+15+9≈45.6． 答：建筑物GH 高为45.6米．第22题图23．解：(1)如图，过点C 作CG ⊥AB 于点G ，DF ⊥CG 于点F . 则在R t△CBG 中，由题意知∠CBG =30°，∴CG=12BC=13015222⨯==7.5.∵∠DAG=90°，∴四边形ADFG是矩形.∴GF= AD=1.5 ，∴CF= CG-GF=7.5－1.5=6. 在R t△CDF中，∠CFD=90º，∵∠DCF=53°，∴cos∠DCF=CF CD，∴6103cos535CFCD===︒(海里)．答：CD两点距离为10海里．（2）如图，设渔政船调整方向后t小时能与捕渔船相会合，由题意知CE=30t，DE=1.5×2×t=3t，∠EDC=53°，过点E作EH⊥CD于点H，则∠EHD=∠CHE=90º，∴sin∠EDH=EH ED，∴EH=ED sin53°=4123=55t t ⨯，∴在Rt△EHC中，sin∠ECD=12253025tEHCE t==．答：sin∠ECD=225．第23题图。