分离定律和自由组合定律

分离定律、自由组合定律和连锁定律一、分离定律（一）孟德尔的豌豆杂交实验1. 实验材料- 孟德尔选用豌豆作为实验材料，是因为豌豆是自花传粉、闭花受粉植物，自然状态下一般都是纯种；而且豌豆具有易于区分的相对性状，例如高茎和矮茎、圆粒和皱粒等。

2. 一对相对性状的杂交实验- 孟德尔以高茎豌豆和矮茎豌豆为亲本（P）进行杂交，得到的子一代（F₁）全部表现为高茎。

然后让F₁自交，得到的子二代（F₂）中出现了高茎和矮茎两种性状，且高茎与矮茎的数量比接近3:1。

3. 对分离现象的解释- 生物的性状是由遗传因子（后来被称为基因）决定的。

显性性状由显性基因控制，如高茎由D基因控制；隐性性状由隐性基因控制，如矮茎由d基因控制。

- 在体细胞中，基因成对存在。

纯种高茎豌豆的基因型为DD，纯种矮茎豌豆的基因型为dd。

- 生物体在形成生殖细胞 - 配子时，成对的基因彼此分离，分别进入不同的配子中。

所以F₁（Dd）产生的配子类型为D和d，且比例为1:1。

- 受精时，雌雄配子的结合是随机的。

F₁自交时，雌雄配子随机结合，会产生DD、Dd、dd三种基因型的后代，其比例为1:2:1，表现型为高茎（DD和Dd）和矮茎（dd），比例为3:1。

4. 对分离现象解释的验证 - 测交实验- 测交是让F₁与隐性纯合子杂交。

F₁（Dd）与隐性纯合子（dd）杂交，后代的基因型为Dd和dd，表现型为高茎和矮茎，比例为1:1。

这一结果验证了孟德尔对分离现象解释的正确性。

（二）分离定律的实质1. 实质内容- 在杂合子的细胞中，位于一对同源染色体上的等位基因，具有一定的独立性；在减数分裂形成配子的过程中，等位基因会随同源染色体的分开而分离，分别进入两个配子中，独立地随配子遗传给后代。

（三）分离定律的应用1. 杂交育种方面- 例如，小麦的抗锈病（显性性状，由A基因控制）和不抗锈病（隐性性状，由a基因控制）是一对相对性状。

如果要选育抗锈病的小麦纯合子（AA），可以让抗锈病小麦（Aa）自交，在F₂中会出现AA、Aa、aa三种基因型，通过不断自交和筛选，最终得到稳定遗传的抗锈病纯合子（AA）。

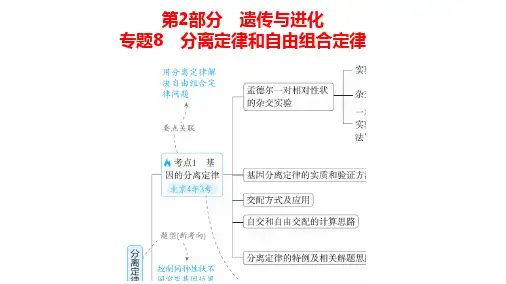
自由组合和分离定律
自由组合定律：在进行组合时，元素之间的自由性质允许它们以多种不同的方式组合，从而形成不同的结构或组合体。

这种组合的灵活性使得我们可以从有限的元素集合中创建
出无限可能的组合。

自由分离定律：在进行分离或解构时，组合体或结构可根据自由性质被分解成其组成
的各个独立元素。

这种分离的自由使得我们可以将复杂的系统或组合体分解为可独立处理
的部分，以便更好地理解或重新组合它们。

在这两个定律中，自由性质扮演了关键的角色。

它们描述了组合和分离的过程中元素
之间的灵活性和独立性，并为我们提供了进行创造性思考和创新的空间。

需要注意的是，
自由并非无限制的，我们仍需遵守一定的规则和限制，以确保组合或分离的过程能够成功
达到预期的目标。

简述分离定律、自由组合定律及其实质。

1）分离定律：
内容：在生物的体细胞中，决定生物体遗传性状的一对遗传因子不相融合，在配子的形成过程中彼此分离，随机分别进入不同的配子中，随配子遗传给后代。

实质：分离定律揭示了一个基因座上等位基因的遗传规律——等位基因随同源染色体的分开而分离。

2）自由组合定律：
内容：具有独立性的两对或多对相对性状的遗传因子进行杂交时，在子一代产生配子时，在同一对遗传因子分离的同时，不同对的遗传因子表现为自由组合。

实质：形成配子时非同源染色体上的基因自由组合。

基因的分离定律和自由组合定律之间的关系基因的分离定律和自由组合定律，听上去有点复杂，但其实它们就像一对小兄弟，各自有各自的个性，却又相辅相成。

咱们先聊聊基因的分离定律，这可是孟德尔的经典之作。

想象一下，一个父母亲有两个孩子，其中一个继承了爸爸的眼睛，另一个则得到了妈妈的笑容。

这种现象其实就是基因在“分离”，每个孩子各自从父母那里“抽取”了一半的基因组合。

就像大伙儿去自助餐一样，随心所欲地挑选，最后拼出一个独特的自己。

这个分离的过程其实是有点随机的，也正是这种随机性，才让每个人都那么独一无二。

然后，咱们再来看看自由组合定律。

它的意思是说，基因在组合的时候就像是调味料，想加什么就加什么。

比如，你的眼睛是爸爸的，头发是妈妈的，鼻子又可能是外公的。

这些基因的组合可是可以自由“调配”的，毫无疑问，每次组合都能造出新的惊喜，像是在做一次奇妙的基因大餐。

就好比你在炒菜，今天想吃青椒炒鸡蛋，明天又想来点西红柿炒蛋，每次做出来的味道都不尽相同，但每道菜都有它的独特魅力。

自由组合让遗传的多样性达到了极致，想象一下，如果每个人都长得一模一样，那生活得多无趣呀！两者之间的关系就像一对搭档。

分离定律负责“分工”，而自由组合则负责“合作”。

前者确保了基因可以在下一代中自由流动，而后者则让这些基因能够以各种各样的方式结合在一起。

这种“兄弟情”是自然选择的基石，给了物种进化的无限可能。

生物界就像一场盛大的派对，大家都在不停地变换舞伴，结果跳出了一曲又一曲的精彩舞蹈。

想想那些千奇百怪的动物和植物，都是这些基因“分离”和“组合”出来的，真是令人叹为观止啊！基因的奇妙之处在于，它们就像一把钥匙，打开了生命的各种可能性。

分离定律和自由组合定律共同编织出了一幅五彩斑斓的遗传图景。

比如，在动物王国，像小狗和小猫这样可爱的生物，它们的外形和性格，都是基因在“玩耍”的结果。

就像有的人天生就会唱歌，有的人则对数字情有独钟，这都是遗传的魅力所在。

基因分离定律和自由组合定律的关系及相关比例
基因分离定律和自由组合定律是遗传学中两个重要的定律，它们之间存在着一定的关系和相关比例。

基因分离定律是指同一基因的两个等位基因在生殖细胞分裂过程中分离到不同的配子中，每个配子只携带一个等位基因。

这个定律是遗传学的基础，也是遗传变异和遗传演化的重要基础。

自由组合定律是指不同基因之间在配子组合过程中是相互独立的，即每一个基因的两个等位基因的组合方式与其他基因的等位基因的组合方式无关。

这个定律提出了遗传性状的多样性和复杂性，也是基因组遗传学和基因工程技术的基础。

两个定律之间的关系是基因分离定律是自由组合定律的特殊情况，即当基因之间没有连锁互作时，基因的等位基因的组合方式符合自由组合定律，同时基因的等位基因在生殖细胞分裂过程中分离到不同的配子中，符合基因分离定律。

根据统计学原理，基因分离定律和自由组合定律是遗传学中最基本的两个定律，它们之间的比例是1:1，即在基因分离和组合过程中，符合基因分离定律和自由组合定律的比例是相等的。

综上所述，基因分离定律和自由组合定律是遗传学中两个基本的定律，它们之间存在着一定的关系和比例，这些定律为理解基因的遗传规律和遗传变异提供了重要的理论支持。

- 1 -。

基因的分离定律和自由组合定律引言基因是生物遗传信息的基本单位，它决定了个体的遗传特征。

基因的分离定律和自由组合定律是遗传学的基本原理，对于理解基因的传递和变异具有重要意义。

本文将详细探讨基因的分离定律和自由组合定律的概念、实验证据以及在实际应用中的意义。

I. 基因的分离定律基因的分离定律是指在杂交过程中，父本的两个基因分离并独立地传给子代的定律。

这一定律由格里高利·孟德尔在19世纪提出，并通过豌豆杂交实验得到了验证。

A. 孟德尔的豌豆实验孟德尔通过对豌豆的杂交实验，发现了基因的分离定律。

他选取了具有明显差异的性状进行杂交，例如花色、种子形状等。

通过连续进行多代的杂交实验，孟德尔观察到了一些规律性的现象。

B. 孟德尔定律的内容孟德尔总结出了三个基本定律： 1. 第一定律：也称为单因素遗传定律或分离定律。

即在杂交过程中，两个互相对立的基因副本（等位基因）分别来自于父本的两个基因组合，并独立地传给子代。

这就保证了基因的纯合性和杂合性的维持。

2. 第二定律：也称为双因素遗传定律或自由组合定律。

即两个不同的性状在杂交过程中独立地传递给子代。

这说明基因在遗传过程中是相互独立的。

3. 第三定律：也称为自由组合定律的互换定律。

即在同一染色体上的基因通过互换（交叉互换）来进行重组，从而形成新的基因组合。

C. 孟德尔定律的意义孟德尔的豌豆实验揭示了基因的分离和自由组合的规律，为后续的遗传学研究奠定了基础。

这些定律对于理解基因的传递、变异以及遗传规律具有重要意义。

此外，孟德尔的定律还为遗传育种提供了理论依据，对农业和生物学领域产生了深远的影响。

II. 自由组合定律自由组合定律是指在杂交过程中，不同染色体上的基因在配子形成过程中独立地组合的定律。

这一定律由托马斯·亨特·摩尔根等科学家在20世纪初通过果蝇实验得到了验证。

A. 摩尔根的果蝇实验摩尔根通过对果蝇的杂交实验，发现了基因的自由组合定律。

自由组合定律与分离定律一、自由组合定律自由组合定律是数学中的一个重要原理，用于描述集合中的元素之间的组合关系。

它指出，对于一个集合中的元素，可以自由地进行组合，得到新的集合。

1.1 定义假设A和B是两个集合，A中有m个元素，B中有n个元素。

那么根据自由组合定律，可以得到一个新的集合C，它包含了A和B中所有可能的组合。

1.2 示例假设A={a, b}，B={1, 2}，那么根据自由组合定律，可以得到集合C={a1, a2, b1, b2}，其中a1表示集合A中的元素a和集合B中的元素1的组合。

1.3 应用自由组合定律在实际应用中有着广泛的应用，特别是在组合数学、概率论和计算机科学等领域。

在组合数学中，自由组合定律可以用于求解排列组合问题，计算不同元素之间的组合数量。

在概率论中，自由组合定律可以用于计算事件的样本空间，从而计算事件的概率。

在计算机科学中，自由组合定律可以用于生成所有可能的组合，从而解决搜索、排列和组合等问题。

二、分离定律分离定律是集合论中的一个基本原理，用于描述集合中的元素之间的分离关系。

它指出，对于一个集合中的元素，可以根据某种条件将其分离出来，得到一个新的集合。

2.1 定义假设A是一个集合，P(x)是一个关于x的命题。

那么根据分离定律，可以得到一个新的集合B，它包含了满足命题P(x)的所有元素。

2.2 示例假设A={1, 2, 3, 4, 5}，P(x)表示x是一个偶数。

那么根据分离定律，可以得到集合B={2, 4}，其中2和4是满足命题P(x)的元素。

2.3 应用分离定律在实际应用中也有着广泛的应用，特别是在集合论、逻辑学和数据库等领域。

在集合论中，分离定律可以用于定义集合的特性，从而进行集合的划分和分类。

在逻辑学中，分离定律可以用于推理和证明，根据给定的条件分离出满足条件的元素。

在数据库中，分离定律可以用于查询和过滤数据，根据给定的条件分离出满足条件的记录。

三、自由组合定律与分离定律的关系自由组合定律和分离定律在某种程度上是相互关联的，它们都描述了集合中元素之间的关系，但侧重点有所不同。