数字电路第8章 数字系统设计基础-习题答案

习题8.1.1电路如图所示，试写出输出F 与输入A ，B ，C 的逻辑关系式。

并画出逻辑图。

+20 V -10 VA B图8.01 习题8.1.1的图解：F AB C =+C8.1.2 晶体管非门电路如图所示，已知U CC V =15 ，U B V =-9 ，R C k =3 Ω， R B k =20 Ω， β=40，求：(1) 求晶体管的集电极临界饱和电流I CS 和基极临界饱和电流I BS ;(2)当输 入电压U I V =5时，要使晶体管饱和导通，试求R X 值 (设 U BE V =06.)。

(3)写出它的逻辑符号。

u Iu OA图8.02 习题8.1.2的图 解：(1) I U R I I CS CC C BS CS mA mAmA mA ≈=====15355400125β. (2) 如 图 所 示I I I I U R R I U U R B BE X XBE B BmA =+=-==--'=-12125449620..故 I R ÓB X =+-449620.. 又 I BS mA =0125. 得 R X k =727.ΩEI 1u I(3) 逻 辑 符 号8.1.3 已知逻辑门电路及输入波形如图所示，试画出各输出F 1、F 2、F 3的波形， 并写出逻辑式。

&"1"F 1≥1"0"F 2B ≥1F 3ABCF 1F 2F 3AABC图8.03 习题8.1.3的图解：CF 2F 3F A A 11=⋅=F A B C3=++F B B20=+=AB F 18.1.4 已知逻辑电路及其输入波形如图所示 ，试分别画出输出 F 1，F 2 的波形 。

（a ） （b ） 图8.04 习题8.1.4的图解：F 2F 1图1图2A 1B 1A 2B 28.2.1 某 逻 辑 电 路 的 状 态 表 如 下，其 输 入 变 量 为 A ，B ，C ，输 出 为F ，试 写 A B C F 018(a)(b) 表8.01 习题8.2.1的表解：(a) F ABC =(b)F ABC A B C A B C ==++=++8.2.2 已知逻辑电路输入A ，B ，C 及输出F 的波形如图所示，试分别列出状态表，写出逻辑式，画出逻辑图。

第8章半导体存储器和可编程逻辑器件8-1存储器按读写功能以及信息的可保存性分别分为哪几类？并简述各自的特点。

解答：存储器按读写功能可分为只读存储器（ROM）和随机存储器（RAM）。

随机存取存储器在工作过程中，既可从其任意单元读出信息，又可以把外部信息写入任意单元。

因此，它具有读、写方便的优点，但由于具有易失性，所以不利于数据的长期保存。

只读存储器在正常工作时其存储的数据固定不变，只能读出，不能随时写入。

ROM为非易失性器件，当器件断电时，所存储的数据不会丢失。

存储器按信息的可保存性可分为易失性存储器和非易失性存储器。

易失性存储器在系统关闭时会失去存储的信息，它需要持续的电源供应以维持数据。

非易失存储器在系统关闭或无电源供应时仍能保持数据信息。

8-2什么是SRAM？什么是DRAM？它们在工作原理、电路结构和读/写操作上有何特点？解答：SRAM（Static Random Access Memory）为静态随机存储器，其存储单元是在静态触发器的基础上附加控制电路构成的。

DRAM（Dynamic Random Access Memory）为动态随机存储器，常利用MOS管栅极电容的电荷存储效应来组成动态存储器，为了避免存储信息的丢失，必须定时地对电路进行动态刷新。

SRAM的数据由触发器记忆，只要不断电，数据就能保存，但其存储单元所用的管子数目多，因此功耗大，集成度受到限制。

DRAM一般采用MOS管的栅极电容来存储信息，由于电荷保存时间有限，为避免存储数据的丢失，必须由刷新电路定期刷新，但其存储单元所用的管子数目少，因此功耗小，集成度高。

SRAM速度非常快，但其价格较贵；DRAM的速度比SRAM慢，不过它比ROM 快。

8-3若RAM的存储矩阵为256字⨯4位，试问其地址线和数据线各为多少条？解答：存储矩阵为256字⨯4位的RAM地址线为8根，数据线为4根。

8-4某仪器的存储器有16位地址线，8位数据线，试计算其最大存储容量是多少？解答：最大存储容量为216⨯8=524288=512k bit（位）8-5用多少片256⨯4位的RAM可以组成一片2K⨯8位的RAM？试画出其逻辑图。

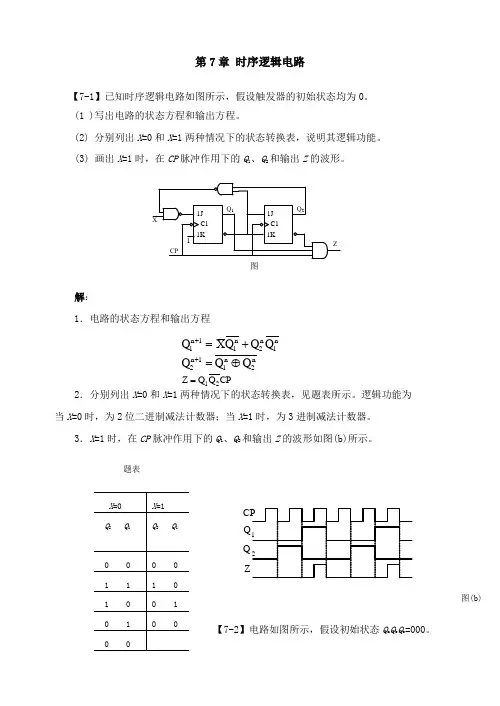
第7章 时序逻辑电路【7-1】已知时序逻辑电路如图所示，假设触发器的初始状态均为0。

(1 )写出电路的状态方程和输出方程。

(2) 分别列出X =0和X =1两种情况下的状态转换表，说明其逻辑功能。

(3) 画出X =1时，在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。

1J 1KC11J 1KC1Q 1Q 2CPXZ1图解：1．电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2．分别列出X =0和X =1两种情况下的状态转换表，见题表所示。

逻辑功能为 当X =0时，为2位二进制减法计数器；当X =1时，为3进制减法计数器。

3．X =1时，在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图(b)所示。

题表Q Q Z图(b)【7-2】电路如图所示，假设初始状态Q a Q b Q c =000。

(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。

(2) 试分析该电路构成的是几进制的计数器。

Q c图解：1．写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2．写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q QQ Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3．列出状态转换表见题表，状态转换图如图(b)所示。

图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4．由FF a 、FF b 和FF c 构成的是六进制的计数器。

【7-3】在二进制异步计数器中，请将正确的进位端或借位端（Q 或Q ）填入下表解：题表7-3下降沿触发 由 Q 端引出进位 由Q 端引出借位触发方式 加法计数器 减法计数器上升沿触发 由Q 端引出进位 由Q 端引出借位【7-4】电路如图(a)所示，假设初始状态Q 2Q 1Q 0=000。

第8章习题参考答案1. 如果认为CPU等待设备的状态信号是处于非工作状态(即踏步等待),那么在下面几种主机与设备之间的数据传送中：A主机与设备是串行工作的；B 主机与设备是并行工作的，C 主程序与设备是并行运行的。

A .程序查询方式B .程序中断方式C . DMA方式2. 中断向量地址是B。

A•子程序入口地址 B •中断服务程序入口地址C•中断服务程序入口地址指示器 D •例行程序入口地址3•利用微型机制作了对输入数据进行采样处理的系统。

在该系统中，每抽取一个输入数据就要中断CPU 一次，中断处理程序接收采样的数据，将其放到主存的缓冲区内。

该中断处理需时x秒，另一方面缓冲区内每存储n个数据，主程序就将其取出进行处理，这种处理需时y秒。

因此该系统可以跟踪到每秒 A 次的中断请求。

A . n/ (n 次 + y)B . n/(x + y) n C. min(1 /x, n/y)4•采用DMA方式传送数据时，每传送一个数据就要占用一个 C 的时间。

A .指令周期B .机器周期C.存储周期 D .总线周期5. 通道的功能是：⑴ 控制外围设备，⑵ 组织外围设备和内存之间进行数据传输______ 。

按通道的工作方式分，通道有选择通道、数组多路通道和字节多路通道三种类型。

6. 在图8.9中，当CPU对设备B的中断请求进行服务时，如设备A提出请求，CPU能够响应吗？为什么？如果设备B 一提出请求总能立即得到服务，问怎样调整才能满足此要求？答：不能，因为A、B是同级别的中断。

要使设备B一提出请求总能立即得到服务，除非将B提高到上一级，并令IM3=0，即构成一个3级IR。

7. 在图& 9中，假定CPU取指并执行一条指令的时间为t1,保护现场需t2,恢复现场需t3,中断周期需t4，每个设备的设备服务时间为t A , t B,…，t G。

试计算只有设备A , D, G时的系统中断饱和时间。

答：依次处理设备A，设备D，设备G的时间为：T1 = t1+t2+t3+t4+t AT2 = t1+t2+t3+t4+t DT3 = t1+t2+t3+t4+t G总时间为T = T1+T2+T 3 = 3*( t 1+t2+t3+t4)+ t A + t D + t G&设某机有5级中断；L o, L1, L2, L3, L4，其中断响应优先次序为：L o最高，L1次之，L4最低。

第8章存储器与可编程逻辑器件8.1存储器概述自测练习1．存储器中可以保存的最小数据单位是（）。

（a）位（b）字节（c）字2．指出下列存储器各有多少个基本存储单元？多少存储单元？多少字？字长多少？（a）2K×8位（）（）（）（）（b）256×2位（）（）（）（）（c）1M×4位（）（）（）（）3．ROM是（）存储器。

（a）非易失性（b）易失性（c）读/写（d）以字节组织的4．数据通过（）存储在存储器中。

（a）读操作（b）启动操作（c）写操作（d）寻址操作5．RAM给定地址中存储的数据在（）情况下会丢失。

（a）电源关闭（b）数据从该地址读出（c）在该地址写入数据（d）答案（a）和（c）6．具有256个地址的存储器有（）地址线。

（a）２５６条（b）６条（c）8条（d）16条7．可以存储２５６字节数据的存储容量是（）。

（a）２５６×１位（b）２５６×８位（c）１Ｋ×４位（d）２Ｋ×１位答案：1． a2．（a）2048×8；2048；2048；8（b）512；256；256；2（c）1024×1024×4；1024×1024；1024×1024；43．a4．c5．d6．c7．b8.2随机存取存储器（RAM）自测练习1.动态存储器（DRAM）存储单元是利用（）存储信息的，静态存储器（SRAM）存储单元是利用（）存储信息的。

2.为了不丢失信息，DRAM必须定期进行（）操作。

3.半导体存储器按读、写功能可分成（）和（）两大类。

4.RAM电路通常由（）、（）和（）三部分组成。

5.6116RAM有（）根地址线，（）根数据线，其存储容量为（）位。

答案：1．栅极电容，触发器2．刷新3．只读存储器，读/写存储器4．地址译码，存储矩阵，读/写控制电路5．11，8，2K×8位8.3 只读存储器（ROM）自测练习1．ROM可分为（）、（）、（）和（）几种类型。

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

第1章习题及解答将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（）2（3）（1101101）2 （4）（）2（5）（）2（6）（）2（7）（）2（8）（）2题解：（1）（11011）2 =（27）10 （2）（）2 =（151）10（3）（1101101）2 =（109）10 （4）（）2 =（255）10（5）（）2 =（）10（6）（）2 =（）10（7）（）2=（）10（8）（）2 =（）10将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（1）2（3）（）2 （4）（）2题解：（1）（1010111）2 =（57）16 =（127）8（2）（0）2 =（19A）16 =（632）8（3）（）2 =（）16 =（）8（4）（）2 =（2C.61）16 =（）8将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（）10（3）（）10 （4）（）10题解：（1）（43）10 =（01000011）8421BCD（2）（）10 =（.00010010）8421BCD（3）（）10 =（）8421BCD（4）（）10 =（.0001）8421BCD将下列有符号的十进制数表示成补码形式的有符号二进制数。

（1） +13 （2）−9 （3）+3 （4）−8题解：（1） +13 =（01101）2（2）−9 =（10111）2（3） +3 =（00011）2（4）−8 =（11000）2用真值表证明下列各式相等。

（1）BA+=+B+BBAA（2）()()()=⊕A⊕CACABB（3）()C BA+=+BCA（4）CAB++A=AABC题解：（1）证明BA+=++BABBA（2）证明()()()ACABCBA⊕=⊕（3）证明()C BACBA+=+（4）证明CAB++=AACBA用逻辑代数公式将下列逻辑函数化成最简与或表达式。

（1）D++A=F+BCBCACA（2）()()D++=F+AACCDA（3）()()B++F+=B+DCDBDDA（4）()D++F+=ADCBCBA（5）()C A B C B AC F ⊕++= （6）()()C B B A F ⊕⊕= 题解：（1）BC A D C A BC C A B A F +=+++= （2）()()CD A D CD A C A A F +=+++=（3）()()C B B A D B D A C B D D D B F ++=++++= （4）()D C B A D C B AD C B A F +=+++= （5）()C B AC C A B C B AC F +=⊕++=（6）()()C A BC B A C B B A F ++=⊕⊕=或C A C B AB ++= 用卡诺图将下列逻辑函数化成最简与或表达式。

第8章 Verilog有限状态机设计8.1 有限状态机摩尔型（Moore）状态机米里型（Mealy）状态机用状态机设计模5计数器module fsm(clk,clr,z,qout);input clk,clr; output reg z; output reg[2:0] qout; always @(posedge clk or posedge clr) //此过程定义状态转换begin if(clr) qout<=0; //异步复位else case(qout)3'b000: qout<=3'b001;3'b001: qout<=3'b010;3'b010: qout<=3'b011;3'b011: qout<=3'b100;3'b100: qout<=3'b000;default: qout<=3'b000;/*default语句*/endcaseendalways @(qout) /*此过程产生输出逻辑*/ begin case(qout)3'b100: z=1'b1;default:z=1'b0;endcaseendendmodule8.2 有限状态机的几种描述方式“101”序列检测器的Verilog 描述（三个过程）module fsm1_seq101(clk,clr,x,z);input clk,clr,x; output reg z; reg[1:0] state,next_state;parameter S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10; /*状态编码，采用格雷（Gray ）编码方式*/always @(posedge clk or posedge clr) /*该过程定义当前状态*/begin if(clr) state<=S0; //异步复位，s0为起始状态else state<=next_state;end always @(state or x) /*该过程定义次态*/begin case (state)S0:begin if(x) next_state<=S1;else next_state<=S0; end S1:begin if(x) next_state<=S1;else next_state<=S2; endS2:beginif(x) next_state<=S3; else next_state<=S0; end S3:b e g i ni f(x)next_state<=S1;else next_state<=S2; enddefault:next_state<=S0;/*default语句*/ endcaseend always @(state)/*该过程产生输出逻辑*/ begin case(state)S3: z=1'b1;default:z=1'b0; endcaseendendmodule“101”序列检测器的Verilog描述（三个过程）“101”序列检测器（单过程描述）module fsm4_seq101(clk,clr,x,z);input clk,clr,x; output reg z; reg[1:0] state; parameter S0=2'b00,S1=2'b01,S2=2'b11,S3=2'b10;/*状态编码，采用格雷（Gray）编码方式*/always @(posedge clk or posedge clr)Begin if(clr) state<=S0; //异步复位，s0为起始状态else case(state)S0:begin if(x) begin state<=S1; z=1'b0;endelse begin state<=S0; z=1'b0;endendS1:begin if(x) begin state<=S1; z=1'b0;endelse begin state<=S2; z=1'b0;endendS2:begin if(x) begin state<=S3; z=1'b0;endelse begin state<=S0; z=1'b0;endendS3:begin if(x) begin state<=S1; z=1'b1;endelse begin state<=S2; z=1'b1;endenddefault:begin state<=S0; z=1'b0;end /*default语句*/ endcase endendmodule8.3 状态编码常用的编码方式一位热码编码选择对话框（Quartus Ⅱ）在Verilog语言中，有两种方式可用于定义状态编码，分别用parameter和'define语句实现，比如要为state0、state1、state2、state3四个状态定义码字为：00、01、11、10，可采用下面两种方式。

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

【最新整理，下载后即可编辑】
数字逻辑习题
1.仅用NOR门来构造下面函数的逻辑网络：H=(XY)’Z’
2.仅用NAND门来构造下面的函数的逻辑网络：D=（A+B）B’
3.求出由下面逻辑网络产生的函数G的最简单形式
4.卡诺图化简：G（A，B，C，D）=Σm（2,3,4,7,8,14,15）
5. 卡诺图化简：G（A，B，C，D）=Σm（0,1,3,4,6,7,12,13,14）
6.卡诺图化简：G（A，B，C，D）=Σm（0,4,5,6，7,8,13,14,15）
7．卡诺图化简：G（A，B，C，D）=Σm（1,2,3,4,6,7,9,12,13）
8.采用一个组合电路来控制一个十进制的七段显示，此电路有4个输入，并提供用压缩十进制数表示的4位代码（0（d）=0000,……8(d)=1000,9(d)=1001）。

7个输出用来定义哪段激活，以显示给定的十进制数
（1）写出这个电路的真值表
（2）用sop形式表示真值表
（3）用pos形式表示真值表（4）写出各段化简的表达式
7.时序电路分析
Q
Q
SET
CLR
D
X
Clock
Y
补充：
【最新整理，下载后即可编辑】。