电动力学 郭硕鸿 第三版 第1次课(附录1)

电动⼒学-郭硕鸿-第三版-课后题⽬整理（复习备考专⽤）（可编辑修改word版）2 电动⼒学答案2. 设u 是空间坐标 x , y , z 的函数，证明：f (u ) = d fd uu ，A (u ) = u d A，d u第⼀章电磁现象的普遍规律1. 根据算符? 的微分性与向量性，推导下列公式：( A B ) = B ( A ) + (B ) A + A ( B ) + ( A )BA ? (? ? A ) = 1 ?A 2- (A ? ?) A ? ? A (u ) = ?u ? d Ad u证明：3. 设 r = 的距离， r 为源点 x ' 到场点 x 的⽅向规定为从源点指向场点。

4. 应⽤⾼斯定理证明 ?Vd V ? ? f= d S ? f ，应⽤斯托克斯S （1）证明下列结果，并体会对源变量求微商与对场变量求微（Stokes ）定理证明 ?d S ? ?= ? d l商的关系：r = -' r = r / r ；SL(1/ r ) = -'(1/ r ) = -r / r 3； ? ? (r / r 3 ) = 0 ；(r / r 3 ) = -'(r / r 3 ) = 0 ，(r ≠ 0) 。

（ 2）求 ? ?r ， ? ? r ， (a ? ?)r ， ?(a ? r ) ， ? ?[E 0 sin(k ? r )] 及 ? ?[E 0 sin(k ? r )]，其中a 、 k 及 E 0 均为常向量。

(x - x ')2 + ( y - y ')2 + (z - z ')25. 已知⼀个电荷系统的偶极矩定义为 p (t ) =V( x ', t )x ' d V '，6. 若 m 是常向量，证明除 R = 0 点以外，向量 A =（m ? R ）/ R 3的旋度等于标量 = m ? R / R 3 的梯度的负值，即利⽤电荷守恒定律 ? ? J + ?t= 0 证明 p 的变化率为：A = -，其中 R 为坐标原点到场点的距离，⽅向由原d p = ? J ( x ', t )d V 点指向场点。

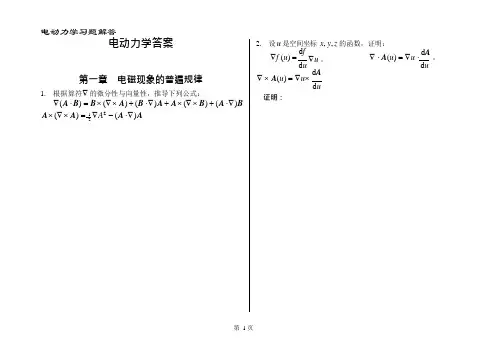
2 电动力学答案2. 设u 是空间坐标 x , y , z 的函数，证明：∇f (u ) = d fd u∇u ，∇ ⋅ A (u ) = ∇u ⋅ d A，d u第一章 电磁现象的普遍规律1. 根据算符∇ 的微分性与向量性，推导下列公式：∇( A ⋅ B ) = B ⨯ (∇ ⨯ A ) + (B ⋅ ∇) A + A ⨯ (∇ ⨯ B ) + ( A ⋅ ∇)BA ⨯ (∇ ⨯ A ) = 1 ∇A 2- (A ⋅ ∇) A ∇ ⨯ A (u ) = ∇u ⨯ d Ad u证明：⎰ 3. 设 r = 的距离， r 为源点 x ' 到场点 x 的方向规定为从源点指向场点。

4. 应用高斯定理证明 ⎰Vd V ∇ ⨯ f= d S ⨯ f ，应用斯托克斯S （1）证明下列结果，并体会对源变量求微商与对场变量求微 （Stokes ）定理证明 ⎰d S ⨯ ∇= ⎰ d l商的关系：∇r = -∇' r = r / r ；SL∇(1/ r ) = -∇'(1/ r ) = -r / r 3； ∇ ⨯ (r / r 3 ) = 0 ；∇ ⋅ (r / r 3 ) = -∇'⋅(r / r 3 ) = 0 ，(r ≠ 0) 。

（ 2） 求 ∇ ⋅r ， ∇ ⨯ r ， (a ⋅ ∇)r ， ∇(a ⋅ r ) ， ∇ ⋅[E 0 sin(k ⋅ r )] 及 ∇ ⨯[E 0 sin(k ⋅ r )]，其中a 、 k 及 E 0 均为常向量。

(x - x ')2 + ( y - y ')2 + (z - z ')25. 已知一个电荷系统的偶极矩定义为 p (t ) =⎰V( x ', t )x ' d V '，∂6. 若 m 是常向量，证明除 R = 0 点以外，向量 A =（m ⨯ R ）/ R 3的 旋 度 等 于 标 量 = m ⋅ R / R 3 的 梯 度 的 负 值 ， 即利用电荷守恒定律 ∇ ⋅ J + ∂t= 0 证明 p 的变化率为：∇ ⨯ A = -∇，其中 R 为坐标原点到场点的距离，方向由原d p = ⎰ J ( x ', t )d V 点指向场点。

电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性，推导下列公式：B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇AA A A )()(221∇⋅-∇=⨯∇⨯A 解：（1）)()()(c c A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=c c c cB A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=（2）在（1）中令B A =得：A A A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇，所以 AA A A A A )()()(21∇⋅-⋅∇=⨯∇⨯ 即 AA A A )()(221∇⋅-∇=⨯∇⨯A 2. 设u 是空间坐标z y x ,,的函数，证明：u u f u f ∇=∇d d )( ， u u u d d )(A A ⋅∇=⋅∇， uu u d d )(AA ⨯∇=⨯∇ 证明：（1）z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(z y x z uu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d d u uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e （2）z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d d uu z u y u x u u A u A u A z y x z z y y x x d d )()d d d d d d (Ae e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++= （3）uA u A u A z u y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=z x y y z x x y z y u A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇= 3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。

电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性，推导下列公式：B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇A A A A )()(221∇⋅-∇=⨯∇⨯A解：（1）)()()(c c A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=c c c cB A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=（2）在（1）中令B A =得：A A A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇，所以 A A A A A A )()()(21∇⋅-⋅∇=⨯∇⨯即 A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数，证明：u u f u f ∇=∇d d )( ， u u u d d )(A A ⋅∇=⋅∇， uu u d d )(AA ⨯∇=⨯∇ 证明：（1）z y x zu f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(z y x z u u f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d d u uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e （2）z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d duu z u y u x u u A u A u A z y x z z y y x x d d )()d d d d d d (Ae e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++=（3）uA u A u A z u y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=z x y y z x x y z y u A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇= 3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。

郭硕鸿《电动力学》课后答案第 2 页电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性，推导下列公式：B A B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇ A A A A )()(221∇⋅-∇=⨯∇⨯A 解：（1）)()()(cc A B B A B A ⋅∇+⋅∇=⋅∇B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=cc c c B A B A A B A B )()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=（2）在（1）中令B A =得：AA A A A A )(2)(2)(∇⋅+⨯∇⨯=⋅∇，所以 A A A A A A )()()(21∇⋅-⋅∇=⨯∇⨯ 即 A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数，证明：u u f u f ∇=∇d d )( ， u u u d d )(A A ⋅∇=⋅∇， uu u d d )(AA ⨯∇=⨯∇ 证明： （1）z y x z u f y u f x u f u f e e e ∂∂+∂∂+∂∂=∇)()()()(zy x zuu f y u u f x u u f e e e ∂∂+∂∂+∂∂=d d d d d du uf z u y u x u u f z y x ∇=∂∂+∂∂+∂∂=d d )(d d e e e（2）z u A y u A x u A u z y x ∂∂+∂∂+∂∂=⋅∇)()()()(A zuu A y u u A x u u A z y x ∂∂+∂∂+∂∂=d d d d d du z u y u x u u A u A u A z y x z z y y x x dd)()d d d d d d (e e e e e e ⋅∇=∂∂+∂∂+∂∂⋅++=第 3 页（3）u A u A u A zu y u x u uu z y x zy x d /d d /d d /d ///d d ∂∂∂∂∂∂=⨯∇e e e Azx y y z x x y z yu u A x u u A x u u A z u u A z uu A y u u A e e e )d d d d ()d d d d ()d d d d (∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=zx y y z x x y z yu A x u A x u A z u A z u A y u A e e e ])()([])()([])()([∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=)(u A ⨯∇=3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。

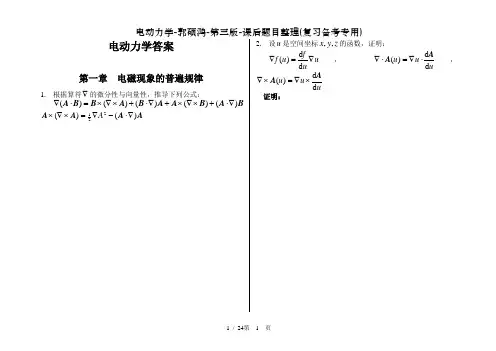
电动力学答案第一章 电磁现象的普遍规律1. 根据算符∇的微分性与向量性，推导下列公式：BA B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数，证明：u uf u f ∇=∇d d )(，uu u d d )(A A ⋅∇=⋅∇，uu u d d )(A A ⨯∇=⨯∇ 证明：3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x的距离，r 的方向规定为从源点指向场点。

（1）证明下列结果，并体会对源变量求微商与对场变量求微商的关系：r r r /'r =-∇=∇ ； 3/)/1(')/1(r r r r -=-∇=∇ ；0)/(3=⨯∇r r ；0)/(')/(33=⋅-∇=⋅∇r r r r ， )0(≠r 。

（2）求r ⋅∇ ，r ⨯∇ ，r a )(∇⋅ ，)(r a ⋅∇ ，)]sin([0r k E ⋅⋅∇及)]sin([0r k E ⋅⨯∇ ，其中a 、k 及0E 均为常向量。

4. 应用高斯定理证明fS f ⨯=⨯∇⎰⎰SVV d d ，应用斯托克斯（Stokes ）定理证明⎰⎰=∇⨯LSϕϕl S d d5. 已知一个电荷系统的偶极矩定义为 'd '),'()(V t t Vx x p ⎰=ρ，利用电荷守恒定律0=∂∂+⋅∇tρJ 证明p 的变化率为：⎰=V V t td ),'(d d x J p6. 若m 是常向量，证明除0=R 点以外，向量3/R ）（R m A ⨯=的旋度等于标量3/R R m ⋅=ϕ的梯度的负值，即ϕ-∇=⨯∇A ，其中R 为坐标原点到场点的距离，方向由原点指向场点。

7. 有一内外半径分别为1r 和2r 的空心介质球，介质的电容率为ε，使介质球内均匀带静止自由电荷f ρ，求：（1）空间各点的电场；（2）极化体电荷和极化面电荷分布。