中考数学压轴题矩形问题精选解析一

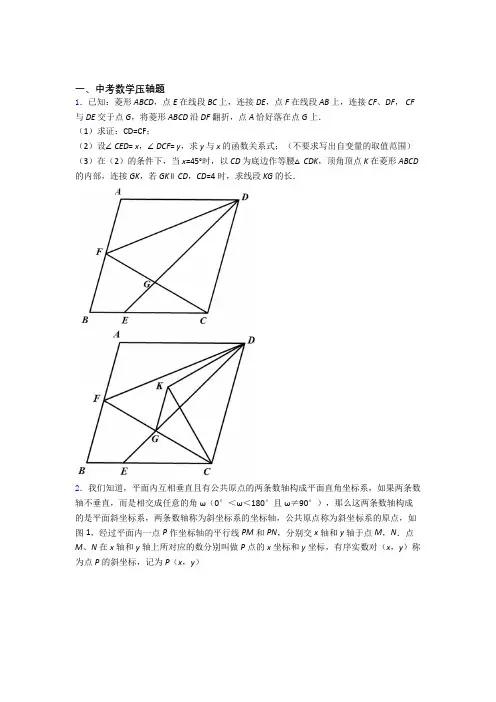
一、中考数学压轴题1．已知：菱形ABCD，点E 在线段BC 上，连接DE，点F 在线段AB 上，连接CF、DF， CF 与DE 交于点G，将菱形ABCD 沿DF 翻折，点A 恰好落在点G 上．（1）求证：CD=CF；（2）设∠CED= x，∠DCF= y，求y 与x 的函数关系式；（不要求写出自变量的取值范围）（3）在（2）的条件下，当x=45°时，以CD 为底边作等腰△CDK，顶角顶点K 在菱形ABCD 的内部，连接GK，若GK∥CD，CD=4 时，求线段KG 的长．2．我们知道，平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系，如果两条数轴不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么这两条数轴构成的是平面斜坐标系，两条数轴称为斜坐标系的坐标轴，公共原点称为斜坐标系的原点，如图1，经过平面内一点P作坐标轴的平行线PM和PN，分别交x轴和y轴于点M，N．点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标，有序实数对（x，y）称为点P的斜坐标，记为P（x，y）（1）如图2，ω＝45°，矩形OABC中的一边OA在x轴上，BC与y轴交于点D，OA＝2，OC＝1．①点A、B、C在此斜坐标系内的坐标分别为A，B，C．②设点P（x，y）在经过O、B两点的直线上，则y与x之间满足的关系为．③设点Q（x，y）在经过A、D两点的直线上，则y与x之间满足的关系为．（2）若ω＝120°，O为坐标原点．①如图3，圆M与y轴相切原点O，被x轴截得的弦长OA＝23，求圆M的半径及圆心M的斜坐标．②如图4，圆M的圆心斜坐标为M（23，23），若圆上恰有两个点到y轴的距离为1，则圆M的半径r的取值范围是．3．如图，AB∥CD，定点E，F分别在直线AB，CD上，平行线AB，CD之间有一动点P．（1）如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为．（2）如图3，当∠EPF＝90°，F P平分∠EFC时，求证：EP平分∠AEF；（3）如图4，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．①若∠EPF＝60°，则∠EQF＝．②猜想∠EPF与∠EQF的数量关系，并说明理由；4．“阅读素养的培养是构建核心素养的重要基础，重庆十一中学校以‘大阅读’特色课程实施为突破口，着力提升学生的核心素养．”全校师生积极响应和配合，开展各种活动丰富其课余生活．在数学兴趣小组中，同学们从书上认识了很多有趣的数．其中有一个“和平数”引起了同学们的兴趣．描述如下：一个四位数，记千位上和百位上的数字之和为x ，十位上和个位上的数字之和为y ，如果x y =，那么称这个四位数为“和平数”． 例如：1423，14x =+，23y =+，因为x y =，所以1423是“和平数”．（1）直接写出：最小的“和平数”是________，最大的“和平数”是__________； （2）求同时满足下列条件的所有“和平数”：①个位上的数字是千位上的数字的两倍；②百位上的数字与十位上的数字之和是12的倍数；（3）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后这两个“和平数”为“相关和平数”．例如：1423于4132为“相关和平数”求证：任意的两个“相关和平数”之和是1111的倍数．5．如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根，且其中一个根为另一个根的一半，则称这样的方程为“半等分根方程”．（1）①方程2280x x --= 半等分根方程（填“是”或“不是”）；②若(1)()0x mx n -+=是半等分根方程，则代数式2252m mn n ++= ； （2）若点(,)p q 在反比例函数8x y =的图象上，则关于x 的方程260px x q -+=是半等分根方程吗？并说明理由； （3）如果方程20ax bx c ++=是半等分根方程，且相异两点(1,)M t s +，(4,)N t s -都在抛物线2y ax bx c =++上，试说明方程20ax bx c ++=的一个根为53． 6．如图，在菱形ABCD 中，AB a ，60ABC ∠=︒，过点A 作AE BC ⊥，垂足为E ，AF CD ⊥，垂足为F ．（1）连接EF ，用等式表示线段EF 与EC 的数量关系，并说明理由；（2）连接BF ，过点A 作AK BF ⊥，垂足为K ，求BK 的长(用含a 的代数式表示)； （3）延长线段CB 到G ，延长线段DC 到H ，且BG CH =，连接AG ，GH ，AH ． ①判断AGH 的形状，并说明理由；②若12,(33)2ADH a S ==+，求sin GAB ∠的值．7．在平面直角坐标系xOy 中，对于点A 和图形M ，若图形M 上存在两点P ，Q ，使得3AP AQ =，则称点A 是图形M 的“倍增点”．（1）若图形M 为线段BC ，其中点()2,0B -，点()2,0C ，则下列三个点()1,2D -，()1,1E -，()0,2F 是线段BC 的倍增点的是_____________；（2）若O 的半径为4，直线l ：2y x =-+，求直线l 上O 倍增点的横坐标的取值范围；（3）设直线1y x =-+与两坐标轴分别交于G ，H ，OT 的半径为4，圆心T 是x 轴上的动点，若线段GH 上存在T 的倍增点，直接写出圆心T 的横坐标的取值范围．8．∠MON=90°，点A ，B 分别在OM 、ON 上运动（不与点O 重合）．（1）如图①，AE 、BE 分别是∠BAO 和∠ABO 的平分线，随着点A 、点B 的运动，∠AEB= °（2）如图②，若BC 是∠ABN 的平分线，BC 的反向延长线与∠OAB 的平分线交于点D ①若∠BAO=60°，则∠D= °．②随着点A ，B 的运动，∠D 的大小会变吗？如果不会，求∠D 的度数；如果会，请说明理由．（3）如图③，延长MO 至Q ，延长BA 至G ，已知∠BAO ，∠OAG 的平分线与∠BOQ 的平分线及其延长线相交于点E 、F ，在△AEF 中，如果有一个角是另一个角的3倍，求∠ABO 的度数．9．如图一，矩形ABCD 中，AB=m ，BC=n ，将此矩形绕点B 顺时针方向旋转θ（0°＜θ＜90°）得到矩形A 1BC 1D 1，点A 1在边CD 上．（1）若m=2，n=1，求在旋转过程中，点D 到点D 1所经过路径的长度；（2）将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2，点D 2在BC 的延长线上，设边A 2B 与CD 交于点E ，若161A E EC =-，求n m 的值． （3）如图二，在（2）的条件下，直线AB 上有一点P ，BP=2，点E 是直线DC 上一动点，在BE 左侧作矩形BEFG 且始终保持BE n BG m =，设AB=33，试探究点E 移动过程中，PF 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．10．如图，直角三角形ABC ∆中，90460ACB AC A ∠︒=∠︒＝，，＝，O 为BC 中点，将ABC ∆绕O 点旋转180︒得到DCB ∆．一动点P 从A 出发，以每秒1的速度沿A B D →→的路线匀速运动，过点P 作直线PM ，使PM AC ⊥．（1）当点P 运动2秒时，另一动点Q 也从A 出发沿A B D →→的路线运动，且在AB 上以每秒1的速度匀速运动，在BD 上以每秒2的速度匀速运动，过Q 作直线QN 使//QN PM ，设点Q 的运动时间为t 秒，(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ，求S 关于t 的函数关系式，并求出S 的最大值．（2）当点P 开始运动的同时，另一动点R 从B 处出发沿B C D →→的路线运动，且在BC 上以每秒3的速度匀速运动，在CD 上以每秒2的速度匀度运动，是否存在这样的P R 、，使BPR ∆为等腰三角形？若存在，直接写出点P 运动的时间m 的值，若不存在请说明理由．11．问题背景：如图（1），ABC 内接于O ，过点A 作O 的切线l ，在l 上任取一个不同于点A 的点P ，连接PB PC 、，比较BPC ∠与BAC ∠的大小，并说明理由．问题解决：如图（2），A （0，2）、B （0，4），在x 轴正半轴上是否存在一点P ，使得cos APB ∠最小？若存在，求出点P 的坐标；若不存在，请说明理由．拓展应用：如图（3），四边形ABCD 中，//AB CD ，AD CD ⊥于D ，E 是AB 上一点，AE AD =，P 是DE 右侧四边形ABCD 内一点，若8AB =，11CD =，tan 2C =，9DEP S =，求sin APB ∠的最大值．12．如图所示，在平面直角坐标系中，点(),C m m 在一三象限角平分线上，点(),0B n 在x 轴上，且m=2n -+2n -+4，点A 在y 轴的正半轴上；四边形AOBC 的面积为6 （1）求点A 的坐标；（2）P 为AB 延长线上一点，//PQ OC ，交CB 延长线于Q ，探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由；（3）作AD 平行CB 交CO 延长线于D ，BE 平分CBx ∠，BE 反向延长线交CO 延长线于，若设ADO α∠=，F β∠=，试求2αβ+的值．13．如图,矩形ABCD 中，AD >AB ，连接AC ，将线段AC 绕点A 顺时针旋转90∘得到线段AE ，平移线段AE 得到线段DF (点A 与点D 对应，点E 与点F 对应)，连接BF ，分别交直线AD ，AC 于点G ，M ，连接EF ．(1) 依题意补全图形；(2) 求证：EG ⊥AD ；(3) 连接EC ，交BF 于点N ，若AB =2，BC =4，设MB =a ，NF =b ，试比较()()11a b ++与9+6214．在菱形ABCD 中，点P 是对角线BD 上一点，点M 在CB 的延长线上，且PC PM =， 连接PA ．()1如图①，求证：PA PM =；()2如图②，连接,AM PM 与AB 交于点,120O ADC ︒∠=求证 =PC AM ；()3连接AM ，当 90ADC ︒∠=时，PC 与AM 的数量关系是15．如图，抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点，与y 轴交于点B ．()1求这条抛物线的顶点坐标；()2已知AD AB =(点D 在线段AC 上)，有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动：同时另一个点Q 以某一速度从点B 沿线段BC 移动，经过()t s 的移动，线段PQ 被BD 垂直平分，求t 的值；()3在()2的情况下，抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在，请求出点M 的坐标：若不存在，请说明理由．16．在平行四边形ABCD 中，60B ∠=︒，点E ，F 分别在边AB ，AD 上，且60ECF ∠=︒．（1）如图1，若AB BC =，求证：AE AF BC +=；（2）如图2，若4AB BC ==，且点E 为AB 的中点，连接BF 交CE 于点M ，求FM ；（3）如图3，若AB kBC =，探究线段BE 、DF 、BC 三之间的数量关系，说明理由．17．已知抛物线y=﹣x 2﹣2x+3交x 轴于点A 、C （点A 在点C 左侧），交y 轴于点B ．（1）求A ，B ，C 三点坐标；（2）如图1，点D 为AC 中点，点E 在线段BD 上，且BE=2DE ，连接CE 并延长交抛物线于点M ，求点M 坐标；（3）如图2，将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ，连接CG ，点P 为△ACG 内一点，连接PA 、PC 、PG ，分别以AP 、AG 为边，在它们的左侧作等边△APR 和等边△AGQ ，求PA+PC+PG 的最小值，并求当PA+PC+PG 取得最小值时点P 的坐标（直接写出结果即可）．18．已知：矩形ABCD 内接于⊙O ，连接 BD ，点E 在⊙O 上，连接 BE 交 AD 于点F ，∠BDC+45°=∠BFD ，连接ED ．（1）如图 1，求证：∠EBD=∠EDB ；（2）如图2，点G 是 AB 上一点，过点G 作 AB 的垂线分别交BE 和 BD 于点H 和点K ，若HK=BG+AF ，求证：AB=KG ；（3）如图 3，在（2）的条件下，⊙O 上有一点N ，连接 CN 分别交BD 和 AD 于10点 M 和点 P ，连接 OP ，∠APO=∠CPO ，若 MD=8，MC= 3，求线段 GB 的长．19．已知：AB 为⊙O 的直径，点C 为弧AB 的中点，点D 为⊙O 上一点，连接CD ，交AB 于点M ，AE 为∠DAM 的平分线，交CD 于点E ．（1）如图1，连接BE ，若∠ACD=22°，求∠MBE 的度数；（2） 如图2，连接DO 并延长，交⊙O 于点F ，连接AF ，交CD 于点N ．①求证：DM 2+CN 2=CM 2；②如图3，当AD=1，AB=10时，请直接写出．．．．线段ME 的长． 20．如图，抛物线25y ax bx =+-交x 轴于点A 、B （A 在B 的左侧），交y 轴于点C ，且OB OC =，()2,0A -．（1）求抛物线的解析式；（2）点P 为第四象限抛物线上一点，过点P 作y 轴的平行线交BC 于点D ，设P 点横坐标为t ，线段PD 的长度为d ，求d 与t 的函数关系式．（不要求写出t 的取值范围） （3）在（2）的条件下，F 为BP 延长线上一点，且45PFC ∠=︒，连接OF 、CP 、PB ，FOB ∆的面积为3600169，求PBC ∆的面积． 21．如图，已知ABF 为等腰直角三角形，90BAF ∠=︒，D 、C 为直线AF 上两点，且满足DF AC =，连接BD 、BC ，过点A 作AE BD ⊥于点E ，交BF 于点H ，连接CH ．（1）若30BAE ∠=︒，1BE =，求DE 的长；（2）若点M 是线段BF 上的动点，连AM 并延长交BD 于N ，当M 在线段BF 的什么位置上时，AH BN =？请说明理由；（3）在（2）的结论下，判断线段CH 、AH 、BD 的数量关系．请说明理由．22．如图1，以AB 为直径作⊙O ，点C 是直径AB 上方半圆上的一点，连结AC ，BC ，过点C 作∠ACB 的平分线交⊙O 于点D ，过点D 作AB 的平行线交CB 的延长线于点E ．（1）如图1，连结AD ，求证：∠ADC ＝∠DEC ．（2）若⊙O 的半径为5，求CA •CE 的最大值．（3）如图2，连结AE ，设tan ∠ABC ＝x ，tan ∠AEC ＝y ，①求y 关于x 的函数解析式；②若CB BE ＝45，求y 的值． 23．发现来源于探究．小亮进行数学探究活动，作边长为a 的正方形ABCD 和边长为b 的正方形AEFG （a>b ），开始时，点E 在AB 上，如图1．将正方形AEFG 绕点A 逆时针方向旋转．（1）如图2，小亮将正方形AEFG 绕点A 逆时针方向旋转，连接BE 、DG ，当点G 恰好落在线段BE 上时，小亮发现DG ⊥BE ，请你帮他说明理由．当a=3，b=2时，请你帮他求此时DG 的长．（2）如图3，小亮旋转正方形AEFG ，点E 在DA 的延长线上，连接BF 、DF ．当FG 平分∠BFD 时，请你帮他求a ：b 及∠FBG 的度数．（3）如图4，BE 的延长线与直线DG 相交于点P ，a=2b ．当正方形AEFG 绕点A 从图1开始，逆时针方向旋转一周时，请你帮小亮求点P 运动的路线长（用含b 的代数式表示）．24．如图，二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ，另一个交点为A ，且与y 轴相交于C 点（1）则m =_________；C 点坐标为___________；（2）在直线BC 上方的抛物线上是否存在一点M ，使得它与B ，C 两点构成的三角形面积最大，若存在，求出此时M 点坐标；若不存在，请简要说明理由．（3）P 为抛物线上一点，它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时，求点P 的坐标；②点P 的横坐标为(04)t t <<，当t =________时，四边形PBQC 的面积最大．25．附加题：在平面直角坐标系中，抛物线21y ax a =-与y 轴交于点A ，点A 关于x 轴的对称点为点B ，（1）求抛物线的对称轴；（2）求点B 坐标（用含a 的式子表示）；（3）已知点11,P a ⎛⎫ ⎪⎝⎭，(3,0)Q ，若抛物线与线段PQ 恰有一个公共点，结合函数图像，求a 的取值范围．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．D解析：（1）见解析；（2）y=1603x +；（2）2 【解析】【分析】（1）根据翻折的性质得△DFG ≌△DFA ，从而推导得出∠FDC=∠DFG ，进而得到CF=DC ； （2）在等腰△DGC 和等腰△CFD 中，可用y 表示出∠GDC 、∠FDC 的值，从而求出∠ADF ，根据∠ADE=∠DEC ，得出y 与x 的关系式；（3）先证△KCD 是等腰直角三角形，根据CD 的长得到KC 的值，然后再△KGC 中求得KG 的值.【详解】（1）∵将菱形ABCD 沿DF 翻折，点A 恰好落在点G 上∴△DFG ≌△DFA ，∠AFD=∠FDC∴∠AFD=∠DFG∴∠FDC=∠DFG∴CF=DC ；（2）∵AD=DG=DC=FC ，∠DCF=y∴在△DGC 中，∠DGC=y ，∠GDC=180－2y在△CFD 中，∠CFD=∠CDF=902y -∴∠FDG=∠FDC －∠GDC=3902y - ∴∠ADF=∠FDG=3902y -，∴∠ADE=3y －180 ∵AD ∥BC∴∠ADE=∠DEC ，即3y －180=x化简得：y=1603x +； （3）如下图，过点K 作CD 的垂线，交CD 于点I ，延长KG 交BC 于点L ，过点C 作GL 的垂线，交GL 于点Q ，过点C 作GD 的垂线，交GD 于点N ，∵x=45°，∴y=75°，∠ADE=x=45°∴∠DGC=∠DCG=75°，∴∠NDC=30°，∴∠ADC=45°+30°=75°，∵四边形ABCD是菱形，∴∠B=75°，∵KG∥DC，∴KG∥AB，∠KGD=∠NDC=30°，∴∠GLC=∠B=75°，∠KGC=30°+75°=105°，∴∠LGC=75°，∴∠CGL=∠CGN，∴GC是∠LGN的角平分线，∴CQ=CN，∵CD=4，∠CDE=30°，∴在Rt△CND中，CN=2，∴CQ=2，∵KG∥CD，∴∠QKI=∠KIC=90°∵CQ⊥KL∴四边形CQKI是矩形，∵CK=KD，KI⊥CD，∴CI=ID=2，∴CI=CQ=2，∴矩形CQKI是正方形∴IK=CQ=2，∴在Rt△KIC中，CK=22，如下图，过点G作CK的垂线，交CK于点M，∴△KGM是等腰直角三角形，△GMC是直角三角形，且∠C=30°，设GM=x，则在Rt△GKM中，KM=GM=x，在Rt△GMC中，CG=2x，3x，∴322解得：62∴2=232x.【点睛】本题考查菱形的性质和翻折的性质，需要注意，翻折后的图形和翻折前的图形时完全相等的，这个条件不可忽略.2．B解析：（1）①（2，0），（12），（﹣12y2x；③y＝﹣22x2；（2）①半径为2，M（3333）；②2＜r＜4【解析】【分析】（1）①如图2−1中，作BE∥OD交OA于E，CF∥OD交x轴于F．求出OE、OF、CF、OD、BE即可解决问题；②如图2−2中，作BE∥OD交OA于E，作PM∥OD交OA于M．利用平行线分线段成比例定理即可解决问题；③如图3−3中，作QM∥OA交OD于M．利用平行线分线段成比例定理即可解决问题；（2）①如图3中，作MF⊥OA于F，作MN∥y轴交OA于N．解直角三角形即可解决问题；②如图4中，连接OM，作MK∥x轴交y轴于K，作MN⊥OK于N交⊙M于E、F．求出FN＝NE＝1时，⊙M的半径即可解决问题；【详解】解：（1）①如图2﹣1中，作BE∥OD交OA于E，CF∥OD交x轴于F．由题意OC ＝CD ＝1，OA ＝BC ＝2，∴BD ＝OE ＝1，OD ＝CF ＝BE＝2， ∴A(2,0)，B(1,2)，C(﹣1,2)，故答案为：A(2,0)，B(1,2)，C(﹣1,2)．②如图2﹣2中，作BE ∥OD 交OA 于E ，作PM ∥OD 交OA 于M ．∵OD ∥BE ，OD ∥PM ，∴BE ∥PM ，∴BE OE PM OM=， ∴21y x=， ∴y ＝2x ．故答案为：y ＝2x ．③如图2﹣3中，作QM ∥OA 交OD 于M ．222MQ DM OA DOx y ∴=-∴= ∴222y x =-+故答案为：y＝﹣22x+2．（2）①如图3中，作MF⊥OA于F，作MN∥y轴交OA于N．∵ω＝120°，OM⊥y轴，∴∠MOA＝30°，∵MF⊥OA，OA＝23，∴OF＝FA＝3，∴FM＝1，OM＝2FM＝2，∴圆M的半径为2∵MN∥y轴，∴MN⊥OM，∴MN＝233，ON＝2MN＝433，∴M4323,33⎛⎫⎪ ⎪⎝⎭．②如图4中，连接OM，作MK∥x轴交y轴于K，作MN⊥OK于N交⊙M于E、F．∵MK∥x轴，ω＝120°，∴∠MKO＝60°，∵MK＝OK＝3∴△MKO是等边三角形，∴MN＝3，当FN＝1时，MF＝3﹣1=2，当EN＝1时，ME＝3+1=4，观察图象可知当⊙M的半径r的取值范围为2＜r＜4．故答案为：2＜r＜4．【点睛】本题考查圆综合题、平行线分线段成比例定理、等边三角形的判定和性质、平面斜坐标系等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考压轴题．3．E解析：（1）∠EPF=∠AEP+∠PFC，∠AEP+∠EPF+∠PFC=360°；（2）见解析；（3）①150°，∠EQF=180°－12∠EPF【解析】【分析】（1）如下图，过点P作AB的平行线，根据平行线的性质可推导出角度关系；（2）如下图，根据（1）的结论，可得∠AEP+∠PFC=∠EPF=90°，利用△EPF内角和为180°可推导得出∠PEF+∠PFE=90°，从而得出∠PEF=∠AEP；（3）①根据（1）的结论知：∠AEP+∠PFC=∠EPF=60°，再利用角平分线的性质得出∠PEQ+∠PFQ=150°，最后在四边形EPFQ中得出结论；②根据（1）的结论知：∠AEP+∠PFC=∠EPF°，再利用角平分线的性质得出∠PEQ+∠PFQ=180°－1EPF2，最后在四边形EPFQ中得出结论．【详解】（1）如下图，过点P作PQ∥AB∵PQ∥AB，AB∥CD，∴PQ∥CD ∴∠AEP=∠EPQ，∠QPF=∠PFC 又∵∠EPF=∠EPQ+∠QPF∴∠EPF=∠AEP+∠PFC如下图，过点P作PQ∥AB同理，AB ∥QP ∥CD∴∠AEP+∠QPE=180°，∠QPF+∠PFC=180°∴∠AEP+∠EPF+∠PFC=∠AEP+∠EPQ+∠QPF+∠PFC=360°（2）根据（1）的结论知：∠AEP+∠PFC=∠EPF=90°∵PF 是∠CFE 的角平分线，∴∠PFC=∠PFE在△PEF 中，∵∠EPF=90°，∴∠PEF+∠PFE=90°∴∠PEF+∠PFE=∠AEP+∠PFC∴∠PEF=∠AEP ，∴PE 是∠AEF 的角平分线（3）①根据（1）的结论知：∠AEP+∠PFC=∠EPF=60°∴∠BEP+∠PFD=180°－∠AEP+180°－∠PFC=300°∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=QEB ，∠PFQ=∠QFD∴∠PEQ+∠PFQ=150°在四边形PEQF 中，∠EQF=360°－∠EPF －(∠PEQ+∠PFQ)=360°－60°－150°=150° ②根据（1）的结论知：∠AEP+∠PFC=∠EPF∴∠BEP+∠PFD=180°－∠AEP+180°－∠PFC=360°－∠EPF∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=∠QEB ，∠PFQ=∠QFD∴∠PEQ+∠PFQ=()1360EPF 2∠︒－=180°－1EPF 2∠ ∴在四边形PEQF 中： ∠EQF=360°－∠EPF －(∠PEQ+∠PFQ)=360°－EPF ∠－(180°－1EPF 2∠)=180°－1EPF 2∠ 【点睛】本题考查“M ”型模型，解题关键在过两条平行线中间的点作已知平行线的平行线，然后利用平行线的性质进行角度转化可推导结论．4．（1）1001；9999；（2）2754和4848；（3）见解析【解析】【分析】（1）根据“和平数”的定义可直接得出最小的“和平数”是1001，最大的“和平数”是9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤，则个位数字是2a ，又由029a ≤≤得到a 的可能取值为1，2，3，4；根据百位上的数字与十位上的数字之和是12的倍数，可知m +n =12，得到122a m +=，由a 的可能取值可得m 的取值，即可求得符合条件的“和平数”；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ，计算它们的和，根据“和平数”的定义可知a+b=c+d ，因式分解可得原式= 1111(a+b )，即可证明．【详解】解：（1）根据“和平数”的定义可得：最小的“和平数”1001，最大的“和平数”9999，故答案为1001；9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤，则个位数字是2a ，又∵029a ≤≤，∴a 的可能取值为1，2，3，4；∵百位上的数字与十位上的数字之和是12的倍数，∴m+n =0或m+n =12，∵“和平数”中a+m =n+2a ，当m+n =0时，即m=n =0，则此时a =0，不符合题意，∴m+n =12，∴a+m =12−m +2a ，解得：122a m +=， ∵a 的可能取值为1，2，3，4；且m 为正整数，∴m 的可能取值为7，8；当a =2时，m =7，这个“和平数”是2754；当a =4时，m =8，这个“和平数”是4848；综上所述，满足条件的“和平数”是2754和4848；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ， ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知：a+b =c+d ，∴原式1100()11()a b a b =+++1111()a b =+，∵a ，b 为正整数，则1111()a b +能被1111整除，即(100010010)(100010010)a b c d b a d c +++++++能被1111整除，∴任意的两个“相关和平数”之和是1111的倍数．【点睛】本题考查新定义运算、因式分解的应用；能够读懂题意，根据数的特点，确定数的取值范围，进行正确的因式分解是解题关键．5．（1）①不是；②0；（2）若点(,)p q 在反比例函数8y x =的图象上，则关于x 的方程260px x q -+=是半等分根方程，理由详见解析；（3）详见解析【解析】【分析】（1）①解方程2280x x --=，根据“半等分根方程”定义作出判断即可；②解方程(1)()0x mx n -+=得11x =，2n x m =-，所以12n m -=或2n m -=，即：n =-2m 或m =-2n ，分别代入代数式2252m mn n ++=结果均为0 （2）根据点(,)p q 在反比例函数8y x =的图象上，得到8q p =，代入260px x q -+=，得到关于x 的方程2860px x p-+=，解方程，用含p 的式子表示x ，根据“半等分根方程”定义判断即可；（3）根据两点(1,)M t s +，(4,)N t s -都在抛物线上，且纵坐标相等，可以求出对称轴为52x =，根据方程20ax bx c ++=是半等分根方程，得到两根关系，根据抛物线对称轴为 12522x x +=，即可求出两个根，问题得证． 【详解】解：（1）①解方程2280x x --=得124,2x x ==-，不符合“半等分根方程”定义， 故答案为：不是；②解方程(1)()0x mx n -+=得11x =，2n x m =-，所以12n m -=或2n m -=，即：n =-2m 或m =-2n ，当n =-2m 时，()()22225522022m mn n m m n m ++=+-+-=； 当m =-2n 时，()()22225522022m mn n n n n n ++=-+-+=； 故答案为：0；（2）若点(,)p q 在反比例函数8y x =的图象上，则关于x 的方程260px x q -+=是半等分根方程理由：∵点(,)p q 在反比例函数8y x =的图象上 ∴8q p=代入方程260px x q -+=得： 2860px x p -+=解得：12x p =，24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程（3）∵相异两点(1,)M t s +，(4,)N t s -都在抛物线2y ax bx c =++上， ∴抛物线的对称轴为：(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有：12522x x += 所以153x =，2103x = 所以方程20ax bx c ++=的一个根为53得证． 【点睛】本题为“新定义问题”，考查了学生自主学习的能力，解决此题关键是理解新定义概念，并结合所学数学知识进行解答．6．E解析：（1）EF =，见解析；（2）BK =；（3）①AGH 是等边三角形，见解析；②14 【解析】【分析】（1）连接EF ，AC ，由菱形的性质，可证Rt AEB Rt AFD ∆≅∆，然后得到AEF ∆为等边三角形，由解直角三角形得到AE =，即可得到答案；（2）由菱形的性质和等边三角形的性质，求出AF 的长度，然后得到BF 的长度，然后由相似三角形的性质，得到AB BK FB BA=，即可求出答案； （3）①由等边三角形的性质，先证明ABG ACH ≅，然后得到AG AH =，然后得到60BAH GAB GAH ︒∠+∠=∠=，即可得到答案；②由三角形的面积公式得到1DH =，然后得到AHF △为等腰直角三角形，再由解直角三角形的性质，即可求出答案．【详解】解：（1）EF =；理由：∵四边形ABCD 是菱形，60ABC ∠=︒，,60,//AB AD BC ABC ADC AD BC ︒∴==∠=∠=，120BAD ︒∴∠=，∵AE BC ⊥，垂足为E ，AF CD ⊥，垂足为F ，90AEB AFD ︒∴∠=∠=Rt AEB Rt AFD ∴∆≅∆，,30AE AF BAE DAF ∴=∠=∠=︒，60EAF ∴∠=︒，AEF ∴∆为等边三角形，EF AE ∴=.连接AC ，1602BAC BAD ︒∴∠=∠= 30EAC ︒∴∠= 在Rt AEC ∆中，tan EC EAC AE ∠=3AE EC ∴=，3EF EC ∴=（2）如图：∵四边形ABCD 是菱形，60,ABC AB a ︒∠==， ACD ∴是等边三角形，//,,60AB CD AD CD a ADC ︒==∠=.AF CD ⊥，垂足为F ，1,902CF DF a BAF AFD ︒∴==∠=∠= 在Rt ADF 中，sin AF ADF AD ∠=， 3AF ∴=在Rt ABF 中，22BF AB AF =+，72BF a ∴= AK BF ⊥，垂足为K ，90AKB FAB ︒∴∠=∠=ABK FBA ∠=∠~Rt AKB Rt FAB ∴∆∆，AB BK FB BA∴=， 27BK a ∴=， （3）如图：①AGH 是等边三角形.理由：连接AC .,60AB BC ABC ︒=∠=，ABC ∴为等边三角形，,60AB AC ABC ACB ︒∴=∠=∠=，120ABG ︒∴∠=. //AB CD ，60BCH ABC ︒∴∠=∠=，120ACH ︒∴∠=ABG ACH ∴∠=∠，又BG CH =，ABG ACH ∴≅，,AG AH GAB HAC ∴=∠=∠.60BAH HAC BAC ︒∠+∠=∠=，60BAH GAB GAH ︒∴∠+∠=∠=，AGH ∴为等边三角形；②ADC 为等边三角形，2,1AD DC AC CF DF ∴=====，AF ∴=.1(32ADH S =， 11(322DH ∴⨯=，1DH ∴=1CH DH CD ∴=-=，HF DH DF =-=AF HF ∴=，AHF ∴为等腰直角三角形，45AHF ︒∴∠=.过点C 作CM AH ⊥，垂足为M .在Rt CMH 中，sin CM CHM CH∠=， 12CM ∴=， 在Rt AMC 中，sin CM MAC AC ∠=， 1sin 4MAC ∴∠=. 又GAB HAC ∠=∠， 1sin sin 4GAB HAC ∴∠=∠=； 【点睛】本题考查了解直角三角形，相似三角形的判定和性质，等边三角形的判定和性质，菱形的性质，等腰三角形的判定和性质，全等三角形的判定和性质，解题的关键是熟练掌握所学的定理和性质，正确作出辅助线进行解题．7．A解析：（1）()1,1E -；（2）12m -≤≤-或01m ≤≤3）9t ≤≤.【解析】【分析】（1）首先要理解点A 是图形M 的“倍增点”的定义，将三个点逐一代入验证即可； （2）分两种情况:①点"倍增点”在O 的外部，分别求得“倍增点”横坐标的最大值和最小值，②点"倍增点"在O 的内部，依次求得“倍增点"横坐标的最大值和最小值，即可确定“倍增点”横坐标的范围；（3）分别求得线段GH 两端点为T "倍增点”时横坐标的最大值和最小值即可．【详解】（1）()1,2D -到线段BC 的距离为2，22(12)(20)1332DC =--+-=<⨯∴()1,2D -不是线段BC 的倍增点；()1,1E -到线段BC 的距离为1，22(12)(10)103EC =--+-=>,∴在线段BC 上必存在一点P 使EP=3，∴()1,1E -是线段BC 的倍增点；()0,2F 到线段BC 的距离为2，22(02)(20)2232FC =-+-=<⨯∴()0,2F 不是线段BC 的倍增点；综上，()1,1E -是线段BC 的倍增点；（2）设直线l 上“倍增点”的横坐标为m ，当点在O 外时，222(2)8,m m +-+≤解方程222(2)8m m +-+=，得1131m =+，2131m =-当点在O 内部时，22224(2)3(44(2))m m m m ++-+≥--+-+解得：m≥0或m≤-2∴直线l 上“倍增点”的橫坐标的取值范围为1312m -≤≤-或0131m ≤≤+；（3）如图所示，当点G(1,0)为T "倍增点"时，T(9,0)，此时T 的横坐标为最大值，当点H(0,1)为T “倍增点”时，则T(63，此时T 的横坐标为最小值；∴圆心T(t, 0)的横坐标的取值范围为：639t -≤≤．【点睛】在正确理解点A 是图形M 的“倍增点”定义的基础上，利用（1）判断是否是倍增点的不等关系式，即可列不等式组求解范围．8．A解析：（1）135°；（2）①45°，②不发生变化，45°；（3）60°或45°【解析】【分析】（1）利用三角形内角和定理、两角互余、角平分线性质即可求解；（2）①利用对顶角相等、两角互余、两角互补、角平分线性质即可求解；②证明和推理过程同①的求解过程；（3）由（2）的证明求解思路，不难得出EAF ∠=90°，如果有一个角是另一个角的3倍，所以不确定是哪个角是哪个角的三倍，所以需要分情况讨论；值得注意的是，∠MON=90°，所以求解出的∠ABO 一定要小于90°，注意解得取舍.【详解】（1）()11801802118090180451352AEB EBA BAE OBA BAO ∠=︒-∠-∠=︒-∠+∠=︒-⨯︒=︒-︒=︒（2）①如图所示AD 与BO 交于点E ，()9060301180307521909030602180180756045OBA DBO NBC DEB OEA OAB D DBE DEB ∠=︒-︒=︒∠=∠=︒-︒=︒∠=∠=︒-∠=︒-︒=︒∠=︒-∠-∠=︒-︒-︒=︒②∠D 的度数不随A 、B 的移动而发生变化设BAD α∠=，因为AD 平分∠BAO ，所以2BAO α∠=，因为∠AOB=90°，所以180902ABN ABO AOB BAO α∠=︒-∠=∠+∠=+。

中考数学抛物线压轴题之矩形（1）如图1，点P为抛物线上位于x轴下方一点，连接PB，PD，当S△PBD最大时，连接AP，以PB为边向上作正△BPQ，连接AQ，点M与点N为直线AQ上的两点，MN＝2且点N位于M点下方，连接DN，求DN+MN+AM的最小值（2）如图2，在第（1）问的条件下，点C关于x轴的对称点为E，将△BOE绕着点A逆时针旋转60°得到△B′O′E′，将抛物线y＝沿着射线PA方向平移，使得平移后的抛物线C′经过点E，此时抛物线C′与x轴的右交点记为点F，连接E′F，B′F，R为线段E’F上的一点，连接B′R，将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT，在平面内找一个点S，使得以B′、R、T、S为顶点的四边形为矩形，求点S的坐标．2．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＜0）与x轴交于A（﹣2，0）、B（4，0）两点，与y轴交于点C，且OC＝2OA．（1）试求抛物线的解析式；（2）直线y＝kx+1（k＞0）与y轴交于点D，与抛物线交于点P，与直线BC交于点M，记m＝，试求m 的最大值及此时点P的坐标；（3）在（2）的条件下，点Q是x轴上的一个动点，点N是坐标平面内的一点，是否存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形？如果存在，请求出点N的坐标；如果不存在，请说明理由．3．如图，在平面直角坐标系xOy中，O为坐标原点，抛物线y＝a（x+3）（x﹣1）（a＞0）与x轴交于A，B 两点（点A在点B的左侧）．（1）求点A与点B的坐标；（2）若a＝，点M是抛物线上一动点，若满足∠MAO不大于45°，求点M的横坐标m的取值范围．（3）经过点B的直线l：y＝kx+b与y轴正半轴交于点C．与抛物线的另一个交点为点D，且CD＝4BC．若点P在抛物线对称轴上，点Q在抛物线上，以点B，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．4．如图，一次函数y＝x+3与坐标轴交于A、C两点，过A、C两点的抛物线y＝ax2﹣2x+c与x轴交于另一点B抛物线顶点为E，连接AE．（1）求该抛物线的函数表达式及顶点E坐标；（2）点P是线段AE上的一动点，过点P作PF平行于y轴交AC于点F，连接EF，求△PEF面积的最大值及此时点P的坐标；（3）若点M为坐标轴上一点，点N为平面内任意一点，是否存在这样的点，使A、E、M、N为顶点的四边形是以AE为对角线的矩形？如果存在，请直接写出N点坐标；若不存在，请说明理由．5．如图1，抛物线y＝﹣x2+x﹣2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，直线AE：y＝x﹣与抛物线相交于另一点E，点D为抛物线的顶点．（1）求直线BC的解析式及点E的坐标；（2）如图2，直线AE上方的抛物线上有一点P，过点P作PF⊥BC于点F，过点P作平行于y轴的直线交直线BC于点G，当△PFG周长最大时，在y轴上找一点M，在AE上找一点N，使得PM+MN+NE值最小，请求出此时N点的坐标及PM+MN+NE的最小值；（3）在第（2）问的条件下，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点N，E，R，S为顶点的四边形为矩形？若存在，请直接写出点S的坐标；若不存在，请说明理由．6．如图：在平面直角坐标系中，直线l：y＝x﹣与x轴交于点A，经过点A的抛物线y＝ax2﹣3x+c的对称轴是x＝．（1）求抛物线的解析式；（2）平移直线l经过原点O，得到直线m，点P是直线m上任意一点，PB⊥x轴于点B，PC⊥y轴于点C，若点E在线段OB上，点F在线段OC的延长线上，连接PE，PF，且PF＝3PE．求证：PE⊥PF；（3）若（2）中的点P坐标为（6，2），点E是x轴上的点，点F是y轴上的点，当PE⊥PF时，抛物线上是否存在点Q，使四边形PEQF是矩形？如果存在，请求出点Q的坐标，如果不存在，请说明理由．7．如图，已知抛物线y＝x2+bx+c与直线AB：y＝﹣x+相交于点A（1，0）和B（t，），直线AB交y轴于点C．（1）求抛物线的解析式及其对称轴；（2）点D是x轴上的一个动点，连接BD、CD，请问△BCD的周长是否存在最小值？若存在，请求出点D的坐标，并求出周长最小值；若不存在，请说明理由．（3）设点M是抛物线对称轴上一点，点N在抛物线上，以点A、B、M、N为顶点的四边形是否可能为矩形？若能，请求出点M的坐标，若不能，请说明理由．8．如图，在平面直角坐标系中，直线l：y＝kx+h与x轴相交于点A（﹣1，0），与y轴相交于点C，与抛物线y＝﹣x2+bx+3的一交点为点D，抛物线过x轴上的AB两点，且CD＝4AC．（1）求直线l和抛物线的解析式；（2）点E是直线l上方抛物线上的一动点，求当△ADE面积最大时，点E的坐标；（3）设P是抛物线对称轴上的一点，点Q在抛物线上，四边形APDQ能否为矩形？若能，请直接写出点P 的坐标；若不能，请说明理由．9．如图，抛物线y＝x2+hx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．（1）求经过A，B，C三点的抛物线的函数表达式；（2）点P是线段BD上一点，当PE＝PC时，求点P的坐标；（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物上点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是矩形，且MG＝2FM时，请求出点M的坐标．10．如图，已知二次函数y＝m2x2﹣2mx﹣3（m是常数，m＞0）的图象与x轴分别相交于点A、B（点A位于点B的左侧），与y轴交于点C，对称轴为直线l．点C关于l的对称点为D，连接AD．点E为该函数图象上一点，AB平分∠DAE．（1）①线段AB的长为．②求点E的坐标；（①、②中的结论均用含m的代数式表示）（2）设M是该函数图象上一点，点N在l上．探索：是否存在点M．使得以A、E、M、N为顶点的四边形是矩形？如果存在，求出点M坐标；如果不存在，说明理由．11．如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣2ax﹣3a（a＜0）与x轴交于A，B两点（点A在点B 的左侧），经过点A的直线l：y＝kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD＝4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；（2）点E是直线l上方的抛物线上的一点，若△ACE的面积的最大值为，求a的值；（3）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．12．如图，抛物线y＝﹣x2+2x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D和点C 关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求直线AD的解析式；（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH周长的最大值；（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．13．如图，已知在平面直角坐标系xOy中，O是坐标原点，抛物线y＝﹣x2+bx+c（c＞0）的顶点为D，与y 轴的交点为C，过点C作CA∥x轴交抛物线于点A，在AC延长线上取点B，使BC＝AC，连接OA，OB，BD 和AD．（1）若点A的坐标是（﹣4，4）．①求b，c的值；②试判断四边形AOBD的形状，并说明理由；（2）是否存在这样的点A，使得四边形AOBD是矩形？若存在，请直接写出一个符合条件的点A的坐标；若不存在，请说明理由．14．如图，已知二次函数的图象过点A（0，﹣3），B（，），对称轴为直线x＝﹣，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC＝MP，MD＝OM，OE＝ON，NF＝NP．（1）求此二次函数的解析式；（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．15．如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x＝﹣1．（1）求抛物线对应的函数关系式；（2）动点Q从点O出发，以每秒1个单位长度的速度在线段OA上运动，同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动，过点Q作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒．①当t为何值时，四边形OMPQ为矩形；②△AON能否为等腰三角形？若能，求出t的值；若不能，请说明理由．16．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＜0）与x轴交于A（﹣2，0）、B（4，0）两点，与y轴交于点C，且OC＝2OA．（1）试求抛物线的解析式；（2）直线y＝kx+1（k＞0）与y轴交于点D，与抛物线交于点P，与直线BC交于点M，记m＝，试求m 的最大值及此时点P的坐标；（3）在（2）的条件下，点Q是x轴上的一个动点，点N是坐标平面内的一点，是否存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形？如果存在，请求出点N的坐标；如果不存在，请说明理由．17．如图，在平面直角标系中，抛物线C：y＝与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为y轴正半轴上一点．且满足OD＝OC，连接BD，（1）如图1，点P为抛物线上位于x轴下方一点，连接PB，PD，当S△PBD最大时，连接AP，以PB为边向上作正△BPQ，连接AQ，点M与点N为直线AQ上的两点，MN＝2且点N位于M点下方，连接DN，求DN+MN+AM的最小值（2）如图2，在第（1）问的条件下，点C关于x轴的对称点为E，将△BOE绕着点A逆时针旋转60°得到△B′O′E′，将抛物线y＝沿着射线PA方向平移，使得平移后的抛物线C′经过点E，此时抛物线C′与x轴的右交点记为点F，连接E′F，B′F，R为线段E’F上的一点，连接B′R，将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT，在平面内找一个点S，使得以B′、R、T、S为顶点的四边形为矩形，求点S的坐标．1．【解答】解：（1）如图1，过点D作DD'∥MN，且DD'＝MN＝2，连接D'M；过点D'作D'J⊥y轴于点J；作直线AP，过点M作MH⊥AP于点H，过点D'作D'K⊥AP于点K∵y＝＝0解得：x1＝﹣3，x2＝1∴A（﹣3，0），B（1，0）∵x＝0时，y＝＝﹣∴C（0，﹣），OC＝∴OD＝OC＝，D（0，）设P（t，t2+t﹣）（﹣3＜t＜1）设直线PB解析式为y＝kx+b，与y轴交于点G∴解得：∴直线PB：y＝（t+）x﹣t﹣，G（0，﹣t﹣）∴DG＝﹣（﹣t﹣）＝t+∴S△BPD＝S△BDG+S△PDG＝DG•x B+DG•|x P|＝DG•（x B﹣x P）＝（t+）（1﹣t）＝﹣（t2+4t﹣5）∴t＝﹣＝﹣2时，S△BPD最大∴P（﹣2，﹣），直线PB解析式为y＝x﹣，直线AP解析式为y＝﹣x﹣3∴tan∠ABP＝＝∴∠ABP＝30°∵△BPQ为等边三角形∴∠PBQ＝60°，BP＝PQ＝BQ∴BA平分∠PBQ∴PQ⊥x轴，PQ与x轴交点I为PQ中点∴Q（﹣2，）∴Rt△AQI中，tan∠QAI＝∴∠QAI＝∠PAI＝60°∴∠MAH＝180°﹣∠PAI﹣∠QAI＝60°∵MH⊥AP于点H∴Rt△AHM＝90°，sin∠MAH＝∴MH＝AM∵DD'∥MN，DD'＝MN＝2∴四边形MNDD'是平行四边形∴D'M＝DN∴DN+MN+AM＝2+D'M+MH∵D'K⊥AP于点K∴当点D'、M、H在同一直线上时，DN+MN+AM＝2+D'M+MH＝2+D'K最短∵DD'∥MN，D（0，）∴∠D'DJ＝30°∴D'J＝DD'＝1，DJ＝DD'＝∴D'（1，）∵∠PAI＝60°，∠ABP＝30°∴∠APB＝180°﹣∠PAI﹣∠ABP＝90°∴PB∥D'K设直线D'K解析式为y＝x+d，把点D'代入得：+d＝解得：d＝∴直线D'K：y＝x+把直线AP与直线D'K解析式联立得：解得：∴K（﹣，）∴D'K＝∴DN+MN+AM的最小值为（2）连接B'A、BB'、EA、E'A、EE'，如图2∵点C（0，﹣）关于x轴的对称点为E∴E（0，）∴tan∠EAB＝∴∠EAB＝30°∵抛物线C'由抛物线C平移得到，且经过点E∴设抛物线C'解析式为：y＝x2+mx+，∵A（﹣3，0），P（﹣2，﹣），E（0，），B（1，0），∴BE∥PA，BE＝PA，∴抛物线C'经过点A（﹣3，0），∴×9﹣3m+＝0解得：m＝∴抛物线C'解析式为：y＝x2+x+∵x2+x+＝0，解得：x1＝﹣3，x2＝﹣1∴F（﹣1，0）∵将△BOE绕着点A逆时针旋转60°得到△B′O′E′∴∠BAB'＝∠EAE'＝60°，AB'＝AB＝1﹣（﹣3）＝4，AE'＝AE＝∴△ABB'、△AEE'是等边三角形∴∠E'AB＝∠E'AE+∠EAB＝90°，点B'在AB的垂直平分线上∴E'（﹣3，2），B'（﹣1，2）∴B'E'＝2，∠FB'E'＝90°，E'F＝∴∠B'FE'＝30°，∠B'E'F＝60°①如图3，点T在E'F上，∠B'TR＝90°过点S作SW⊥B'E'于点W，设翻折后点E'的对应点为E'' ∴∠E'B'T＝30°，B'T＝B'E'＝∵△B′E′R翻折得△B'E''R∴∠B'E''R＝∠B'E'R＝60°，B'E''＝B'E'＝2∴E''T＝B'E''﹣B'T＝2﹣∴Rt△RTE''中，RT＝E''T＝2﹣3∵四边形RTB'S是矩形∴∠SB'T＝90°，SB'＝RT＝2﹣3∴∠SB'W＝∠SB'T﹣∠E'B'T＝60°∴B'W＝SB'＝﹣，SW＝SB'＝3﹣∴x S＝x B'﹣B'W＝，y S＝y B'+SW＝3+∴S（，3+）②如图4，点T在E'F上，∠B'RT＝90°过点S作SX⊥B'F于点X∴E'R＝B'E'＝1，点E'翻折后落在E'F上即为点T∴B'S＝RT＝E'R＝1∵∠SB'X＝90°﹣∠RB'F＝30°∴XS＝B'S＝，B'X＝B'S＝∴x S＝x B'+XS＝﹣，y S＝y B'﹣B'X＝∴S（﹣，）③如图5，点T在B'F上，∠B'TR＝90°∴RE''∥E'B'，∠E''＝∠B'E'R＝60°∴∠E'BE''＝∠E'RE''＝120°∴四边形B'E'RE''是平行四边形∵E'R＝E''R∴▱B'E'RE''是菱形∴B'E'＝E'R∴△B'E'R是等边三角形∵∠B'SR＝90°，即RS⊥B'E'∴点S为B'E'中点∴S（﹣2，2）综上所述，使得以B′、R、T、S为顶点的四边形为矩形的点S坐标为（，3+）或（﹣，）或（﹣2，2）．2．【解答】解：（1）因为抛物线y＝ax2+bx+c经过A（﹣2，0）、B（4，0）两点，所以可以假设y＝a（x+2）（x﹣4），∵OC＝2OA，OA＝2，∴C（0，4），代入抛物线的解析式得到a＝﹣，∴y＝﹣（x+2）（x﹣4）或y＝﹣x2+x+4或y＝﹣（x﹣1）2+．（2）如图1中，由题意，点P在y轴的右侧，作PE⊥x轴于E，交BC于F．∵CD∥PE，∴△CMD∽△FMP，∴m＝＝，∵直线y＝kx+1（k＞0）与y轴交于点D，则D（0，1），∵BC的解析式为y＝﹣x+4，设P（n，﹣n2+n+4），则F（n，﹣n+4），∴PF＝﹣n2+n+4﹣（﹣n+4）＝﹣（n﹣2）2+2，∴m＝＝﹣（n﹣2）2+，∵﹣＜0，∴当n＝2时，m有最大值，最大值为，此时P（2，4）．（3）存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形．①当DP是矩形的边时，有两种情形，a、如图2﹣1中，四边形DQNP是矩形时，有（2）可知P（2，4），代入y＝kx+1中，得到k＝，∴直线DP的解析式为y＝x+1，可得D（0，1），E（﹣，0），由△DOE∽△QOD可得＝，∴OD2＝OE•OQ，∴1＝•OQ，∴OQ＝，∴Q（，0）．根据矩形的性质，将点P向右平移个单位，向下平移1个单位得到点N，∴N（2+，4﹣1），即N（，3）b、如图2﹣2中，四边形PDNQ是矩形时，∵直线PD的解析式为y＝x+1，PQ⊥PD，∴直线PQ的解析式为y＝﹣x+，∴Q（8，0），根据矩形的性质可知，将点D向右平移6个单位，向下平移4个单位得到点N，∴N（0+6，1﹣4），即N（6，﹣3）．②当DP是对角线时，设Q（x，0），则QD2＝x2+1，QP2＝（x﹣2）2+42，PD2＝13，∵Q是直角顶点，∴QD2+QP2＝PD2，∴x2+1+（x﹣2）2+16＝13，整理得x2﹣2x+4＝0，方程无解，此种情形不存在，综上所述，满足条件的点N坐标为（，3）或（6，﹣3）．3．【解答】解：（1）y＝a（x+3）（x﹣1），令y＝0，则x＝1或﹣3，故点A、B的坐标分别为：（﹣3，0）、（1，0）；（2）抛物线的表达式为：y＝（x+3）（x﹣1）…①，当∠MAO＝45°时，如图所示，则直线AM的表达式为：y＝x…②，联立①②并解得：m＝x＝4或﹣3（舍去﹣3），故点M（4，7）；②∠M′AO＝45°时同理可得：点M（﹣2，﹣1）；故：﹣2≤m≤4；（3）①当BD是矩形的对角线时，如图2所示，过点Q作x轴的平行线EF，过点B作BE⊥EF，过点D作DF⊥EF，抛物线的表达式为：y＝ax2+2ax﹣3a，函数的对称轴为：x＝﹣1，抛物线点A、B的坐标分别为：（﹣3，0）、（1，0），则点P的横坐标为：﹣1，OB＝1，而CD＝4BC，则点D的横坐标为：﹣4，故点D（﹣4，5a），即HD＝5a，线段BD的中点K的横坐标为：＝﹣，则点Q的横坐标为：﹣2，则点Q（﹣2，﹣3a），则HF＝BE ＝3a，∵∠DQF+∠BQE＝90°，∠BQE+∠QBE＝90°，∴∠QBE＝∠DQF，∴△DFQ∽△QEB，则，，解得：a＝（舍去负值），同理△PGB≌△DFQ（AAS），∴PG＝DF＝8a＝4，故点P（﹣1，4）；②如图3，当BD是矩形的边时，作DI⊥x轴，QN⊥x轴，过点P作PL⊥DI于点L，同理△PLD≌△BNQ（AAS），∴BN＝PL＝3，∴点Q的横坐标为4，则点Q（4，21a），则QN＝DL＝21a，同理△PLD∽△DIB，∴，即，解得：a＝（舍去负值），LI＝26a＝，故点P（﹣1，），；综上，点P的坐标为：P（﹣1，4）或（﹣1，）．4．【解答】解：（1）一次函数y＝x+3与坐标轴交于A、C两点，则点A、C的坐标为（﹣3，0）、（0，3），将点A、C的坐标代入二次函数表达式得：，解得：，故抛物线的表达式为：y＝﹣x2﹣2x+3，顶点E（﹣1，4）；（2）将点A、E的坐标代入一次函数表达式并解得：直线AE的表达式为：y＝2x+6，设点P（x，2x+6），则点F（x，x+3），S△PEF＝PF×（x E﹣x）＝×（2x+6﹣x﹣3）（﹣1﹣x）＝﹣（x+3）（x+1），当x＝﹣2时，S△PEF有最大值为，此时点P（﹣2，2）；（3）点A、E的坐标分别为（﹣3，0）、（﹣1，4），AE2＝20，①当点M（m，0）在x轴上时，设点N（s，t），则AE＝MN，且AE中点坐标为MN中点坐标，即：，解得：，故点N（﹣3，4）；②当点M在y轴上时，同理可得：点N（﹣4，3）或（﹣4，1）；综上，点N坐标为：N（﹣3，4）或（﹣4，3）或（﹣4，1）．5．【解答】解：（1）当y＝0时，，解得x1＝1，x2＝4 所以点A（1，0），B（4，0）设BC直线解析式为y＝kx+b，将B、C坐标代入得，解得所以直线BC的解析式为联立方程，解得，∴点E坐标为（）（2）设P（），G（）PG＝（）﹣（）＝﹣当△PFG周长最大时，线段PG最长＜0，所以PG有最大值当m＝2时，PG最大，P点坐标为（2，）如图，作P点关于y轴的对称点P'，在AE下方作∠AEQ＝30°，过点p'作P'Q⊥EQ，垂足为Q，P'Q交x轴于S，交AE于N，作P'T⊥x轴，垂足为T，ER⊥x轴，垂足为R则P'Q＝PM+MN+NE由题意可知，P'（﹣2，），∠P'ST＝60°在Rt△P'ST中，tan∠p'ST＝＝∴TS＝3∴S点坐标为（1，0）设P'S直线解析式为y＝kx+b将P'、S坐标代入得，解得所以P'S直线解析式y＝+在Rt△EHR中tan∠EHR＝＝∴HR＝∴H（，0）∴SH＝∴SQ＝∵P'S＝∴P'Q＝所以PM+MN+NE的最小值为．点N坐标为（1，0）（3）如图所示，设R1的纵坐标长度为m当NE为矩形对角线时可证△NA1R1∽△R1ZE，∴＝∴＝解得m1＝﹣，m2＝﹣﹣（舍去）∴R1的坐标为（，﹣+）可证△NB1S1≌△EZR1∴S1坐标为（，+）同理S2坐标为（，﹣）当NE为矩形的一边时，如图可证△S3HN≌△R3FE≌△R3GE在Rt△R3GE中，GE＝，由三角函数可得EF＝∴HN＝，S3H＝∴S3坐标为（，）同理可得S4坐标为（，﹣）6．【解答】解：（1）当y＝0时，x﹣＝0，解得x＝4，即A（4，0），抛物线过点A，对称轴是x＝，得，解得，抛物线的解析式为y＝x2﹣3x﹣4；（2）∵平移直线l经过原点O，得到直线m，∴直线m的解析式为y＝x．∵点P是直线m上任意一点，∴设P（3a，a），则PC＝|3a|，PB＝|a|．又∵PF＝3PE，设PB＝n，PC＝3n，PE＝m，PF＝3m，则CF＝＝3，BE＝，∴＝＝＝3，∵∠PCF＝∠PBE＝90°，∴△PCF∽△PBE，∴∠FPC＝∠EPB．∵∠CPE+∠EPB＝90°，∴∠FPC+∠CPE＝90°，∴FP⊥PE．（3）如图所示，点E在点B的左侧时，设E（a，0），则BE＝6﹣a．∵CF＝3BE＝18﹣3a，∴OF＝20﹣3a．∴F（0，20﹣3a）．∵PEQF为矩形，∴＝，＝，∴Q x+6＝0+a，Q y+2＝20﹣3a+0，∴Q x＝a﹣6，Q y＝18﹣3a．将点Q的坐标代入抛物线的解析式得：18﹣3a＝（a﹣6）2﹣3（a﹣6）﹣4，解得：a＝4或a＝8（舍去）．∴Q（﹣2，6）．如下图所示：当点E在点B的右侧时，设E（a，0），则BE＝a﹣6．∵CF＝3BE＝3a﹣18，∴OF＝3a﹣20．∴F（0，20﹣3a）．∵PEQF为矩形，∴＝，＝，∴Q x+6＝0+a，Q y+2＝20﹣3a+0，∴Q x＝a﹣6，Q y＝18﹣3a．将点Q的坐标代入抛物线的解析式得：18﹣3a＝（a﹣6）2﹣3（a﹣6）﹣4，解得：a＝8或a＝4（舍去）．∴Q（2，﹣6）．综上所述，点Q的坐标为（﹣2，6）或（2，﹣6）．7．【解答】解：（1）对于y＝﹣x+，令y＝得x＝﹣4，∴B（﹣4，）．分别把A（1，0）和B（﹣4，）代入y＝x2+bx+c，得解得，则该抛物线解析式为：y＝x2+x﹣，∵﹣＝﹣1，∴对称轴为直线x＝﹣1；（2）直线AB：y＝﹣x+相交于点C（0，），作点C关于x轴的对称点C′，则C′（0，﹣），连接BC′交x轴于点D，根据“两点之间线段最短”可得BD+CD的和最小，从而△BCD的周长也最小，∵B（﹣4，），C′（0，﹣），∴直线BC′的解析式为y＝﹣x﹣．令y＝0，可得x＝﹣，∴D（﹣，0），∴当△BCD的周长最小时，点D的坐标为（﹣，0），最小周长＝BC+BC′＝+＝5+2；（3）①若AB为四边形的边长，作AE⊥AB，交y轴于点E，又OA⊥CE，∴△AOC∽△EOA，∴OE＝2OA＝2，∴E（0，﹣2）∴直线AE为y＝2x﹣2，令2x﹣2＝x2+x﹣，解得x1＝x2＝1，∴直线AE与抛物线只有一个交点为A，∴不存在满足题意的矩形；②若AB为四边形的对角线，当四边形是平行四边形时，对角线互相平分，有x A+x B＝x M+x N，即：1+（﹣4）＝﹣1+x N，解得x N＝﹣2．把x N＝﹣2代入y＝x2+x﹣，得y N＝﹣，由y A+y B＝y M+y N得：y M＝4，∴M（﹣1，4），N（﹣2，﹣），此时MN＝＝，AB＝＝，∴MN＝AB，∴平行四边形AMBN为矩形，综上，能为矩形，M（﹣1，4）．8．【解答】解：（1）将A（﹣1，0）代入y＝﹣x2+bx+3，得b＝2，所以抛物线的解析式为y＝﹣x2+2x+3，过点D作DF⊥x轴于点F，如图1易证△AOC∽△AFD，∴，∵CD＝4AC，∴＝，∴点D横坐标为4，把x＝4代入y＝﹣x2+2x+3，得y＝﹣5，∴D（4，﹣5），把x＝4，y＝﹣5；x＝﹣1，y＝0代入y＝kx+h，解得，k＝﹣1，h＝﹣1，∴直线l的解析式为y＝﹣x﹣1．（2）过点E作EM⊥x轴，交AD于点M，如图2设点E（m，﹣m2+2m+3），则M（m，﹣m﹣1），∴EM＝﹣m2+2m+3﹣（﹣m﹣1）═﹣m2+3m+4，∴S△ADE＝（﹣m2+3m+4）＝，当m＝时，△ADE的面积最大，此时，E（，）．（3）不存在理由如下：∵抛物线的对称轴为直线x＝1，设P（1，m），如图4，则易得Q（2，3），m＝﹣5a﹣3＝﹣8，则P（1，﹣8），PQ2＝12+112＝122，PD2＝32+32＝18QD2＝22+82＝68，∴PD2+QD2≠PQ2，∴∠PDQ≠90°，此时平行四边形ADPQ不是矩形，9．【解答】解：（1）抛物线y＝x2+hx+c，即：a＝1，抛物线过A（﹣1，0），B（3，0）两点，则抛物线的表达式为：y＝（x+1）（x﹣3）＝x2﹣2x﹣3；（2）点C（0，﹣3），函数的对称轴为：x＝1，故点E（1，0），点D（1，﹣4），将点BD代入一次函数表达式：y＝kx+b并解得：直线BD的表达式为：y＝2x﹣6，设点P（m，2m﹣6），PE＝PC时，则：m2+（2m﹣6+3）2＝（m﹣1）2+（2m﹣6）2，解得：m＝2，故点P（2，﹣2）；（3）设点M的坐标为（a，0），则点G的坐标为（a，﹣a2+2a+3），∵以F、M、N、G为顶点的四边形是矩形，∴MG＝2FM时，|a2﹣2a﹣3|＝2|a﹣2|，解得：a＝或2，故点M的坐标为：（2，0）或（2﹣，0）或（，0）或（﹣，0）．10．【解答】解：（1）①令y＝0，则（mx﹣3）（mx+1）＝0，∴x＝﹣或x＝，∴A（﹣，0），B（，0），∴AB＝，。

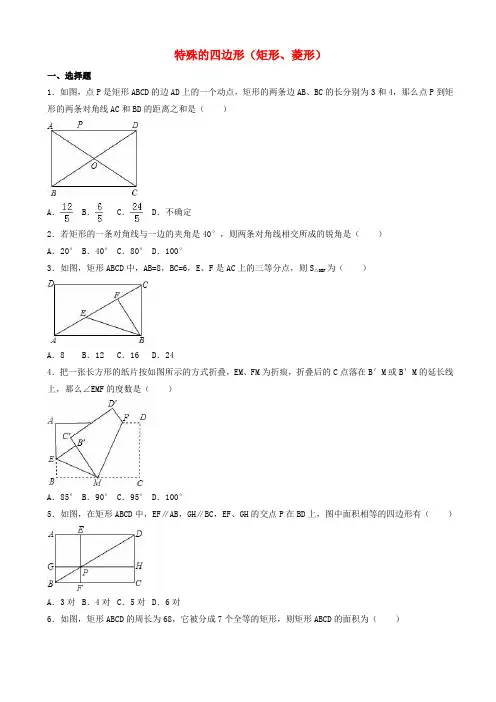
特殊的四边形（矩形、菱形）一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A．20° B．40° C．80° D．100°3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．244．把一张长方形的纸片按如图所示的方式折叠，EM、FM为折痕，折叠后的C点落在B′M或B′M的延长线上，那么∠EMF的度数是（）A．85° B．90° C．95° D．100°5．如图，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有（）A．3对B．4对C．5对D．6对6．如图，矩形ABCD的周长为68，它被分成7个全等的矩形，则矩形ABCD的面积为（）A．98 B．196 C．280 D．2847．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A． B．C．D．68．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108°D．72°9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）A．1 B．2 C．D．10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．111．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）A．26 B．13 C．30 D．6.515．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m217．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是cm．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB= cm，BC= cm．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB= 度．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC= 度，∠FCA= 度．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF= ．（写出一条线段即可）24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是°．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是cm，面积是cm2．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为cm．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件（写一个即可）．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是．33．已知四边形ABCD为平行四边形，要使四边形ABCD为菱形，还应添加条件．34．用两张对边平行的纸条交叉重叠放在一起，则四边形ABCD为；两张纸条互相垂直时，四边形ABCD 为；若两张纸条的宽度相同，则四边形ABCD为．三、解答题35．如图1中的矩形ABCD，沿对角线AC剪开，再把△ABC沿着AD方向平行移动，得到图2．在图2中，△ADC≌△C′BA′，AC∥A′C′，A′B∥DC．除△DAC与△C′BA′外，指出有哪几对全等的三角形（不能添加辅助线和字母）？选择其中一对加以证明．36．如图，在▱ABCD的纸片中，AC⊥AB，AC与BD相交于点O，将△ABC沿对角线AC翻转180°，得到△AB′C．（1）以A，C，D，B′为顶点的四边形是矩形吗（请填“是”、“不是”或“不能确定”）；（2）若四边形ABCD的面积S=12cm2，求翻转后纸片重叠部分的面积，即S△ACE= cm2．37．如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，那么MN⊥BD成立吗？试说明理由．38．如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2020厘米后停下，则这只蚂蚁停在点．39．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．特殊的四边形（矩形、菱形）参考答案与试题解析一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定【考点】矩形的性质；相似三角形的判定与性质．【专题】压轴题；动点型．【分析】过P点作PE⊥AC，PF⊥BD，由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD，根据和，即和，两式相加得PE+PF=，即为点P到矩形的两条对角线AC和BD的距离之和．【解答】解：法1：过P点作PE⊥AC，PF⊥BD∵矩形ABCD∴AD⊥CD∴△PEA∽△CDA∴∵AC=BD==5∴…①同理：△PFD∽△BAD∴∴…②∴①+②得：∴PE+PF=即点P到矩形的两条对角线AC和BD的距离之和是．法2：连结OP．∵AD=4，CD=3，∴AC==5，又∵矩形的对角线相等且互相平分，∴AO=OD=2.5cm，∴S△APO+S△POD=×2.5•PE+×2.5•PF=×2.5（PE+PF）=×3×4，∴PE+PF=．故选：A．【点评】根据矩形的性质，结合相似三角形求解．2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A．20° B．40° C．80° D．100°【考点】矩形的性质．【专题】计算题．【分析】根据矩形的性质，得△BOC是等腰三角形，再由等腰三角形的性质进行答题．【解答】解：图形中∠1=40°，∵矩形的性质对角线相等且互相平分，∴OB=OC，∴△BOC是等腰三角形，∴∠OBC=∠1，则∠AOB=2∠1=80°．故选C．【点评】本题主要考查了矩形的性质，对角线相等且互相平分，矩形被对角线分成四个等腰三角形．3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．24【考点】矩形的性质．【专题】压轴题．【分析】要求S△BEF只要求出底边EF以及EF边上的高就可以，高可以根据△ABC的面积得到，EF=AC，根据勾股定理得到AC，就可以求出EF的长，从而求出△EFG的面积．【解答】解：S△ABC=×8×6=24．又E、F是AC上的三等分点．∴S△BEF=S△ABC=8．故选A．【点评】本题运用了勾股定理，已知直角三角形的两直角边，求斜边上的高，这类题的解决方法是需要熟记的内容．4．把一张长方形的纸片按如图所示的方式折叠，EM、FM为折痕，折叠后的C点落在B′M或B′M的延长线上，那么∠EMF的度数是（）A．85° B．90° C．95° D．100°【考点】翻折变换（折叠问题）．【分析】根据折叠的性质：对应角相等，对应的线段相等，可得．【解答】解：根据图形，可得：∠EMB′=∠EMB，∠FMB′=∠FMC，∵∠FMC+∠FMB′+∠EMB′+∠BME=180°，∴2（∠EMB′+∠FMB′）=180°，∵∠EMB′+∠FMB′=∠FME，∴∠EMF=90°．故选B．【点评】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．5．如图，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有（）A．3对B．4对C．5对D．6对【考点】矩形的性质．【专题】压轴题．【分析】本题考查了矩形的性质，得出△EPD≌△HDP，则S△EPD=S△HDP，通过对各图形的拼凑，得到的结论．【解答】解：在矩形ABCD中，∵EF∥AB，AB∥DC，∴EF∥DC，则EP∥DH；故∠PED=∠DHP；同理∠DPH=∠PDE；又PD=DP；所以△EPD≌△HDP；则S△EPD=S△HDP；同理，S△GBP=S△FPB；则（1）S梯形BPHC=S△BDC﹣S△HDP=S△ABD﹣S△EDP=S梯形ABPE；（2）S□AGPE=S梯形ABPE﹣S△GBP=S梯形BPHC﹣S△FPB=S□FPHC；（3）S梯形FPDC=S□FPHC+S△HDP=S□AGPE+S△EDP=S梯形GPDA；（4）S□AGHD=S□AGPE+S□HDPE=S□PFCH+S□PHDE=S□EFCD；（5）S□ABFE=S□AGPE+S□GBFP=S□PFCH+S□GBFP=S□GBCH故选C．【点评】本题是一道结论开放题，掌握矩形的性质，很容易得到答案．6．如图，矩形ABCD的周长为68，它被分成7个全等的矩形，则矩形ABCD的面积为（）A．98 B．196 C．280 D．284【考点】矩形的性质．【专题】计算题．【分析】等量关系为：5个小矩形的宽等于2个小矩形的长；6个小矩形的宽加一个小矩形的长等于大长方形周长的一半．【解答】解：设小矩形宽为x，长为y．则大矩形长为5x或2y，宽为x+y．依题意有x+y+5x==34；5x=2y．解得：x=4，y=10．则大矩形长为20，宽为14．所以大矩形面积为280．故选C．【点评】本题考查了矩形的面积和一种很重要的思想：方程思想．7．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A． B．C．D．6【考点】翻折变换（折叠问题）；勾股定理．【分析】先根据图形翻折变换的性质求出AC的长，再由勾股定理及等腰三角形的判定定理即可得出结论．【解答】解：∵△CEO是△CEB翻折而成，∴BC=OC，BE=OE，∠B=∠COE=90°，∴EO⊥AC，∵O是矩形ABCD的中心，∴OE是AC的垂直平分线，AC=2BC=2×3=6，∴AE=CE，在Rt△ABC中，AC2=AB2+BC2，即62=AB2+32，解得AB=3，在Rt△AOE中，设OE=x，则AE=3﹣x，AE2=AO2+OE2，即（3﹣x）2=32+x2，解得x=，∴AE=EC=3﹣=2．故选：A．【点评】本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．8．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108°D．72°【考点】翻折变换（折叠问题）；矩形的性质．【专题】计算题．【分析】根据∠A MD′=36°和折叠的性质，得∠NMD=∠NMD′=72°；根据平行线的性质，得∠BNM=∠NMD=72°；根据折叠的性质，得∠D′=∠D=90°；根据四边形的内角和定理即可求得∠NFD′的值．【解答】解：∵∠AMD′=36°，∴∠NMD=∠NMD′=72°．∵AD∥BC，∴∠BNM=∠NMD=72°．又∵∠D′=∠D=90°，∴∠NFD′=360°﹣72°×2﹣90°=126°．故选B．【点评】此题综合运用了折叠的性质、平行线的性质、四边形的内角和定理．9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）A．1 B．2 C．D．【考点】菱形的性质；勾股定理．【专题】计算题．【分析】根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2，从而可求得BC的长．【解答】解：∵AC=2BC，∠B=90°，∴AC2=AB2+BC2，∴（2BC）2=32+BC2，∴BC=．故选：D．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．1【考点】翻折变换（折叠问题）．【分析】连BH，根据折叠的性质得到∠1=∠2，EB=EH，BH⊥EG，则∠EBH=∠EHB，又点E是AB的中点，得EH=EB=EA，于是判断△AHB为直角三角形，且∠3=∠4，根据等角的余角相等得到∠1=∠3，因此有∠1=∠2=∠3=∠4．【解答】解：连BH，如图，∵沿直线EG将纸片折叠，使点B落在纸片上的点H处，∴∠1=∠2，EB=EH，BH⊥EG，而∠1＞60°，∴∠1≠∠AEH，∵EB=EH，∴∠EBH=∠EHB，又∵点E是AB的中点，∴EH=EB=EA，∴△AHB为直角三角形，∠AHB=90°，∠3=∠4，∴∠1=∠3，∴∠1=∠2=∠3=∠4．故选B．【点评】本题考查了折叠的性质：折叠前后的两个图形全等，即对应角相等，对应线段相等．也考查了若三角形一边上的中线等于这边的一半，则此三角形为直角三角形．11．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm【考点】翻折变换（折叠问题）．【专题】压轴题．【分析】延长A1E交CD于点G，由题意知GE=EH，FH=GF，则阴影部分的周长与原矩形的周长相等．【解答】解：延长A1E交CD于点G，由题意知，GE=EH，FH=GF，四边形EHD1A1≌四边形EGDA，∴AD=A1D1，AE=A1E，DG=D1H，FH=FG，∴阴影部分的周长=矩形的周长=（12+6）×2=36cm．故选：B．【点评】本题利用了翻折的性质：对应图形全等，对应边相等．12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形【考点】矩形的判定．【专题】证明题．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．【解答】解：A、有一个角是直角的平行四边形是矩形，正确；B、有三个角是直角的四边形是矩形，正确；C、对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形，错误；D、对角线互相平分且相等的四边形是矩形，正确．故选C．【点评】本题主要考查的是矩形的判定定理．（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°【考点】矩形的判定．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形．据此判断．【解答】解：A、一个角为直角的平行四边形为矩形，故A正确．B、矩形的对角线平分且相等，故B正确．C、∠BCD+∠ADC=180°，但∠BCD不一定与∠ADC相等，根据矩形的判定定理，故C不正确．D、因为∠BAD=∠BCD，故AB∥CD，又因为，∠ABC=∠ADC=90°，根据矩形的判定（有一个角是直角的平行四边形是矩形），故D正确．故选C．【点评】本题考查的是矩形的判定定理，但考生应注意的是由矩形的判定引申出来的各图形的判定．难度一般．14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）A．26 B．13 C．30 D．6.5【考点】勾股定理；直角三角形斜边上的中线．【分析】由勾股定理可以求出斜边，再根据直角三角形中斜边上的中线等于斜边的一半可以求出斜边中线的长．【解答】解：由勾股定理知，斜边c==13，∵直角三角形中斜边上的中线等于斜边的一半知，∴斜边中线的长=×13=6.5．故选D．【点评】本题考查了勾股定理和直角三角形的性质：斜边上的中线等于斜边的一半．15．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．【考点】剪纸问题．【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有4条边，并且这4条边还相等，从而可以得到剪下的图形展开后一定是菱形．【解答】解：根据题意折叠剪图可得，剪下的四边形四条边相等，根据四边形等的四边形是菱形可得剪下的图形是菱形，故选：A．【点评】此题考查了剪纸问题，关键是掌握菱形的判定方法：四边形等的四边形是菱形．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m2【考点】菱形的性质．【专题】几何图形问题．【分析】菱形对角线互相垂直平分，所以OA2+OB2=AB2，根据已知可得AB=5，BO=4，利用勾股定理求得AO，即可求得AC的长，根据AC、BD即可求菱形ABCD的面积，即可解题．【解答】解：根据题意可得：BD=8m，则BO=DO=4m，∵菱形周长为20m，∴AB=5m，∵菱形对角线互相垂直平分，∴OA2+OB2=AB2，∴AO==3（m），∴AC=6（m），故菱形的面积S=×6×8=24（m2）．故选D．．【点评】本题考查了菱形对角线互相垂直平分的性质，菱形面积的计算，本题中根据勾股定理求AO的值是解题的关键．17．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形【考点】菱形的判定；作图—复杂作图．【分析】关键菱形的判定定理（有四边都相等的四边形是菱形）判断即可．【解答】解：由图形作法可知：AD=AB=DC=BC，∴四边形ABCD是菱形，故选：B．【点评】本题主要考查对作图﹣复杂作图，菱形的判定等知识点的理解和掌握，能熟练地运用性质进行推理是解此题的关键．18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD【考点】菱形的判定．【专题】几何图形问题．【分析】首先根据题意画出图形，然后由DE∥AC、DF∥AB，判定四边形DEAF为平行四边形，再由菱形的判定定理求解即可求得答案；注意掌握排除法在选择题中的应用．【解答】解：如图，∵DE∥AC、DF∥AB，∴四边形DEAF为平行四边形，A、∵AD平分∠BAC，DF∥AB，∴∠BAD=∠CAD，∠BAD=∠ADF，∴∠CAD=∠ADF，∴AF=DF，∴四边形DEAF为菱形；B、∵AB=AC且BD=CD，∴AD平分∠BAC，同理可得：四边形DEAF为菱形；C、∵由AD为中线，得不到AD平分∠BAC，证不出四边形DEAF的邻边相等，∴不能判断四边形DEAF为菱形；D、∵AD⊥EF，∴▱DEAF是菱形．故选C．【点评】此题考查了菱形的判定．此题难度不大，注意掌握数形结合思想的应用．二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是28 cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的一组邻边和一条对角线组成一个直角三角形，解题即可．【解答】解：根据矩形的性质得到△ABC是直角三角形，因为对角线AC=10cm，AB：BC=3：4，根据勾股定理得到BC2=AC2﹣（BC）2=100﹣BC2解得BC=8，AB=6，故它的周长=2×8+2×6=28cm．故答案为28．【点评】本题考查对矩形的性质以及勾股定理的运用．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB= 10 cm，BC= 7 cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的对边相等以及所给的三角形的周长可得到和所求线段相关的两个式子，进而求解．【解答】解：设AB=a，BC=b．∴2OA=2OB=AC=，2a+2b=34，即a+b=17．由题意可知△AOB的周长+7=△ABC的周长．∴AB+OA+OB+7=AB+BC+AC．∴a++7=a+b+．即b=7，a=17﹣7=10．即AB=10，BC=7．故答案为，10，7．【点评】本题综合考查了矩形的性质及勾股定理的运用．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB= 35 度．【考点】矩形的性质；三角形内角和定理．【专题】计算题．【分析】根据矩形对角线的性质得到△OAB的形状，进而求得底角的度数．【解答】解：∵矩形的对角线相等且互相平分．∴OA=OC．∴△AOB是等腰三角形．∴∠OAB=∠OBA．∵∠OAB+∠OBA+∠AOB=180°．∴2∠OAB+110°=180°．∴∠O AB=35°．故答案为35．【点评】本题考查矩形的性质以及三角形内角和定理．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC= 90 度，∠FCA= 45 度．【考点】矩形的性质；全等三角形的判定与性质．【专题】计算题．【分析】两个大小完全一样的矩形拼成“L”形图案所构成的△AFG≌△CAB，所以AF=AC，∠FAC=90°，∠FCA=45度．【解答】解：由已知△AFG≌△CAB，∴∠AFG=∠CAB，AF=AC∵∠AFG+∠FAG=90°，∴∠CAB+∠FA G=90°，∴∠FAC=90°．又∵AF=AC，∴∠FCA=（180°﹣90°）×=45°．故答案为：90；45．【点评】根据矩形的性质得到全等三角形，进而求得△AFC是等腰直角三角形．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF= BE ．（写出一条线段即可）【考点】矩形的性质；全等三角形的判定与性质．【专题】几何图形问题．【分析】根据矩形的性质得出AD∥BC，推出∠AFD=∠B，推出∠DAF=∠AEB，根据全等三角形的判定推出△AFD≌△EBA即可．【解答】解：DF=BE，理由是：∵四边形ABCD是矩形，DF⊥AE，∴∠B=∠AFD=90°，AD∥BC，∴∠DAF=∠AEB，在△AFD和△EBA中∴△AFD≌△EBA（AAS），∴DF=BE，故答案为：DF=BE．【点评】本题考查了全等三角形的性质和判定，平行线的性质，全等三角形的性质和判定的应用，关键是推出△AFD≌△EBA，注意：矩形的四个角都是直角，矩形的对边平行．24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是62 °．【考点】翻折变换（折叠问题）．【专题】压轴题；操作型．【分析】易得∠DED′的度数，除以2即为所求角的度数．【解答】解：∵∠CED′=56°，∴∠DED′=180°﹣56°=124°，∵∠AED=∠AED′，∴∠AED=∠DED′=62°．故答案为：62．【点评】考查翻折变换问题；用到的知识点为：翻折前后得到的角相等．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为40.5 ．【考点】菱形的性质．【分析】根据相邻两内角的度数比为1：5，可求出一个30°角，根据周长为36，求出菱形的边长，根据直角三角形里30°角的性质求出高，从而求出面积．【解答】解：作AE⊥BC于E点，∵其相邻两内角的度数比为1：5，∴∠B=180°×=30°，∵菱形ABCD的周长为36，∴AB=BC=×36=9．∴AE=×9=．∴菱形的面积为：BC•AE=9×=40.5．故答案为：40.5．【点评】本题考查菱形的性质，菱形的邻角互补，四边相等．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是20 cm，面积是24 cm2．【考点】菱形的性质；勾股定理．【分析】根据菱形的面积等于两对角线乘积的一半可得到其面积，根据菱形的性质可求得其边长，从而可得到其周长．【解答】解：如图，四边形ABCD是菱形，BD，AC分别是其对角线且BD=6，AC=8，求其面积和周长．∵四边形ABCD是菱形，BD，AC分别是其对角线，∴BD⊥AC，BO=OD=3cm，AO=CO=4cm，∴AB=5cm，∴菱形的周长=5×4=20cm；S菱形=×6×8=24cm2．故本题答案为：20cm；24cm2．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是AC⊥BD ．【考点】中点四边形．【分析】根据三角形的中位线定理，可以证明所得四边形的两组对边分别和两条对角线平行，所得四边形的两组对边分别是两条对角线的一半，再根据平行四边形的判定就可证明该四边形是一个平行四边形；所得四边形要成为矩形，则需有一个角是直角，故对角线应满足互相垂直．【解答】解：如图，∵E，F分别是边AB，BC的中点，∴EF∥AC，EF=AC，同理HG∥AC，HG=AC，∴EF∥HG，EF=HG，∴四边形EFGH是平行四边形；要使四边形EFGH是矩形，则需EF⊥FG，即AC⊥BD；故答案为：AC⊥BD．【点评】此题主要考查了三角形的中位线定理的运用．同时熟记此题中的结论：顺次连接四边形各边中点所得四边形是平行四边形；顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为2cm．【考点】菱形的性质．【专题】计算题．【分析】根据菱形的性质及勾股定理即可求得其边长的值．【解答】解：菱形的两条对角线分别是4cm，8cm，得到两条对角线相交所构成的直角三角形的两直角边是×4=2和×8=4，那么根据勾股定理得到它的斜边即菱形的边长=2cm．故答案为2【点评】本题考查菱形的性质以及勾股定理．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件此题答案不唯一，如AC⊥BD或AB=AD 等（写一个即可）．【考点】菱形的判定．【专题】开放型．【分析】由四边形ABCD是平行四边形，根据菱形的判定定理求解即可求得答案．【解答】解：∵四边形ABCD是平行四边形，∴当AC⊥BD或AB=AD时，四边形ABCD是菱形．故答案为：此题答案不唯一，如AC⊥BD或AB=AD等．【点评】此题考查了菱形的判定．此题难度不大，注意熟记定理是解此题的关键．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为或．【考点】菱形的性质．【专题】压轴题；分类讨论．【分析】根据题意得，应分P与A在BD的同侧与异侧两种情况进行讨论．【解答】解：当P与A在BD的异侧时：连接AP交BD于M，∵AD=AB，DP=BP，∴AP⊥BD（到线段两端距离相等的点在垂直平分线上），在直角△ABM中，∠BAM=30°，∴AM=AB•cos30°=3，BM=AB•sin30°=3，∴PM==，∴AP=AM+PM=4；当P与A在BD的同侧时：连接AP并延长AP交BD于点MAP=AM﹣PM=2；当P与M重合时，PD=PB=3，与PB=PD=2矛盾，舍去．AP的长为4或2．故答案为4或2．【点评】本题注意到应分两种情况讨论，并且注意两种情况都存在关系AP⊥BD，这是解决本题的关键．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是3．【考点】轴对称﹣最短路线问题；菱形的性质．【专题】几何图形问题．【分析】根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC与P，可得答案．【解答】解：∵菱形的性质，∴AC是BD的垂直平分线，AC上的点到B、D的距离相等．连接BE交AC于P点，PD=PB，PE+PD=PE+PB=BE，在Rt△ABE中，由勾股定理得BE==3，故答案为：3．【点评】本题考查了轴对称，对称轴上的点到线段两端点的距离相等是解题关键．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是 5 ．【考点】轴对称﹣最短路线问题；勾股定理；菱形的性质．【专题】计算题．【分析】AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，根据菱形的性质推出N是AD中点，P与O重合，推出PE+PF=NF=AB，根据勾股定理求出AB的长即可．【解答】解：AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，∴PN=PE，∵四边形ABCD是菱形，∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，∵E为AB的中点，∴N在AD上，且N为AD的中点，∵AD∥CB，∴∠ANP=∠CFP，∠NAP=∠FCP，。

专题02与特殊四边形有关问题的压轴题之四大题型目录【题型一与矩形有关问题的压轴题】 (1)【题型二与菱形有关问题的压轴题】 (14)【题型三与正方形形有关问题的压轴题】 (25)【题型四与特殊平行四边形中新定义探究问题压轴题】 (37)【题型一与矩形有关问题的压轴题】由题意知，60DAN ∠=︒，4AD AB ==∴cos 602AN AD =⋅︒=，sin DN AD =⋅∴3tan 2DN DGN GN ∠==，∵FBG △是等腰三角形，∴11124BM GM BG AB ====，∴3AM =，由题意，设5AB BC x ==，则4OB x =【变式训练】1．（2023·浙江·一模）如图1，菱形ABCD 中，=60B ∠︒，2AB =，E 是边BC 上一动点（不与点B 、C 重合）连结DE ，点C 关于直线DE 的对称点为C '，连结AC '并延长交直线DE 于点P 、F 是AC '的中点，连结DC '、DF ．(1)填空：DC '=________；FDP ∠=________．(2)如图2，将题中条件“=60B ∠︒”改成“90B Ð=°”，其余条件均不变，连结BP 线段间的数量关系，并对你的猜想加以证明．(3)在（2）的条件下，连结AC ．①若动点E 运动到边BC 的中点处时，求ACC '△的面积；90GAP∴∠=︒，四边形ABCD是菱形，Ð∴四边形ABCD是正方形，90ADC BAD∴∠=∠=︒，AB AD=，由（1）得：12 FDP ADC ∠=∠AD C D'=，AF C F'=，∠=∠=由（2）得：APB G∴∠=∠+∠= BPD BPA DPFBPD BCD∴∠=∠=︒，90∴B、P、C、D四点共圆， 四边形ABCD是正方形，∴=，OA OC上，∴在OA12ACC S AC C M ''∴=⋅ ，222AC AB == ，1222ACC S C M ''∴=⨯= ∴当C M '取最大时，S △22BD AC == ，122DM BD ∴==，2C M C D DM ''∴=-=-()2222ACC S '∴=-= 故ACC '△面积的最大值为=，求证：(1)在线段BC上取一点T，使CE CT(2)图中7AE=．AB=，1∆周长的最大值和最小值；①点F在线段BC上，求EFG②记点F关于直线AB的轴对称点为点【答案】(1)见解析(2)①最小值为93，最大值为343；60FEG ∠=︒ ，60TEC ∠=︒，FET TEG GEC TEG ∴∠+∠=∠+∠，FET GEC ∴∠=∠，在FET ∆和GEC ∆中，FET GEC ET CE FTE GCE ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ΔΔEFT EGC ASA ∴≅，FT CG ∴=；（2）解：①如下图，当点F 与点B 重合时，同（1）可得，FE GF =，60FEG ∠=︒ ，FEG ∴∆是等边三角形，同理可得，当点F 在BC 边上时，FEG ∆均是等边三角形，当FE BC ⊥时，EF 最短，如下图，7AB AC == ，1AE =，716CE AC AE ∴=-=-=，又60ACF ∠=︒ ，30CEF ∴∠=︒，过点E 作EH BC ⊥于H ，则3CH =，33EH =，734BH BC CH ∴=-=-=，在Rt BHE 中，2BE BH EH =+∴作CM AB ⊥于M ，点F 关于AB 的对称点N 在OF ON CM ∴==，37322CM BC ABC BC =⋅∠==，732OF ∴=，连接BN，点N与点F关于AB对称，ABN ABC∴∠=∠=︒，60，∠=︒BAC602CF BC BF ∴=-=，02CF ∴<<或14CF >．【点睛】本题考查了菱形的性质，等边三角形判定和性质，相似三角形判定和性质，轴对称性质等知识，解决问题的关键是证明三角形相似．【题型二与菱形有关问题的压轴题】(1)求证：CBE FEB ∠=∠．(2)当A ，F ，C 三点共线时，用含(3)若5AB AE =，BCF △能否是等腰三角形？若能，求【答案】(1)见解析由对称得BE AC ⊥，∴90ABE BAC ∠+∠=︒，∵90DAC BAC ∠+∠=︒，∴ABE DAC ∠=∠．=(如图3)，则5a=若FB BCn=，∴5若FC BC =（如图4），由NC (2260251313a na a na ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭解得132n =∴n 的值为5013或5或132．【点睛】题目主要考查矩形及折叠的性质，相似三角形的判定和性质，勾股定理解三角形等，理解题意，进行分类讨论，作出相应图形是解题关键．【变式训练】1．（2023·浙江金华·校联考三模）如图，在矩形ABCD 中，4AB =，2AD =，动点P 从点A 开始以每秒2个单位长度沿AB 向终点B 运动，同时，动点Q 从点C 开始沿C D A --以每秒3个单位长度向终点A 运动，它们同时到达终点．连接PQ 交AC 于点E ．过点E 作EF PQ ⊥，交直线CD 于点F ．1AQ AD DQ =-=，(23AP CD =同理：AME ABC ∽△△，∴12EM BC AM AB ==，∴22AM EM h ==．若点F 在Q 的右侧，如图3，当FEQ △作PH CD ⊥于点H ，而B PHQ ∠=∠=∴ABC PHQ ∽，则2AB H PH Q BC ==，∴112QH PH ==．∵222242=+=+AC AB BC 又∵32CE AE =∴24555AE AC ==．∵由FEQ ABC ∽△△结合对顶角可得：由90FEQ NEG ∠=∠=︒，得FEN ∠∴Rt Rt FEN QEG ∽△△，∴2EN EF EG EQ==．同理可得：12AG BC EG AB ==，(1)如图（1），当0α=︒，求n m的值．(2)如图2，若090α︒≤≤︒，求m 关于n 的数量关系．(3)若CEF △旋转至A ，E ，F 三点共线，求m 的值．【答案】(1)5 四边形ABCD 是矩形，90ADC BCE ∴∠=∠=︒，AD =在Rt ABC ∆中，由勾股定理得：在Rt CEF ∆中，4CE =，3EF =，5CF ∴=，∴3EF =，63AB ==，在Rt ABC ∆中，由勾股定理得：在Rt CEF ∆中，4CE =，3EF =，5CF ∴=，∴34EF CE =，6384AB BC ==，同理得：AFC BEC ∆∆∽，∴54AC AF BC BE ==，AF =48211255BE AF -∴==综上，821125BE +=或BE 【点睛】本题考查了矩形的性质、旋转的性质、勾股定理以及相似三角形的判定和性质等知识，熟练掌握【题型三与正方形形有关问题的压轴题】(1)如图1，过点E 作EG CD ⊥，EF BC ⊥，连接(2)如图2，连结EC ，过点E 作EC 的垂线交①求证：EQC 为等腰三角形；②连结PC ，若2BQ k CQ =，且2DE =，求【答案】(1)结论：AE FG =，AE FG ⊥．详见解析(2)①详见解析；②2244k k ++FG EC =，可得结论；（2）①过点E 作EM AB ⊥于点M ，EN BC ⊥于点N ，分别证明EP EC =，EQ EP =，可得结论；②延长ME 交CD 与点K ．则四边形EKCN 是矩形，证明2CQ =，BQ k =，利用勾股定理求解．【详解】（1）解：结论：AE FG =，AE FG ⊥．理由：连接EC ，延长AE 交FG 与点J ，交CD 于点K ．四边形ABCD 是正方形，BA BC ∴=，AB ∠45E CBE =∠=︒，90BCD ∠=︒，BE BE = ，()SAS ABE CBE ∴≌ ，AE CE ∴=，BAE BCE ∠=∠，EG CD ⊥ ，EF CB ⊥，90EGC EFC FCG ∴∠=∠=∠=︒，∴四边形EFCG 是矩形，∴=FG CE ，AE FG ∴=，EG FC = ，90GEF CFE ∠=∠=︒，EF FE =，()SAS GEF CFE ∴≌△△，ECF EGF ∴∠=∠，BAE EGF ∠=∠ ，∵AB CD ∥，BAE EKG ∴∠=∠，EGF EKG ∴∠=∠，90GEK EKG ∠+∠=︒ ，90GEK EGJ ∴∠+∠=︒，四边形ABCD是正方形，∴∠=∠，EBA EBC⊥，EN CB EM AB⊥∴=，EM ENEMB ENB MBN∠=∠=∠【变式训练】(1)判断线段AE、BF的位置关系并说明理由．(2)连接AC交BF于点H，连接EH，如图②；①若点E是BC的中点，当5HF=时，求线段AE②设正方形ABCD的面积为1S，四边形CEHF的面积为【答案】(1)垂直，理由见解析(1)探索并证明AG 与BF 有怎样的位置和数量关系；(2)转动DEF 至如图2位置时，（1）中的结论是否仍然成立？若成立，请证明：若不成立，请说明理由．(3)若122DE AD ==，DEF 绕着点D 旋转过程中，请直接写出【答案】(1)2BF AG =，BF AG ⊥，证明见解析(2)仍然成立，证明见解析(3)221221CG -≤≤+四边形ABCD 为正方形，AB BC CD AD ∴===，DE DF = ，AD DE CD DF ∴-=-，即在ABE 和CBF V 中，AB CB BAE BCF =⎧⎪，四边形ABCD 为正方形，AB BC CD AD ∴===，90BAE BCF ∠=∠=︒，9090ADE EDC CDF EDC ∠+∠=︒∠+∠=︒ ，，ADE CDF \Ð=Ð，在ADE V 和CDF 中，AD CD ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩，()SAS ADE CDF ∴≌V V ，AE CF ∴=，DAE DCF ∠=∠，在BGM 和EGA △中，BG GE AGE MGB AG MG =⎧⎪∠=∠⎨⎪=⎩，()SAS BGM EGA ∴ ≌，AE BM GAE M ∴=∠=∠，，90180M MBC BAM ∠+∠+︒+∠=︒ ，90BAM GAE DAE ∠+∠+∠=︒，MBC EAD ∴∠=∠，9090ABM MBC BCF DCF ∠=︒+∠∠=︒+∠ ，，ABM BCF ∴∠=∠，在ABM 和BCF △中，令E 点所在圆的半径为R ，G 点所在圆的半径为 122DE AD ==，4AB AD ∴==，2AC BD AB ==+1222BO CO BD ∴===，:1:2BG BE = ，:1:2r R ∴=，(1)求证：DG FG=．(2)如图2，当点E是中点时，求tan CGE∠的值．(3)如图3，当23BEDG=时，连接CF并延长交AB于点，求CFCH的值．【答案】(1)见解析(2)3 4 2∴EFM EGC △∽△，△∴EF EM EG EC =，即25x x =CF CM CH CB =，即12CF CH =2CF 【题型四与特殊平行四边形中新定义探究问题压轴题】【解决问题】：(3)如图3，点P 是正方形ABCD 的AB 边上一动点（不与A 、B 重合）位置，连接DE 并延长，与CP 的延长线交于点F ，连接AF ，若∵四边形ABCD 和四边形∴ABF ABD ∠=∠∴B ，F ，D 三点在一条直线上．∵GF AB ⊥，DA ∴BGF 和BAD∵四边形ABCD 和四边形∴45ABD GBF ∠=∠=∴BGF ∆和BAD ∆为等腰直角三角形，∴ABG ABF ∠+∠=∠∴ABG DBF ∠=∠，∴ABG DBF ∽，∴2DF BD ==；∵ABG DBF ∽，∴GAB BDF ∠=∠．∵ANM DNB ∠=∠，∴BAG AMN ∠+∠=∴AMN ABD ∠=∠=即直线DF 与直线AG∵四边形ABCD为正方形，=，∴BC CD由折叠的性质可得：=，∴CE CD⊥，∵CQ DF∠=∠．∴ECQ DCQ【变式训练】(1)如图1，在四边形ABCD 中，,90AD BC A ∠=︒∥，对角线BD 平分ADC ∠四边形．(2)如图2，在6×5的方格纸中，A ，B ，C 三点均在格点上，若四边形ABCD 合条件的格点D ．（3）如图，过C 作CQ AD ⊥于Q ，可得四边形ABCQ 是矩形，AQ BC =，AD BC ∥，证明四边形ACBE 为平行四边形，可得8BE AC ==，AE BC =，设BC AE x ==，而10DE =，10AD x =-，()10210DQ x x x =--=-，由新定义可得CD CB x ==，由勾股定理可得：()22222108x x x --=-，再解方程可得答案．【详解】（1）解：∵,90AD BC A ∠=︒∥，∴18090ABC A ∠=︒-∠=︒，ADB CBD ∠=∠，∵对角线BD 平分ADC ∠，∴ADB CDB ∠=∠，∴CBD CDB ∠=∠，∴CD CB =，∴四边形ABCD 为邻等四边形．（2）解：1D ，2D ，3D 即为所求；（3）如图，过C 作CQ AD ⊥于Q ，∵90DAB ABC ∠=∠=︒，∴四边形ABCQ 是矩形，∴,AQ BC AB CQ ==，AD BC ∥，∵BE AC ∥，∴四边形ACBE 为平行四边形，∴8BE AC ==，AE BC =，设BC AE x ==，而10DE =，问题探究：(1)如图1，等边ABC 边长为3，垂直于BC 边的等积垂分线段长度为______；(2)如图2，在ABC 中，8AB =，63BC =，30B ∠=︒，求垂直于BC 边的等积垂分线段长度；(3)如图3，在四边形ABCD 中，90A C ∠=∠=︒，6AB BC ==，3AD =，求出它的等积垂分线段长．∵ABC 是等边三角形，∴3sin 602AD AB ︒==，∴332AD =，（2）解：如图2中，线段在Rt ABH 中，∵90AHB ∠=︒，∴142AH AB ==，3BH AH =∵63BC =，11在Rt ABC △中，∵90A ∠=∴2223BD AD BD =+=+∵EH AB ∥，∴EH DH DE AB DB AD==，∵EF AD∥，∴ADH EHD∠=∠，∵ADB BDC∠=∠，∴EDH EHD∠=∠，∴ED EH=，论的思想解决问题是关键．。

2021年中考数学冲刺 挑战压轴题专题汇编（湖南长沙卷）03挑战压轴题（解答题（一））1. （2020年长沙中考第23题）在矩形ABCD 中，E 为DC 边上一点，把△ADE 沿AE 翻折，使点D 恰好落在BC 边上的点F 。

（1）求证：△ABF ∽△FCE ；（2）若AB=32，AD=4，求EC 的长；（3）若EC DE AE 2=-，记∠BAF=α，∠FAE=β，求βαtan tan +的值。

【答案】（1）见解析 （2）332 （3）332 【解析】（1）由题可知，∠AFE=∠D=90°，∴∠AFB+∠CFE=90°∵∠AFB+∠BAF=90°，∴∠CFE=∠BAF又∵∠B=∠C∴△ABF ∽△FCE（1）由题可知，AF=AD=4∴BF=2)32(42222=-=-AB AF∴CF=BC-BF=AD-BF=4-2=2又∵△ABF ∽△FCE ， ∴ABCF BF CE = 即：3222=CE ∴CE=332 （2）AF EF CF CE AF EF AB BF +=+=+βαtan tan 设CE=1，DE=x 则AE=x+2 AD=4422+=-x DE AE ，AB=CD=x+1∴BF=32222++-=-x x AB AF CF=1-222-=x CE EF∵△ABF ∽△FCE x x x x EF CF AF AB 14412-=++∴=∴， ∴xx x x x 111212-•+=++）（ 解得：x=2 ∴33232231tan tan =+=+βα2.（2019年长沙中考第24题）根据相似多边形定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．（1）某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．①条边成比例的两个凸四边形相似；（ 命题）②三个角分别相等两个凸四边形相似；（ 命题）③两个大小不同的正方形相似．（ 命题）（2）如图1，在四边形ABCD 和四边形A 1B 1C 1D 1中，∠ABC =∠A 1B 1C 1，∠BCD =∠B 1C 1D 1，111111AB BC CD A B B C C D ==，求证：四边形ABCD 与四边形A 1B 1C 1D 1相似．（3）如图2，四边形ABCD 中，AB ∥CD ，AC 与BD 相交于点O ，过点O 作EF ∥AB 分别交AD ，BC 于点E ，F ．记四边形ABFE 的面积为S 1，四边形EFDE 的面积为S 2，若四边形ABFE 与四边形EFCD 相似，求21S S 的值． 【答案】（1）①假，②假，③真；（2）见解析 ；（3）121S S = 【分析】（1）根据相似多边形的定义即可判断．（2）根据相似多边形的定义证明四边成比例，四个角相等即可．（3）四边形ABFE 与四边形EFCD 相似，证明相似比是1即可解决问题，即证明DE=AE即可．【详解】解（1）①四条边成比例的两个凸四边形相似，是假命题，角不一定相等．②三个角分别相等的两个凸四边形相似，是假命题，边不一定成比例．③两个大小不同的正方形相似．是真命题．故答案为假，假，真．（2）证明：分别连接BD ，B 1D 1111BCD B C D ∠=∠，且1111BC CD B C C D = 111BCD BC D ∴∽， 111CDB C D B ∴∠=∠，111C B D CBD ∠=∠，111111BD BC CD B D B C C D ==， 1111BD AB B D A B ∴=，111ABC A B C ∠=∠，111ABD A B D ∴∠=∠， 111ABD A B D ∴∽，1111AD AB A D A B =，1A A ∠=∠，111ADB A D B ∠=∠， 11111111AB BC CD AD A B B C C D A D ∴===，111ADC A DC ∠=∠，1A A ∠=∠，111ABC A B C ∠=∠，111BCD BC D ∠=∠∴四边形ABCD 与四边形A 1B 1C 1D 1相似. （3）如图2中，∵四边形ABFG 与四边形EFCD 相似DE EF AE AB∴=，EF OE OF =+， DE OE OF AE AB +∴=，EF AB CD ， DE OE AD AB ∴=，DE OC OF AD AB AB ==，DE DE OE OF AD AD AB AB ∴+=+， 2DE DE AD AE ∴=，AD DE AE =+，21DE AE AE∴=+， 2AE DE AE ∴=+，即AE =DE 121S S ∴=，3.（2018年长沙中考第24题）如图，在△ABC 中，AD 是边BC 上的中线，∠BAD=∠CAD ，CE ∥AD ，CE 交BA 的延长线于点E ，BC=8，AD=3．（1）求CE 的长；（2）求证：△ABC 为等腰三角形．（3）求△ABC 的外接圆圆心P 与内切圆圆心Q 之间的距离．【分析】（1）证明AD 为△BCE 的中位线得到CE=2AD=6；（2）通过证明△ABD ≌△CAD 得到AB=AC ；（3）如图，连接BP 、BQ 、CQ ，先利用勾股定理计算出AB=5，设⊙P 的半径为R ，⊙Q的半径为r ，在Rt △PBD 中利用勾股定理得到（R ﹣3）2+42=R 2，解得R=，则PD=，再利用面积法求出r=，即QD=，然后计算PD+QD即可．【解答】（1）解：∵AD是边BC上的中线，∴BD=CD，∵CE∥AD，∴AD为△BCE的中位线，∴CE=2AD=6；（2）证明：∵BD=CD，∠BAD=∠CAD，AD=AD，∴△ABD≌△CAD，∴AB=AC，∴△ABC为等腰三角形．（3）如图，连接BP、BQ、CQ，在Rt△ABD中，AB==5，设⊙P的半径为R，⊙Q的半径为r，在Rt△PBD中，（R﹣3）2+42=R2，解得R=，∴PD=PA﹣AD=﹣3=，∵S△ABQ+S△BCQ+S△ACQ=S△ABC，∴•r•5+•r•8+•r•5=•3•8，解得r=，即QD=，∴PQ=PD+QD=+=．答：△ABC的外接圆圆心P与内切圆圆心Q之间的距离为．1.（2020·湖南长沙市·九年级月考）定义：有且仅有一组对角相等的凸四边形叫做“准平行四边形”．例如：凸四边形ABCD 中，若A C ∠=∠，B D ∠≠∠，则称四边形ABCD 为准平行四边形．（1）如（图①），A 、B 、C 、D 是⊙O 上的四个点，60APC CPB ∠=∠=︒，延长BP 到Q ，使AQ AP =．求证：四边形AQBC 是准平行四边形；（2）如（图②），准平行四边形ABCD 内接于⊙O ，AB AD ≠，BC DC =，若⊙O 的半径为5，6AB =，求AC 的长；（3）如（图③），在Rt ABC △中，90C ∠=︒，30A ∠=︒，2BC =，若四边形ABCD 是准平行四边形，且BCD BAD ∠≠∠，请直接写出BD 长的最大值．【答案】（1）见解析；（2）（3）2【分析】（1）可证APQ 是等边三角形，可得60Q QAP ∠=︒=∠，由圆的内接四边形的性质可得60QPA ACB Q ∠=∠=︒=∠，由四边形内角和定理可证QAC QBC ∠≠∠，可得结论；（2）如图②，连接BD ，由准平行四边形定义可求90BAD BCD ∠=∠=︒，可得BD 是直径，由勾股定理可求8AD =，将ABC ∆绕点C 顺时针旋转90︒得到CDH ∆，可得6AB DH ==，AC CH =，90ACH ∠=︒，ABC CDH ∠=∠，由勾股定理可求AC 的长；（3）如图③，作ACD △的外接圆O ，过点O 作OE AC ⊥于E ，OF BC ⊥于F ，由准平行四边形定义可求60ABC ADC ∠=∠=︒，可得120AOC ∠=︒，由等腰三角形的性质和直角三角形的性质，可求1OE =，22CO OE ==，由勾股定理可求OB ，由当点D 在BO 的延长线时，BD 的长有最大值，即可求解．【详解】解：证明：（1）∵60APC CPB ∠=∠=︒，∴60APQ ∠=︒，且AQ AP =，∴APQ 是等边三角形，∴60Q QAP ∠=︒=∠，∵四边形APBC 是圆内接四边形，∴60QPA ACB ∠=∠=︒，∵360Q ACB QAC QBC ∠+∠+∠+∠=︒，∴240QAC QBC ∠+∠=︒，且120120QAC QAP BAC PAB PAB ∠=∠+∠+∠=︒+∠>︒，∴120QBC ∠<︒，∴QAC QBC ∠≠∠，且60QPA ACB Q ∠=∠=︒=∠，∴四边形AQBC 是准平行四边形．（2）如图②，连接BD ，∵AB AD ≠，BC DC =，∴ABD ADB ∠≠∠，CBD CDB ∠=∠，∴ABC ADC ∠≠∠，∵四边形ABCD 是准平行四边形，∴BAD BCD ∠=∠，∵四边形ABCD 是圆内接四边形，∴180BAD BCD ∠+∠=︒，180ABC ADC ∠+∠=︒，∴90BAD BCD ∠=∠=︒，∴BD 是直径，∴10BD =，∴8AD =，将ABC 绕点C 顺时针旋转90°得到CDH △，∴6AB DH ==，AC CH =，90ACH ∠=︒，ABC CDH ∠=∠，∵180ABC ADC ∠+∠=︒，∴180ADC CDH ∠+∠=︒，∴点A ，点D ，点H 三点共线，∴14AH AD DH =+=，∵222AC CH AH +=，∴22196AC =，∴AC =（3）如图③，作ACD ∆的外接圆O ，过点O 作OE AC ⊥于E ，OF BC ⊥于F ，90C ∠=︒，30A ∠=︒，2BC =，60ABC ∴∠=︒，60ABC ∠=︒，AC ==四边形ABCD 是准平行四边形，且BCD BAD ∠≠∠，60ABC ADC ∴∠=∠=︒，120AOC ∴∠=︒，且OE AC ⊥，OA OC =，30ACO CAO ∴∠=∠=︒，CE AE =，1OE ∴=，22CO OE ==，OE AC ⊥，OF BC ⊥，90ECF ∠=︒，∴四边形CFOE 是矩形，CE OF ∴==1OE CF ==，3BF BC CF ∴=+=，BO ∴==当点D 在BO 的延长线时，BD 的长有最大值，BD ∴长的最大值2BO OD =+=．【点睛】本题是圆的综合题，考查了圆的有关知识，旋转的性质，矩形的判定和性质，勾股定理等知识，理解准平行四边形的定义是本题的关键，添加恰当辅助线是本题的难点．2.（2020·长沙市南雅中学）我们定义：对角线垂直的凸四边形叫做“准筝形”．如图 1，四边形 ABCD 中，AC ⊥BD ，则四边形 ABCD 是“准筝形”．（1）“三条边相等的准筝形是菱形”是 命题；（填“真” 或“假”）（2）如图 1，在准筝形 ABCD 中，AD ＝3，AB ＝2，BC ＝4，求 CD 的长．（3）如图 2， 在准筝形 ABCD 中，AC 与 BD 交于点 O ，点 P 在线段 AD 上，AP ＝2，且 AD ＝3，AO =32，在BD 上存在移动的线段EF，E 在 F 的左侧，且EF＝1，使四边形AEFP 周长最小，求此时OE 的长度．【答案】（1）真；（2（3【分析】（1）先根据在准筝形ABCD中，AC⊥BD，BC=CD=AD，设AC与BD交于点O，得出OA=OC，OB=OD，推出四边形ABCD是平行四边形，再根据AD=CD，即可证明四边形ABCD是菱形，即可得出结论；（2）设AC与BD交于点O，根据AC⊥BD，得到AB2=AO2+BO2，AD2=AO2+DO2，CD2=CO2+DO2，BC2=OB2+OC2，可得AB2+CD2=AD2+BC2=OA2+OB2+OC2+OD2，根据AD=3，АВ=2，BC=4，即可求出CD；（3）过P作PG⊥AO于G，过A作AM//EF且AM=EF，作M点关于OD的对称点N，连接MN交OD于H，交PG于R，连接PN交OD于F，先证明四边形AEFM是平行四边形，得到AE=MF，根据M、N关于OD对称，得出MF=NF，推出当且仅当N、F、P三点共线时，AE+PF取得最小值，根据AP=2，EF=1，得出当AE+PE取得最小值时，四边形AEFP周长取得最小值，然后证明四边形AOHM是矩形，得出АМ=ОН=EF=1，OA=MН=HN=32，根据在Rt△AOD中，OA=32，AD=3，PG⊥OA，求出AG=12AP=1，，RN=HN+HR=2，证明△NHF∽△NRP，得出HFRP=NHNR=34，求出HF=34PR=)314，根据OF=ОН+HF=OE+EF，ОН=EF=1，即可得出OЕ．【详解】解：（1）三条边相等的准筝形是菱形是真命题，，在准筝形ABCD中，AC⊥BD，BC=CD=AD，设AC与BD交于点O，∴OA=OC，OB=OD，∴四边形ABCD是平行四边形，∵AD=CD，∴四边形ABCD是菱形，∴三边相等的准筝形是菱形，故答案为：真；（2）设AC与BD交于点O，∵AC⊥BD，∴AB2=AO2+BO2，AD2=AO2+DO2，CD2=CO2+DO2，BC2=OB2+OC2，∴AB2+CD2=AD2+BC2=OA2+OB2+OC2+OD2，∵AD=3，АВ=2，BC=4，∴22+CD2=32+42，∴∴CD（3）过P作PG⊥AO于G，过A作AM//EF且AM=EF，作M点关于OD的对称点N，连接MN交OD于H，交PG于R，连接PN交OD于F，∵AM//EF，AM=EF，∴四边形AEFM是平行四边形，∴AE=MF，∵M、N关于OD对称，∴MF=NF，∴AE+PF=MF+PF=NF+PF≥PN，∴当且仅当N、F、P三点共线时，AE+PF取得最小值，∵AP=2，EF=1，∴当AE+PE取得最小值时，四边形AEFP周长取得最小值，∵AM//OD，ОA//MН，∠AOD=90°，∴四边形AOHM是矩形，∴АМ=ОН=EF=1，OA=MН=HN=32，在Rt△AOD中，OA=32，AD=3，∴∠ADO=30°，∵PG⊥OA，∴PG∥OD，∴∠APG=∠ADO=30°，∴AG=12AP=1，∴，∵HR=32-1=12，∴RN=HN+HR=2，∵PG//OD，∴△NHF∽△NRP，∴HFRP=NHNR=34，∴HF=34PR=)314∵OF=ОН+HF=OE+EF ，ОН=EF=1，∴，故四边形AEFP 周长最小时，OE 【点睛】本题属于四边形综合题，考查了菱形的判定和性质，相似三角形的判定和性质，勾股定理，含30度角的直角三角形的性质，掌握这些知识点灵活运用是解题关键．3．（2020·长沙市明德天心中学）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“邻好四边形”．(1)概念理解：如图1，在四边形ABCD 中，添加一个条件，使得四边形ABCD 是“邻好四边形”，请写出你添加的一个条件________；(2)概念延伸：下列说法正确的是________．(填入相应的序号)①对角线互相平分的“邻好四边形”是菱形；②一组对边平行，另一组对边相等的“邻好四边形”是菱形；③有两个内角为直角的“邻好四边形”是正方形；④一组对边平行，另一组对边相等且有一个内角是直角的“邻好四边形”是正方形；(3)问题探究：如图2，小红画了一个Rt ABC ∆，其中90ABC ∠=︒，2AB =，1BC =，并将Rt ABC ∆沿B 的平分线BB '方向平移得到A B C '''∆，连结AA '，BC '，要使平移后的四边形ABC A ''是“邻好四边形”应平移多少距离(即线段BB '的长)？【答案】（1）AB=AD；（2）①④；（3）21或2【分析】（1）根据定义添加一组邻边相等即可；（2）先利用平行四边形的判定定理得平行四边形，再利用“邻好四边形”定义得邻边相等，得出结论；（3）由平移的性质易得BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，“邻好四边形”定义分类讨论，由勾股定理得出结论．【详解】（1）AB=BC或BC=CD或AD=CD或AB=AD．答案：AB=AD；（2）①正确，理由为：∵四边形的对角线互相平分，∴这个四边形是平行四边形，∵四边形是“邻好四边形”，∴这个四边形有一组邻边相等，∴这个“邻好四边形”是菱形；②不正确，理由为：一组对边平行，另一组对边相等的“邻好四边形”也有可能是等腰梯形；③不正确，理由为：有两个内角为直角的“邻好四边形”不是平行四边形时，该结论不成立；④正确，理由为：一组对边平行，另一组对边相等且有一个内角是直角可得到“四个角都是直角”，则该四边形是矩形，根据“邻边相等的矩形为正方形”，所以④的说法正确．故答案是：①④；（3）∵∠ABC=90°，AB=2，BC=1，∴∵将Rt△ABC平移得到△A′B′C′，∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，（I）如图1，当AA′=AB时，BB′=AA′=AB=2；（II）如图2，当AA′=A′C′时，BB′=AA′=A′C′=5；（III）当A′C′=BC′=5时，如图3，延长C′B′交AB于点D，则C′B′⊥AB，∵BB′平分∠ABC，∴∠ABB′=12∠ABC=45°， ∴∠BB′D=′∠ABB′=45°∴B′D=BD ，设B′D=BD=x ，则C′D=x+1，BB′=2x ，∵在Rt △BC′D 中，BD 2+C′D 2=BC′2∴x 2+（x+1）2=(5)2，解得：1212x x ==-，(不合题意，舍去)， ∴BB′=22=（Ⅳ）当BC′=AB=2时，如图4，同理可得：BD 2+C′D 2=BC′2，设B′D=BD=x ，则x 2+（x+1）2=22， 解得：121717x x -+--==（不合题意，均舍去）， ∴BB′=22142-=． 综上所述，要使平移后的四边形ABC′A′是“邻好四边形”应平移251214-+． 4．（2021·全国九年级）如图，点E 是ABC ∆的内心，AE 的延长线和ABC ∆的外接圆相交于点D ，交BC于F ．（1）若40ABC =∠，80C ∠=，求CBD ∠的度数；（2）求证：DB DE =；（3）若6AB =，4AC =，5BC =，求DE 的长．【答案】（1）30°；（2）见解析；（3）【分析】（1）由三角形的内心定义和同弧所对的圆周角相等即可解答；（2）连接BE ，根据三角形的内心定义和同弧所对的圆周角相等证得∠DBE ＝∠BED ，从而依据等角对等边即可证得；（3）利用已知和角平分线的性质得32AB BF AC CF ==，进而求得BF 、CF 的值，再证明△BDF ∽△ACF 和△DBF ∽△DAB ，利用相似三角形的性质得到关于BD 的方程，解之即可解答﹒【详解】（1）∵40ABC =∠，80C ∠=，∴∠BAC=180º-∠ABC-∠C=60º，∵E 是内心，∴∠BAD ＝∠CAD=12∠BAC=30º， 由同弧所对的圆周角相等得：∠CBD=∠CAD=30º；（2）证明：连接BE ，∵E 是内心，∴∠ABE ＝∠CBE ，∠BAD ＝∠CAD ．∵∠CBD ＝∠CAD ，∴∠CBD ＝∠BAD ，∵∠BAD+∠ABE ＝∠BED ，∠CBE+∠CBD ＝∠DBE ，∴∠DBE ＝∠BED ，∴ DE ＝DB ；（3）∵∠BAD ＝∠CAD ，AB=6，AC=4，BC=5 ∴32AB BF AC CF == ∴ BF=3，CF=2∵∠DBC ＝∠D AC ，∠BFD=∠AFC∴ △BDF ∽△ACF ∴42,2BD AC BF DF DF CF AF CF====， ∴,62BD DF DF AF BF CF ===， ∵∠BAD ＝∠CAD=∠DBC ，∠BDF=∠ADB∴ △DBF ∽△DAB ∴BD DF DA BD=，∴22•()62BD BD DF AD DF AF DF ⎛⎫==+=+ ⎪⎝⎭，∴BD =BD=DE ，∴DE =【点睛】本题考查了三角形的内心定义、圆的外接圆、同弧所对的圆周角相等、相似三角形的判定与性质，解答的关键是正确理解三角形的内心定义，熟练掌握同弧所对的圆周角相等，进而创造三角形相似的条件，进行相关的证明或计算．5．（2020·长沙市南雅中学九年级开学考试）如图1，在平面直角坐标系中，已知点A ，B 的坐标分别为()0,6A和()B -，点E 为x 轴正半轴上的一个动点，过点A 、B 、E 作ABE △的外接圆C ，连结AC 并延长交圆于点D ，连结BD 、DE ．（1）求证：OAE BAD ∠=∠．（2）当15AD =时，求OE 的长度．（3）如图2，连结OD ，求线段OD 的最小值及当OD 最小时ABE △的外接圆圆心C 的坐标．【答案】（1）见解析；（2）92；（3）OD 最小值为9，C （，34） 【分析】（1）根据圆周角定理得出∠ABD=90°，再根据同弧所对的圆周角相等得出∠ADB=∠AEB ，从而证明结论； （2）根据条件算出AB ，证明△ABD ∽△AOE ，得出AB AO AD AE=，解得AE ，再根据勾股定理算出OE 的长； （3）设直线BD 与y 轴交于点F ，得出当OD ⊥BD 时，OD 最小，通过解直角三角形算出OD ，BD ，过点D 作DG ⊥BE 于点G ，设OG=x ，利用勾股定理解出OG 和DG ，从而得到点D 坐标，结合点A 坐标得出圆心C 的坐标.【详解】解：（1）由题意可得：AD 为⊙O 的直径，∴∠ABD=∠AOE=90°，∵∠ADB=∠AEB ，∠AOE=90°∴∠OAE=∠BAD ；（2）∵()0,6A 和()B -，∴OA=6，OB=∴12=，∵AD=15，由（1）得：∠OAE=∠BAD ，∠ABD=∠AOE ，∴△ABD ∽△AOE ， ∴AB AO AD AE=， 即12615AE=， 解得：AE=152，∴92==； （3）设直线BD 与y 轴交于点F ，∵AB ⊥BD ，∴∠OBD=∠OAB=90°-∠ABO ，直线AB 位置不变，∴直线BD 位置不变，∴当OD ⊥BD 时，OD 最小，此时，OD=OB×sin ∠OBD=OB×sin ∠OAB=×OB AB =，=过点D 作DG ⊥BE 于点G ，设OG=x ，则BG=，在△OBD 中，BD 2-BG 2=OD 2-OG 2，即(()22229x x -=-，解得：x=2，即OG=2，=92， 由题意可得点D 在第三象限，∴点D坐标为（2-，92-），而点A （0，6）， ∴点C坐标为（022，9622-+），即（，34）.【点睛】本题属于圆的综合题，涉及了圆周角定理，相似三角形的判定与性质、三角函数值的知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来． 6．（2021·长沙九年级模考）如图，O 为ABC ∆的外接圆，D 为OC 与AB 的交点，E 为线段OC 延长线上一点，且EAC ABC ∠=∠．(1)求证：直线AE 是O 的切线．(2)若D 为AB 的中点，6CD =，16AB =．①求O 的半径；②求ABC的内心到点O的距离．【答案】(1)证明见解析;(2)①253;②5．【分析】（1）连接AO，并延长AO交⊙O于点F，连接CF，由圆周角定理的推论可得∠ACF=90°，可得∠F+∠FAC=90°，由∠EAC=∠ABC，可得∠EAC+∠FAC=90°，即可完成证明；(2)①由垂径定理可得OD⊥AB，AD=BD=8，由勾股定理可求⊙O的半径；②作∠CAB的平分线交CD于点H，连接BH，过点H作HM⊥AC，HN⊥BC，则点H是△ABC的内心，由三角形内心的性质可得HM=HN=HD，由三角形的面积公式可求HD的值，即可完成解答．【详解】(1)证明：如图：连接AO，并延长AO交⊙O于点F，连接CF，∵AF是直径，∴∠ACF=90°，∴∠F+∠FAC=90°，∵∠F=∠ABC，∠ABC=∠EAC，∴∠EAC=∠F，∴∠EAC+∠FAC=90°，∴∠EAF=90°，∵AO是半径，∴直线AE是⊙O的切线；(2)①如图，连接AO，∵D为AB的中点，OD过圆心，∴OD⊥AB，AD=BD=12AB=8，∵AO2=AD2+DO2，∴AO2=82+（AO-6）2，∴AO=253，∴⊙O的半径为253；②如图，作∠CAB的平分线交CD于点H，连接BH，过点H作HM⊥AC，HN⊥BC，∵OD⊥AB，AD=BD，∴AC=BC，∴CD平分∠ACB，即点H是△ABC的内心，∴MH=NH=DH，在Rt△ACD中，10AC BC====，∵S△ABC=S△ACH+S△ABH+S△BCH，∴12×16×6=12×10×MH+12×16×DH+12×10×NH，∴DH=83，∵OH=CO－CH=CO－（CD－DH），∴2586533OH⎛⎫=--=⎪⎝⎭.【点睛】本题是圆的综合题，考查了圆周角定理、垂径定理、切线的判定、角平分线性质、勾股定理等知识，熟练运用这些性质定理进行推理是解答本题的关键．7．（2020·湖南长沙市·九年级月考）定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形ABCD 中，若,A C B D ∠=∠∠≠∠，则称四边形ABCD 为准平行四边形.（1）如图①，,,,A P B C 是O 上的四个点，60APC CPB ∠=∠=︒，延长BP 到Q ，使AQ AP =.求证:四边形AQBC 是准平行四边形；（2）如图②，准平行四边形ABCD 内接于O ，,AB AD BC DC +=，若O 的半径为5,6AB =，求AC 的长；（3）如图③，在Rt ABC 中，90,30,2C A BC ∠=︒∠=︒=，若四边形ABCD 是准平行四边形，且BCD BAD ∠≠∠，请直接写出BD 长的最大值.【答案】（1）见解析；（2）（3）2【分析】（1）先根据同弧所对的圆周角相等证明三角形ABC 为等边三角形，得到∠ACB=60°，再求出∠APB=60°，根据AQ=AP 判定△APQ 为等边三角形，∠AQP=∠QAP=60°，故∠ACB=∠AQP ，可判断∠QAC ＞120°，∠QBC ＜120°，故∠QAC≠∠QBC ，可证四边形AQBC 是准平行四边形；（2）根据已知条件可判断∠ABC≠∠ADC ，则可得∠BAD=∠BCD=90°，连接BD ，则BD 为直径为10，根据BC=CD 得△BCD 为等腰直角三角形，则∠BAC=∠BDC=45°，在直角三角形BCD 中利用勾股定理或三角函数求出BC 的长，过B 点作BE ⊥AC ，分别在直角三角形ABE 和△BEC 中，利用三角函数和勾股定理求出AE 、CE 的长，即可求出AC 的长.（3）根据已知条件可得：∠ADC=∠ABC=60°，延长BC 到E 点，使BE=BA ，可得三角形ABE 为等边三角形，∠E=60°，过A 、E 、C 三点作圆o ，则AE 为直径，点D 在点C 另一侧的弧AE 上（点A 、点E 除外），连接BO 交弧AE 于D 点，则此时BD 的长度最大，根据已知条件求出BO 、OD 的长度，即可求解.【详解】（1）∵60APC CPB ∠=∠=︒∴∠ABC=∠BAC=60°∴△ABC 为等边三角形，∠ACB=60°∵∠APQ=180°-∠APC-∠CPB=60°又AP=AQ∴△APQ 为等边三角形∴∠AQP=∠QAP=60°∴∠ACB=∠AQP∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB ＞120°故∠QBC=360°-∠AQP-∠ACB-∠QAC ＜120° ∴∠QAC≠∠QBC∴四边形AQBC 是准平行四边形（2）连接BD ，过B 点作BE ⊥AC 于E 点∵准平行四边形ABCD 内接于O ，,≠=AB AD BC DC∴∠ABC≠∠ADC ，∠BAD=∠BCD∵∠BAD+∠BCD=180°∴∠BAD=∠BCD=90°∴BD 为O 的直径∵O 的半径为5∴BD=10∵BC=CD,∠BCD=90°∴∠CBD=∠BDC=45°∴BC=BD ⨯ sin ∠BDC=102⨯，∠BAC=∠BDC=45° ∵BE ⊥AC∴∠BEA=∠BEC=90°∴AE=AB ⨯sin ∠BAC=6⨯2∵∠ABE=∠BAE=45°∴BE=AE=在直角三角形BEC 中，=∴AC=AE+EC=（3）在Rt ABC 中，90,30∠=︒∠=︒C A∴∠ABC=60°∵四边形ABCD 是准平行四边形，且BCD BAD ∠≠∠∴∠ADC=∠ABC=60°延长BC 到E 点，使BE=BA ，可得三角形ABE 为等边三角形，∠E=60°，过A 、E 、C 三点作圆o ，因为∠ACE=90°，则AE 为直径，点D 在点C 另一侧的弧AE 上（点A 、点E 除外），此时，∠ADC=∠AEC=60°，连接BO 交弧AE 于D 点，则此时BD 的长度最大.在等边三角形ABE 中，∠ACB=90°，BC=2∴AE=BE=2BC=4∴OE=OA=OD=2∴BO ⊥AE∴BO=BE ⨯sin ∠E=4⨯∴BD=BO+0D=2+即BD 长的最大值为2+【点睛】本题考查的是新概念及圆的相关知识，理解新概念的含义、掌握圆的性质是解答的关键，本题的难点在第（3）小问，考查的是与圆相关的最大值及最小值问题，把握其中的不变量作出圆是关键.8.（2020·长沙市天心区明德启南中学九年级期末）如图1，⊙O是△ABC的外接圆，AB是直径，D是⊙O 外一点且满足∠DCA＝∠B，连接AD．（1）求证：CD是⊙O的切线；（2）若AD⊥CD，AB＝10，AD＝8，求AC的长；（3）如图2，当∠DAB＝45°时，AD与⊙O交于E点，试写出AC、EC、BC之间的数量关系并证明．【答案】（1）见解析；（2）AC的长为（3）AC＝BC，理由见解析【分析】(1)连接OC,由直径所对圆周角是直角可得∠ACB=90°,由OC=OB得出∠OCB=∠B,由因为∠DCA=∠B,从而可得∠DCA=∠OCB,即可得出∠DCO=90°;(2) 由题意证明△ACD∽△ABC,根据对应边成比例列出等式求出AC即可;(3) 在AC上截取AF使AF＝BC，连接EF、BE，通过条件证明△AEF≌△BEC,根据性质推出△EFC为等腰直角三角形,即可证明AC、EC、BC的数量关系．【详解】(1)证明：连接OC，如图1所示：∵AB是⊙O的直径，∴∠ACB＝90°，∵OC＝OB，∴∠B＝∠OCB，∵∠DCA＝∠B，∴∠DCA＝∠OCB，∴∠DCO＝∠DCA+∠OCA＝∠OCB+∠OCA＝∠ACB＝90°，∴CD⊥OC，∴CD是⊙O的切线；(2)解：∵AD⊥CD∴∠ADC＝∠ACB＝90°又∵∠DCA＝∠B∴△ACD∽△ABC∴AC ADAB AC=，即810ACAC=，∴AC＝即AC的长为(3)解：AC＝BC；理由如下：在AC上截取AF使AF＝BC，连接EF、BE，如图2所示：∵AB是直径，∴∠ACB＝∠AEB＝90°，∵∠DAB＝45°，∴△AEB为等腰直角三角形，∴∠EAB＝∠EBA＝∠ECA＝45°，AE＝BE，在△AEF和△BEC中，AE BEEAF EBC AF BC=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△BEC(SAS)，∴EF＝CE，∠AFE＝∠BCE＝∠ACB+∠ECA＝90°+45°＝135°，∴∠EFC＝180°﹣∠AFE＝180°﹣135°＝45°，∴∠EFC＝∠ECF＝45°，∴△EFC为等腰直角三角形．∴CF，∴AC＝AF+CF＝BC．【点睛】本题考查圆与三角形的结合,关键在于牢记基础性质,利用三角形的相似对应边以及三角形的全等进行计算．。

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图，在矩形ABCD 中，AB =8，AD =4，点E 是矩形ABCD 内部一动点，且∠BEC =90°，点P 是AB 边上一动点，连接PD 、PE ，则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹，利用“将军饮马”模型将PE 进行转化即可求解．【详解】解：如图，设点O 为BC 的中点，由题意可知，点E 在以BC 为直径的半圆O 上运动，作半圆O 关于AB 的对称图形(半圆O ')，点E 的对称点为E 1，连接O 'E 1,则PE =PE 1，∴当点D 、P 、E 1、O '共线时，PD +PE 的值最小，最小值为DE 1的长，如图所示，在Rt △DCO '中，CD =8，CO '=6，∴DO '=82+62=10，又∵O 'E 1=2，∴DE 1=DO '-O 'E 1=8，即PD +PE 的最小值为8，故选：A ．【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理，利用“将军饮马”模型将PE 进行转化时解题的关键．2(2023·安徽黄山·校考模拟预测)如图，在平面直角坐标系中，二次函数y =32x 2-32x -3的图象与x 轴交于点A ，C 两点，与y 轴交于点B ，对称轴与x 轴交于点D ，若P 为y 轴上的一个动点，连接PD ，则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，可求得∠ABO =30°，从而得出PE =12PB ，进而得出PD +12PB =PD +EP ，进一步得出结果．【详解】解：如图，作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，抛物线的对称轴为直线x =--322×32=12，∴OD =12，当x =0时，y =-3，∴OB =3，当y =0时，32x 2-32x -3=0，∴x 1=-1，x 2=2，∴A (-1,0)，∴OA =1，∵tan ∠ABO =OA OB =13=33，∴∠ABO =30°，∴PE =12PB ，∴12PB +PD =PD +PE ≥DF ，当点P 在P 时，PD +PE 最小，最大值等于DF ，在Rt △ADF 中，∠DAF =90°-∠ABO =60°，AD =OD +PA =12+1=32，∴DF =AD ⋅sin ∠DAE =32×32-334，∴12PB +PD 最小=DF =334，故选：A ．【点睛】本题以二次函数为背景，考查了二次函数与一元二次方程之间的关系，解直角三角形等知识，解决问题的关键是用三角函数构造12PB ．3(2023秋·浙江金华·九年级统考期末)如图，正方形ABCD 的边长为4，点E 是正方形ABCD 内的动点，点P 是BC 边上的动点，且∠EAB =∠EBC ．连结AE ，BE ，PD ，PE ，则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°，即可得点E 在以AB 为直径的半圆上移动，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，问题随之得解．【详解】解：∵四边形ABCD 是正方形，∴∠ABC =90°，∴∠ABE +∠EBC =90°，∵∠EAB =∠EBC ，∴∠EAB +∠EBA =90°，∴∠AEB =90°，∴点E 在以AB 为直径的半圆上移动，如图，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，E∵∠G =90°，FG =BG =AB =4，∴OG =6，OA =OB =OE =2，∴OF =FG 2+OG 2=213，∴EF =OF -OE =213-2，故PE +PD 的长度最小值为213-2，故选：A ．【点睛】本题考查了轴对称-最短路线问题，正方形的性质，勾股定理，正确的作出辅助线，得出点E 的运动路线是解题的关键．4(2022秋·安徽池州·九年级统考期末)如图，Rt △ABC 中，∠C =90°，AC =4，BC =3，点P 为AC 边上的动点，过点P 作PD ⊥AB 于点D ，则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，点P 即为所求作的点，此时PB +PD 有最小值，连接AB ，根据对称性的性质，可知：BP =B P ，△ABC ≅△AB C ，根据S △ABB =S △ABC +S △AB C =2S △ABC ，即可求出PB +PD 的最小值．【详解】解：如下图，作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，连接AB ，点P 即为所求作的点，此时PB +PD 有最小值，根据对称性的性质，可知：BP =B P ，在Rt △ABC 中，∠ACB =90°,AC =4,BC =3，∴AB =AC 2+BC 2=5，根据对称性的性质，可知：△ABC ≅△AB C ，∴S △ABB =S △ABC +S △ABC =2S △ABC ，即12×AB ⋅B D =2×12BC ⋅AC ，∴5B D =24，∴B D =245，故选：B ．【点睛】本题考查了轴对称一最短路线问题，解题的关键是掌握轴对称的性质．5(2023秋·甘肃定西·八年级校考期末)如图所示，在△ABC 中，∠ABC =68°，BD 平分∠ABC ，P 为线段BD 上一动点，Q 为 边AB 上一动点，当AP +PQ 的值最小时，∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ，连接PE ，证明△PBQ ≌△PBE SAS ，得出PE =PQ ，说明AP +PQ =AP +PE ，找出当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ 最小，过点A 作AE ⊥BC 于点E ，交BD 于点P ，根据三角形外角的性质可得答案．【详解】解：在BC 上截取BE =BQ ，连接PE ，如图：∵BD 平分∠ABC ，∠ABC =68°，∴∠ABD =∠CBD =12∠ABC =34°，∵BP =BP ，∴△PBQ ≌△PBE SAS ，∴PE =PQ ，∴AP +PQ =AP +PE ，∴当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ最小，过点A作AE ⊥BC 于点E ，交BD 于点P ，如图：∵∠AEB =90°，∠CBD =34°，∴∠APB =∠AEB +∠CBD =124°．故选：D ．5【点睛】本题主要考查了角平分线的定义，三角形全等的判定和性质，垂线段最短，三角形内角和定理与三角形的外角的性质，解题的关键是找出使AP +PQ 最小时点P 的位置．6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图，E 为正方形ABCD 边AD 上一点，AE =1，DE =3，P 为对角线BD 上一个动点，则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点，根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长，求出EC 的长即可.【详解】连接EC ，交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长.∵AE =1，DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选：A【点睛】本题主要考查了正方形的性质和两点之间线段最短，这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图，正方形ABCD 的边长为4，点M 在DC 上，且DM =1，N 是AC 上一动点，则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称，连接BM 交AC 于N ′，N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可．【详解】∵四边形ABCD 是正方形，∴点B 与D 关于直线AC 对称，6连接BD ，BM 交AC 于N ′，连接DN ′，∴当B 、N 、M 共线时，DN +MN 有最小值，则BM 的长即为DN +MN 的最小值，∴AC 是线段BD 的垂直平分线，又∵CD =4，DM =1∴CM =CD -DM =4-1=3，在Rt △BCM 中，BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5．故选：D ．【点睛】本题考查的是轴对称-最短路线问题及正方形的性质，先作出D 关于直线AC 的对称点，由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键．8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图，在平面直角坐标系中，二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点，与x 轴交于点C (3,0)，若P 是x 轴上一动点，点D 的坐标为(0,-1)，连接PD ，则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ，根据2PD +PC =2PD +22PC =2PD +PJ ，求出DP +PJ 的最小值即可解决问题．【详解】解：连接BC ，过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ．∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0)，∴b =2，∴二次函数的解析式为y =-x 2+2x +3，令y =0，-x 2+2x +3=0，解得x =-1或3，∴A (-1，0)，令x =0，y =3，∴B (0，3)，∴OB =OC =3，∵∠BOC =90°，∴∠OBC =∠OCB =45°，∵D(0，-1)，∴OD =1，BD =4，∵DH ⊥BC ，∴∠DHB =90°，设DH =x ，则BH =x ,∵DH 2+BH 2=BD 2，7∴x =22，∴DH =22，∵PJ ⊥CB ，∴∠PJC =90°，∴PJ =22PC ，∴2PD +PC =2PD +22PC =2PD +PJ ，∵DP +PJ ≥DH ，∴DP +PJ ≥22，∴DP +PJ 的最小值为22，∴2PD +PC 的最小值为4．故选：A ．【点睛】本题考查了二次函数的相关性质，以及等腰直角三角形的判定和性质，垂线段最短等知识，得到∠OBC =∠OCB =45°，PJ =22PC 是解题的关键．9(2022·山东泰安·统考中考真题)如图，四边形ABCD 为矩形，AB =3，BC =4．点P 是线段BC 上一动点，点M 为线段AP 上一点．∠ADM =∠BAP ，则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°，得出点M 在O 点为圆心，以AO 为半径的圆上，从而计算出答案．【详解】设AD 的中点为O ，以O 点为圆心，AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心，以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时，BM 最短∵BO 2=AB 2+AO 2，AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选：D ．【点睛】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．810(2022·河南·校联考三模)如图1，正方形ABCD 中，点E 是BC 的中点，点P 是对角线AC 上的一个动点，设AP =x ，PB +PE =y ，当点P 从A 向点C 运动时，y 与x 的函数关系如图2所示，其中点M 是函数图象的最低点，则点M 的坐标是()A.42，35B.22,35C.35,22D.35,42【答案】A【分析】根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，从而确定正方形的边长为6，根据将军饮马河原理，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，利用相似三角形，计算AG 的长即为横坐标．【详解】如图，根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，∵点E 是BC 的中点，∴BC =6，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，∵四边形ABCD 是正方形，AB =6，∴CE ∥AD ，AC =62+62=62，DE =62+32=35，∴△CGE ∽△AGD ，∴CG AG =CE AD =12，∴AC AG=32，∴AG =42，故点M 的坐标为(42，35)，故A 正确．故选：A ．【点睛】本题考查了正方形的性质，三角形相似的判定和性质，函数图像信息的获取，将军饮马河原理，熟练掌握正方形的性质，灵活运用三角形相似，构造将军饮马河模型求解是解题的关键．2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图，矩形ABCD ，AB =4，BC =8，E 为AB 中点，F 为直线BC 上动点，B 、G 关于EF 对称，连接AG ，点P 为平面上的动点，满足∠APB =12∠AGB ，则DP 的最小值．【答案】210-22【分析】由题意可知，∠AGB =90°，可得∠APB =12∠AGB =45°，可知点P 在以AB 为弦，圆周角∠APB =45°的9圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)，设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，可知△AOB 为等腰直角三角形，求得OA =22AB =22=OP ，AQ =OQ =22OA =2，QD =AD -AQ =6，OD =OQ 2+QD 2=210，再由三角形三边关系可得：DP ≥OD -OP =210-22，当点P 在线段OD 上时去等号，即可求得DP 的最小值．【详解】解：∵B 、G 关于EF 对称，∴BH =GH ，且EF ⊥BG∵E 为AB 中点，则EH 为△ABG 的中位线，∴EH ∥AG ，∴∠AGB =90°，∵∠APB =12∠AGB ，即∠APB =12∠AGB =45°，∴点P 在以AB 为弦，圆周角∠APB =45°的圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，则OA =OB =OP ，∵∠APB =45°，∴∠AOB =90°，则△AOB 为等腰直角三角形，∴OA =22AB =22=OP ，又∵E 为AB 中点，∴OE ⊥AB ，OE =12AB =AE =BE ，又∵四边形ABCD 是矩形，∴∠BAD =90°，AD =BC =8，∴四边形AEOQ 是正方形，∴AQ =OQ =22OA =2，QD =AD -AQ =6，∴OD =OQ 2+QD 2=210，由三角形三边关系可得：DP ≥OD-OP =210-22，当点P 在线段OD 上时去等号，∴DP 的最小值为210-22，故答案为：210-22．【点睛】本题考查轴对称的性质，矩形的性质，隐形圆，三角形三边关系，正方形的判定及性质，等腰直角三角形的判定及性质，根据∠APB =12∠AGB =45°得知点P 在以AB 为弦，圆周角∠APB =45°的圆上是解决问题的关键．12(2023春·江苏连云港·八年级期中)如图，在边长为8的正方形ABCD 中，点G 是BC 边的中点，E 、F 分别是AD 和CD 边上的点，则四边形BEFG 周长的最小值为．【答案】2410【分析】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G ，根据两点之间线段最短即可解决问题．【详解】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G∵EB =EB ,FG =FG ，∴BE +EF +FG +BG =B E +EF +FG +BG ，∵EB +EF +FG ≥B G ，∴四边形BEFG 的周长的最小值=BG +B G ，∵正方形ABCD 的边长为8∴BG =4，BB =16，BG =12，∴B G =162+122=20，∴四边形BEFG 的周长的最小值为=4+20=24．故答案为：24．【点睛】本题考查轴对称求线段和的最短问题，正方形的性质，勾股定理，解题的关键是学会利用轴对称解决最短问题．13(2022·湖南湘潭·校考模拟预测)如图，菱形草地ABCD 中，沿对角线修建60米和80米两条道路AC <BD ，M 、N 分别是草地边BC 、CD 的中点，在线段BD 上有一个流动饮水点P ，若要使PM +PN 的距离最短，则最短距离是米．【答案】50【分析】作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，根据菱形的性质和勾股定理求出BC 长，即可得出答案．【详解】解：作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，∵四边形ABCD 是菱形，∴AC ⊥BD ，∠QBP =∠MBP ，即Q 在AB 上，∵MQ ⊥BD ，∴AC ∥MQ ，∴M 为BC 中点，∴Q 为AB 中点，∵N 为CD 中点，四边形ABCD 是菱形，∴BQ ∥CD ，BQ =CN ，∴四边形BQNC 是平行四边形，∴NQ =BC ，设AC 与BD 的交点为点O ，∵四边形ABCD 是菱形，∴AC ⊥BD，OC =12AC =30米，OB =12BD =40米，∴BC =OB 2+OC 2=50米，∴PM +PN 的最小值是50米．故答案为：50．11【点睛】本题考查了轴对称-最短路线问题，平行四边形的性质和判定，菱形的性质，勾股定理的应用，解此题的关键是能根据轴对称找出P 的位置．14(2023春·江苏·九年级校考阶段练习)如图，正方形ABCD 的边长为4，⊙B 的半径为2，P 为⊙B 上的动点，则2PC -PD 的最大值是．【答案】2【分析】解法1，如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，连接PM 、DM ，推得2PC -PD=2PC -22PD =2PC -PM ，因为PC -PM ≤MC ，求出MC 即可求出答案．解法2：如图：连接BD 、BP 、PC ，在BD 上做点M ，使BM BP =24，连接MP ，证明△BMP ∼△BPD ，在BC 上做点N ，使BN BP=12，连接NP ，证明△BNP ∼△BPC ，接着推导出2PC -PD =22MN ，最后证明△BMN ∼△BCD ，即可求解．【详解】解法1如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，∴∠PDM =45，DM =PM =22PD ，∵四边形ABCD 正方形∴∠BDC =45°，DB DC=2又∵∠PDM =∠PDB +MDB ，∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ，DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为：2．解法2如图：连接BD 、BP 、PC根据题意正方形ABCD 的边长为4，⊙B 的半径为2∴BP =2，BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ，使BM BP=24，则BM =22，连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ，BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24，则PD =22PM ∵BP BC =24=12在BC 上做点N ，使BN BP=12，则BN =1，连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ，BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12，则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ，BM BC =224=28，BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为：2．【点睛】本题考查正方形的性质，相似三角形，勾股定理等知识，难度较大，熟悉以上知识点运用是解题关键．15(2023秋·广东广州·九年级统考期末)如图，四边形ABCD 中，AB ∥CD ，AC ⊥BC ，∠DAB =60°，AD =CD =4，点M 是四边形ABCD 内的一个动点，满足∠AMD =90°，则△MBC 面积的最小值为．【答案】63-4【分析】取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则OM +ME ≥OF ，通过计算得出当O ,M ,E 三点共线时，ME 有最小值，求出最小值即可．【详解】解：如图，取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则13OM +ME ≥OF ，∵AB ∥CD ，∠DAB =60°，AD =CD =4，∴∠ADC =120°，∵AD =CD ，∴∠DAC =30°，∴∠CAB =30°，∵AC ⊥BC ，∴∠ACB =90°∴∠B =90°-30°=60°，∴∠B =∠DAB ，∴四边形ABCD 为等腰梯形，∴BC =AD =4，∵∠AMD =90°，AD =4，OA =OD ，∴OM =12AD =2，∴点M 在以点O 为圆心，2为半径的圆上，∵AB ∥CD ，∴∠GCF =∠B =60°，∴∠DGO =∠CGF =30°，∵OF ⊥BC ，AC ⊥BC ，∴∠DOG =∠DAC =30°=∠DGO ，∴DG =DO =2，∴OG =2OD ⋅cos30°=23，GF =3，OF =33，∴ME ≥OF -OM =33-2，∴当O ,M ,E 三点共线时，ME 有最小值33-2，∴△MBC 面积的最小值为=12×4×33-2 =63-4．【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点，点M 位置的确定是解题关键．16(2023春·全国·八年级专题练习)如图，在等边△ABC 中，BD ⊥AC 于D ，AD =3cm ．点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ，点M 为线段BD 上一动点，连接PM ,QM ，则PM +QM 的最小值为cm ．【答案】5【分析】如图所示，作点P 关于BD 的对称点P ，且点P 在BC 上，则PM +QM =P M+QM ，当P ,M ,Q 在同一条直线上时，有最小值，证明四边形PP QA 是平行四边形，P Q =AP =AB -BP ，由此即可求解．【详解】解：如图所示，作点P 关于BD 的对称点P ，∵△ABC 是等边三角形，BD ⊥AC ，∴∠ABD =∠DBC =12∠ABC =12×60°=30°，14∴点P 在BC 上，∴P M =PM ，则PM +QM =P M +QM ，当P ,M ,Q 在同一条直线上时，有最小值，∵点P 关于BD 的对称点P ，∠ABD =∠DBC =30°，∴PP ⊥BM ，BP =BP =1cm ，∴∠BP P =60°，∴△BPP 是等边三角形，即∠BP P =∠C =60°，∴PP ∥AC ，且PP =AQ =1cm ，∴四边形PP QA 是平行四边形，∴P Q =AP =AB -BP ，在Rt △ABD 中，∠ABD =30°，AD =3，∴AB =2AD =2×3=6，∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5，故答案为：5．【点睛】本题主要考查动点与等边三角形，对称-最短路径，平行四边形的判定和性质的综合，理解并掌握等边三角形得性质，对称-最短路径的计算方法，平行四边形的判定和性质是解题的关键．17(2022秋·山东菏泽·九年级校考阶段练习)如图，在周长为12的菱形ABCD 中，DE =1，DF =2，若P 为对角线AC 上一动点，则EP +FP 的最小值为．【答案】3【分析】作F 点关于BD 的对称点F ，连接EF 交BD 于点P ，则PF =PF ，由两点之间线段最短可知当E 、P 、F 在一条直线上时，EP +FP 有最小值，然后求得EF 的长度即可．【详解】解：作F 点关于BD 的对称点F ，则PF =PF ，连接EF '交BD 于点P ．∴EP +FP =EP +F P ．由两点之间线段最短可知：当E 、P 、F '在一条直线上时，EP +FP 的值最小，此时EP +FP =EP +F P =EF ．∵四边形ABCD 为菱形，周长为12，∴AB =BC =CD =DA =3，AB ∥CD ，∵AF =2，AE =1，∴DF =AE =1，∴四边形AEF D 是平行四边形，∴EF =AD =3．∴EP +FP 的最小值为3．故答案为：3．【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题，明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键．18(2023春·上海·八年级专题练习)如图，直线y =x +4与x 轴，y 轴分别交于A和B ，点C 、D 分别为线段AB 、OB 的中点，P 为OA 上一动点，当PC +PD 的值最小时，点P 的坐标为．15【答案】(-1,0)【分析】直线y =x +4与x 轴，y 轴分别交于A 和B ，可求出点A ，B 的坐标，点C 、D 分别为线段AB 、OB 的中点，可求出点C 、D 的坐标，作点C 关于x 轴的对称点C ，连接C D 与x 轴的交点就是所求点P 的坐标．【详解】解：直线y =x +4与x 轴，y 轴分别交于A 和B ，∴当y =0，x =-4，即A (-4,0)；当x =0，y =4，即B (0,4)，∵点C 、D 分别为线段AB 、OB 的中点，∴C (-2,2)，D (0,2)，如图所示，过点C 关于x 轴的对称点C，∴C (-2,-2)，∴直线C D 的解析式为：y =2x +2，当y =0，x =-1，即P (-1,0)，故答案为：(-1,0)．【点睛】本题主要考查一次函数与最短线段的综合，掌握对称中最短线段的解题方法是解题的关键．19(2023秋·黑龙江鸡西·九年级统考期末)如图，抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧)，与y 轴交于点C ，在其对称轴上有一动点M ，连接MA ,MC ,AC ，则△MAC 周长的最小值是．【答案】32+10【分析】根据“将军饮马”模型，先求出A 1,0 ,B 3,0 ,C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，从而C △MAC =CA +CM +MA =CA +CM +MB ，AC =OA 2+OC 2=10，则△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，从而得到CB =OC 2+OB 2=32，即可得到答案．【详解】解：∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧)，与y 轴交于点C ，16∴当y =0时，0=x 2-4x +3解得x =1或x =3，即A 1,0 ,B 3,0 ；当x =0时，y =3，即C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，即MA =MB ，∴C △MAC =CA +CM +MA =CA +CM +MB ，∵AC =OA 2+OC 2=10，∴△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，∵CB =OC 2+OB 2=32，∴△MAC 周长的最小值为CA +CB =32+10，故答案为：32+10．【点睛】本题考查动点最值问题与二次函数综合，涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识，熟练掌握动点最值的常见模型是解决问题的关键．20(2023秋·浙江温州·九年级校考期末)如图所示，∠ACB =60°，半径为2的圆O 内切于∠ACB．P 为圆O 上一动点，过点P 作PM 、PN 分别垂直于∠ACB 的两边，垂足为M 、N ，则PM +2PN 的取值范围为．【答案】6-23≤PM +2PN ≤6+23【分析】根据题意，本题属于动点最值问题-“阿氏圆”模型，首先作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示，通过代换，将PM +2PN 转化为PN +12PM =PN +HP =NH ，得到当MP 与⊙O 相切时，MF 取得最大值和最小值，分两种情况，作出图形，数形结合解直角三角形即可得到相应最值，进而得到取值范围．【详解】解：作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示：∵PM ⊥AC ，PN ⊥CB ，∴∠PMC =∠PNC =90°，∴∠MPN =360°-∠PMC -∠PNC -∠C =120°，∴∠MPH =180°-∠MPN =60°，∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ，∴PN +12PM =PN +HP =NH ，∵MF =NH ，∴当MP 与⊙O 相切时，MF 取得最大和最小，①连接OP ，OG ，OC ，如图1所示：可得：四边形OPMG 是正方形，∴MG =OP =2，在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG +GM =2+23，在Rt △CMF 中，MF =CM ⋅sin60°=3+3，∴HN =MF =3+3，即PM +2PN =212PM +PN =2HN =6+23；②连接OP ，OG ，OC ，如图2所示：可得：四边形OPMG 是正方形，17∴MG =OP =2，由上同理可知：在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG -GM =23-2，在Rt △CMF 中，MF =CM ⋅sin60°=3-3，∴HN =MF =3-3，即PM +2PN =212PM +PN =2HN =6-23，∴6-23≤PM +2PN ≤6+23．故答案为：6-23≤PM +2PN ≤6+23．【点睛】本题考查动点最值模型-“阿氏圆”，难度较大，掌握解决动点最值问题的方法，熟记相关几何知识，尤其是圆的相关知识是解决问题的关键．3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图，已知抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，交y 轴于点C ．(1)求抛物线的解析式，连接BC ，并求出直线BC 的解析式；(2)请在抛物线的对称轴上找一点P ，使AP +PC 的值最小，此时点P 的坐标是；(3)点Q 在第一象限的抛物线上，连接CQ ，BQ ，求出△BCQ 面积的最大值．【答案】(1)y =-x 2+3x +4；y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ，B 4,0 两点，代入抛物线解析式，可得到抛物线解析式，从而得到C 0,4 ，再设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入，即可求解；(2)连接BC ，PB ，根据题意可得A 、B 关于抛物线的对称轴直线x =32对称，从而得到当P 在直线AB 上三点共线时，AP +CP 的值最小，把x =32代入直线BC 的解析式，即可求解；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，可得QD =-d 2+4d ，从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8，即可求解；【详解】(1)解：(1)∵抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，∴a -b +4=016a +4b +4=0，解得：a =-1b =3 ，18∴抛物线的解析式为y =-x 2+3x +4；∵抛物线与y 轴的交点为C ，∴C 0,4 ，设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入得：4k +b =0b =4 ，解得：k =-1b =4 ，∴直线BC 的解析式为y =-x +4；(2)如图，连接BC ，PB ，∵y =-x 2+3x +4=-x -32 2+74，∴抛物线的对称轴为直线x =32，根据题意得：A 、B 关于抛物线的对称轴直线x =32对称，∴AP =BP ，∴AP +CP =BP +CP ≥BC ，即当P 在直线AB 上时，AP +CP 的值最小，∴当x =32时，y =-32+4=52，∴P 32,52 ，故答案是：32,52 ；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，∴QD =-d 2+3d +4 --d +4 =-d 2+4d ，∵B 4,0 ，∴OB =4，∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8，当d =2时，S ΔBCQ 取最大值，最大值为8，∴△BCQ 的最大面积为8；【点睛】本题主要考查了二次函数的图像和性质，利用数形结合思想和分类讨论思想是解题的关键．22(2023秋·江苏淮安·八年级统考期末)如图1，直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，过点B 的直线交x 轴负半轴于点C -3,0 ．(1)请直接写出直线BC 的关系式：(2)在直线BC 上是否存在点D，使得S △ABD =S △AOD 若存在，求出点D 坐标：若不存请说明理由；(3)如图2，D 11,0 ，P 为x 轴正半轴上的一动点，以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ，连接QA ,QD ．请直接写出QB -QD 的最大值：．19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时，S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点，可求出点B 的坐标，再用待定系数法即可求解；(2)设D (a ,2a +6)，分别用含a 的式子表示出出S △AOD ,S △ABD ，由此即可求解；(3)△BPQ 是等腰直角三角形，设P (m ,0)(m >0)，可表示出QB ，再证Rt △BOP ≌Rt △PTQ (AAS )，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值，可求得点R 的坐标，根据勾股定理即可求解．【详解】(1)解：∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，令x =0，则y =6，∴B (0,6)，且C -3,0 ，设直线BC 的解析式为y =kx +b ，∴b =6-3k +b =0，解得，k =2b =6 ，∴直线BC 的解析式为y =2x +6，故答案为：y =2x +6．(2)解：由(1)可知直线BC 的解析式为y =2x +6，直线AB 的解析式为y =-x +6，∴A (6,0),B (0,6),C (-3,0)，∴OA =6,BO =6,OC =3，如图所示，点D 在直线BC 上，过点D 作DE ⊥x 轴于E ，∴设D (a ,2a +6)，E (a ,0)，∴S △ABC =12AC ·OB =12×(6+3)×6=27，S △ADC =12AC ·DE =12×(6+3)×a =92a ，S △AOD =12OA ·DE =12×6×a =3a ，∴S △ABD =S △ABC -S △ADC =27-92a ，若S △ABD =S △AOD ，则27-92a =3a ，当a >0时，27-92a =3a ，解得，a =185，即D 185,665 ；当a <0时，27+92a =-3a ，解得，a =-185，即D -185,-65 ；综上所述，当D 185,665 或D -185,-65时，S △ABD =S △AOD ．(3)解：已知A (6,0),B (0,6),D (11,0)，设P (m ,0)(m >0)，∴在Rt △BOP 中，OB =6,OP =m ，∵△BPQ 是等腰直角三角形，∠BPQ =90°，∴BP =QP ；如图所示，过点Q 作QT ⊥x 轴于T ，20在Rt △BOP ,Rt △PTQ 中，∠BOP =∠PTQ =90°，∠BPO +∠QPA =∠QPA +∠PQT =90°，∴∠BPO =∠PQT ，∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP，∴Rt △BOP ≌Rt △PTQ (AAS )，∴OP =TQ =m ，OB =PT =6，∴AT =OP +PT -OA =m +6-6=m ，∴AT =QT ，且QT ⊥x 轴，∴△ATQ 是等腰直角三角形，∠QAT =45°，则点Q 的轨迹在射线AQ 上，如图所示，作点D 关于直线AQ 的对称点R，连接QR ,BR ,AR ，A (6,0)，B (0,6)，D (11,0)，∵△ATQ 是等腰直角三角形，即∠QAT =45°，根据对称性质，∴∠QAR =45°，∴RA ⊥x 轴，且△DQA ≌△RQA ，∴AR =AD =11-6=5，则R (6,5)，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值；∴由勾股定理得：BR =62+(6-5)2=37，故答案为：37．【点睛】本题主要考查一次函数，几何的综合，掌握待定系数法求解析式，将军饮马问题，等腰直角三角形的性质，勾股定理是解题的关键．23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中，∠B =60°．(1)如图1，若AC >BC ，CD 平分∠ACB 交AB 于点D ，且AD =3BD ．证明：∠A =30°；(2)如图2，若AC <BC ，取AC 中点E ，将CE 绕点C 逆时针旋转60°至CF ，连接BF 并延长至G ，使BF =FG ，猜想线段AB 、BC 、CG 之间存在的数量关系，并证明你的猜想；(3)如图3，若AC =BC ，P 为平面内一点，将△ABP 沿直线AB 翻折至△ABQ ，当3AQ +2BQ +13CQ 取得最小值时，直接写出BPCQ的值．【答案】(1)见解析(2)BC =AB +CG ，理由见解析(3)213+33913【分析】(1)过点D 分别作BC ，AC 的垂线，垂足为E ，F ，易得DE =DF ，由∠B =60°，可得DE =DF =32BD ，由AD =3BD ，求得sin A =DE AD=12，可证得∠A =30°；(2)延长BA ，使得BH =BC ，连接EH ，CH ，易证△BCH 为等边三角形，进而可证△BCF ≌△HCE SAS ，可得BF =HE ，∠BFC =∠HEC ，可知∠AEH =∠CFG ，易证得△AEH ≌△CFG SAS ，可得AH =CG ，由BC =BH =AB +AH =AB +CG 可得结论；(3)由题意可知△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，可得CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，可知△ACQ ∽△MCN ，可得MN =32AQ ，由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ，N 都在线段BM 上时，3AQ +2BQ+13CQ 有最小值，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，可得CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，可证△CBR ∽△MBT ，得BR CR =BT MT ，设BC =a 由等边三角形的性质，可得CM =32a ，进而可得CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，结合BR CR=BTMT 可得：BQ +213CQ 313CQ =a +334a 34a ，可得BQ CQ =213+33913，由翻折可知，BP =BQ ，可求得BP CQ的值．【详解】(1)证明：过点D 分别作BC ，AC 的垂线，垂足为E ，F ，∵CD 平分∠ACB ，DE ⊥BC ，DF ⊥AC ，∴DE =DF ，又∵∠B =60°，∴DE =BD ⋅sin60°=32BD ，则DE =DF =32BD ，又∵AD =3BD ，∴sin A =DE AD =32BD3BD=12，∴∠A =30°；(2)BC =AB +CG ，理由如下：延长BA ，使得BH =BC ，连接EH ，CH ，∵∠ABC =60°，BH =BC ，∴△BCH 为等边三角形，∴CB =CH ，∠BCH =60°，∵CE 绕点C 逆时针旋转60°至CF ，∴CE =CF ，∠ECF =60°，则∠BCH -∠ACB =∠ECF -∠ACB ，∴∠ECH =∠FCB ，∴△BCF ≌△HCE SAS ，∴BF =HE ，∠BFC =∠HEC ，则∠AEH =∠CFG ，∵BF =FG ，∴BF =HE =FG ，又∵E 为AC 中点，∴AE =CE =CF ，∴△AEH ≌△CFG SAS ，∴AH =CG ，∴BC =BH =AB +AH =AB +CG ；(3)∵∠ABC =60°，AC =BC ，∴△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，则CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，∴sin ∠CQN =CN QN =313，cos ∠CQN =CQ QN =213，则∠ACM =∠QCN =90°，∴∠ACM -∠ACN =∠QCN -∠ACN ，则∠ACQ =∠MCN∴△ACQ ∽△MCN ，∴MN AQ =CM CA=32，即：MN =32AQ ，∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即：点Q ，N 都在线段BM 上时，3AQ +2BQ +13CQ 有最小值，如下图，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，则∠BRC =∠BTM =90°，CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，又∵∠CBR =∠MBT ，∴△CBR ∽△MBT ，∴BR CR=BT MT ，∵△ABC 是等边三角形，设BC =a ∴∠ACB =60°，AC =BC =a ，则CM =32a ，∵∠ACM =90°，∴∠MCT =30°，则CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，则由BR CR=BT MT 可得：BQ +213CQ 313CQ =a +334a34a ，整理得：133BQ CQ +23=4+333，得BQ CQ=213+33913，由翻折可知，BP =BQ ，∴BP CQ =BQ CQ=213+33913．【点睛】本题属于几何综合，考查了解直角三角形，等边三角形的判定及性质，全等三角形的判定及性质，相似三角形的判定及性质，旋转的性质以及费马点问题，掌握费马点问题的解决方法，添加辅助线构造全等三角形和相似三角形是解决问题的关键．24(2023春·江苏·八年级专题练习)定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在Rt △ABC 中，∠A =90°，AB =AC ，点D 、E 分别在边AB 、AC 上，AD =AE ，连接DE 、DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，且连接PM 、PN ．(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”．(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置，连接BD ，CE ，试判断PM 与PN 是否为“等垂线段”，并说明理由．(3)拓展延伸把△ADE 绕点A 在平面内自由旋转，若DE =2，BC =4，请直接写出PM 与PN 的积的最大值．。

2021年中考数学压轴题专项训练《四边形》1．如图①，在矩形ABCD中，已知BC＝8cm，点G为BC边上一点，满足BG＝AB＝6cm，动点E以1cm/s的速度沿线段BG从点B移动到点G，连接AE，作EF⊥AE，交线段CD于点F．设点E移动的时间为t（s），CF的长度为y（cm），y与t的函数关系如图②所示．（1）图①中，CG＝ 2 cm，图②中，m＝ 2 ；（2）点F能否为线段CD的中点？若可能，求出此时t的值，若不可能，请说明理由；（3）在图①中，连接AF，AG，设AG与EF交于点H，若AG平分△AEF的面积，求此时t 的值．解：（1）∵BC＝8cm，BG＝AB＝6cm，∴CG＝2cm，∵EF⊥AE，∴∠AEB+∠FEC＝90°，且∠AEB+∠BAE＝90°，∴∠BAE＝∠FEC，且∠B＝∠C＝90°，∴△ABE∽△ECF，∴，∵t＝6，∴BE＝6cm，CE＝2cm，∴∴CF＝2cm，∴m＝2，故答案为：2，2；（2）若点F是CD中点，∴CF＝DF＝3cm，∵△ABE∽△ECF，∴，∴∴EC2﹣8EC+18＝0∵△＝64﹣72＝﹣8＜0，∴点F不可能是CD中点；（3）如图①，过点H作HM⊥BC于点M，∵∠C＝90°，HM⊥BC，∴HM∥CD，∴△EHM∽△EFC，∴∵AG平分△AEF的面积，∴EH＝FH，∴EM＝MC，∵BE＝t，EC＝8﹣t，∴EM＝CM＝4﹣t，∴MG＝CM﹣CG＝2﹣，∵，∴∴CF＝∵EM＝MC，EH＝FH，∴MH＝CF＝∵AB＝BG＝6，∴∠AGB＝45°，且HM⊥BC，∴∠HGM＝∠GHM＝45°，∴HM＝GM，∴＝2﹣，∴t＝2或t＝12，且t≤6，∴t＝2．2．问题提出：（1）如图1，△ABC的边BC在直线n上，过顶点A作直线m∥n，在直线m上任取一点D，连接BD、CD，则△ABC的面积＝△DBC的面积．问题探究：（2）如图2，在菱形ABCD和菱形BGFE中，BG＝6，∠A＝60°，求△DGE的面积；问题解决：（3）如图3，在矩形ABCD中，AB＝12，BC＝10，在矩形ABCD内（也可以在边上）存在一点P，使得△ABP的面积等于矩形ABCD的面积的，求△ABP周长的最小值．解：问题提出：（1）∵两条平行线间的距离一定，∴△ABC与△DBC同底等高，即△ABC的面积＝△DBC的面积，故答案为：＝；问题探究：（2）如图2，连接BD，∵四边形ABCD，四边形BGFE是菱形，∴AD∥BC，BC∥EF，AD＝AB，BG＝BE，∴∠A＝∠CBE＝60°，∴△ADB是等边三角形，△BGE是等边三角形，∴∠ABD＝∠GBE＝60°，∴BD∥GE，∴S△DGE＝S△BGE＝BG2＝9；（3）如图3，过点P作PE∥AB，交AD于点E，∵△ABP的面积等于矩形ABCD的面积的，∴×12×AE＝×12×10∴AE＝8，作点A关于PE的对称点A'，连接A'B交PE于点P，此时△ABP周长最小，∴A'E＝AE＝8，∴AA'＝16，∴A'B＝＝＝20，∴△ABP周长的最小值＝AP+AB+PB＝A'P+PB+AB＝20+12＝32．3．（1）方法感悟：如图①，在正方形ABCD中，点E、F分别为DC、BC边上的点，且满足∠EAF＝45°，连接EF．将△ADE绕点A顺时针旋转90°得到△ABG，易证△GAF≌△EAF，从而得到结论：DE+BF＝EF．根据这个结论，若CD＝6，DE＝2，求EF的长．（2）方法迁移：如图②，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，且∠EAF＝∠BAD，试猜想DE，BF，EF之间有何数量关系，证明你的结论．（3）问题拓展：如图③，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，试探究线段EF、BE、FD之间的数量关系，请直接写出你的猜想（不必说明理由）．解：（1）方法感悟：∵将△ADE绕点A顺时针旋转90°得到△ABG，∴GB＝DE＝2，∵△GAF≌△EAF∴GF＝EF，∵CD＝6，DE＝2∴CE＝4，∵EF2＝CF2+CE2，∴EF2＝（8﹣EF）2+16，∴EF＝5；（2）方法迁移：DE+BF＝EF，理由如下：如图②，将△ADE绕点A顺时针旋转90°得到△ABH，由旋转可得，AH＝AE，BH＝DE，∠1＝∠2，∠D＝∠ABH，∵∠EAF＝∠DAB，∴∠HAF＝∠1+∠3＝∠2+∠3＝∠BAD，∴∠HAF＝∠EAF，∵∠ABH+∠ABF＝∠D+∠ABF＝180°，∴点H、B、F三点共线，在△AEF和△AHF中，∴△AEF≌△AHF（SAS），∴EF＝HF，∵HF＝BH+BF，∴EF＝DE+BF．（3）问题拓展：EF＝BF﹣FD，理由如下：在BC上截取BH＝DF，∵∠B+∠ADC＝180°，∠ADC+∠ADF＝180°，∴∠B＝∠ADF，且AB＝AD，BH＝DF，∴△ABH≌△ADF（SAS）∴∠BAH＝∠DAF，AH＝AD，∵∠EAF＝∠BAD，∴∠DAE+∠BAH＝∠BAD，∴∠HAE＝∠BAD＝∠EAF，且AE＝AE，AH＝AD，∴△HAE≌△FAE（SAS）∴HE＝EF，∴EF＝HE＝BE﹣BH＝BE﹣DF．4．如图1，在▱ABCD中，AB＝3cm，BC＝5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图2，设移动时间为t（s）（0＜＜4），连结PQ，MQ，解答下列问题：（1）当t为何值时，PQ∥MN？（2）当t为何值时，∠CPQ＝45°？（3）当t为何值时，PQ⊥MQ？解：（1）∵AB＝3cm，BC＝5cm，AC⊥AB，∴AC＝＝4cm，∵MN∥AB，PQ∥MN，∴PQ∥AB，∴，∴，∴t＝s（2）如图2，过点Q作QE⊥AC，则QE∥AB，∴，∴，∴CE＝，QE＝t，∵∠CPQ＝45°，∴PE＝QE＝t，∴t+t+t＝4，∴t＝s（3）如图2，过点P作PF⊥BC于F点，过点M作MH⊥BC，交BC延长线于点H，∴四边形PMHF是矩形，∴PM＝FH＝5，∵∠A＝∠PFC＝90°，∠ACB＝∠PCF，∴△ABC∽△FPC，∴，∴＝∴PF＝，CF＝，∴QH＝5﹣FQ＝5﹣（CF﹣CQ）＝，∵PQ⊥MQ，∴∠PQF+∠MQH＝90°，且∠PQF+∠FPQ＝90°，∴∠FPQ＝∠MQH，且∠PFQ＝∠H＝90°，∴△PFQ∽△QHM，∴，∴∴t＝s．5．问题背景：如图1，在正方形ABCD的内部，作∠DAE＝∠ABF＝∠BCG＝∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得四边形EFGH是正方形．类比探究：如图2，在正△ABC的内部，作∠1＝∠2＝∠3，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）．（1）△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；（2）△DEF是否为正三角形？请说明理由；（3）如图3，进一步探究发现，△ABD的三边存在一定的等量关系，设BD＝a，AD＝b，AB＝c，请探索a，b，c满足的等量关系．（1）△ABD≌△BCE≌△CAF；理由如下：∵△ABC是正三角形，∴∠CAB＝∠ABC＝∠BCA＝60°，AB＝BC＝AC，又∵∠1＝∠2＝∠3，∴∠ABD＝∠BCE＝∠CAF，在△ABD、△BCE和△CAF中，，∴△ABD≌△BCE≌△CAF（ASA）；（2）△DEF是正三角形；理由如下：∵△ABD≌△BCE≌△CAF，∴∠ADB＝∠BEC＝∠CFA，∴∠FDE＝∠DEF＝∠EFD，∴△DEF是正三角形；（3）c2＝a2+ab+b2．作AG⊥BD于G，如图所示：∵△DEF是正三角形，∴∠ADG＝60°，在Rt△ADG中，DG＝b，AG＝b，在Rt△ABG中，c2＝（a+b）2+（b）2，∴c2＝a2+ab+b2．6．如图，在四边形ABCD中，AC是对角线，∠ABC＝∠CDA＝90°，BC＝CD，延长BC交AD 的延长线于点E．（1）求证：AB＝AD；（2）若AE＝BE+DE，求∠BAC的值；（3）过点E作ME∥AB，交AC的延长线于点M，过点M作MP⊥DC，交DC的延长线于点P，连接PB．设PB＝a，点O是直线AE上的动点，当MO+PO的值最小时，点O与点E是否可能重合？若可能，请说明理由并求此时MO+PO的值（用含a的式子表示）；若不可能，请说明理由．（1）证明：∵∠ABC＝∠CDA＝90°，∵BC＝CD，AC＝AC，∴Rt△ABC≌Rt△ADC（HL）．∴AB＝AD．（2）解：∵AE＝BE+DE，又∵AE＝AD+DE，∴AD＝BE．∵AB＝AD，∴AB＝BE．∴∠BAD＝∠BEA．∵∠ABC＝90°，∴∠BAD═45°．∵由（1）得△ABC≌△ADC，∴∠BAC＝∠DAC．∴∠BAC═22.5°．（3）解：当MO+PO的值最小时，点O与点E可以重合，理由如下：∵ME∥AB，∴∠ABC＝∠MEC＝90°，∠MAB＝∠EMA．∵MP⊥DC，∴∠MPC＝90°．∴∠MPC＝∠ADC＝90°．∴PM∥AD．∴∠EAM＝∠PMA．由（1）得，Rt△ABC≌Rt△ADC，∴∠EAC＝∠MAB，∴∠EMA＝∠AMP．即MC平分∠PME．又∵MP⊥CP，ME⊥CE，∴PC＝EC．如图，连接PB，连接PE，延长ME交PD的延长线于点Q．设∠EAM＝α，则∠MAP＝α．在Rt△ABE中，∠BEA＝90°﹣2α．在Rt△CDE中，∠ECD＝90°﹣∠BEA＝2α．∵PC＝EC，∴∠PEB＝∠EPC＝∠ECD＝α．∴∠PED＝∠BEA+∠PEB＝90°﹣α．∵ME∥AB，∴∠QED＝∠BAD＝2α．当∠PED＝∠QED时，∵∠PDE＝∠QDE，DE＝DE，∴△PDE≌△QDE（ASA）．∴PD＝DQ．即点P与点Q关于直线AE成轴对称，也即点M、点E、点P关于直线AE的对称点Q，这三点共线，也即MO+PO的值最小时，点O与点E重合．因为当∠PED＝∠QED时，90°﹣α＝2α，也即α＝30°．所以，当∠ABD＝60°时，MO+PO取最小值时的点O与点E重合．此时MO+PO的最小值即为ME+PE．∵PC＝EC，∠PCB＝∠ECD，CB＝CD，∴△PCB≌△ECD（SAS）．∴∠CBP＝∠CDE＝90°．∴∠CBP+∠ABC＝180°．∴A，B，P三点共线．当∠ABD＝60°时，在△PEA中，∠PAE＝∠PEA＝60°．∴∠EPA＝60°．∴△PEA为等边三角形．∵EB⊥AP，∴AP＝2AB＝2a．∴EP＝AE＝2a．∵∠EMA＝∠EAM＝30°，∴EM＝AE＝2a．∴MO+PO的最小值为4a．7．已知：如图，在正方形ABCD中，点E在AD边上运动，从点A出发向点D运动，到达D 点停止运动．作射线CE，并将射线CE绕着点C逆时针旋转45°，旋转后的射线与AB边交于点F，连接EF．（1）依题意补全图形；（2）猜想线段DE，EF，BF的数量关系并证明；（3）过点C作CG⊥EF，垂足为点G，若正方形ABCD的边长是4，请直接写出点G运动的路线长．解：（1）补全图形如图1所示：（2）线段DE，EF，BF的数量关系为：EF＝DE+BF．理由如下：延长AD到点H，使DH＝BF，连接CH，如图2所示：∵四边形ABCD是正方形，∴∠BCD＝∠ADC＝∠B＝90°，BC＝DC，∴∠CDH＝90°＝∠B，在△CDH和△CBF中，，∴△CDH≌△CBF（SAS）．∴CH＝CF，∠DCH＝∠BCF．∵∠ECF＝45°，∴∠ECH＝∠ECD+∠DCH＝∠ECD+∠BCF＝45°．∴∠ECH＝∠ECF＝45°．在△ECH和△ECF中，，∴△EC H≌△ECF（SAS）．∴EH＝EF．∵EH＝DE+DH，∴EF＝DE+BF；（3）由（2）得：△ECH≌△ECF（SAS），∴∠CEH＝∠CEF，∵CD⊥AD，CG⊥EF，∴CD＝CG＝4，∴点G的运动轨迹是以C为圆心4为半径的弧DB，∴点G运动的路线长＝＝2π．8．如图，在正方形ABCD中，P是边BC上的一动点（不与点B，C重合），点B关于直线AP的对称点为E，连接AE．连接DE并延长交射线AP于点F，连接BF．（1）若∠BAP＝α，直接写出∠ADF的大小（用含α的式子表示）；（2）求证：BF⊥DF；（3）连接CF，用等式表示线段AF，BF，CF之间的数量关系，并证明．（1）解：由轴对称的性质得：∠EAP＝∠BAP＝α，AE＝AB，∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∴∠DAE＝90°﹣2α，AD＝AE，∴∠ADF＝∠AED＝（180°﹣∠DAE）＝（90°+2α）＝45°+α；（2）证明：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∵点E与点B关于直线AP对称，∴∠AEF＝∠ABF，AE＝AB．∴AE＝AD．∴∠ADE＝∠AED．∵∠AED+∠AEF＝180°，∴在四边形ABFD中，∠ADE+∠ABF＝180°，∴∠BFD+∠BAD＝180°，∴∠BFD＝90°∴BF⊥DF；（3）解：线段AF，BF，CF之间的数量关系为AF＝BF+CF，理由如下：过点B作BM⊥BF交AF于点M，如图所示：∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°，∴∠ABM＝∠CBF，∵点E与点B关于直线AP对称，∠BFD＝90°，∴∠MFB＝∠MFE＝45°，∴△BMF是等腰直角三角形，∴BM＝BF，FM＝BF，在△AMB和△CFB中，，∴△AMB≌△CFB（SAS），∴AM＝CF，∵AF＝FM+AM，∴AF＝BF+CF．9．如图1，已知等腰Rt△ABC中，E为边AC上一点，过E点作EF⊥AB于F点，以为边作正方形，且AC＝3，EF＝．（1）如图1，连接CF，求线段CF的长；（2）将等腰Rt△ABC绕点旋转至如图2的位置，连接BE，M点为BE的中点，连接MC，MF，求MC与MF关系．解：（1）如图1，∵△ABC是等腰直角三角形，AC＝3，∴AB＝3，过点C作CM⊥AB于M，连接CF，∴CM＝AM＝AB＝，∵四边形AGEF是正方形，∴AF＝EF＝，∴MF＝AM﹣AF＝﹣，在Rt△CMF中，CF＝＝＝；（2）CM＝FM，CM⊥FM，理由：如图2，过点B作BH∥EF交FM的延长线于H，连接CF，CH，∴∠BHM＝∠EFM，∵四边形AGEF是正方形，∴EF＝AF∵点M是BE的中点，∴BM＝EM，在△BMH和△EMF中，，∴△BMH≌△EMF（AAS），∴MH＝MF，BH＝EF＝AF∵四边形AGEF是正方形，∴∠FAG＝90°，EF∥AG，∵BH∥EF，∴BH∥AG，∴∠BAG+∠ABH＝180°，∴∠CBH+∠ABC+∠BAC+∠CAG＝180°．∵△ABC是等腰直角三角形，∴BC＝AC，∠ABC＝∠BAC＝45°，∴∠CBH+∠CAG＝90°，∵∠CAG+∠CAF＝90°，∴∠CBH＝∠CAF，在△BCH和△ACF中，，∴△BCH≌△ACF（SAS），∴CH＝CF，∠BCH＝∠ACF，∴∠HCF＝∠BCH+∠BCF＝∠ACF+∠BCF＝90°，∴△FCH是等腰直角三角形，∵MH＝MF，∴CM＝FM，CM⊥FM；10．如图将正方形ABCD绕点A顺时针旋转角度α（0°＜α＜90°）得到正方形AB′C′D′．（1）如图1，B′C′与AC交于点M，C′D′与AD所在直线交于点N，若MN∥B′D′，求α；（2）如图2，C′B′与CD交于点Q，延长C′B′与BC交于点P，当α＝30°时．①求∠DAQ的度数；②若AB＝6，求PQ的长度．解：（1）如图1中，∵MN∥B′D′，∴∠C′MN＝∠C′B′D′＝45°，∠C′NM＝∠C′D′B′＝45°，∴∠C′MN＝∠C′NM，∴C′M＝C′N，∵C′B′＝C′D′，'∴MB′＝ND′，∵AB′＝AD′，∠AB′M＝∠AD′N＝90°，∴△AB′M≌△AD′N（SAS），∴∠B′AM＝∠D′AN，∵∠B′AD′＝90°，∠MAN＝45°，∴∠B′AM＝∠D′AN＝22.5°，∵∠BAC＝45°，∴∠BAB′＝22.5°，∴α＝22.5°．（2）①如图2中，∵∠AB′Q＝∠ADQ＝90°，AQ＝AQ，AB′＝AD，∴Rt△AQB′≌Rt△AQD（HL），∴∠QAB′＝∠QAD，∵∠BAB′＝30°，∠BAD＝90°，∴∠B′AD＝30°，∴∠QAD＝∠B′AD＝30°．②如图2中，连接AP，在AB上取一点E，使得AE＝EP，连接EP．设PB＝a．∵∠ABP＝∠AB′P＝90°，AP＝AP，AB＝AB′，∴Rt△APB≌Rt△APB′（HL），∴∠BAP＝∠PAB′＝15°，∵EA＝EP，∴∠EAP＝∠EPA＝15°，∴∠BEP＝∠EAP+∠EPA＝30°，∴PE＝AE＝2a，BE＝a，∵AB＝6，∴2a+a＝6，∴a＝6（2﹣）．∴PB＝6（2﹣），∴PC＝BC﹣PB＝6﹣6（2﹣）＝6﹣6，∵∠CPQ+∠BPB′＝180°，∠BAB′+∠BPB′＝180°，∴∠CPQ＝∠BAB′＝30°，∴PQ＝＝＝12﹣4．11．已知，如图1，在边长为2的正方形ABCD中，E是边AB的中点，点F在边AD上，过点A作AG⊥EF，分别交线段CD、EF于点G、H（点G不与线段CD的端点重合）．（1）如图2，当G是边CD中点时，求AF的长；（2）设AF＝x，四边形FHGD的面积是y，求y关于x的函数关系式，并写出x的取值范围；（3）联结ED，当∠FED＝45°时，求AF的长．解：（1）∵E是AB的中点，AB＝2，∴AE＝AB＝1，同理可得DG＝1，∵AG⊥EF，∴∠AHF＝∠HAF+∠AFH＝90°，∵四边形ABCD是正方形，∴∠ADG＝90°＝∠DAG+∠AGD，∴∠AFH＝∠AGD，∵∠EAF＝∠ADG＝90°，∴△EAF∽△ADG，∴，即，∴AF＝；（2）如图1，由（1）知：△EAF∽△ADG，∴，即，∴DG＝2x，∵∠HAF＝∠DAG，∠AHF＝∠ADG＝90°，∴∠AHF∽△ADG，∴＝，∴＝，∴AH＝＝，FH＝＝，∴y＝S△ADG﹣S△AFH，＝，＝2x﹣，如图2，当G与C重合时，∵EF⊥AG，∴∠AHE＝90°，∵∠EAH＝45°，∴∠AEH＝45°，∴AF＝AE＝1，∴0＜x＜1；∴y关于x的函数关系式为：y＝2x﹣（0＜x＜1）；（3）如图3，过D作DM⊥AG，交BC于M，连接EM，延长EA至N，使AN＝CM，连接DN，设CM＝a，则AN＝a，∵AD＝CD，∠NAD＝∠DCM＝90°，∴△NAD≌△MCD（SAS），∴∠ADN＝∠CDM，DN＝DM，∵EF⊥AG，DM⊥AG，∴EF∥DM，∴∠EDM＝∠FED＝45°，∴∠ADE+∠CDM＝∠EDM＝45°，∴∠NDA+∠ADE＝∠NDE＝∠EDM，∵ED＝ED，∴△NDE≌△MDE（SAS），∴EN＝EM＝a+1，∵BM＝2﹣a，在Rt△EBM中，由勾股定理得：BE2+BM2＝EM2，∴12+（2﹣a）2＝（a+1）2，a＝，∵∠AEF+∠EAG＝∠EAG+∠DAG，∴∠AEF＝∠DAG＝∠CDM，∴tan∠AEF＝tan∠CDM，∴，∴，∴AF＝．12．如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD．试证明：AB2+CD2＝AD2+BC2；（3）解决问题：如图3，△ACB中，∠ACB＝90°，AC⊥AG且AC＝AG，AB⊥AE且AE＝AB，连结CE、BG、GE．已知AC＝4，AB＝5，求GE的长．解：（1）四边形ABCD是垂美四边形，理由如下：连接AC，BD，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴AC是线段BD的垂直平分线，∴四边形ABCD是垂美四边形；（2）∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得，AD2+BC2＝AO2+DO2+BO2+CO2，AB2+CD2＝AO2+BO2+CO2+DO2，∴AD2+BC2＝AB2+CD2；故答案为：AB2+CD2＝AD2+BC2；（3）∵∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，∴四边形CGEB是垂美四边形，由（2）得，CG2+BE2＝CB2+GE2，∵AC＝4，AB＝5，∴BC＝3，CG＝4，BE＝5，∴GE2＝CG2+BE2﹣CB2＝73，∴GE＝．13．如图1，四边形ACEB，连接BC，∠ACB＝∠BEC＝90°，D在AB上，连接CD，∠ACD＝∠ABC，BE＝CD．（1）求证：四边形CDBE为矩形；（2）如图2，连接DE，DE交BC于点O，若tan∠A＝2，在不添加任何辅助线和字母的情况下，请直接写出图中所有长度与AD的长度相等的线段．（1）证明：∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵∠ACD＝∠ABC，∴∠A+∠ACD＝90°，∴∠ADC＝90°，∴∠BDC＝180°﹣90°＝90°＝∠BEC，在Rt△BCD和Rt△CBE中，，∴Rt△BCD≌Rt△CBE（HL），∴BD＝CE，∵CD＝BE，∴四边形CDBE是平行四边形，又∵∠BEC＝90°，∴四边形CDBE为矩形；（2）解：图中所有长度与AD的长度相等的线段为AC＝OC＝OB＝OD＝OE＝AD．理由如下：由（1）得：四边形CDBE为矩形，∠ADC＝90°，∴BC＝DE，OD＝OE，OB＝OC，∴OC＝OB＝OD＝OE＝BC，∵∠ADC＝∠ACB＝90°，∴tan∠A＝2＝＝，∴CD＝2AD，BC＝2AC，∴AC＝＝＝AD，∴DE＝BC＝2AC，∴OC＝OB＝OD＝OE＝BC＝AC＝AD，∴AC＝OC＝OB＝OD＝OE＝AD．14．如图在直角坐标系中，四边形ABCO为正方形，A点的坐标为（a，0），D点的坐标为（0，b），且a，b满足（a﹣3）2+|b﹣|＝0．（1）求A点和D点的坐标；（2）若∠DAE＝∠OAB，请猜想DE，OD和EB的数量关系，说明理由．（3）若∠OAD＝30°，以AD为三角形的一边，坐标轴上是否存在点P，使得△PAD为等腰三角形，若存在，直接写出有多少个点P，并写出P点的坐标，选择一种情况证明．解：（1）∵（a﹣3）2+|b﹣|＝0，∴a＝3，b＝，∴D（0，），A（3，0）；（2）DE＝OD+EB；理由如下：如图1，在CO的延长线上找一点F，使OF＝BE，连接AF，在△AOF和△ABE中，，∴△AOF≌△ABE（SAS），∴AF＝AE，∠OAF＝∠BAE，又∵∠OAB＝90°，∠DAE＝，∴∠BAE+∠DAO＝45°，∴∠DAF＝∠OAF+∠DAO＝45°，∴∠DAF＝∠EAD，在△AFD和△AED中，，∴△AFD≌△AED（SAS），∴DF＝DE＝OD+EB；（3）有3种情况共6个点：①当DA＝DP时，如图2，Rt△ADO中，OD＝，OA＝3，∴AD＝＝＝2，∴P1（﹣3，0），P2（0，3），P3（0，﹣）；②当AP4＝DP4时，如图3，∴∠ADP4＝∠DAP4＝30°，∴∠OP4D＝60°，Rt△ODP4中，∠ODP4＝30°，OD＝，∴OP4＝1，∴P4（1，0）；③当AD＝AP时，如图4，∴AD＝AP5＝AP6＝2，∴P5（3+2，0），P6（3﹣2，0），综上，点P的坐标为：∴P（﹣3，0）或（0，3）或（0，﹣）或（1，0）或（3+2，0）或（3﹣2，0）．证明：P5（3+2，0），∵∠OAD＝30°且△ADO是直角三角形，又∵AO＝3，DO＝，∴DA＝2，而P5A＝|3+2﹣3|＝2，∴P5A＝DA，∴△P5AD是等腰三角形．15．已知，在四边形ABCD中，点M、N、P、Q分别为边AB、AD、CD、BC的中点，连接MN、NP、PQ、MQ．（1）如图1，求证：四边形MNPQ为平行四边形；（2）如图2，连接AC，AC分别交MN、PQ于点E、F，连接BD，BD分别交MQ、NP于点G、H，AC与BD交于点O，且AC⊥BD，若tan∠ADB＝，在不添加任何辅助线的情况下，请直接写出图2中所有长度等于OD的线段．（1）证明：如图1，连接BD．∵Q，P分别是BC，CD的中点，所以PQ∥BD，PQ＝BD．∵M，N分别是AB，AD的中点．∴MN∥BD，MN＝BD．∴PQ∥MN，且PQ＝MN．∴四边形MNPQ是平行四边形．（2）解：∵四边形MNPQ是平行四边形，AC⊥BD，∴四边形MNPQ是矩形，∴四边形NHOE和四边形EOGM都是矩形，∴NH＝OE＝MG＝AE＝，∵tan∠ADB＝，∴，∴NH＝OE＝MG＝AE＝．即长度等于OD的线段有NH，OE，MG，AE．。

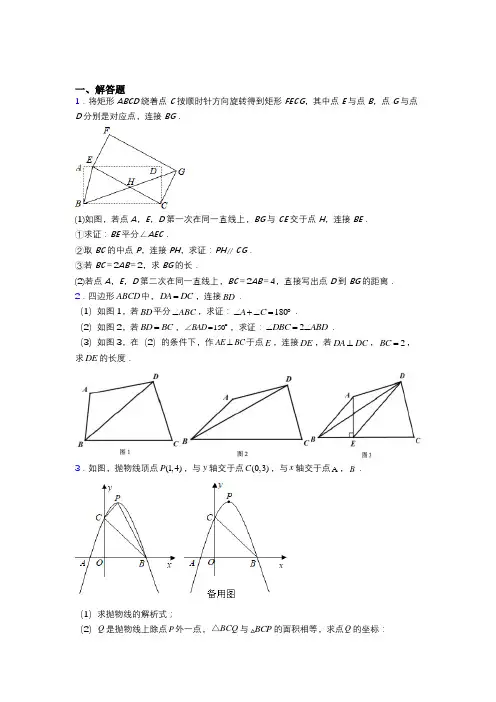
一、解答题1．将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，其中点E 与点B ，点G 与点D 分别是对应点，连接BG ．(1)如图，若点A ，E ，D 第一次在同一直线上，BG 与CE 交于点H ，连接BE ． ①求证：BE 平分∠AEC ．②取BC 的中点P ，连接PH ，求证：PH ∥CG ． ③若BC ＝2AB ＝2，求BG 的长．(2)若点A ，E ，D 第二次在同一直线上，BC ＝2AB ＝4，直接写出点D 到BG 的距离． 2．四边形ABCD 中，DA DC =，连接BD ．（1）如图1，若BD 平分ABC ∠，求证：180A C ∠+∠=︒． （2）如图2，若BD BC =，150=︒∠BAD ，求证：2DBC ABD ∠=∠．（3）如图3，在（2）的条件下，作AE BC ⊥于点E ，连接DE ，若DA DC ⊥，2BC =，求DE 的长度．3．如图，抛物线顶点(1,4)P ，与y 轴交于点(0,3)C ，与x 轴交于点A ，B ．（1）求抛物线的解析式；（2）Q 是抛物线上除点P 外一点，BCQ △与BCP 的面积相等，求点Q 的坐标：（3）M 是线段BC 上方抛物线上一个动点，过点M 作x 轴的垂线，交线段BC 于点D ，再过点M 做MN //x 轴交抛物线于点N ，连结DN ，请问是否存在点M 使MDN △为等腰直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．4．某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：观察与猜想（1）①如图1，在正方形ABCD 中，点E ，F 分别是AB ，AD 上的两点，连接DE ，CF ，DE CF ⊥，则DECF的值为 ； ②如图2，在矩形ABCD 中，7AD =，4CD =，点E 是AD 上的一点，连接CE ，BD ，且CE BD ⊥，则CEBD的值为 ； 类比探究（2）如图3，在四边形ABCD 中，90A B ∠=∠=︒，点E 为AB 上一点，连接DE ，过点C 作DE 的垂线交ED 的延长线于点G ，交AD 的延长线于点F ，求证：DE AB CF AD ⋅=⋅；拓展延伸（3）如图4，在Rt ABD △中，90BAD ∠=︒，3AB =，9AD =，将Rt ABD △沿BD 翻折，点A 落在点C 处得CBD ，点E ，F 分别在边AB ，AD 上，连接DE ，CF ，DE CF ⊥．请问DECF是定值吗？若是求出其值，若不是说明理由； 5．如图，在平面直角坐标系中，ABC 的边AB 在x 轴上，且OB OA >，以AB 为直径的圆过点C ．若点C 的坐标为()0,4，10AB =，（1）求抛物线的解析式；（2）点P为该函数在第一象限内的图象上一点（不与BC重合)，过点P作PQ BC⊥，垂足为点Q，连接PC．若以点P、C、Q为顶点的三角形与COA相似，求点P的坐标；（3）若ACB∠平分线所在的直线l交x轴与点E，过点E任作一直线l'分别交射线CA，CB（点C除外）于点M，N．则11CM CN+的是否为定值？若是，求出该定值；若不是，请说明理由．6．在平面直角坐标系xOy中，规定：抛物线y＝a（x﹣h）2+k的“伴随直线”为y＝a（x﹣h）+k．例如：抛物线y＝2（x+1）2﹣3的“伴随直线”为y＝2（x+1）﹣3，即y＝2x﹣1．（1）在上面规定下，抛物线y＝（x+1）2﹣5的顶点坐标为_____，“伴随直线”为_____．（2）如图，顶点在第一象限的抛物线y＝a（x﹣1）2﹣4a（a≠0）与其“伴随直线”相交于点A，B（点A在点B的左侧），与x轴交于点C，D．①若△ABC为等腰三角形时，求a的值；②如果点P（x，y）是直线BC上方抛物线上的一个动点，△PBC的面积记为S，当S取得最大值274时，求a的值．7．如图1，抛物线y＝ax2﹣94x+c与x轴交于A（﹣1，0）和B两点，与y轴交于C（0，﹣3），E为抛物线顶点，抛物线的对称轴交x轴于点H．（1）求抛物线的解析式；（2）已知点3(0,2)2F，点P在对称轴右侧的抛物线上运动，连接PO，PO与对称轴交于点D，连接DF．当DF平分∠ODE时，求点P的坐标；（3）如图2，平移对称轴EH交抛物线于M，交直线BC于N．以N为圆心，NM为半径作⊙N．当⊙N与坐标轴相切时，请直接写出⊙N的半径长．8．等腰Rt△ABC，CA＝CB，D在AB上，CD＝CE，CD⊥CE．（1）如图1，连接BE，求证：AD＝BE．（2）如图2，连接AE，CF⊥AE交AB于F，T为垂足，①求证：FD＝FB；②如图3，若AE交BC于N，O为AB中点，连接OC，交AN于M，连FM、FN，当S OF2+BF2的最小值．52FMN9．如图，在△ABC中，AB＝AC，⊙是△ABC的外接圆，连接BO并延长交边AC于点D．（1）如图1，求证：∠BAC＝2∠ABD；（2）如图2，过点B作BH⊥AC于点H，延长BH交⊙O于点G，连接OC，CG，OC交BG于点F，求证：BF＝2HG；（3）如图3，在（2）的条件下，若AD＝2，CD＝3，求线段BF的长．10．问题背景如图（1），△ABC 为等腰直角三角形，∠BAC ＝90°，直线l 绕着点A 顺时针旋转，过B ，C 两点分别向直线l 作垂线BD ，CE ，垂足为D ，E ，此时△ABD 可以由△CAE 通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小（取最小旋转角度）． 尝试应用如图（2），△ABC 为等边三角形，直线l 绕着点A 顺时针旋转，D 、E 为直线l 上两点，∠BDA ＝∠AEC ＝60°．△ABD 可以由△CAE 通过旋转变换得到吗？若可以，请指出旋转中心O 的位置并说明理由；拓展创新如图（3）在问题背景的条件下，若AB ＝2，连接DC ，直接写出CD 的长的取值范围．11．如图1，菱形ABCD 绕点A 顺时针旋转()0180αα︒<<︒，得到菱形AEFG ，连接AC ，AF 、分别与BD ，EG 相交于点O ，O '．射线BD ，GE 交于点P ，BPG β∠=．（1）当90α=︒时，四边形AOPO '的形状为 ． （2）求α与β的数量关系．（3）如图2．连接PA ，若42BAD ∠=°，PA PB =，求α的值．（4）如图3，连接PC ，PF ，若5AB =，4BD =，四边形AFPC 能否为菱形？若能，直接写出α的值和AP 的长；若不能，请说明理由．12．如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），与y轴交于点A （0，a），且a、p满足+（p﹣1）2＝0．(1)求直线AP的解析式；(2)如图1，直线x＝﹣2与x轴交于点N，点M在x轴上方且在直线x＝﹣2上，若△MAP 的面积等于6，请求出点M的坐标；(3)如图2，已知点C（﹣2，4），若点B为射线AP上一动点，连接BC，在坐标轴上是否存在点Q，使△BCQ是以BC为底边的等腰直角三角形，直角顶点为Q，若存在，请求出点Q坐标；若不存在，请说明理由．13．我们把方程（x﹣m）2＋（y﹣n）2＝r2称为圆心为（m，n）、半径长为r的圆的标准方程．例如，圆心为（1，﹣2）、半径长为3的圆的标准方程是（x﹣1）2＋（y＋2）2＝9．如图，在平面直角坐标系中，⊙C与x轴交于A，B两点，且点B的坐标为（8，0），与y轴相切于点D（0，4），过点A，B，D的抛物线的顶点为E．(1)求⊙C的标准方程；(2)试判断直线AE 与⊙C 的位置关系，并说明理由； (3)连接CE ，求sin∠AEC 的值．14．如图，ABC 为O 的内接三角形，AB 为O 的直径，过点A 作O 的切线交BC 的延长线干点D ．(1)求证：ABC ∽；(2)若E 为AD 上一点，使得，连接OE ，求证：OE 平分；(3)若点F 为直径AB 下方半圆的中点，连接CF 交AB 于点G ，且，2AB =，求CG的长．15．如图，在平面直角坐标系中，抛物线y ＝ax 2＋bx ＋2与直线y ＝x ﹣2交于点A （m ，0）和点B （﹣2，n ），与y 轴交于点C ．(1)求抛物线的解析式及顶点D 的坐标；(2)若向下平移抛物线，使顶点D 落在x 轴上，原来的抛物线上的点P 平移后的对应点为P '，若，求点P 的坐标；(3)在抛物线上是否存在点Q ，使△QAB 的面积是△ABC 面积的一半？若存在，直接写出点Q 的坐标；若不存在，请说明理由．16．已知抛物线24y ax bx =++（a ≠0）与x 轴交于点A （3-，0）、B （2，0），与y 轴交于点C ，直线y mx n =+经过两点A 、C ．(1)求a，b的值；(2)如图1，点Р在已知抛物线上，且位于第二象限，当四边形PABC的面积最大时，求点P的坐标．(3)如图2，将已知抛物线向左平移12个单位，再向下平移2个单位．记平移后的抛物线为'y，若抛物线'y与原抛物线的对称轴交于点Q．点E是新抛物线'y的对称轴上一动点，在（2）的条件下，当△PQE是等腰三角形时，请直接写出点E的坐标．17．如图，已知四边形ABCD内接于⊙O，直径DF交BC于点G．(1)如图1，求证：∠BAD－∠BCF＝90°；(2)如图2，连接AC，当∠BAC＝∠CFD＋∠ACD时，求证：CA＝CB；(3)如图3，在（2）的条件下，AC交DF于点H，∠BAC＝∠DGB，45CGBG，AC＝9，求△CDH的面积．18．设抛物线y=ax2+bx-2与x轴交于两个不同的点A（-1，0）、B（m，0），与y轴交于点C．且∠ACB=90度．(1)求m 的值；(2)求抛物线的解析式，并验证点D （1，﹣3）是否在抛物线上；(3)已知过点A 的直线y =x +1交抛物线于另一点E ．问：在x 轴上是否存在点P ，使以点P 、B 、D 为顶点的三角形与△AEB 相似？若存在，请求出所有符合要求的点P 的坐标；若不存在，请说明理由．19．图形的旋转变换是研究数学相关问题的重要手段之一，在研究三角形的旋转过程中，发现下列问题：如图1，在ABC 中，AB AC =，BAC α∠=，MN 分别为AB 、BC 边上一点，连接MN ，且MN AC ∥，将ABC 绕点B 在平面内旋转．(1)观察猜想ABC 绕点B 旋转到如图2所示的位置，若60α=︒，则AMCN的值为______． (2)类比探究若90α=︒，将ABC 绕点B 旋转到如图3所示的位置，求AMCN的值． (3)拓展应用若90α=︒，M 为AB 的中点，4AB =，当AM BN ⊥时，请直接写出CN 的值． 20．如图1，在菱形ABCD 中，对角线AC 与BD 相交于点O ，且AC ＝16，BD ＝12． （1）求菱形ABCD 的面积及周长；（2）点M 是射线DA 上一个动点，作射线BM ，交射线CA 于点E ．将射线BM 绕点B 逆时针旋转后交射线CA 于点N ，旋转角为∠MBN ，且∠MBN ＝12BAD ∠，连接MN ．①如图2，当点N 与点O 重合时，求△AMN 的周长；②当AE ＝BE 时，请直接写出AM 的长为 ； ③BN ＝35时，请直接写出AM 的长为 ．【参考答案】**科目模拟测试一、解答题1．(1)7 57221【解析】 【分析】（1）①根据旋转的性质得到CB CE =，求得EBC BEC ∠=∠，根据平行线的性质得到EBC BEA ∠=∠，于是得到结论；②如图1，过点B 作CE 的垂线BQ ，根据角平分线的性质得到AB BQ =，求得=CG BQ ，根据全等三角形的性质得到BH GH =，根据三角形的中位线定理即可得到结论； ③如图2，过点G 作BC 的垂线GM ，解直角三角形即可得到结论．（2）如图3，连接DB ，DG ，过G 作GP BC ⊥交BC 的延长线于P ，GN DC ⊥交DC 的延长线于N ，根据旋转的性质得到4==CE BC ，2CD AB ==，解直角三角形得到1NG =，3PG =(1)解：①证明：矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，CB CE ∴=，EBC BEC ∴∠=∠，又//AD BC ，EBC BEA ∴∠=∠，BEA BEC ∴∠=∠，BE ∴平分AEC ∠；②证明：如图1，过点B 作CE 的垂线BQ ，BE 平分AEC ∠，BA AE ⊥，BQ CE ⊥，AB BQ ∴=，CG BQ ∴=，90BQH GCH ∠=∠=︒，BQ AB CG ==，BHQ GHC ∠=∠，()BHQ GHC AAS ∴∆≅∆，BH GH ∴=，即点H 是BG 中点， 又点P 是BC 中点，//PH CG ∴；③解：如图2，过点G 作BC 的垂线GM ，22BC AB ==，1BQ ∴=，30BCQ ∴∠=︒，90ECG ∠=︒，60GCM ∴∠=︒，1CG AB CD ===，3GM ∴12CM =，222253()()722BG BM MG ∴=+=+=； (2)解：如图3，连接DB ，DG ，过G 作GP BC ⊥交BC 的延长线于P ，GN DC ⊥交DC 的延长线于N ，24BC AB ==，2AB ∴=，将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，4CE BC ∴==，2CD AB ==，点A ，E ，D 第二次在同一直线上，90CDE ，12CD CE ∴=， 30DEC ∴∠=︒，60DCE ∴∠=︒，30NCG ∴∠=︒，2CG =，1NG ∴=，3PG =523DBG DBC DCG BCG S S S S ∆∆∆∆∴=++=+2227BG BP PG +257221DBG S DM BG ∆∴= 【点睛】本题考查了旋转的性质，全等三角形的判定和性质，矩形的性质，三角形的中位线定理，勾股定理，解直角三角形，解题的关键是正确地作出辅助线．2．（1）见解析；（2）见解析；（32【解析】【分析】（1）过点D 分别作DF BC ⊥于点F ，DE BA ⊥交BA 的延长线于点E ，根据角平分线的性质可得ED FD =，结合已知条件HL 证明Rt DAE ≌Rt DCF △，继而可得C EAD ∠=∠，根据平角的定义以及等量代换即可证明180BAD BCD ∠+∠=︒；（2）过点D 分别作DF BC ⊥于点F ，DE BA ⊥交BA 的延长线于点E ，过点B 作BG DC ⊥，根据含30度角的直角三角形的性质可得12ED AD =，根据三线合一，可得12DG DC =，进而可得DE DG =，根据角平分线的判定定理可推出12ABD DBG DBC ∠=∠=∠，进而即可证明2DBC ABD ∠=∠； （3）先证明四边形DMEF 是矩形，证明△MAD ≌FCD ，进而证明四边形DMEF 是正方形，设ABD α∠=，根据（2）的结论以及三角形内角和定理，求得15α=︒，进而求得30DBC ∠=︒，根据含30度角的直角三角形的性质，即可求得EF ，进而在Rt DEF △中，勾股定理即可求得DE 的长．【详解】（1）如图，过点D 分别作DF BC ⊥于点F ，DE BA ⊥交BA 的延长线于点E ，BD 平分ABC ∠，ED FD ∴=DA DC =，在Rt DAE 与Rt DCF △中AD DC ED FD =⎧⎨=⎩∴Rt DAE ≌Rt DCF △（HL ）C EAD ∴∠=∠180DAB EAD DAB C ∴∠+∠=∠+∠=︒即180BAD BCD ∠+∠=︒（2）如图，过点D 作DE BA ⊥交BA 的延长线于点E ，过点B 作BG DC ⊥，BD BC = 11,22DG GC DC DBG CBG DBC ∴==∠=∠=∠ 150=︒∠BAD ，18015030EAD ∴∠=︒-︒=︒12ED AD ∴= DA DC =ED DG ∴=,ED BE DG BG ⊥⊥EBD GBD ∴∠=∠12ABD DBC ∴∠=∠ 即2DBC ABD ∠=∠（3）如图，过点D 分别作DF BC ⊥于点F ，DM EA ⊥交EA 的延长线于点M ，AE BC ⊥，,DM ME DF FE ⊥⊥∴四边形DMEF 是矩形90MDF ∴∠=︒90MDA ADF ∴∠+∠=︒DA DC⊥90ADC∴∠=︒90ADF FDC∴∠+∠=︒FDC MDA∴∠=∠在△MAD与FCD中MDA FDCDMA DFCDA DC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△MAD≌FCDDM DF∴=，MDA FDC∠=∠∴四边形DMEF是正方形DF EF∴=设ABDα∠=∴22DBC ABDα∠=∠=BD BC=()11802902BDC BCDαα∴∠=∠=︒-=-90MDA FDC BCDα∴∠=∠=︒-∠=90DAE M MDAα∴∠=∠+∠=︒+150BAD∠=︒60BAEα∴∠=-在BAE中9030ABE BAEα∠=︒-∠=︒+23ABE ABD DBCααα∠=∠+∠=+=15α∴=︒230DBCα∴∠==︒2BD =112122DF BD∴==⨯=在Rt DEF△中，1EF DF==DE∴==【点睛】本题考查了三角形全等的性质与判定，角平分线的性质与判定，三角形内角和定理，三角形的外角性质，勾股定理，正方形的性质与判定，正确的添加辅助线是解题的关键．3．（1）2y x 2x 3=-++；（2）1(2,3)Q ，2317117(,)22Q +--，3317117(,)22Q --+；（3）存在，(2,3)M 或5175317(,)22--+ 【解析】【分析】 （1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入求出a ，即可得出答案；（2）①过P 作PQ //BC ，交抛物线于点Q ，如图1所示；②求出点G 坐标，可得2PG GH ==，过H 作直线23Q Q //BC ，交x 轴于点H ，分别求出Q 的坐标即可；（3）MDN △为等腰直角三角形，则MN MD =，求出MN 、MD 的长度即可列出等量关系式，从而得出答案．【详解】（1）设2(1)4(0)y a x a =-+≠，把C(0,3)代入抛物线解析式得：43a +=，即1a =-，则抛物线解析式为22(1)423 y x x x =--+=-++；（2）由(3,0)B ，C(0,3)，得到直线BC 解析式为3y x =-+，①过P 作1PQ //BC ，交抛物线于点1Q ，如图1所示，(1,4)P ，∴直线PQ 解析式为5y x =-+，联立得：2235y x x y x ⎧=-++⎨=-+⎩， 解得：14x y =⎧⎨=⎩或23x y =⎧⎨=⎩， 即1(2,3)Q ；②过P 作PH x ⊥轴，交BC 于点G ，交x 轴于点H ，令1x =，代入3y x =-+，得2y =，(1,2)G ∴，2PG GH ∴==，过H 作直线23Q Q //BC ，则直线23Q Q 解析式为1y x =-+，联立得：2231y x x y x ⎧=-++⎨=-+⎩，解得：x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧⎪⎪⎨⎪=⎪⎩2Q ∴，3Q ， 综上所述：点Q 的坐标为1(2,3)Q，2Q，3Q ； （3）MDN △为等腰直角三角形，则MN MD =，点()2,23M m m m -++，令x m =，代入3y x =-+得：3y m =-+，(,3)D m m ∴-+，函数的对称轴为：1x =，则点N 的横坐标为：2m -，则|22|MN m =-，2223(3)3MD m m m m m =-++--+=-+，2223m m m ∴-=-+，2223m m m -=-+或2223m m m -+=-+，解得：12m =或21m =-（舍）或3m =4m = 当2m =时，2233m m -++=，当m =223m m -++= 故点M 的坐标为：(2,3)或． 【点睛】 本题考查了二次函数综合题，设计知识有：用待定系数法求函数解析式、同底等高的面积计算、等腰直角三角形的性质，一次函数与二次函数交点问题，熟练掌握相关知识点是解决本题的关键．4．（1）①1；②47；②见解析；（3）是定值，53 【解析】【分析】（1）①如图1，设DE 与CF 交于点G ，由正方形的性质得出∠A =∠FDC =90°，AD =CD ，可证明△AED ≌△DFC （AAS ），由全等三角形的性质得出DE =CF ，则可得出结论；②如图2，设DB 与CE 交于点G ，根据矩形性质得出∠A =∠EDC =90°，由直角三角形的性质证出∠ECD =∠ADB ，由相似三角形的判定定理证出△DEC ∽△ABD 即可；（2）如图3，过点C 作CH ⊥AF 交AF 的延长线于点H ，证明△DEA ∽△CFH ，由相似三角形的性质得出DE AD CF CH =，则可得出结论； （3）过点C 作CG ⊥AD 于点G ，连接AC 交BD 于点H ，CG 与DE 相交于点O ，根据等积关系可得AH 、DH 和CG 的长，，再证明△DEA ∽△CFG ，得出比例线段DE AD CF CG=则可求出答案．【详解】解：（1）①如图1，设DE 与CF 交于点G ，∵四边形ABCD 是正方形，∴∠A =∠FDC =90°，AD =CD ，∵DE ⊥CF ，∴∠DGF =90°，∴∠ADE +∠CFD =90°，∠ADE +∠AED =90°，∴∠CFD =∠AED ，在△AED 和△DFC 中，A FDC CFD AED AD CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△AED ≌△DFC （AAS ），∴DE =CF ，∴DE CF=1 故答案为：1；②如图2，设DB 与CE 交于点G ，∵四边形ABCD 是矩形，∴∠A=∠EDC=90°，∵CE⊥BD，∴∠DGC=90°，∴∠CDG+∠ECD=90°，∠ADB+∠CDG=90°，∴∠ECD=∠ADB，∵∠CDE=∠A，∴△DEC∽△ABD，∴4,7 CE DCBD AD==，故答案为：47．（2）证明：如图3，过点C作CH⊥AF交AF的延长线于点H，∵CG⊥EG，∴∠G=∠H=∠A=∠B=90°，∴四边形ABCH为矩形，∴AB=CH，∠FCH+∠CFH=∠DFG+∠FDG=90°，∴∠FCH=∠FDG=∠ADE，∠A=∠H=90°，∴△DEA∽△CFH，∴DE AD CF CH=，∴DE AD CF AB=，∴DE•AB=CF•AD；（3）是定值，如图4，过点C作CG⊥AD于点G，连接AC交BD于点H，CG与DE相交于点O，则AC BD ⊥于H∵CF ⊥DE ，GC ⊥AD ，∴∠FCG +∠CFG =∠CFG +∠ADE =90°，∴∠FCG =∠ADE ，∠BAD =∠CGF =90°，∴△DEA ∽△CFG ， ∴DE AD CF CG=， 在Rt △ABD 中，AD =9，AB =3， ∴222293310BD AB AD ++ 又1122AD AB BD AH = ∴93910310AD AB AH BD ⨯=== ∴AC =2AH 91052222910279()101010DH AD AH =-=- ∵1122ADC S AC DH AD CG ∆=⋅=⋅， ∴192711010925102CG =⨯， ∴CG =275，由（1）可得，ADE GCF ∆∆∴952735DE AD CF CG ===【点睛】此题是相似形综合题，主要考查了正方形的性质，矩形的性质，勾股定理，相似三角形的判定与性质，全等三角形的判断和性质，三角形的面积，解本题的关键是熟练掌握相似三角形的判定与性质．5．（1）213442y x x =-++；（2）点P 的坐标为：（6，4171，2172）；（3）11NC MC += 【解析】【分析】（1）根据题意，先证明AOC ∆∽COB ∆，得到AO OC CO OB=，求出点A 、B 的坐标，然后利用待定系数法，即可求出抛物线解析式；（2）根据题意，可分为两种情况：AOC ∆∽PQC ∆或AOC ∆∽CQP ∆，结合解一元二次方程，相似三角形的判定和性质，分别求出点P 的坐标，即可得到答案；（3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，然后由角平分线的性质定理，得到EI =EJ ，再证明△MEI ∽△MNC ，△NEJ ∽△NMC ，得到111NC MC EI +=，然后求出EI 一个定值，即可进行判断．【详解】解：（1）∵以AB 为直径的圆过点C ，∴∠ACB =90°，∵点C 的坐标为()0,4，∴CO ⊥AB ，∴∠AOC =∠COB =90°，∴∠ACO +∠OCB =∠ACO +∠OAC =90°，∴∠OCB =∠OAC ,∴AOC ∆∽COB ∆， ∴AO OC CO OB =， ∵4CO =，10AO BO AB +==，∴10AO OB =-， ∴1044OB OB-=， 解得：2OB =或8OB =，经检验，满足题意，∵OB OA >，∴8OB =，∴点A 为（2-，0），点B 为（8，0）．设抛物线的解析式为2y ax bx c =++，把点A 、B 、C 三点的坐标代入，有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩，解得：14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式为213442y x x =-++； （2）根据题意，如图：当AOC ∆∽PQC ∆时，∴ACO PCQ ∠=∠，∵90ACO OCB ∠+∠=︒，∴90PCQ OCB ∠+∠=︒， ∴PC ⊥OC ，∴点P 的纵坐标为4，当4y =时，有2134442x x -++=， 解得：16x =或20x =（舍去）；∴点P 的坐标为（6，4）；当AOC ∆∽CQP ∆时，则此时BC 垂直平分OP ，作PG ⊥y 轴，垂足为G ，如上图， ∴90CQP AOC ∠=∠=︒，∴AC ∥OP ，∴∠ACO =∠POG ，∵90PGO AOC ∠=∠=︒，∴AOC ∆∽PGO ∆，∴AO OC PG GO=， 设点P 为（x ，213442x x -++）， ∴PG x =，213442GO x x =-++， ∴22413442x x x =-++， 解得：171x =， ∵点P 在第一象限， ∴171x =，∴2134217242x x -++=，∴点P 的坐标为（171-，2172-）；综合上述，点P 的坐标为：（6，4）或（171-，2172-）；（3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，如图：∵CE 是∠ACB 的角平分线，∴EI =EJ ， ∵EI ∥CN ，EJ ∥CM ，∴△MEI ∽△MNC ，△NEJ ∽△NMC ，∴EI ME NC MN =，EJ NE MC MN =， ∴1EI EJ ME NE NC MC MN MN +=+=， ∴1EI EI NC MC +=， ∴111NC MC EI+=， ∵△ACO ∽△AEI ， ∴12AI AO EI CO ==， ∵222425AC =+∵AC AI IC AI EI =+=+，2512EI -=， 解得：45EI =∴11135NC MC EI +== ∴11NC MC+是一个定值． 【点睛】本题考查了二次函数的综合应用，求二次函数的解析式，二次函数的性质，相似三角形的判定和性质，解一元二次方程，角平分线的性质定理等知识，解题的关键是熟练掌握题意，正确的作出辅助线，运用数形结合的思想进行解题．6．（1）（﹣1，﹣5），y ＝x ﹣4；（2）①a 的值为a ＝﹣2． 【解析】【分析】（1）由“伴随直线”的定义即可求解； （2）①先求y ＝a （x −1）2−4a 的伴随直线为y ＝ax −5a ，再联立方程组2(1)45y a x a y ax a ⎧=--⎨=-⎩，求出A （1，−4a ），B （2，−3a ），C （−1，0），D （3，0），由于当△ABC 为等腰三角形时，只存在一种可能为AC ＝BC ，即可求a 的值；②先求直线BC 解析式为y ＝−ax −a ，过P 作x 轴的垂线交BC 于点Q ，设点P 的横坐标为x ，则P [x ，a （x −1）2−4a ]，Q （x ，−ax −a ），23127()228PBC S a x a ∆=--，即可求面积的最大值，进而求a 的值．【详解】（1）∵抛物线y ＝（x +1）2﹣5，∴顶点坐标为（﹣1，﹣5），“伴随直线”为y ＝x ﹣4，故答案为：（﹣1，﹣5），y ＝x ﹣4；（2）①由“伴随直线”定义可得：y ＝a （x ﹣1）2﹣4a 的伴随直线为y ＝ax ﹣5a ， 联立2(1)45y a x a y ax a ⎧=--⎨=-⎩， 解得14x y a =⎧⎨=-⎩或23x y a =⎧⎨=-⎩， ∴A （1，﹣4a ），B （2，﹣3a ），在y ＝a （x ﹣1）2﹣4a 中，令y ＝0可解得x ＝﹣1或x ＝3，∴C （﹣1，0），D （3，0），∴AC 2＝4+16a 2，BC 2＝9+9a 2，∵当△ABC 为等腰三角形时，只存在一种可能为AC ＝BC ，∴AC 2＝BC 2，即4+16a 2＝9+9a 2，解得=a ∵抛物线开口向下，∴a =∴若△ABC 为等腰三角形时，a 的值为 ②设直线BC 的解析式为y ＝kx +b ，∵B （2，﹣3a ），C （﹣1，0），∴200k b k b +=⎧⎨-+=⎩，解得k a b a =-⎧⎨=-⎩，∴直线BC 解析式为y ＝﹣ax ﹣a ，如图，过P 作x 轴的垂线交BC 于点Q ，设点P 的横坐标为x ，∴P [x ，a （x ﹣1）2﹣4a ]，Q （x ，﹣ax ﹣a ），∵P 是直线BC 上方抛物线上的一个动点， ∴22219(1)4(2)()24PQ a x a ax a a x x a x ⎡⎤=--++=--=--⎢⎥⎣⎦， ∴23127()228PBC S a x a ∆=--， ∴当12x =时，△PBC 的面积有最大值278-a ， ∴S 取得最大值274时，即272784-=a ，解得a ＝﹣2．【点睛】本题考查二次函数的综合应用，熟练掌握二次函数的图象及性质，理解新定义，将所求问题转化为直线与抛物线的知识是解题的关键．7．（1）y ＝239344x x --；（2）点P 的坐标为：13313-13313-或(3，3)；（3）⊙N 的半径为163或83或1． 【解析】【分析】（1）代入点A 、C 的坐标求出解析式；（2）先求出直线OD 的解析式，再和二次函数为的解析式y ＝239344x x -+联立即可求解；（3）先求出直线BC 的解析式，设N (m ，3m 34-)，则M (m ，239344m m --)，求出MN 的距离，最后利用“当⊙N 与y 轴相切时，MN =m ”，得出结果．【详解】解：（1）将点A （-1，0），C （0，3）代入抛物线的解析式得，9043a c c ⎧++=⎪⎨⎪=-⎩， 解得343a c ⎧=⎪⎨⎪=-⎩， 故二次函数的解析式为y ＝239344x x --； （2）∵抛物线y ＝239344x x --=23325()423x --， ∴抛物线的顶点E 的坐标为(325,23-)， ∵DF 平分∠ODE ，∴∠ODF =∠FDE ，∵EH ∥y 轴，∴∠FDE =∠OFD ，∴OD =OF ，∵(0,F ， ∴OD =OF设D (32，m )，则OD ²=223()2m +，即2(=223()2m +，解得：m =-32或32， ∴D (32，32-)或(32，32)， 设直线OD 的解析式为y =kx ， ∴32-=32k 或32=32k ，解得：k =-1或k =1， ∴直线OD 的解析式为：y =x 或y =－x ， 联立239344y x y x x =⎧⎪⎨=--⎪⎩或239344y x y x x =-⎧⎪⎨=--⎪⎩， 解得：x舍去)；或x =3或43-(舍去)； ∴y3， ∴点P 的坐标为：或(3，3)；（3）由（1）得二次函数为：y ＝239344x x --， 当y =0时，239344x x --=0，解得：121,4x x =-=， ∴B (4，0)，设直线BC 为：y =kx +b ，经过点C (0，-3)，则有043k b b =+⎧⎨=-⎩， 解得：343k b ⎧=⎪⎨⎪=-⎩ ， ∴直线BC 为：y=334x -， 设N (m ，3m 34-)，则M (m ，239344m m --)， ∴MN =M N y y -=239333444m m m ---+=2334m m - 当⊙N 与y 轴相切时，MN =m ， ∴2334m m -=m ， 解2334m m -=m ，得m =163或0(舍去)， 解2334m m -=-m ，得m =83或0(舍去)， ∴⊙N 的半径为163或83； 当⊙N 与x 轴相切时，MN =334m -+， ∴2334m m -=334m -+，解2334m m -=334m -+，得m =4(舍去)或-1(舍去)， 解2334m m -=3m 34-，得m =4(舍去)或1， ∴⊙N 的半径为1；综上，⊙N 的半径为163或83或1．【点睛】本题考查了待定系数法求二次函数及一次函数的解析式，两点之间的距离公式，圆的切线的性质，解本题的关键用方程的思想解决问题．8．（1）见解析；（2）①见解析；②202【解析】【分析】（1）利用SAS 证明△ACD ≌△BCE ，从而利用全等三角形的性质即可得出结论；（2）①过点D 作DH ⊥CF 于H ，过点B 作BG ⊥CF ，交CF 的延长线于G ，首先证明△ACT ≌△BCG 及△DCH ≌△ECT ，得到CT ＝BG ，CT ＝DH ，通过等量代换得出DH ＝BG ，再证明△DHF ≌△BGF ，则可证明结论；②首先利用等腰三角形的性质和ASA 证明△AOM ≌△COF ，则有OM ＝OF ，然后利用等腰直角三角形的性质得出FK 2，然后利用三角形的面积得出OF×BF ＝2，最后利用平方的非负性和完全平方公式求解即可．【详解】证明：（1）∵△ABC 是等腰直角三角形，AC =BC ，∴∠ACB =90°，∵CD ⊥CE ，∴∠ACB ＝∠DCE ＝90°，∴∠ACD +∠BCD =∠BCE +∠BCD ，即∠ACD ＝∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BCE （SAS ），∴AD ＝BE ；（2）①如图2，过点D 作DH ⊥CF 于H ，过点B 作BG ⊥CF ，交CF 的延长线于G ，∵CF ⊥AE ，∴∠ATC =∠ATF =90°，∴∠ACT +∠CAT ＝90°，又∵∠ACT +∠BCG ＝90°，∴∠CAT ＝∠BCG ，在△ACT 和△CBG 中，90CAT BCG ATC CGB AC CB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴△ACT ≌△CBG （AAS ），∴CT ＝BG ，同理可证△DCH ≌△ECT ，∴CT ＝DH ，∴DH ＝BG ，在△DHF 和△BGF 中，90DFH BFG DHF BGF DH BG ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴△DHF ≌△BGF （AAS ），∴DF ＝BF ；②如图3，过点F 作FK ⊥BC 于K ， ∵等腰Rt △ABC ，CA ＝CB ，点O 是AB 的中点， ∴AO ＝CO ＝BO ，CO ⊥AB ，∠ABC ＝45°， ∴∠OCF +∠OFC ＝90°，∵AT ⊥CF ，∴∠ATF =90°，∴∠OFC +∠FAT ＝90°，∴∠FAT ＝∠OCF ，在△AOM 和△COF 中，90MAO FCO OA OCAOM COF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△AOM ≌△COF （ASA ），∴OM ＝OF ，又∵CO ⊥AO ，∴∠OFM ＝∠OMF ＝45°，222MF OF OM =+， ∴∠OFM ＝∠ABC ，MF， ∴MF //BC ，∴∠MFK =∠BKF =90°，∵∠ABC ＝45°，FK ⊥BC ，∴∠ABC ＝∠BFK ＝45°，∴FK ＝BK ，∵222BF FK BK =+，∴FK＝22BF，∵S△FMN＝52，∴12×MF×FK＝52，∴2OF×22BF＝102，∴OF×BF＝102，∵（BF﹣OF）2≥0，∴BF2+OF2﹣2BF×OF≥0，∴BF2+OF22＝2∴BF2+OF2的最小值为2．【点睛】本题主要考查全等三角形的判定及性质，等腰直角三角形的性质与判定，平行线的性质与判定，三角形面积，完全平方公式等等，掌握等腰直角三角形的性质与判定和全等三角形的判定方法及性质是解题的关键．9．（1）证明见解析；（2）证明见解析，（3）157 BF=【解析】【分析】（1）连接OA并延长AO交BC于E，证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论，（2）利用直角三角形两锐角互余、圆周角定理进行导角，得出MCG△和△FCG是等腰三角形，得出BM=MC=FG=CG，MH=HG，进而由BF=BM+MH-FH=FG-FH+HG，得出结论；（3）过O点作OP⊥AC，由垂径定理得出12PD=，再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==，由勾股定理进而可求BH，再利用相似三角形对应边成比例求出HG，即可得BF长．【详解】解：（1）连接OA并延长AO交BC于E，∵AB=AC，∴AB AC=，∵AE过圆心O，∴AE BC⊥，BE EC=，∴∠BAC=2∠BAE，∵OA=OB，∴∠ABD=∠BAE，∴∠BAC=2∠ABD；（2）如解图（2），连接OA并延长AO交BC于E，AE交BF于M，连接MC，设2BACα∠=，则ABD BAE EACα∠=∠=∠=∵AE=EC，AE⊥BC，∴BM=MC，∴∠MBC=∠MCB，∵BG⊥AC，AE⊥BC，∴∠EAC+∠ACE=90°，∠HBC+∠ACE=90°，∴EAC HBC MCBα∠=∠=∠=，∴2CMG MBC MCBα∠=∠+∠=，∵BC BC=，∴2G BACα∠=∠=，∴∠G=∠CMG，∴CG =CM =BM ，∵AC ⊥BG ，∴MH =HG ，∵OA =OC ，∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-，∵180FCG CFG G ∠=︒-∠-∠，即180(90)290FCG ααα∠=︒-︒--=︒-，∴FCG CFG ∠=∠，∴FG =CG ，∴BM =MC =FG =CG ，又∵MH =HG ，∴BF =BM +MH -FH =FG -FH +HG ，∴BF =2HG ．（3）过O 点作OP ⊥AC ，如解图（3）∵AO 是∠BAC 的角平分线，∴点O 到AB 、AC 的距离相等， ∴ABO ADO SAB BO S AD OD==， ∵AD =2，CD =3，∴AB =AC =5， ∴5=2BO OD ，即：2=7OD BD ， ∵OP ⊥AC ， ∴52AP PC ==，12PD =， ∵BH AC ⊥， ∴OP //BH ，∴27DP OP OD DH BH BD ===， ∴7724DH DP ==， ∴154AH AD DH =+=，5-4HC DC DH ==，∵在Rt ABH中，BH==∵BAH G∠=∠，AHB GHC∠=∠，∴AHB GHC△△，∴AH BHHG CH=即：AH HC BH HG=，51544=⨯，∴HG=，由（2）得BF=2HG，∴BF=【点睛】本题是圆的综合题，主要考查了圆周角定理，涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点，解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系，从而利用相似或勾股定理解题．10．（1）旋转中心为BC边的中点O，旋转方向为逆时针，旋转角度为90°；（2）可以，旋转中心为为等边△ABC三边垂直平分线的交点O，理由见解析；（3）11CD≤≤【解析】【分析】问题背景（1）根据等腰直角三角形的性质，以及旋转的性质确定即可；尝试应用（2）首先通过证明△ABD和△CAE全等说明点A和点B对应，点C和点A对应，从而作AB和AC的垂直平分线，其交点即为旋转中点；拓展创新（3）首先确定出D点的运动轨迹，然后结合点与圆的位置关系，分别讨论出CD 最长和最短时的情况，并结合勾股定理进行求解即可．【详解】解：问题背景（1）如图所示，作AO⊥BC，交BC于点O，由等腰直角三角形的性质可知：∠AOC=90°，OA=OC，∴点A是由点C绕点O逆时针旋转90°得到，同理可得，点B是由点A绕点O逆时针旋转90°得到，点D是由点E绕点O逆时针旋转90°得到，∴△ABD可以由△CAE通过旋转变换得到，旋转中心为BC边的中点O，旋转方向为逆时针，旋转角度为90°；尝试应用（2）∵△ABC 为等边三角形，∴AB =AC ，∠BAC =60°，∵∠DAC =∠DAB +∠BAC =∠AEC +∠EAC ，∠BAC =∠AEC =60°，∴∠DAB =∠ECA ，在△ABD 和△CAE 中，BDA AEC DAB ECA AB CA ∠⎪∠⎧=∠∠=⎪⎨⎩= ∴△ABD ≌△CAE (AAS )，∴△ABD 的A 、B 、D 三点的对应点分别为△CAE 的C 、A 、E 三点，则AC 、AB 分别视作两组对应点的连线，此时，如图所示，作AC 和AB 的垂直平分线交于点O ，∵△ABC 为等边三角形，∴由等边三角形的性质可知，OC =OA =OB ，∠AOC =120°，∴△ABD 可以由△CAE 通过旋转变换得到，旋转中心为为等边△ABC 三边垂直平分线的交点O ；拓展创新（3）由（1）知，在直线l 旋转的过程中，总有∠ADB =90°，∴点D 的运动轨迹为以AB 为直径的圆，如图，取AB 的中点P ，连接CP ，交⊙P 于点Q ，则当点D 在CP 的延长线时，CD 的长度最大，当点D 与Q 点重合时，CD 的长度最小，即CQ 的长度，∵AB =AC ，AB =2，∴AP =1，AC =2，在Rt △APC 中，225CP AP AC =+=，由圆的性质，PD =AP =1，∴PD =PQ =1，∴51CD CP PD =+=+，51CQ CP PQ =-=-，∴CD 的长的取值范围为：5151CD -≤≤+．【点睛】本题主要考查旋转三要素的确定，以及旋转的性质，主要涉及等腰直角三角形和等边三角形的性质，全等三角形的判定与性质，以及动点最值问题，掌握旋转的性质，确定出动点的轨迹，熟练运用圆的相关知识点是解题关键．11．（1）正方形；（2）α+β=180°；（3）α=96°；（4）能，α的值为120°，AP 的长为221．【解析】【分析】（1）由旋转的性质得到AO =AO ′，∠OAO ′=90°，由菱形的性质得到∠POA =∠AO ′P =90°，可以推出四边形AOPO ′为正方形；（2）利用旋转的性质推出∠AEP +∠AEG =∠AEP +∠ABD =180°，再结合四边形的内角和即可推出结论；（3）结合已知条件可分别先求出各部分角度，然后结合旋转的性质推出∠BPG 的度数，再结合（2）的结论求解即可；（4）利用勾股定理即可求得AO 的长，根据菱形的性质推出BD 是AC 的垂直平分线，证明△PAC 是等边三角形，即可求解．【详解】：（1）当α=90°时，四边形AOPO ′的形状为正方形．∵菱形AEFG 是菱形ABCD 旋转得到的，且点O ，O ′是对角线的交点，∴AO=AO′，∠OAO′=90°，∠POA=∠AO′P=90°，∴四边形AOPO′为正方形，故答案为：正方形；（2）由题意△BAD≌△EAG，∴∠ABD=∠AEG，∵射线BD，GE交于点P，∴∠AEP+∠AEG=∠AEP+∠ABD=180°，在四边形ABPE中，∠BAE+∠BPG=360°-（∠AEP+∠ABD）=180°，∴∠BAE=a，∠BPG=β，∴α+β=180°；（3）由菱形的性质知，AB=AD，△ABD为等腰三角形，∴当∠BAD=42°时，∠ABD=∠ADB=69°，∵PA=PB，∴∠ABP=∠BAP=69°，∴∠BPA=42°，∵AO=AO′，∴PA平分∠BPG，即：∠BPA=∠GPA=42°，∴∠BPG=84°，即：β=84°，由①知：α +β=180°，∴α=180°-84°=96°；（4）能，理由如下：连接PA，∵四边形ABCD 是菱形，且对角线交点为O ，AB =5，BD =4，∴BO =DO =2，AO =CO ，∠BOA =90°，∴AO =CO 2221AB BO -=∴AC 21 同理：21,AF 由旋转对称性可得,PC PF =∴ 当30CPB ∠=︒时，2221,PC CO PF ===∴ 四边形AFPC 是菱形，∵四边形ABCD 是菱形，∴BD 是AC 的垂直平分线，∴PC =PA ，∴△PAC 是等边三角形，∴PA =PC 21PAC =60°，∴∠CAF =120°，即α的值为120°，AP 的长为21【点睛】本题是四边形综合题，考查了菱形的性质，旋转的性质，勾股定理，等腰三角形的性质，等边三角形的判定和性质等，解答时灵活运用菱形的性质和旋转变化的性质是解题关键．12．(1)y =3x -3；(2)（-2，3）；(3)Q 的坐标为（-72，0）或（0，74）或（0，132） 【解析】【分析】（1）根据算术平方根的非负性及偶次方的非负性得到a +3=0，p -1=0，求出a ，p ，得到点P ，A 的坐标，设直线AP 的解析式为y=kx+b ，利用待定系数法求出函数解析式；（2）过M 作MD交x 轴于D ，连接AD ，由MD ，△MAP 的面积等于6，顶点△DAP 的面积等于6，求出DP ，得到点D 坐标，求出直线DM 的解析式，即可求出M 的坐标；（3）设B （t ，3t -3），分三种情况，①当点Q 在轴负半轴时，过B 作BE ⊥x 轴于E ，证明△BEQ ≌△QNC （AAS ），得到O Q=QE-OE=ON+QN ，即4-t =2+3-3t ，求出t 值即可；②当Q在y轴正半轴上时，过C作CF⊥y轴于F，过B作BG⊥y轴于G，证明△CQF≌△QBG（AAS），得到O Q=OG-QG=OF-QF，即3t-3-2=4-t，求出t即可；③当Q在y轴正半轴上时，过点C作CF⊥y轴于F，过B作BT⊥y轴于T，同②可证△CFQ≌△QTB（AAS），得到OQ=OT+QT=OF+QF，即3t-3+2=4+t，求出t值即可．(1)解：∵+（p﹣1）2＝0．∴a+3=0，p-1=0，解得a=-3，p=1，∴P(1,0)，A(0,-3)，设直线AP的解析式为y=kx+b，∴，解得，∴直线AP的解析式为y=3x-3；(2)解：过M作MD交x轴于D，连接AD，∵MD，△MAP的面积等于6，∴△DAP的面积等于6，∴，即，∴DP=4，∴D（-3，0）设直线DM的解析式为y=3x+c，则，∴c=9，∴直线DM的解析式为y=3x+9，令x=-2，得y=3，∴M（-2，3）；(3)解：存在设B（t，3t-3），。

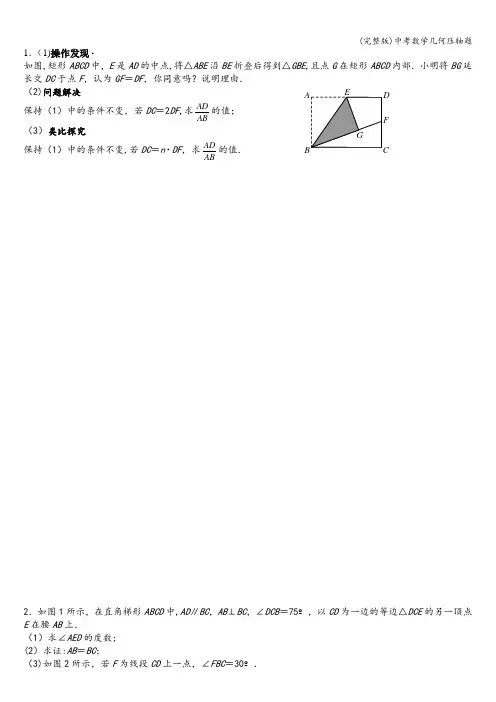
1．（1)操作发现·如图,矩形ABCD中，E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF＝DF，你同意吗？说明理由．（2)问题解决Array AD的值；保持（1）中的条件不变，若DC＝2DF,求AB（3）类比探究AD的值．保持（1）中的条件不变,若DC＝n·DF，求AB2．如图1所示，在直角梯形ABCD中,AD∥BC，AB⊥BC，∠DCB＝75º，以CD为一边的等边△DCE的另一顶点E在腰AB上．求 错误!的值．3。

如图①,在等腰梯形ABCD 中，AD ∥BC ，AE ⊥BC 于点E ，DF ⊥BC 于点F ．AD ＝2cm ，BC ＝6cm ，AE ＝4cm ．点P 、Q 分别在线段AE 、DF 上，顺次连接B 、P 、Q 、C ，线段BP 、PQ 、QC 、CB 所围成的封闭图形记为M ．若点P在线段AE 上运动时，点Q 也随之在线段DF 上运动,使图形M 的形状发生改变，但面积始终．．为10cm 2．设EP ＝x cm ，FQ ＝y cm,解答下列问题： （1)直接写出当x ＝3时y 的值;（2)求y 与x 之间的函数关系式,并写出自变量x 的取值范围； (3）当x 取何值时,图形M 成为等腰梯形?图形M 成为三角形？ （4）直接写出线段PQ 在运动过程中所能扫过的区域的面积．ABCDE 图1ABCDE图2FADA DP4．如图①，将一张矩形纸片对折,然后沿虚线剪切，得到两个（不等边）三角形纸片△ABC ,△A 1B 1C 1．（1）将△ABC ，△A 1B 1C 1如图②摆放，使点A 1与B 重合，点B 1在AC 边的延长线上,连接CC 1交BB 1于点E ．求证：∠B 1C 1C ＝∠B 1BC ．（2）若将△ABC ，△A 1B 1C 1如图③摆放,使点B 1与B 重合，点A 1在AC 边的延长线上，连接CC 1交A 1B 于点F ．试判断∠A 1C 1C 与∠A 1BC 是否相等，并说明理由．图 ①ABC A 1B 1C 1C 1C B 1B A(A 1)E图 ②5．将一副三角尺如图拼接:含30°角的三角尺（△ABC ）的长直角边与含45°角的三角尺(△ACD )的斜边恰好重合．已知AB ＝32，P 是AC 上的一个动点．（1）当点P 运动到∠ABC 的平分线上时，连接DP ，求DP 的长; （2）当点P 在运动过程中出现PD ＝BC 时，求此时∠PDA 的度数； （3）当点P 运动到什么位置时，以D ，P ，B ,Q 为顶点的平行四边形的顶点Q 恰好在边BC 上？求出此时□DPBQ 的面积．A BCD6．如图1，已知长方形ABED ，点C 是边DE 的中点，且AB ＝2AD ． （1）判断△ABC 的形状，并说明理由;（2）保持图1中ABC 的固定不变,绕点C 旋转DE 所在的直线MN 到图2中的位置（当垂线段AD 、BE 在直线MN 的同侧），试探究线段AD 、BE 、DE 长度之间有什么关系？并给予证明；(3）保持图2中△ABC 的固定不变，继续绕点C 旋转DE 所在的直线MN 到图3中的位置(当垂线段AD 、BE 在直线MN 的异侧)．试探究线段AD 、BE 、DE 长度之间有什么关系?并给予证明．AB CDE图1ABC D E图3NM ABCDE图2NM7．如图1，梯形ABCD 中,AD ∥BC ，AB ＝AD ＝CD ，∠BAD ＝120°，∠MAN ＝60°,将图1中的∠MAN 绕点A 按逆时针方向旋转α角（0°＜α＜120°),边AM 、AN 分别交直线BC 、CD 于E 、F 两点． （1）当0°＜α≤60°时，其他条件不变,如图2、如图3所示．①如图2，判断线段BE 、DF 、EF 的数量关系,并直接写出结论；②如图3，①中的结论是否依然成立?若成立，请利用图3证明；若不成立，说明理由． （2）当60°＜α＜120°时，其他条件不变,请在图4中画出一个．．符合条件的图形，直接写出所画图形中线段BE 、DF 、EF 的数量关系．图1 AB C DMN 图2 ABC DMNE F图3ABCD M FEN图4ABCD。

2020中考数学专题突破训练：填空压轴题（含解析）1.如图，矩形ABCD中，AB=2，BC=3，点E为AD上一点，且∠ABE=30°，将△ABE沿BE翻折，得到△A′BE，连接CA′并延长，与AD相交于点F，则DF的长为．解：如图作A′H⊥BC于H．∵∠ABC=90°，∠ABE=∠EBA′=30°，∴∠A′BH=30°，∴A′H=BA′=1，BH=A′H=，∴CH=3﹣．∵△CDF∽△A′HC，∴ =，∴ =，∴DF=6﹣2．故答案为：6﹣2．2.数学课上，老师提出如下问题：△ABC是⊙O的内接三角形，OD⊥BC于点D.请借助直尺，画出△ABC中∠BAC的平分线.晓龙同学的画图步骤如下：（1）延长OD交»BC于点M；（2）连接AM交BC于点N.所以线段AN为所求△ABC中∠BAC的平分线.请回答：晓龙同学画图的依据是.【答案】垂径定理，等弧所对的圆周角相等．3.如图，在平面直角坐标系中，△P1OA1，△P2A1A2，△P3A2A3，…都是等腰直角三角形，其直角顶点P1（3，3），P2，P3，…均在直线y=﹣x+4上．设△P1OA1，△P2A1A2，△P3A2A3，…的面积分别为S1，S2，S3，…，依据图形所反映的规律，S2018=．【分析】分别过点P1.P2.P3作x轴的垂线段，先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高，继而求得三角形的面积，得出面积的规律即可得出答案．【解答】解：如图，分别过点P1.P2.P3作x轴的垂线段，垂足分别为点C.D.E，∵P1（3，3），且△P1OA1是等腰直角三角形，∴OC=CA1=P1C=3，设A1D=a，则P2D=a，∴OD=6+a，∴点P2坐标为（6+a，a），将点P 2坐标代入y=﹣x+4，得：﹣（6+a ）+4=a ，解得：a=，∴A 1A 2=2a=3，P 2D=，同理求得P 3E=、A 2A 3=，∵S 1=×6×3=9.S 2=×3×=、S 3=××=、……∴S 2018=，故答案为：．4．阅读下面材料：小亮的作法如下：C老师说：“小亮的作法正确”请回答：小亮的作图依据是_________________________________________________．【答案】两点确定一条直线；同圆或等圆中半径相等；5.如图①，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A 逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为BC=DC+EC ；探索：如图②，在Rt△ABC与Rt△ADE中，AB=AC，AD=AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；应用：如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD的长．【分析】（1）证明△BAD≌△CAE，根据全等三角形的性质解答；（2）连接CE，根据全等三角形的性质得到BD=CE，∠ACE=∠B，得到∠DCE=90°，根据勾股定理计算即可；（3）作AE⊥AD，使AE=AD，连接CE，DE，证明△BAD≌△CAE，得到BD=CE=9，根据勾股定理计算即可．【解答】解：（1）BC=DC+EC，理由如下：∵∠BAC=∠DAE=90°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE，∴BD=CE，∴BC=BD+CD=EC+CD，故答案为：BC=DC+EC；（2）BD2+CD2=2AD2，理由如下：连接CE，由（1）得，△BAD≌△CAE，∴BD=CE，∠ACE=∠B，∴∠DCE=90°，∴CE2+CD2=ED2，在Rt△ADE中，AD2+AE2=ED2，又AD=AE，∴BD2+CD2=2AD2；（3）作AE⊥AD，使AE=AD，连接CE，DE，∵∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAD′，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴BD=CE=9，∵∠ADC=45°，∠EDA=45°，∴∠EDC=90°，∴DE==6，∵∠DAE=90°，∴AD=AE=DE=6．6.如图，是按一定规律排成的三角形数阵，按图中数阵的排列规律，第9行从左至右第5个数是【分析】由图形可知，第n行最后一个数为=，据此可得答案．【解答】解：由图形可知，第n行最后一个数为=，∴第8行最后一个数为==6，则第9行从左至右第5个数是=，故答案是 7．已知：在四边形ABCD 中，∠ABC =∠ADC =90º，M 、N 分别是CD 和BC 上的点．求作：点M 、N ，使△AMN 的周长最小．作法：如图，（1）延长AD ，在AD 的延长线上截取DA ´=DA ；（2）延长AB ，在AB 的延长线上截取B A″=BA ；（3）连接A′A″，分别交CD 、BC 于点M 、N ．则点M 、N 即为所求作的点．请回答：这种作法的依据是_____________．【答案】①线段垂直平分线的定义（或线段垂直平分线的判定，或轴对称的性质即对称点的 连线段被对称轴垂直平分）②线段垂直平分线上的点到线段两个端点的距离相等（线段垂直平分线的性质）；③两点之间线段最短.8.如图，∠MON=30°，点B 1在边OM 上，且OB 1=2，过点B 1作B 1A 1⊥OM 交ON 于点A 1，以A 1B 1为边在A 1B 1右侧作等边三角形A 1B 1C 1；过点C 1作OM 的垂线分别交OM 、ON 于点B 2.A 2，以A 2B 2ABC D A ''A 'N M DC BA为边在A2B2的右侧作等边三角形A2B2C2；过点C2作OM的垂线分别交OM、ON于点B3.A3，以A3B3为边在A3B3的右侧作等边三角形A3B3C3，…；按此规律进行下去，则△A n B n+1C n的面积为（）2n﹣2×．（用含正整数n的代数式表示）【解答】解：由题意△A1A2C1是等边三角形，边长为，△A2A3C2是等边三角形，边长为×，△A3A4C3是等边三角形，边长为××=（）2×，△A4A5C4是等边三角形，边长为×××=（）3×，…，△A n B n+1C n的边长为（）n﹣1×，∴△A n B n+1C n的面积为×[（）n﹣1×]2=（）2n﹣2×．9.如图1，将矩形ABCD折叠，使BC落在对角线BD上，折痕为BE，点C落在点C′处，若∠ADB=46°，则∠DBE的度数为23 °．解∵四边形ABCD是矩形，∴AD∥BC，∴∠ADB=∠DBC=46°，由翻折不变性可知，∠DBE=∠EBC=∠DBC=23°，故答案为23．10. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系xOy 中，矩形ABCD 的边AB 在x 轴上，，，边AD 长为5. 现固定边AB ，“推”矩形使点D 落在y 轴的正半轴上（落点记为），相应地，点C 的对应点的坐标为 .【答案】(7,4)11.如图，正方形AOBO 2的顶点A 的坐标为A （0，2），O 1为正方形AOBO 2的中心；以正方形AOBO 2的对角线AB 为边，在AB 的右侧作正方形ABO 3A 1，O 2为正方形ABO 3A 1的中心；再以正方形ABO 3A 1的对角线A 1B 为边，在A 1B 的右侧作正方形A 1BB 1O 4，O 3为正方形A 1BB 1O 4的中心；再以正方形A 1BB 1O 4的对角线A 1B 1为边在A 1B 1的右侧作正方形A 1B 1O 5A 2，O 4为正方形A 1B 1O 5A 2的中心：…；按照此规律继续下去，则点O 2018的坐标为 （21010﹣2，21009） ．【分析】由题意Q 1（1，1），O 2（2，2），O 3（，4，2），O 4（，6，4），O 5（10，4），O 6（14，8）…观察可知，下标为偶数的点的纵坐标为2，下标为偶数的点在直线y=x+1上，点O 2018的纵坐标为21009，可得21009=x+1，同侧x=21010﹣2，可得点O 2018的坐标为（21010﹣2，21009）．【解答】解：由题意Q 1（1，1），O 2（2，2），O 3（，4，2），O 4（，6，4），O 5（10，4），O 6（14，8）…观察可知，下标为偶数的点的纵坐标为2，(3,0)A -(4,0)B D 'C'下标为偶数的点在直线y=x+1上，∵点O 2018的纵坐标为21009， ∴21009=x+1，∴x=21010﹣2，∴点O 2018的坐标为（21010﹣2，21009）． 故答案为（21010﹣2，21009）． 12．在平面直角坐标系xOy 中，点(2,)A m -绕坐标原点O 顺时针旋转90︒后，恰好落在右图中阴影区域（包括边界）内，则m 的取值范围是 .【答案】532m ≤≤ 13.为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋，检查员将这些金蛋按1﹣2018的顺序进行标号．第一次先取出编号为单数的金蛋，发现其中没有有奖金蛋，他将剩下的金蛋在原来的位置上又按1﹣1009编了号（即原来的2号变为1号，原来的4号变为2号……原来的2018号变为1009号），又从中取出新的编号为单数的金蛋进行检验，仍没有发现有奖金蛋……如此下去，检查到最后一枚金蛋才是有奖金蛋，问这枚有奖金蛋最初的编号是 1024 ．【解答】解：∵将这些金蛋按1﹣2018的顺序进行标号，第一次先取出编号为单数的金蛋，发现其中没有有奖金蛋，∴剩余的数字都是偶数，是2的倍数，；∵他将剩下的金蛋在原来的位置上又按1﹣1009编了号，又从中取出新的编号为单数的金蛋进行检验，仍没有发现有奖金蛋，∴剩余的数字为4的倍数，以此类推：2018→1009→504→252→126→63→31→15→7→3→1共经历10次重新编号，故最后剩余的数字为：210=1024．故答案为：1024．14．下面是“作以已知线段为斜边的等腰直角三角形”的尺规作图过程．请回答：在上面的作图过程中，①ABC △是直角三角形的依据是 ；②ABC △是等腰三角形的依据是 ．【答案】①直径所对的圆周角为直角OQB②线段垂直平分线上的点与这条线段两个端点的距离相等15.按一定顺序排列的一列数叫做数列，如数列：，，，，…，则这个数列前2018个数的和为_____．【答案】【解析】【分析】根据数列得出第n个数为，据此可得前2018个数的和为，再用裂项求和计算可得．【详解】由数列知第n个数为，则前2018个数的和为===1﹣=，故答案为：．16.下面是“作三角形一边上的高”的尺规作图过程.已知：△ABC.求作：△ABC的边BC上的高AD.作法：如图，（1）分别以点B和点C为圆心，BA,CA为半径作弧,两弧相交于点E；请回答：该尺规作图的依据是．【答案】与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；三角形的高的定义.17.下面是按一定规律排列的代数式：a2，3a4，5a6，7a8，…则第8个代数式是15a16．【分析】直接利用已知单项式的次数与系数特点得出答案．【解答】解：∵a2，3a4，5a6，7a8，…∴单项式的次数是连续的偶数，系数是连续的奇数，∴第8个代数式是：（2×8﹣1）a2×8=15a16．故答案为：15a16．。