(完整word版)北京林业大学2011-2012概率论与数理统计试卷

哈工大 2012年秋季学期概率论与数理统计 试题一、填空题（每小题3分，共5小题，满分15分）1．设事件A 、B 相互独立，事件B 、C 互不相容，事件A 与C 不能同时发生，且()()0.5P A P B ==，()0.2P C =，则事件A ，B 和C 中仅C 发生或仅C 不发生的概率为__________ ．2．设随机变量X 服从参数为2的指数分布， 则21e X Y-=-的概率密度为()Y f y =______ ____．3．设随机变量X 的概率密度为21e ,0()20, 0xx x f x x -⎧>⎪=⎨⎪≤⎩，利用契比雪夫不等式估计概率≥<<)51(X P ______．4．已知铝的概率密度2~(,)X N μσ，测量了9次，得 2.705x =，0.029s =，在置信度0.95下，μ的置信区间为______ ____．5．设二维随机变量(,)X Y 服从区域{(,)|01,02}G x y x y =≤≤≤≤上的均匀分布，令),min(Y X Z =，),max(Y X W =, 则)1(≥+W Z P = ．（0.0250.050.050.025(8)23060,(8)18595,(9) 1.8331,(9) 2.2622t t t t =⋅=⋅==()1.960.975Φ=，()1.6450.95Φ=)二、选择题（每小题3分，共5小题，满分15分）（每小题给出的四个选项中，只有一个是符合题目要求的，把所选项的字母填在题后的括号内）1．设0()1, 0()1, ()()P A P B P B A P B <<<<=，则与上式不等价的是（A ）A 与B 不相容. （B ）()()P B A P B A =.（C ）)()(A P B A P =. （D ）)()(A P B A P =． 【 】2．设总体X 服从参数为λ的泊松分布，12,,,n X X X 是来自X 的样本，X 为样本均值，则 （A ）1EX λ=，21DX n λ=． （B ）,λ=X E n X D λ=． （C ）,nX E λ=2n X D λ=． （D ）,λ=X E λn X D 1=． 【 】 3．设随机变量X 的概率密度为2, 01()0, x x f x <<⎧=⎨⎩其他，则)2(DX EX X P ≥-等于（A）99-. （B）69+. （C ）928-6. （D）69-． 【 】 4．如下四个函数，能作为随机变量X 概率密度函数的是（A ）⎪⎩⎪⎨⎧≤>+=0,00,11)(2x x x x f . （B ）0,157(),1116160, 1x f x x x x <-⎧⎪⎪=+-≤<⎨⎪≥⎪⎩.（C ）1()e ,.2xf x x -=∈R . （D ）1e ,0()0,0x x f x x -⎧->=⎨≤⎩ . 【 】5．设12,,,n X X X 为来自总体2~(,)X N μσ的一个样本，统计量2)(1μ-=X Sn Y 其中X 为样本均值，2S 为样本方差，则 【 】 （A ）2~(1)Y x n -（B ）~(1)Y t n -（C ）~(1,1)Y F n - （D ）~(1,1)Y F n -．三、（8分）假设某段时间内来到百货公司的顾客数服从参数为λ的Poisson 分布，而在百货公司里每个顾客购买电视机的概率均为p ，且顾客之间是否购买电视机相互独立，试求=A “该段时间内百货公司售出k 台电视机”的概率（假设每顾客至多购买一台电视机）。

一、填空题(每小题3分，共15分）1． 设事件B A ,仅发生一个的概率为0.3，且5.0)()(=+B P A P ，则B A ,至少有一个不发生的概率为__________。

答案：0.3解：3.0)(=+B A B A P即)(25.0)()()()()()(3.0AB P AB P B P AB P A P B A P B A P -=-+-=+=所以1.0)(=AB P9.0)(1)()(=-==AB P AB P B A P 。

2． 设随机变量X 服从泊松分布，且)2(4)1(==≤X P X P ，则==)3(X P ______.答案:161-e解答：λλλλλ---==+==+==≤e X P e eX P X P X P 2)2(,)1()0()1(2由 )2(4)1(==≤X P X P 知 λλλλλ---=+e e e 22 即 0122=--λλ 解得 1=λ，故161)3(-==e X P3． 设随机变量X 在区间)2,0(上服从均匀分布，则随机变量2X Y =在区间)4,0(内的概率密度为=)(y f Y _________。

答案：04,()()0,.Y Y X y f y F y f <<'===⎩其它解答：设Y 的分布函数为(),Y F y X 的分布函数为()X F x ,密度为()X f x 则2()()()((Y X X F y P Y y P X y P X F F =≤=≤=≤≤=-因为~(0,2)X U，所以(0X F =，即()Y X F y F = 故04,()()0,.Y Y Xyf y F y f<<'===⎩其它另解在(0,2)上函数2y x=严格单调，反函数为()h y=所以04,()0,.Y Xyf y f<<==⎩其它4．设随机变量YX,相互独立，且均服从参数为λ的指数分布，2)1(-=>eXP，则=λ_________，}1),{min(≤YXP=_________。

一. 填空题（每空题 2 分，共计 60 分）1、A、B是两个随机事件，已知p(A )0.4, P(B) 0.5,p( AB) 0.3 ，则p(A B)0.6 ,p(A - B)0.1，P( A B )= 0.4 ,p(A B)0.6 。

2、一个袋子中有大小相同的红球 6 只、黑球 4 只。

（1）从中不放回地任取 2 只，则第一次、第二次取红色球的概率为：1/3。

（2）若有放回地任取2只，则第一次、第二次取红色球的概率为：9/25。

（3）若第一次取一只球观查球颜色后，追加一只与其颜色相同的球一并放入袋中后，再取第二只，则第一次、第二次取红色球的概率为：21/55。

3、设随机变量 X 服从 B（2，0.5 ）的二项分布，则p X 1 0.75, Y 服从二项分布 B(98, 0.5), X 与 Y 相互独立 , 则 X+Y服从 B(100,0.5) ，E(X+Y)= 50 ，方差 D(X+Y)= 25 。

4、甲、乙两个工厂生产同一种零件，设甲厂、乙厂的次品率分别为0.1 、0.15 ．现从由甲厂、乙厂的产品分别占60%、40%的一批产品中随机抽取一件。

（1）抽到次品的概率为：0.12 。

（2）若发现该件是次品，则该次品为甲厂生产的概率为：0.5 ．5、设二维随机向量( X ,Y)的分布律如右，则 a 0.1, E( X ) 0.4 ，X 0 1X与 Y 的协方差为: - 0.2Y，-1 0.2 0.3Z X Y2的分布律为 : z 1 21 0.4 a概率0.6 0.46、若随机变量X ~ N(2,4)且(1) 0.8413 ，(2) 0.9772 ,则 P{ 2 X 4}0.815，Y 2X 1,则Y~N( 5，16）。

7、随机变量X、Y 的数学期望E(X)= -1，E(Y)=2,方差D(X)=1，D(Y)=2,且X、Y相互独立，则：E(2X Y)-4，D(2X Y)6。

8、设D（X）25，D（Y）1，Cov ( X ,Y ) 2 ，则 D（ X Y）309、设X1,, X 26是总体 N (8,16) 的容量为26 的样本，X为样本均值，S2为样本方差。

2012概率论与数理统计试卷答案-内编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2012概率论与数理统计试卷答案-内）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2012概率论与数理统计试卷答案-内的全部内容。

(完整word版）2012概率论与数理统计试卷答案—内亲爱的读者：本文内容由我和我的同事精心收集整理后编辑发布到文库，发布之前我们对文中内容进行详细的校对,但难免会有错误的地方，如果有错误的地方请您评论区留言，我们予以纠正，如果本文档对您有帮助,请您下载收藏以便随时调用。

下面是本文详细内容。

最后最您生活愉快 ~O（∩_∩）O ~暨南大学考试试卷答案1．设A 、B 、C 为三个事件,则事件“A 、B 、C 中恰有两个发生”可表示为（ C ). A ．AB AC BC ++； B. A B C ++; C. ABC ABC ABC ++； D 。

ABC2.。

设在 Bernoulli 试验中，每次试验成功的概率为)10(<<p p ，重复独立进行3 次试验, 至少失败一次的概率为 ( B ). A 。

3)1(p -; B. 31p -; C 。

3(1)p -； D 。

)1()1()1(223p p p p p -+-+-。

3. 设12,,,,n ηηη⋅⋅⋅⋅⋅⋅是相互独立且具有相同分布的随机变量序列, 若 1n E η=,方差存在,(1,2,),n =⋅⋅⋅ 则1lim ||3ni n i n P n η→∞=⎛⎫-<=⎪⎝⎭∑（ B )。

A. 0; B 。

1; C 。

1;3 D. 12。

课程考试标准答案和评分标准（题目类型是指：填空、选择、判断、名词解释、简答、论述、案例分析等） 一、（填空题）（3721''⨯=）： 1、 0.5 2、 0.2 3、164、 1-a5、 37.256、 23λ+7、 (0,1)N 二、（选择题）（3721''⨯=）：1、B2、B3、C4、B5、C6、 C7、 D三、计算题（本大题共5小题，共计58分）1、（本小题分值10分）解：设从甲袋取到白球的事件为A ，从乙袋取到白球的事件为B ，则根据全概率公式有()()(|)()(|)P B P A P B A P A P B A =+ ……………………8分211150.417323412=⨯+⨯== ……………………10分 2、（本小题分值10分）解：设电子元件损坏的概率为p ，则{200}p P X =≤2002006001()600xf x dx e dx --∞==⎰⎰……………………4分 200600013|1xee--=-=- ……………………6分根据贝努力模型，至少有一个元件损坏的概率为：1331(1)1(1)p e ---=--（或者2113333ee e ----++） . ……………………10分3、（本小题分值12分） 解：（1）1221()()(2)E X xf x dx x dx x x dx +∞-∞==+-⎰⎰⎰ ………4分3312201|()|133x x x =+-= …………6分 （2） 因为122232017()()(2)6E X x f x dx x dx x x dx +∞-∞==+-=⎰⎰⎰……9分 所以2271()()[()]166D XE X E x =-=-= ………………………12分 4、（本小题分值 12分）（1）数学期望是一阶原点矩为110()2)E X μ===⎰ …………………………….3分其样本矩为X =所以22ˆ1x x θ-⎛⎫= ⎪-⎝⎭为θ的矩估计值。

北京林业大学 2007--2008学年第二学期考试试卷试卷名称： 数理统计II （B 卷） 课程所在院系： 理学院 考试班级： 学号： 姓名： 成绩：试卷说明：1. 本次考试为闭卷考试。

本试卷共4页，共八大部分，请勿漏答；2. 考试时间为120分钟，请掌握好答题时间；3. 答题之前，请将试卷上的考试班级、学号、姓名填写清楚；4. 所有试题答案写在试卷上；5. 答题完毕，请将试卷交回，不得带出考场；6. 考试中心提示：请你遵守考场纪律，参与公平竞争!答题中可能用到的数据：8944.0)25.1(=Φ，9599.0)75.1(=Φ，(0.4243)0.6228Φ=，(1.414)0.9213Φ=， 0.025 1.96z =，,.)(.7764240250=t ,.)(.14311402502=χ20.025(5)12.833χ=一、选择题（在每个小题四个备选答案中选出一个正确答案，每小题３分，总计２１分） 1. 设A 、B 为任意两事件，且,()0,A B P B ⊂>则下列选择必然成立的是 (C) 。

()()()A P A P A B <; ()()()B P A P A B >;()()()C P A P A B ≤ ; ()()()D P A P A B ≥2. 对于事件A ，B ，下列命题正确的是 (D) （A ）若A ，B 互不相容，则A 与B 也互不相容。

（B ）若A ，B 相容，那么A 与B 也相容。

（C ）若A ，B 互不相容，且概率都大于零，则A ，B 也相互独立。

（D ）若A ，B 相互独立，那么A 与B 也相互独立。

３.设123,,X X X 相互独立同服从参数3λ=的泊松分布，令1231()3Y X X X =++，则2()E Y = (C) ．(A) 1. (B) 9. (C)10. (D ）6.４．每次试验结果相互独立，设每次试验成功的概率为p 。

2011 至 2012 学年第 1 学期 考试时间： 120 分钟 课程名称： 概率论与数理统计 （B ）卷 考试形式：（闭卷）年级： 10 专业： 全校相关专业 ；层次：（本）一、填空题（每小题2分，共20分） 1、0.7； 2、)16,1(N ； 3、10； 4、1,1==B A ； 5、44； 6、2720；7、 8、32，9、75，10、111-∑=n i i X n 。

二、选择题（每题2分，共20分）11、（B ）； 12、（D ）； 13、（D ）； 14、（B ）； 15、（C ）；16、（B ）；17、（A ）；18、（B ）； 19、（A ）； 20、（B ）. 三、计算题（共60分）21、(8分) 解： 设 i A ={第i 次取得新球}，i=1,2. (1) 设C={第二次才取得新球}，有12C A A =12121464()()()(|)10915P C P A A P A P A A ===⨯=， ………2分 (2) 设事件 D = {发现其中之一是新球}，E = {其中之一是新球，另一个也是新球}12121651()()()(|)1093P ED P A A P A P A A ===⨯= ………4分 121212121121()()()()1()(|)()(|)31644613310910915P D P A A P A A P A A P A P A A P A P A A =++=++=+⨯+⨯= ………6分 ()1/35(|)()13/1513P E D P E D P D ===. ………8分22、(10分)解设随机变量X 与Y 相互独立，且均服从[]0,2上的均匀分布，令U X Y =-，试求()D U 。

解：易知X 与Y 的联合密度函数为()1,,,(,)40,x y D f x y ⎧∈⎪=⎨⎪⎩其他，其中(){},02,02D x y x y =≤≤≤≤（2分）12E(U)=E X-Y 43Dx y dxdy ⎡⎤=-⋅=⎣⎦⎰⎰，（3分） ()()222212E(U )=E X-Y E X-Y 43Dx y dxdy ⎡⎤⎡⎤==-⋅=⎣⎦⎣⎦⎰⎰，（3分） ()()()2229D UE U E U =-=。

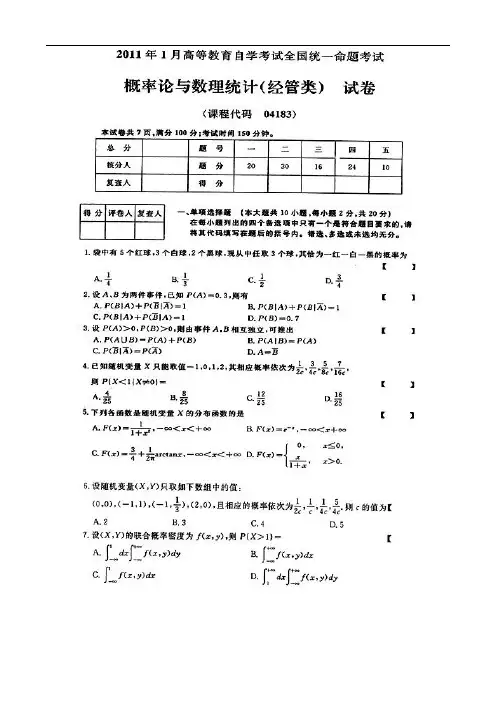
全国2011年4月高等教育自学考试 概率论与数理统计(经管类)试题课程代码：04183一、单项选择题(本大题共10小题，每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设A ，B ，C 为随机事件，则事件“A ，B ，C 都不发生”可表示为( ) A ．B.BC C ．ABC D.2．设随机事件A 与B 相互独立，且P(A)=，P(B)=，则P(A B)=( )A ． B.C ． D.3．设随机变量X ～B(3，0.4)，则P{X≥1}=( ) A.0.352 B.0.432 C.0.784 D.0.9364.已知随机变量X 的分布律为 ，则P{-2<X≤4 }=( )A.0.2B.0.35C.0.55D.0.8 5.设随机变量X 的概率密度为f(x)=，则E(X)，D(X)分别为 ( )A.-3，B.-3，2C.3，D.3，26.设二维随机变量(X,Y)的概率密度为f(x,y)=则常数c=( )X -1 2 5 P 0.2 0.35 0.45A. B.C.2D.47.设随机变量X~N(-1,22)，Y~N(-2,32)，且X与Y相互独立，则X-Y~( )A.N(-3，-5)B.N(-3,13)C.N (1，)D.N(1，13)8.设X,Y为随机变量，D(X)=4，D(Y)=16，Cov(X,Y)=2，则XY=( )A. B.C. D.9.设随机变量X~2(2)，Y~2(3)，且X与Y相互独立，则( )A.2(5)B.t(5)C.F(2，3)D.F(3,2)10.在假设检验中，H0为原假设，则显著性水平的意义是( )A.P{拒绝H0| H0为真}B. P {接受H0| H0为真}C.P {接受H0| H0不真}D. P {拒绝H0| H0不真}二、填空题(本大题共15小题，每小题2分，共30分)请在每小题的空格中填上正确答案。

北京交通大学2013〜2014学年第一学期概率论与数理统计期末考试试卷（ A 卷）某些标准正态分布的数值X 0.34 0.53 0.675 1.16 1.74 1.96 2.33 2.58 Q(x )0.66310.70190.750.8770.95910.9750.990.995其中①［X 是标准正态分布的分布函数.一.（本题满分8分）某人钥匙丢了，他估计钥匙掉在宿舍里、教室里以及路上的概率分别为0.4、0.35和0.25，而钥匙在上述三个地方被找到的概率分别为 0.5、0.65和0.45 •如果钥匙最终被找到， 求钥匙是在路上被找到的概率.解：设B = “钥匙被找到”.A 二“钥匙掉在宿舍里”，A ?二“钥匙掉在教室里”，A 3二“钥匙掉在路上”.由Bayes 公式，得PA 3B = 3PA 3PBA3Z P （A P （B A ）i 10.25 0.450.2083 .0.4 0.5 0.35 0.65 0.25 0.45二.（本题满分8分）抛掷3枚均匀的硬币，设事件A 」「至多出现一次正面 \B =「正面与反面都出现1判断随机事件 A 与B 是否相互独立（4分）？如果抛掷 4枚均匀的硬币，判断上述随机事件 A 与B 是否相互独立（4分）？100解:⑴如果抛掷3枚硬币，则样本点总数为21 2 3=8 .P A 丄丄，P B 丄丄，P AB ，8 28 4 8所以有 P AB =- =1 3二PAPB ，因此此时随机事件A 与B 是相互独立的. 8 2 4⑵ 如果抛掷4枚硬币，则样本点总数为24=16.514 74 1P A ， P B， P AB 二1616 8 16 4P AB — - =P A P B ，因此此时随机事件 A 与B 不是相互独立的. 416 8.（本题满分8分）设随机变量X 的密度函数为0 ： x :: 1其它E X (4 分)；⑵ plx E X / (4 分).解::: 1E (X )= J xf (x dx = J x 4(1 - x j dx1⑵ P 〈XE X ［；-P a 0.2 ； = j 41 -x 3dx0.2所以有 求：⑴ 1=4 x - 3x 2 3x 3ddx=4 丄1 3」124 5 丿 10.2.52013-2014学年第一学期概率论与数理统计学期末考试试卷（ A 卷）答案 Page 2 of 9100四.（本题满分8分） 某加油站每周补给一次汽油，如果该加油站每周汽油的销售量 度函数为0 ： x :: 100 其它1=4 1 _3x 3x 2dx =40.2 X-3X 2x 」x 2 4 0.2 25 60.409662 5 X （单位：千升）是一随机变量，其密试问该加油站每次的储油量需要多大，才能把一周内断油的概率控制在2%以下?解：设该加油站每次的储油量为a •则由题意，a应满足0 ：：： a ::: 100 ,而且P X a <0.02 .而P(X > a )= [ f (x dx = [ f (x dx + [ f (x )dx = [—x 1 -a 20 I 100丿1」100100所以，应当有,1」兰0.02.、一 100 丿 所以，得 1 一上 <V0.02，即 1 —1002 兰 2 , 100 100 因此有 a -100 1 -5 0.02 =54.2694948因此可取a = 55 （千升）,即可使一周内断油的概率控制在5%以下.五.（本题满分8分）设平面区域D 是由双曲线 , x 0以及直线y =x , x =2所围，二维随机变量 xX, Y 服从区域D 上的均匀分布.求：⑴ 二维随机变量 X, Y 的联合密度函数f x, y （4分）；⑵随机变量丫的边缘密度函数 f Y y （4分）.解：⑴区域D 的面积为2* 1 2 A = J x-— dx =（2x 2- In x ） = 6- In 2 ,x 丿 r 1所以，二维随机变量 X, Y 的联合密度函数为10 (x, y 弹 D1 ⑵当丄"£1时，2-be 2 / 、 1 1 1fY (y )— J f (X, ydx- f dx -2——“ h —1— (x, y )^ D f (x ，y )=【6-l n2y6—1 n2 ；6—In 2 I y 丿y所以，随机变量Y 的边际密度函数为必求出Y 的密度函数，只需指出Y 是哪一种分布，以及分布中的参数即可.）解：由于X 1 ~ N 0,匚2 , X 2~N0,-2，而且X 1与X 2相互独立，所以X 1 X 2 ~ N 0,2；「2 , X 1—X 2~N0,2匚2 .-be卜八f x.y dx =16 —In 22dx1 6 —In 22-y •六.（本题满分8分）f Y（y ）=«其它设随机变量 X 与Y 满足：var X =2 , var Y =4 , cov X ,Y = 1 ,再设随机变量U = 2X - 3Y ,V =3X -2丫，求二维随机变量 U, V 的相关系数:-U ,V .解：var U = var 2X -3Y =4 var X 9 var Y -12cov X, Y [=4 2 9 4 -12 =32 , var V =var3X-2Y = 9var X i 亠 4 var Y -12 cov X, Y ]=9 24 4-12 =22 ,cov U , V =cov 2X -3Y, 3X - 2Y^6var X 6var X -4cov X, Y -9cov X, Y [=6 26 4-13 1 =23.所以，二维；U ,V_covU,_V . 23 =23“8668451157、var U var V . 32 . 228、1123七.（本题满分8分）设X 1, X 2是取自正态总体 N 0,匚2中的一个样本.试求随机变量X^X 2 “―X22的分布（不1 6 — l n21 < y ::: 1 2由于covX1 X2,X r _X2= v a rX1-v a rX2=0 ,所以, 广X1 +X2 2＜屈丿21，_X2相互独立.所以，Y二乂+x2丫l X1- X2 丿「X1 +X2 22 X1 二X2 i占b八.（本题满分8分）某射手射击，他打中10环的概率为0.5，打中9环的概率为0.3，打中8环的概率为0.1，打中7环的概率为0.05，打中6环的概率为0.05 .他射击100次，试用中心极限定理近似计算他所得的总环数介于900环与930环之间的概率.x 1.25 1.30 1.35 1.40①(x)0.8944 0.90230 0.91149 0.91924解:设X k表示该射手射击的第则X k的分布律为X k 10 9 8 7 6P 0.5 0.3 0.1 0.05 0.05所以，E X k1=10 0.5 9 0.3 8 0.1 7 0.05 6 0.05 715,=102 0.5 92 0.3 82 0.1 - 72 0.05 62 0.05 =84.95,所以，D X k二EX： -Ex k2=84.95-9.152=1.2275.因此，X1, X2,…，X100是独立同分布的随机变量，故1 0 0P 9002X k 兰930『P1 0 0 1 0 0 1 0 0 1 0 0900、E X k ' X k-' E X k 930、E X k k £.：：：k =1km.：：：k T一,1 0 0 — 110 0「D X k ' D X k[k d . k=11 0 0' D X kk =12,而且X1 X2, X1 —X2服从二元正态分布，所以X1 X2与X1 —X2相互独立./ 100送 X k —100x9.15=P —1.35388 兰 7 l J100 汉 1.2275「Q1.35 ］尬［1.35 U 1.35 -1 =2 0.91149 -1 =0.82289 .九.(本题满分9分)设随机变量X 与Y 相互独立而且同分布，其中随机变量X 的分布列为P^X =1 j p 0, P 「X =0 =1 - p 0 ,再设随机变量”1 X +Y 为偶数 Z =」0 X +Y 为奇数■-⑴ 写出随机变量 X, Z 的联合分布律以及 X 与Z 各自的边缘分布律；⑵ 问p 取什么值时，随机变量X 与Z 相互独立？解：⑴X 与Z 的联合分布列以及X 与Z 各自的边际分布列为其中 P 〈X =0, Z =0丄 P 「X =0,Y =1丄 P 〈X =0：PY =1、p 1 - p ； P 〈X =0, Z =1 丄 P 「X =0,Y =0 .；S x "pY =0 .；h ［1 - p 2；P ：X =1, Z =0 ； = P ：X =1, Y =0 ； = P ：X =1P "Y =0^= p 1 — p ； P^X =1, Z =1 ； = P 「X =1, Y =1 ；S x=1 ；=P 2 ；900-100 9.15 J00 1.2275100X k -100 9.15•：：： 一k -J100x 1.2275930-100 9.15 -<1 00 1.2275<1.35388)第6页共9页⑵如果X 与Z 相互独立，则有P ：X =1, Z =0、p 1 一 p 二 P 「X =＜：piz =0、p 2p 1 一 p ， 1 1解方程 p1-P 二p ・2p1 — p ，得p =—.并且当p =-时，有221Pi • X1 1 1 044211 1 1 4 4 21 1 p j22可以验证，此时X 与Z 是相互独立的.十.（本题满分9分）两台相同型号的自动记录仪，每台无故障工作的时间分别为X 和Y ，假设X 与Y 相互独立，都服从参数为冬-5的指数分布.X 的密度函数为由题意，知 ^X Y ，设T 的密度函数为f T t ，则-be-bef T t = f X x f Y t - x dx 二 5e _5x f Y t - x dx-:作变换 u=t-x ，贝U du =-dx ，当x =0时，u =t ；当x - 时，u —；匚.代入上式，得f （x5e _5xx 0 xE0现首先开动其中一台，当其损坏停用时另一台自动开动，直至第二台记录仪损坏为止.令: T :从开始到第二台记录仪损坏时记录仪的总共工作时间，试求随机变量T 的概率密度函数.解:5e*xX 的密度函数为fx （x ）=」x 0 x 乞0丫的密度函数为fY （y ）= “ 5e^ytf r (t )= - \5e~^~ F Y (U du =5e~ Je 5u fY(u dut-20当仁0时，由f Y y =0，知f r t =o ； 当t 0时，tf T t =5e® e 5u 5e“u du =25te^综上所述，可知随机变量T 的密度函数为（本题满分9分） 设总体X 的密度函数为1 _ixf x;e 二，-：：:x26其中二0是未知参数. X 1，…，X n 是从中抽取的一个样本•求解：r 的似然函数为1_（日）=口 f （X i ；日 Ay^exh —4 送 X i ；＞， y（2日）I 日-‘ 则有‘ / 1 nIn L （e ）=—nln （2&）— —为 x i ，对。

2008－2009学年 第1学期 概率论与数理统计(46学时) A一、单项选择题（本大题共5小题，每小题3分，共15分）。

1、A B 、为两个随机事件，若()0P AB =，则（A ）A B 、一定是互不相容的； （B ）AB 一定是不可能事件； （C ）AB 不一定是不可能事件； （D ）()0P A =或()0P B =.2、二维离散型随机变量(,)X Y 的分布律为(,)F x y 为(,)X Y 的联合分布函数，则(1.5,1.5)F 等于（A ）1/6； （B ）1/2； （C ）1/3； （D ）1/4.3、X Y 、是两个随机变量，下列结果正确的是 （A ）若()E XY EXEY =,则X Y 、独立； （B ）若X Y 、不独立,则X Y 、一定相关；（C ）若X Y 、相关,则X Y 、一定不独立； （D ）若()D X Y DX DY -=+,则X Y 、独立.YX 0 1 2 1 1/61/3 0 21/41/61/124、总体2212~(,),,,,,n X N X X X μσμσ均未知，为来自X 的一个简单样本，X 为样本均值，2S 为样本方差。

若μ的置信度为0.98的置信区间为(X c X c -+，则常数c 为（A ）0.01(1)t n -； （B ）0.01()t n ；（C ）0.02(1)t n -； （D ）0.02()t n .5、随机变量12,,,n X X X 独立且都服从(2,4)N 分布，则__11ni i X X n ==∑服从（A ）(0,1)N ； （B ）(2,4)N n ；（C ）(2,4)N n n ； （D ）4(2,)N n .二、填空题（本大题共5小题，每小题3分，共15分）。

6、已知A B 、为两个随机事件，若()0.6,()0.1,P A P AB ==则(|)P A AB =1.7、已知随机变量X 服从区间(0,2)上的均匀分布，则(2)E X =（ ）.8、已知连续型随机变量X 的概率密度函数为2,01()0,x x f x <<⎧=⎨⎩其它，则概率(||12)P X <=（ ）.9、随机变量12(3,),(3,)33Xb Yb ,且,X Y 独立，则()D X Y -=（ ）.10、已知随机变量,1,2,3i X i =相互独立，且都服从(0,9)N 分布，若随机变量2222123()(3)Y a X X X χ=++，则常数a =（ ）.三、解答题（本大题共6小题，每小题10分，共60分）。

北京林业大学20 11--2012学年第一学期考试试卷课程名称： 数理统计B （A 卷） 课程所在学院： 理学院 考试班级 学号 姓名 成绩 试卷说明：1. 本次考试为闭卷考试。

本试卷共计 4 页，共 十 大部分，请勿漏答；2. 考试时间为 120 分钟，请掌握好答题时间；3. 答题之前，请将试卷和答题纸上的考试班级、学号、姓名填写清楚；4. 答案写在本试卷上；5. 答题完毕，请将试卷和答题纸正面向外对叠交回，不得带出考场； 考试中心提示：请你遵守考场纪律，诚信考试、公平竞争！一、填空（每题2分，共10分） 1．袋中有红球4只，黑球3只，不放回地从中任取2只，则这2只球的颜色不相同的概率等于 。

2．若事件A 、B 满足P AB P A B ()()= 且3/1)(=A P ，则P B ()= 。

3．已知()221212(,)~X Y Nr μμσσ，，，，，如果X 和Y 独立, 那么r = 。

4．已知X 的概率密度函数||1()2x X f x e -=，则3Y X =的概率密度函数()Y f y = 。

5．设总体X 服从参数为2的泊松(Poisson)分布，),,(81X X 是来自总体X 的容量为8的样本，X是样本均值，那么()2E X= 。

二、单项选择题（每题2分，共10分）1. 设连续型随机变量X 的分布函数⎪⎩⎪⎨⎧>≤≤+<=ππx x b kx x x F ,10,0,0)(，则以下正确的答案是 。

A ．1,b k π== ；B ．1/,0b k π==；C ．0,1/b k π==；D ．,1b k π==2.设2~(3,) X N σ，{34}0.4P X <<=,则{2}P X ≤= 。

A ． 0.1 ；B ．0.2 ；C ．0.3；D ．0.93.设X 的方差4DX =, Y 的方差1DY =，X 和Y 相关系数,6.0=XY ρ则32X Y -的方差(32)D X Y -= 。

概率论与数理统计期末考试填空与单项选择暂无对应题库，您可以自行用小号刷题获取题库A。

1•B.•C。

0。

7••A.P｛Y=2X—1}=1•B。

P｛Y=-2X—1｝=10。

00/3。

00•C。

P{Y=—2X+1｝=1•D.P{Y=2X+1}=1正确答案：D你错选为B3单选（3分)已知P（A）=0。

9；，则P(A—BC）=得分/总分•A。

0。

4•B.0.6•C.0。

7•D。

0。

8正确答案：C你没选择任何选项4单选(3分）设随机变量X和Y都服从正态分布，且它们不相关，则得分/总分•A。

X和Y一定独立•B.X和Y不一定独立•C.（X,Y）一定服从二维正态分布•D。

X+Y服从一维正态分布正确答案：B你没选择任何选项5单选(3分）设X1，X2，……为独立同分布随机变量序列,且Xi(i=1,2，……）均服从参数为4的指数分布。

则当n比较大时,近似服从得分/总分•A.•B。

•C。

•D.正确答案:A你没选择任何选项6填空(3分)随机变量X的概率密度为则常数T=__________？得分/总分你没有填写答案正确答案：17填空（3分）甲、乙、丙三人同时独立地向同一个目标射击一次,命中率分别为0.8、0。

6、0。

5，则目标被击中的概率为_______?(答案保留两位小数)得分/总分你没有填写答案正确答案：0。

968填空（3分）若随机事件A与B互不相容，并且P（A)= p, P（B）=q, 则_______?得分/总分你没有填写答案正确答案：q9填空(3分）一个袋子中装有3个红色球，5个白色球，甲取出了一个红球，不再放回袋子中，乙也从袋子中摸一个球，他取出红球的概率是_______？（答案保留两位小数）得分/总分你没有填写答案正确答案:0。

2910填空（3分）设随机变量X1，X2，X3相互独立，其中X1在区间[0,6］上服从均匀分布,X2服从正态分布N（0，4），X3服从参数为λ=3的泊松分布，记Y=X1-2X2+3X3，则D（Y）=_________？得分/总分你没有填写答案正确答案：46本部分由7道计算题组成，每道题均为10分。