Excel数据管理与图表分析 双因素方差分析

统计学中的几个基本概念1、同质（homogeneity）与变异（variation）严格地讲，同质是指被研究指标的影响因素完全相同。

但在医学研究中，有些影响因素往往是难以控制的（如遗传、营养等），甚至是未知的。

所以，在统计学中常把同质理解为对研究指标影响较大的、可以控制的主要因素尽可能相同。

例如研究儿童的身高时，要求性别、年龄、民族、地区等影响身高较大的、易控制的因素要相同，而不易控制的遗传、营养等影响因素可以忽略。

同质基础上的个体差异称为变异。

如同性别、同年龄、同民族、同地区的健康儿童的身高、体重不尽相同。

事实上，客观世界充满了变异，生物医学领域更是如此。

哪里有变异，哪里就需要统计学。

若所研究的同质群体中所有个体一模一样，只需观察任一个体即可，无须进行统计研究。

2、总体（population）与样本（sample）任何统计研究都必须首先确定观察单位（observed unit），亦称个体（individual）。

观察单位是统计研究中最基本的单位，可以是一个人、一个家庭、一个地区、一个样品、一个采样点等。

总体是根据研究目的确定的同质观察单位的全体，或者说，是同质的所有观察单位某种观察值（变量值）的集合。

例如欲研究山东省2002年7岁健康男孩的身高，那么，观察对象是山东省2002年的7岁健康男孩，观察单位是每个7岁健康男孩，变量是身高，变量值（观察值）是身高测量值，则山东省2002年全体7岁健康男孩的身高值构成一个总体。

它的同质基础是同地区、同年份、同性别、同为健康儿童。

总体又分为有限总体（finite population）和无限总体（infinite population）。

有限总体是指在某特定的时间与空间范围内，同质研究对象的所有观察单位的某变量值的个数为有限个，如上例；无限总体是抽象的，无时间和空间的限制，观察单位数是无限的，如研究碘盐对缺碘性甲状腺病的防治效果，该总体的同质基础是缺碘性甲状腺病患者，同用碘盐防治；该总体应包括已使用和设想使用碘盐防治的所有缺碘性甲状腺病患者的防治效果，没有时间和空间范围的限制，因而观察单位数无限，该总体为无限总体。

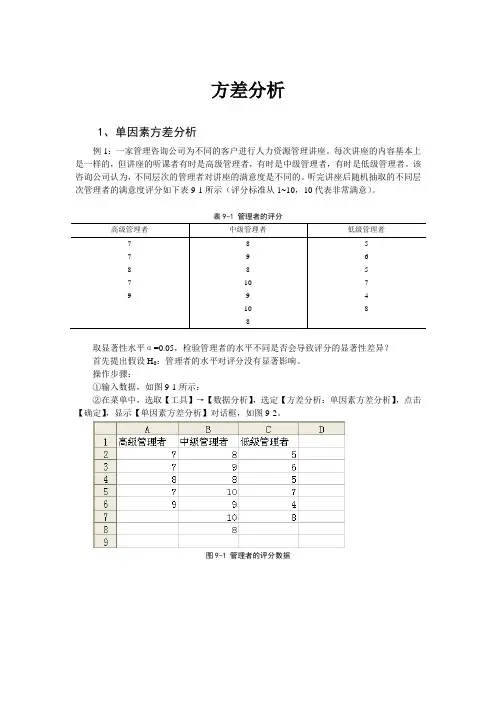
方差分析1、单因素方差分析例1：一家管理咨询公司为不同的客户进行人力资源管理讲座。

每次讲座的内容基本上是一样的，但讲座的听课者有时是高级管理者，有时是中级管理者，有时是低级管理者。

该咨询公司认为，不同层次的管理者对讲座的满意度是不同的。

听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1所示（评分标准从1~10，10代表非常满意）。

表9-1 管理者的评分高级管理者中级管理者低级管理者7 8 57 9 68 8 57 10 79 9 410 88取显著性水平α=0.05，检验管理者的水平不同是否会导致评分的显著性差异？首先提出假设H0：管理者的水平对评分没有显著影响。

操作步骤：①输入数据，如图9-1所示：②在菜单中，选取【工具】→【数据分析】，选定【方差分析：单因素方差分析】，点击【确定】，显示【单因素方差分析】对话框，如图9-2。

图9-1 管理者的评分数据图9-2 单因素方差分析对话框③在“输入区域”框输入数据矩阵（首坐标：尾坐标），可选为“A1：C8”，点选“标志位于第一行”，在“分组方式”框选定“列”，指定显著水平α＝0.05，输出选项的输出区域可为工作表的任何位置，本例选择在I4处。

④点击【确定】，则得输出结果，如下图9-3所示。

图9-3 单因素方差分析结果图9-3是一个单因素方差分析结果的报告。

第一个表是有关各样本的一些描述统计量，它可以作为方差分析的参考信息。

第二个表是方差分析结果。

其中SS 表示平方和，df 为自由度，MS 表示均方，F 为检验的统计量，P-value 为用于检验的P 值，F crit 为给定α水平下的临界值。

从方差分析表可以看到，由于68232.375573.11=>=αF F ，所以拒绝原假设，即管理者的水平对评分的影响是显著的。

在进行决策时，可以直接利用方差分析表中的P 值与显著性水平α的值进行比较，若 P ＜α，则拒绝原假设；若P ＞α，则不能拒绝原假设。

EXCEL方差分析实例在Excel中进行方差分析可以使用数据分析工具包中的Anova: Single Factor分析工具。

下面我们使用一个实例来演示如何进行方差分析。

假设有一个实验，研究不同品牌汽车轮胎的寿命是否有差异。

我们随机选择了3个品牌的轮胎，每个品牌选择了10个样本。

寿命的数据如下所示：品牌1:500,510,505,495,485,490,500,495,505,500品牌2:490,485,480,495,500,495,505,500,510,495品牌3:505,500,495,490,485,500,500,495,500,505首先，将数据输入到Excel的工作表中。

在A列中输入"品牌1", "品牌2", "品牌3"，在B列中分别输入对应品牌的寿命数据，共30个数据点。

然后，在Excel的菜单栏中选择"数据"，点击"数据分析"按钮。

如果"数据分析"按钮没有显示，可以在Excel选项中打开数据分析工具包。

在"数据分析"对话框中选择"Anova:Single Factor"，点击"确定"。

在"Anova: Single Factor"对话框中，将输入范围设置为包含我们的数据，即B1:B30。

选择"纵向位置"为第一列。

点击"确定"。

Excel将显示方差分析的结果。

在"Anova: Single Factor"结果窗口中，我们可以看到各个组的平均值、方差、观测次数等信息。

方差分析的结果也可以在工作表中显示。

在C1单元格中输入"组间平方和"，在D1单元格中输入"组内平方和"，在E1单元格中输入"总平方和"，在F1单元格中输入"自由度组间"，在G1单元格中输入"自由度组内"，在H1单元格中输入"自由度总"，在I1单元格中输入"组间均方"，在J1单元格中输入"组内均方"，在K1单元格中输入"F值"，在L1单元格中输入"P值"。

第1章Excel统计分析功能概述1.1 Excel 2003新功能1．列表功能在Microsoft Office Excel 2003 中，可以在工作表中创建列表以将相关数据分组并对其进行操作。

Excel 2003既可以对现有数据创建列表，也可从空白区域创建列表。

在指定一个范围作为列表后，可以很容易地管理和分析独立于该列表外部其他数据的数据。

此外，可以通过与Microsoft Windows SharePoint Services 集成来与其他人共享包含在列表内的信息。

默认情况下，列表中每一列都已在标题行中启用了“自动筛选”，该功能可以快速筛选或排序数据。

与Microsoft Windows SharePoint Services集成Excel列表可以通过与Microsoft Windows SharePoint Services的无缝集成来对包含在列表内的信息进行协作。

可以通过发布列表来在SharePoint网站上基于Excel列表创建SharePoint列表。

如果选择将列表链接到SharePoint网站，则在同步该列表时，在Excel中对列表所做的任何更改都将反映在SharePoint网站上。

还可以使用Excel编辑现有的Microsoft Windows SharePoint Services 列表。

2．改进的统计函数在Excel 2003中，下列统计函数（包括四舍五入结果）的外观以及精确性都已增强：BINOMDIST、CHIINV、CONFIDENCE、CRITBINOM、DSTDEV、DSTDEVP、DV AR、DV ARP、FINV、FORECAST、GAMMAINV、GROWTH、HYPGEOMDIST、INTERCEPT、LINEST、LOGEST、LOGINV、LOGNORMDIST、NEGBINOMDIST、NORMDIST、NORMINV、NORMSDIST、NORMSINV、PEARSON、POISSON、RAND、RSQ、SLOPE、STDEV、STDEV A、STDEVP、STDEVPA、STEYX、TINV、TREND、V AR、V ARA、V ARP、V ARPA、ZTEST上述函数的计算结果可能与Excel以前版本中的结果有所不同。

双因素方差分析一、无交互作用下的方差分析设A 与B 是可能对试验结果有影响的两个因素，相互独立，无交互作用。

设在双因素各种水平的组合下进行试验或抽样，得数据结构如下表：表中每行的均值.i X （i=1,2,…r ）是在因素A 的各个水平上试验结果的平均数；每列的均值jX .(j=1,2,…,n)是在因素B 的各种水平上试验的平均数。

以上数据的离差平方和分解形式为：SST=SSA+SSB+SSE （6.13） 上式中：∑∑-=2)(X X SST ij(6.14)∑-=∑∑-=2.2.)()(X X n X XSSA i i (6.15)∑-=∑∑-=2.2)()(X Xr X XSSB j j（6.16）∑+-∑-=2..)(X X X X SSE ji ij(6.17)SSA 表示的是因素A 的组间方差总和，SSB 是因素B 的组间方差总和，都是各因素在不同水平下各自均值差异引起的；SSE 仍是组内方差部分，由随机误差产生。

各个方差的自由度是：SST 的自由度为nr-1，SSA 的自由度为r-1，SSB 的自由度为n-1，SSE 的自由度为nr-r-n-1=（r-1）(n-1)。

各个方差对应的均方差是：对因素A 而言： 1-=r SSA MSA （6.18） 对因素B 而言： 1-=n SSB MSB （6.19）对随机误差项而言：1---=n r nr SSEMSE （6.20）我们得到检验因素A 与B 影响是否显著的统计量分别是：)]1)(1(,1[~---=n r r F MSE MSA F A （6.21）)]1)(1(,1[~---=n r n F MSE MSBF B （6.22）【例6-2】某企业有三台不同型号的设备，生产同一产品，现有五名工人轮流在此三台设备上操作，记录下他们的日产量如下表。

试根据方差分析说明这三台设备之间和五名工人之间对日产量的影响是否显著？（α=0.05）。

Excel中的数据分析工具假设检验和方差分析Excel中的数据分析工具——假设检验和方差分析数据分析在现代社会中扮演着重要的角色，而Excel作为一款常用的办公软件，在数据分析方面具有强大的功能和工具。

本文将重点介绍Excel中的数据分析工具——假设检验和方差分析。

一、假设检验假设检验是一种统计方法，用于确定一个样本是否代表着整个总体的特征。

它通过对样本数据进行分析，来推断和判断总体的参数。

Excel提供了多种假设检验的方法，常用的有t检验和z检验。

1. t检验t检验用于对一个总体或两个总体的均值是否存在显著差异进行判断。

在Excel中，可以通过T.TEST()函数进行t检验的计算。

该函数的语法为：T.TEST(array1, array2, tails, type)。

其中，array1和array2分别表示两个样本的数据范围，tails表示尾部情况（单尾或双尾），type表示两个样本是否具有相等的方差。

2. z检验z检验用于判断一个样本均值和总体均值的显著性差异。

在Excel 中，可以通过Z.TEST()函数进行z检验的计算。

该函数的语法为：Z.TEST(array, x, sigma)。

其中，array表示样本数据范围，x表示总体均值的猜测值，sigma表示总体标准差。

二、方差分析方差分析是一种用于分析多个样本之间差异性的统计方法。

它可以用于判断一个因素是否对样本产生了显著影响。

Excel中提供了ANOVA()函数来进行方差分析的计算。

方差分析可以分为单因素方差分析和双因素方差分析两种情况。

1. 单因素方差分析单因素方差分析用于对一个因素（变量）的多个水平（组别）之间的差异进行比较。

在Excel中，可以通过使用ANOVA()函数进行单因素方差分析的计算。

该函数的语法为：ANOVA(data, group)。

其中，data表示包含多个组别数据的范围，group表示包含组别标识的范围。

2. 双因素方差分析双因素方差分析用于分析两个因素（变量）对样本数据的影响。