习题1举例说明光传播中几何光学各基本定律的现象和应用

大学物理中的几何光学光的传播与反射现象大学物理课程中，几何光学是一个重要的分支，研究光的传播和反射现象。

在这个领域内，我们可以了解到光是如何在空间中传播的以及光线与物体的相互作用。

本文将介绍几何光学的基本原理和应用，探讨光的传播和反射现象。

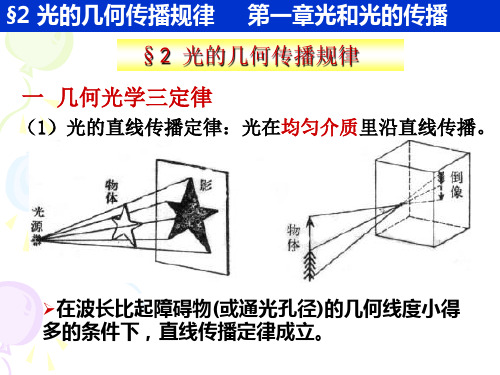
一、光的传播光是一种电磁波，由电场和磁场交替变化而形成。

当光线穿过介质边界时，会发生折射现象。

根据斯涅尔定律，入射角和折射角之间的正弦值成正比。

这可以用下面的公式表示：\[ \frac{n_1}{n_2}=\frac{\sin{\theta_1}}{\sin{\theta_2}} \]其中，\( n_1 \) 和 \( n_2 \) 是两个介质的折射率，\( \theta_1 \) 是入射角，\( \theta_2 \) 是折射角。

除了折射现象，光线在传播过程中还会发生衍射和干涉现象。

衍射是指当光线通过一个小孔或者绕过一个障碍物时，会产生弯曲和扩散的效应。

干涉是指两束或多束光线相遇时产生的加强或减弱的现象。

这些现象都可以通过几何光学的原理解释。

二、反射现象光线遇到物体表面时，会发生反射现象。

光的反射符合反射定律，即入射角和反射角相等，且在同一平面内。

这可以用下面的公式表示：\[ \theta_i = \theta_r \]其中，\( \theta_i \) 是入射角，\( \theta_r \) 是反射角。

反射现象在我们日常生活中随处可见。

例如，镜子的表面就是一个光线的良好反射体。

借助反射现象，我们可以制造各种光学仪器和设备，如反光镜、望远镜等。

三、应用实例几何光学的原理和方法在许多实际应用中都发挥着重要作用。

以下是几个常见的应用实例：1. 透镜的成像原理透镜是一种光学器件，利用折射和反射来改变光线的传播方向。

根据透镜的形状和折射率，可以产生不同的成像效果。

凸透镜和凹透镜可以分别形成实像和虚像，这些成像原理和方法在光学显微镜、眼镜等领域得到广泛应用。

2. 光纤通信光纤通信是一种基于光的传输技术，利用光纤内部的全反射原理实现信息传输。

1.1_几何光学的基本定律第一节几何光学的基本定律几何光学是以光线的概念为基础，采用几何的方法研究光在介质中的传播规律和光学系统的成像特性按几何光学的观点，光经过介质的传播问题可归结为四个基本定律：光的直线传播定律、光的独立传播定律、光的反射定律和折射定律ref: 几何光学的发展先秦时代《墨经》330-260BC 欧几里德《反射光学》965-1038AD 阿勒·哈增《光学全书》十七世纪开普勒、斯涅尔、笛卡儿、费马折射定律的确立，使几何光学理论得到很快的发展。

1.光波、光线、光束light waves、raysand beams·光波光波是一种电磁波，是一定频率范围内的电磁波，波长比一般的无线电波的短可见光：400nm-760nm紫外光：5-400nm红外光：780nm-40μm近红外：780nm-3μm中红外：3μm－6μm远红外：6μm－40μm·光源light sources光源：任何能辐射光能的的物体点光源：无任何尺寸，在空间只有几何位置的光源实际中是当光源的大小与其辐射光能的作用距离相比可忽略不计，则视为点光源光学介质optical mediums光学介质：光从一个地方传至另一个地方的空间。

空气、水、玻璃?各向同性介质:光学介质的光学性质不随方向而改变各向异性介质：单晶体（双折射现象）均匀介质：光学介质的不同部分具有相同的光学性质均匀各向同性介质·波前wave front波前：某一瞬间波动所到达的位置构成的曲面波面：传播过程中振动相位相同的各点所连结成的曲面在任何的时刻都只能有一个确定的波前；波面的数目则是任意多的?球面波：波面为球面的波，点光源平面波：无穷远光源柱面波：线光源光线：传输光能的有方向的几何线在各向同性介质中，光沿着波面的法线方向传输，所以波面的法线就是光线光束光束：具有一定关系的光线的集合同心光束：同一个发光点发出或相交于同一点平行光束：发光点位于无穷远，平面光波像散光束：既不相交于一点，又不平行，但有一定关系的光线的集合，与非球面的高次曲面光波相对应同心光束平行光束ref: 像散光束·光线既不平行，又不相交，波面为曲面。

几何光学的三个基本定律一、引言几何光学是研究光在直线传播过程中的行为的光学分支。

其理论基础是几何光学三个基本定律，这些定律揭示了光在透明介质中的传播规律。

本文将详细介绍这三个基本定律，并探讨它们对光学现象的解释和应用。

二、第一定律：直线传播定律直线传播定律是几何光学中最基本的定律，它表明光线在均匀介质中直线传播。

光的传播路径可以用直线表示，且沿一定方向传播。

这意味着光线在不同介质之间传播时会发生折射，但在同一介质内则是直线传播。

三、第二定律：反射定律反射定律是几何光学的第二个基本定律，它描述了光线在界面上的反射行为。

根据反射定律，入射光线与法线的夹角等于反射光线与法线的夹角，而且入射光线、反射光线和法线在同一平面内。

这个定律解释了为什么我们能够看到镜子中的自己，以及为什么我们可以利用反射现象制作反光镜和平面镜。

四、第三定律：折射定律折射定律是几何光学中的第三个基本定律，它描述了光线在不同介质中的折射行为。

根据折射定律，入射光线、折射光线和法线在同一平面内，而且入射角和折射角之间的正弦比等于两个介质的折射率之比。

这个定律解释了为什么我们能看到水中的鱼和游泳池底部的景物，以及为什么光能够通过透镜形成清晰的图像。

1. 折射率的定义折射率是指光在某一介质中的速度与真空中速度之比。

高折射率的介质会使光线偏折得更多，而低折射率的介质则会使光线偏折得较少。

2. 斯涅尔定律斯涅尔定律是折射定律的一种特殊形式，适用于光线从一介质射入另一介质的情况下。

根据斯涅尔定律，入射角、折射角和两个介质的折射率之比满足一个简单的数学关系式。

五、光学现象的应用几何光学的三个基本定律在光学现象的解释和应用中起着重要的作用。

以下是几个常见光学现象及其与定律的关系：1. 倒影倒影是一种反射现象，发生在平面镜或其他光滑表面上。

根据反射定律，镜子中的物体通过镜面反射形成倒立的像。

这个现象在我们日常生活中的镜子和反光材料中得到了广泛应用。

2. 折射折射是光线在不同介质之间传播时发生的偏折现象。

微型专题 几何光学的原理及应用[学科素养与目标要求]物理观念：1.知道光的直线传播规律.2.知道光的反射定律、折射定律和全反射的规律.3.知道光的可逆原理.科学思维：1.会根据几何光学的基本原理画出光路图.2.会利用几何关系找出相应的角、边关系.一、几何光学的基本原理及应用几何光学就是以光线为工具，研究光的传播规律.解几何光学的题目，首先根据几何光学的基本原理画出光路图，然后利用几何关系找出相应的角、边关系. 几何光学研究的是光线传播的规律，主要包括五条基本规律. 1.光的直线传播规律：光在同一种均匀介质中沿直线传播 2.光的反射定律(1)反射光线与入射光线、法线在同一平面内，反射光线、入射光线分居在法线两侧. (2)反射角等于入射角. 3.光的折射定律折射光线与入射光线、法线在同一平面内，折射光线、入射光线分居在法线两侧；入射角的正弦与折射角的正弦成正比.公式：n 12＝sin θ1sin θ2.其中θ1为入射光线与法线的夹角，θ2为折射光线与法线的夹角. 4.光的全反射规律 发生全反射的条件是： (1)由光密介质射向光疏介质； (2)入射角θ≥临界角C ，其中sin C ＝1n .5.光的可逆原理在反射、折射和直线传播中，光路都是可逆的.例1 如图1所示，一棱镜的截面为直角三角形ABC ，∠A ＝30°，斜边AB ＝a .棱镜材料的折射率为 2.在此截面所在的平面内，一条光线以45°的入射角从AC 边的中点M 射入棱镜.画出光路图，并求光线从棱镜射出的点的位置(不考虑光线沿原路返回的情况).图1答案 见解析解析 设入射角为θ1，折射角为θ2，由折射定律得sin θ1sin θ2＝n ①由已知条件及①式得θ2＝30°②如果入射光线在法线的右侧，光路图如图甲所示.设出射点为F ，由θ2＝30°得光线垂直于AB 射出，且由几何关系可得AF ＝38a ③甲即出射点在AB 边上离A 点38a 的位置.如果入射光线在法线的左侧，光路图如图乙所示.乙设折射光线与AB 边的交点为D .由几何关系可知，在D 点的入射角θ＝60°④ 设全反射的临界角为C ，则sin C ＝1n ⑤由⑤式和已知条件得C ＝45°⑥ 因此，光在D 点发生全反射.设此光线的出射点为E ，由几何关系得 ∠DEB ＝90°，BD ＝a －2AF ⑦ BE ＝BD sin 30°⑧ 联立③⑦⑧式得BE ＝18a即出射点在BC 边上离B 点18a 的位置.求解几何光学的题目首先要画出光路图，然后利用相应的公式结合几何知识分析边、角关系.而光从光密介质射到光疏介质时，首先要判断是否发生了全反射. 二、全反射和临界角的综合问题 分析光的全反射、临界角问题的一般思路(1)确定光是由光疏介质进入光密介质，还是由光密介质进入光疏介质. (2)若光是由光密介质进入光疏介质，根据公式sin C ＝1n确定临界角.(3)画出恰好发生全反射的光路图，利用几何知识分析边、角关系，找出临界角.(4)以恰好发生全反射的光线为比较对象来判断其他光线是否发生全反射，从而画出其他光线的光路图.例2 (2018·全国卷Ⅱ)如图2，△ABC 是一直角三棱镜的横截面，∠A ＝90°，∠B ＝60°.一细光束从BC 边的D 点折射后，射到AC 边的E 点，发生全反射后经AB 边的F 点射出.EG 垂直于AC 交BC 于G ，D 恰好是CG 的中点.不计多次反射.图2(1)求出射光相对于D 点的入射光的偏角；(2)为实现上述光路，棱镜折射率的取值应在什么范围？ 答案 (1)60° (2)233≤n <2解析 (1)光线在BC 面上发生折射，由折射定律有sin i 1＝n sin r 1①式中，n 为棱镜的折射率，i 1和r 1分别是该光线在BC 面上的入射角和折射角.光线在AC 面上发生全反射，由反射定律有i 2＝r 2②式中i 2和r 2分别是该光线在AC 面上的入射角和反射角.光线在AB 面上发生折射，由折射定律有n sin i 3＝sin r 3③式中i 3和r 3分别是该光线在AB 面上的入射角和折射角. 由几何关系得i 2＝r 2＝60°，r 1＝i 3＝30°④F 点的出射光相对于D 点的入射光的偏角为δ＝(r 1－i 1)＋(180°－i 2－r 2)＋(r 3－i 3)⑤由①②③④⑤式得δ＝60°⑥(2)光线在AC 面上发生全反射，光线在AB 面上不发生全发射，有n sin i 2≥n sin C >n sin i 3⑦ 式中C 是全反射临界角，满足n sin C ＝1⑧由④⑦⑧式知，棱镜的折射率n 的取值范围应为233≤n <2.⑨[学科素养] 光在穿过有形介质时，往往要发生多次折射和反射，所以常把全反射现象和一般的折射问题综合起来考查.在解题时，要边计算、边作图、边考虑几何关系，三个环节同步进行，才能得到合理的情况.例2体现了“物理观念”和“科学思维”的学科素养.针对训练 如图3所示，ABC 为一透明材料制成的柱形光学元件的横截面，该种材料的折射率n ＝3，AC 是一半径为R 的14圆弧，O 为圆弧的圆心，ABCO 构成正方形，在O 处有一点光源.从点光源射到圆弧AC 的光线进入透明材料后首次射向AB 或BC 界面时，有一部分不能从AB 或BC 界面直接射出.下面的问题只研究进入透明材料后首次射向AB 或BC 界面的光线，已知AB 面上的P 点到A 点的距离为33R .求：图3(1)从P 点射出的光线的折射角；(2)AB 和BC 横截面上没有光线射出部分的总长度. 答案 (1)60° (2)(2－2)R解析 (1)设射向P 点的光线入射角为θ1，折射角为θ2，如图所示， tan θ1＝33R R ＝33，θ1＝30°，故sin θ1＝12根据折射定律有n ＝sin θ2sin θ1＝ 3解得θ2＝60°(2)设临界角为C ，射向M 点的光线恰好发生全反射，则有sin C ＝1n ＝33，由数学知识可得tan C ＝22AB 横截面没有光线射出部分的长度 BM ＝(1－tan C )R ＝(1－22)R 同理可知BC 横截面没有光线射出部分的长度为(1－22)R 两横截面上没有光线射出部分的总长度 l ＝2(1－22)R ＝(2－2)R .1.(几何光学的基本原理及应用)(2018·四川资阳二诊)如图4所示，一个三棱镜的截面为等腰直角△ABC ，腰长为a ，∠A ＝90°.一束细光线沿此截面所在平面且平行于BC 边的方向从真空射到AB 边上的中点M ，光在M 点发生折射后射到AC 边上，并刚好在AC 边上发生全反射.已知真空中的光速为c ，试求：图4(1)该棱镜材料的折射率n ； (2)光从AB 边到AC 边的传播时间t . 答案 见解析解析 (1)设光从AB 边射入时入射角为i ，折射角为α，射到AC 边上N 点时入射角为β，作出光路图如图所示.根据折射定律：n ＝sin i sin α光在AC 边上恰好发生全反射： sin β＝1n又由几何关系：α＋β＝90°，i ＝45° 联立解得：n ＝62(2)由图中几何关系可得M 、N 间距x ＝a 2sin α光在棱镜内传播的速度v ＝c n ，t ＝xv联立解得：t ＝32a4c2.(全反射和临界角的综合问题)用某种透明材料制成的一块柱体形棱镜的水平截面图如图5所示，左侧ABOD 为长方形，右侧DOF 为以O 为圆心的14圆.光线从真空以入射角θ1＝60°射到棱镜AB 面，经折射后，光线到达BF 面上的O 点并恰好不从BF 面射出.图5(1)画出光路图；(2)求该棱镜的折射率n 和光线在棱镜中传播的速度大小v (光在真空中的传播速度c ＝3×108 m/s). 答案 (1)见解析图 (2)72 677×108 m/s 解析 (1)光路图如图所示(2)设光线在AB 面的折射角为θ2，折射光线与OD 的夹角为C ，则n ＝sin θ1sin θ2由题意可知，光线在BF 面恰好发生全反射sin C ＝1n由图可知，θ2＋C ＝90° 联立以上各式解得n ＝72，又n ＝cv ，可解得v＝677×108 m/s.3.(全反射和临界角的综合问题)一个半圆柱形玻璃砖，其横截面是半径为R的半圆，AB为半圆的直径，O为圆心，如图6所示，玻璃的折射率为n＝ 2.图6(1)一束平行光垂直射向玻璃砖的下表面，若光线到达上表面后，都能从该表面射出，则入射光束在AB上的最大宽度为多少？(2)一细束光线在O点左侧与O相距32R处垂直于AB从下方入射，求此光线从玻璃砖射出点的位置.答案见解析解析(1)在O点左侧，设从E点射入的光线进入玻璃砖后在上表面的入射角恰好等于发生全反射的临界角θ，则OE区域的入射光线经上表面折射后都能从玻璃砖射出，如图甲.甲由全反射条件有sin θ＝1n①由几何关系有OE＝R sin θ②由对称性可知，若光线都能从上表面射出，光束的宽度最大为l＝2OE③联立①②③式，代入已知数据得l＝2R④(2)设光线在距O点32R的C点射入后，在上表面的入射角为α，由几何关系及①式和已知条件得α＝60°>θ⑤光线在玻璃砖内会发生三次全反射，最后由G点射出，如图乙，乙由反射定律和几何关系得OG ＝OC ＝32R ⑥ 射到G 点的光有一部分被反射，沿原路返回到达C 点射出.1.(2018·西安中学高二第二学期期中)如图1所示，△ABC 为一直角三棱镜的横截面，∠BAC ＝30°，现有两条间距为d 的平行单色光线垂直于AB 面射入三棱镜，已知棱镜对该单色光的折射率为 3.图1(1)若两条单色光线均能从AC 面射出，求两条单色光线从AC 面射出后的距离；(2)若第三条单色光线垂直于AB 面射入三棱镜，到达AC 面恰好能发生全反射，若真空中光速为c ，求这条光线在三棱镜中的传播速度. 答案 见解析解析 (1)如图所示，两条单色光线在AC 面的折射点分别为D 、E ，由图中几何关系可知，入射角i ＝30°则根据光的折射定律有sin r sin i ＝n得r ＝60°在直角三角形DEF 中∠EDF ＝30° 所以EF ＝12DE ＝12·d cos 30°＝33d .(2)由题意结合光路图知入射的临界角为30°，n 2＝1sin 30°＝2，则光在三棱镜中的传播速度v ＝c2.2.(2018·唐山一中高二第二学期期中)如图2所示为安全防盗门上的观察孔(俗称“猫眼”)，直径为d，为了扩大向外观察的范围，在孔中完全嵌入折射率为n＝3的玻璃，玻璃由圆柱体和顶角为60°的球冠组成，猫眼的平面部分正好和安全门内表面平齐，球冠的边缘恰好和防盗门外表面平齐.若要让房间里的人能看到门外全部的景象，门的厚度不能超过多少？图2答案3 3d解析若要让房间的人能看到门外全部的景象，则沿平行门方向射向C处的光线能够折射经过A点即可.光路如图所示：根据光的折射定律有sin 60°sin γ＝n可得γ＝30°由几何关系知∠CAB＝30°则门的厚度最大为BC＝AB tan 30°＝33d.3.(2018·青岛一中高二第二学期第一次模拟考试)如图3所示是一个半球形透明物体的侧视图，现在有一细束单色光沿半径OA方向入射，保持入射方向不变，不考虑光线在透明物体内部的反射.图3(1)将细光束平移到距O点33R处的C点，此时透明物体左侧恰好不再有光线射出，求透明物体对该单色光的折射率；(2)若细光束平移到距O点0.5R处，求出射光线与OA轴线的交点与O点的距离. 答案(1)3(2)3R解析 (1)如图甲所示，甲光束由C 处水平射入，在B 处恰好发生全反射，∠OBC 为临界角，由几何关系有sin ∠OBC ＝33R R ＝33，则折射率n ＝1sin ∠OBC ＝ 3.(2)如图乙所示，乙光束由D 点水平射入，在E 点发生折射，入射角为∠OED ＝α，折射角为∠NEF ＝β，折射率n ＝sin βsin α＝3，sin α＝12R R ＝12 联立解得：sin β＝32，β＝60° 由几何关系可知：∠FOE ＝α＝30°，∠OFE ＝β－α＝30°＝α，则出射光线与OA 轴线的交点F 与O 点的距离为：OF ＝2R cos 30°＝3R .4.(2018·四川宜宾一诊)如图4所示，横截面为直角三角形的玻璃砖ABC ，AC 边长为L ，∠B ＝30°.两条同种色光的光线P 、Q ，从AC 边中点射入玻璃砖，其中光线P 垂直AC 边，光线Q 与AC 边夹角为45°.发现光线Q 第一次到达BC 边后垂直BC 边射出，已知真空中的光速为c .求：图4(1)玻璃砖的折射率.(2)光线P 由进入玻璃砖到第一次从BC 边射出经过的时间.答案 (1)2 (2)56L 6c解析 (1)作出光路图如图所示：光线Q 在AC 边的入射角i ＝45°由几何关系可知在AC 边的折射角r ＝30°由折射定律得n ＝sin i sin r＝ 2 (2)光线P 在玻璃砖中传播时s 1＝L 2tan 30°＝32L s 2＝L 2cos 30°＝33L P 在玻璃砖内传播的速度v ＝c n，则所要求的时间为t ＝s 1＋s 2v 由以上各式可得t ＝56L 6c. 5.如图5所示，圆形的光学仪器(斜线阴影)内有一个半径为2R 的圆形空腔，空腔左面侧壁上有一台激光器，可以沿空腔的直径方向发出在真空中速度为c 的激光束.空腔中放置了一个比空腔略小(半径可视为2R )的折射率为2的透明圆柱状光学材料，光学材料的圆心在空腔的圆心O 点，并且材料中被挖掉了一块半径为R 的截面为半圆形的柱体(圆心和O 点重合)，挖掉的部分为真空.(反射与折射在同一界面时只考虑折射)图5(1)求激光从发出到照射到空腔壁的时间.(2)激光器始终开启，若光学材料围绕空腔圆心O 点顺时针转动90°，空腔壁上能被激光照射到的圆弧长度为多少？(只考虑反射光线照射的圆弧长度)答案 (1)7R c (2)2πR 3解析 (1)光在半圆真空中的传播时间为t 1＝R c光学材料中光速为v ＝c n ，传播距离为3R 传播时间为：t 2＝3R v ＝6R c总时间t ＝t 1＋t 2＝7R c(2)在O 处，光从光密介质射入光疏介质，设发生全反射的临界角为C ，则sin C ＝1n，解得C ＝30°，所以照射的弧长范围为l ＝2πR 3. 6.如图6所示，由两种不同透明介质制成的直角三棱镜甲和乙，并排放在一起刚好构成一截面为正三角形的棱镜，甲的折射率为n 1＝1.5，一细光束由AB 边的中点O 斜射入棱镜甲，已知入射光线在AB 边的入射角的正弦值为sin i ＝0.75，经折射后该光束刚好在棱镜乙的AC 边发生全反射，最后从BC 边射出，已知真空中的光速为c ＝3×108 m/s ，AB 边的长度为l ＝6 cm ，求该细光束在棱镜中的传播时间.图6答案 3.75×10－10 s解析 由题意可知该细光束在棱镜甲中的传播速度为：v 1＝c n 1＝2×108 m/s 设该细光束在AB 边的折射角为θ，由折射定律可得：n 1＝sin i sin θ，得到：θ＝30°由几何关系可知，细光束在棱镜甲中的折射光线与AB 边的夹角为90°－30°＝60°，故折射光线与底边BC 平行，光线进入棱镜乙时传播方向不变.因光束刚好在AC 边发生全反射，由几何知识得到，光线在AC 边的入射角为90°－60°＝30°，即发生全反射的临界角为：C ＝30°设棱镜乙的折射率为n 2，则有sin C ＝1n 2，得到：n 2＝2，则该细光束在棱镜乙中的传播速度为v 2＝c n 2＝1.5×108 m/s 由几何关系可知：OE ＝l 4＝1.5 cm ，EF ＝l 4＝1.5 cm ，FD ＝l 2＝3 cm 则该光束在棱镜中的传播时间为：t ＝OE v 1＋EF ＋FD v 2＝3.75×10－10 s. 7.(2018·沈阳东北育才学校高二下学期期中)如图7所示，有一透明玻璃砖的截面，其上面的部分是半径为R 的半圆，下面是边长为2R 的正方形，在玻璃砖的两侧面距离R 处，分别放置和侧面平行的足够大的光屏，已知玻璃砖的折射率n ＝53，一束光线按图示方向从左侧光屏的P 点射出，过M 点射入玻璃砖，恰好经过半圆部分的圆心O ，且∠MOA ＝45°，光在真空中的传播速度为c .求：图7(1)光在玻璃砖中发生全反射的临界角；(2)光从P 点发出到第一次传播到右侧光屏上所用的时间.答案 (1)37° (2)(322＋4)R 3c解析 (1)设光在玻璃砖中发生全反射的临界角为C ，则：n ＝1sin C ，解得：sin C ＝35，C ＝37° (2)由于光射到玻璃砖的平面上时的入射角均为i ＝45°>C ＝37°，则射到玻璃砖面上的光线发生全反射，其光路图如图所示.由几何知识可得，光在玻璃砖和光屏之间传播的距离x 1＝2(22－1)R传播的时间t 1＝x 1c ＝(42－2)R c光在玻璃砖内传播的距离：x 2＝(42＋2)R光在玻璃砖内传播的速度为v ＝c n ＝35c 光在玻璃砖内传播的时间t 2＝x 2v ＝(202＋10)R 3c光从P 点发出到第一次传播到右侧光屏上所用时间：t ＝t 1＋t 2＝(322＋4)R 3c .。

光的传播规律(几何光学)一、光的直线传播1．光在的介质中沿直线传播，各种频率的光在真空中传播速度：C＝ m/s；说明：①直线传播的前提条件是在介质。

否则，可能发生偏折。

如从空气进入水中（介质）；“海市蜃楼”现象（介质）。

②同一种频率的光在不同介质中的传播速度是不同的。

不同频率的光在同一种介质中传播速度一般也不同（与机械波不同）。

在同一种介质中，频率越低的光其传播速度越。

③当障碍物或孔的尺寸和光的波长可以相比或者比波长小时，发生明显的现象，光线可以偏离原来的传播方向。

2、日食和月食：若图中的P是月球，则地球上的某区域处在区域内将看到日全食；处在区域内将看到日偏食；处在区域内将看到日环食。

将看到月全食；处在区域内将看到月偏食；由于日、月、地的大小及相对位置关系决定看月球不可能运动到区域D内，所以不存在月环食的自然光现象。

二、平面镜的作用和成像特点（1）作用：只改变光束的传播方向，不改变光束的聚散性质．（2）成像特点：的像，物和像关于镜面．（3）像与物方位关系:上下不颠倒，左右要交换Array【例1】某物体左右两侧各有一竖直放置的平面镜，两平面镜相互平行，物体距离左镜4m，右镜8m，如图所示，物体在左镜所成的像中从右向左数的第三个像与物体的距离是（）A、24mB、32mC、40mD、48m三、光的反射1、反射现象：光从一种介质射到另一种介质的界面上再返回原介质的现象．2．反射定律：在同一平面内，且反射光线和入射光线分居两侧，等于．3．分类：光滑平面上的反射现象叫做反射。

发生在粗糙平面上的反射现象叫做反射。

4．光路可逆原理：所有几何光学中的光现象，光路都是可逆的．121．折射现象：光从一种介质斜．射入另一种介质，传播方向发生改变的现象． 2．折射定律： 在同一平面内，折射光线、入射光线分居 两侧， 跟 成正比．3．在折射现象中光路是可逆的．4、折射率．①定义：光从真空射入某种介质, 跟 之比,叫做介质的折射率．注意：指光从 射入 ．②公式：n= = = = ，折射率总 1． ③各种色光性质比较：红光的折射率最 ，频率最 ，在同种介质中（除真空外）v 最 ，波长最 ，从同种介质射向真空时全反射的临界角C 最 ，以相同入射角在介质间发生折射时的折射角最 。

第1章习题1. 举例说明光传播中几何光学各基本定律的现象和应用。

（略）2. 证明光线通过二表面平行的玻璃板时，出射光线与入射光线的方向平行。

（略）3. 光线由水中射向空气，求在界面处发生全反射时的临界角。

当光线由玻璃内部射向空气时，临界角又为多少？（n水=1.333，n玻璃=1.52）（略）4. 一根没有包外层的光纤折射率为1.3，一束光线以u1为入射角从光纤的一端射入，利用全反射通过光纤，求光线能够通过光纤的最大入射角u1max。

实际应用中，为了保护光纤，在光纤的外径处加一包层，设光纤的内芯折射率为1.7，外包层的折射率为1.52，问此时光纤的最大入射角u2max为多少？解：如图所示，n0sin u= n1sin i1，i1+i2=90°，恰能发生全反射时i2=arcsin(n2/n1)u=(1)没有外包层，即n2=n0=1，u1max=43.6°(2)有外包层，u2max=35.4°5. 在上一习题中，若光纤的长度为2m，直径为20μm，设光纤平直，问以最大入射角入射的光线从光纤的另一端射出时，经历了多少次反射？解：以有外包层时的情况计算，u2max=35.4°，i1=19.9°，l1=27.6μm 2m / (2*27.6μm) = 36231，经历了36231次反射6. 一个18mm高的物体位于折射球面前180mm处，球面半径r=30mm，n=1，n’=1.52，求像的位置、大小、正倒及虚实状况。

解：如图，可以按近轴光路计算，y=18mm，l=-180mm，r=30mm，n=1，n’=1.52根据折射球面的物像关系公式：n n n n l l r''--='，l ’=129.1mm 8.5mm l ry y l r'-'-==-+，倒立的实像7. 简化眼把人眼的成像归结为一个曲率半径为5.7mm ，介质折射率为1.333的单球面折射，求这种简化眼的焦点位置和光焦度。