多缝夫琅禾费衍射现象仿真实现及分析

矩孔的夫琅和费衍射原理及仿真分析摘要：利用光波的标量衍射理论推导夫琅和费衍射的原理并列出矩孔衍射在观察平面上的复振幅公式，进而在MA TLAB中写出对应的程序代码，再进行模拟仿真并分析不通条件下观察屏上的衍射光强强度分布图。

关键词：夫琅和费衍射；矩孔；复振幅；光强；正文部分(一)应用在科学实验和生产实践中，经常遇到一些狭缝（如光谱仪狭缝）或者微孔的精确测量问题，这些狭缝或者微孔的尺寸大小，或者由于其他原因不能直接精确测量。

这时，可以通过对狭缝或者微孔的较宽的夫琅和费衍射图样进行测量，进而来间接确定狭缝或者微孔的尺寸。

另外，在全息信息光学技术中，图像的再现过程出理也应用了是夫琅和费衍射原理。

(二) 理论基础下图为课程设计过程的流程图光的衍射是光的波动性的主要标志之一最初的理论：一定波长的波穿过与波长可比的小孔时会发生衍射现象;通过凸透镜可以将衍射条纹更好的显示在衍射屏上,便于观察.实际理论：波的波面发生任何形式的形变（通过相位物体）或者说波面（波前）上光场的复振幅分布受到任何空间的调制，都将导致衍射现象的产生，而使通过障碍或者是孔以后的光场复振幅重新分布。

其中，导致衍射发生的“障碍物”称“作衍射屏”。

下图介绍的是光波的衍射现象示意图及衍射中的三个波前：光波的标量衍射理论：1.惠更斯-菲涅耳原理波前（波面）上的每一点都可以看作为一个发出球面子波的次级扰动中心，在后一个时刻这些子波的包络面就是此时此刻新的波前。

A 为离点光源单位距离处的波振幅；R 是波面'∑的半径。

1.1.设单色点光源s 在波面'∑上任意一点Q 产生复振幅如下：~e x p ()Q A E i k R R=1.2.衍射屏上面元d σ在P 点的复振幅可以表示如下：~e x p ()e x p ()()()A i k R i k r d E P C K d R rθσ=1.3.波面∑的子波对P 点产生的复振幅总和为：~exp()exp()()()C A ikR ikr E P k d Rrθσ=∑⎰⎰2. 菲涅耳-基尔霍夫衍射公式：由于菲涅耳理论本身的缺陷，所以从波动微分方程出发，利用场论中的Green 定理及电磁场的边值条件，其中倾斜因子为()k θ和常数C 均在下面所设。

实验报告模板夫琅禾费衍射实验目的：1.了解夫琅禾费衍射的基本原理；2.学习使用夫琅禾费衍射实验装置；3.观察并分析不同样品在夫琅禾费衍射下的衍射图案。

实验器材：1.光源2.狭缝3.凸透镜4.样品5.荧光屏6.尺子7.定位器8.纸刀实验步骤：1.将光源放置在一固定位置上，调节光源的亮度。

2.在光源与样品之间插入狭缝，通过调节狭缝的宽度控制光的入射角度。

3.将凸透镜放置在样品后方，用于调节光的焦距。

4.将样品放置在夫琅禾费衍射实验装置的特定位置上，用定位器进行固定。

5.将荧光屏放置在样品的后方，用尺子测量荧光屏与样品的距离。

6.关闭实验室的其他光源，打开荧光屏后的灯光，确保实验环境的暗度。

7.使用纸刀将荧光屏上的荧光图案记录下来。

实验数据：1.光源的亮度调节为80%；2.狭缝的宽度为0.1毫米；3.凸透镜的焦距为20毫米；4.样品为一种光栅结构材料；5.荧光屏与样品的距离为40厘米。

实验结果：观察到荧光屏上出现了一系列的亮暗条纹，这些条纹呈现出规律的分布格局。

根据夫琅禾费衍射的原理，我们可以从衍射图案中得到一些有关样品的信息。

通过测量亮暗条纹的间距、角度等数据，可以计算出样品的光栅常数、衍射角等参数。

实验讨论：1.根据实验结果，我们可以推断样品中的光栅结构的特点。

例如，光栅常数越大，亮暗条纹的间距越小。

2.实验中的光源亮度、狭缝宽度、凸透镜焦距、样品类型等因素都会对实验结果产生影响。

在进行实验时，我们需要注意控制这些因素，以保证实验的准确性和可重复性。

3.通过比较不同样品的衍射图案，我们可以分析不同材料的光学特性，进一步了解材料的结构和性质。

实验总结：本次实验通过使用夫琅禾费衍射实验装置，观察并分析了不同样品在夫琅禾费衍射下的衍射图案。

通过实验我们深入了解了夫琅禾费衍射的原理和应用，提高了实验操作的技巧和实验数据处理的能力。

实验结果对于研究材料的光学特性和结构具有重要意义，为今后的相关研究提供了基础和指导。

大学物理创新性试验实验项目：单缝﹑双缝﹑多缝衍射现象仿真实验专业班级：材料成型及控制工程0903班姓名：曹惠敏学号：090201097目录1光的衍射2衍射分类3实验现象4仿真模拟5实验总结光的衍射光在传播路径中，遇到不透明或透明的障碍物，绕过障碍物，产生偏离直线传播的现象称为光的衍射。

光的衍射现象是光的波动性的重要表现之一.波动在传播过程中,只要其波面受到某种限制,如振幅或相位的突变等,就必然伴随着衍射的发生. 然而,只有当这种限制的空间几何线度与波长大小可以比拟时,其衍射现象才能显著地表现出来.所有光学系统,特别是成像光学系统,一般都将光波限制在一个特定的空间域内,这使得光波的传播过程实际上就是一种衍射过程.因此,研究各种形状的衍射屏在不同实验条件下的衍射特性,对于深刻理解衍射的实质,研究光波在不同光学系统中的传播规律分析复杂图像的空间频谱分布以及改进光学滤波器设计等具有非常重要的意义.随着计算机技术的飞速发展, 计算机仿真已深入各种领域。

光的干涉与衍射既是光学的主要内容 , 也是人们研究与仿真的热点。

由于光波波长较短,与此相应的复杂形状衍射屏的制作较困难,并且实验过程中对光学系统及环境条件的要求较高.因而在实际的实验操作和观察上存在诸多不便. 计算机仿真以其良好的可控性、无破坏、易观察及低成本等优点,为数字化模拟现代光学实验提供了一种极好的手段. 本次实验利用MATLAB软件实现对任意形状衍射屏的夫琅禾费衍射实验的计算机仿真。

衍射分类⒈菲涅尔衍射菲涅尔衍射：入射光与衍射光不都是平行光的衍射。

惠更斯提出，媒质上波阵面上的各点，都可以看成是发射子波的波源，其后任意时刻这些子波的包迹，就是该时刻新的波阵面。

菲涅尔充实了惠更斯原理，他提出波前上每个面元都可视为子波的波源，在空间某点P的振动是所有这些子波在该点产生的相干振动的叠加，称为惠更斯－菲涅尔原理。

惠更斯－菲涅尔原理能定性地描述衍射现象中光的传播问题，成为我们解释光的各类衍射现象的理论依据。

多矩孔夫琅禾费衍射1 技术指标仿照研究单矩孔夫琅禾费衍射和多狭缝夫琅禾费衍射规律，研究多矩孔夫琅禾费衍射的规律，并利用Matlab仿真。

要求：研究一维多矩孔夫琅禾费衍射的规律和二维多矩孔夫琅禾费衍射的规律，并用Matlab来进行编程计算，绘制曲线，进行仿真处理。

2 基本原理一维多矩孔夫琅禾费衍射是多个单矩孔在一维空间发生的夫琅禾费衍射,根据光波的叠加原理,一维多矩孔夫琅禾费衍射可以看做是光波透过多个单矩孔发生夫琅禾费衍射相互叠加并相互干涉的结果。

同理，二维多矩孔夫琅禾费衍射是多个单矩孔在二维空间发生夫琅禾费衍射并相互叠加相互干涉的结果。

下面，根据单矩孔夫琅禾费衍射光强分布的推导，来逐步分析一维多矩孔夫琅禾费衍射和二维夫琅禾费衍射的光强分布规律。

2.1 矩孔夫琅禾费衍射2.1.1 矩孔夫琅禾费衍射装置矩孔夫琅禾费衍射实验装置如图1所示。

设用于夫琅禾费衍射实验的光源为单色光源，实验时，让平行光垂直入射到矩孔上，在矩孔后置一焦距为f的会聚透镜，在透镜的像方焦平面上置一接收光屏，则在光屏上能观测到衍射图样。

图1 矩孔夫琅禾费衍射实验装置图2.1.2 矩孔夫琅禾费衍射光强分布如图1，设波长为λ的单色平行光垂直入射到宽度为（轴方向），宽度为b（轴方向）的矩孔上，若矩孔上的光场强度分布均匀，则瞳孔函数为常数，即.夫琅禾费矩孔衍射的衍射场为（1）式中，分别表示轴和轴方向上的衍射角；=A;=为真空中的波数；为光波从坐标原点出发达到P（,）的光程。

在积分过程中不变的常量为。

由光强分布公式=及（1）式可知，夫琅禾费衍射的光强分布为，（2）式中，*=（）。

2.2 一维多矩孔夫琅禾费衍射由单狭缝夫琅禾费衍射光强分布公式及公式（2）可知，当公式（2）中的时（即轴方向衍射角为0），与的比值是1，此时光强与单狭缝夫琅禾费衍射光强分布公式相同，也就是说，单狭缝夫琅禾费衍射是单矩孔夫琅禾费衍射的特例，当矩孔的长或者宽是时，二者等价。

夫琅禾费衍射和菲涅尔衍射班级：物理1903 姓名：王高文 学号：41721176 同组人员：修为轩实验目的：测量单缝衍射的光强分布，验证光强分布理论；观察几类夫琅禾费衍射现象，加深对光的衍射现象和理论的理解。

实验原理：A 单缝衍射光强分布 202sin uI I u ，其中sin a u；a 为单缝宽度， 为光波波长，为衍射角。

当 =0时，u=0，此时光强为最大，这是中央零级亮条纹，称为主级强。

当sin ka时，u k ，这时 I =0，出现暗条纹。

实际上 很小，可以认为sin ，即暗条纹在ka的位置出现。

其他的亮条纹所在位置：sin 1.43, 2.46 3.47a a a，，，，次级强相对于主级强的强度分别为0.047,0.017,0.008...I I B 矩形孔衍射光强分布 22022sin sin I ,I，其中sin sin a b a b；，a 和b 为矩形孔边长， 为光波波长，a 和b 为衍射角。

C 圆孔衍射光强分布 2102J u I I u，式中， 1J u 为一阶贝塞尔函数；2sin a u;a 为圆孔半径， 为光波波长， 为衍射角。

根据贝塞尔函数的性质，当u=0时，即 =0时， 00I I I .这说明圆孔衍射的中心始终是一个亮点，并且强度取最大值，其他各级次强度极大值位置：'''123sin 0.819,sin 1.333,sin 1.84a a a，，，极小值位置123sin 0.610,sin 1.116,sin 1.619a a a，，，次级强相对主级强的相对强度分别为0.0175,0.0042,0.0016...I I D 双缝或双孔夫琅禾费衍射设狭缝宽度或圆孔半径为a，两狭缝或两圆孔的间距为d，双缝 220sin ()cos u I I u ，式中sin sin a b；， 为光波波长，为衍射角。

双孔 2120'2cos 'J I I，式中 1'J 为一阶贝塞尔函数；2sin 'a，sin b， 为光波波长， 为衍射角。

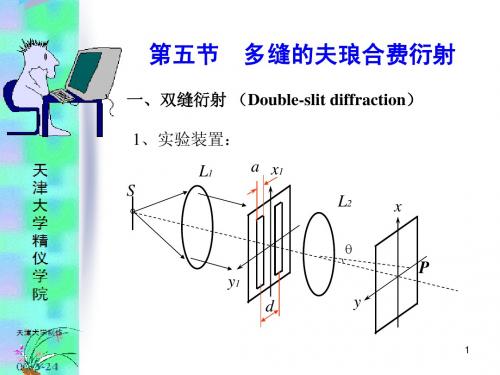
4、多缝的夫琅和费衍射，使用平行光照明，观察衍射图样随点光源位置（光源上下移动）的变化 θθθ图4-1 图4-2多缝夫琅禾费衍射如图4-1所示。

由于相邻单缝在P 点产生的夫琅禾费衍射的幅值与中心单缝的相同，只是产生一个相位差θλπδsin 2d =，故，经证明，P 点处的光强为：220)2sin 2sin ()sin ()(δδααN I P I =， 其中θλπαsin a =，θλπδsin 2d =。

因而，程序代码如下：clear %清除原有变量Lambda=600*(1e-9); %设置波长为600nma=0.005*(1e-3); %设置衍射屏参数：缝宽为0.005mm ， 缝距为0.02mmd=0.02*(1e-3);f=0.01; %汇聚透镜焦距设置为1cmN=20; %设置缝数为20ni=1000;x=linspace(-0.005,0.005,ni); %将衍射屏按照狭缝方向分为ni 个微元 for k=1:nisn=x(k)/sqrt(x(k).^2+f^2);alpha=pi*a*sn/Lambda; %算各微元对应的α和δ值delta=2*pi*d*sn/Lambda;I(k)=(sin(alpha)/alpha).^2*(sin(N*delta/2)/sin(delta/2)).^2; %求出各处的光强endfigure(gcf); %显示图像NCLevels=250;Br=I*NCLevels;image(0,x,Br);colormap(gray(NCLevels));title('二维强度分布');运行后结果如图4-2所示。

将光源上下移动的结果如图4-3所示：图4-3 图4-4点光源发出的光经过准直透镜后形成倾斜入射的平行光，倾斜角度为i 。

此时，P 点强度的公式为：220)sin ()sin ()(ββααN I P I =， 其中)sin (sin i a -=θλπα，)sin (sin i d -=θλπβ。