输出反馈极点配置
- 格式:pdf
- 大小:344.07 KB
- 文档页数:53



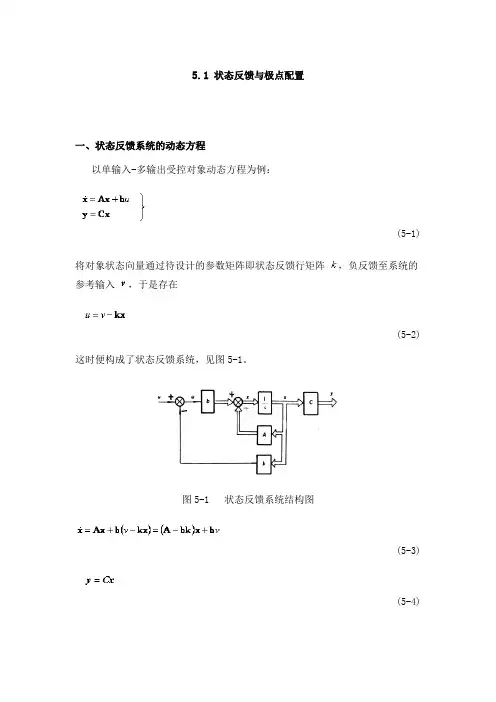
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。





第五章静态输出反馈、观测器和静态输出反馈观测器和动态补偿器§5-1静态输出反馈和极点配置一、静态输出反馈的性质若给定线性时不变系统方程为=+=A B C xx u y x (5-1)若取静态输出反馈控制律u =K y +v (5-2)可以得到闭环系统的动态方程为(),(53)A BKCBC xx v y x =++=−(),=++=A BKC B C xx v y x xCBvyx∫AK闭环系统结构图)不改变系统的可观测性定理5-1反馈规律(5-2)不改变系统的可观测性。
证明根据等式()−+−−⎡⎤⎡⎤⎡⎤I A BCK IBK I A s s (5-4)0=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦C I C (54)由于(5-4)式右端第一个矩阵是非奇异阵,因此)式右端第个矩阵是非奇异阵,因此对任意的s 和K ,均有⎡()(55)s s rank rank −+−⎤⎡⎤=−⎢⎥⎢⎥⎣⎦⎣⎦I A BKC I A C C 证完。
可见,系统(A +BKC , C )可观测的充分必要条件)可观测这表明是系统(A , C )可观测。
这表明静态输出反馈不改变系统的可观测性。
)不可观测由(55)可知如果系统(A , C )不可观测,由(5-5)可知,静态输出反馈不会改变系统的不可观测模态。
推论:u =K y +v 的反馈律不改变系统的可控性。
把中看作态馈证明:把(A +BKC )中的KC 看作是状态反馈增益阵,而状态反馈不改变系统的可控性。
证完。
二、循环矩阵定义:称为是循环的系指其最小多项式1. 循环矩阵的定义:n ×n 方阵A 称为是循环的,系指其最小多项式就是特征多项式。
等价的提法有:1).s I −A 的Smith 标准形只有一个非1的不变因子;2)A 的若当形中一个特征值只有一个若当块2).A 的若当形中一个特征值只有一个若当块。
特别地,有:1A A )若的所有特征值互异,则为循环阵。
为循环矩阵则存在向量b 2)若A 为循环矩阵,则存在向量b , 使221,,,,,−−"b Ab A b Ab Abn n A b n 可张成一个维空间,即(,)可控。


实现输出反馈极点配置的数值方法
邱海明;付明义
【期刊名称】《自动化学报》
【年(卷),期】1991(017)003
【摘要】本文讨论了用数值方法实现输出反馈极点配置的问题.求解反馈阵的矩阵方程被等效成非线性向量方程,用牛顿迭代法可求得反馈阵.本文推导了牛顿迭代法所需的导数公式:并给出有关算例.还可将非线性向量方程化作性能指标,用寻优的方法求得所需的输出反馈阵.
【总页数】5页(P345-349)
【作者】邱海明;付明义
【作者单位】不详;不详
【正文语种】中文
【中图分类】O231
【相关文献】
1.基于粒子群优化极点配置的空燃比输出反馈控制 [J], 何德峰;张露宽;郭海锋
2.条形区域极点配置静态输出反馈可靠控制 [J], 徐艺超;王福忠;姚波
3.梯形区域极点配置静态输出反馈可靠控制 [J], 徐艺超;姚波;王福忠;
4.基于区域极点配置的静态输出反馈可靠控制 [J], 房志铭;姚波;王福忠
5.基于扇形区域极点配置的静态输出反馈H∞控制 [J], 姚波;谷美萱;王福忠;何新因版权原因,仅展示原文概要,查看原文内容请购买。
实验二 状态反馈与极点配置一、实验目的a) 掌握状态反馈极点配置的设计方法。
b) 掌握运用模拟运算放大电路实现状态反馈。
c) 验证极点配置理论。
二、实验仪器a) TDN —AC/ACS 型自动控制系统实验箱一台b) 示波器c) 万用表三、实验原理和电路为了更好地达到系统所要求的各种性能指针,需要通过设计系统控制器,改善原有系统的性能。
由于系统的性能与其极点分布位置有密切关系,因而极点配置是系统设计的关键。
极点配置就是利用状态反馈或输出反馈使闭环系统的极点位于所希望的极点位置。
在系统综合设计中,状态反馈和输出反馈是两种常用的反馈形式,而在现代控制理论中系统的物理特性是采用系统内部状态变量来描述的,利用内部状态变量乘以系数(向量)与系统参考输入综合构成的反馈系统,具有更优的控制效果。
1、单输入单输出状态反馈的极点配置受控系统如图2-1,图2-1受控系统其中状态变量1()1/G S S =,2()1/(0.051)G S S =+,状态变量1x 、2x ,对系统进行极点配置,达到系统期望的性能指针:输出超调量5%P M ≤;峰值时间0.5p t s ≤;系统频宽10b ω≤;跟踪误差0p e =(对于阶跃输入)。
i. 确定受控系统的状态空间模型211()()x u x G S =-,122()x x G S =,1y x =,系统的状态方程为:.11.2220200101x x u x x ⎡⎤-⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦;[]1210x y x ⎡⎤=⎢⎥⎣⎦ ii.确定期望的极点21P M e ζ-=;21p n t ωζ=-;22412244b ωωζζζ=-+-+可解得0.707ζ≥,选0.707ζ=;9n ω≥由10b ω≤选10n ω=。
这样期望极点为:*17.077.07j λ=-+*27.077.07j λ=--iii. 确定状态反馈矩阵K原系统特征多项式:12110det()...2020n s n sI A s a s a s a s s ---=++++=++期望的闭环系统特征多项式:**212det()()()14.1100sI A BK s s s s λλ--=--=++ 计算K :K =[10020-,14.120-]=[80,-5.9]计算变换矩阵p :1111111[...]...1n n n a p A b Ab b a a ----⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1/20011p ⎡⎤=⎢⎥-⎣⎦[][]1/20080 5.99.9 5.911K K p ⎡⎤==-=-⎢⎥-⎣⎦iv. 确定输入放大系数L闭环传递函数为2()20/(14.1100)G s s s =++系统要求跟踪阶跃信号误差为0则000lim(1())lim (1/()/)1/5p t s e y t s s G s s L →→==-=-=- 得L=52、极点配置的系统结构图图2-2极点配置后的系统将原系统的反馈线路与状态x1反馈线路合并后图2-3极点配置后的系统一、实验内容及步骤1、根据图2-4接线图2-4极点配置后系统的模拟电路M、峰值时间2、输入阶跃信号,用示波器观察并记录系统输出的波形,测量超调量Pt。
第五章静态输出反馈、观测器和静态输出反馈观测器和动态补偿器§5-1静态输出反馈和极点配置一、静态输出反馈的性质若给定线性时不变系统方程为=+=A B C xx u y x (5-1)若取静态输出反馈控制律u =K y +v (5-2)可以得到闭环系统的动态方程为(),(53)A BKCBC xx v y x =++=−(),=++=A BKC B C xx v y x xCBvyx∫AK闭环系统结构图)不改变系统的可观测性定理5-1反馈规律(5-2)不改变系统的可观测性。
证明根据等式()−+−−⎡⎤⎡⎤⎡⎤I A BCK IBK I A s s (5-4)0=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦C I C (54)由于(5-4)式右端第一个矩阵是非奇异阵,因此)式右端第个矩阵是非奇异阵,因此对任意的s 和K ,均有⎡()(55)s s rank rank −+−⎤⎡⎤=−⎢⎥⎢⎥⎣⎦⎣⎦I A BKC I A C C 证完。
可见,系统(A +BKC , C )可观测的充分必要条件)可观测这表明是系统(A , C )可观测。
这表明静态输出反馈不改变系统的可观测性。
)不可观测由(55)可知如果系统(A , C )不可观测,由(5-5)可知,静态输出反馈不会改变系统的不可观测模态。
推论:u =K y +v 的反馈律不改变系统的可控性。
把中看作态馈证明:把(A +BKC )中的KC 看作是状态反馈增益阵,而状态反馈不改变系统的可控性。
证完。
二、循环矩阵定义:称为是循环的系指其最小多项式1. 循环矩阵的定义:n ×n 方阵A 称为是循环的,系指其最小多项式就是特征多项式。
等价的提法有:1).s I −A 的Smith 标准形只有一个非1的不变因子;2)A 的若当形中一个特征值只有一个若当块2).A 的若当形中一个特征值只有一个若当块。
特别地,有:1A A )若的所有特征值互异,则为循环阵。
为循环矩阵则存在向量b 2)若A 为循环矩阵,则存在向量b , 使221,,,,,−−"b Ab A b Ab Abn n A b n 可张成一个维空间,即(,)可控。
因此,单输入系统(A, b )可控的充分必要条件是:A 是循环的且b 是A 的生成元。
可控且为循环阵则几乎对2. 循环阵与可控性:,)))×=A B A A B A b p ρρ若(可控,且为循环阵,则几乎对所有的1实向量,都有(,(,为可控。
引理1*:注:若A 非循环阵,可求K 1使得(A+BK 1, B )可控。
ρ[][]11121120K p nn n n n u u u x x x −×−×=∈""R,),×∈A B K Rp n若(可控,则对几乎所有的特征值各不相同因此是循环的引理2*:A BK A BK +的特征值各不相同,因此+是循环的。
3. 用状态反馈进行极点配置的循环矩阵算法:引理1*和引理2*提供了另一种状态反馈极点配置的算法(免去了第四章求K1的算法):1)根据引理2*,容易找到一个矩阵K1,使得A+BK1是且根据定理循环的,且根据定理4-2,(A+BK1,B)与(A, B)有相同的可控子空间;根据引理容易找到中的个向量使得2)1*,容易找到Im B中的一个向量b,使得(A+BK1,b)是可控的;)此时可按单输入系统极点配置原理构造状态反馈阵3)此时可按单输入系统极点配置原理构造状态反馈阵。
三、用于输出反馈极点配置问题中的几个定理推论5-2若(A, B)可控,A是循环矩阵,则存在向量b∈Im B,使(A, b)可控。
证明:这是引理1*的一个推论。
5-4设(A,B,C)可控可观测,则存在个推论54)可控可观测则存在一个p×q矩阵H,使(A+BHC,B)可控,(A+BHC, C)可观测,并且A+BHC是循环矩阵,即它的最)可观测并且是循环矩阵即它的最小多项式是n次。
例5-3给定系统为(A , B , C )如下1100110⎡⎤⎥⎥00⎡⎤00⎡00010⎢⎢=⎢⎥A 0010⎢⎥⎢⎥=⎢⎥B 100001⎤=⎢⎥⎣⎦C 0001⎢⎥⎣⎦01⎢⎥⎣⎦1100010110⎡⎤⎢⎥⎡⎤0000110001⎢⎥=+=⎢⎥⎢⎥⎣⎦⎢⎥H A BHC ⎣⎦可知(A +BHC ,B )可控,(A +BHC ,C )可观测,且A +BHC 是循环矩阵,它的最小多项式为4次。
四、用静态输出反馈配置极点首先研究单输多输出的系统以说明用静态1.单输入系统可配置n 个极点的条件首先研究单输入多输出的系统,以说明用静态输出反馈配置极点时所遇到的困难,而这些困难是用全部状态变量作反馈时所未遇到的用全部状态变量作反馈时所未遇到的。
1,,,A b A R b R C C R ×××=+∈∈=∈n n n q nxx u y x (5-11)121,[](512)×=+=∈−K K R "q q u y v k k k 由此可得闭环系统的动态方程为()(513)x x v =++−A bKC b2.单输入系统q 个极点的配置问题进一步的问题是:若rank C =q ,是否可以任意配置q 个极点或任意接近它们呢?我们有定理5—55-11rank C =设单输入系统(5)可控,q ,则总存在常值向量K ,使得q 个特征值任意接近于预先给定的q 个值,这些值中如有复数,应共轭成对出现。
证明设预先给定个值为12,,,qλλλ""并设它们彼此不同。
根据前面的推导:问题:1).为保证S 非奇异,为什么需要C 行满秩?考虑⎡102000C ⎤=⎢⎥⎦⎣2). 从数学和物理意义上解释为什么可对λi 稍稍)什i 进行摄动?3). 剩下的n −q 个特征值的位置在什么地方?3.多输入系统的极点配置问题定理5-6(A ,B ,C )可控可观测,rank B =p ,rank C =q则存在矩阵K ,使A +BKC 有max{p ,q }个特征值任意接近于预先给定的max{p ,q }个复数值。
证明不是循环阵则根据54总有使:若A 不是循环阵,则根据推论5-4,总有K 1,使得A +BK 1C 是循环阵。
又根据推论5-2,1Im ,(,)b B b BL A BK C b ∃∈⇔=+使得可控-55,K ⇒2根据定理,存在使得12A BK C bK C=C A B(K LK )C ++1212K A BK C BLK C=A ++++可任意接近个特征值。
qT T T ,,)A C B 另一方面(可控可观测,用上面的证明意味存T K 在,使得T T T TA C KB +的个特征值可任意接近于指定的个值。
p p T T T T T T T ,,)+A BKC A C B 注意到与其对偶系统(证完。
A C K B max{p, q}之+有相同的特征值。
故采用此种方法可以配置个特征值。
完剩下的?这是一个严重n −max{p ,q }个特征值的去向? 这是个严重的问题,因为若有根位于右半平面,将导致系统失去稳定性而无法工作此时极点配置便没有意义去稳定性而无法工作,此时极点配置便没有意义。
定理5-7若(A,B,C)可控可观测,rank B=p,rank C=q,且A有n个不同的特征值,则对几乎所有的(B,C)对,存在个p×q的输出反馈增益矩阵K,使得闭环对,存在一个系统A+BKC的特征值有max{p,q}−1个是任意指定的A的特征值(复数成对指定),以及(复数成对指定)以及{,p+q}({p,q})s=min{n−1}−(max{−1)个是任意接近于任意指定的值(复数成对)。
注:指定的根+任意接近的根= max{p ,q }−1+ min{n , {}1i {1}58)可控可观测p +q −1}−max{p ,q }+1= min{n , p +q −1} 定理5-8若(A ,B ,C )可控可观测,rank B =rank C =p ,q ,则对几乎所有的矩阵对(B ,C ),存在一个输出反使得馈增益阵K ,使得A +BKC 有−min{n ,p +q 1}个特征值设置得任意接近于min{n ,p +q −1}个任意指定的值(复数成对)。
特别,在p +q ≥n +1的情况下,几乎所有的线性时不变系统都可通过输出反馈来使之镇定。
证明:仅就四种情况之一(min{n , p +q −1}是奇数,a {)证明如下5-6max{p , q }是偶数) 证明如下:1)由定理56 ,可找到K 1,使得A +BK 1C 配置max{p , q } (1)个指定的极点,并使其中至少有一个是实的;若有必要稍稍摄动使2)若有必要,稍稍摄动K 1,使A +BK 1C 之特征值互不相同(循环阵,满足定理5-7)。
利用定理5-7,可找到K 2,使得在保留C {A +B K 1C 的max{p , q }−1个指定的极点max{, 中至少有一个是实的)(因为a {p ,q }中至少有个是实的)的同时,再由A+B K1C+B K2C= A+B(K1+K2)C设置i{{1)min{n,p+q−1}−(max{p,q}−1)个指定的特征值。
这样K=K K1+K2就给出了所要的反馈增益阵。
3)总共配置的极点个数是,−min{n, p+q1}定理5-8的证明过程事实上给出了一种多变量实种多变系统输出反馈配置极点的两步算法:56使得1)定理5-6可找到K1,使得A+BK1C配置max{,{p,q}个指定的极点且使A+BK1C之特征值互不相同(故57)至少有一个是A+BK1C是循环阵满足定理5-7 )、至少有一个是实的;2)按定理5-7找到K2;则K=K1+K2就给出了所要的反馈增益阵。
就给了所要的反馈增阵例5-6考虑系统010000⎡⎤⎡⎤0000101000,,0001000010A B C=⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎢容易验证定理5—8的条件满足。
现用输出反馈u =K y 来000001⎥⎢⎥⎣⎦⎣⎦配置极点。
取12k k ⎡⎤特征方程式为34K=k k ⎢⎥⎣⎦42141423()()0k k k k k k λλ+−+−=取何值仅能置个极点但不论K 取何值,仅能配置2个极点。
但=m in {,1}3n p q +−这说明定理的结论并不是对所有的(B ,C )都成立,而仅仅是对几乎所有的(B ,C )对成立。
57例5-7系统A 、B 、C 阵如下010100⎡⎡⎡1000110010⎤⎤⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎣⎦A B C 00011⎢⎥⎢⎥⎣⎦⎣⎦要找出个输出反馈增益阵使得闭环极点任意接近要找出一个输出反馈增益阵使得闭环极点任意接近指定的三个极点{–1, –2, –5}。