数据结构- 串的模式匹配算法:BF和 KMP算法
- 格式:pdf
- 大小:571.80 KB
- 文档页数:11


串的两种模式匹配算法 模式匹配(模范匹配):⼦串在主串中的定位称为模式匹配或串匹配(字符串匹配) 。
模式匹配成功是指在主串S中能够找到模式串T,否则,称模式串T在主串S中不存在。
以下介绍两种常见的模式匹配算法:1. Brute-Force模式匹配算法暴风算法,⼜称暴⼒算法。
算法的核⼼思想如下: 设S为⽬标串,T为模式串,且不妨设: S=“s0s1s2…sn-1” , T=“t0t1t2 …tm-1” 串的匹配实际上是对合法的位置0≦i≦n-m依次将⽬标串中的⼦串s[i…i+m-1]和模式串t[0…m-1]进⾏⽐较:若s[i…i+m-1]=t[0…m-1]:则称从位置i开始的匹配成功,亦称模式t在⽬标s中出现;若s[i…i+m-1]≠t[0…m-1]:从i开始的匹配失败。
位置i称为位移,当s[i…i+m-1]=t[0…m-1]时,i称为有效位移;当s[i…i+m-1] ≠t[0…m-1]时,i称为⽆效位移。
算法实现如下: (笔者偷懒,⽤C#实现,实际上C# String类型已经封装实现了该功能)1public static Int32 IndexOf(String parentStr, String childStr)2 {3 Int32 result = -1;4try5 {6if (parentStr.Length > 1 && childStr.Length > 1)7 {8 Int32 i = 0;9 Int32 j = 0;10while (i < parentStr.Length && j < childStr.Length)11 {12if (parentStr[i] == childStr[j])13 {14 i++;15 j++;16 }17else18 {19 i = i - j + 1;20 j = 0;21 }22 }23if (i < parentStr.Length)24 {25 result = i - j;26 }27 }28 }29catch (Exception)30 {31 result = -1;32 }33return result;34 } 该算法的时间复杂度为O(n*m) ,其中n 、m分别是主串和模式串的长度。

BF算法与KMP算法BF(Brute Force)算法是普通的模式匹配算法,BF算法的思想就是将⽬标串S的第⼀个字符与模式串T的第⼀个字符进⾏匹配,若相等,则继续⽐较S的第⼆个字符和 T的第⼆个字符;若不相等,则⽐较S的第⼆个字符和T的第⼀个字符,依次⽐较下去,直到得出最后的匹配结果。
BF算法实现:1int BF(char S[],char T[],int pos)2 {//c从第pos位开始搜索匹配3int i=pos,j=0;4while(S[i+j]!='\0'&&T[j]!='\0')5 {6if(S[i+j]==T[j])7 j++;8else9 {10 i++;11 j=0;12 }13 }14if(T[j]=='\0')15return i+1;16else17return -1;18 }BF算法⽐较直接,是⼀种蛮⼒算法,该算法最坏情况下要进⾏M*(N-M+1)次⽐较,为O(M*N),下⾯来看⼀个效率⾮常⾼的字符串匹配算KMP算法完成的任务是:给定两个字符串S和T,长度分别为n和m,判断f是否在S中出现,如果出现则返回出现的位置。
常规⽅法是遍历KMP算法思想:实例1优化的地⽅:如果我们知道模式中a和后⾯的是不相等的,那么第⼀次⽐较后,发现后⾯的的4个字符均对应相等,可见a下次匹配的位置实例2由于abc 与后⾯的abc相等,可以直接得到红⾊的部分。
⽽且根据前⼀次⽐较的结果,abc就不需要⽐较了,现在只需从f-a处开始⽐较即可。
说明主串对应位置i的回溯是不必要的。
要变化的是模式串中j的位置(j不⼀定是从1开始的,⽐如第⼆个例⼦)j的变化取决于模式串的前后缀的相似度,例2中abc和abc(靠近x的),前缀为abc,j=4开始执⾏。
下⾯我们来看看Next()数组:定义:(1)next[0]= -1 意义:任何串的第⼀个字符的模式值规定为-1。

数据结构—串的模式匹配数据结构—串的模式匹配1.介绍串的模式匹配是计算机科学中的一个重要问题,用于在一个较长的字符串(称为主串)中查找一个较短的字符串(称为模式串)出现的位置。
本文档将详细介绍串的模式匹配算法及其实现。
2.算法一:暴力匹配法暴力匹配法是最简单直观的一种模式匹配算法,它通过逐个比较主串和模式串的字符进行匹配。
具体步骤如下:1.从主串的第一个字符开始,逐个比较主串和模式串的字符。
2.如果当前字符匹配成功,则比较下一个字符,直到模式串结束或出现不匹配的字符。
3.如果匹配成功,返回当前字符在主串中的位置,否则继续从主串的下一个位置开始匹配。
3.算法二:KMP匹配算法KMP匹配算法是一种改进的模式匹配算法,它通过构建一个部分匹配表来减少不必要的比较次数。
具体步骤如下:1.构建模式串的部分匹配表,即找出模式串中每个字符对应的最长公共前后缀长度。
2.从主串的第一个字符开始,逐个比较主串和模式串的字符。
3.如果当前字符匹配成功,则继续比较下一个字符。
4.如果当前字符不匹配,则根据部分匹配表的值调整模式串的位置,直到模式串移动到合适的位置。
4.算法三:Boyer-Moore匹配算法Boyer-Moore匹配算法是一种高效的模式匹配算法,它通过利用模式串中的字符出现位置和不匹配字符进行跳跃式的匹配。
具体步骤如下:1.构建一个坏字符规则表,记录模式串中每个字符出现的最后一个位置。
2.从主串的第一个字符开始,逐个比较主串和模式串的字符。
3.如果当前字符匹配成功,则继续比较下一个字符。
4.如果当前字符不匹配,则根据坏字符规则表的值调整模式串的位置,使模式串向后滑动。
5.算法四:Rabin-Karp匹配算法Rabin-Karp匹配算法是一种基于哈希算法的模式匹配算法,它通过计算主串和模式串的哈希值进行匹配。
具体步骤如下:1.计算模式串的哈希值。
2.从主串的第一个字符开始,逐个计算主串中与模式串长度相同的子串的哈希值。

字符串模式匹配算法系列(⼀):BF算法算法背景:BF(Brute Force)算法,是⼀种在字符串匹配的算法中,⽐较符合⼈类⾃然思维⽅式的⽅法,即对源字符串和⽬标字符串逐个字符地进⾏⽐较,直到在源字符串中找到完全与⽬标字符串匹配的⼦字符串,或者遍历到最后发现找不到能匹配的⼦字符串。
算法思路很简单,但也很暴⼒。
算法原理:假设源字符串为“⾮常地⾮常地⾮常地喜欢你”,我们想从中寻找⽬标字符串“⾮常地⾮常地喜欢”,则BF算法的过程可以表述如下:第1轮:将源字符串和⽬标字符串对齐,并下标0开始逐个向后⽐较每个字符。
结果发现双⽅的第1个字符都是“⾮”、第2个字符都是“常”、……,但到了第7个字符时发现不⼀致:源字符串为“⾮”、⽬标字符串为“喜”,因此这⼀轮匹配不成功。
第2轮:将⽬标字符串整体向后移动1个字符的位置(即将⽬标字符串的第1个字符与源字符串的第2个字符对齐),并开始逐个向后⽐较每个字符,结果发现两个字符串的第1个字符就不⼀致,因此这⼀轮匹配也不成功。
第3轮:类似地,将⽬标字符串整体向后移动1个字符的位置(即将⽬标字符串的第1个字符与源字符串的第3个字符对齐),并开始逐个向后⽐较,结果发现两个字符串的第1个字符就不⼀致,因此这⼀轮匹配也不成功。
第4轮:这⼀轮终于发现,⽬标字符串的每个字符都能和源字符串对应起来,匹配成功!因此算法结束并根据需要返回相应的信息(⽐如返回这⼀轮源字符串遍历起始点的位置下标3)算法实现:BF算法的python实现如下:1#!/usr/bin/env python2#-*- coding: utf-8 -*-3import sys4import pdb56 reload(sys)7 sys.setdefaultencoding('utf-8')8910class BruteForce(object):11"""BF算法12成员变量:13 str_s: 源字符串14 str_t: ⽬标字符串15"""16def__init__(self, str_s, str_t):17 self.str_s = str_s18 self.str_t = str_t1920def run(self):21"""完全匹配则返回源字符串匹配成功的起始点的下标,否则返回-122"""23 base = 0 # 记录源字符串与⽬标字符串对齐的基准点24 len_s = len(self.str_s)25 len_t = len(self.str_t)2627while base + len_t <= len_s:28 step = 029while step < len_t:30if str_t[step] == self.str_s[base + step]:31# 当前字符相同,则继续⽐较下⼀个字符32 step += 133continue34# 当前字符不相同,则结束次轮⽐较,更新base基准位置,启动下⼀轮⽐较35 base += 136break37# 完全匹配成功,算法结论,返回匹配成功的基准点位置下标38if step == len_t:39return base40# 遍历了所有情况,最终匹配失败,返回-141return -1424344if__name__ == '__main__':45 str_s = u"⾮常地⾮常地⾮常地喜欢你"46 str_t = u"⾮常地⾮常地喜欢"47 model = BruteForce(str_s, str_t)48print model.run()复杂度分析:时间复杂度:假设源字符串长度为m,⽬标字符串长度为n,则:最好情况下是第⼀轮就成功匹配,则时间复杂度为O(n);最坏情况下是遍历到最后才成功匹配,或者遍历到最后发现匹配不成功,则时间复杂度为O(n*(m-n+1)),⼀般实际使⽤时m >> n,所以可以认为趋近于O(m*n);空间复杂度:由于不需要额外的存储空间,所以空间复杂度为O(1)算法评估:整个算法其实就循环执⾏如下两个步骤:⼀、从每⼀轮的基准点开始⽐较两个字符串;⼆、如发现不能完全匹配⽬标字符串,将⽬标字符串向后挪动⼀个字符的位置(即更新基准点);如果想优化算法性能,那就简单分析⼀下:步骤⼀基本没有优化的空间:两个字符串⽐较就是需要从前向后逐个字符看是否匹配;步骤⼆可能有优化的空间:每轮发现不匹配时,⽬标字符串只能向后挪动⼀个字符的距离,所以会想到能否多往后挪动⼏个字符的距离?这样不就减少了步骤⼀⽐较的轮次数,从⽽加快速度了吗?这基本就是KMP算法的思路,下⼀篇会详细介绍。

天津市大学软件学院实验报告课程名称:串匹配算法实验姓名:***学号:**********班级:业务1114串匹配问题一、实验题目:给定一个主串,在该主串中查找并定位任意给定字符串。
二、实验目的:(1)深刻理解并掌握蛮力法的设计思想;(2)提高应用蛮力法设计算法的技能;(3)理解这样一个观点:用蛮力法设计的算法,一般来说,经过适度的努力后,都可以对算法的第一个版本进行一定程度的改良,改进其时间性能。
三、实验分析:串匹配问题的BF算法1 在串S中和串T中设比较的下标i=1和j=1;2 循环直到S中所剩字符个数小于T的长度或T中所有字符均比较完2.1 k=i2.2 如果S[i]=T[j],则比较S和T的下一字符,否则2.2 将i和j回溯(i=k+1; j=1)3 如果T中所有字符均比较完,则匹配成功,返回k否则匹配失败,返回0时间复杂度:设匹配成功发生在si处,则在i-1趟不成功的匹配中比较了(i-1)m次,第i趟成功匹配共比较了m次,所以总共比较了i m次,因此平均比较次数是:pi(i m)=(i m)=一般情况下,m<<n,因此最坏情况下时间复杂度是Ο(n m)。
串匹配问题的KMP算法实现过程:在串S和串T中高比较的起始下标i和j;循环直到S中所剩字符小于T的长度或T的所有字符均比较完(如果S[i]=T[j],则继续比较S和T的下一个字符;否则将j向右滑动到next[j]位置,即j=next[j];如果j=0,则将i和j分别+1,准备下趟比较,至于其中的next在此不作详细讲解);如果T中所有字符均比较完,则匹配成功,返回匹配的起始下标;否则匹配失败,返回0。
时间复杂度:Ο(n m),当m<<n时,KMP算法的时间复杂性是Ο(n)。
四、实验所用语言和运行环境C++,运行环境Microsoft Visual C++ 6.0五、实验过程的原始记录BF算法程序代码#include<iostream.h>#include<string>void main(){cout<<"请输入主串并且以0和回车结束"<<endl;char s[100];char t[100];for(int m=0;m<100;m++){cin>>s[m];if(s[m]=='0'){s[m]='\0';break;}}cout<<"您输入的主串为:";for(int o=0;o<strlen(s);++o){cout<<s[o];}cout<<endl;cout<<"主串长度:";cout<<strlen(s);cout<<endl<<endl;cout<<"请输入子串并且以0和回车结束"<<endl;for(int n=0;n<100;n++){cin>>t[n];if(t[n]=='0'){t[n]='\0';break;}}cout<<"您输入的子串为:";for(int a=0;a<strlen(t);++a){cout<<t[a];}cout<<endl;cout<<"子串长度:";cout<<strlen(t);cout<<endl;cout<<endl<<"++++++++BF算法++++++++"<<endl;int i,j,k,y=0;for(i=0;i<strlen(s)-strlen(t)+1;){k=i;for(j=0;j<strlen(t);)if(s[i]==t[j]){if(j==strlen(t)-1){cout<<"找到了相同的字串:";cout<<"位置在主串的第"<<i-j+1<<"的位置上";cout<<endl;y=1;break;}++i;++j;}else{j=0;break;}}i=k+1;if(y==1)break;}if(i==strlen(s)-strlen(t)+1&&j!=strlen(t)-1){cout<<"没有找到可以匹配的子串"<<endl;}}程序执行结果:查找到了子串没有查找到子串程序代码#include<iostream.h>#include<string>//前缀函数值,用于KMP算法int GETNEXT(char t[],int b){int NEXT[10];NEXT[0]=-1;int j,k;j=0;k=-1;while(j<strlen(t)){if ((k==-1)||(t[j]==t[k])){j++;k++;NEXT[j]=k;}else k=NEXT[k];}b=NEXT[b];return b;}int KMP(char s[],char t[]){int a=0;int b=0;int m,n;m=strlen(s); //主串长度n=strlen(t); //子串长度cout<<endl<<"+++++++++KMP算法++++++++++++"<<endl;while(a<=m-n){while(s[a]==t[b]&&b!=n){a++;b++;}if(b==n){cout<<"找到了相应的子串位置在主串:"<<a-b+1<<endl;return 0;}b=GETNEXT(t,b);a=a-b;if(b==-1) b++;}cout<<"没有找到匹配的子串!"<<endl;return 0;}void main(){cout<<"请输入主串并且以0和回车结束"<<endl;char s[100];char t[100];for(int m=0;m<100;m++){cin>>s[m];if(s[m]=='0'){s[m]='\0';break;}}cout<<"您输入的主串为:";for(int o=0;o<strlen(s);++o){cout<<s[o];}cout<<endl;cout<<"主串长度:";cout<<strlen(s);cout<<endl<<endl;cout<<"请输入子串并且以0和回车结束"<<endl;for(int n=0;n<100;n++){cin>>t[n];if(t[n]=='0'){t[n]='\0';break;}}cout<<"您输入的子串为:";for(int a=0;a<strlen(t);++a){cout<<t[a];}cout<<endl;cout<<"子串长度:";cout<<strlen(t);cout<<endl;KMP(s,t);}程序执行结果:查找到子串没有查到子串。




两种常见的模式匹配算法(代码实现)BF算法(暴⼒法)不多解释,直接上代码:// BF算法 O(mn)int bf(SString s, SString t, int pos){int i = pos, j = 0;while (i < s.length && j < t.length){if (s.ch[i] == t.ch[j]){i++;j++;} else {i = i - j + 1;j = 0;}}if (j >= t.length)return i - t.length;elsereturn -1;}// 另⼀个版本的BF算法 - O(mn)int pm(SString s, SString t, int pos){for (int i = pos; i <= s.length-t.length; i++){bool status = true;for (int j = 0; j < t.length; j++){if (s.ch[i+j] != t.ch[j]){status = false;break;}}if (status)return i;}return -1;}KMP算法KMP算法较难理解,在⼤⼆上数据结构这门课的时候就没有搞懂,今天花了点时间终于把它看懂了。
KMP算法相⽐BF算法,其改进主要在使⽤了⼀个前后缀匹配数组next(我⾃⼰起的名⼉~)来记录前缀和后缀的匹配信息,以使得在发现主串与模式串的⽐较中出现不匹配时,主串指针⽆需回溯,并根据前后缀匹配数组中的信息,向后移动,从⽽减少了多余的⽐较。
代码实现:// KMP算法int kmp(SString &s, SString &t, int pos){int next[t.length], j = 0, i = 0;get_next(t, next);while (i < s.length && j < t.length){if (j == -1 || s.ch[i] == t.ch[j]){i++; j++;} elsej = next[j];}if (j >= t.length)return i-t.length;elsereturn -1;}void get_next(SString &t, int next[]){ int i = 0, j = -1;next[0] = -1;while (i < t.length - 1){if (j == -1 || t.ch[i] == t.ch[j]){i++; j++;next[i] = j;} else {j = next[j];}}}参考博客:(讲得⾮常好,但是没有代码实现)(进⼀步理解)(含代码实现)可运⾏的整体代码:#include<iostream>#define MAXLEN 100#define CHUNKSIZE 50using namespace std;// 串的普通顺序存储typedef struct {char ch[MAXLEN+1];int length;}SString;// 串的堆式顺序存储//typedef struct {// char *ch;// int length;//}SString;// 串的链式存储typedef struct chunk{char ch[CHUNKSIZE];struct chunk *next;}Chunk;typedef struct {Chunk *head, *tail;int length;}LString;// 普通顺序存储的初始化操作void SsInit(SString &s){s.length = 0;}void SsInput(SString &s){char c;while ((c = getchar()) != '\n'){s.ch[s.length++] = c;}}void printString(SString &s){for (int i = 0; i < s.length; i++){cout << s.ch[i];}cout << endl;}// BF算法 - O(mn)int pm(SString s, SString t, int pos){for (int i = pos; i <= s.length-t.length; i++){ bool status = true;for (int j = 0; j < t.length; j++){if (s.ch[i+j] != t.ch[j]){status = false;break;}}if (status)return i;}return -1;}// 另⼀种版本的BF算法 O(mn) - 与暴⼒法相似int bf(SString s, SString t, int pos){int i = pos, j = 0;while (i < s.length && j < t.length){if (s.ch[i] == t.ch[j]){i++;j++;} else {i = i - j + 1;j = 0;}}if (j >= t.length)return i - t.length;elsereturn -1;}// KMP算法int kmp(SString &s, SString &t, int pos){int next[t.length], j = 0, i = 0;get_next(t, next);while (i < s.length && j < t.length){if (j == -1 || s.ch[i] == t.ch[j]){i++; j++;} elsej = next[j];}if (j >= t.length)return i-t.length;elsereturn -1;}void get_next(SString &t, int next[]){int i = 0, j = -1;next[0] = -1;while (i < t.length - 1){if (j == -1 || t.ch[i] == t.ch[j]){i++; j++;next[i] = j;} else {j = next[j];}}}int main(){SString s, t;SsInit(s);SsInput(s);SsInit(t);SsInput(t);int loc = -1;// loc = pm(s, t, 0); // loc = bf(s, t, 0);loc = kmp(s, t, 0); cout << loc << endl; }。
实验四串【实验目的】1、掌握串的存储表示及基本操作;2、掌握串的两种模式匹配算法:BF和KMP。
3、了解串的应用。
【实验学时】2学时【实验预习】回答以下问题:1、串和子串的定义串的定义:串是由零个或多个任意字符组成的有限序列。
子串的定义:串中任意连续字符组成的子序列称为该串的子串。
2、串的模式匹配串的模式匹配即子串定位是一种重要的串运算。
设s和t是给定的两个串,从主串s的第start个字符开始查找等于子串t的过程称为模式匹配,如果在S中找到等于t的子串,则称匹配成功,函数返回t在s中首次出现的存储位置(或序号);否则,匹配失败,返回0。
【实验内容和要求】1、按照要求完成程序exp4_1.c,实现串的相关操作。
调试并运行如下测试数据给出运行结果:•求“This is a boy”的串长;•比较”abc3”和“abcde“;表示空格•比较”english”和“student“;•比较”abc”和“abc“;•截取串”white”,起始2,长度2;•截取串”white”,起始1,长度7;•截取串”white”,起始6,长度2;•连接串”asddffgh”和”12344”;#include<stdio.h>#include<string.h>#define MAXSIZE 100#define ERROR 0#define OK 1/*串的定长顺序存储表示*/typedef struct{char data[MAXSIZE];int length;} SqString;int strInit(SqString *s);/*初始化串*/int strCreate(SqString *s); /*生成一个串*/int strLength(SqString *s); /*求串的长度*/int strCompare(SqString *s1,SqString *s2); /*两个串的比较*/int subString(SqString *sub,SqString *s,int pos,int len);/*求子串*/int strConcat(SqString *t,SqString *s1,SqString *s2);/*两个串的连接*//*初始化串*/int strInit(SqString *s){s->length=0;s->data[0]='\0';return OK;}/*strInit*//*生成一个串*/int strCreate(SqString *s){printf("input string :");gets(s->data);s->length=strlen(s->data);return OK;}/*strCreate*//*(1)---求串的长度*/int strLength(SqString *s){return s->length;}/*strLength*//*(2)---两个串的比较,S1>S2返回>0,s1<s2返回<0,s1==s2返回0*/int strCompare(SqString *s1,SqString *s2){int i;for(i=0;i<s1->length&&i<s2->length;i++){if(s1->data[i]>s2->data[i]){return 1;}if(s1->data[i]<s2->data[i]){return -1;}}return 0;}/*strCompare*//*(3)---求子串,sub为返回的子串,pos为子串的起始位置,len为子串的长度*/int subString(SqString *sub,SqString *s,int pos,int len) {int i;if(pos<1||pos>s->length||len<0||len>s->length-pos+1) {return ERROR;}sub->length=0;for(i=0;i<len;i++){sub->data[i]=s->data[i+pos-1];sub->length++;}sub->data[i]='\0';return OK;}/*subString*//*(4)---两个串连接,s2连接在s1后,连接后的结果串放在t中*/int strConcat(SqString *t,SqString *s1,SqString *s2){int i=0,j=0;while(i<s1->length){t->data[i]=s1->data[i];i++;}while(j<s2->length){t->data[i++]=s2->data[j++];}t->data[i]='\0';t->length=s1->length+s2->length;return OK;}/*strConcat*/int main(){int n,k,pos,len;SqString s,t,x;do{printf("\n ---String--- \n");printf(" 1. strLentgh\n");printf(" 2. strCompare\n");printf(" 3. subString\n");printf(" 4. strConcat\n");printf(" 0. EXIT\n");printf("\n ---String---\n");printf("\ninput choice:");scanf("%d",&n);getchar();switch(n){case 1:printf("\n***show strLength***\n");strCreate(&s);printf("strLength is %d\n",strLength(&s));break;case 2:printf("\n***show strCompare***\n");strCreate(&s);strCreate(&t);k=strCompare(&s,&t); /*(5)---调用串比较函数比较s,t*/if(k==0)printf("two string equal!\n");else if(k<0)printf("first string<second string!\n");elseprintf("first string>second string!\n");break;case 3:printf("\n***show subString***\n");strCreate(&s);printf("input substring pos,len:");scanf("%d,%d",&pos,&len);if(subString(&t,&s,pos,len))printf("subString is %s\n",t.data);elseprintf("pos or len ERROR!\n");break;case 4:printf("\n***show subConcat***\n");strCreate(&s);strCreate(&t);if(strConcat(&x,&s,&t)) /*(6)---调用串连接函数连接s&t*/printf("Concat string is %s",x.data);elseprintf("Concat ERROR!\n");break;case 0:exit(0);default:break;}}while(n);return 0;}2、按照要求完成程序exp4_2.c,实现BF&KMP串的模式匹配算法。
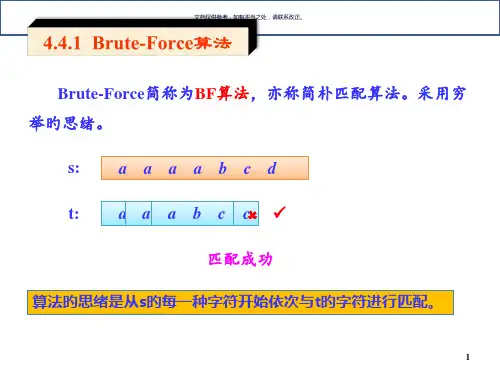
数据结构- 串的模式匹配算法:BF和KMP算法Brute-Force算法的思想Brute-Force算法的基本思想是:1) 从目标串s 的第一个字符起和模式串t的第一个字符进行比较,若相等,则继续逐个比较后续字符,否则从串s 的第二个字符起再重新和串t进行比较。
2) 依此类推,直至串t 中的每个字符依次和串s的一个连续的字符序列相等,则称模式匹配成功,此时串t的第一个字符在串s 中的位置就是t 在s中的位置,否则模式匹配不成功。
Brute-Force算法的实现c语言实现:1.// Test.cpp : Defines the entry point for the console application.2.//3.#include "stdafx.h"4.#include <stdio.h>5.#include "stdlib.h"6.#include <iostream>ing namespace std;8.9.//宏定义10.#define TRUE 111.#define FALSE 012.#define OK 113.#define ERROR 014.15.#define MAXSTRLEN 10016.17.typedef char SString[MAXSTRLEN + 1];18./************************************************************************/19./*20.返回子串T在主串S中第pos位置之后的位置,若不存在,返回021.*/22./************************************************************************/23.int BFindex(SString S, SString T, int pos)24.{25.if (pos <1 || pos > S[0] ) exit(ERROR);26.int i = pos, j =1;27.while (i<= S[0] && j <= T[0])28. {29.if (S[i] == T[j])30. {31. ++i; ++j;32. } else {33. i = i- j+ 2;34. j = 1;35. }36. }37.if(j > T[0]) return i - T[0];38.return ERROR;39.}40.41.42.43.void main(){44. SString S = {13,'a','b','a','b','c','a','b','c','a','c','b','a','b'};45. SString T = {5,'a','b','c','a','c'};46.int pos;47. pos = BFindex( S, T, 1);48. cout<<"Pos:"<<pos;49.}2.1 算法思想:每当一趟匹配过程中出现字符比较不等时,不需要回溯I指针,而是利用已经的带的“部分匹配”的结果将模式向右滑动尽可能远的一段距离后,继续进行比较。
即尽量利用已经部分匹配的结果信息,尽量让i不要回溯,加快模式串的滑动速度。
需要讨论两个问题:①如何由当前部分匹配结果确定模式向右滑动的新比较起点k?②模式应该向右滑多远才是高效率的?现在讨论一般情况:假设主串:s: …s(1)s(2) s(3) ……s(n)‟ ; 模式串:p: …p(1)p(2) p(3)…..p(m)‟现在我们假设主串第i个字符与模式串的第j(j<=m)个字符…失配‟后,主串第i个字符与模式串的第k(k<j)个字符继续比较。
此时,s(i)≠p(j):由此,我们得到关系式:即得到到1 到 j -1 的"部分匹配"结果:‘P(1)P(2) P(3)…..P(j-1)’= ’ S(i-j+1)……S(i-1)’从而推导出k 到j- 1位的“部分匹配”:即P的j-1~j-k=S前i-1~i- (k -1))位‘P(j - k + 1) …..P(j-1)’ = ’S(i-k+1)S(i-k+2)……S(i-1)’由于s(i)≠p(j),接下来s(i)将与p(k)继续比较,则模式串中的前(k-1)个字符的子串必须满足下列关系式,并且不可能存在k‟>k满足下列关系式:(k<j)有关系式:即(P的前k- 1 ~ 1位=S前i-1~i-(k-1) )位) ,:‘P(1) P(2) P(3)…..P(k-1)’= ’S(i-k+1)S(i-k+2)……S(i-1)’现在我们把前面总结的关系综合一下,有:由上,我们得到关系:‘p(1)p(2) p(3)…..p(k-1)’ = ‘p(j - k + 1) …..p(j-1)’反之,若模式串中满足该等式的两个子串,则当匹配过程中,主串中的第i 个字符与模式中的第j个字符等时,仅需要将模式向右滑动至模式中的第k个字符和主串中的第i个字符对齐。
此时,模式中头k-1个字符的子串…p(1)p(2) p(3)…..p(k-1)‟必定与主串中的第i 个字符之前长度为k-1 的子串‟s(j-k+1)s(j-k+2)……s(j-1)‟相等,由此,匹配仅需要从模式中的第k 个字符与主串中的第i 个字符比较起继续进行。
若令next[j] = k ,则next[j] 表明当模式中第j个字符与主串中相应字符“失配”时,在模式中需要重新和主串中该字符进行的比较的位置。
由此可引出模式串的next函数:根据模式串P的规律:‘p(1)p(2) p(3)…..p(k-1)’ = ‘p(j - k + 1) …..p(j-1)’由当前失配位置j(已知) ,可以归纳计算新起点k的表达式。
由此定义可推出下列模式串next函数值:模式匹配过程:KMP算法的实现:第一步,先把模式T所有可能的失配点j所对应的next[j]计算出来;第二步:执行定位函数Index_kmp(与BF算法模块非常相似)1.int KMPindex(SString S, SString T, int pos)2.{3.if (pos <1 || pos > S[0] ) exit(ERROR);4.int i = pos, j =1;5.while (i<= S[0] && j <= T[0])6. {7.if (S[i] == T[j]) {8. ++i; ++j;9. } else {10. j = next[j+1];11. }12. }13.if(j > T[0]) return i - T[0];14.return ERROR;15.}完整实现代码:1.// Test.cpp : Defines the entry point for the console application.2.//3.#include "stdafx.h"4.#include <stdio.h>5.#include "stdlib.h"6.#include <iostream>ing namespace std;8.9.//宏定义10.#define TRUE 111.#define FALSE 012.#define OK 113.#define ERROR 014.15.#define MAXSTRLEN 10016.17.typedef char SString[MAXSTRLEN + 1];18.19.void GetNext(SString T, int next[]);20.int KMPindex(SString S, SString T, int pos);21./************************************************************************/22./*23.返回子串T在主串S中第pos位置之后的位置,若不存在,返回024.*/25./************************************************************************/26.int KMPindex(SString S, SString T, int pos)27.{28.if (pos <1 || pos > S[0] ) exit(ERROR);29.int i = pos, j =1;30.int next[MAXSTRLEN];31. GetNext( T, next);32.while (i<= S[0] && j <= T[0])33. {34.if (S[i] == T[j]) {35. ++i; ++j;36. } else {37. j = next[j];38. }39. }40.if(j > T[0]) return i - T[0];41.return ERROR;42.}43.44./************************************************************************/45./* 求子串next[i]值的算法46.*/47./************************************************************************/48.void GetNext(SString T, int next[])49.{ int j = 1, k = 0;50. next[1] = 0;51.while(j < T[0]){52.if(k == 0 || T[j]==T[k]) {53. ++j; ++k; next[j] = k;54. } else {55. k = next[k];56. }57. }58.}59.60.void main(){61. SString S = {13,'a','b','a','b','c','a','b','c','a','c','b','a','b'};62. SString T = {5,'a','b','c','a','c'};63.int pos;64. pos = KMPindex( S, T, 1);65. cout<<"Pos:"<<pos;66.}2.2 求串的模式值next[n]k值仅取决于模式串本身而与相匹配的主串无关。