高2021届高2018级高三第一轮复习小专题训练30分钟第四章小题型38

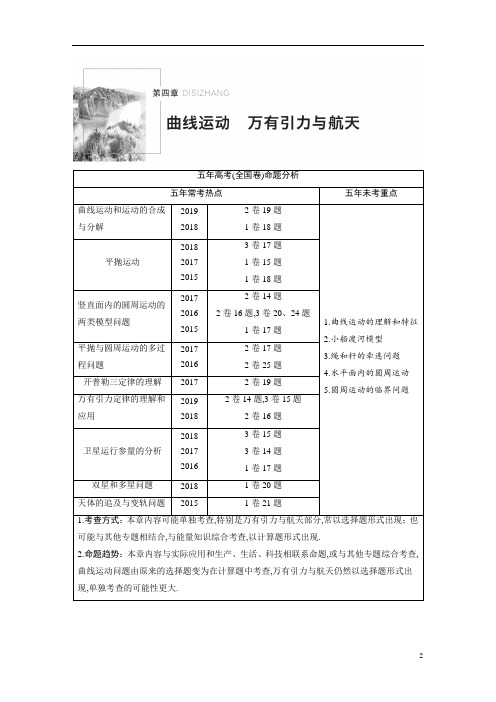
五年高考(全国卷)命题分析五年常考热点五年未考重点曲线运动和运动的合成与分解201920182卷19题1卷18题1.曲线运动的理解和特征2.小船渡河模型3.绳和杆的牵连问题4.水平面内的圆周运动5.圆周运动的临界问题平抛运动2018201720153卷17题1卷15题1卷18题竖直面内的圆周运动的两类模型问题2017201620152卷14题2卷16题,3卷20、24题1卷17题平抛与圆周运动的多过程问题201720162卷17题2卷25题开普勒三定律的理解20172卷19题万有引力定律的理解和应用201920182卷14题,3卷15题2卷16题卫星运行参量的分析2018201720163卷15题3卷14题1卷17题双星和多星问题20181卷20题天体的追及与变轨问题20151卷21题1.考查方式：本章内容可能单独考查,特别是万有引力与航天部分,常以选择题形式出现；也可能与其他专题相结合,与能量知识综合考查,以计算题形式出现.2.命题趋势：本章内容与实际应用和生产、生活、科技相联系命题,或与其他专题综合考查,曲线运动问题由原来的选择题变为在计算题中考查,万有引力与航天仍然以选择题形式出现,单独考查的可能性更大.第1讲 曲线运动 运动的合成与分解一、曲线运动1.速度的方向：质点在某一点的速度方向,沿曲线在这一点的切线方向.2.运动的性质：做曲线运动的物体,速度的方向时刻在改变,所以曲线运动一定是变速运动.3.运动的条件：物体所受合力的方向跟它的速度方向不在同一条直线上或它的加速度方向与速度方向不在同一条直线上.4.合外力方向与轨迹的关系物体做曲线运动的轨迹一定夹在合外力方向与速度方向之间,速度方向与轨迹相切,合外力方向指向轨迹的“凹”侧.判断正误 (1)做曲线运动的物体加速度方向一定变化.( × ) (2)物体在恒力作用下不可能做曲线运动.( × ) (3)物体在变力作用下可以保持速率不变.( √ ) 二、运动的合成与分解 1.遵循的法则位移、速度、加速度都是矢量,故它们的合成与分解都遵循平行四边形定则. 2.合运动与分运动的关系(1)等时性：合运动和分运动经历的时间相等,即同时开始、同时进行、同时停止. (2)独立性：一个物体同时参与几个分运动,各分运动独立进行,不受其他运动的影响. (3)等效性：各分运动的规律叠加起来与合运动的规律有完全相同的效果. 3.运动性质的判断⎩⎨⎧加速度(或合外力)⎩⎪⎨⎪⎧ 变化：非匀变速运动不变：匀变速运动加速度(或合外力)方向与速度方向⎩⎪⎨⎪⎧共线：直线运动不共线：曲线运动4.两个直线运动的合运动性质的判断标准：看合初速度方向与合加速度方向是否共线.两个互成角度的分运动 合运动的性质 两个匀速直线运动匀速直线运动 一个匀速直线运动、一个匀变速直线运动匀变速曲线运动两个初速度为零的匀加速直线运动匀加速直线运动两个初速度不为零的匀变速直线运动如果v合与a合共线,为匀变速直线运动如果v合与a合不共线,为匀变速曲线运动自测(2019·广东深圳市4月第二次调研)2018珠海航展,我国五代战机“歼20”再次闪亮登场.表演中,战机先水平向右,再沿曲线ab向上(如图1),最后沿陡斜线直入云霄.设飞行路径在同一竖直面内,飞行速率不变.则沿ab段曲线飞行时,战机()图1A.所受合外力大小为零B.所受合外力方向竖直向上C.竖直方向的分速度逐渐增大D.水平方向的分速度不变[参考答案]C[试题解析] 战机在同一竖直面内做曲线运动,且运动速率不变,由于速度方向是变化的,则速度是变化的,故战机的加速度不为零,根据牛顿第二定律可知,战机所受的合外力不为零,故A错误；战机在同一竖直面内做匀速率曲线运动,则所受合外力与速度方向垂直,由于速度方向时刻在变,则合外力的方向也时刻在变化,并非始终都竖直向上,故B错误；由以上分析可知,战机所受合外力方向始终与速度方向垂直,对合外力和速度在竖直方向和水平方向上进行分解可知,竖直方向上做加速运动,水平方向上做减速运动,故竖直方向分速度逐渐增大,水平方向分速度逐渐减小,故C正确,D错误.1.条件物体受到的合外力方向与速度方向始终不共线.2.特征(1)运动学特征：做曲线运动的物体的速度方向时刻发生变化,即曲线运动一定为变速运动.(2)动力学特征：由于做曲线运动的物体所受合外力一定不为零且和速度方向始终不在同一条直线上(做曲线运动的条件).合外力在垂直于速度方向上的分力改变物体速度的方向,合外力在沿速度方向上的分力改变物体速度的大小.(3)轨迹特征：曲线运动的轨迹始终夹在合外力的方向与速度的方向之间,而且向合外力的一侧弯曲.(4)能量特征：如果物体所受的合外力始终和物体的速度垂直,则合外力对物体不做功,物体的动能不变；若合外力不与物体的速度方向垂直,则合外力对物体做功,物体的动能发生变化. 例1(2020·江西上饶市重点中学六校第一次联考)下列关于运动和力的叙述中,正确的是()A.做曲线运动的物体,其加速度方向一定是变化的B.物体做圆周运动,所受的合力一定是向心力C.物体所受合力恒定,该物体速率随时间一定均匀变化D.物体运动的速率在增加,所受合力一定做正功[参考答案]D[试题解析] 做曲线运动的物体,其加速度方向不一定是变化的,例如平抛运动,选项A错误；物体做匀速圆周运动时,所受的合力一定是向心力,选项B错误；物体所受合力恒定,该物体速率随时间不一定均匀变化,例如平抛运动,选项C错误；根据动能定理可知,物体运动的速率在增加,所受合力一定做正功,选项D正确.变式1如图2是某物体做匀变速曲线运动的轨迹的示意图.已知该物体在B点的加速度方向与速度方向垂直,物体在B点处的速度方向如图所示,则下列说法正确的是()图2A.C点的速率小于B点的速率B.A点的加速度比C点的加速度大C.C点的速率大于B点的速率D.从A点到C点加速度方向与速度方向的夹角先增大后减小,速率先减小后增大[参考答案]C[试题解析] 物体做匀变速曲线运动,即物体整个运动过程中加速度不变,所以物体经过C点时的加速度与A点相同,故选项B错误；由物体在B点的加速度方向与速度方向垂直可知,物体的加速度方向竖直向下,则由题图可知,B点到C点的加速度方向与速度方向夹角小于90°,则C 点的速率比B点速率大,故选项A错误,C正确；由题图可知,A点加速度方向与速度方向夹角大于90°,C点的加速度方向与速度方向夹角小于90°,从A点到C点加速度方向与速度方向的夹角一直减小,物体的速率先减小后增大,故选项D错误.1.基本思路：分析运动的合成与分解问题时,一般情况下按运动效果进行分解.2.解题关键：两个方向上的分运动具有等时性,这常是处理运动分解问题的关键点.3.注意问题：要注意分析物体在两个方向上的受力及运动规律,分别在两个方向上列式求解.例2(2019·江西宜春市第一学期期末)如图3所示是物体在相互垂直的x方向和y方向运动的v－t图象.以下判断正确的是()图3A.在0～1 s内,物体做匀速直线运动B.在0～1 s内,物体做匀变速直线运动C.在1～2 s内,物体做匀变速直线运动D.在1～2 s内,物体做匀变速曲线运动[参考答案]C[试题解析] 在0～1 s内,物体水平方向为匀速直线运动,竖直方向为匀加速直线运动,则合运动为匀变速曲线运动,故选项A、B错误；在1～2 s内,物体水平方向初速度为：v0x＝4 m/s,加速度为：a x＝4 m/s2,竖直方向初速度为：v0y＝3 m/s,加速度为：a y＝3 m/s2,根据平行四边形定则合成可以得到合速度为v＝5 m/s,合加速度为a＝5 m/s2,而且二者方向在同一直线上,则根据曲线运动条件可知,合运动为匀变速直线运动,故选项C正确,D错误.变式2(2020·福建厦门市期末调研)如图4所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物()图4A.帆船朝正东方向航行,速度大小为vB.帆船朝正西方向航行,速度大小为vC.帆船朝南偏东45°方向航行,速度大小为2vD.帆船朝北偏东45°方向航行,速度大小为2v[参考答案]D[试题解析] 以帆板为参照物,帆船具有正东方向的速度v和正北方向的速度v,所以帆船相对帆板的速度v相对＝2v,方向为北偏东45°,D正确.1.船的实际运动：是水流的运动和船相对静水的运动的合运动.2.三种速度：船在静水中的速度v船、水的流速v水、船的实际速度v.3.两类问题、三种情景渡河时间最短当船头方向垂直河岸时,渡河时间最短,最短时间t min＝dv船渡河位移最短如果v船>v水,当船头方向与上游河岸夹角θ满足v船cos θ＝v水时,合速度垂直河岸,渡河位移最短,等于河宽d如果v船＜v水,当船头方向(即v船方向)与合速度方向垂直时,渡河位移最短,等于d v水v船4.分析思路例3(多选)甲、乙两船在同一河流中同时开始渡河,河水流速为v0,两船在静水中的速率均为v,甲、乙两船船头均与河岸成θ角,如图5所示,已知甲船恰能垂直河岸到达河正对岸的A 点,乙船到达河对岸的B点,A、B之间的距离为L,则下列判断正确的是()图5A.乙船先到达对岸B.若仅是河水流速v 0增大,则两船的渡河时间都不变C.不论河水流速v 0如何改变,只要适当改变θ角,甲船总能到达正对岸的A 点D.若仅是河水流速v 0增大,则两船到达对岸时,两船之间的距离仍然为L [参考答案]BD[试题解析] 将小船的运动分解为平行于河岸和垂直于河岸两个方向,由分运动和合运动具有等时性,知甲、乙两船到达对岸的时间相等,渡河的时间t ＝dv sin θ,故A 错误；若仅是河水流速v 0增大,渡河的时间t ＝dv sin θ,则两船的渡河时间都不变,故B 正确；只要甲船速度大于水流速度,不论河水流速v 0如何改变,甲船总能到达河的正对岸A 点,故C 错误；若仅是河水流速v 0增大,则两船到达对岸时间不变,根据速度的分解,船在水平方向相对于静水的分速度仍不变,则两船之间的距离仍然为L ,故D 正确.变式3 如图6所示,河水流动的速度为v 且处处相同,河宽度为a .在船下水点A 的下游距离为b 处是瀑布.为了使小船渡河安全(不掉到瀑布里去),则( )图6A.小船船头垂直河岸渡河时间最短,最短时间为t ＝bvB.小船轨迹垂直河岸渡河位移最小,渡河速度最大,最大速度为v max ＝a 2＋b 2vbC.当小船沿轨迹AB 渡河时,船在静水中的最小速度为v min ＝a vb D.当小船沿轨迹AB 渡河时,船在静水中的最小速度为v min ＝a v a 2＋b 2[参考答案]D[试题解析] 小船船头垂直河岸渡河时间最短,最短时间为t ＝av 船,故选项A 错误；小船轨迹垂直河岸渡河,位移最小,大小为a ,但船头必须指向上游,合速度不是最大,故选项B 错误；小船沿轨迹AB 运动,船在静水中的速度最小时,速度方向与AB 垂直,可得v min ＝a v a 2＋b 2,故选项C 错误,D正确.1.模型特点沿绳(杆)方向的速度分量大小相等. 2.思路方法合速度→绳(杆)拉物体的实际运动速度v分速度→⎩⎪⎨⎪⎧其一：沿绳(杆)的速度v 1其二：与绳(杆)垂直的速度v 2方法：v 1与v 2的合成遵循平行四边形定则. 3.解题原则把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.常见的模型如图7所示.图7模型1 绳端速度分解模型例4 质量为m 的物体P 置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P 与小车,P 与滑轮间的细绳平行于斜面,小车以速率v 水平向右做匀速直线运动,重力加速度为g .当小车与滑轮间的细绳和水平方向成夹角θ2时(如图8),下列判断正确的是( )图8A.P 的速率为vB.P 的速率为v cos θ2C.绳的拉力等于mg sin θ1D.绳的拉力小于mg sin θ1 [参考答案]B[试题解析] 将小车速度沿绳子和垂直绳子方向分解为v 1、v 2,P 的速率v P ＝v 1＝v cos θ2,A 错误,B 正确；小车向右做匀速直线运动,θ2减小,P 的速率增大,绳的拉力大于mg sin θ1,C 、D 错误. 变式4 A 、B 两物体通过一根跨过光滑轻质定滑轮的不可伸长的轻绳相连放在水平面上,现物体A 以v 1的速度向右匀速运动,当绳被拉成与水平面夹角分别是α、β时,如图9所示,物体B 的运动速度为(绳始终有拉力)( )图9A.v 1sin αsin βB.v 1cos αsin βC.v 1sin αcos βD.v 1cos αcos β [参考答案]D[试题解析] 设物体B 的运动速度为v B ,速度分解如图甲所示,则有v B ＝v 绳B cos β①物体A 的合运动对应的速度为v 1,它的速度分解如图乙所示,则有v 绳A ＝v 1cos α② 由于对应同一根绳,其长度不变,故v 绳B ＝v 绳A ③ 联立①②③式解得v B ＝v 1cos αcos β,选项D 正确.模型2 杆端速度分解模型例5 (2019·山东济南市3月模拟)曲柄连杆结构是发动机实现工作循环,完成能量转换的主要运动零件,如图10所示,连杆下端连接活塞Q ,上端连接曲轴P .在工作过程中,活塞Q 在汽缸内上下做直线运动,带动曲轴绕圆心O 旋转,若P 做线速度大小为v 0的匀速圆周运动,则下列说法正确的是( )图10A.当OP 与OQ 垂直时,活塞运动的速度等于v 0B.当OP 与OQ 垂直时,活塞运动的速度大于v 0C.当O 、P 、Q 在同一直线时,活塞运动的速度等于v 0D.当O 、P 、Q 在同一直线时,活塞运动的速度大于v 0 [参考答案]A[试题解析] 当OP 与OQ 垂直时,设∠PQO ＝θ,此时活塞的速度为v ,将P 的速度分解为沿杆方向和垂直于杆方向的速度；将活塞的速度v 分解为沿杆方向和垂直于杆方向的速度,则此时v 0cos θ＝v cos θ,即v ＝v 0,选项A 正确,B 错误；当O 、P 、Q 在同一直线时,P 沿杆方向的速度为零,则活塞运动的速度等于0,选项C 、D 错误.变式5 (2019·陕西宝鸡市高考模拟检测(二))如图11所示的机械装置可以将圆周运动转化为直线上的往复运动.连杆AB 、OB 可绕图中A 、B 、O 三处的转轴转动,连杆OB 在竖直面内的圆周运动可通过连杆AB 使滑块在水平横杆上左右滑动.已知OB 杆长为L ,绕O 点沿逆时针方向匀速转动的角速度为ω,当连杆AB 与水平方向夹角为α,AB 杆与OB 杆的夹角为β时,滑块的水平速度大小为( )图11A.ωL sin βsin αB.ωL cos βsin αC.ωL cos βcos αD.ωL sin βcos α[参考答案]D[试题解析] 设滑块的水平速度大小为v ,A 点的速度的方向沿水平方向,如图将A 点的速度分解,根据运动的合成与分解可知,沿杆方向的分速度：v A 分＝v cos α,B 点做圆周运动,实际速度是圆周运动的线速度,可以分解为沿AB 杆方向的分速度和垂直于AB 杆方向的分速度,如图,设B 的线速度为v ′,则：v B 分＝v ′cos θ＝v ′cos (β－90°)＝v ′cos (90°－β)＝v ′sin β,v ′＝ωL , 又二者沿杆方向的分速度是相等的,即：v A 分＝v B 分 联立可得：v ＝ωL sin βcos α,故D 正确.1.下列关于力与运动的叙述中正确的是()A.物体所受合力方向与运动方向有夹角时,该物体速度一定变化,加速度也变化B.物体做圆周运动,所受的合力一定指向圆心C.物体运动的速率在增加,所受合力方向与运动方向夹角小于90°D.物体在变力作用下有可能做曲线运动,做曲线运动物体一定受到变力作用[参考答案]C[试题解析] 物体所受合力方向与运动方向有夹角时,该物体速度一定变化,但加速度不一定变化,如平抛运动,A错误；若物体做变速圆周运动,则存在一个切向加速度,合力不指向圆心,B错误；合力方向与运动方向夹角小于90°时合力做正功,速度增大,C正确；如果变力与速度方向不共线,则做曲线运动,但做曲线运动的物体受到的合力可以为恒力,如平抛运动,D错误.2.如图1所示,长为L的直杆一端可绕固定轴O无摩擦转动,另一端靠在以水平速度v匀速向左运动、表面光滑的竖直挡板上,当直杆与竖直方向夹角为θ时,直杆端点A的线速度为()图1A.vsin θ B.v sin θ C.vcos θ D.v cos θ[参考答案]C[试题解析] 将直杆端点A的线速度进行分解,如图所示,由图中的几何关系可得：v0＝vcos θ,选项C正确,选项A、B、D错误.3.(多选)(2020·广东韶关市质检)在杂技表演中,猴子沿竖直杆向上做初速度为零、加速度为a 的匀加速运动,同时人顶着直杆以速度v0水平匀速前进,经过时间t,猴子沿杆向上移动的高度为h,人顶杆沿水平地面移动的距离为x,如图2所示.关于猴子的运动情况,下列说法中正确的是()图2A.相对地面的运动轨迹为直线B.相对地面做匀加速曲线运动C.t时刻猴子相对地面速度的大小为v0＋atD.t时间内猴子相对地面的位移大小为x2＋h2[参考答案]BD[试题解析] 猴子在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,合速度与合加速度不在同一条直线上,所以猴子运动的轨迹为曲线,故A错误.猴子在水平方向上的加速度为零,在竖直方向上有恒定的加速度,根据运动的合成,知猴子做曲线运动的加速度不变,做匀加速曲线运动,故B正确.t时刻猴子在水平方向上的分速度为v0,在竖直方向上的分速度为at,所以合速度v＝v02＋(at)2,故C错误.在t时间内猴子在水平方向和竖直方向上的分位移分别为x和h,根据运动的合成,知合位移大小为x2＋h2,故D正确.4.(2019·福建厦门市第一次质量检查)在演示“做曲线运动的条件”的实验中,有一个在水平桌面上向右做直线运动的小铁球,第一次在其速度方向上放置条形磁铁,第二次在其速度方向上的一侧放置条形磁铁,如图3所示,虚线表示小铁球的运动轨迹.观察实验现象,以下叙述正确的是()图3A.第一次实验中,小铁球的运动是匀变速直线运动B.第二次实验中,小铁球的运动类似平抛运动,其轨迹是一条抛物线C.该实验说明做曲线运动物体的速度方向沿轨迹的切线方向D.该实验说明物体做曲线运动的条件是物体受到的合外力的方向与速度方向不在同一直线上[参考答案]D[试题解析] 第一次实验中,小铁球受到沿着速度方向的引力作用,做直线运动,并且引力随着距离的减小而变大,加速度变大,则小铁球的运动是非匀变速直线运动,选项A错误；第二次实验中,小铁球所受的磁铁的引力方向总是指向磁铁,是变力,故小球的运动不是类平抛运动,其轨迹也不是一条抛物线,选项B错误；该实验说明物体做曲线运动的条件是物体受到的合外力的方向与速度方向不在同一直线上,但是不能说明做曲线运动物体的速度方向沿轨迹的切线方向,选项C错误,D正确.5.如图4所示,在灭火抢救过程中,消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业.为了节省救援时间,消防队员沿梯子匀加速向上运动的同时消防车匀速后退,则关于消防队员的运动,下列说法正确的是()图4A.消防队员做匀加速直线运动B.消防队员做匀变速曲线运动C.消防队员做变加速曲线运动D.消防队员水平方向的速度保持不变[参考答案]B[试题解析] 根据运动的合成,知合速度的方向与合加速度的方向不在同一条直线上,其合加速度的方向、大小不变,所以消防队员做匀变速曲线运动,故A、C错误,B正确.将消防队员的运动分解为水平方向和竖直方向,知水平方向上的最终的速度为匀速后退的速度和沿梯子方向速度在水平方向上的分速度的合速度,因为沿梯子方向的速度在水平方向上的分速度在变,所以消防队员水平方向的速度在变,故D错误.6.如图5所示,河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水＝3400x(m/s)(x的单位为m),让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船＝4 m/s,则下列说法中正确的是()图5A.小船渡河的轨迹为直线B.小船在河水中的最大速度是5 m/sC.小船在距南岸200 m处的速度小于在距北岸200 m处的速度D.小船渡河的时间是160 s[参考答案]B[试题解析] 小船在南北方向上为匀速直线运动,在东西方向上先加速,到达河中间后再减速,速度与加速度不共线,小船的合运动是曲线运动,A错.当小船运动到河中间时,东西方向上的分速度最大,为3 m/s,此时小船的合速度最大,最大值v m＝5 m/s,B对.小船在距南岸200 m处的速度等于在距北岸200 m处的速度,C错.小船的渡河时间t＝800 m4 m/s＝200 s,D错.7.(2019·山东烟台市期中)在一光滑的水平面上建立xOy平面直角坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的x－t图象和v y－t图象分别如图6甲、乙所示,求：图6(1)运动后4 s 内质点的最大速度的大小；(2)4 s 末质点离坐标原点的距离.[参考答案](1)2 5 m/s (2)8 m[试题解析] (1)由题图可知,质点沿x 轴正方向做匀速直线运动,速度大小为v x ＝x 1t 1＝2 m/s ,在运动后4 s 内,沿y 轴方向运动的最大速度为v y m ＝4 m/s,则运动后4 s 内质点运动的最大速度为v m ＝v x 2＋v y m 2＝2 5 m/s.(2)0～2 s 内质点沿y 轴正方向做匀加速直线运动,2～4 s 内先沿y 轴正方向做匀减速直线运动,再沿y 轴负方向做初速度为零的匀加速直线运动,此过程加速度大小为a ＝Δv Δt ＝62m/s 2＝3 m/s 2则质点沿y 轴正方向做匀减速运动的时间t 2＝v 1a ＝23s 则由题图乙可知,运动后的4 s 内沿y 轴方向的位移y ＝12×2×⎝⎛⎭⎫2＋23 m －12×4×(2－23) m ＝0 因此4 s 末质点离坐标原点的距离等于沿x 轴方向的位移由题图甲可知,4 s 末质点离坐标原点的距离s ＝x 1＝8 m.。

45分钟单元能力训练卷(四)[考查范围：第四单元分值：100分]一、选择题(本大题共14小题，每小题4分，共计56分。

在每小题列出的四个选项中，只有一项是符合题目要求的)1．2018年10月11日，国务院关于修改《中华人民共和国资源税暂行条例》的决定对外公布，将于2018年11月1日起施行。

这意味着去年6月开始在新疆试点的资源税改革终于要推向全国。

资源税的征收( )①表明宏观调控在资源配置中的基础性作用②政府运用经济手段调控资源配置③有利于推动资源节约型、环境友好型社会建设④表明市场具有盲目性和滞后性的缺陷A．①② B．③④ C．②③ D．①④2．近年来，我国出现了一系列食品安全事件。

一些企业在没有通过质量认证的情况下，把大量的食品添加剂应用于食品生产。

这表明市场具有( )A．盲目性 B．滞后性 C．自发性 D．开放性爆炒3．漫画《爆炒》给我们的启示是( )A．必须充分发挥市场的调节作用B．必须充分加强国家的宏观调控C．必须不断提高商品的社会必要劳动时间D．必须不断降低商品的个别劳动时间4．下图横向箭头显示的是一种宏观经济的收缩过程，纵向箭头显示的是针对过程中各环节相应的调控手段。

在市场经济条件下，政府应采用的手段是( )A．① B．② C．③ D．④5．为活跃农村消费市场，山东省财政厅、经贸委联合发出通知，“家电下乡”时间延长至2018年11月底，家电下乡产品扩展为彩电、冰箱、手机、洗衣机四大类，补贴金额仍然执行按销售价格的13%给予补贴。

此举( )①是政府在运用行政手段扩大内需②有利于扩大内需，促进经济增长③有利于提高农村居民的生活水平④是市场在调节家电资源的优化配置A．①② B．②③ C．①④ D．③④6．漫画《躲风头》告诉我们( )①市场调节具有盲目性和滞后性②必须规范市场秩序，强调诚实守信③取消市场在资源配置中的基础性地位④市场需要法律、道德的规范和引导A．①② B．③④C．②④ D．①③7．中国银监会有关负责人2018年8月12日表示，银监会将督促和引导银行业金融机构加大对保障性住房的信贷支持力度。

命题角度1Fe2＋、Fe3＋的性质及转化1.下列试剂中,不能使Fe2＋转化为Fe3＋的是()①氯气②NaCl溶液③酸性KMnO4溶液④稀硝酸⑤盐酸⑥NaNO3溶液A.①②③B.①③④C.②④⑤D.②⑤⑥2.(2019·烟台质检)FeCO3与砂糖混用可以作补血剂,实验室里制备FeCO3的流程如下图所示,下列说法不正确的是()A.可利用KSCN溶液检验FeSO4溶液是否变质B.沉淀过程中有CO2气体放出C.过滤操作的常用玻璃仪器有烧杯、漏斗和玻璃棒D.产品FeCO3在空气中高温分解可得到纯净的FeO3.将几滴KSCN(SCN－是“类似卤离子”)溶液加入到含有Fe3＋的酸性溶液中,溶液变为红色,将该红色溶液分为两份；①向其中一份溶液中加入适量KMnO4溶液,红色褪去；②向另一份溶液中通入SO2,红色也褪去。

下列说法中不正确的是()A.①中红色褪去的原因是KMnO4将SCN－氧化,使Fe(SCN)3消失B.②中红色褪去的原因是SO2将Fe3＋还原为Fe2＋C.②中红色褪去的原因是SO2将SCN－还原D.SCN－在适当条件下可失去电子被氧化剂氧化为(SCN)24.某同学在实验室进行铁盐与亚铁盐相互转化的实验。

实验Ⅰ：将Fe3＋转化为Fe2＋(1)Fe3＋与Cu粉发生反应的离子方程式为_______________________________________________________________________________________________________________。

(2)探究白色沉淀产生的原因,请填写实验方案。

实验方案现象 结论步骤1：取4mL________mol·L －1CuSO 4溶液,向其中滴加3滴0.1 mol·L－1KSCN 溶液产生白色沉淀CuSO 4溶液与KSCN 溶液反应产生了白色沉淀步骤2：取________________________________________________________________________ ________________________________________________________________________无明显现象查阅资料已知：①SCN －的化学性质与I －相似②2Cu 2＋＋4I －===2CuI ↓＋I 2Cu 2＋与SCN －反应的离子方程式为_____________________________________________ ________________________________________________________________________。

第四节 函数y =A sin ()x ωϕ+的图象及三角函数模型的简单应用强化训练1.将函数y =sin2x 的图象向左平移4π个单位长度,再向上平移1个单位长度,所得图象的函数解析式是( ) A.y =2cos 2x B.y =2sin 2xC.y =1+sin (2)4x π+D.y =cos2x答案:A解析:将函数y =sin2x 的图象向左平移4π个单位长度,得到函数y =sin 2()4x π+,即y =sin (2)2x π+=cos2x 的图象,再向上平移1个单位长度,所得图象的函数解析式为y =1+cos2x =2cos 2x ,故选A.2.已知函数f (x )=sin ()(4x x ωπ+∈R 0)ω,>的最小正周期为π,将y =f (x )的图象向左平移(0)ϕϕ>个单位长度,所得图象关于y 轴对称,则ϕ的一个值是( )A.2π B.38πC.4πD.8π答案:D解析:由已知,周期为π22πωω=,=,则结合平移公式和诱导公式可知平移后是偶函数,sin [2()]4x ϕπ++=±cos2x ,故选D.3.将函数y =sin x 的图象向左平移(02ϕϕ≤<π)个单位后,得到函数y =sin ()6x π-的图象,则ϕ等于( ) A.6π B.56πC.76πD.116π答案:D解析:由函数y =sin x 向左平移ϕ个单位得到y =sin ()x ϕ+的图象,由条件知函数y =sin ()x ϕ+可化为函数y =sin ()6x π-,比较各答案易知,只有y =sin 11()6x π+=sin ()6x π-,所以选D 项.4.要得到函数y =sin x 的图象,只需将函数y =cos(x -)3π的图象 .答案:向右平移6π个单位长度 解析:y =sin x =cos ()2x π-=cos ()2x π-=cos [()]36x ππ--.∴将y =cos ()3x π-的图象向右平移6π个单位长度可得到y =sin x 的图象.课后作业题组一 函数y =A sin ()x ωϕ+图象的作法和变换 1.函数y =cos (x x ∈R )的图象向左平移2π个单位长度后,得到函数y =g(x )的图象,则g(x )的解析式为 ( ) A.g(x )=-sin x B.g(x )=sin x C.g(x )=-cos x D.g(x )=cos x答案:A解析:y =cos ()2x π+=-sin x . 2.为得到函数y =cos ()3x π+的图象,只需将函数y =sin x 的图象( ) A.向左平移6π个单位长度B.向右平移π个单位长度C.向左平移56π个单位长度D.向右平移56π个单位长度答案:C解析:y =sin x =cos ()2x π-=cos 5()36x ππ+-.3.已知函数f (x )=sin ()(4x x ωπ+∈R 0)ω,>的最小正周期为π,为了得到函数g(x )=cos x ω的图象,只需将y =f (x )的图象( ) A.向左平移8π个单位长度B.向右平移8π个单位长度C.向左平移4π个单位长度D.向右平移4π个单位长度答案:A解析:由题知2ω=, 所以f (x )=sin (2)x π+ =cos [(2)]24x ππ-+=cos (2)4x π-=cos 2()8x π-,故选择A.4.(2018课标全国,理11)设函数f (x )=sin (x ω+)ϕ+cos (x ω+)(0ϕω>,|ϕ|)2π<的最小正周期为π,且f (-x )=f (x ),则( )A.f (x )在(0)2π,上单调递减B.f (x )在3()44ππ,上单调递减C.f (x )在(0)2π,上单调递增D.f (x )在3()44ππ,上单调递增答案:A解析:∵f (x )=sin ()x ωϕ++cos ()x ωϕ+=(x ω+ϕ+)4π,又∵f (x )的最小正周期为π,∴2πω=π,即2ω=.又f (-x )=f (x ),故f (x )是偶函数, 即42k ππϕ+=+π(k ∈Z )k ϕ,=π(4k π+∈Z ).因|ϕ|2π<,取k=0,则4ϕπ=,从而()f x =x ,且在(0)2π,上单调递减,故选A.5.函数y =sin (2)3x π-在区间[2π-,π]内的简图是( )答案:A6.已知函数y =f (x )的图象上的每一点的纵坐标扩大到原来的4倍,横坐标扩大到原来的2倍,然后把所得的图象沿x 轴向左平移2π个单位长度,这样得到的曲线和y =2sin x 的图象相同,则函数y =f (x )的解析式为 . 答案:12y =-cos2x 解析:y =2sin x y =2sin ()2x π-y =2sin (2)2x π-y =12sin (2)2x π-12=-cos2x .7.已知函数12y =sin (2)6x x π+,∈R . (1)求它的振幅、周期、初相;(2)用五点法作出它的简图;(3)该函数的图象可由y =sin (x x ∈R )的图象经过怎样的平移和伸缩变换得到? 解:(1)函数12y =sin (2)6x π+的振幅为12,周期为π,初相为6π. (2)列表:画简图如下图所示:(3)方法一:函数y =sin x 的图象函数y =sin ()6x π+的图象函数y =sin(2x +)6π的图象函数y =12sin(2x +)6π的图象.方法二:函数y =sin x 的图象函数y =sin2x 的图象函数y =sin(2x +)6π的图象函数y =12sin(2x +)6π的图象. 题组二 求函数y =Asin ()x b ωϕ++的解析式 8.已知简谐运动f (x )=2sin ()(3x ϕπ+|ϕ|)2π<的图象经过点(0,1),则该简谐运动的最小正周期T 和初相ϕ分别为( )A.66T ϕπ=,= B.63T πϕ=,=C.T=6π6ϕπ,=D.T=6ππϕ,=答案:A解析:263T ππ==,又∵f (0)=2sin 1ϕ=,∴sin 12ϕ=.∵|ϕ|2π<,∴6ϕπ=.9.函数f (x )=A sin ()(x ωϕ+其中00A ω>,>,|ϕ|)2π<的图象如图所示,则f (0)等于( )A.1B.12答案:D解析:由题图可知A =1,22274()123T ππωππ===,⨯-∴f (x )=sin (2)x ϕ+, ()3f π=sin (2)03ϕπ⨯+=. ∵A>0,|ϕ|2π<,∴3πϕ=.∴f (0)=sin (0)3π+=sin 3π=10.已知函数y =sin ()x ωϕ+(0ω>,-πϕ≤π<)的图象如图所示,则ϕ= .答案:910π解析:由题图可知,T=2(2π35)42ππ-=,∴45ω=.把(2π,1)代入y =sin 4()5x ϕ+,有1=sin 8()5πϕ+,∴910πϕ=.11.已知函数f (x )=2sin ()(0x ωϕω+>,-π0)ϕ<<的图象如图所示,则7()12f π= .答案:0解析:由题中图象知最小正周期5222()3443T ππππω=-==,故3ω=,又4x π=时,f (x )=0,即2sin (3)04πϕ⨯+=,又-π0ϕ<<,可得ϕ=34π-,所以7()212f π=sin 73(3)0124ππ⨯-=.12.已知函数f (x )=A sin ()(00x A ωϕω+>,>,|ϕ|)2π<的部分图象如图所示.(1)求函数f (x )的解析式;(2)如何由函数y =2sin x 的图象通过适当的变换得到函数f (x )的图象,写出变换过程. 解:(1)由题中图象知A =2,f (x )的最小正周期54()126T ππ=⨯-=π,故22Tπω==,将点(2)6π,代入f (x )的解析式得sin ()13ϕπ+=,又|ϕ|2π<, ∴6ϕπ=.故函数f (x )的解析式为f (x )=2sin (2)6x π+. (2)变换过程如下:y =2sin x 图象y =2sin ()6x π+y =2sin (2)6x π+;另解:y =2sin x y =2sin2xy =2sin (2)6x π+.。

[高2021届高2018级高三数学一轮专题训练24]第五讲 函数y ＝A sin(ωx ＋φ)的图象及应用A 组基础巩固一、单选题1.将函数f (x )的图象上所有点向右平移π4个单位长度，得到函数g (x )的图象.若函数g (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|＜π2)的部分图象如图所示，则函数f (x )的解析式为( C )A.f (x )＝sin(x ＋5π12)B.f (x )＝－cos(2x ＋π3)C.f (x )＝cos(2x ＋π3)D.f (x )＝sin(2x ＋7π12)【试题解答】 根据函数g (x )的图象可知A ＝1，12T ＝π3＋π6＝π2，T ＝π＝2πω，ω＝2，所以g (x )＝sin(2x＋φ)，所以g (π3)＝sin(2π3＋φ)＝0，所以2π3＋φ＝π＋k π，k ∈Z ，φ＝π3＋k π，k ∈Z ，又因为|φ|＜π2，所以φ＝π3，所以g (x )＝sin(2x ＋π3)，将g (x )＝sin(2x ＋π3)的图象向左平移π4个单位长度后，即可得到函数f (x )的图象，所以函数f (x )的解析式为f (x )＝g (x ＋π4)＝sin[2(x ＋π4)＋π3]＝sin(π2＋2x ＋π3)＝cos(2x ＋π3).2.(2020·浙江金华十校期末)要得到函数y ＝cos (2x ＋π3)的图象，只需将函数y ＝cos 2x 的图象( B )A.向左平移π3个单位B.向左平移π6个单位C.向右平移π6个单位D.向右平移π3个单位【试题解答】 ∵y ＝cos (2x ＋π3)＝cos [2(x ＋π6)]，∴要得到函数y ＝cos (2x ＋π3)的图象，只需将函数y＝cos 2x 的图象向左平移π6个单位.3.(2020·河南豫南九校联考)将函数y ＝sin (x －π4)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再向右平移π6个单位，则所得函数图象的解析式为( B )A.y ＝sin (x 2－5π24)B.y ＝sin (x 2－π3)C.y ＝sin (x 2－5π12)D.y ＝sin (2x －7π12)【试题解答】 函数y ＝sin (x －π4)经伸长变换得y ＝sin (x 2－π4)，再作平移变换得y ＝sin [12(x －π6)－π4]＝sin (x 2－π3).4.(2020·安徽省宿州市高三上学期检测)已知函数f (x )＝A sin (ωx ＋φ)(A >0，ω>0,0＜φ＜π2)的部分图象如图所示，若将函数f (x )的图象上点的纵坐标不变，横坐标缩短到原来的14，再向右平移π6个单位，所得到的函数g (x )的解析式为( D )A.g (x )＝2sin 14xB.g (x )＝2sin 2xC.g (x )＝2sin (14x －π6)D.g (x )＝2sin (2x －π6)【试题解答】 由图象可得A ＝2，T 4＝π，故T ＝4π，ω＝12，∴f (x )＝2sin (12x ＋φ)，∵点(0,1)在函数的图象上，∴f (0)＝2sin φ＝1，∴sin φ＝12，又0＜φ＜π2，∴φ＝π6，∴f (x )＝2sin (12x ＋π6)，将函数f (x )的图象上点的纵坐标不变，横坐标缩短到原来的14所得图象对应的解析式为y ＝2sin (12×4x＋π6)＝2sin (2x ＋π6)，然后再向右平移π6个单位，所得图象对应的解析式为y ＝2sin [2(x －π6)＋π6]＝2sin (2x －π6)，即g (x )＝2sin (2x －π6)，选D.5.设函数f (x )＝sin (ωx ＋φ)＋cos (ωx ＋φ)(ω>0，|φ|＜π2)的最小正周期为π，且f (－x )＝f (x )，则( A )A.f (x )在(0，π2)上单调递减B.f (x )在(0，π2)上单调递增C.f (x )在(π4，3π4)上单调递增D.f (x )在(π2，π)上单调递减【试题解答】 f (x )＝sin (ωx ＋φ)＋cos (ωx ＋φ)＝2sin (ωx ＋φ＋π4).由函数f (x )的最小正周期T ＝2πω＝π，得ω＝2. 由f (－x )＝f (x )，得φ＋π4＝π2＋k π(k ∈Z )，即φ＝π4＋k π(k ∈Z ).又∵|φ|＜π2，∴φ＝π4.∴f (x )＝2sin (2x ＋π2)＝2cos 2x .若2x ∈(0，π)，则x ∈(0，π2)，∴f (x )在(0，π2)上单调递减.故选A.6.已知曲线C ：y ＝sin (2x ＋φ)(|φ|＜π2)的一条对称轴方程为x ＝π6，曲线C 向左平移θ(θ>0)个单位长度，得到的曲线E 的一个对称中心为(π6，0)，则|φ－θ|的最小值是( A )A.π12B.π4C.π3D.5π12【试题解答】 因为曲线C ：y ＝sin (2x ＋φ)(|φ|＜π2)的一条对称方程为x ＝π6，所以sin (π3＋φ)＝±1，则π3＋φ＝π2＋k π，k ∈Z .因为|φ|＜π2，所以φ＝π6.可得曲线C ：y ＝sin (2x ＋π6)，向左平移θ个单位长度，得曲线E ：y ＝sin (2x ＋2θ＋π6).由曲线E 的对称中心为(π6，0)，得2×π6＋2θ＋π6＝k π，k ∈Z ，所以θ＝12k π－π4，k ∈Z ，则|φ－θ|＝⎪⎪⎪⎪π4＋π6－12k π(k ∈Z )的最小值为：π12.故选A. 二、多选题7.(2020·辽宁省实验中学期中改编)已知函数y ＝A sin (ωx ＋φ)＋B (A >0，ω>0，|φ|＜π2)的部分图象如图，则下面不正确的是( ABC )A.A ＝4B.ω＝1C.B ＝4D.φ＝π6【试题解答】 根据函数y ＝A sin (ωx ＋φ)＋B 的图象知，A ＝2，B ＝2，∴A ，C 错误；设函数的最小正周期为T ，则14T ＝512π－π6＝π4，∴T ＝2πω＝π，解得ω＝2，B 错误；当x ＝π6时，ωx ＋φ＝2×π6＋φ＝2k π＋π2(k ∈Z )，且|φ|＜π2，∴φ＝π6，∴D 正确.故选A 、B 、C.8.已知函数f (x )＝3sin ωx ＋cos ωx (ω>0)的图象相邻两条对称轴之间的距离是π2，则该函数的一个单调递增区间为( AD )A.[－π3，π6]B.[－5π12，π12]C.[－π6，2π3]D.[2π3，7π6]【试题解答】 根据已知得f (x )＝3sin ωx ＋cos ωx ＝2(32sin ωx ＋12cos ωx )＝2sin (ωx ＋π6).根据相邻两条对称轴之间的距离是π2，得T ＝π，所以2πω＝π，即ω＝2，所以函数f (x )＝2sin (2x ＋π6).再根据正弦函数的单调性可得该函数的单调递增区间是2k π－π2≤2x ＋π6≤2k π＋π2(k ∈Z )，解得k π－π3≤x ≤k π＋π6(k ∈Z ).令k ＝0,1即可求得其一个单调递增区间是[－π3，π6]、[2π3，7π6].故选A 、D.三、填空题9.(1)为了得到函数y ＝sin (x ＋1)的图象，只需把函数y ＝sin x 的图象上所有的点向__左__平移__1__个单位长度.(2)为了得到函数y ＝sin (2x ＋1)的图象，只需把函数y ＝sin 2x 的图象上所有的点向__左__平移 12 个单位长度.10.已知函数f (x )＝2sin (π3x ＋φ)(|φ|＜π2)的图象经过点(0,1)，则该函数的振幅为__2，周期T 为__6，频率为 16 ，初相φ为 π6.【试题解答】 振幅A ＝2，T ＝2ππ3＝6，f ＝16，因为图象过点(0,1)，所以1＝2sin φ，所以sin φ＝12，又|φ|＜π2，所以φ＝π6.11.(2020·南昌模拟)将函数f (x )＝sin (ωx ＋φ)(ω>0，－π2＜φ＜π2)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π6个单位长度得到y ＝sin x 的图象，则f (π6)＝ 2.【试题解答】 将y ＝sin x 的图象向左平移π6个单位长度，再把横坐标伸长到原来的2倍，纵坐标不变，得f (x )＝sin (12x ＋π6)，所以f (π6)＝sin (12·π6＋π6)＝sin π4＝22.12.(2020·重庆模拟)已知函数y ＝A sin (ωx ＋φ)(A >0，ω>0，|φ|＜π2)的图象上有一个最高点的坐标为(2，2)，由这个最高点到其右侧相邻最低点间的图象与x 轴交于点(6,0)，则此解析式为 y ＝2sin (π8x ＋π4) .【试题解答】 由题意得：A ＝2，T 4＝6－2，T ＝16，ω＝2πT ＝π8，又sin (π8×2＋φ)＝1，π4＋φ＝π2＋2k π(k∈Z )，又|φ|＜π2，所以φ＝π4，所以函数解析式为y ＝2sin (π8x ＋π4).四、解答题13.(2020·江西南昌实验中学月考)已知函数f (x )＝2sin (12x ＋π6).(1)用“五点法”在如图所示的虚线方框内作出函数f (x )在一个周期内的简图(要点：列表与描点，建立直角坐标系)；(2)函数f (x )的图象可以通过函数g (x )＝2cos x 的图象经过“先伸缩后平移”的规则变换而得到，请写出一个这样的变换.【试题解答】 (1)列表如下：x －π3 2π3 5π3 8π3 11π3 12x ＋π6 0 π2 π 3π2 2π f (x )2－2图象如图所示：(2)g (x )＝2cos x ＝2sin (x ＋π2)，先将横坐标伸长为原来的2倍，得到y ＝2sin (x 2＋π2)，再向右平移2π3个单位，得到f (x )＝2sin (12x ＋π6).(答案不唯一)14.(2020·河北沧州模拟)已知函数f (x )＝A sin (ωx ＋φ)(A >0，ω>0，|φ|＜π2)的部分图象如图所示.(1)求函数f (x )的解析式，并求它的对称中心的坐标；(2)将函数f (x )的图象向右平移m (0＜m ＜π2)个单位，得到的函数g (x )为偶函数，求函数y ＝f (x )g (x )＋34(x∈[－π12，π6])的最值及相应的x 值.【试题解答】 (1)根据图象知A ＝3，34T ＝11π12－π6＝3π4，∴T ＝2πω＝π，∴ω＝2，∴f (x )＝3sin (2x ＋φ).将点(π6，3)代入，即3sin (π3＋φ)＝ 3.又|φ|＜π2，∴φ＝π6，∴f (x )＝3sin (2x ＋π6).令2x ＋π6＝k π(k ∈Z )，解得x ＝k π2－π12(k ∈Z )，∴f (x )的对称中心的坐标为(k π2－π12，0)(k ∈Z ).(2)g (x )＝3sin (2x －2m ＋π6)，∵g (x )为偶函数，∴－2m ＋π6＝k π＋π2(k ∈Z )，∴m ＝－k π2－π6(k ∈Z ).又∵0＜m ＜π2，∴m ＝π3，∴g (x )＝3sin (2x －π2)＝－3cos 2x ，∴y ＝f (x )g (x )＋34＝－3cos 2x sin (2x ＋π6)＋34＝－3cos 2x ·(32sin 2x ＋12cos 2x )＋34＝－334sin 4x －32×1＋cos 4x 2＋34＝－32(32sin 4x ＋12cos 4x )＝－32sin (4x ＋π6).又∵x ∈[－π12，π6]，∴4x ＋π6∈[－π6，5π6].∴sin (4x ＋π6)∈[－12，1]，∴y max ＝34，此时x ＝－π12；y min ＝－32，此时x ＝π12.B 组能力提升1.(2020·郑州市第一次质量预测)若将函数f (x )＝12sin (2x ＋π3)图象上的每一个点都向左平移π3个单位长度，得到g (x )的图象，则函数g (x )的单调递增区间为( A )A.[k π＋π4，k π＋3π4](k ∈Z )B.[k π－π4，k π＋π4](k ∈Z )C.[k π－2π3，k π－π6](k ∈Z )D.[k π－π12，k π＋5π12](k ∈Z )【试题解答】 将函数f (x )＝12sin (2x ＋π3)图象上的每一个点都向左平移π3个单位长度，得到函数g (x )＝12sin [2(x ＋π3)＋π3]＝12sin (2x ＋π)＝－12sin 2x 的图象，令π2＋2k π≤2x ≤3π2＋2k π(k ∈Z )，可得π4＋k π≤x ≤3π4＋k π(k ∈Z )，因此函数g (x )的单调递增区间为[k π＋π4，k π＋3π4](k ∈Z ).故选A.2.如果存在正整数ω和实数φ使得函数f (x )＝sin 2(ωx ＋φ)的图象如图所示(图象经过点(1,0))，那么ω的值为( B )A.1B.2C.3D.4【试题解答】 由f (x )＝sin 2(ωx ＋φ)＝1－cos (2ωx ＋2φ)2及其图象知，12＜12×2π2ω＜1，即π2＜ω＜π，所以正整数ω＝2或3.由函数f (x )的图象经过点(1,0)，得f (1)＝1－cos (2ω＋2φ)2＝0，得2ω＋2φ＝2k π(k ∈Z )，即2φ＝2k π－2ω(k ∈Z ).由图象知f (0)>12，即1－cos 2φ2＝1－cos 2ω2>12，得cos 2ω＜0，所以ω＝2.故选B.3.(多选题)(2020·吉林通化月考改编)已知ω>0，a >0，f (x )＝a sin ωx ＋3a cos ωx ，g (x )＝2cos (ax ＋π6)，h (x )＝f (x )g (x ).这3个函数在同一直角坐标系中的部分图象如图所示，则函数g (x )＋h (x )的图象的一条对称轴方程可以为( AC )A.x ＝π12B.x ＝13π6C.x ＝－23π12D.x ＝－29π12【试题解答】 ∵f (x )＝a sin ωx ＋3a cos ωx ＝2a sin (ωx ＋π3)，g (x )＝2cos (ax ＋π6)，又由函数图象可知，f (x )的最大值为2，可得a ＝1，∴f (x )＝2sin (ωx ＋π3)，g (x )＝2cos (x ＋π6)，由图象可知，f (x )的周期为π，∴ω＝2，h (x )＝f (x )g (x )＝2sin (2x ＋π3)2cos (x ＋π6)＝2sin (x ＋π6)，x ≠k π＋π3(k ∈Z ).那么函数g (x )＋h (x )＝2cos (x ＋π6)＋2sin (x ＋π6)＝22sin (x ＋π6＋π4)＝22sin (x ＋5π12)，x ≠k π＋π3(k ∈Z ).令x ＋5π12＝π2＋k π(k ∈Z ).可得对称轴方程为x ＝π12＋k π(k ∈Z )，当k ＝0时，x ＝π12，当k ＝－2时，可得x ＝－23π12.故选A 、C.4.(2020·四川达州高级中学诊断)已知f (x )＝2sin (2x －π6)－m 在x ∈[0，π2]上有两个零点，则实数m 的取值范围为( C )A.(1,2)B.[1,2]C.[1,2)D.(1,2]【试题解答】 f (x )＝2sin (2x －π6)－m ＝0，即m ＝2sin (2x －π6)记g (x )＝2sin (2x －π6)，x ∈[0，π2]其图象如下图，由图可知m 的取值范围是[1,2)，故选C.5.某同学用“五点法”画函数f (x )＝A sin (ωx ＋φ)(ω>0，|φ|＜π2)在某一个周期内的图象时，列表并填入了部分数据，如下表：ωx ＋φ 0 π2 π 3π2 2π x π3 5π6 A sin (ωx ＋φ)5－5(1)(2)将y ＝f (x )图象上所有点向左平行移动θ(θ>0)个单位长度，得到y ＝g (x )的图象.若y ＝g (x )图象的一个对称中心为(5π12，0)，求θ的最小值.【试题解答】 (1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6.数据补全如下：且函数表达式为f (x )＝5sin (2x －π6).(2)由(1)知f (x )＝5sin (2x －π6)，得g (x )＝5sin (2x ＋2θ－π6).因为y ＝sin x 图象的对称中心为(k π，0)，k ∈Z ， 所以令2x ＋2θ－π6＝k π，k ∈Z ，解得x ＝k π2＋π12－θ，k ∈Z .由于函数y ＝g (x )图象的一个对称中心为(5π12，0)，令k π2＋π12－θ＝5π12，k ∈Z ， 解得θ＝k π2－π3，k ∈Z .由θ>0可知，当k ＝1时，θ取得最小值π6.。

[高2021届高2018级高三数学一轮专题训练27]第四章 平面向量、数系的扩充与复数的引入第一讲 平面向量的概念及其线性运算A 组基础巩固一、单选题 1.设a 0为单位向量，①若a 为平面内的某个向量，则a ＝|a |a 0； ②若a 与a 0平行，则a ＝|a |a 0； ③若a 与a 0平行且|a |＝1，则a ＝a 0. 上述命题中，假命题的个数是( D ) A.0 B.1 C.2D.3【试题解答】 向量是既有大小又有方向的量，a 与|a |a 0的模相同，但方向不一定相同，故①是假命题；若a 与a 0平行，则当a 为零向量时，a 的方向任意；当a 不为零向量时，a 与a 0的方向有两种情况：一是同向，二是反向，反向时a ＝－|a |a 0，故②③也是假命题，综上所述，假命题的个数是3.故选D.2.D 是△ABC 的边AB 上的中点，则向量CD →等于( A ) A.－BC →＋12BA →B.－BC →－12BA →C.BC →－12BA →D.BC →＋12BA →【试题解答】 如图所示，CD →＝CB →＋BD →＝CB →＋12BA →＝－BC →＋12BA →.故选A.3.如图所示的方格纸中有定点O ，P ，Q ，E ，F ，G ，H ，则OP →＋OQ →＝( D )A.OH →B.OG →C.EO →D.FO →【试题解答】 在方格纸上作出OP →＋OQ →，如图所示，则容易看出OP →＋OQ →＝FO →，故选D.4.(2018·课标全国Ⅰ)设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB →＋FC →＝( A ) A.AD → B.12AD → C.BC →D.12BC → 【试题解答】 EB →＋FC →＝12(AB →＋CB →)＋12(AC →＋BC →)＝12(AB →＋AC →)＝AD →，故选A.5.(2020·重庆高三二诊)已知两个非零向量a ，b 互相垂直，若向量m ＝4a ＋5b 与n ＝2a ＋λb 共线，则实数λ的值为( C )A.5B.3C.52D.2【试题解答】 因为向量m ＝4a ＋5b 与n ＝2a ＋λb 共线，所以存在实数t ，使得m ＝t n ，即4a ＋5b ＝t (2a ＋λb )，又向量a ，b 互相垂直，故a ，b 不共线，所以⎩⎪⎨⎪⎧2t ＝4，tλ＝5，解得⎩⎪⎨⎪⎧t ＝2，λ＝52.故选C.6.(2020·黑龙江统一仿真模拟)点G 为△ABC 的重心(三角形三边中线的交点)，设BG →＝a ，GC →＝b ，则AB →＝( D )A.32a －12b B.32a ＋12b C.2a －bD.b －2a【试题解答】 如图，EB →＋BG →＝EG →，即12AB →＋BG →＝12GC →， 故AB →＝GC →－2BG →＝b －2a .故选D. 二、多选题7.(2020·湖北枣阳白水高中期中改编)下列说法正确的是( BC )A.单位向量都相等B.模为0的向量与任意向量共线C.平行向量一定是共线向量D.任一向量与它的相反向量不相等【试题解答】 对于A ，单位向量的模相等，方向不一定相同，所以A 错误；对于B ，模为0的向量为零向量，零向量和任意向量共线，所以B 正确；对于C ，共线向量是方向相同或相反的非零向量，也叫平行向量，所以C 正确；对于D ，零向量与它的相反向量相等，所以D 错误，故选B 、C 正确.8.(2020·广东仲元中学期中改编)在平行四边形ABCD 中，下列结论错误的是( AC ) A.|AB →|＝|AD →|一定成立 B.AC →＝AB →＋AD →一定成立 C.AD →＝CB →一定成立 D.BD →＝AD →－AB →一定成立【试题解答】 在平行四边形ABCD 中，AC →＝AB →＋AD →一定不成立，AD →＝CB →一定不成立，BD →＝AD →－AB →一定成立，但|AB →|＝|AD →|不一定成立，故选A 、C.三、填空题9.如图所示，下列结论不正确的是__②④__.①PQ →＝32a ＋32b ；②PT →＝－32a －32b ；③PS →＝32a －12b ；④PR →＝32a ＋b .【试题解答】 由a ＋b ＝23PQ →，知PQ →＝32a ＋32b ，①正确；由PT →＝32a －32b ，从而②错误；PS →＝PT →＋b ，故PS →＝32a －12b ，③正确；PR →＝PT →＋2b ＝32a ＋12b ，④错误.故正确的为①③.10.设a 和b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于__－4__.【试题解答】 ∵A ，B ，D 三点共线，∴AB →∥BD →.∵AB →＝2a ＋k b ，BD →＝BC →＋CD →＝a －2b ，∴k ＝－4.故填－4.11.(2020·河南三市联考)若AP →＝12PB →，AB →＝(λ＋1)BP →，则λ＝ －52.【试题解答】 由AP →＝12PB →可知，点P 是线段AB 上靠近点A 的三等分点，则AB →＝－32BP →，所以λ＋1＝－32，解得λ＝－52.12.如图所示，已知∠B ＝30°，∠AOB ＝90°，点C 在AB 上，OC ⊥AB ，若用OA →和OB →来表示向量OC →，则OC →＝ 34OA →＋14OB → .【试题解答】 易知OC →＝OA →＋AC →＝OA →＋14AB →＝OA →＋14(OB →－OA →)＝34OA →＋14OB →.四、解答题13.(1)设e 1，e 2是两个不共线向量，已知AB →＝2e 1－8e 2，CB →＝e 1＋3e 2，CD →＝2e 1－e 2. ①求证：A ，B ，D 三点共线；②若BF →＝3e 1－k e 2，且B ，D ，F 三点共线，求实数k 的值；(2)已知a 、b 不共线，若向量k a ＋b 与a ＋k b 共线反向，求实数k 的值.【试题解答】 (1)①证明：由已知得BD →＝CD →－CB →＝(2e 1－e 2)－(e 1＋3e 2)＝e 1－4e 2， ∵AB →＝2e 1－8e 2，∴AB →＝2BD →，又AB →与BD →有公共点B ， ∴A ，B ，D 三点共线. ②由①可知BD →＝e 1－4e 2，又BF →＝3e 1－k e 2，由B ，D ，F 三点共线，得BF →＝λBD →， 即3e 1－k e 2＝λe 1－4λe 2，∴⎩⎪⎨⎪⎧λ＝3，－k ＝－4λ，解得k ＝12， (2)∵k a ＋b 与a ＋k b 共线反向， ∴存在实数λ使k a ＋b ＝λ(a ＋k b )(λ＜0).∴⎩⎪⎨⎪⎧k ＝λ，kλ＝1.∴k ＝±1.又λ＜0，∴k ＝－1. B 组能力提升1.在平行四边形ABCD 中，若|AB →＋AD →|＝|AB →－AD →|，则四边形ABCD 的形状为( C ) A.梯形B.菱形C.矩形D.正方形【试题解答】如图，因为AB →＋AD →＝AC →，AB →－AD →＝DB →，所以|AC →|＝|DB →|.由对角线长相等的平行四边形是矩形可知，四边形ABCD 是矩形.2.(2020·广西玉林高中模拟)设D ，E ，F 分别为△ABC 三边BC ，CA ，AB 的中点，则DA →＋2EB →＋3FC →＝( D )A.12AD →B.32AD →C.12AC → D.32AC → 【试题解答】 ∵D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，∴DA →＋2EB →＋3FC →＝12(BA →＋CA →)＋2×12(AB →＋CB →)＋3×12(AC →＋BC →)＝12BA →＋12CA →＋AB →＋CB →＋32AC →＋32BC →＝12AB →＋12BC →＋AC →＝32AC →.3.(2020·江西南昌莲塘一中质检)已知a ，b 是不共线的向量，AB →＝λa ＋b ，AC →＝a ＋μb (λ，μ∈R )，若A ，B ，C 三点共线，则λ，μ的关系一定成立的是( A )A.λμ＝1B.λμ＝－1C.λ－μ＝－1D.λ＋μ＝2【试题解答】 ∵AB →与AC →有公共点A ，∴若A ，B ，C 三点共线，则存在一个实数t 使AB →＝tAC →，即λa＋b ＝t a ＋μt b ，则⎩⎪⎨⎪⎧λ＝t ，μt ＝1，消去参数t 得λμ＝1；反之，当λμ＝1时，AB →＝1μa ＋b ，此时存在实数1μ使AB →＝1μAC →，故AB →和AC →共线 .∵AB →与AC →有公共点A ，∴A ，B ，C 三点共线.故选A.4.(2020·四川成都七中一诊)已知点O ，A ，B 不在同一条直线上，点P 为该平面上一点，且2OP →＝2OA →＋BA →，则( B )A.点P 在线段AB 上B.点P 在线段AB 的反向延长线上C.点P 在线段AB 的延长线上D.点P 不在直线AB 上【试题解答】 ∵2OP →＝2OA →＋BA →，∴2OP →－2OA →＝BA →，即2AP →＝BA →，∴点P 在线段AB 的反向延长线上，故选B.5.(2020·甘肃诊断)设D 为△ABC 所在平面内一点，BC →＝－4CD →，则AD →＝( B ) A.14AB →－34AC →B.14AB →＋34AC →C.34AB →－14AC →D.34AB →＋14AC →【试题解答】 解法一：设AD →＝xAB →＋yAC →，由BC →＝－4CD →可得，BA →＋AC →＝－4CA →－4AD →，即－AB →－3AC →＝－4xAB →－4yAC →，则⎩⎪⎨⎪⎧－4x ＝－1，－4y ＝－3，解得⎩⎨⎧x ＝14，y ＝34，即AD →＝14AB →＋34AC →，故选B.解法二：在△ABC 中，BC →＝－4CD →，即－14BC →＝CD →，则AD →＝AC →＋CD →＝AC →－14BC →＝AC →－14(BA →＋AC →)＝14AB →＋34AC →，故选B.。

1.如图均为电化学装置,下列有关叙述正确的是()A.装置①中,b电极发生氧化反应B.装置②中,铁棒上析出红色固体C.装置③中,若电镀前两电极质量相等,电镀完成后二者质量差为5.12 g,则电镀时待镀铁制品应与电源负极相连,外电路转移0.08 mol电子D.装置④中,离子交换膜应为阴离子交换膜2.(2019·沈阳一中检测)金属镍有广泛的用途。

粗镍中含有少量Fe、Zn、Cu、Pt等杂质,可用电解法制备高纯度的镍,下列叙述正确的是(已知：氧化性Fe2＋<Ni2＋<Cu2＋)()A.阳极发生还原反应,其电极反应式：Ni2＋＋2e－===NiB.电解过程中,阳极质量的减少与阴极质量的增加相等C.电解后,溶液中存在的金属阳离子只有Fe2＋和Zn2＋D.电解后,电解槽底部的阳极泥中只有Cu和Pt3.锂硫电池是一种新型储能电池,放电时的总反应为2Li＋x S===Li2S x。

以该电池为电源制备甲烷的原理如图所示。

下列说法正确的是()A.b为锂硫电池的负极B.锂硫电池的正极反应式为Li －e －===Li ＋C.阳极反应式为CO ＋3CO 2－3＋2H 2O －2e －===4HCO －3D.该装置工作时溶液中的c (CO 2－3)增大4.(2019·山东临沂一模)Cu 2O 是一种半导体材料,基于绿色化学理论设计的制取Cu 2O 的电解池示意图如下,电解总反应为2Cu ＋H 2O=====电解Cu 2O ＋H 2↑。

下列说法正确的是( )A.石墨电极上产生氢气B.铜电极发生还原反应C.铜电极接直流电源的负极D.当有0.1 mol 电子转移时,有0.1 mol Cu 2O 生成5.如图A 为碱性硼化钒(VB 2)—空气电池示意图,两极用离子交换膜隔开,VB 2放电时生成两种氧化物。

若用该电池为电源,用惰性电极电解硫酸铜溶液,实验装置如图B 所示。

则下列说法错误的是( )A.碱性硼化钒(VB 2)—空气电池中使用阴离子交换膜B.外电路中电子由VB 2电极流向c 电极C.电解过程中,b 电极表面产生的气体可以收集后充入A 池中的电极循环利用D.VB 2电极发生的电极反应为2VB 2－22e －＋11H 2O===V 2O 5＋2B 2O 3＋22H ＋6.(2019·泸州质检)装置(Ⅰ)为铁镍(Fe －Ni)可充电的碱性电池：Fe ＋NiO 2＋2H 2O 放电充电Fe(OH)2＋Ni(OH)2；装置(Ⅱ)为电解示意图。

2018年高考英语一轮复习专题4.２Worｋing tｈｅｌａnd(讲)(含解析）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望（2018年高考英语一轮复习专题4．2 Workiｎｇ the land(讲)（含解析）)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为2０１8年高考英语一轮复习专题4.2 Wｏrking the land(讲）（含解析）的全部内容。

专题4。

２ Wｏrkｉng tｈｅｌand背诵这篇范文【河南省南阳市第一中学2０１8届高三实验班第一次考试】假如你是李华,暑假期间，你将参加学生代表团，回访去年来你校交流的瑞典（Sweｄeｎ)某中学. 请你给去年来访时住在你家的Peteｒ写信.要点如下:1。

时间: ８月20日至8月3１日;2。

参加人员:教师1人,学生30 人 ;3。

希望Peｔer带你参观该市的足球俱乐部.注意：1。

词数1０0左右;２。

可以适当增加细节，以使行文连贯；3. 信的开头和结尾已给出,不计入总词数.Dear Ｐeteｒ，＿＿_______＿_＿_＿__＿______________＿__＿＿＿_＿_____＿___＿____＿_＿_____＿___＿＿____＿__＿______＿____＿____＿_＿_＿__＿________＿_＿_＿＿_＿______＿＿＿_＿___＿____＿__＿______＿_______＿＿__＿_＿＿_＿_＿_____＿___＿____________＿________＿____＿___＿____＿_＿＿_____＿___＿＿_＿____＿＿____＿_＿___＿＿___＿__＿____＿___＿____＿＿__＿＿_＿＿_＿____＿＿_＿_＿__＿_＿_＿_＿____＿_＿_____＿______＿_____＿_＿__________＿_＿__＿_＿＿＿＿_＿_________＿__________＿＿＿______＿__＿_＿＿__＿__＿___＿_＿_________＿_＿＿＿_＿__＿____＿＿＿____＿________＿______＿_____＿_____＿＿_______＿＿____＿_＿＿_______＿_____＿_____＿＿_______＿_____＿_＿__＿__＿＿____________＿_____＿＿＿＿_＿＿___＿_＿＿＿___＿____＿___＿＿__＿_________＿_____＿＿＿＿________＿＿_______＿_____＿__＿＿__________＿________＿__________＿__＿____＿_____＿______________________＿____＿_____＿____＿__＿_＿_＿_＿___＿_＿＿＿_Ｙouｒｓ，Ｌｉ Hua【参考范文】Ｄeaｒ Peｔer，How timｅｆlies! Ｉt’s almost a ｙeａｒsincｅｙｏｕ reｔurned ｔo Sｗede ｎ。

[考案1]第一章综合过关规范限时检测(时间：45分钟满分100分)一、单选题(本大题共7个小题，每小题5分，共35分，在每小题给出的四个选项中只有一个是符合题目要求的)1.(2020·兰州市高三诊断考试)已知集合A＝{x∈N|－1＜x＜4}，B⊆A，则集合B中的元素个数至多是(B)A.3B.4C.5D.6【试题解答】因为A＝|x∈N|－1＜x＜4}＝{0,1,2,3}，且B⊆A，所以集合B中的元素个数至多是4，故选B.2.(2018·课标全国Ⅲ，1)已知集合A＝{x|x－1≥0}，B＝{0,1,2}，则A∩B＝(C)A.{0}B.{1}C.{1,2}D.{0,1,2}【试题解答】本题考查集合的运算.∵A＝{x|x－1≥0}＝{x|x≥1}，B＝{0,1,2}，∴A∩B＝{1,2}，故选C.3.(2020·成都市二诊)设全集U＝R，集合A＝{x|－1＜x＜3}，B＝{x|x≤－2或x≥1}，则A∩(∁U B)＝(A)A.{x|－1＜x＜1}B.{x|－2＜x＜3}C.{x|－2≤x＜3}D.{x|x≤－2或x>－1}【试题解答】由题意知∁U B＝{x|－2＜x＜1}，则A∩(∁U B)＝{x|－1＜x＜3}∩{x|－2＜x＜1}＝{x|－1＜x＜1}.4.(2020·宁夏中卫模拟)命题“若a2＋b2＝0，则a＝0且b＝0”的逆否命题是(D)A.若a2＋b2≠0，则a≠0且b≠0B.若a2＋b2≠0，则a≠0或b≠0C.若a＝0且b＝0，则a2＋b2≠0D.若a≠0或b≠0，则a2＋b2≠0【试题解答】命题“若a2＋b2＝0，则a＝0且b＝0”的逆否命题是“若a≠0或b≠0，则a2＋b2≠0”，故选D.5.(2020·山东潍坊重点高中联考)毛泽东同志在《清平乐·六盘山》中的两句诗为“不到长城非好汉，屈指行程二万”，假设诗句的前一句为真命题，则“到长城”是“好汉”的(B)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【试题解答】解法一：由“不到长城非好汉”可知，要想成为好汉必须到过长城，因此“到长城”是“好汉”的必要不充分条件.解法二：设¬p为不到长城，推出¬q非好汉，即¬p⇒¬q，由原命题与其逆否命题等价可知q⇒p，即好汉⇒到长城，故“到长城”是“好汉”的必要不充分条件.故选B.6.下列命题中，真命题是( D )A.命题“若a >b ，则ac 2>bc 2”B.命题“若a ＝b ，则|a |＝|b |”的逆命题C.命题“当x ＝2时，x 2－5x ＋6＝0”的否命题D.命题“终边相同的角的同名三角函数值相等”的逆否命题【试题解答】 命题“若a >b ，则ac 2>bc 2”是假命题，如a >b 且c ＝0时，ac 2＝bc 2；命题“若a ＝b ，则|a |＝|b |”的逆命题为“若|a |＝|b |，则a ＝b ”是假命题；命题“当x ＝2时，x 2－5x ＋6＝0”的否命题为“若x ≠2，则x 2－5x ＋6≠0”是假命题；命题“终边相同的角的同名三角函数值相等”是真命题，其逆否命题与原命题等价，为真命题，故选D.7.(2020·广东汕头模拟)已知命题p ：关于x 的方程x 2＋ax ＋1＝0没有实根；命题q ：∀x >0，均有2x －a >0.若“¬p ”和“p ∧q ”都是假命题，则实数a 的取值范围是( C )A.(－∞，－2)B.(－2,1]C.(1,2)D.(1，＋∞)【试题解答】 若方程x 2＋ax ＋1＝0没有实根，则判别式Δ＝a 2－4＜0，即－2＜a ＜2，即p ：－2＜a ＜2.∀x >0,2x －a >0则a ＜2x ，当x >0时，2x >1，则a ≤1，即q ：a ≤1.∵¬p 是假命题，∴p 是真命题.∵p ∧q 是假命题，∴q 是假命题，即⎩⎪⎨⎪⎧－2<a <2，a >1，得1＜a ＜2.故选C. 二、多选题(本大题共3个小题，每小题5分，共15分，在每小题给出的四个选项中，有多项符合题目要求全部选对的得5分，部分选对的得3分，有选错的得0分)8.(2020·重庆市第一次调研抽测改编)已知集合A ＝{1,2，m }，B ＝{3,4}，若A ∪B ＝{1,2,3,4}，则实数m 可以为( CD )A.1B.2C.3D.4 【试题解答】 解法一：由题意知m 是B 中的元素，则m ＝3或4，故选C 、D.解法二：由集合中元素的互异性知，m ≠1且m ≠2，故排除选项A 、B ，选C 、D.9.(2020·福建三明一中期中改编)下列选项中错误的有( ABC )A.命题“若x 2＝1，则x ＝1”的否命题为：“若x 2＝1，则x ≠1”B.“A ≠∅”是“A ∩B ≠∅”的充分不必要条件C.命题“∃x ∈R ，使得x 2＋x －1＜0”的否定是“∀x ∈R ，均有x 2＋x －1>0”D.命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题【试题解答】 对于A ，命题“若x 2＝1，则x ＝1”的否命题为：“若x 2≠1，则x ≠1”∴A 错误； 对于B ，由“A ≠∅”是得不到“A ∩B ≠∅”，即“A ≠∅”是“A ∩B ≠∅”不充分条件，由“A ∩B ≠∅”可知“A ≠∅”，即“A ≠∅”是“A ∩B ≠∅”必要条件，故“A ≠∅”是“A ∩B ≠∅”必要不充分条件，∴B 错误；对于C ，命题“∃x ∈R ，使得x 2＋x －1＜0”的否定是“∀x ∈R ，使得x 2＋x －1≥0”，∴C 错误； 对于D ，命题“若x ＝y ，则sin x ＝sin y ”为真命题，根据互为逆否命题的两个命题同真假，可知，命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题，∴D 正确；故A 、B 、C.10.(2020·凤城市第一中学高一月考改编)不等式1≤|x |≤4成立的充分不必要条件为( AB )A.[－4，－1]B.[1,4]C.[－4，－1]∪[1,4]D.[－4,4]【试题解答】 由不等式1≤|x |≤4，解得：－1≤x ≤－1或1≤x ≤4，对于A ，B 选项中的集合是不等式解集的真子集，∴不等式1≤|x |≤4成立的充分不必要条件为A ，B.故选A 、B.三、填空题(本大题共4小题，每小题5分，共20分.把答案填在题中的横线上)11.(2018·湖南卷)已知集合U ＝{1,2,3,4}，A ＝{1,3}，B ＝{1,3,4}，则A ∪(∁U B )＝__{1,2,3}__. 【试题解答】 ∵∁U B ＝{2}，∴A ∪(∁U B )＝{1,2,3}.12.(2020·江西上饶模拟)命题“∀x ∈R ，|x |＋x 2≥0”的否定是 ∃x 0∈R ，|x 0|＋x 20＜0 .【试题解答】 因为全称命题的否定是特称命题，所以命题“∀x ∈R ，|x |＋x 2≥0”的否定是“∃x 0∈R ，|x 0|＋x 20＜0”.13.(2020·湖南常德一中模拟)条件p ：1－x ＜0，条件q ：x >a ，若p 是q 的充分不必要条件，则a 的取值范围是__(－∞，1)__.【试题解答】 p ：x >1，若p 是q 的充分不必要条件，则p ⇒q 但qp ，也就是说，p 对应的集合是q 对应的集合的真子集，所以a ＜1.14.(2020·衡水金卷A 信息卷(五)，14)命题p ：若x >0，则x >a ；命题q ：若m ≤a －2，则m ＜sin x (x ∈R )恒成立.若p 的逆命题，q 的逆否命题都是真命题，则实数a 的取值范围是__[0,1)__.【试题解答】 命题p 的逆命题是若x >a ，则x >0，故a ≥0.因为命题q 的逆否命题为真命题，所以命题q 为真命题，则a －2＜－1，解得a ＜1.则实数a 的取值范围是[0,1).四、解答题(本大题共2个小题，共30分，解答应写出文字说明、证明过程或演算步骤)15.(本小题满分15分)已知集合A ＝{x |x 2－6x ＋8＜0}，B ＝{x |(x －a )(x －3a )＜0}，a ∈R .(1)若x ∈A 是x ∈B 的充分条件，求实数a 的取值范围；(2)若A ∩B ＝∅，求实数a 的取值范围.【试题解答】 A ＝{x |x 2－6x ＋8＜0}＝{x |2＜x ＜4}，B ＝{x |(x －a )(x －3a )＜0}.(1)当a ＝0时，B ＝∅，不符合题意，当a >0时，B ＝{x |a ＜x ＜3a }，要满足题设条件，则⎩⎪⎨⎪⎧a ≤2，3a ≥4，解得43≤a ≤2. 当a ＜0时，B ＝{x |3a ＜x ＜a }，要满足题设条件，则⎩⎪⎨⎪⎧3a ≤2，a ≥4，无解. 综上可知：43≤a ≤2. (2)要满足A ∩B ＝∅.当a >0时，B ＝{x |a ＜x ＜3a }，则a ≥4或3a ≤2，即0＜a ≤23或a ≥4， 当a ＜0时，B ＝{x |3a ＜x ＜a }，则a ≤2或3a ≥4，即a ＜0，当a ＝0时，B ＝∅，满足题意.综上可知：a ≤23或a ≥4. 16.(本小题满分15分)设命题p ：方程x 28－a ＋y 2a －4＝1表示焦点在x 轴上的椭圆，命题q ：函数f (x )＝13x 3＋3(3－a )2x 2＋9x 无极值. (1)若p 为真命题，求实数a 的取值范围；(2)若“p ∧q ”为假命题，“p ∨q ”为真命题，求实数a 的取值范围.【试题解答】 (1)由⎩⎪⎨⎪⎧ 8－a >0a －4>08－a >a －4得4＜a ＜6， ∴实数a 的取值范围为(4,6).(2)由题意知p ，q 一真一假，q 为真时，则f ′(x )＝x 2＋3(3－a )x ＋9≥0恒成立，∴Δ＝9(3－a )2－36≤0得1≤a ≤5，若p 真q 假，5＜a ＜6；若q 真p 假，1≤a ≤4.综上，实数a 的取值范围是[1,4]∪(5,6).。