图论之二部图图形解析

二分体图论
1.定义
二分图，又称二部图，是图论中的一种特殊模型。

设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集（A,B），并且图中每条边（i,j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G是一个二分图。

2.判定
无向图G={V, E},如果可以把结点分成不相交的两部分，即X和Y，使得每条边的其中一个端点在X中，另一个端点在Y中，则称图G 是二分图。

二分图-无奇数图
无向图G为二分图的充分必要条件是，G至少有两个顶点,且其所有回路的长度均为偶数。

3.性质
1.最小点覆盖=最大匹配数
2.最小边覆盖=点数-最小点覆盖（最大匹配数）
3.最小路径覆盖=原图的结点数-新图的最大匹配数。

4.最大独立集=点数-最小点覆盖（最大匹配数）
4.匹配
二分图匹配：给定一个二分图G={V, E}，将E的子集M称作一个匹配，如果M中的任意两条边都没有公共端点。

多重匹配：二分图中某些点可以被匹配多次。

最大匹配：包含的边数最多的匹配。

X(Y) -完全匹配：X(Y)中的所有顶点都出现在匹配M中。

完全匹配：所有的点都在匹配边上的匹配（M既是X-完全匹配，又是Y-完全匹配）。

最佳匹配：如果G为加权二分图，则权值和最大的完美匹配称为最佳匹配。

5.相关算法：
二分图最大匹配：匈牙利算法、HK算法、网络流最大流
二分图多重匹配：网络流最大流
二分图最佳匹配：KM算法、网络流最大流。

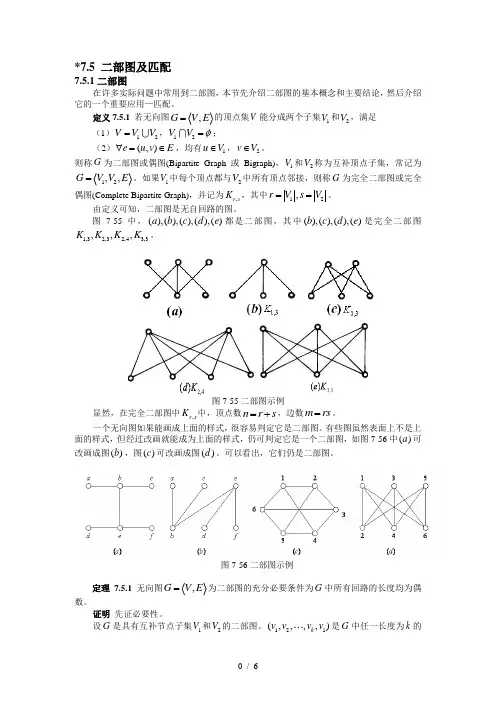
*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图，本节先介绍二部图的基本概念和主要结论，然后介绍它的一个重要应用—匹配。

定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ，满足（1）12V V V =，12V V φ=；（2）(,)e u v E ∀=∈，均有1u V ∈，2v V ∈。

则称G 为二部图或偶图(Bipartite Graph 或Bigraph)，1V 和2V 称为互补顶点子集，常记为12,,G V V E =。

如果1V 中每个顶点都与2V 中所有顶点邻接，则称G 为完全二部图或完全偶图(Complete Bipartite Graph)，并记为,r s K ，其中12,r V s V ==。

由定义可知，二部图是无自回路的图。

图7-55中，(),(),(),(),()a b c d e 都是二部图，其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。

图7-55二部图示例显然，在完全二部图中,r s K 中，顶点数n r s =+，边数m rs =。

一个无向图如果能画成上面的样式，很容易判定它是二部图。

有些图虽然表面上不是上面的样式，但经过改画就能成为上面的样式，仍可判定它是一个二部图，如图7-56中()a 可改画成图()b ，图()c 可改画成图()d 。

可以看出，它们仍是二部图。

图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。

证明 先证必要性。

设G 是具有互补节点子集1V 和2V 的二部图。

121(,,,,)k v v v v 是G 中任一长度为k 的回路，不妨设11v V ∈，则211m v V +∈，22m v V ∈，所以k 必为偶数，不然，不存在边1(,)k v v 。

再证充分性。

设G 是连通图，否则对G 的每个连通分支进行证明。

二分图的最优匹配（KM算法）KM算法用来解决最大权匹配问题：在一个二分图内，左顶点为X，右顶点为Y，现对于每组左右连接XiYj有权wij，求一种匹配使得所有wij的和最大。

基本原理该算法是通过给每个顶点一个标号（叫做顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。

设顶点Xi的顶标为A[ i ]，顶点Yj的顶标为B[ j ]，顶点Xi与Yj之间的边权为w[i,j]。

在算法执行过程中的任一时刻，对于任一条边(i,j)，A[ i ]+B[j]>=w[i,j]始终成立。

KM算法的正确性基于以下定理：若由二分图中所有满足A[ i ]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

首先解释下什么是完备匹配，所谓的完备匹配就是在二部图中，X点集中的所有点都有对应的匹配或者是Y点集中所有的点都有对应的匹配，则称该匹配为完备匹配。

这个定理是显然的。

因为对于二分图的任意一个匹配，如果它包含于相等子图，那么它的边权和等于所有顶点的顶标和；如果它有的边不包含于相等子图，那么它的边权和小于所有顶点的顶标和。

所以相等子图的完备匹配一定是二分图的最大权匹配。

初始时为了使A[ i ]+B[j]>=w[i,j]恒成立，令A[ i ]为所有与顶点Xi关联的边的最大权，B[j]=0。

如果当前的相等子图没有完备匹配，就按下面的方法修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止。

我们求当前相等子图的完备匹配失败了，是因为对于某个X顶点，我们找不到一条从它出发的交错路。

这时我们获得了一棵交错树，它的叶子结点全部是X顶点。

现在我们把交错树中X顶点的顶标全都减小某个值d，Y顶点的顶标全都增加同一个值d，那么我们会发现：1）两端都在交错树中的边(i,j)，A[ i ]+B[j]的值没有变化。

也就是说，它原来属于相等子图，现在仍属于相等子图。

2）两端都不在交错树中的边(i,j)，A[ i ]和B[j]都没有变化。

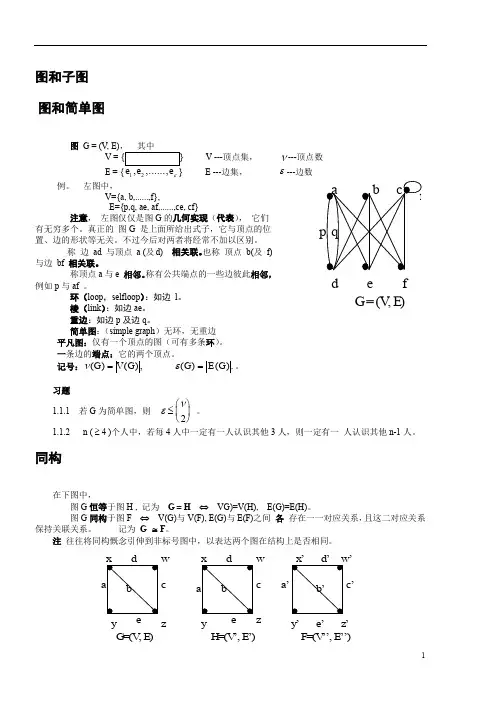
图和子图 图和简单图图 G = (V, E)V ---顶点集，ν---顶点数12ε E ---边集， ε---边数例。

左图中， V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意， 左图仅仅是图G 的几何实现（代表）， 它们有无穷多个。

真正的 图G 是上面所给出式子，它与顶点的位置、边的形状等无关。

不过今后对两者将经常不加以区别。

称 边 ad 与顶点 a (及d) 相关联。

也称 顶点 b(及 f) 与边 bf 相关联。

称顶点a 与e 相邻。

称有公共端点的一些边彼此相邻，例如p 与af 。

环（loop ，selfloop ）：如边 l 。

棱（link ）：如边ae 。

重边：如边p 及边q 。

简单图：（simple graph ）无环，无重边 平凡图：仅有一个顶点的图（可有多条环）。

一条边的端点：它的两个顶点。

记号：νε()(),()().G V G G E G ==。

习题1.1.1 若G 为简单图，则εν≤⎛⎝ ⎫⎭⎪2 。

1.1.2 n ( ≥ 4 )个人中，若每4人中一定有一人认识其他3人，则一定有一 人认识其他n-1人。

同构在下图中， 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。

图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系，且这二对应关系保持关联关系。

记为 G ≅F。

注 往往将同构慨念引伸到非标号图中，以表达两个图在结构上是否相同。

de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。

完全图(complete graph) Kn空图（empty g.） ⇔ E = ∅ 。

V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。

图论内容提要第一章图的基本概念图的基本概念；二部图及其性质；图的同构；关联矩阵与邻接矩阵。

路、圈与连通图；最短路问题。

树及其基本性质；生成树；最小生成树。

第二章图的连通性割点、割边和块；边连通与点连通；连通度；Whitney定理；可靠通信网络的设计。

第三章匹配问题匹配与最大匹配；完美匹配；二部图的最大匹配；指派问题与最大权匹配。

第四章欧拉图与哈密尔顿图欧拉图；中国邮递员问题；哈密尔顿图；旅行商问题。

第五章支配集、独立集、覆盖集与团支配集、点独立集、点覆盖集、边覆盖集与团的概念及其求法。

第六章图的着色问题点着色；边着色；平面图；四色猜想；色多项式；色数的应用。

第七章网络流理论有向图；网络与网络流的基本概念；最大流最小割定理；求最大流的标号算法；最小费用流问题；最小费用最大流；网络流理论的应用。

主要参考书[1] J.A. Bondy and U.S. Murty, Graph theory with applications, 1976, 有中译本（吴望名等译）。

[2] B.Bollobas, Modern graph theory (现代图论)，科学出版社，2001。

[3] 蒋长浩，图论与网络流，中国林业出版社，2001。

[4] 田丰，马仲蕃，图与网络流理论，科学出版社，1987。

[5] 徐俊明，图论及其应用，中国科技大学出版社，1998。

[6] 王树禾，图论及其算法，中国科技大学出版社，1994。

[7] 殷剑宏，吴开亚，图论及其算法，中国科技大学出版社，2003。

第一章 图的基本概念§1.1 图的基本概念1. 图(graph)：一集元素及它们之间的某种关系。

具体地说，图是一个二元组),(E V ，其中集合V 称为顶点集，集合E 是V V ⨯的一个子集（无序对，元素可重复），称为边集。

例1.1.1 ),(E V G =，其中},,,,{54321v v v v v V =，)},(),,(),,(),,(),,(),,(),,{(55515153433221v v v v v v v v v v v v v v E =。

二分图二分图又称作二部图，是图论中的一种特殊模型。

设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

1定义简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。

2辨析示例区别二分图，关键是看点集是否能分成两个独立的点集。

上图中U和V构造的点集所形成的循环圈不为奇数，所以是二分图。

上图中U和V和W构造的点集所形成的的循环圈为奇数，所以不是二分图。

3必要条件无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。

证先证必要性。

设G为二分图<X，E，Y>。

由于X，Y非空，故G至少有两个顶点。

若C为G 中任一回路，令C=(v0,v1,v2，…，v l-1,v l=v0)其中诸vi(i=0,1，…，l）必定相间出现于X及Y中，不妨设{v0,v2,v4，…，v l=v0}&Iacute;X{v1,v3,v5，…，v l-1}&Iacute;Y因此l必为偶数，从而C中有偶数条边。

再证充分性。

设G的所有回路具有偶数长度，并设G为连通图（不失一般性，若G不连通，则可对G的各连通分支作下述讨论）。

令G的顶点集为V，边集为E，现构作X，Y，使<X，E，Y>=G。

取v0&Icirc;V，置X={v|v=v0或v到v0有偶数长度的通路}Y=V-XX显然非空。

现需证Y非空，且没有任何边的两个端点都在X中或都在Y中。

由于|V|≥2并且G为一连通图，因此v0必定有相邻顶点，设为v1，那么v1&Icirc;Y；故Y不空。

设有边（u,v），使u&Icirc;X，v&Icirc;X。

那么，v0到u有偶数长度的通路，或u=v0；v0到v有偶数长度的通路，或v=v0。

二分图的概念二分图又称作二部图，是图论中的一种特殊模型。

设G=(V, E)是一个无向图。

如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。

二分图的性质定理：当且仅当无向图G的每一个回路的次数均是偶数时，G才是一个二分图。

如果无回路，相当于任一回路的次数为0，故也视为二分图。

二分图的判定如果一个图是连通的，可以用如下的方法判定是否是二分图：在图中任选一顶点v，定义其距离标号为0，然后把它的邻接点的距离标号均设为1，接着把所有标号为1的邻接点均标号为2（如果该点未标号的话），如图所示，以此类推。

标号过程可以用一次BFS实现。

标号后，所有标号为奇数的点归为X部，标号为偶数的点归为Y部。

接下来，二分图的判定就是依次检查每条边，看两个端点是否是一个在X部，一个在Y部。

如果一个图不连通，则在每个连通块中作判定。

二分图匹配给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

图中加粗的边是数量为2的匹配。

最大匹配选择边数最大的子图称为图的最大匹配问题(maximal matching problem)如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

图中所示为一个最大匹配，但不是完全匹配。

增广路径增广路径的定义：设M为二分图G已匹配边的集合，若P是图G中一条连通两个未匹配顶点的路径（P的起点在X部，终点在Y部，反之亦可），并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

增广路径是一条“交错轨”。

也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且起点和终点还没有被选择过，这样交错进行,显然P有奇数条边（为什么？）红边为三条已经匹配的边。

从X部一个未匹配的顶点x4开始，找一条路径：x4,y3,x2,y1,x1,y2x4,y3,x2,y1,x1,y2因为y2是Y部中未匹配的顶点，故所找路径是增广路径。