高考数学预测试题(5)预测题文
- 格式:pdf
- 大小:240.47 KB
- 文档页数:10

2022-2023年高考《数学(文科)》预测试题(答案解析)全文为Word可编辑,若为PDF皆为盗版,请谨慎购买!第壹卷一.综合考点题库(共50题)1.A.(1, 2)B.(1,﹣ 2)C.(﹣ 1, 2)D.(﹣ 1,﹣ 2)正确答案:A本题解析:2.阿基米德(公元前 287 年﹣公元前 212 年,古希腊)不仅是著名的哲学家、物理学家,也是著名的数学家,他利用“逼近法” 得到椭圆的面积除以圆周率π 等于椭圆的长半轴长与短半轴长的乘积.在平面直角坐标系 Oxy 中,椭圆 C:(a>b >0)的面积为2√3π,两焦点与短轴的一个顶点构成等边三角形.过点(1, 0)的直线l 与椭圆 C 交于不同的两点 A, B.(1)求椭圆 C 的标准方程;(2)设椭圆 C 的左、右顶点分别为 P, Q,直线 PA 与直线 x=4 交于点 F,试证明 B, Q,F 三点共线;(3)求△AOB 面积的最大值.正确答案:本题解析: 暂无解析3.已知命题 p : ∃x∈N*, lgx <0, q : ∀x∈R, cosx≤1, 则下列命题是真命题的是()A.p∧qB.(¬p ) ∧qC.p∧(¬q )D.¬(p∨q)正确答案:B本题解析:4.如图, 网格纸上小正方形的边长为 1, 粗实线画出的是某几何体的三视图,则该几何体的体积为()A.36B.24C.12D.6正确答案:C本题解析:5.分别统计了甲、乙两位同学 16 周的各周课外体育运动时长(单位:h),得如下茎叶图:则下列结论中错误的是()A.甲同学周课外体育运动时长的样本中位数为 7.4B.乙同学周课外体育运动时长的样本平均数大于 8C.甲同学周课外体育运动时长大于 8 的概率的估计值大于 0.4D.乙同学周课外体育运动时长大于 8 的概率的估计值大于 0.6正确答案:C本题解析:暂无解析6.A.AB.BC.CD.D正确答案:A 本题解析:7.A.AB.BC.CD.D正确答案:C 本题解析:暂无解析8.A.AB.BC.CD.D正确答案:C 本题解析:9.点 P 在焦点为 F 1 (﹣ c , 0)、 F 2 (c , 0) 的椭圆 C 上, PF 1 交 y 轴于点 Q , 且△PQF 2为正三角形, 若|OQ|=1, 则椭圆 C 的标准方程为正确答案:本题解析:10.A.f(x-1)-1B.f(x-1)+1C.f(x+1)-1D.f(x+1)+1正确答案:B本题解析:11.A.p∧(¬q)B.(¬p)∧(¬q)C.(¬p)∧qD.p∧q正确答案:A本题解析:12.执行右边的程序框图,输出的n= ()A.3B.4C.5D.6正确答案:B本题解析:暂无解析13.正确答案:本题解析:暂无解析14. 设 m、 n 是两条不同的直线,α、β 是两个不同的平面,给出下列四个命题:①若m⊥α,n∥α,则m⊥n;②若m∥n,n∥α,则m∥α;③若m∥n,n⊥β,m∥α,则α⊥β;④若m∩ n=A,m∥α,m∥β,n∥α,n∥β,则α∥β.其中真命题的个数是()A.1B.2C.3D.4正确答案:C本题解析:15.A.AB.BC.CD.D正确答案:B 本题解析:16.A.AB.BC.CD.D正确答案:A 本题解析:17.若 z(1﹣ i)=4i,则|z|=()A.√2B.2√2C.2D.4正确答案:B本题解析:18.设集合 M={x|0<x<4}, N={x| 1/3≤x≤5},则M∩ N=()A.{x|0<x≤1/3 }B.{x| 1/3≤x<4}C.{x|4≤x<5}D.{x|0<x≤5}正确答案:B本题解析:19.A.2B.-2C.1/2D.-1/2正确答案:D 本题解析:20.A.AB.BC.CD.D正确答案:B 本题解析:21.A.AB.BC.CD.D正确答案:A本题解析:暂无解析22.A.AB.BC.CD.D正确答案:D 本题解析:23. 已知函数 f(x)=|2x﹣ 1|+|2x+1|,记不等式 f(x)<4 的解集为 M.(1)求 M;(2)设 a,b∈M,证明: |ab|﹣ |a|﹣ |b|+1>0.正确答案:本题解析:暂无解析24.A.14B.12C.6D.3正确答案:D本题解析:暂无解析25.已知某几何体的三视图如图所示,则该几何体的内切球的半径等于()A.AB.BC.CD.D正确答案:A 本题解析:26.A.2B.√2C.3D.√3正确答案:A 本题解析:27.A.AB.BC.CD.D正确答案:B 本题解析:28.A.AB.BC.CD.D正确答案:A 本题解析:29.A.B.C.D.正确答案:A本题解析:由已知可得命题p为真命题,命题q为真命题,所以p∧q为真命题,故选A30.如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM (1)证明:平面PAM⊥平面PBD(2)若PD= DC=1 ,求四棱锥P- ABCD的体积.正确答案:31. 已知函数 f(x)=2|x﹣ 1|﹣ |x+1|.(1)在答题卡所给出的网格坐标系中作出函数 f(x)的图象(不要求写作法),并直接写出函数 f(x)的最小值;(2)已知函数 g(x)=|x+a|﹣ 2|x﹣ a|,若存在 x 1 ,x 2 ∈R 使 f(x 1 ) +5=g(x 2 ),求实数a 的取值范围.正确答案:本题解析:暂无解析32.我们可以用随机模拟的方法估计π 的值,如图程序框图表示其基本步骤(函数 RAND 是产生随机数的函数,它能随机产生(0, 1)内的任何一个实数).若输出的结果为 781,则由此可估计π 的近似值为()A.3.119B.3.124C.3.132D.3.151正确答案:B 本题解析:33.正确答案:本题解析:暂无解析34.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得 1 分,否则得 0 分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得 2 分的概率()A.1/3B.2/3C.1/6D.1/2正确答案:C本题解析:35.设(1+ 2i)a+b=2i,其中a,b为实数,则( )A.a=1,b=-1B.a=1,b=1C.a=-1,b= 1D.a=-1,b=-1正确答案:A本题解析:暂无解析36.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据 L 和小数记录法的数据 V满足 L=5+lgV.已知某同学视力的五分记录法的数据为 4.9,则其视力的小数记录法的数据约为()A.1.5B.1.2C.0.8D.0.6 正确答案:C本题解析:37.已知直线 l 1 , l 2 ,l 1 ⊥l 2 于点 H,A∈l 1 且|AH|=36,B∈l 2 ,点 M 在线段 AB 的垂直平分线上且MB⊥l 2 ,则|MA|的最小值为()A.9B.18C.36D.72正确答案:B本题解析:38.设λ∈R,则“λ=﹣3” 是“直线2λx+(λ﹣ 1) y﹣ 1=0 与直线 6x+(1﹣λ)y﹣ 4=0 平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件正确答案:A本题解析:39. 已知函数 f(x)=|2x﹣ a|﹣ |x+1|.(1)当 a=2 时,求不等式 f(x)<1 的解集;(2)若 a>0,不等式 f(x) +2>0 恒成立,求实数 a 的取值范围正确答案:本题解析:暂无解析40.A.AB.BC.CD.D正确答案:B本题解析:41.某校从高一年级学生中随机抽取 40 名学生,将他们的期中考试数学成绩(满分 100 分,成绩均为不低于 40 分的整数)分成六段: [40, 50), [50, 60),…, [90,100]后得到如图的频率分布直方图.(1)求图中实数 a 的值;(2)若该校高一年级共有学生 1000 人,试估计该校高一年级期中考试数学成绩不低于60 分的人数.(3)若从样本中数学成绩在[40, 50)与[90, 100]两个分数段内的学生中随机选取 2名学生,试用列举法求这 2 名学生的数学成绩之差的绝对值大于 10 的概率.正确答案:本题解析:暂无解析42.庄子说:一尺之锤,日取其半,万世不竭.这句话描述的是一个数列问题.现用程序框图描述,如图所示,若输入某个正数 n后,输出的则输入的 n的值为()A.7B.6C.5D.4正确答案:C 本题解析:43.如图所示,平面PAB⊥平面 ABCD,底面 ABCD 是边长为 8 的正方形,∠APB=90° ,点 E, F分别是 DC, AP 的中点.(1)证明:DF∥平面 PBE;(2)若 AB=2PA,求四棱锥 P﹣ ABED 的体积.正确答案:本题解析:暂无解析44.已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球0的球面上,则当该四棱锥的体积最大时,其高为()A.AB.BC.CD.D正确答案:C本题解析:暂无解析45.正确答案:本题解析:暂无解析46.随着我国经济总量的日益增长和社会财富的不断积累,投资理财观念已经深入普通国人家庭.“投资理财情绪指数” 是根据互联网用户搜索某种理财产品相应关键词的次数为基础所得到的统计指标.指数越大,表示互联网用户对该理财产品的关注度也越高.如图是 2022 年上半年某种理财产品的投资理财情绪指数走势图.根据该走势图,下列结论正确的是()A.这半年中,互联网用户对该理财产品的关注度不断增强B.这半年中,互联网用户对该理财产品的关注度呈周期性变化C.从这半年的投资理财情绪指数来看, 2 月份的方差大于 4 月份的方差D.从这半年的投资理财情绪指数来看, 5 月份的平均值小于 6 月份的平均值正确答案:C本题解析:47.已知 A, B, C 是半径为 1 的球 O 的球面上的三个点,且AC⊥BC, AC=BC=1,则三棱锥 O﹣ ABC 的体积为()A.AB.BC.CD.D正确答案:A 本题解析:48.A.(﹣ 4,﹣ 2)B.(﹣ 2,﹣ 1)C.(1, 2)D.(2, 4)正确答案:B本题解析:49.近几年,随着大众鲜花消费习惯的转变,中国进入一个鲜花消费的增长期.根据以往统计,某地一鲜花店销售某种 B 级玫瑰花,在连续统计的 320 天的玫瑰花售卖中,每天的玫瑰花的销售量(单位:支)与特殊节日的天数如表:(1)填写上表,判断是否有 99%的把握认为“每天的玫瑰花的销售量与特殊节日有关”?(2)若按分层抽样的方式,从上述表格的特殊节日中抽取 5 天作为一个样本,再从这个样本中抽取 2 天加以分析研究,求这两天玫瑰花的销售量在[120, 160]内的概率.正确答案:本题解析:暂无解析50.如图,在一个正方体内放入两个半径不相等的球 O 1 、 O 2 ,这两个球相外切,且球 O 1 与正方体共顶点 A 的三个面相切,球 O 2 与正方体共顶点 B 1 的三个面相切,则两球在正方体的面 AA 1 C 1 C 上的正投影是()A.AB.BC.CD.D正确答案:B 本题解析:。

2024学年安徽省屯溪一中高考数学试题(课标版)押题卷解析注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数有三个不同的零点 (其中),则 的值为( )A .B .C .D .2.已知函数()log (|2|)(0a f x x a a =-->,且1a ≠),则“()f x 在(3,)+∞上是单调函数”是“01a <<”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件3.射线测厚技术原理公式为0tI I e ρμ-=,其中0I I ,分别为射线穿过被测物前后的强度,e 是自然对数的底数,t 为被测物厚度,ρ为被测物的密度,μ是被测物对射线的吸收系数.工业上通常用镅241(241Am )低能γ射线测量钢板的厚度.若这种射线对钢板的半价层厚度为0.8,钢的密度为7.6,则这种射线的吸收系数为( )(注:半价层厚度是指将已知射线强度减弱为一半的某种物质厚度,ln 20.6931≈,结果精确到0.001) A .0.110B .0.112C .0.114D .0.1164.在ABC ∆中,“cos cos A B <”是“sin sin A B >”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件5.已知点2F 为双曲线222:1(0)4x y C a a -=>的右焦点,直线y kx =与双曲线交于A ,B 两点,若223AF B π∠=,则2AF B 的面积为( )A .22B .23C .2D .36.某高中高三(1)班为了冲刺高考,营造良好的学习氛围,向班内同学征集书法作品贴在班内墙壁上,小王,小董,小李各写了一幅书法作品,分别是:“入班即静”,“天道酬勤”,“细节决定成败”,为了弄清“天道酬勤”这一作品是谁写的,班主任对三人进行了问话,得到回复如下: 小王说:“入班即静”是我写的;小董说:“天道酬勤”不是小王写的,就是我写的; 小李说:“细节决定成败”不是我写的.若三人的说法有且仅有一人是正确的,则“入班即静”的书写者是( ) A .小王或小李B .小王C .小董D .小李7.已知f (x )=-1x x e e a+是定义在R 上的奇函数,则不等式f (x -3)<f (9-x 2)的解集为( )A .(-2,6)B .(-6,2)C .(-4,3)D .(-3,4)8.已知函数()sin 2cos 2f x x a x =+的图象的一条对称轴为12x π=,将函数()f x 的图象向右平行移动4π个单位长度后得到函数()g x 图象,则函数()g x 的解析式为( ) A .()2sin(2)12g x x π=- B .()2sin(2)12g x x π=+C .()2sin(2)6g x x π=-D .()2sin(2)6g x x π=+9.如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )A .2019年12月份,全国居民消费价格环比持平B .2018年12月至2019年12月全国居民消费价格环比均上涨C .2018年12月至2019年12月全国居民消费价格同比均上涨D .2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格 10.当0a >时,函数()()2xf x x ax e =-的图象大致是( )A .B .C .D .11.已知某几何体的三视图如图所示,则该几何体的体积是( )A .643B .64C .323D .3212.已知复数z 满足:((1)11)i z i +-=-,则z 的共轭复数为( ) A .12i -B .1i +C .1i -+D .12i +二、填空题:本题共4小题,每小题5分,共20分。

江西省宜春市2023届高三高考模拟文科数学试题一、单选题1.(2023·江西宜春·统考模拟预测)设全集U =R ,{1A x x =<-或}2x ≥,{}2,1,0,1,2B =--,则()U B A ⋂=ð( )A .{}0,1B .{}1,0-C .{}0,1,2D .{}1,0,1-2.(2023·江西宜春·统考模拟预测)已知复数z 满足()1i 2z +=-,则z 等于( )A .1i--B .1i-C .1i+D .1i-+3.(2023·江西宜春·统考模拟预测)非零向量a r ,b r ,c r 满足()a cb ⊥-r r r ,a r 与b r 的夹角为π3,2b =r ,则c r 在a r 上的投影为( )A .-1B.C .1D4.(2023·江西宜春·统考模拟预测)已知实数,x y 满足约束条件0,30,1,x y x y y -≥⎧⎪+-≤⎨⎪≥⎩则23x yz -+=的最大值是( )A .3B .13CD .1275.(2023·江西宜春·统考模拟预测)从棱长为2的正方体内随机取一点,则取到的点到中心的距离不小于1的概率为( )A .π6B .π4C .π16-D .π14-6.(2023·江西宜春·统考模拟预测)若30.04,ln1.04,log 1.04a b c ===则( )A .c b a <<B .b a c <<C .c a b<<D .b<c<a7.(2023·江西宜春·统考模拟预测)在数学和许多分支中都能见到很多以瑞士数学家欧拉命名的常数,公式和定理,若正整数,m n 只有1为公约数,则称,m n 互质,对于正整数(),n n ϕ是小于或等于n 的正整数中与n 互质的数的个数,函数()n ϕ以其首名研究者欧拉命名,称为欧拉函数,例如:()()32,76ϕϕ==,()96ϕ=.记n S 为数列(){}3nϕ的前n 项和,则10S =( )A .9312-B .931-C .10312-D .1031-8.(2023·江西宜春·统考模拟预测)函数()πsin 6f x x ω⎛⎫=+ ⎪⎝⎭的图象(04)ω<<关于直线π6x =对称,将()f x 的图象向左平移π4个单位长度后与函数()y g x =图象重合,下列说法正确的是( )A .函数()g x 图象关于直线π6x =对称B .函数()g x 图象关于点π,06⎛⎫- ⎪⎝⎭对称C .函数()g x 在π0,3⎛⎫⎪⎝⎭单调递减D .函数()g x 最小正周期为π29.(2023·江西宜春·统考模拟预测)在Rt ABC V 中,1,2CA CB ==.以斜边AB 为旋转轴旋转一周得到一个几何体,则该几何体的内切球的体积为( )ABC .32π81D .4π8110.(2023·江西宜春·统考模拟预测)如图,设1F ,2F 是双曲线2222:1(0,0)x y C a b a b -=>>的左右焦点,点A ,B 分别在两条渐近线上,且满足22133OA OF OB =+u u u r u u u u r u u u r ,20OA BF ⋅=u u u r u u u u r,则双曲线C 的离心率为( )A .B .2CD11.(2023·江西宜春·统考模拟预测)已知数列{}n a 满足1321223n n a a a a n+++++=L ,若数列()21n n n a ⎧⎫+⎪⎪⎨⎬+⎪⎪⎩⎭的前n 项和n S ,对任意*N n ∈不等式n S λ<恒成立,则实数λ的取值范围是( )A .1λ>B .1λ≥C .58λ≥D .58λ>12.(2023·江西宜春·统考模拟预测)已知函数()()()ln 1,ln (0)1m xf x xg x x m x m =+-=+>+,且()()120f x g x ==,则()2111em xx -+的最大值为( )A .1B .eC .2eD .1e二、填空题13.(2023·江西宜春·统考模拟预测)已知)114d πa x x -=+⎰,则到点(),0M a 的距离为2的点的坐标可以是___________.(写出一个满足条件的点就可以)14.(2023·江西宜春·统考模拟预测)已知点()()1,1,1,1A B ---,若圆22()(24)1x a y a -+-+=上存在点M 满足3MA MB ⋅=u u u r u u u r,则实数a 的取值的范围是___________.15.(2023·江西宜春·统考模拟预测)已知某线路公交车从6:30首发,每5分钟一班,甲、乙两同学都从起点站坐车去学校,若甲每天到起点站的时间是在6:30--7:00任意时刻随机到达,乙每天到起点站的时间是在6:45-7:15任意时刻随机到达,那么甲、乙两人搭乘同一辆公交车的概率是___________________16.(2023·江西宜春·统考模拟预测)如图,多面体ABCDEF 中,面ABCD 为正方形,DE ⊥平面,ABCD CF DE ∥,且2,1,AB DE CF G ===为棱BC 的中点,H 为棱DE 上的动点,有下列结论:①当H 为DE 的中点时,GH P 平面ABE ;②存在点H ,使得GH AC ⊥;③直线GH 与BE ④三棱锥A BCF -的外接球的表面积为9π.其中正确的结论序号为___________.(填写所有正确结论的序号)三、解答题17.(2023·江西宜春·统考模拟预测)在ABC V 中,角,,A B C 所对的边分别为,,a b c ,且2cos a b c B +=.(1)求证:2C B =;(2)求3cos a bb B+的最小值.18.(2023·江西宜春·统考模拟预测)如图1,在直角梯形ABCD 中,//,90,224AB CD DAB CD AB AD ∠====o ,点E ,F 分别是边,BC CD 的中点,现将CEF △沿EF 边折起,使点C 到达点P 的位置(如图2所示),且2BP =.(1)求证:平面APE ⊥平面ABD ;(2)求点B 到平面ADP 的距离.19.(2023·江西宜春·统考模拟预测)为了缓解日益拥堵的交通状况,不少城市实施车牌竞价策略,以控制车辆数量.某地车牌竞价的基本规则是:①“盲拍”,即所有参与竞拍的人都是网络报价,每个人不知晓其他人的报价,也不知道参与当期竞拍的总人数;②竞价时间截止后,系统根据当期车牌配额,按照竞拍人的出价从高到低分配名额.某人拟参加2023年5月份的车牌竞拍,他为了预测最低成交价,根据竞拍网站的公告,统计了最近5个月参与竞拍的人数(见表):月份2022.122023.12023.22023.32023.4月份编号t12345竞拍人数y (万人)1.72.12.52.83.4(1)由收集数据的散点图发现可用线性回归模型拟合竞拍人数y (万人)与月份编号t 之间的相关关系.请用最小二乘法求y 关于t 的线性回归方程:ˆˆˆy bt a =+,并预测2023年5月份参与竞拍的人数.(2)某市场调研机构对200位拟参加2023年5月份车牌竞拍人员的报价进行抽样调查,得到如下一份频数表:报价区间(万元)[)1,2[)2,3[)3,4[)4,5[)5,6[]6,7频数206060302010(i )求这200位竞拍人员报价X 的平均数x 和样本方差2s (同一区间的报价可用该价格区间的中点值代替);(ii )假设所有参与竞价人员的报价X 可视为服从正态分布()2,N μσ,且μ与2σ可分别由(i )中所求的样本平均数x 及方差2s 估值.若2023年5月份实际发放车牌数是5000,请你合理预测(需说明理由)竞拍的最低成交价.附:()()()121ˆ 1.3niii nii x x y y bx x ==--=≈-∑∑,若()0,1Y N :,则( 1.11)0.8660<=P Y ,( 1.12)0.8686P Y <=.20.(2023·江西宜春·统考模拟预测)已知函数()ln 2f x x x =--.(1)求函数的最小值;(2)若方程()f x a =有两个不同的实数根1x ,2x 且12x x <,证明:1223x x +>.21.(2023·江西宜春·统考模拟预测)在平面直角坐标系xoy 中,已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,左、右焦点分别是12,F F ,以1F 为圆心,6为半径的圆与以2F 为圆心,2为半径的圆相交,且交点在椭圆C 上.(1)求椭圆C 的方程;(2)设过椭圆C 的右焦点2F 的直线12,l l 的斜率分别为12,k k ,且122k k =-,直线1l 交椭圆C 于,M N 两点,直线2l 交椭圆C 于,G H 两点,线段,MN GH 的中点分别为,R S ,直线RS 与椭圆C 交于,P Q 两点,,A B 是椭圆C 的左、右顶点,记PQA △与PQB △的面积分别为12,S S ,证明:12S S 为定值.22.(2023·江西宜春·统考模拟预测)在平面直角坐标系xoy 中,曲线C 的参数方程11222122t t t t x y ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎪=-⎪⎩(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程cos 2sin 10m ρθρθ+-=.(1)求曲线C 的普通方程;(2)若直线l 与曲线C 有两个不同公共点,求m 的取值范围.23.(2023·江西宜春·统考模拟预测)已知函数()244f x x x =++-.(1)求不等式24410x x ++-≥的解集;(2)若()f x 的最小值为m ,正实数a ,b ,c 满足a b c m ++=,求证:11192a b b c c a m++≥+++.参考答案:1.D【分析】先计算得到U A ð,进而求出交集.【详解】{}12U A x x =-≤<ð,故(){}1,0,1U B A =-I ð故选:D 2.A【分析】利用复数的除法运算和共轭复数的定义求解.【详解】由题可得2(1i)1i 1iz -==--=-++,所以1i z =--,故选:A.3.C【分析】根据投影公式计算出正确答案.【详解】由于()a c b ⊥-r r r,所以()0,a c a b a c a a b b c ⋅-=⋅-⋅=⋅=⋅r r r r r r r r r r r ,由于a r 与b r 的夹角为π3,所以πcos 3a c a b a b a ⋅=⋅=⋅⋅=r r r r r r r,c r 在a r 上的投影为1a a c a a⋅==rr r r r .故选:C 4.B【分析】画出可行域,向上平移基准直线20x y -+=到可行域边界位置,由此求得23x y z -+=的最大值.【详解】画出可行域如下图所示,向上平移基准直线20x y -+=到可行域边界点()1,1B 的位置,此时z 取得最大值为1max 12111,3z z --⨯+=-==,.故选:B.5.C【分析】根据几何概型概率问题的计算公式求得正确答案.【详解】点到中心距离小于等于1的几何体是以中心为球心,1为半径的球体.所以,取到的点到中心的距离不小于1的概率为334π1π31126⨯-=-.故选:C 6.A【分析】构造函数()()ln 1f x x x =+-,利用导数判断函数单调性,再结合对数的性质即可判断大小关系.【详解】因为0.04a =,ln1.04b =,3log 1.04c =,当()0,1x ∈时,设()()ln 1f x x x =+-,则()11011xf x x x -'=-=<++,所以()f x 在()0,1上单调递减且()00f =,所以()()()0.04ln 10.040.0400f f =+-<=,即()0.04ln 10.04>+,所以a b >;又因为3e >,所以ln 3ln e 1>=,3ln1.04log 1.03ln1.04ln 3=<,即b c >,所以c b a <<.故选:A.7.D【分析】根据题意分析可得()1323nn ϕ-=⋅,结合等比数列求和公式运算求解.【详解】由题意可知:若正整数3nm ≤与3n不互质,则m 为3的倍数,共有1333n n -=个,故()1133332n n n n ϕ---=⋅=,∵()()113233233n n n n ϕϕ+-⋅==⋅,即数列(){}3n ϕ是以首项()32ϕ=,公比3q =的等比数列,故()1010102133113S -==--.故选:D.8.C【分析】由对称性求得ω,由图象平移变换求得()g x ,然后结合正弦函数的对称性,单调性,周期判断各选项.【详解】由已知ππππ662k ω+=+,62k ω=+,Z k ∈,又04ω<<,∴2ω=,ππ2π()sin[2()sin(2463g x x x =++=+,π2ππ2ππ,Z 632k k ⨯+=≠+∈,A 错;π2ππ2()π,Z 633k k ⨯-+=≠∈,B 错;π(0,3x ∈时,2π2π4ππ3π2(,)(,)33322x +∈⊆,C 正确;()g x 的最小正周期是2ππ2T ==,D 错.故选:C .9.C【分析】根据旋转体的概念得出该旋转体是两个共底面的圆锥的组合体,作出轴截面,得出内切球于心O 位于对称轴AB 上,由平行线性质求得球半径r 后可得球体积.【详解】由题意该几何体是两个共底面的圆锥的组合体,如图是其轴截面,由对称性知其内切球球心O 在AB 上,O 到,CA CB 的距离,OE OF 相等为球的半径,设其为r ,因为C 是直角,所以OECF 是正方形,即CF CE r ==,由//OF CA 得OF BF CA BC =,即212r r -=,解得23r =,球体积为3344232ππ(π33381V r ==⨯=.故选:C .10.C【分析】先求出AB 所在的直线方程,分别与两条渐近线联立方程组,求出,A B 两点的坐标,再根据22133OA OF OB =+u u u r u u u u r u u u r,求出,a c 之间的关系,从而可得双曲线的离心率【详解】由题意:OA b k a = ,20OA BF =u u u r u u u u r Q g ,2OA BF ∴⊥ ,2BF ak b ∴=-所以直线2BF 的方程为:()ay x c b=-- ①直线OA 的方程为:by x a =②直线OB 的方程为:by x a=-③联立①②可得:2a x cab y c⎧=⎪⎪⎨⎪=⎪⎩ ,即2(,)a ab A c c 联立①③可得22222a c x a babcy a b ⎧=⎪⎪-⎨-⎪=⎪-⎩,即22222(,a c abc B a b a b ---又22133OA OF OB =+u u u r u u u u r u u u r Q 22222221(,)(,0)(,)33a ab a c abcc c c a b a b-∴=+--可得222222233()3()a a c c c a b ab abcc a b ⎧=+⎪-⎪⎨-⎪=⎪-⎩ ,化简可得223a c = ,即2e 3=,e ∴= 故选:C 11.C【分析】根据1321223n n a a a a n+++++=L 求得 n a ,再因为对任意*N n ∈不等式n S λ<恒成立,()max n S λ>,求出实数λ的取值范围.【详解】1321223n n a a a a n+++++=L ①,31212231n n a a a a n -++++=-L ②,由①-②可得,当 2n ≥ 时,2n na n=,当211,2n a ==,当2n ≥,()()()122211222111n n n n n n n a n n n n +⎛⎫++==- ⎪ ⎪++⨯⨯+⨯⎝⎭,当1,n =()2318n n n a +=+,所以()()2312131111311228223221282212n n n n S n n n ++⎡⎤⎛⎫⎛⎫⎛⎫=+-++-=+-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⨯⨯⨯+⨯⨯+⨯⎝⎭⎢⎥⎝⎭⎝⎭⎣⎦L ,对任意*N n ∈不等式n S λ<恒成立,所以 ()max n S λ>,()21332528882221181n n S n +⎛⎫=+<+=⎪ ⎪-⨯+⎝⎭⨯.所以58λ≥.故选:C.12.A【分析】根据题意表示出()()21121ln 1e ,x x x x m ++==从而推导出21e 1,xx =+将问题转化为()21111e em m x x m--+=,利用导数求得函数的最值.【详解】()()()()()ln 10,ln 10,1ln 1,11m mf x x x m x x x x =+-=+-==++++()ln0,e ,x xg x x m x m=+==由题意知,()()21121ln 1e ,x x x x m ++==即()()2221121ln 1e e ln e ,x x xx x x m ++===因为0m >,所以21e 1,11xx >+>,设()ln ,1p x x x x =>,则()1ln 0p x x '=+>,()()211e ,xp x p m +==所以211e x x +=,所以()22121111e e e e x m m m x x x m---+==,1(),0e m m t m m -=>,则11(),em mt m --'=当01m <<时,()0;t m '>当1m >时,()0;t m '<所以()t m 在()0,1时单调递增,在()1,+∞时单调递减,所以max ()(1)1,t m t ==故选:A.13.22(2)4x y -+=上的任意一点都可以【分析】根据定积分的几何意义先求出a ,再写出到点(),0M a 的距离为2的点表示一个圆.【详解】由于11d x -⎰表示以()0,0为圆心,1为半径且在第一、二象限的圆弧与坐标轴围成的面积,其面积是半径为1的圆的面积的一半,即为π2.所以)111144π4d d 202ππ2πa x x x x --==⨯+=+=⎰⎰,到点()2,0M 的距离为2的点是圆22(2)4x y -+=上的点.故答案为:22(2)4x y -+=上的任意一点.14.120,5⎡⎤⎢⎥⎣⎦【分析】设(,)M x y ,由数量积的坐标表示求得M 点轨迹是一个圆,然后由圆与圆的位置关系可得a 的范围.【详解】设(,)M x y ,则(1,1),(1,1)MA x y MB x y =----=---u u u r u u u r,2(1)(1)(1)3MA MB x x y ⋅=---+--=u u u r u u u r,即22(1)4x y ++=,M 在以(0,1)-为圆心,2为半径的圆上,由题意该圆与圆22()(24)1x a y a -+-+=有公共点,所以2121-≤≤+,解得1205a ≤≤.故答案为:12[0,]5.15.112【分析】由题意知本题是一个几何概型,设甲和乙到达的分别为6时x +分、6时y +分,则3060x ……,4575y ……,他们能搭乘同一班公交车,则4560x ……,4560y …….试验包含的所有区域是{(,)|3060x y x Ω=……,4575}y ……,他们能搭乘同一班公交车所表示的区域为A ,由此能求出结果.【详解】解:由题意知本题是一个几何概型,设甲和乙到达的分别为6时x +分、6时y +分,则3060x ……,4575y ……,则试验包含的所有区域是{(,)|3060x y x Ω=……,4575}y ……,他们能搭乘同一班公交车所表示的区域为4550{(,)|4550x A x y y ⎧=⎨⎩…………或50555055x y ⎧⎨⎩…………或5560}5560x y ⎧⎨⎩…………,则他们能搭乘同一班公交车的概率5531303012P ⨯⨯==⨯.故答案为:11216.①④【分析】根据线面平行的判定定理,以及线线垂直的判定,结合异面直线所成角,以及棱锥外接球半径的求解,对每一项进行逐一求解和分析即可.【详解】对①:当H 为DE 的中点时,取EA 中点为M ,连接,MH MB ,因为,H M 分别为,ED EA 的中点,故可得MH //AD ,12MH AD =,根据已知条件可知:BG //1,2AD BG AD =,故MH //,BG MH BG =,故四边形HMBG 为平行四边形,则H G //MB ,又MB ⊂平面,ABE HG ⊄平面ABE ,故H G //面ABE ,故①正确;对②:因为ED ⊥平面ABCD ,,⊂DA DC 平面ABCD ,故,DE DA DE DC ⊥⊥,又四边形ABCD 为矩形,故DA DC ⊥,则,,DE DA DC 两两垂直,以D 为坐标原点,建立空间直角坐标系如图所示:则()()()()()2,0,0,0,2,0,2,2,0,0,0,2,1,2,0A C B E G ,设()0,0,H m ,[]0,2m ∈,若GH AC ⊥,则()()1,2,2,2,020GH AC m ⋅=--⋅-=-≠u u u r u u u r,不满足题意,故②错误;对③:()1,2,GH m =--u u u r,()2,2,2BE =--u u u r ,()()()()1222262GH BE m m ⋅=-⨯-+-⨯-+=+u u u r u u u r,GH ==u u u r,BE =u u u r []0,2m ∈,,cos GH =u u u r u=[]0,2m ∈,令2325m y m +=+,设32t m =+,[]2,4t ∈,23t m -=,则29492453ty t t t==-⎛⎫+-+ ⎪⎝⎭,当[]2,4t ∈时,根据对勾函数的性质得4949454,42t t ⎡⎤+-∈⎢⎥⎣⎦,则236,549y ⎡⎤∈⎢⎥⎣⎦,当25y =时,cos ,GH BE u u u r u u u r有最小值,最小值为,故③错误;对④:由题可得CF ⊥平面ABCD ,又面ABCD 为正方形,∴,,AB BC CF AB BC CF C ⊥⊥⋂=,∴AB ⊥平面BCF ,则AB ,BC ,CF 两两垂直,∴AF 为三棱锥A BCF -的外接球的直径,又22222212219AF AB BC CF =++=++=,∴三棱锥A BCF -的外接球表面积为9π,故④正确.故答案为:①④.17.(1)证明见解析(2)最小值为【分析】(1)根据正弦定理边角互化和两角和差正弦化简即可证明.(2)将问题转化32cos 2cos cos a b c B b b B b B++=24cos cos B B =+,根据第一问解得π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,然后结合不等式求解.【详解】(1)在ABC V 中,2cos a b c B +=,由正弦定理得sin sin 2sin cos A B C B +=,又()πA B C =-+,因为()sin sin 2sin cos B C B C B ++=⋅,所以sin cos sin cos sin C B B C B ⋅-⋅=,所以()sin sin C B B -=,又sin 0B >,所以0πC B C <-<<,且πB C B C +-=<,所以B C B =-,故2C B =.(2)由(1)2C B =得()30,πB C B +=∈,所以π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭,因为2cos ,2a b c B C B +==,所以32cos 2cos cos a b c B b b B b B++=2sin cos 2sin 2sin2cos 2sin sin cos sin cos C B B B B BB B B B⋅+⋅+==⋅⋅24cos cos B B=+≥当且仅当24cos cos B B =即cos B =π0,3B ⎛⎫∈ ⎪⎝⎭,即当且仅当π4B =时等号成立,所以当π4B =时,3cos a bb B +的最小值为18.(1)证明见解析【分析】(1)连接,BD BF ,由等腰三角形的性质和勾股定理,证明PE EF ⊥,PE BE ⊥,可证得PE ⊥平面ABD ,即可证得平面APE ⊥平面ABD .(2)取AD 的中点O ,连接,,OE DE PO ,由勾股定理求,,PD PA PO ,又B PAD P ABD V V --=,利用体积法求点B 到平面ADP 的距离.【详解】(1)证明:由题意,连接,BD BF ,因为224CD AB AD ===,//AB CD ,90,DAB F ∠=o 是边CD 的中点,所以2BF CF ==,则BC =又E 是边BC 的中点,则EF BC ⊥,在折起中PE EF ⊥.又222224BE PE BP +=+==,所以PE BE ⊥,又BE EF E =I ,BE ⊂平面ABD ,EF ⊂平面ABD ,故PE ⊥平面ABD ,又PE ⊂平面APE ,所以平面APE ⊥平面ABD .(2)由(1)中取AD 的中点O ,连接,,OE DE PO ,由(1)可知,PE ⊥平面ABD ,所以,,PE DE PE AE PE OE ⊥⊥⊥,而()132OE AB DC =+=,112OD AD ==,所以DE =同理AE =所以PD PA PO ======所以PAD V 是等腰三角形,所以1122PAD S AD PO =⋅=⨯=V 又B PAD P ABD V V --=,即1133PAD ABD S h S PE ⋅=⋅V V ,所以ABD PADS PE h S ⋅==VV =,即点B 到平面ADP19.(1)0.41.7ˆ12=+yt ,预测2023年5月份参与竞拍的人数为3.73万人(2)(i ) 3.5x =,2 1.7s =;(ii )预测竞拍的最低成交价为4.943万元【分析】(1)由已知公式求得线性回归方程,6t =代入回归方程可得预测值;(2)(i )由均值与方差公式计算出均值与方差;(ii )由预测值求得报价在最低成交价以上人数占总人数比例,然后由正态分布的性质求得预测竞拍的最低成交价.【详解】(1)11(12345)3,(1.7 2.1 2.5 2.8 3.4) 2.555t y =++++==++++=,55211149162555, 1.7 4.27.511.21741.6,ii i i i tt y ===++++==++++=∑∑,241.653 2.5ˆˆ0.41, 2.50.413 1.275553ba -⨯⨯∴===-⨯=-⨯,y 关于t 的线性回归方程0.41.7ˆ12=+y t 2023年5月份对应6t =,所以0.416 1.27 3.73ˆ=⨯+=y所以预测2023年5月份参与竞拍的人数为3.73万人.(2)(i )由题意可得:1.50.12.50.33.50.34.50.155.50.16.50.05 3.5x =⨯+⨯+⨯+⨯+⨯+⨯=22222(1.5 3.5)0.1(2.5 3.5)0.3(3.5 3.5)0.3(4.5 3.5)0.15s =-⨯+-⨯+-⨯+-⨯22(5.5 3.5)0.1(6.5 3.5)0.05 1.7+-⨯+-⨯=(ii )2023年5月份实际发放车牌数是5000,设预测竞拍的最低成交价为a 万元,根据竞价规则,报价在最低成交价以上人数占总人数比例为5000100%13.40%37300⨯≈根据假设报价X 可视为服从正态分布()22,, 3.5, 1.7, 1.3===≈N μσμσσ,令 3.51.3--==X X Y μσ,由于( 1.11)0.8660<=P Y ,1( 1.11)0.1340P Y ∴-<=,3.5() 1.110.86601.3a P Y a P Y -⎛⎫∴<=<== ⎪⎝⎭,所以 3.5 1.111.3a -=得 4.943=a ,所以预测竞拍的最低成交价为4.943万元.20.(1)1-(2)证明见解析【分析】(1)利用导数法求函数最值的步骤解求解;(2)根据题意构造函数()()()2F x f x f x =--,()0,1x ∈.对函数求导,利用导函数的正负判断函数的单调性,进而利用函数的最值得出()()212f x f x >-,再结合(1)中函数的单调性即可得证.【详解】(1)由题意可知:函数()ln 2f x x x =--的定义域为:()0,∞+.则()11f x x'=-,令()0f x '=,解得1x =.当()0,1x ∈,()0f x '<,函数()f x 单调递减;当()1,x ∈+∞,()0f x ¢>,函数()f x 单调递增.所以1x =为极小值点,且()()min 11f x f ==-.所以函数()f x 的最小值为1-.(2)根据题意可知:()()12f x f x =,根据(1)设101x <<,21x >,构造函数()()()2F x f x f x =--,()0,1x ∈.()()()()()221202x F x f x f x x x -'''=+-=<-,所以()F x 在()0,1上单调递减.则有()()10F x F <=,也即()()1120f x f x -->.因为()()12f x f x =,所以()()2120f x f x -->,也即()()212f x f x >-因为121x ->,21x >,由(1)可知()f x 在()1,+∞上单调递增,所以212x x >-,也即122x x +>.由已知21x >,所以1223x x +>.21.(1)2211612x y +=;(2)证明见解析.【分析】(1)根据离心率的定义和椭圆定义求得,a c ,再计算出b 后得椭圆方程;(2)设()()1122,,,M x y N x y ,直线方程代入椭圆方程,利用韦达定理求得中点,R S 的坐标,当直线PQ 斜率存在时,设直线:PQ y mx n =+,点,R S 在直线PQ 上,代入整理得12,k k 是一个一元二次方程的根,由韦达定理得12k k ,从而得出,m n 关系,得出直线PQ 过定点E ,再确定直线PQ 斜率不存在时也过这个定点E ,然后结合该定点得出三角形面积比.【详解】(1)依题意得12622c a a⎧=⎪⎨⎪+=⎩,则4,2,a c =⎧⎨=⎩则22212b a c =-=,所以椭圆C 的方程为2211612x y +=;(2)直线()11:2l y k x =-,设()()1122,,,M x y N x y ,由122(2)11612y k x x y =-⎧⎪⎨+=⎪⎩得()2222111341616480k x k x k +-+-=,所以2112211634k x x k +=+,211221164834k x x k -=+,且0∆>,则中点211221186,3434k k R k k ⎛⎫- ⎪++⎝⎭,同理可算222222286,3434k k S k k ⎛⎫- ⎪++⎝⎭①当直线斜率存在时,设直线:PQ y mx n =+,点,R S 在直线PQ 上,点,R S 坐标代入整理得()()21122284630,84630,m n k k n m n k k n ⎧+++=⎪⎨+++=⎪⎩易知12,k k 为方程()284630m n k k n +++=的两个根,则123284n k k m n==-+,所以1611n m =-,所以直线16:11PQ y mx m =-,则直线恒过点16,011E ⎛⎫⎪⎝⎭②当直线的斜率不存在时,由对称性可知12k k =-,由122k k =-,不妨设12k k ==,所以221222128816343411k k k k ==++,直线16:11PQ x =过16,011⎛⎫⎪⎝⎭,根据①②可知,直线PQ 恒过点16,011E ⎛⎫⎪⎝⎭,因为PQA △的面积11212S AE y y =⋅-,PQB △的面积21212S BE y y =⋅-,所以121641511167411AE S S BE +===-.【点睛】方法点睛:椭圆中的直线过定点问题的解决方法:斜率存在时,设出直线方程为y mx n =+,根据已知条件确定,m n 的关系后,由直线方程得出定点坐标.本题中,动直线PQ 是由点,R S 确定的,因此可由已知直线12,l l 确定,R S 的坐标,再把坐标代入所设直线方程,发现12,k k 是一个一元二次的两根,这样可由韦达定理求得,m n 的关系,得出结论.22.(1)()22441x y x -=≥(2)4m <<【分析】(1)在曲线C 的参数方程中消去参数t ,可得出曲线C 的普通方程,利用基本不等式求出x 的取值范围,即可得解;(2)求出直线l 的普通方程,分析可知直线l 与双曲线2214y x -=的右支有两个交点,将直线l 与双曲线2214y x -=方程联立,利用直线与双曲线的位置关系可得出关于m 的不等式组,即可解得实数m 的取值范围.【详解】(1)因为112122t t x ⎛⎫=+≥ ⎪⎝⎭()222222221422,2441122,2t t t t x x y x y ⎧=++⎪⎪-=≥⎨⎪=+-⎪⎩则则曲线的普通方程为()22441x y x -=≥(2)cos 2sin 10m ρθρθ+-=则210mx y +-=由得()22210,1,14mx y y x x +-=⎧⎪⎨-=≥⎪⎩得()22162170m x mx -+-=有两个不等正根()22222160,Δ468160,20,1617016m m m m m m ⎧-≠⎪=+->⎪⎪⎨->⎪-⎪⎪->-⎩则4m <<23.(1)[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦(2)证明见解析【分析】(1)利用零点分段法分类讨论,分别求出不等式的解集,即可得解;(2)利用绝对值三角不等式求出()f x 的最小值,即m 的值,再利用柯西不等式证明即可.【详解】(1)不等式24410x x ++-≥,所以224410x x x ≤-⎧⎨---+≥⎩,解得103x ≤-,或2424410x x x -<<⎧⎨+-+≥⎩,解得24x ≤<,或424410x x x ≥⎧⎨++-≥⎩,解得4x ≥,所以原不等式解集为[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦.(2)()244242f x x x x x x =++-=++-++()2406x x ≥+--+=,当且仅当2x =-时取得,即min ()6f x =,所以6a b c m ++==,因为()1112a b c a b b c a c ⎛⎫++⨯++ ⎪+++⎝⎭()111a b b c c a a b b c c a ⎛⎫=+++++++ ⎪+++⎝⎭()()()111a b b c c a a b b c c a ⎛⎫=+++++++⎡⎤ ⎪⎣⎦+++⎝⎭222222⎡⎤⎡⎤⎢⎥=++++⎢⎥⎣⎦⎢⎥⎣⎦2≥()21119=++=,当且仅当12a b c ===时取等号,所以()1119922a b b c c a a b c m ++≥=+++++成立.。

2024年高考数学模拟试卷请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为12F F ,,过2F 作一条直线与双曲线右支交于A B ,两点,坐标原点为O ,若22215OA a b BF a =+=,,则该双曲线的离心率为( ) A .152B .102C .153D .1032.已知非零向量a 、b ,若2b a =且23a b b -=,则向量b 在向量a 方向上的投影为( ) A .32b B .12b C .32b -D .12b -3.如图,ABC 中260A B ∠=∠=︒,点D 在BC 上,30BAD ∠=︒,将ABD △沿AD 旋转得到三棱锥B ADC '-,分别记B A ',B D '与平面ADC 所成角为α,β,则α,β的大小关系是( )A .2αβα<≤B .23αβα≤≤C .2βα≤,23αβα<≤两种情况都存在D .存在某一位置使得3a β>4.己知集合{|13}M y y =-<<,{|(27)0}N x x x =-,则M N ⋃=( ) A .[0,3)B .70,2⎛⎤ ⎥⎝⎦C .71,2⎛⎤- ⎥⎝⎦D .∅5.已知α、,22ππβ⎛⎫∈- ⎪⎝⎭,αβ≠,则下列是等式sin sin 2αβαβ-=-成立的必要不充分条件的是( )A .sin sin αβ>B .sin sin αβ<C .cos cos αβ>D .cos cos αβ<6.正ABC ∆的边长为2,将它沿BC 边上的高AD 翻折,使点B 与点C 间的距离为3,此时四面体A BCD -的外接球表面积为( ) A .103πB .4πC .133πD .7π7.若,则( ) A .B .C .D .8.若双曲线()22210x y a a-=>的一条渐近线与圆()2222x y +-=至多有一个交点,则双曲线的离心率的取值范围是( ) A .)2,⎡+∞⎣B .[)2,+∞C .(2D .(]1,29.数列{}n a 满足:21n n n a a a +++=,11a =,22a =,n S 为其前n 项和,则2019S =( ) A .0B .1C .3D .410.设复数z 满足31ii z=+,则z =( )A .1122i + B .1122-+i C .1122i - D .1122i -- 11.已知平面向量a ,b ,c 满足:0,1a b c ⋅==,5a c b c -=-=,则a b -的最小值为( ) A .5B .6C .7D .812.已知点2F 为双曲线222:1(0)4x y C a a -=>的右焦点,直线y kx =与双曲线交于A ,B 两点,若223AF B π∠=,则2AF B 的面积为( )A .22B .23C .2D .3二、填空题:本题共4小题,每小题5分,共20分。

重庆高考数学(文科)预测试题(5)参考数据与公式:柱体的体积公式 V S h = (表示柱体的底面积,h 表示柱体的高)锥体的体积公式 13V S h = (其中S 表示锥体的底面积,h 表示锥体的高)由列联表中数据计算2K 的公式 22()()()()()n ad bc K a b c d a c b d -=++++临界值表第I 卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将你认为正确的选项前面的代号填入答题卷相应的表格中1.设全集U R =,集合{|09}A x x =<<,{|44}B x Z x =∈-<<,则集合B A C U )(中元素的个数为( )A .3B .4C .5D .62.若i 是虚数单位,设()()11,,2ia b i a b R i+=++∈-,则复数Z a bi =+在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.函数()sin()(0)3f x x πωω=->的最小正周期为π,则函数()f x 的单调递增区间( )A .5[,]66k k ππππ-+()k Z ∈B .511[,]66k k ππππ++()k Z ∈C .5[,]1212k k ππππ-+()k Z ∈D .511[,]1212k k ππππ++()k Z ∈4.已知等差数列{}n a 中22a =,则其前3项的积3T 的取值范围是( ) A .(],4-∞ B .(],8-∞ C .[)4,+∞ D .[)8,+∞ 5.如果执行右边的程序框图,那么输出的k =( )A .4B .5C .6D .7 6.已知圆C 与直线 0x y -=及40x y --=都相切,圆心在直线 0x y +=上,则圆C 的方程为( )A .22(11)2x y -++=)( B .22(11)2x y ++-=)( C .22(11)2x y -+-=)( D .22(11)2x y +++=)( 7.已知双曲线的渐近线方程为230,x y ±=(0,5)F -为双曲线的一个焦点,则双曲线的方程为( )A .22149y x -=B .2213131100225y x -=C .22194x y -=D .22131********y x -=8.下列四个命题:①()()0f a f b <为函数 ()f x 在区间 (,)a b 内存在零点的必要不充分条件;②从总体中抽取的样本1122(,),(,),(,),n n x y xy x y …,若记1111,,n ni i i i X x Y y n n ====∑∑则回归直线ˆybx a =+必过点(,)X Y ;③设点P 是ABC ∆所在平面内的一点,且2BC BA BP +=,则P 为线段AC 的中点;④若空间两点 (1,2,1),(2,0,)A B m -2m =. 其中真命题的个数为( )A .1个B .2个C .3 个D .4个9.已知定义在R 上的函数()y f x =满足()()f x f x =--,当0x <时,'()0f x <.若120x x +<,且120x x <,则12()()f x f x +的值( )A .恒正B .恒负C .可正可负D .可能等于010.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之积为10的概率为( )A .1144B .1160C .1180D .1360第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,满分25分.11.若函数 ()log (3)a f x m x =+-的图像恒过点(4,2),则 22()4x x m g x m +=+的最大值是 .12.已知直线1:30l x y ++=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是13.对于有线性相关关系的变量y x ,,测得一组数据如下表:根据上表得它们的回归直线方程为a x y ˆ52.10ˆ+=,据此模型来预 测当20=x 时,y 的估计值为14.已知函数5(6),()(4)4(6),2x a x f x ax x -⎧>⎪=⎨-+≤⎪⎩是R 上的单调递增函数,则实数a 的取值范围是 15.已知过抛物线22(0)y px p =>的焦点F的直线与抛物线交于,A B 两点,且AF BF >,则AF BF= .三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.(本小题满分13分)在三边互不相等的 ABC ∆中,已知 45,tan .3AB BC A ===(1)求AC 的值;(2)求cos(2)A C +的值.17.(本小题满分13分)某校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按[)[)[)40,50,50,60,60,70,[)[)[]70,80,80,90,90,100分组,得到成绩分布的频率分布直方图(如图).(1)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;(3)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写下面22⨯列联表,并问是否有99%的把握认为“18.(本小题满分13分)如图是某三棱柱被截去一部分后的直观图与三视图的侧视图、俯视图.在直观图中,2CF AD =,M 是FD 的中点. 侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.(1)求该几何体的体积; (2)求证:EM ACFD ⊥平面.19.(本小题满分12分)已知圆 22:2O x y +=交x 轴正半轴于点A ,点F 满足2OF OA =,以F 为右焦点的椭圆 C . (1)求椭圆 C 的标准方程;(2)设过圆 O 上一点P 的切线交直线 2x =于点Q ,求证:PF OQ ⊥.20. (本小题满分12分)设数列 {}n a 的前n 项和为n S ,且 *21()n n S a n N =-∈. (1)求数列 {}n a 的通项公式;(2)设数列 {}n na 的前n 项和为n T ,对任意 *n N ∈,比较2n T与 n S 的大小.21.(本小题满分12分)设0a >,函数 2()xe f x x a=+.(1)求函数 ()f x 的单调区间; (2)当12x =时,函数 ()f x 取得极值,证明:对于任意的 1213,[,],22x x ∈12()()f x f x |-重庆高考数学(文科)参考答案一、 BDCBB ABBAC二、11.1.12..13. 211.8 14. [)7,8 15.3 三、16.(Ⅰ)由4tan 3A =知,由余弦定理,222525cos AC AC A =+-⨯⨯,即 2650AC AC -+=,1,5AC AC ∴==或(舍去). …………………6分(Ⅱ)cos C ==,sin C ∴,2247sin 22sin cos ,cos22cos 12525A A A A A ===-=-cos(2)cos2cos sin 2sin A C A C A C ∴+=-= …………………12分17.(Ⅰ)高一合格率为0.02100.03100.02100.01100.8⨯+⨯+⨯+⨯==80﹪; ………4分(Ⅱ)高一样本的平均数为10102030201045556575859572100100100100100100⨯+⨯+⨯+⨯+⨯+⨯=,据此,可以估计高一年级这次知识竞赛的学生的平均成绩为72分. ………8分 (Ⅲ)2200(80402060)9.5 6.63510010014060K ⨯-⨯=≈>⨯⨯⨯.所以有99%的把握认为“这次知识竞赛的成绩与年级有关系”. ………12分 18.(Ⅰ)CF P,P PQ BC BE Q,取中点过作∥交于PD,QD,AD CP AD=CP 连结∥且,ACPD 四边形为平行四边形,AC PD ∴∥,PDQ ABC ∴平面∥面,2D-EFPQ DQP-ABC 11V=V +V =2sin 60223∴⨯︒⨯+三棱柱…………6分(Ⅱ)由三视图可知,ABC CBEF ⊥平面平面,FC ABC ⊥平面, 取AC 中点N ,连结MN,BN ,BN AC,ABC ∆⊥中, 又FC ABC,BN FC,⊥∴⊥平面BN ACFD ∴⊥平面MN MN=BE=3,∥CF ∥AD∥BE,又BN EM ∴∴四边形BEMN 为平行四边形,∥EM ACFD ∴⊥平面. …………12分19.(Ⅰ)(1,0)A F .椭圆1,c =e =,a ∴=2221b a c =-=, 221x y ∴+=椭圆D 的方程为2. ………………5分(Ⅱ)设点()11,P x y ,过点P 的圆的切线方程为 ()1111x y y x x y -=-- 即()1111xy x x y y =--+。

2023年广东省揭阳市高考数学押题试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={x∈Z|﹣1<x≤2},B={x||x|≤1},则A∩B=()A.{x|0<x≤1}B.{x|﹣1<x≤1}C.{1}D.{0,1}2.(5分)复数z=2﹣i5(其中i为虚数单位)的共轭复数为()A.2﹣i B.2+i C.1D.33.(5分)已知单位向量,,,满足+=,则向量和的夹角为()A.B.C.D.4.(5分)“”是“方程表示的曲线为双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件5.(5分)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数n'与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有()A.648个B.720个C.810个D.891个6.(5分)已知圆M:(x﹣a)2+(y﹣1)2=r2(r>0),若圆M与x轴交于A,B两点,且=,则r=()A.2B.2C.D.17.(5分)如图1,洛书是一种关于天地空间变化脉络的图案,2014年正式入选国家级非物质文化遗产名录,其数字结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,形成图2中的九宫格,将自然数1,2,3,…,n2放置在n行n列(n≥3)的正方形图表中,使其每行、每列、每条对角线上的数字之和(简称“幻和”)均相等,具有这种性质的图表称为“n阶幻方”.洛书就是一个3阶幻方,其“幻和”为15.则7阶幻方的“幻和”为()A.91B.169C.175D.1808.(5分)已知函数f(x)=sin x+sin2x在(0,a)上有4个零点,则实数a的最大值为()A.πB.2πC.πD.3π二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.(多选)9.(5分)进入21世纪以来,全球二氧化碳排放量增长迅速,自2000年至今,全球二氧化碳排放量增加了约40%,我国作为发展中国家,经济发展仍需要大量的煤炭能源消耗.如图是2016﹣2020年中国二氧化碳排放量的统计图表(以2016年为第1年).利用图表中数据计算可得,采用某非线性回归模型拟合时,;采用一元线性回归模型拟合时,线性回归方程为,.则下列说法正确的是()A.由图表可知,二氧化碳排放量y与时间x正相关B.由决定系数可以看出,线性回归模型的拟合程度更好C.利用线性回归方程计算2019年所对应的样本点的残差为﹣0.30D.利用线性回归方程预计2025年中国二氧化碳排放量为107.24亿吨(多选)10.(5分)将函数图象上所有的点向右平移个单位长度,得到函数g(x)的图象,则下列说法正确的是()A.g(x)的最小正周期为πB.g(x)图象的一个对称中心为C.g(x)的单调递减区间为D.g(x)的图象与函数的图象重合(多选)11.(5分)已知函数,g(x)=f(x+1).若实数a,b(a,b均大于1)满足g(3b﹣2a)+g(﹣2﹣a)>0,则下列说法正确的是()A.函数f(x)在R上单调递增B.函数g(x)的图象关于(1,0)中心对称C.D.log a(a+1)>log b(b+1)(多选)12.(5分)如图,已知正方体ABCD﹣A1B1C1D1顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n 次后仍在底面ABCD上的概率为P n,则下列说法正确的是()A.B.P n+1=+C.点Q移动4次后恰好位于点C1的概率为0D.点Q移动10次后恰好回到点A的概率为三、填空题:本题共4小题,每小题5分,共20分.13.(5分)若正数a,b满足ab=4,则的最小值为.14.(5分)已知抛物线y2=2px(p>0),若过点(1,2)的直线l与抛物线恒有公共点,则p的值可以是.(写出一个符合题意的答案即可)15.(5分)2022年3月,中共中央办公厅、国务院办公厅印发了《关于构建更高水平的全民健身公共服务体系的意见》,再次强调持续推进体育公园建设.如图,某市拟建造一个扇形体育公园,其中,OA=OB=2千米.现需要在OA,OB,上分别取一点D,E,F,建造三条分健走长廊DE,DF,EF,若DF⊥OA,EF⊥OB,则DE+EF+FD 的最大值为千米.16.(5分)在四面体ABCD中,已知AB=CD=AC=BD=2,AD=BC=4,记四面体ABCD外接球的球心到平面ABC的距离为d1,四面体ABCD内切球的球心到点A的距离为d2,则的值为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知△ABC内角A,B,C的对边分别为a,b,c,满足4a sin B=3b cos A.(1)求cos A的值;(2)若△ABC的面积为,求的值.18.(12分)已知数列{a n}满足,a2=4.(1)求数列{a n}的通项公式;(2)记数列的前n项和为S n,求证:S n<2.19.(12分)如图1,正方形ABCD中,E,F分别为边BC,AD的中点,将四边形EFDC 沿直线EF折起,使得平面CDFE⊥平面ABEF.如图2,点M,N分别满足,.(1)求证:AN⊥平面BMN;(2)求平面AFM与平面BMN夹角的余弦值.20.(12分)数据显示,中国直播购物规模近几年保持高速增长态势,而直播购物中的商品质量问题逐渐成为人们关注的重点.已知某顾客在直播电商处购买了n(n∈N+)件商品.(1)若n=10,且买到的商品中恰好有2件不合格品,该顾客等可能地依次对商品进行检查.求顾客检查的前4件商品中不合格品件数X的分布列.(2)抽检中发现直播电商产品不合格率为0.2.若顾客购买的n件商品中,至少有两件合格产品的概率不小于0.9984,求n的最小值.21.(12分)已知椭圆C:+=1(a>b>0)的离心率为,且经过点P(1,).(1)求椭圆C的方程;(2)A,B为椭圆C上两点,直线PA与PB倾斜角互补,求△PAB面积的最大值.22.(12分)已知函数f(x)=ln|x|+a cos x+bx,其中a≥0,b∈R.(1)当a=0时,若f(x)存在大于零的极值点,求b的取值范围.(2)若存在x1,(其中x1≠x2),使得曲线y=f(x)在点(x1,f(x1))与点(x2,f(x2))处有相同的切线,求a的取值范围.2023年广东省揭阳市高考数学押题试卷参考答案与试题解析一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={x∈Z|﹣1<x≤2},B={x||x|≤1},则A∩B=()A.{x|0<x≤1}B.{x|﹣1<x≤1}C.{1}D.{0,1}【解答】解:集合A={x∈Z|﹣1<x≤2}={0,1,2},B={x||x|≤1}={x|﹣1≤x≤1},则A∩B={0,1}.故选:D.2.(5分)复数z=2﹣i5(其中i为虚数单位)的共轭复数为()A.2﹣i B.2+i C.1D.3【解答】解:∵z=2﹣i5=2﹣i4+1=2﹣i,∴,故选:B.3.(5分)已知单位向量,,,满足+=,则向量和的夹角为()A.B.C.D.【解答】解:单位向量,,,满足+=,∴()2=1+1+2cos<>=1,解得cos<>=﹣,∴0≤<>≤π,∴向量和的夹角为.故选:A.4.(5分)“”是“方程表示的曲线为双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【解答】解:∵方程表示的曲线为双曲线,⇔(2a﹣1)a<0⇔0<a<,∴是方程表示的曲线为双曲线的充要条件,故选:C.5.(5分)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n为自然数,且n的各位数字反向排列所得自然数n'与n相等,这样的n称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有()A.648个B.720个C.810个D.891个【解答】解:根据题意,五位“回文数”的万位数字不能为0,有9种情况,千位、百位数字都有10种情况,则五位“回文数”共有9×10×10=900个,其中,各位数字完全相同的情况有9种,则所有5位数中是“回文数”且各位数字不全相同的共有900﹣9=891个,故选:D.6.(5分)已知圆M:(x﹣a)2+(y﹣1)2=r2(r>0),若圆M与x轴交于A,B两点,且=,则r=()A.2B.2C.D.1【解答】解:∵圆M:(x﹣a)2+(y﹣1)2=r2(r>0),∴圆心M(a,1),半径为r,圆心到x轴的距离为1,∵圆M与x轴交于A,B两点,且=,∴可设|AB|=,|MB|=t(t>0),∴由垂径定理可得,,即,解得t=2,∴圆的半径r=t=2.故选:B.7.(5分)如图1,洛书是一种关于天地空间变化脉络的图案,2014年正式入选国家级非物质文化遗产名录,其数字结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,形成图2中的九宫格,将自然数1,2,3,…,n2放置在n行n列(n≥3)的正方形图表中,使其每行、每列、每条对角线上的数字之和(简称“幻和”)均相等,具有这种性质的图表称为“n阶幻方”.洛书就是一个3阶幻方,其“幻和”为15.则7阶幻方的“幻和”为()A.91B.169C.175D.180【解答】解:将自然数1,2,3,…,n2放置在n行n列(n≥3)的正方形图表中,使其每行、每列、每条对角线上的数字之和(简称“幻和”)均相等,故当n=7时,S=1+2+3+…+49=,故7阶幻方的“幻和”为×=175.故选:C.8.(5分)已知函数f(x)=sin x+sin2x在(0,a)上有4个零点,则实数a的最大值为()A.πB.2πC.πD.3π【解答】解:∵f(x)=sin x+sin2x=sin x(1+2cos x)在(0,a)上有4个零点,∴sin x=0或cos x=﹣,∴x=kπ(k∈Z且k≠0)或x=2kπ±(k∈Z),当sin x=0在(0,a)上取到第二个零点,但取不到第三个零点时,a∈(2π,3π];当y=cos x与y=﹣在(0,a)上取到第三个交点时的x的值为,∴满足题意的实数a的最大值为,故选:C.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.(多选)9.(5分)进入21世纪以来,全球二氧化碳排放量增长迅速,自2000年至今,全球二氧化碳排放量增加了约40%,我国作为发展中国家,经济发展仍需要大量的煤炭能源消耗.如图是2016﹣2020年中国二氧化碳排放量的统计图表(以2016年为第1年).利用图表中数据计算可得,采用某非线性回归模型拟合时,;采用一元线性回归模型拟合时,线性回归方程为,.则下列说法正确的是()A.由图表可知,二氧化碳排放量y与时间x正相关B.由决定系数可以看出,线性回归模型的拟合程度更好C.利用线性回归方程计算2019年所对应的样本点的残差为﹣0.30D.利用线性回归方程预计2025年中国二氧化碳排放量为107.24亿吨【解答】解:对于A,由图表可知,图象中的点呈上升趋势,即二氧化碳排放量y与时间x正相关,故A正确,对于B,∵,∴线性回归模型的拟合程度更好,故B正确,对于C,2019年,对应x=4,2019年所对应的样本点的残差为98.06﹣(1.58×4+91.44)=0.3,故C错误,对于D,2025年,对应x=10,预计2025年中国二氧化碳排放量为1.58×10+91.44=107.24亿吨,故D正确.故选:ABD.(多选)10.(5分)将函数图象上所有的点向右平移个单位长度,得到函数g(x)的图象,则下列说法正确的是()A.g(x)的最小正周期为πB.g(x)图象的一个对称中心为C.g(x)的单调递减区间为D.g(x)的图象与函数的图象重合【解答】解:将函数图象上所有的点向右平移个单位长度,得到函数g(x)=cos(2x﹣)的图象,对于A:函数的最小正周期为π,故A正确;对于B:当x=时,g()=0,故B正确;对于C:令(k∈Z),整理得函数的单调递减区间为,故C正确;对于D:函数g(x)=cos(2x﹣)=,故D错误.故选:ABC.(多选)11.(5分)已知函数,g(x)=f(x+1).若实数a,b(a,b均大于1)满足g(3b﹣2a)+g(﹣2﹣a)>0,则下列说法正确的是()A.函数f(x)在R上单调递增B.函数g(x)的图象关于(1,0)中心对称C.D.log a(a+1)>log b(b+1)【解答】解:对于A,∵>=|2x|,∴+2x>0在R上恒成立,∴f(x)定义域为R,即f(x)的定义域关于原点对称,∵f(x)+f(﹣x)=ln[(+2x)(﹣2x)]=ln1=0,∴f(x)为奇函数,∴函数f(x)的图象关于点(0,0)中心对称,∵y=x3,y=+2x,y=lnx在(0,+∞)上单调递增,∴函数数在(0,+∞)上单调递增,∴函数f(x)在R上单调递增,故A正确;对于B,∵g(x)=f(x+1)的图象是将y=f(x)的图象向左平称一个单位得到,∴函数g(x)的图象关于点(﹣1,0)中心对称,故B错误;对于C,∵函数g(x)的图象关于点(﹣1,0)中心对称,∴g(a)+g(﹣2﹣a)=0,∴﹣g(﹣2﹣a)=g(a),∵g(3b﹣2a)+g(﹣2﹣a)>0,∴g(3b﹣2a)>﹣g(﹣2﹣a)=g(a),∵g(x)相当于f(x)向左平移1个单位,∴g(x)和f(x)单调性相同,∴函数g(x)在R上单调递增,∴3b﹣2a>a,∴b>a>1,∴e a﹣b<e0=1<,故C错误;对于D,令h(x)=(x>1),∴h′(x)=(x>1),令s(x)=xlnx(x>1),则s′(x)=lnx+1>0,∴s(x)在(1,+∞)上单调递增,∴xlnx<(x+1)ln(x+1),∴h′(x)=<0,∴h(x)在(1,+∞)上单调递减,∵b>a>1,∴h(a)>h(b),∴log a(a+1)>log b(b+1),故D正确.故选:AD.(多选)12.(5分)如图,已知正方体ABCD﹣A1B1C1D1顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n 次后仍在底面ABCD上的概率为P n,则下列说法正确的是()A.B.P n+1=+C.点Q移动4次后恰好位于点C1的概率为0D.点Q移动10次后恰好回到点A的概率为【解答】解:在正方体中,每一个顶点由3个相邻的点,其中两个在同一底面,∴当点Q在下底面时,随机移动一次仍在下底面的概率为,在上底面时,随机移动一次回到下底面的概率为,∴P2==,故A正确;P n+1=+=,故B错误;点Q由点A移动到点C1处至少需要3次,任意折返都需要2次移动,∴移动4次后不可能到达点C1,故C正确;由于P n+1=+,∴,且P1﹣=,∴,∴P n=,∴P9=,∴点Q移动10次后恰好回到点A的概率为=,故D正确.故选:ACD.三、填空题:本题共4小题,每小题5分,共20分.13.(5分)若正数a,b满足ab=4,则的最小值为3.【解答】解:因为a>0,b>0,且ab=4,所以≥2=2×=2×=3,当且仅当=,即a=,b=6时取“=”,所以+的最小值为3.故答案为:3.14.(5分)已知抛物线y2=2px(p>0),若过点(1,2)的直线l与抛物线恒有公共点,则p的值可以是不小于2的实数.(写出一个符合题意的答案即可)【解答】解:抛物线方程为y2=2px(p>0),若过点(1,2)的直线l与抛物线恒有公共点,则点(1,2)在抛物线内部或在抛物线上,可得22≤2p,即p≥2.∴p的值可以是不小于2的实数.故答案为:不小于2的实数.15.(5分)2022年3月,中共中央办公厅、国务院办公厅印发了《关于构建更高水平的全民健身公共服务体系的意见》,再次强调持续推进体育公园建设.如图,某市拟建造一个扇形体育公园,其中,OA=OB=2千米.现需要在OA,OB,上分别取一点D,E,F,建造三条分健走长廊DE,DF,EF,若DF⊥OA,EF⊥OB,则DE+EF+FD的最大值为千米.【解答】解:据题意,设∠BOF=α,则∠DOF=,结合OF=2,EF=2sinα,,α∈(),显然O,E,F,D四点共圆,且直径为2,故,DE=,所以DE+EF+FD=+2(sinα+sin())=,易知,当时,原式取得最大值.故答案为:.16.(5分)在四面体ABCD中,已知AB=CD=AC=BD=2,AD=BC=4,记四面体ABCD外接球的球心到平面ABC的距离为d1,四面体ABCD内切球的球心到点A的距离为d2,则的值为.【解答】解:由题意可将四面体ABCD放在一个长方体中,如图所示,设长宽高为a,b,c,则,解得,设外接球的半径为R1,则,在△ABC中,,则,设△ABC的外接圆半径为r,则,则,所以,可得,设四面体ABCD内切球的半径为R2,因为四面体的各个面都相等,且,则,解得,因为d1=R2,四面体的各个面都相等,则外接球的球心到各个面的距离相等,所以外接球的球心和内切球的球心重合,所以,所以.故答案为:.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知△ABC内角A,B,C的对边分别为a,b,c,满足4a sin B=3b cos A.(1)求cos A的值;(2)若△ABC的面积为,求的值.【解答】解:(1)因为4a sin B=3b cos A,由正弦定理得:4sin A sin B=3sin B cos A,因为sin B>0,所以4sin A=3cos A,又因为sin2A+cos2A=1,A∈(0,),所以;(2)由(1)及余弦定理知,整理得:5b2+5c2﹣5a2=8bc,①由面积公式:,整理得:5a2﹣5c2=3bc,②由①②得:5b2=11bc,所以.18.(12分)已知数列{a n}满足,a2=4.(1)求数列{a n}的通项公式;(2)记数列的前n项和为S n,求证:S n<2.【解答】解:(1)∵﹣=1,∴{}是以1为公差的等差数列,又∵a2=4,﹣=1,∴=1,∴=n,则a n=n2;(2)证明:由(1)可知==<==2(﹣),所以S n=++•••+<2[(1﹣)+(﹣)+•••+(﹣)]=2﹣,又n∈N*,故S n=2﹣<2.19.(12分)如图1,正方形ABCD中,E,F分别为边BC,AD的中点,将四边形EFDC 沿直线EF折起,使得平面CDFE⊥平面ABEF.如图2,点M,N分别满足,.(1)求证:AN⊥平面BMN;(2)求平面AFM与平面BMN夹角的余弦值.【解答】解:(1)证明:连结AE交BN于点G,连结MG,设AB=2,因为平面CDFE⊥平面ABEF,平面CDFE∩平面ABEF=EF,CE⊂平面CDFE,CE⊥EF,所以CE⊥平面ABEF,因为点N是EF的中点,NE∥AB,所以AG=2GE,又因为AM=2MC,所以MG∥CE,所以MG⊥平面ABEF,因为AN⊂平面ABEF,所以MG⊥AN,又AB=2,,所以AN⊥NB,因为NB∩MG=G,NB,MG⊂平面BMN,所以AN⊥平面BMN.(2)如图,分别以FA,FE,FD所在直线为x,y,z轴建立空间直角坐标系,所以F(0,0,0),A(1,0,0),,所以,,设平面AFM的法向量为,由,解得,令y=1,得,由(1)知平面BMN的法向量为,设平面AFM与平面BMN的夹角为θ,所以,所以平面AFM与平面BMN夹角的余弦值为.20.(12分)数据显示,中国直播购物规模近几年保持高速增长态势,而直播购物中的商品质量问题逐渐成为人们关注的重点.已知某顾客在直播电商处购买了n(n∈N+)件商品.(1)若n=10,且买到的商品中恰好有2件不合格品,该顾客等可能地依次对商品进行检查.求顾客检查的前4件商品中不合格品件数X的分布列.(2)抽检中发现直播电商产品不合格率为0.2.若顾客购买的n件商品中,至少有两件合格产品的概率不小于0.9984,求n的最小值.【解答】解:(1)由题意可知,X的取值为0,1,2.,,.所以顾客检查的前4件商品中不合格品件数X的分布列为X015P(2)记“顾客购买的n件商品中,至少有两件合格产品”为事件A,则,由题意可知1﹣(1+4n)⋅0.2n≥0.9984,所以(1+4n)⋅0.2n≤0.0016,即(1+4n)⋅0.2n﹣4≤1,设f(n)=(1+4n)⋅0.2n﹣4,则f(n+1)﹣f(n)=(5+4n)⋅0.2n﹣3﹣(1+4n)⋅0.2n ﹣4=﹣16n⋅0.2n﹣3<0,所以f(n+1)<f(n),因为f(5)=21×0.2=4.2>1,f(6)=25×0.04=1,所以当n≥6时,f(n)≤1成立,所以n的最小值为6.21.(12分)已知椭圆C:+=1(a>b>0)的离心率为,且经过点P(1,).(1)求椭圆C的方程;(2)A,B为椭圆C上两点,直线PA与PB倾斜角互补,求△PAB面积的最大值.【解答】解:(1)由题意得:,解得:,,∴椭圆方程为.(2)由题意可知直线AB的斜率一定存在,设直线AB的方程为y=kx+t,A(x1,y1),B(x2,y2),将y=kx+t代入得:(k2+3)x2+2ktx+t2﹣6=0,∴,,则y1+y2=kx1+t+kx2+t=k(x1+x2)+2t=,x1y2+x2y1=x1(kx2+t)+x2(kx1+t)=kt(x1+x2)+2ktx1x2=,∵直线PA和直线PB的倾斜角互补,∴,化简可得:,即,即,∵直线AB不过点P,∴,∴,,则,又点P到直线AB的距离为,∵Δ=12t2﹣24(t2﹣6)>0,∴,∴,当且仅当时等号成立,∴△PAB面积最大值为.22.(12分)已知函数f(x)=ln|x|+a cos x+bx,其中a≥0,b∈R.(1)当a=0时,若f(x)存在大于零的极值点,求b的取值范围.(2)若存在x1,(其中x1≠x2),使得曲线y=f(x)在点(x1,f(x1))与点(x2,f(x2))处有相同的切线,求a的取值范围.【解答】解:(1)由题意知f(x)=ln|x|+bx,.①若b≥0,当x∈(0,+∞)时,f'(x)>0,f(x)单调递增,无极值点;②若b<0,当x∈(0,﹣)时,f'(x)<0,f(x)单调递减;当x∈(﹣,+∞)时,f'(x)>0,f(x)单调递增;f(x)在(0,+∞)上存在唯一的极小值点﹣,故b的取值范围是(﹣∞,0).(2)由题意,f(x)在点(x1,f(x1))处的切线方程为y﹣f(x1)=f'(x1)(x﹣x1),即y=f'(x1)x﹣x1f'(x1)+f(x1),同理f(x)在点(x2,f(x2))处的切线方程为y=f'(x2)x﹣x2f'(x2)+f(x2),因为两切线相同,所以,化简得,令h(x)=ax sin x+ln|x|+a cos x,,当时,h'(x)>0,h(x)单调递增;当时,h'(x)<0,h(x)单调递减.注意到h(x)为偶函数,且x1≠x2,h(x1)=h(x2),故x1+x2=0,令,注意到g(x)的奇函数,所以当x1+x2=0时,g(x1)+g(x2)=0,又因为g(x1)=g(x2),故g(x1)=g(x2)=0,因为a>0,,所以,当时,g(x)单调递减,,当时,g(x)单调递减,.故,所以,即a∈[,+∞).。

高三数学考试(文科)本试题卷分为选择题和非选择题两部分,共23小题,时量120分钟,满分150分。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={xly =-/I=x },则CRA=A.{xix 《O} B.{xix ζ1}已{xJx >O }D. {xlx>l}2.复数z =i(l 一i)+2在复平面内对应的点位于A.第一象限B.第二象限 c.第三象限D.第四象限3.在等比数列{a ,.}中,若αs =2,句句=句,则{a ,.}的公比q =A . ./2B. 2C .2./2D.44.己知某班共有学生46人,该班语文老师为了了解学生每天阅读课外书籍的时长情况,决定利用随机数表法从全班学生中抽取10人进行调查.将46名学生按01,02,…,46进行编号.现提供随机数表的第7行至第9行:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 . 21 12 34 2978 64 56 07 8252 42 07 44 3815 51 00 13 4299 66 02 79 54若从表中第7行第41列开始向右依次读取2个数据,每行结束后,下一行依然向右读数,则得到的第8个样本编号是A. 07 B. 12 C. 39 D 44 5.已知函数f(x )是定义在R上的奇函数,且f(x-3)=f (到+1,则f(6=A.一1B.1C. -2D.26.己知函数f(x )=「'-lnx-a ,若对任意的zε口,+oo ,f(x )注0成立,则a的最大值是A.In 2B ._l c.1D.e7.勾股定理,在我国又称为“商高定理”,最早的证明是由东叹末期数学家赵爽在为《周静算经》作注时给出的,他利用了句股困方图,此图被称为“赵爽弦图”.“赵爽弦图”是由四个金等的直角三角形和中间的一个小正方形组成的大正方形图案(如图所示〉,若在大正方形内随机取一点,该9点落在小正方形内的概率为币’则“赵爽弦图”里的直角三角形中最小角的正弦值为2一盯人 B.v'3434c 主. 17D. .JI 于17[高三数学第l 页(共4页)文科]@Q!巳·HEN·8己知椭圆C :王+亏=l的左、右顶起分别是A ,B ,。

备战09高考数学――名师精编预测题跟踪演练详解系列五1.(本小题满分14分)已知椭圆)0(12222>>=+b a by ax 的左、右焦点分别是F 1(-c ,0)、F 2(c ,0),Q是椭圆外的动点,满足.2||1a Q F =点P 是线段F 1Q 与该椭圆的交点,点T 在线段F 2Q 上,并且满足.0||,022≠=⋅TF TF PT(Ⅰ)设x 为点P 的横坐标,证明x ac a P F +=||1;(Ⅱ)求点T 的轨迹C 的方程;(Ⅲ)试问:在点T 的轨迹C 上,是否存在点M , 使△F 1MF 2的面积S=.2b 若存在,求∠F 1MF 2的正切值;若不存在,请说明理由.本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应用,以及综合运用数学知识解决问题的能力.满分14分. (Ⅰ)证法一:设点P 的坐标为).,(y x由P ),(y x 在椭圆上,得.)()()(||222222221x ac a xab bc x y c x P F +=-++=++=由0,>+-≥+≥a c x ac a a x 知,所以 .||1x ac a P F +=………………………3分证法二:设点P 的坐标为).,(y x 记,||,||2211r P F r P F ==则.)(,)(222221y c x r y c x r ++=++=由.||,4,211222121x a c a r P F cx r r a r r +===-=+得 证法三:设点P 的坐标为).,(y x 椭圆的左准线方程为.0=+x a c a由椭圆第二定义得ac cax P F =+||||21,即.||||||21x a c a cax ac P F +=+=由0,>+-≥+-≥a c x ac a a x 知,所以.||1x ac a P F +=…………………………3分(Ⅱ)解法一:设点T 的坐标为).,(y x当0||=PT 时,点(a ,0)和点(-a ,0)在轨迹上.当|0||0|2≠≠TF PT 且时,由0||||2=⋅TF PT ,得2TF PT ⊥. 又||||2PF PQ =,所以T 为线段F 2Q 的中点. 在△QF 1F 2中,a Q F OT ==||21||1,所以有.222a yx =+综上所述,点T 的轨迹C 的方程是.222a y x =+…………………………7分解法二:设点T 的坐标为).,(y x 当0||=PT 时,点(a ,0)和点(-a ,0)在轨迹上. 当|0||0|2≠≠TF PT 且时,由02=⋅TF PT ,得2TF PT ⊥.又||||2PF PQ =,所以T 为线段F 2Q 的中点.设点Q 的坐标为(y x '',),则⎪⎪⎩⎪⎪⎨⎧'=+'=.2,2y y c x x因此⎩⎨⎧='-='.2,2y y c x x ①由a Q F 2||1=得.4)(222a y c x ='++' ② 将①代入②,可得.222a y x =+综上所述,点T 的轨迹C 的方程是.222a y x =+……………………7分(Ⅲ)解法一:C 上存在点M (00,y x )使S=2b 的充要条件是⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x 由③得a y ≤||0,由④得.||20cby ≤ 所以,当cb a 2≥时,存在点M ,使S=2b ;当cba2<时,不存在满足条件的点M.………………………11分③ ④当cb a 2≥时,),(),,(002001y x c MF y x c MF --=---=,由2222022021b c a y c x MF MF =-=+-=⋅,212121cos ||||MF F MF MF MF MF ∠⋅=⋅,22121sin ||||21b MF F MF MF S =∠⋅=,得.2tan 21=∠MF F解法二:C 上存在点M (00,y x )使S=2b 的充要条件是⎪⎩⎪⎨⎧=⋅=+.||221,2022020b y c a y x由④得.||20cby ≤ 上式代入③得.0))((2224220≥+-=-=cba cba cb a x于是,当cba 2≥时,存在点M ,使S=2b ;当cba2<时,不存在满足条件的点M.………………………11分当cba 2≥时,记cx y k k cx y k k M F M F -==+==00200121,,由,2||21a F F <知︒<∠9021MF F ,所以.2|1|tan212121=+-=∠k k k k MF F (14)分2.(本小题满分12分)函数)(x f y =在区间(0,+∞)内可导,导函数)(x f '是减函数,且.0)(>'x f 设m kx y x +=+∞∈),,0(0是曲线)(x f y =在点()(,00x f x )得的切线方程,并设函数.)(m kx x g +=(Ⅰ)用0x 、)(0x f 、)(0x f '表示m ; (Ⅱ)证明:当)()(,),0(0x f x g x ≥+∞∈时;(Ⅲ)若关于x 的不等式),0[231322+∞≥+≥+在x b ax x 上恒成立,其中a 、b 为实数,求b 的取值范围及a 与b 所满足的关系.本小题考查导数概念的几何意义,函数极值、最值的判定以及灵活运用数形结合的思想判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运用数学基本关系解决问③ ④题的能力.满分12分(Ⅰ)解:).()(000x f x x f m '-=…………………………………………2分 (Ⅱ)证明:令.0)(),()()(),()()(00=''-'='-=x h x f x f x h x f x g x h 则 因为)(x f '递减,所以)(x h '递增,因此,当0)(,0>'>x h x x 时;当0)(,0<'<x h x x 时.所以0x 是)(x h 唯一的极值点,且是极小值点,可知)(x h 的最小值为0,因此,0)(≥x h 即).()(x f x g ≥…………………………6分(Ⅲ)解法一:10≤≤b ,0>a 是不等式成立的必要条件,以下讨论设此条件成立. 0)1(,122≥-+-+≥+b ax x b ax x 即对任意),0[+∞∈x 成立的充要条件是.)1(221b a -≤另一方面,由于3223)(x x f =满足前述题设中关于函数)(x f y =的条件,利用(II )的结果可知,3223x b ax =+的充要条件是:过点(0,b )与曲线3223x y=相切的直线的斜率大于a ,该切线的方程为.)2(21b x b y +=-于是3223x b ax≥+的充要条件是.)2(21b a ≥…………………………10分综上,不等式322231x b ax x ≥+≥+对任意),0[+∞∈x 成立的充要条件是.)1(2)2(2121b a b -≤≤- ①显然,存在a 、b 使①式成立的充要条件是:不等式.)1(2)2(2121b b -≤- ②有解、解不等式②得.422422+≤≤-b ③因此,③式即为b 的取值范围,①式即为实数在a 与b 所满足的关系.…………12分(Ⅲ)解法二:0,10>≤≤a b 是不等式成立的必要条件,以下讨论设此条件成立. 0)1(,122≥-+-+≥+b ax x b ax x 即对任意),0[+∞∈x 成立的充要条件是.)1(221b a -≤………………………………………………………………8分令3223)(x b ax x -+=φ,于是3223x b ax ≥+对任意),0[+∞∈x 成立的充要条件是.0)(≥x φ 由.0)(331--==-='ax xa x 得φ当30-<<a x 时;0)(<'x φ当3->a x 时,0)(>'x φ,所以,当3-=a x 时,)(x φ取最小值.因此0)(≥x φ成立的充要条件是0)(3≥-a φ,即.)2(21-≥b a ………………10分综上,不等式322231x b ax x≥+≥+对任意),0[+∞∈x 成立的充要条件是.)1(2)2(2121b a b -≤≤- ①显然,存在a 、b 使①式成立的充要条件是:不等式2121)1(2)2(b b -≤- ②有解、解不等式②得.422422+≤≤-b因此,③式即为b 的取值范围,①式即为实数在a 与b 所满足的关系.…………12分3.(本小题满分12分)已知数列{}n a 的首项15,a =前n 项和为n S ,且*15()n n S S n n N +=++∈(I )证明数列{}1n a +是等比数列;(II )令212()nn f x a x a x a x =+++ ,求函数()f x 在点1x =处的导数(1)f '并比较2(1)f '与22313n n -的大小.解:由已知*15()n n S S n n N +=++∈可得12,24n n n S S n -≥=++两式相减得()1121n n n n S S S S +--=-+即121n n a a +=+从而()1121n n a a ++=+当1n =时21215S S =++所以21126a a a +=+又15a =所以211a =从而()21121a a +=+故总有112(1)n n a a ++=+,*n N ∈又115,10a a =+≠从而1121n n a a ++=+即数列{}1n a +是等比数列;(II )由(I )知321nn a =⨯-因为212()n n f x a x a x a x =+++ 所以112()2n n f x a a x na x -'=+++从而12(1)2n f a a na '=+++ =()()23212321(321)n n ⨯-+⨯-++⨯-=()232222n n +⨯++⨯ -()12n +++ =()1(1)31262n n n n ++-⋅-+由上()()22(1)23131212n f n n n '--=-⋅-()21221n n --=()()1212121(21)nn n n -⋅--+=12(1)2(21)nn n ⎡⎤--+⎣⎦① 当1n =时,①式=0所以22(1)2313f n n '=-; 当2n =时,①式=-120<所以22(1)2313f n n '<- 当3n ≥时,10n ->又()011211nnn nn n nn C C C C -=+=++++ ≥2221n n +>+所以()()12210nn n ⎡⎤--+>⎣⎦即①0>从而2(1)f '>22313n n -4.(本小题满分14分) 已知动圆过定点,02p⎛⎫⎪⎝⎭,且与直线2p x =-相切,其中0p >.(I )求动圆圆心C 的轨迹的方程;(II )设A 、B 是轨迹C 上异于原点O 的两个不同点,直线O A 和O B 的倾斜角分别为α和β,当,αβ变化且αβ+为定值(0)θθπ<<时,证明直线A B 恒过定点,并求出该定点的坐标.解:(I )如图,设M 为动圆圆心,,02p⎛⎫⎪⎝⎭为记为F ,过点M 作直线2p x =-的垂线,垂足为N ,由题意知:M F M N =即动点M 到定点F 与定直线2p x =-的距离相等,由抛物线的定义知,点M 的轨迹为抛物线,其中,02pF ⎛⎫⎪⎝⎭为焦点,2p x =-为准线,所以轨迹方程为22(0)y px P =>;(II )如图,设()()1122,,,A x y B x y ,由题意得12x x ≠(否则αβπ+=)且12,0x x ≠所以直线A B 的斜率存在,设其方程为y kx b =+,显然221212,22y y x x pp==,将y kx b =+与x =22(0)y px P =>联立消去x,得2220k y p y p b -+=由韦达定理知121222,p pb y y y y kk+=⋅=①(1)当2πθ=时,即2παβ+=时,ta n ta n 1αβ⋅=所以121212121,0y y x x y y x x ⋅=-=,221212204y y y y p-=所以2124y y p =由①知:224pb p k=所以2.b pk =因此直线A B 的方程可表示为2y kx Pk =+,即(2)0k x P y +-=所以直线A B 恒过定点()2,0p -(2)当2πθ≠时,由αβθ+=,得tan tan()θαβ=+=tan tan 1tan tan αβαβ+-=122122()4p y y y y p+-将①式代入上式整理化简可得:2tan 2p b pkθ=-,所以22tan p b pk θ=+,此时,直线A B 的方程可表示为y kx =+22tan ppk θ+即2(2)0tan p k x p y θ⎛⎫+--= ⎪⎝⎭所以直线A B 恒过定点22,tan p p θ⎛⎫- ⎪⎝⎭所以由(1)(2)知,当2πθ=时,直线A B 恒过定点()2,0p -,当2πθ≠时直线A B 恒过定点22,tan p p θ⎛⎫- ⎪⎝⎭. 5.(本小题满分12分)已知椭圆C 1的方程为1422=+yx,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (Ⅰ)求双曲线C 2的方程; (Ⅱ)若直线2:+=kx y l 与椭圆C 1及双曲线C 2都恒有两个不同的交点,且l 与C 2的两个交点A 和B 满足6<⋅OB OA (其中O 为原点),求k 的取值范围.解:(Ⅰ)设双曲线C 2的方程为12222=-by a x ,则.1,31422222==+=-=b c b a a 得再由故C 2的方程为.1322=-yx(II )将.0428)41(1422222=+++=++=kx x k yxkx y 得代入由直线l 与椭圆C 1恒有两个不同的交点得,0)14(16)41(16)28(22221>-=+-=∆kk k即 .412>k ①0926)31(1322222=---=-+=kx x k yxkx y 得代入将.由直线l 与双曲线C 2恒有两个不同的交点A ,B 得.131.0)1(36)31(36)26(,0312222222<≠⎪⎩⎪⎨⎧>-=-+-=∆≠-k k k k k k 且即)2)(2(,66319,3126),,(),,(22+++=+<+<⋅--=⋅-=+B A B A B A B A B A B A B A B A B B A A kx kx x x y y x x y y x x OB OA kx x kk x x y x B y x A 而得由则设.1373231262319)1(2)(2)1(222222-+=+-⋅+--⋅+=++++=kk kk k kk x x k x x kB A B A.0131315,613732222>--<-+kk kk 即于是解此不等式得.31151322<>k k或 ③由①、②、③得.11513314122<<<<kk或故k 的取值范围为)1,1513()33,21()21,33()1513,1( ----6.(本小题满分12分)数列{a n }满足)1(21)11(1211≥+++==+n a nn a a nn n 且.(Ⅰ)用数学归纳法证明:)2(2≥≥n a n ;(Ⅱ)已知不等式)1(:,0)1l n (2≥<><+n e a x x x n 证明成立对,其中无理数e=2.71828….(Ⅰ)证明:(1)当n=2时,222≥=a ,不等式成立. (2)假设当)2(≥=k k n 时不等式成立,即),2(2≥≥k a k那么221))1(11(1≥+++=+kk k a k k a . 这就是说,当1+=k n 时不等式成立.根据(1)、(2)可知:22≥≥n a k 对所有成立. (Ⅱ)证法一:由递推公式及(Ⅰ)的结论有 )1.()2111(21)11(221≥+++≤+++=+n a nn a nn a n nnn n两边取对数并利用已知不等式得 n nn a nn a ln )2111ln(ln 21++++≤+.211ln 2nn nn a +++≤ 故nn n n n a a 21)1(1ln ln 1++≤-+ ).1(≥n上式从1到1-n 求和可得 121212121)1(1321211ln ln -++++-++⨯+⨯≤-n n nn a a.22111121121121111)3121(211<-+-=--⋅+--++-+-=nnn nn即).1(,2ln 2≥<<n ea a n n 故(Ⅱ)证法二:由数学归纳法易证2)1(2≥->n n n n对成立,故).2()1(1)1(11(21)11(21≥-+-+<+++=+n n n a n n a nn a n nn n令).2())1(11(),2(11≥-+≤≥+=+n b n n b n a b nn n n 则取对数并利用已知不等式得 n n b n n b ln ))1(11ln(ln 1+-+≤+).2()1(1ln ≥-+≤n n n b n上式从2到n 求和得 )1(1321211ln ln 21-++⨯+⨯≤-+n n b b n.11113121211<--++-+-=nn因).2(3,3ln 1ln .313ln 11122≥=<+<=+=+++n ee b b a b n n 故故1,,,2,132222121≥<<<≥<-<+n e a e a e a n e e a n n 对一切故又显然成立. 7.(本小题满分12分)已知数列:,}{且满足的各项都是正数n a .),4(,21,110N n a a a a n n n ∈-==+(1)证明;,21N n a a n n ∈<<+ (2)求数列}{n a 的通项公式a n . 解:(1)方法一 用数学归纳法证明:1°当n=1时,,23)4(21,10010=-==a a a a∴210<<a a ,命题正确. 2°假设n=k 时有.21<<-k k a a 则)4(21)4(21,1111k k k k k k a a a a a a k n ---=-+=--+时).4)((21))((21)(211111k k k k k k k k k k a a a a a a a a a a ---=+---=-----而.0,04.0111<-∴>--<----k k k k k k a a a a a a又.2])2(4[21)4(2121<--=-=+k k k k a a a a∴1+=k n 时命题正确.由1°、2°知,对一切n ∈N 时有.21<<+n n a a金太阳新课标资源网 金太阳新课标资源网方法二:用数学归纳法证明:1°当n=1时,,23)4(21,10010=-==a a a a ∴2010<<<a a ;2°假设n=k 时有21<<-k k a a 成立, 令)4(21)(x x x f -=,)(x f 在[0,2]上单调递增,所以由假设有:),2()()(1f a f a f k k <<-即),24(221)4(21)4(2111-⨯⨯<-<---k k k k a a a a也即当n=k+1时 21<<+k k a a 成立,所以对一切2,1<<∈+k k a a N n 有 (2)下面来求数列的通项:],4)2([21)4(2121+--=-=+n n n n a a a a 所以21)2()2(2--=-+n n a an n n n n n n n n b b b b b a b 22212122222112)21()21(21)21(2121,2-+++----==⋅-=--=-=-= 则令,又b n =-1,所以1212)21(22,)21(---=+=-=n nn n n b a b 即。

预测题(5)本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分.满分150分.考试时间120分钟.第I 卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合}4,3,2,1{=U ,}2,1{=A ,}4,2{=B ,则=)(B A C U ( )2.3. 4 5 6.则第三组的频率是( )A .0.12B .0.21C .0.15D . 0.287.已知流程图如右图所示,该程序运行后,为使输出的b 值为16,则循环体的判断框内①处应填( ) A. 2 B. 3 C. 5 D. 78910于111213n 11122012301030立.类似地,在正项等比数列{}n b 中,有_____________________成立.14.给出下列命题:①对∀实数y ,都∃一个实数x ,使得43y x =;②两个非零向量a 与b 垂直的充要条件是|a +b |=|a -b |;③如果两条直线b a ,和平面M 满足M a ⊥,且M b ⊥,则b a //;④∃一个实数x ,使230x x -+≤.其中,假命题的序号是_________. 15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) A. (不等式选讲选做题)不等式112x x +≥+的实数解集为以2:l 161718 如图,在四棱锥P ABCD -中,底面ABCD 是正方 形,侧棱PD ⊥底面ABCD ,4,3PD DC ==,E 是PC 的中点.(I )证明://PA BDE 平面;(II )求PAD ∆以PA 为轴旋转所围成的几何体体积.19.(本小题满分12分)一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:其中1234567i =,,,,,,. (Ⅰ)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图.,20A 、B 两点,若||23AB =,求直线 21.(本小题满分14分) 已知函数323()(2)632f x ax a x x =-++-. (I )当2a >时,求函数()f x 极小值; (II )试讨论曲线()y f x =与x 轴公共点的个数.一、选择题1.B .(){1,24}{3}.U U C A B C == , 2.C .22(1)1211i i i i i-+=+-=--. 3.B . 因为tan 1k θ=<-,0θπ≤<,所以34πθπ<<. 4.B .由题意知02πθ-<<,从而tan 0θ<.此时有5.6. 7.选8.数3)9.的最小值为3.10.D . 设),(y x p ,则(,),(,),a aM y y N y y b b- 于是 (,0)(,0)a aPM PN y x y x b b⋅=-⋅-- ()()a a y x y x b b =---22222222222221()a a b x y b x a y a b b b=-=-==,所以 2PM NP PM PN a ⋅=-⋅=- .11.. ∵180754560A ∠=--= .∴10sin 45sin 60x = ,∴x =. 12.④. 用三视图的概念容易做出只有圆锥满足题意,应填④. 13.30302110201211b b b b b b =.由算术平均数类比几何平均数,容易得出30302110201211b b b b b b =.14.①④. 分别判断命题如下:于x ,2令222242k x k πππππ-≤+≤+,得388k x k ππππ-≤≤+. 所以,单调递增区间为3,,88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. ……………………6分(II )解法1:当]3,0[π∈x ,112,4412t x πππ⎡⎤=+∈⎢⎥⎣⎦,由11,,412y t t ππ⎡⎤=∈⎢⎥⎣⎦的图象可知,当2t π=时,y 9分当1112t π=时,y111122π=.所以,值域12⎣. ……………………12分 解法2:若30π≤≤x ,则1211424πππ≤+≤x ,4sin 426)64sin(12sin 1211sin πππππ<-=-==, ……………………9分17所以21n n a =-. …………………………………….12分 解法2:由已知得12n n n a a +-=, 则212a a -=;2322a a -=; 3432a a -=;112n n n a a ---=(2)n ≥.累加得23112222n n a a --=++++ . 即2311222221n n n a -=+++++=- .当1n =时,11a =也成立,所以数列{}n a 的通项公式21n n a =-.………..12分 18.(I )连接,A C 交BD 于O ,连接EO . …………2分19.(Ⅰ)散点图如图………………………………………………4分(Ⅱ)7i=13245i ix y=∑,25x =,15.43y =,7215075i i x ==∑,2()4375n x =∴71722170.797()i ii ii x y x yb xx ==-⋅=≈-∑∑, ………………………………………………7分20和(因为OQ OM ON =+ ,所以()()00,,2x y x y = 即0x x =,02yy =. ………………8分 又因为22004x y +=,所以224(0)4y x y +=≠,所以Q 点的轨迹方程是221(0)416x y y +=≠, ………………11分 这说明轨迹是中心在原点,焦点在y 轴,长轴为8、短轴为4的椭圆,除去短轴端点 . …………13分21. (I )'22()33(2)63()(1),f x ax a x a x x a=-++=-- ………3分 ()f x 极小值为(1)2af =-. ………6分(II。

(5)数列——2024年高考数学真题模拟试题专项汇编一、选择题1.[2024届·重庆市第八中学·模拟考试]已知数列{}n a 的前n 项和为n S ,设甲:{}n a 是等差数列,乙:()12n n a a n S +=,则甲是乙的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.[2024届·长沙市第一中学·模拟考试]定义:在数列{}n a 中,()*211n n n na a d n a a +++-=∈N ,其中d 为常数,则称数列{}n a 为“等比差”数列.已知“等比差”数列{}n a 中,1231,3a a a ===,则2422a a =()A.1763B.1935C.2125D.23033.[2024届·浙江温州·二模]已知等差数列{}n a 的前n 项和为n S ,公差为d ,且{}n S 单调递增.若55a =,则d ∈()A.50,3⎡⎫⎪⎢⎣⎭B.100,7⎡⎫⎪⎢⎣⎭C.50,3⎛⎫ ⎪⎝⎭D.100,7⎛⎫ ⎪⎝⎭4.[2024届·合肥一六八中学·模拟考试]数列{}n a 中,12n n a a +=+,518a =,则1210a a a ++⋅⋅⋅+=()A.210B.190C.170D.1505.[2024届·辽宁省实验中学·模拟考试]设数列{}n a 满足13a =,134n n a a n +=-,若21485n n n n n b a a +++=,且数列{}n b 的前n 项和为n S ,则n S =()A.2169n n ⎛⎫- ⎪+⎝⎭B.42369n n ++ C.1169n n ⎛⎫+ ⎪+⎝⎭D.2169n n ⎛⎫+ ⎪+⎝⎭二、多项选择题6.[2024届·辽宁省实验中学·模拟考试]等差数列{}n a 中,10a >,则下列命题正确的是()A.若374a a +=,则918S = B.若150S >,160S <,则2289a a >C.若125a a +=,349a a +=,则7817a a += D.若810a S =,则90S >,100S <7.[2024届·江苏省前黄高级中学·一模]已知等差数列{}n a 的前n 项和为n S ,{}n a 的公差为d ,则()A.13713S S = B.5274S a a =+C.若{}n na 为等差数列,则1d =- D.若为等差数列,则12d a=8.[2024届·山东临沂·二模]已知{}n a 是等差数列,n S 是其前n 项和,则下列命题为真命题的是()A.若349a a +=,7818a a +=,则125a a +=B.若2134a a +=,则1428S =C.若150S <,则78S S >D.若{}n a 和{}1n n a a +⋅都为递增数列,则0n a >三、填空题9.[2024年新课标Ⅱ卷高考真题]记n S 为等差数列{}n a 的前n 项和.若347a a +=,2535a a +=,则10S =__________.10.[2024届·河南许昌·模拟考试校考]抛掷一枚不均匀的硬币,正面向上的概率为14,反面向上的概率为34,记n 次抛掷后得到偶数次正面向上的概率为n a ,则数列{}n a 的通项公式n a =____________.11.[2024届·河北衡水·二模联考]已知等差数列{}n a (公差不为0)和等差数列{}n b 的前n 项和分别为n S ,n T ,如果关于x 的实系数方程21003100310030x S x T -+=有实数解,则以下1003个方程()201,2,,1003i i x a x b i -+== 中,有实数解的方程至少有_________个.四、双空题五、解答题13.[2024届·辽宁省实验中学·模拟考试]已知正项数列{}n a 的前n 项和为n S ,且满足2844n n n S a a =++.(1)求数列{}n a 的通项公式;(2)若11212n n n n b a n --⎧⎪=⎨⎪⎩为奇数为偶数,{}n b 的前n 项和为n T ,求2n T .14.[2024届·山西长治·一模校考]已知正项等比数列{}n a 满足142n n n a a +=,n *∈N .(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足21n nn b a +=,设其前n 项和为n S ,求证:5n S <.15.[2024届·湖北·模拟考试联考]记n S 为公比不为1的等比数列{}n a 的前n 项和54218,88,21a a a a S -=-+=.(1)求n a ;(2)设22log n n b a =,由{}n a 与{}n b 的公共顶从小到大组成数列{}n c ,求{}n c 的前n 项和n T .参考答案1.答案:C 2.答案:B解析:因为数列{}n a 是“等比差”数列,所以()211n n n na a d n a a ++++-=∈N ,因为1231,3a a a ===,所以32212a a d a a =-=,所以有2113211212,2,,2n n n n n n n n a a a a a aa a a a a a ++++--=-=-= ,累和,得()*2221111221232,n n n n n n a a aa n n n n n a a a a ++++--=⇒=+⇒=-≥∈N ,因此有1212123,25,,1n n n n a a an n a a a ---=-=-= ,累积,得1(23)(25)1135(23)nn a n n a n a =--⇒=⨯⨯⨯⨯- ,所以2422135414345193513541a a ⨯⨯⨯⨯⨯==⨯⨯⨯ ,3.答案:A 4.答案:C解析:由12n n a a +=+知数列{}n a 是公差为2-的等差数列,所以()()121056551816534170a a a a a ++⋅⋅⋅+=+=⨯+=⨯=.故选:C.5.答案:D解析:由134n n a a n +=-可得()[]12113(21)n n a n a n +-++=-+⎡⎤⎣⎦,13a =,∴1(211)0a -⨯+=,则可得数列{}(21)n a n -+为常数列0,即(21)0n a n -+=,∴21n a n =+,∴2485(21)(23)221111(21)(23)(21)(23)(21)(23)2123n n n n n b n n n n n n n n +++++===+=+-++++++++,∴111111112((1)3557212332369n S n n n n n n n =+-+-++-=+-=+++++ .故选:D.6.答案:ACD解析:等差数列{}n a 中,10a >,对于A ,374a a +=,193799()9()2182a a S a a ++===,A 正确;对于B ,11515815()1502a a S a +=>=,则80a >,116168916()8()02a a S a a +==+<,则890a a +<,980a a <-<,因此22898989()()0a a a a a a -=+-<,即2289a a <,B 错误;对于C ,()()563412213a a a a a a +=+-+=,则()()785634217a a a a a a +=+-+=,C 正确;对于D ,设{}n a 的公差为d ,由810a S =,得1171045a d a d +=+,解得1938d a =-,则9111189369()019S a d a a =+=->,1011815(2)038S a a =-<,D 正确.故选:ACD 7.答案:BD 解析:A 选项,()1137137********2a a a S a +⨯===,而77,S a 不一定相等,A 不正确;B 选项,因为()1553552a a S a +==,()273334445a a a d a d a +=-++=,所以5274S a a =+,故B 正确;C 选项,因为()()2111n na n a n d n d a d n =+-=+-⎡⎤⎣⎦,若{}n na 为等差数列,则()()()()()22111111n n n a na n d a d n n d a d n++-=++-+---12nd a =+,要想12nd a +为常数,则0d =,故C 不正确;D 选项,由题可知()2111222n n n d d d S na n a n -⎛⎫=+=+- ⎪⎝⎭,若=为关于n 的一次函数,所以102da -=,即12d a =,故D 正确.故选:BD 8.答案:BC 解析:9.答案:95解析:解法一:设{}n a 的公差为d ,由3411123257a a a d a d a d +=+++=+=,()25111334475a a a d a d a d +=+++=+=,解得14a =-,3d =,则101104595S a d =+=.解法二:设{}n a 的公差为d ,由34257a a a a +=+=,2535a a +=,得21a =-,58a =,故52352a a d -==-,611a =,则()1101056105519952a aS a a +=⨯=+=⨯=.10.答案:11122n +⎛⎫+ ⎪⎝⎭解析:根据题意有:抛掷n 次偶数次正面向上的情况由抛掷1n -次偶数次正面向上的情况下第n 次反面向上,或抛掷1n -次奇数次正面向上的情况下第n 次正面向上组成,可得递推关系为()1113144n n n a a a --=-+,构造数列1111222n n a a -⎛⎫-=- ⎪⎝⎭,所以1112124n n a a --=-,即数列12n a ⎧⎫-⎨⎬⎩⎭是以112a -为首项,以12为公比的等比数列,又抛一次硬币,偶数次正面向上为0次,此时134a =,所以1131242a -=-,所以11131111242222n n n n a a -+⎛⎫⎛⎫⎛⎫-=-⨯⇒=+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,故答案为:11122n +⎛⎫+ ⎪⎝⎭.11.答案:502解析:由题意得,210031003410030S T -⨯≥,又因为1100310035021003()10032a a S a +==,1100310035021003()10032b b T b +==,代入得250250240a b -≥,要使方程()201,2,,1003i i x a x b i -+== 有实数解,则240(1,2,,1003)i i a b i -≥= ,显然第502个方程有解,设方程2110x a x b -+=与方程1003321000x a x b -+=的判别式分别为1∆,1003∆,则22222110031100311100310031100311003502()(4)(4)4()422a a ab a b a a b b b +∆+∆=-+-=+-+≥-⨯,即2250211003502502502(2)82(4)02a b a b ∆+∆≥-=-≥,等号成立的条件11003a a =,所以10∆≥,10030∆≥中至少一个成立,同理可得20∆≥,10020∆≥中至少一个成立,…,5010∆≥,5030∆≥中至少一个成立,且5020∆≥,综上,在所给的1003个方程中,有实根的方程最少502个,故答案为:502.13.答案:(1)42n a n =-(2)224123n n T n n -=+-解析:(1)2844n n n S a a =++ ①2111844n n n S a a ---∴=++②①-②整理得11()(4)0,2n n n n a a a a n --+--=≥ 数列{}n a 是正项数列,14,2n n a a n -∴-=≥当1n =时,21111844, 2.S a a a =++=由可得∴数列{}n a 是以2为首项,4为公差的等差数列,42n a n ∴=-;(2)由题意知,1223n n n b n n -⎧=⎨-⎩为奇数为偶数,故()()24222122215943n n T n -=+++++++++- ()()114143142n n n ⨯-+-=+-24123n n n -=+-.14.答案:(1)2n n a =(2)证明见解析解析:(1)设正项等比数列{}n a 的公比为(0)q q >,由142n n n a a +=,得11242n n n a a+++=,两式相除得24q =,则2q =,又1242a a =,即214a =,而10a >,则12a =,所以数列{}n a 的通项公式是112n n n a a q -==.(2)由(1)知212n nn b +=,则23357212222n n n S +=++++ ,于是231135212122222n n n n n S +-+=++++ ,两式相减得112111111(1)3111213215252212222222221212n n n n n n n n S n --+++-+++=++++-=+-=-- ,因此2552n n n S +=-,而2502n n +>恒成立,则25552n n +-<.所以5n S <.15.答案:(1)1(2)n n a -=--;(2){}n c 是首项为2,公比为4的等比数列;()2413nn T =-解析:(1)设{}n a 的公比为(1)q q ≠,因为542188a a a a -=-+,所以()54218a a a a -=--,所以354218a a q a a -==--,解得2q =-.又()6161211a q S q -==-,解得11a =-.故1(2)n n a -=--.(2)因为22222log log 222n n n b a n -===-,又{}n a 是首项为-1,公比为-2的等比数列,所以{}n c 是首项为2,公比为4的等比数列,所以()()214241143n nn T -==--.。
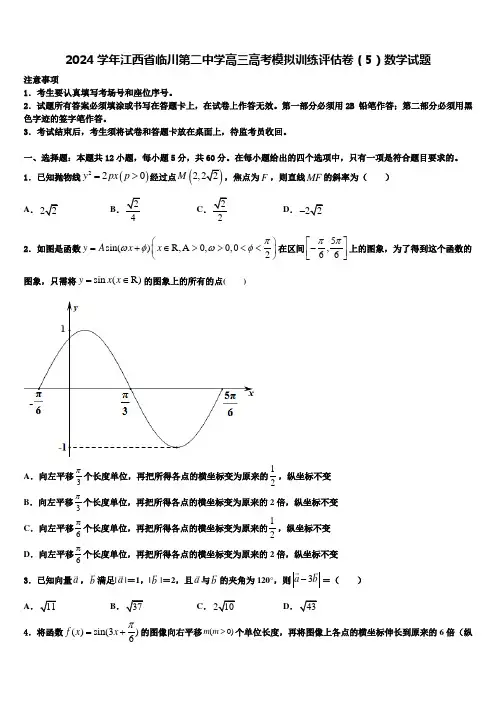
2024学年江西省临川第二中学高三高考模拟训练评估卷(5)数学试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知抛物线()220y px p =>经过点()2,22M ,焦点为F ,则直线MF 的斜率为( )A .22B .24C .22D .22-2.如图是函数sin()R,A 0,0,02y A x x πωφωφ⎛⎫=+∈>><< ⎪⎝⎭在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象,为了得到这个函数的图象,只需将sin (R)y x x =∈的图象上的所有的点( )A .向左平移3π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 B .向左平移3π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变C .向左平移6π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 D .向左平移6π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 3.已知向量a ,b 满足|a |=1,|b |=2,且a 与b 的夹角为120°,则3a b -=( ) A 11B 37C .10D 434.将函数()sin(3)6f x x π=+的图像向右平移(0)m m >个单位长度,再将图像上各点的横坐标伸长到原来的6倍(纵坐标不变),得到函数()g x 的图像,若()g x 为奇函数,则m 的最小值为( )A .9πB .29π C .18π D .24π5.已知直线1:240l ax y ++=,2:(1)20l x a y +-+=,则“1a =-”是“12l l ”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.设()f x x =,点()00O ,,()01A ,,()()n A n f n ,,*n N ∈,设n n AOA θ∠=对一切*n N ∈都有不等式22223122222sin sin sin sin 123n nθθθθ+++⋅⋅⋅⋅⋅⋅+ 222t t <--成立,则正整数t 的最小值为( ) A .3B .4C .5D .67.设双曲线221x y a b+=的一条渐近线为2y x =-,且一个焦点与抛物线24x y =的焦点相同,则此双曲线的方程为( ) A .225514x y -= B .225514y x -= C .225514y x -= D .225514x y -= 8.抛物线的焦点是双曲线的右焦点,点是曲线的交点,点在抛物线的准线上,是以点为直角顶点的等腰直角三角形,则双曲线的离心率为( ) A .B .C .D .9.集合{2,0,1,9}的真子集的个数是( ) A .13B .14C .15D .1610.如图所示点F 是抛物线28y x =的焦点,点A 、B 分别在抛物线28y x =及圆224120x y x +--=的实线部分上运动, 且AB 总是平行于x 轴, 则FAB ∆的周长的取值范围是( )A .(6,10)B .(8,12)C .[6,8]D .[8,12]11.已知集合A ={0,1},B ={0,1,2},则满足A ∪C =B 的集合C 的个数为( ) A .4B .3C .2D .112.已知O 为坐标原点,角α的终边经过点(3,)(0)P m m <且10sin 10m α=,则sin 2α=( ) A .45B .35C .35D .45-二、填空题:本题共4小题,每小题5分,共20分。
新高考地区考试题型为8(单选题)+4(多选题)+4(填空题)+6(解答题),其中结构不良型试题是新高考地区新增加的题型,主要涉及解三角形与数列两大模块,以解答题的方式进行考查。
考查学生知识的应用能力,数学建模的核心素养。
能够对已知条件进行综合分析、归纳与抽象,并正确地将实际问题转化为数学模型,再用相关的数学知识,进行合理设计,确定解题方案,进行数学上的计以数学文化为背景的新情景问题,此类试题蕴含浓厚的数学文化气息,将数学知识、方法等融为一体,能有效考查学生在新情景下对知识的理解以及迁移到不同情境中的能力,考查学生发现问题、分析问题和解决问题的能力,例如本卷第A.33B.126.如图所示,当篮球放在桌面并被斜上方一个灯泡子是椭圆,且篮球与桌面的接触点是椭圆的右焦点.若篮球的半径为个单位长度,灯泡垂直照射在平面上的点为离心率e等于()A.23B.347.已知数列{}n a满足:当2k最小值为()A.52B.418.已知0.3e1a=-,ln1.3b=A.c a b>>B.a二、多项选择题:本题共4小题,每小题全部选对的得5分,部分选对的得9.“50米跑”是《国家学生体质健康标准》,则下列说法中正确的是().则())的关系,从该班随机抽取10名$$$.已知之间有线性相关关系,设其回归直线方程为y bx a=+________________kg.,若动圆M与圆1F内切与圆四、解答题:本题共6小题,共17.(10分)已知锐角△ABC 2sin sin 1sin sin A B c B A ab+=+.(1)求角C 的大小;(2)若2a b +=,求c 的取值范围.18.(12分)已知正项数列(1)求n S ;(2)在数列{}n a 的每相邻两项a {}112123n b a a a a a a :,,,,,,19.(12分)“稻草很轻,但是他迎着风仍然坚韧,这就是生命的力量,意志的力量踏实实努力的时候,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现你会切身体会到读书破万卷给予我们的力量.学生进行调查,得到了这800如图所示的频率分布直方图.(1)求a 的值;(2)为进一步了解这800名学生阅读时间的分配情况,从周平均阅读时间在的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取的学生人数为X ,求X 的分布列和数学期望;(3)以样本的频率估计概率,从该校所有学生中随机抽取20名学生,用生周平均阅读时间在(]8,12内的概率,其中0,1,2,,20k =⋅⋅⋅.当20.(12分)在苏州博物馆有一类典型建筑八角亭,既美观又利于采光,其中一角如图所示,为多面体11111ABCDE A B C D E -,AB AE ⊥,AE BC ∥,AB ED ∥,的正方形且平行于底面,11AB A B ∥,1D E ,1B B 的中点分别为(1)证明:FG ∥平面1C CD ;(2)求平面1C CD 与平面11AA B B 夹角的余弦值;(3)一束光从玻璃窗面1C CD 上点1C 射入恰经过点A (假设此时光经过玻璃为直射)上的入射角的正切值.21.(12分)在平面直角坐标系xOy 中,已知椭圆C :(222210x y a b a b+=>>与椭圆C 交于A B 、两点.当直线l 过原点时,3PO AO =.(1)求椭圆C 的标准方程;(2)若存在直线l ,使得PA PB m ⋅=,求m 的取值范围.。
全国18名校2024届高考模拟试卷(数学试题文)试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数2sin cos ()20x x xf x x =+在[2,0)(0,2]ππ-⋃上的图象大致为( ) A . B .C .D .2.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[]0.51-=-,[]1.51=,已知函数12()4324x x f x -=-⋅+(02x <<),则函数[]()y f x =的值域为( ) A .13,22⎡⎫-⎪⎢⎣⎭ B .{}1,0,1-C .1,0,1,2D .{}0,1,23.已知平行于x 轴的直线分别交曲线2ln 21,21(0)y x y x y =+=-≥于,A B 两点,则4AB 的最小值为( )A .5ln 2+B .5ln 2-C .3ln 2+D .3ln 2-4.如图,正四面体P ABC -的体积为V ,底面积为S ,O 是高PH 的中点,过O 的平面α与棱PA 、PB 、PC 分别交于D 、E 、F ,设三棱锥P DEF -的体积为0V ,截面三角形DEF 的面积为0S ,则( )A .08V V ≤,04S S ≤B .08V V ≤,04S S ≥C .08V V ≥,04S S ≤D .08V V ≥,04S S ≥5.若202031i iz i+=+,则z 的虚部是( )A .iB .2iC .1-D .16.已知12,F F 分别为双曲线2222:1x y C a b-=的左、右焦点,点P 是其一条渐近线上一点,且以12F F 为直径的圆经过点P ,若12PF F ∆的面积为b 2233,则双曲线的离心率为( ) A .3B .2C .5D .37.在直角坐标系中,已知A (1,0),B (4,0),若直线x +my ﹣1=0上存在点P ,使得|PA |=2|PB |,则正实数m 的最小值是( ) A .13B .3C .33D .38.在ABC ∆中,60BAC ∠=︒,3AB =,4AC =,点M 满足2B M M C =,则AB AM ⋅等于( ) A .10 B .9C .8D .79.抛物线的准线与双曲线的两条渐近线所围成的三角形面积为,则的值为 ( )A .B .C .D .10.将函数()cos f x x =的图象先向右平移56π个单位长度,在把所得函数图象的横坐标变为原来的1ω(0)>ω倍,纵坐标不变,得到函数()g x 的图象,若函数()g x 在3(,)22ππ上没有零点,则ω的取值范围是( ) A .228(0,][,]939 B .2(0,]9C .28(0,][,1]99D .(0,1]11.为了进一步提升驾驶人交通安全文明意识,驾考新规要求驾校学员必须到街道路口执勤站岗,协助交警劝导交通.现有甲、乙等5名驾校学员按要求分配到三个不同的路口站岗,每个路口至少一人,且甲、乙在同一路口的分配方案共有( ) A .12种B .24种C .36种D .48种12.已知定义在[)0,+∞上的函数()f x 满足1()(2)2f x f x =+,且当[)0,2x ∈时,2()2f x x x =-+.设()f x 在[)22,2n n -上的最大值为n a (*n N ∈),且数列{}n a 的前n 项的和为n S .若对于任意正整数n 不等式()129n k S n +≥-恒成立,则实数k 的取值范围为( )A .[)0,+∞B .1,32⎡⎫+∞⎪⎢⎣⎭C .3,64⎡⎫+∞⎪⎢⎣⎭D .7,64⎡⎫+∞⎪⎢⎣⎭二、填空题:本题共4小题,每小题5分,共20分。
填空题〔5〕数列制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日1.}{n a 的首项11=a ,且521,,a a a 是等比数列且21a a ≠,那么 (1)数列的通项公式n a = . (2)设集合}1001,,111|{13221≤≤∈++++++==*+n N n a a a a a a T T A n n n n ,取集合A 的非空子集B ,假设B B 为“完美子集〞,那么集合A 中的“完美子集〞的个数为 .2.定义:数列n n n n n x x x x x x ++==+231123,1:}{;数列23211:}{nn n n xx y y ++=;数列232132:}{nn nn n x x x z z +++=,那么=+11z y ;假设}{n y 的前n 项乘积为,P }{n z 的前n 项和为Q ,那么=+Q P .3.当n 为正整数时,定义函数)(n N 表示n ,5)10(,3)3(==N N . 记)2()2()1()(nN N N n S +++= .那么(1)=)4(S ; (2)=)(n S .4.]][[)(x x x f =,其中][x 表示不超过x 的最大整数,假设)](,0[*∈∈N n n x 时,)(x f 的值域为n A ,那么=3A ;记||n n A a =,其中||A 表示集合A 中元素的个数,那么=n a.5.数列}{n a 满足:),3,2(11,211 =-==-n a a a n n ,假设数列}{n a 有一个形如B n A a n ++=)sin(ϕω的通项公式,其中ϕω,,,B A 均为实数,且2||,0,0πϕω<>>A ,那么=n a .(只要写出一个通项公式即可)6.数列}{n a 的前n 项和为n S ,假设数列}{n a 的各项按如下规律排列:,1,,2,1,,54,53,52,51,43,42,41,32,31,21nn n n -有如下运算和结论: ①8324=a ; ②数列 ,,,,10987654321a a a a a a a a a a ++++++是等比数列;③数列 ,,,,10987654321a a a a a a a a a a ++++++的前n 项和为42nn T n +=;④假设存在正整数k ,使10,101≥<+k k S S ,那么75=k a .其中正确的结论有 .7.数列}{n a 中,21=a ,][n a 表示n a 的整数局部,)(n a 表示n a 的小数局部,)()(1][1*+∈+=N n a a a n n n ,数列}{n b 中,)(,2,122121*++∈⋅===N n b b b b b n n n , 那么=∑=ni nn ba 1.8.设代数方程0)1(242210=-+-+-nn n x a x a x a a 有n 2个不同的根n x x x ±±±,,,21 ,那么)1()1)(1()1(222222120242210nnn nx x x x x x a xa x a x a a -⋅⋅--=-+-+- ,比拟两边2x 的系数得=1a (用n x x x a ,,,,210 表示);假设展示式+-+-=!7!5!31sin 642x x x x x 对R x ∈,0≠x 成立,那么由于0sin =xx有无多个根: ,,,2,πππn ±±±,于是⋅-⋅⋅--=+-+-)1()21)(1(!7!5!3122222222642πππn x x x x x x ,利用上述结论可得=+++++222131211n. 9.给定集合)3,}(,,,,{321≥∈=n N n a a a a A n ,定义),,1(N j i n j i a a j i ∈≤≤≤+中所有不同值的个数为集合A 两元素和的容量,用)(A L 表示,假设}8,6,4,2{=A , 那么=)(A L ;假设数列}{n a 是等差数列(公差不为0),设集合},,,,{321m a a a a A =,(*∈N m m 为常数)那么)(A L 关于m 的表达式为 .10.}{n a 是公差不为0的等差数列,}{n b 是等比数列,其中25411,7,1b a a b a ====,且存在常数βα, 使得对每一个正整数n 都有βα+=n n b a log ,那么=+βα .答案与解析1.解析:(1)设公方差为d )0(≠d ,那么d n d n a a n )1(1)1(212-+=-+=,又521,,a a a 是等比数列,∴5225122a a a a a =⇒=,又d a d a 41,1522+=+=,∴d d 411+=+,解之可得0,2==d d (舍去),∴12-=n a n .(2)∵12121-++=++n n a a n n ,∴)1212(211212111--+=-++=++n n n n a a n n ,那么)112(2111113221-+=++++++=+n a a a a a a T n n n ,∵1001≤≤n ,∴212012112213201123-≤-+≤-⇒≤+≤n n ,那么集合A 的元素为整数的是6,5,4,3,2,1.又B 的元素都是整数,且B 是集合A 的非空子集,∴集合A 中的“完美子集〞的个数为63126=-. 2.解析:由可得1322323211+=++=++=n n nn n n nn n x x x x x x x x y ,于是有61211==x x y , 113221211++=⋅⋅⋅=⋅⋅⋅=n n n n x x x x x x x y y y P ,另一方面又有232132nn n n x x x z +++= 11322323221111323213213232++-=+-=+++++++-=+++=n n n n nn n n n n n n n n n n n x x x x x x x x x x x x x x x x x . ∴656111=-=z ,11322111)11()11()11(++-=-++-+-=n n n x x x x x x x Q , ∴111111=-+=+++n n x x Q P .3.解析:由题设知,12)12(),()2(-=-=n n N n N n N .(1))]16()4()2([)]15()5()3()1([)4(N N N N N N N S ++++++++= )]16()4()2([)15531(N N N ++++++++=86)1(444)2(44)3(423233=+++=++=+=S S S .(2)]2()4()2([)]12(531[)(nnN N N n S ++++-++++= ∴)1)(1(4)(1≥-+=-n n S n S n ,又1)1(1==N S ,∴3244444)(021+=++++=--n n n n S .4.解析:}9,5,4,1,0{3=A ; 当1+<<n x n 时,n x =][,),(][22n n n nx x x +∈=,故)(x f 可取1,,1,222-++n n n n .当1+=n x 时,2)1()(+=n x f ,又当],0[n x ∈时,显然有2)(nx f ≤,所以na a n n +=+1,又∵,21=a ∴21)2()1()()()(112211+++-+-=+-++-+-=--- n n a a a a a a a a n n n n n , ∴)4(212+-=n n a n .5..解析:∵1111,2--==n n a a a ,∴2,1,21432=-==a a a ,那么数列}{n a 的周期为3, ∴3223πωωπ=⇒=,∴B n A a n ++=)32sin(ϕπ,又,1,21,2321-===a a a 那么有 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+=+--=+-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧-=++=++=++)3(1sin )2(21)sin 21cos 23()1(2)sin 21cos 23(1)4sin(21)34sin(2)32sin(B A B A B A B A B A B A ϕϕϕϕϕϕπϕπϕπ,那么)2()1(-得 23cos 3=ϕA ,)2()1(+得252sin =+-B A ϕ,联立)3(得21=B ,∴23sin -=ϕA 3tan cos sin -==ϕϕϕA A ,又2||πϕ<,∴3πϕ-=,2323)3sin(-=-=-A A π,∴3=A .∴21)332sin(3+-=ππn a n . 6.解析:①8324=a ,故①正确; ②中数列的通项211211n n n n n b n =++++++=是等差数列,不是等比数列; ③中数列的前n 项和为422322212nn n T n +=++++= ,故③正确;④由61042<⇒<+=n n n T n ,而21545525=+=T ,1075747372715<+++++T , 107675747372715>++++++T ,∴75=k a ,故④正确. 故填①③④. 7.解析:261215,241213,221211,24321+=-+=+=-+=+=-+==a a a a ,…,猜测:)(2)1(2*∈+-=N n n a n ,∴}{221n n n n b b b b ⇒⋅=++为等比数列.又∵2,121==b b ,∴,21-=n n b ∴11222)1(2]2)1(2[--⋅+⋅-=⋅+-=⋅n n n n n n n b a ,∴24222)2(22242)2(111-+⋅+⋅-=-⋅++⋅-=++=∑n n n n ni nn n n ba .8.2x 项的系数即可得)111(2222101n x x x a a +++= ,利用这一结论得)1211(1!3122222 ++++⨯=πππn ,变形得61312112222π=+++++ n.9.解析:①∵1486,1284,1064,1082,862,642=+=+=+=+=+=+,∴5)(=A L .②不妨设数列}{n a 是递增等差数列可知m a a a a <<<< 321, 那么mm m m a a a a a a a a a a +<<+<+<<+<+-1213121 ,故)1(m j i a a j i ≤≤≤+中至少有32-m 个不同的数.又据等差数列的性质:当mj i ≤+时,11-++=+j i j i a a a a ;当m j i >+时,m m j i j i a a a a +=+-+,因此每个和)1(m j i a a j i ≤≤≤+等于)2(1m k a a k ≤≤+中一个,或者者等于)12(-≤≤+m l a a m l 32)(-=m A L .或者构造一个简单的等差数列m ,,3,2,1 进展考虑. 10.解析:设}{n a 的公差为d,}{n b 的公比为q ,那么27314=⇒=+=d d a a ,92415=⨯+=a ,那么92==q b ,从而有βα+=-⋅+-19log )1(21n n 对一切正整数n 都成立,从而29log =α,βα+-=-9log 1,求得1,3==βα,那么4=+βα.制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日。
湖北省恩施土家族苗族自治州高级中学2025届高考全国统考预测密卷数学试卷注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.定义运算()()a a b a b b a b ≤⎧⊕=⎨>⎩,则函数()12xf x =⊕的图象是( ). A . B .C .D .2.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为( )A 3B 3C .33D .2333.已知函数()ln ln(3)f x x x =+-,则( ) A .函数()f x 在()0,3上单调递增 B .函数()f x 在()0,3上单调递减 C .函数()f x 图像关于32x =对称 D .函数()f x 图像关于3,02⎛⎫⎪⎝⎭对称 4.设递增的等比数列{}n a 的前n 项和为n S ,已知4403S =,43231030a a a -+=,则4a =( )A .9B .27C .81D .835.设1,0(){2,0xx x f x x -≥=<,则((2))f f -=( )A .1-B .14C .12D .326.抛物线的准线与双曲线的两条渐近线所围成的三角形面积为,则的值为 ( )A .B .C .D .7.已知集合{}|1A x x =>-,集合(){}|20B x x x =+<,那么A B 等于( )A .{}|2x x >-B .{}1|0x x -<<C .{}|1x x >-D .{}|12x x -<<8.执行如图所示的程序框图若输入12n =,则输出的n 的值为( )A .32B .2C .52D .39.已知i 是虚数单位,则( ) A .B .C .D .10.若()5211x a x ⎛⎫+- ⎪⎝⎭的展开式中的常数项为-12,则实数a 的值为( ) A .-2B .-3C .2D .311.已知ABC 是边长为3的正三角形,若13BD BC =,则AD BC ⋅=A .32- B .152 C .32D .152-12.执行程序框图,则输出的数值为( )A .12B .29C .70D .169二、填空题:本题共4小题,每小题5分,共20分。
四川省南部中学高2023届高考模拟检测(五)数学(文科)试题第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|340}M x x x =--<,{|05}N x x =≤≤,则M N ⋂=A .(0,4]B.[0,4)C.[1,0)-D.(1,0]-2.设复数1z ,2z 在复平面内的对应点关于虚轴对称,12z i =+,则12z z =A.-5B.5C.-4+iD.-4-i3.在区间[]2,3-上随机选取一个数X ,则1X ≤的概率为A.45B.35C.25D.154.设变量x,y 满足约束条件360,{20,30,x y x y y +-≥--≤-≤则目标函数z =y -2x 的最小值为A.-7B.-4C.1D.25.奇函数()f x 的定义域为R ,若(2)f x +为偶函数,且(1)1f =,则(8)(9)f f +=A.2- B.1- C.0D.16.设n S 为等差数列{}n a 的前n 项和,83742S a a ==-,,则9a =()A.6B.4C.6- D.27.若sin 2,sin x x 分别是sin θ与cos θ的等差中项和等比中项,则cos2x 的值为()A.1338+ B.1338C.1338D.148.一艘海轮从A 处出发,以每小时40海里的速度沿东偏南50 方向直线航行,30分钟后到达B 处.在C 处有一座灯塔,海轮在A 处观察灯塔,其方向是东偏南20 ,在B 处观察灯塔,其方向是北偏东65 ,那么B 、C 两点间的距离是()A.海里B.C.D.海里9.函数2||2x y x e =-在[]–2,2的图象大致为()A.B.C. D.10.已知直三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若,,,AB AC ⊥112AA O =,则球的半径为 A.3172B. C.132D.11.已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ,左、右顶点分别为,A B 点,P Q 是双曲线C 上关于x 轴对称的两点,且直线PQ 经过点F .如果M 是线段FQ 上靠近点Q 的三等分点,E 在y 轴的正半轴上,且E A M ,,三点共线,,,P E B 三点共线,则双曲线C 的离心率为()A.5B. C. D.612.已知函数f (x )=x (ln x -ax )有两个极值点,则实数a 的取值范围是()A.(-∞,0)B.C.(0,1)D.(0,+∞)第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量a 与b 的夹角为60°,|a |=2,|b |=1,则|a+2b |=______.14.过点(3,1)作圆22(2)(2)4x y -+-=的弦,其中最短的弦长为__________.15.抛物线()220x py p =>的焦点为F ,其准线与22133y x -=相交于A ,B 两点,若ABF △为等边三角形,则p =___________.16.设()f x 与()g x 是定义在同一区间[],a b 上的两个函数,若对任意[],x a b ∈,都有()()1f x g x -≤成立,则称()f x 和()g x 在[],a b 上是“亲密函数”,区间[],a b 称为“亲密区间”.若()234f x x x =-+与()21g x x =-在[],a b 上是“亲密函数”,则b 的最大值______三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.南中数学教研室对高二学生的记忆力x 和判断力y 进行统计分析,所得数据如下表所示:x 681012y2356(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆy bx a =+(3)根据(2)中求出的线性回归方程,预测记忆力为11的学生的判断力.(参考公式: 1221,ni i i n ii x y nx y b a y bx x nx==-==--∑∑)18.已知向量()()sin ,sin ,cos ,cos ,sin 2m A B n B A m n C ==⋅=,且、、A B C 分别为ABC 的三边,,a b c 所对的角.(1)求角C 的大小;(2)若sin ,sin ,sin A C B 成等差数列,且()18CA AB AC ⋅-=,求c 边的长.19.如图,在四棱锥P ABCD -中,AB CD ∥,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.20.已知函数()3211,32f x x ax a =-∈R .(I)当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程;(II)设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.21.在平面直角坐标系xOy 中,已知椭圆C :22221x y a b +=(a >b >0)的离心率为22,椭圆C 截直线y =1所得线段的长度为22(Ⅰ)求椭圆C 的方程;(Ⅱ)动直线l :y =kx +m (m ≠0)交椭圆C 于A ,B 两点,交y 轴于点M .点N 是M 关于O 的对称点,⊙N 的半径为|NO |.设D 为AB 的中点,DE ,DF 与⊙N 分别相切于点E ,F ,求∠EDF 的最小值.22.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线:4cos C ρθ=,直线l 的参数方程为:321x ty t=+⎧⎨=-+⎩(t 为参数),直线l 与曲线C 分别交于,M N 两点.(1)写出曲线C 和直线l 的普通方程;(2)若点(3,1)P -,求11||||PM PN -的值.23.已知函数()2f x m x m x =+--()0m >的最大值为6.(1)求m 的值;(2)若正数x ,y ,z 满足x y z m ++=,求证:xy xz m ≤.四川省南部中学高2023届高考模拟检测(五)数学(文科)试题第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|340}M x x x =--<,{|05}N x x =≤≤,则M N ⋂=A.(0,4] B.[0,4) C.[1,0)- D.(1,0]-【答案】B【详解】试题分析:()()234041014x x x x x --<⇒-+<⇒-<<,故M N ⋂=[0,4),故选B .考点:1.一元二次不等式的解法;2.集合的运算.2.设复数1z ,2z 在复平面内的对应点关于虚轴对称,12z i =+,则12z z =A.-5 B.5C.-4+iD.-4-i【答案】A【详解】试题分析:由题意,得22z i =-+,则12(2)(2)5z z i i =+-+=-,故选A .考点:1、复数的运算;2、复数的几何意义.3.在区间[]2,3-上随机选取一个数X ,则1X ≤的概率为A.45B.35C.25D.15【答案】B【详解】试题分析:在[]2,3-上符合1X ≤的区间为[]2,1-,因为区间[]2,3-的区间长度为5且区间[]2,1-的区间长度为3,所以根据几何概型的概率计算公式可得35P =,故选B.考点:几何概型4.设变量x,y 满足约束条件360,{20,30,x y x y y +-≥--≤-≤则目标函数z =y -2x 的最小值为A.-7B.-4C.1D.2【答案】A 【分析】画图分析【详解】画出原不等式组表示的平面区域如图所示阴影部分,由题意知,当目标函数2z y x =-表示的直线经过点A(5,3)时,z 取得最小值,所以z 的最小值为3257-⨯=-,故选A.【考点定位】本小题考查线性规划的基础知识,难度不大,线性规划知识在高考中一般以小题的形式出现,是高考的重点内容之一,几乎年年必考.5.奇函数()f x 的定义域为R ,若(2)f x +为偶函数,且(1)1f =,则(8)(9)f f +=A.2- B.1- C.0D.1【答案】D 【详解】【分析】试题分析:(2)f x +是偶函数,则()f x 的图象关于直线2x =对称,又()f x 是奇函数,则(0)0f =,且()f x 是周期函数,且周期为8,所以(8)(9)(0)(1)1f f f f +=+=.故选D .考点:函数的奇偶性,周期性.【名师点睛】解函数问题时,有些隐含性质需我们已知条件找出,特别是周期性.当函数具有两个对称时函数一般也是周期函数.当函数()f x 是奇函数,又有对称轴x m =时,则函数一定是周期函数,且周期为4T m =;若()f x 有两条对称轴x a =和x b =,则函数是周期函数,2b a -是函数的一个周期;同样若()f x 有两个对称中心(,0)a 和(,0)b ,则函数是周期函数,2b a -是函数的一个周期;6.设n S 为等差数列{}n a 的前n 项和,83742S a a ==-,,则9a =()A.6B.4C.6- D.2【答案】C【分析】根据题意求出首项和公差,再根据等差数列的通项即可得解.【详解】设等差数列{}n a 的公差为d ,由83742S a a ==-,,得()11187842262a d a d a d ⨯⎧+=+⎪⎨⎪+=-⎩,解得1102a d =⎧⎨=-⎩,所以9186a a d =+=-.7.若sin 2,sin x x 分别是sin θ与cos θ的等差中项和等比中项,则cos2x 的值为()A.1338+ B.1338C.1338D.124【答案】A【分析】根据条件可得2sin 2sin cos x θθ=+,2sin sin cos x θθ=,然后结合同角三角函数的关系,以及恒等变换公式化简,即可得到结果.【详解】依题意可得2sin 2sin cos x θθ=+,2sin sin cos x θθ=,且()22222sin cos sin cos 2sin cos 4sin 22sin 1x x θθθθθθ+=+-=-=,所以()241cos 2cos 220x x -+-=,即24cos 2cos 220x x --=,解得133cos 28x ±=又因为2sin sin cos x θθ=,所以2cos 212sin 1sin 20x x θ=-=-≥,所以133cos 28x +=故选:A8.一艘海轮从A 处出发,以每小时40海里的速度沿东偏南50 方向直线航行,30分钟后到达B 处.在C 处有一座灯塔,海轮在A 处观察灯塔,其方向是东偏南20 ,在B 处观察灯塔,其方向是北偏东65 ,那么B 、C 两点间的距离是()A.海里B.C.D.海里【答案】A【分析】根据给定条件,画出图形,再利用正弦定理解三角形作答.【详解】依题意,如图,在ABC中,5020304065105BAC ABC ∠=-=∠=+=,,则3045402060ACB AB ∠==⨯=,,由正弦定理得sin sin BC AB BAC ACB =∠∠,即20sin30sin45BC =,因此120222BC ⨯==(海里),所以B C 、两点间的距离是海里.9.函数2||2x y x e =-在[]–2,2的图象大致为()A. B.C. D.【答案】D【详解】试题分析:函数2||()2x f x x e =-|在[–2,2]上是偶函数,其图象关于y 轴对称,因为22(2)8e ,08e 1f =-<-<,所以排除,A B 选项;当[]0,2x ∈时,4x y x e '=-有一零点,设为0x ,当0(0,)x x ∈时,()f x 为减函数,当0(,2)x x ∈时,()f x 为增函数.故选:D.10.已知直三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若,,,AB AC ⊥112AA O =,则球的半径为A.B. C.132D.【答案】C【详解】因为直三棱柱中,AB =3,AC =4,AA 1=12,AB ⊥AC ,所以BC =5,且BC 为过底面ABC 的截面圆的直径.取BC 中点D ,则OD ⊥底面ABC ,则O 在侧面BCC 1B 1内,矩形BCC 1B 1的对角线长即为球直径,所以2R =13,即R =13211.已知双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ,左、右顶点分别为,A B 点,P Q 是双曲线C 上关于x 轴对称的两点,且直线PQ 经过点F .如果M 是线段FQ 上靠近点Q 的三等分点,E 在y 轴的正半轴上,且E A M ,,三点共线,,,P E B 三点共线,则双曲线C 的离心率为()A.5B. C.D.6【分析】可设22,,b b P c Q c a a ---⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,,根据E A M ,,三点共线和,,P E B 三点共线,得到a 、c 的关系,即可求出离心率【详解】解:设()()(),0,,0,,0F c A a B a --,点PQ 是双曲线C 上关于x 轴对称的两点,且直线PQ 经过点F ,可得PQ x ⊥轴,令x c =-可得22221c y a b-=,解得2b y a =±可设22,,b b P c Q c a a ---⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,由M 是线段FQ 上靠近点Q 的三等分点,可得22,3b M c a ⎛⎫-- ⎪⎝⎭,由E 在y 轴的正半轴上,可设()0,E e ,由E A M ,,三点共线,可得AM EA k k =,即为223b e a a a c=-+①由,,P E B 三点共线,可得EB BP k k =,即为2b e a ac a-=--,②由①②可得()123a c c a =+-,即为3322c a c a -=+,即5c a =,所以5ce a==.故选:A.【点睛】求椭圆(双曲线)离心率的一般思路:(1)直接求出a 、b 、c ,计算离心率;(2)根据题目的条件,找到a 、b 、c 的关系,消去b ,构造离心率e 的方程或(不等式)即可求出离心率.12.已知函数f (x )=x (ln x -ax )有两个极值点,则实数a 的取值范围是()A.(-∞,0)B.C.(0,1)D.(0,+∞)【答案】B【详解】函数f (x )=x (lnx ﹣ax ),则f′(x )=lnx ﹣ax+x (﹣a )=lnx ﹣2ax+1,令f′(x )=lnx ﹣2ax+1=0得lnx=2ax ﹣1,函数f (x )=x (lnx ﹣ax )有两个极值点,等价于f′(x )=lnx ﹣2ax+1有两个零点,等价于函数y=lnx 与y=2ax ﹣1的图象有两个交点,在同一个坐标系中作出它们的图象(如图)当a=时,直线y=2ax ﹣1与y=lnx 的图象相切,由图可知,当0<a <时,y=lnx 与y=2ax ﹣1的图象有两个交点.则实数a 的取值范围是(0,).故选B .第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量a 与b 的夹角为60°,|a |=2,|b |=1,则|a+2b |=______.【答案】【详解】∵平面向量a 与b 的夹角为060,21a b == ,∴021cos601a b ⋅=⨯⨯= .∴2a b +====故答案为点睛:(1)求向量的夹角主要是应用向量的数量积公式.(2)a =常用来求向量的模.14.过点(3,1)作圆22(2)(2)4x y -+-=的弦,其中最短的弦长为__________.【答案】【详解】最短弦为过点()3,1与圆心连线的垂线与圆相交而成,d ====【考点定位】本题考查直线和圆的位置关系,考查数形结合思想和运算能力.圆的半径、弦心距、半弦构成的直角三角形在解决直线和圆问题常常用到,本题只需要简单判断最短弦的位置就能轻松解答,有时候可能会出现点到直线的距离公式来求弦心距的长度.15.抛物线()220x py p =>的焦点为F ,其准线与22133y x -=相交于A ,B 两点,若ABF △为等边三角形,则p =___________.【答案】6【分析】求出抛物线的焦点和准线方程,求出AB 的长,根据ABF △为等边三角形,得到关于p 的方程,即可求得答案.【详解】抛物线()220x py p =>的焦点为(0,)2p F ,其准线为2p y =-,将2p y =-与22133y x -=联立,得221312x p -=,解得x =,则||AB =,由于ABF △为等边三角形,故||2AB p =,即32p ⋅=,解得6p =,故答案为:616.设()f x 与()g x 是定义在同一区间[],a b 上的两个函数,若对任意[],x a b ∈,都有()()1f x g x -≤成立,则称()f x 和()g x 在[],a b 上是“亲密函数”,区间[],a b 称为“亲密区间”.若()234f x x x =-+与()21g x x =-在[],a b 上是“亲密函数”,则b 的最大值______【答案】4【分析】首先表示出()()f x g x -,令()()1f x g x -≤,即2551x x -+≤,解得x 的取值范围,即可得解.【详解】解:因为()()()22342155f x g x x x x x x -=-+--=-+,若()234f x x x =-+与()21g x x =-在[],a b 上是“亲密函数”,则()()1f x g x -≤,即2551x x -+≤,即21551x x -≤-+≤,解得12x ≤≤或34x ≤≤,即[][]1,23,4x ∈⋃,所以b 的最大值为4.故答案为:4三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.南中数学教研室对高二学生的记忆力x 和判断力y 进行统计分析,所得数据如下表所示:x681012y 2356(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆy bx a =+(3)根据(2)中求出的线性回归方程,预测记忆力为11的学生的判断力.(参考公式: 1221,n i ii n i i x y nx y b a y bx x nx==-==--∑∑ )【答案】(1)答案见解析(2)ˆ0.7 2.3yx =-(3)5.4【分析】(1)根据表格直接画出散点图即可;(2)根据公式分别计算出 ,ba ,即可得到线性回归防尘;(3)根据(2)中的回归方程,将11x =代入计算,即可得到结果.【小问1详解】散点图如下:【小问2详解】446283105126158i i i x y ==⨯+⨯+⨯+⨯=∑()()116810129,2356444x y =+++==+++=4222224*********i i x ==+++=∑2158494140.73444920b -⨯⨯∴===-⨯ ,则 40.79 2.3ay bx =-=-⨯=- ,故线性回归方程为ˆ0.7 2.3yx =-【小问3详解】由(2)中线性回归方程可知,当11x =时,0.711 2.3 5.4y =⨯-=,所以预测记忆力为11的同学的判断力约为5.418.已知向量()()sin ,sin ,cos ,cos ,sin 2m A B n B A m n C ==⋅= ,且、、A B C 分别为ABC 的三边,,a b c 所对的角.(1)求角C 的大小;(2)若sin ,sin ,sin A C B 成等差数列,且()18CA AB AC ⋅-= ,求c 边的长.【答案】(1)π3C =;(2)6c =.【分析】(1)根据数量积的运算,有sin 2m n C ⋅= ,因为2sin cos m n C C ⋅= ,可求得1πcos ,23C C ==;(2)因为sin ,sin ,sin A C B 成等差数列,由正弦定理得2c ab =,因为()18CA AB AC ⋅-= ,所以可得cos 18,36ab C ab ==,由余弦定理()22222cos 3c a b ab C a b ab =+-=+-,即可解得c .【详解】(1)对于ABC ,π,0πA B C C +=-<<,∴()sin sin A B C +=;由()()sin ,sin ,cos ,cos m A B n B A == ,可得sin cos sin cos sin()sin m n A B B A A B C ⋅=+=+= ,又∵sin 2m n C ⋅= ,∴1sin 22sin cos sin ,cos 2C C C C C ==∴=,π(0,π),3C C ∈∴= .(2)由sin ,sin ,sinB A C 成等差数列,得2sin sin sin C A B =+;由正弦定理得2c a b =+,∵()18CA AB AC ⋅-= ,∴18CA CB ⋅= ,即cos 18,36ab C ab ==,由余弦定理()22222cos 3c a b ab C a b ab =+-=+-,∴2224336,36c c c =-⨯=,∴6c =.19.如图,在四棱锥P ABCD -中,AB CD ∥,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.【答案】(1)证明见解析;(2)623+.【详解】试题分析:(1)由90BAP CDP ∠=∠=︒,得AB AP ⊥,CD PD ⊥.从而得AB PD ⊥,进而而AB ⊥平面PAD ,由面面垂直的判定定理可得平面PAB ⊥平面PAD ;(2)设PA PD AB DC a ====,取AD 中点O ,连结PO ,则PO ⊥底面ABCD ,且22,2AD a PO a ==,由四棱锥P ABCD -的体积为83,求出2a =,由此能求出该四棱锥的侧面积.试题解析:(1)由已知90BAP CDP ∠=∠=︒,得AB AP ⊥,CD PD ⊥.由于AB CD ∥,故AB PD ⊥,从而AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)在平面PAD 内作PE AD ⊥,垂足为E .由(1)知,AB ⊥面PAD ,故AB PE ⊥,可得PE ⊥平面ABCD .设AB x =,则由已知可得2AD =,22PE x =.故四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=.由题设得31833x =,故2x =.从而2PA PD ==,22AD BC ==,22PB PC ==.可得四棱锥P ABCD -的侧面积为111222PA PD PA AB PD DC ⋅+⋅+⋅21sin606232BC +︒=+.20.已知函数()3211,32f x x ax a =-∈R .(I)当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程;(II)设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.【答案】(Ⅰ)390x y --=;(Ⅱ)见解析.【详解】试题分析:(Ⅰ)根据导数的几何意义,求出切线的斜率,再用点斜式写出切线方程;(Ⅱ)由()()(sin )g x x a x x =-'-,通过讨论确定()g x 的单调性,再由单调性确定极值.试题解析:(Ⅰ)由题意2()f x x ax '=-,所以,当2a =时,(3)0f =,2()2f x x x =-',所以(3)3f '=,因此,曲线()y f x =在点(3,(3))f 处的切线方程是3(3)y x =-,即390x y --=.(Ⅱ)因为()()()cos sin g x f x x a x x =+--,所以()()cos ()sin cos g x f x x x a x x ''=+---,()()sin x x a x a x=---()(sin )x a x x =--,令()sin h x x x =-,则()1cos 0h x x '=-≥,所以()h x 在R 上单调递增,因为(0)0h =,所以,当0x >时,()0h x >;当0x <时,()0h x <.(1)当a<0时,()()(sin )g x x a x x '=--,当(,)x a ∈-∞时,0x a -<,()0g x '>,()g x 单调递增;当(,0)x a ∈时,0x a ->,()0g x '<,()g x 单调递减;当(0,)x ∈+∞时,0x a ->,()0g x '>,()g x 单调递增.所以当x a =时()g x 取到极大值,极大值是31()sin 6g a a a =--,当0x =时()g x 取到极小值,极小值是(0)g a =-.(2)当0a =时,()(sin )g x x x x '=-,当(,)x ∈-∞+∞时,()0g x '≥,()g x 单调递增;所以()g x 在(,)∞∞-+上单调递增,()g x 无极大值也无极小值.(3)当0a >时,()()(sin )g x x a x x '=--,当(,0)x ∈-∞时,0x a -<,()0g x '>,()g x 单调递增;当(0,)x a ∈时,0x a -<,()0g x '<,()g x 单调递减;当(,)x a ∈+∞时,0x a ->,()0g x '>,()g x 单调递增.所以当0x =时()g x 取到极大值,极大值是(0)g a =-;当x a =时()g x 取到极小值,极小值是31()sin 6g a a a =--.综上所述:当a<0时,函数()g x 在(,)a -∞和(0,)+∞上单调递增,在(,0)a 上单调递减,函数既有极大值,又有极小值,极大值是31()sin 6g a a a =--,极小值是(0)g a =-;当0a =时,函数()g x 在(,)∞∞-+上单调递增,无极值;当0a >时,函数()g x 在(,0)-∞和(,)a +∞上单调递增,在(0,)a 上单调递减,函数既有极大值,又有极小值,极大值是(0)g a =-,极小值是31()sin 6g a a a =--.【考点】导数的几何意义及导数的应用【名师点睛】(1)求函数f (x )极值的步骤:①确定函数的定义域;②求导数f ′(x );③解方程f ′(x )=0,求出函数定义域内的所有根;④检验f ′(x )在f ′(x )=0的根x 0左右两侧值的符号,如果左正右负,那么f (x )在x 0处取极大值,如果左负右正,那么f (x )在x 0处取极小值.(2)若函数y =f (x )在区间(a ,b )内有极值,那么y =f (x )在(a ,b )内绝不是单调函数,即在某区间上单调函数没有极值.21.在平面直角坐标系xOy 中,已知椭圆C :22221x y a b +=(a >b >0)的离心率为22,椭圆C 截直线y =1所得线段的长度为(Ⅰ)求椭圆C 的方程;(Ⅱ)动直线l :y =kx +m (m ≠0)交椭圆C 于A ,B 两点,交y 轴于点M .点N 是M 关于O 的对称点,⊙N 的半径为|NO |.设D 为AB 的中点,DE ,DF 与⊙N 分别相切于点E ,F ,求∠EDF 的最小值.【答案】(Ⅰ)22142x y +=.(II)3π.【详解】试题分析:(Ⅰ)由2c a =得a =,由椭圆C 截直线y =1所得线段的长度为=,求得椭圆的方程为22142x y +=;(Ⅱ)由2224x y y kx m⎧+=⎨=+⎩,解得222(21)4240k x kmx m +++-=,确定222(,)2121km m D k k -++,DN =,结合22NDNF 的单调性求EDF ∠的最小值.试题解析:(Ⅰ)由椭圆的离心率为2,得2222()a a b =-,又当1y =时,2222a x a b =-,得2222a a b -=,所以224,2a b ==,因此椭圆方程为22142x y +=.(Ⅱ)设1122(,),(,)A x y B x y ,联立方程2224y kx m x y =+⎧⎨+=⎩,得222(21)4240k x kmx m +++-=,由0∆>得2242m k <+.(*)且122421km x x k +=+,因此122221m y y k +=+,所以222(,2121km m D k k -++,又(0,)N m -,所以222222(()2121km m ND m k k =-++++整理得2242224(13)(21)m k k ND k ++=+,因为NF m =,所以2422222224(31)831(21)(21)ND k k k k k NF +++==+++.令283,3t k t =+≥,故21214t k ++=,所以2221616111(1)2NDt t NF t t=+=++++.令1y t t=+,所以211y t '=-.当3t ≥时,0'>y ,从而1y t t =+在[3,)+∞上单调递增,因此1103t t +≥,等号当且仅当3t =时成立,此时0k =,所以22134ND NF ≤+=,由(*)得m <<且0m ≠.故12NF ND ≥,设2EDF θ∠=,则1sin 2NF ND θ=≥,所以θ的最小值为π6,从而EDF ∠的最小值为π3,此时直线l 的斜率是0.综上所述:当0k =,(m ∈⋃时,EDF ∠取到最小值π3.【考点】圆与椭圆的方程、直线与圆锥曲线的位置关系【名师点睛】圆锥曲线中的两类最值问题:①涉及距离、面积的最值以及与之相关的一些问题;②求直线或圆锥曲线中几何元素的最值以及这些元素存在最值时确定与之有关的一些问题.常见解法:①几何法,若题目的条件和结论能明显体现几何特征及意义,则考虑利用图形性质来解决;②代数法,若题目的条件和结论能体现一种明确的函数关系,则可先建立起目标函数,再求这个函数的最值,最值常用基本不等式法、配方法及导数法求解.22.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线:4cos C ρθ=,直线l 的参数方程为:321x t y t =+⎧⎨=-+⎩(t 为参数),直线l 与曲线C 分别交于,M N 两点.(1)写出曲线C 和直线l 的普通方程;(2)若点(3,1)P -,求11||||PM PN -的值.【答案】(1)22(2)4x y -+=;250x y --=(2)55【分析】(1)利用极坐标和直角坐标方程得转化公式即可得出曲线C 的普通方程,消去直线l 参数方程中的t 即可得直线l 的普通方程;(2)联立直线l 的参数方程和曲线C 的普通方程得出关于参数的一元二次方程,利用参数t '的几何意义和韦达定理即可求得11||||PM PN -的值.【小问1详解】将:4cos C ρθ=等号两边同时乘以ρ可得24cos ρρθ=,所以224x y x +=;即22(2)4x y -+=;所以曲线C 的普通方程为22(2)4x y -+=;将32:1x t l y t =+⎧⎨=-+⎩消去参数t 可得,32(1)x y =++,整理得250x y --=;即直线l 的普通方程为250x y --=【小问2详解】注意到(3,1)P -在直线l 上,直线l 倾斜角为1tan 2αα=,,cos 2sin αα∴=,22π(0,),sin 0,cos 0,sin cos 12ααααα∈>>+= ,解得525sin ,cos ,55αα==所以直线l 参数方程为2535(515x t t y ⎧=+⎪⎪⎨⎪=-+⎪⎩'''为参数),联立C 的直角坐标方程与l的参数方程得22(+1)1)455t ''+-=整理得225205t ''+-=,设方程的解为12,t t '',则125t t ''+=-,122t t ''=-,12,t t ''异号.不妨设1||PM t '=,2||PN t '=-,有12121211115||||5t t PM PN t t t t ''+-=+==''''.23.已知函数()2f x m x mx =+--()0m >的最大值为6.(1)求m 的值;(2)若正数x ,y ,z 满足x y z m ++=,求证:≤.【答案】(1)2;(2)证明见解析.【分析】(1)利用绝对值三角不等式求出()f x 的最大值,让最大值等于6即可得m 的值;(2)由(1)知,2x y z ++=,由222x x x y z y z ⎛⎫⎛⎫=++=+++ ⎪ ⎪⎝⎭⎝⎭利用基本不等式即可求证.【详解】(1)由题意得()2()(2)3f x x m x m x m x m m =+--≤+--=,因为函数()f x 的最大值为6,所以36m =,即2m =±.因为0m >,所以2m =;(2)由(1)知,2x y z ++=,因为0x >,0y >,0z >,所以222x x x y z y z ⎛⎫⎛⎫=++=+++≥+⎪ ⎪⎝⎭⎝⎭,当且仅当2x y z ==时,即1x =,12y z ==等号成立,22m ≤=≤,当且仅当11,2x y z ===时,等号成立.。
图1一、单项选择题1.已知集合A ={}x |-1≤x ≤2,B ={}0,2,4,则A ⋂B =().A.{}0,2,4 B.{}0,2C.{}x |0≤x ≤4 D.{}x |-1≤x ≤2或x =42.设i 是虚数单位,z ()1+i =i ,则||z =().A.12B.1C. D.23.在平面直角坐标系中,O为坐标原点,A ()4,3,B ()-1,3,则∠AOB 的余弦值为().A. B.C. D.4.已知a ,b 为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是().A.若α//β,a ⊂α,b ⊂β,则a //bB.若a ⊂α,b ⊂β,a //b ,则α//βC.若α⋂β=a ,b ⊂β,b ⊥a ,则α⊥βD.若α⋂β=l ,α⊥β,a ⊂α,a ⊥l ,a //b ,则b ⊥β5.在五边形ABCDE 中 EB =a ,AD =b,M ,N 分别为AE ,BD 的中点,则MN =().A.32a +12b B.23a+13b C.12a +12b D.34a+14b 6.命题p :关于x 的不等式ax 2+ax -x -1<0的解集为()-∞,-1⋃æèöø1a ,+∞的一个充分不必要条件是().A.a ≤-1B.a >0C.-2<a <0D.a <-27.清明节前夕,某校团委决定举办“缅怀革命先烈,致敬时代英雄”主题演讲比赛,经过初赛,共10人进入决赛,其中高一年级2人,高二年级3人,高三年级5人,现采取抽签方式决定演讲顺序,则在高二年级3人相邻的前提下,高一年级2人不相邻的概率为().A.112B.13C.12 D.348.若不等式m cos x -cos 3x -18≤0对任意x ∈æèöø0,π2恒成立,则实数m 的取值范围是().A.æèùû-∞,-94 B.(]-∞,-2C.æèùû-∞,94 D.æèùû-∞,98二、多选题9.已知0<log 12a <log 12b <1,则下列说法正确的是().A.1>a 2>b 2>14B.2>1a >1b >1C.a b -1>b a -1D.1e>e -b >1e 10.函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图1所示,则下列结论正确的是().A.f (x )的最小正周期为2B.把y =f (x )图象上所有点向右平移π12个单位长度后得到函数g (x )=2cos 2x 的图象C.f (x )在区间[π2,11π12]上单调递减D.(π6,0)是y =f (x )图象的一个对称中心11.提丢斯·波得定律是关于太阳系中行星轨道的一个简单的几何学规则,它是在1766年由德国的一位中学老师戴维斯·提丢斯发现的,后来被柏林天文台的台长波得归纳成一条定律,即数列{}a n :0.4,0.7,1.6,2.8,5.2,10,19.6,…,表示的是太阳系第n 颗行星与太阳的平均距离(以天文单位A .U .为单位).现将数列{}a n 的各项乘以10后再减4,得到数列{}b n ,可以发现数列{}b n 从第3项起,每项是前一项的2倍,则下列说法正确的是().A.数列{}b n 的通项公式为b n =3×2n -2B.数列{}a n 的第2021项为0.3×22020+0.4C.数列{}a n 的前n 项和S n =0.4n +0.3×2n -1-0.3D.数列{}nb n 的前n 项和T n =3()n -1∙2n -112.在一张纸上有一圆C :()x +22+y 2=r 2()r >0与点M ()m ,0()m ≠-2,折叠纸片,使圆C 上某一点M ′好与点M 重合,这样的折法每次都会留下一条直线折世世世世世世世世世世世世世世世世世53高考链接痕PQ ,设折痕PQ 与直线M ′C 的交点为T ,则下列说法正确的是().A.当-2-r <m <-2+r 时,点T 的轨迹为椭圆B.当r =1,m =2时,点T 的轨迹方程为x 2-y 23=1C.当m =2,1≤r ≤2时,点T 的轨迹对应曲线的离心率取值范围为[]2,4D.当r =22,m =2时,在T 的轨迹上任取一点S ,过S 作直线y =x 的垂线,垂足为N ,则△SON (O 为坐标原点)的面积为定值三、填空题13.正态分布在概率和统计中占有重要地位,它广泛存在于自然现象、生产和生活实践中,在现实生活中,很多随机变量都服从或近似服从正态分布.在某次大型联考中,所有学生的数学成绩X ~N ()100,225.若成绩低于m +10的同学人数和高于2m -20的同学人数相同,则整数m 的值为_______.14.已知抛物线x 2=4y ,其准线与y 轴交于点P ,则过点P 的抛物线的切线方程为_______.15.在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,其中A =π3,b +c =4,M 为线段BC 的中点,则||AM 的最小值为_______.16.已知四棱锥P -ABCD 的底面为正方形,PA =PB =PC =PD ,AB =2,若四棱锥P -ABCD 的体积为43,则以点P 为球心,以2为半径的球的表面与四棱锥侧面PAB 交线的长度约为_______,该四棱锥P -ABCD 外接球的体积为_______.(参考数据tan 35°≈).四、解答题17.在①S 8=72,②S 5=6a 2,③S 6=S 4+a 5这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列{a n }的前n 项和为S n ,a 3=6,________.若数列{b n }满足b n =2a n ,求数列{a n +b n }的前n 项和T n .18.已知等差数列{}a n 的前n 项和为S n ,且S 4=S 5=-20.(1)求数列{}a n 的通项公式;(2)已知数列{}b n 是以4为首项,4为公比的等比数列,若数列{}a n 与{}b n 的公共项为a m ,记m 由小到大构成数列{}c n ,求{}c n 的前n 项和T n .19.如图2,已知圆台O 1O 的下底面半径为2,上底面半径为1,母线与底面所成的角为π3,AA 1,BB 1为母线,平面AA 1O 1O ⊥平面BB 1O 1O ,M 为BB 1的中点,P 为AM 上的任意一点.(1)证明:BB 1⊥OP ;(2)当点P 为线段AM 的中点时,求平面OPB 与平面OAM 所成锐二面角的余弦值.图220.机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让行人”.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让行人”行为统计数据:月份违章驾驶员人数112021053100495580(1)请利用所给数据求违章人数y 与月份x 之间的回归直线方程y =b x +a ;(2)预测该路口9月份的不“礼让行人”违章驾驶员人数;(3)交警从这5个月内通过该路口的驾驶员中随机抽查70人,调查驾驶员不“礼让行人”行为与驾龄的关系,得到下表:驾龄不超过1年驾龄1年以上不礼让行人2416礼让行人1614能否据此判断有97.5%的把握认为“礼让行人”行为与驾龄有关?参考公式和数据:k 2=n (ad -bc )2(a +b )(c +d )(b +d )(其中n =a +b +c +d ).P (k 2≥k 0)k 00.152.0720.102.7060.053.8410.0255.0240.0106.63521.已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的离心率为12,过椭圆的左、右焦点F 1,F 2分别作倾斜角为π3的两条直线,且这两条直线之间的距离为3.54高考链接(1)求椭圆E 的标准方程;(2)如图3,过F 2与坐标轴不垂直的直线l 与椭圆交于A ,B 两点.过点A 作与x 轴垂直的直线与椭圆交于点Q ,求证:直线QB 过定点.图322.已知函数f (x )=e x-1,g (x )=a sin x ,a ∈R .(1)若a =-1,证明:当x ≥0时,f (x )≥g (x );(2)讨论φ(x )=f (x )-g (x )在x ∈[0,π]上零点的个数.参考答案及解析一、单项选择题1-8BCCDC DDA二、多项选择题9.ACD ;10.CD ;11.CD ;12.ACD.三、填空题;14.x -y -1=0,或x +y +1=0;15.3;16.;9π2.四、解答题17.解:选择①,设公差为d ,因为S 8=72,a 3=6,所以ìíî8a 1+28d =72,a 1+2d =6,解得ìíîa 1=2,d =2,所以a n =2n .因为b n =2a n ,所以b n =22n =4n ,a n +b n =2n +4n ,T n =2(1+2+...+n )+41+42+ (4)=n (n +1)+4(1-4n )1-4=43(4n -1)+n (n +1)=4n +13+n 2+n -43.选择②,设公差为d ,因为S 5=6a 2,所以5a 3=6a 2.因为a 3=6,所以a 2=5,所以d =1,所以a n =n +3.因为b n =2a n ,所以b n =2n +3=8×2n ,所以a n +b n =8×2n +n +3,T n =8(21+22+…+2n )+(1+2+…+n )+3n=8×2(1-2n )1-2+n (n +1)2+3n=16(2n -1)+n (n +1)2+3n =2n +4+12n 2+72n -16.选择③,设公差为d ,因为S 6=S 4+a 5,可得S 6-S 4=a 5,即a 6+a 5=a 5,所以a 6=0.因为a 3=6,所以d =-2,所以a n =-2n +12.因为b n =2a n ,所以b n =2-2n +12=212×2-2n ,T n =-2(1+2+…+n )+12n +212×(4-1+4-2+…+4-n )=-n (n +1)+12n +212×(14+142+…+14n )=2123[1-(14)n]-n 2+11n .18.解:(1)设等差数列{}a n 的公差为d ,因为S 4=S 5=-20,所以a 5=S 5-S 4=0.因为S 5=5a 3=-20,所以a 3=-4,所以d =a 5-a35-3=2,所以a n =a 5+()n -5d =2n -10.(2)由题意知b n =4×4n -1=4n .因为a m =2m -10,所以2m -10=4n ,m =4n+102.因此c n =4n +102=4n2+5.所以T n =42+5+422+5+432+5+⋯+4n 2+5=23×4n +5n -23.19.(1)证明:过点B 1作平面AOB 的垂线,垂足为C ,如图4,则C 是OB 的中点,所以BC =1.又∠OBB 1=π3,所以BB 1=2.连接OB 1,因为BB 1=OB =2,所以△OBB 1为等边三角形.因为点M 为BB 1的中点,所以BB 1⊥OM .因为平面AA 1O 1O ⊥平面BB 1O 1O ,平面AA 1O 1O ⋂平面BB 1O 1O =OO 1,且AO ⊥OO 1,AO ⊂平面AA 1O 1O ,所以AO ⊥平面BB 1O 1O .因为BB 1⊂平面BB 1O 1O ,所以AO ⊥BB 1.又因为AO ⋂OM =O ,AO ⊂平面OMA ,OM ⊂平面OMA ,所以BB 1⊥平面OMA .因为OP ⊂平面OMA ,所以BB 1⊥OP .图4(2)解:以O 为坐标原点,OA ,OB ,OO 1所在直55线分别为x 轴、y 轴、z 轴,建立如图4所示的空间直角坐标系A ()2,0,0,B ()0,2,0,B 1()0,1,3,M æèçç0,32,ø,P æèçø1,34, OP =æèçø1,34,,OB =()0,2,0设平面OPB 的一个法向量为n =()x ,y ,z ,则{OP ∙n =0, OB ∙n =0,即ìíîïïx +34y +=0,2y =0,取z =43,得x =-3,y =0,所以n=()-3,0,43,因为BB 1⊥平面OAM ,所以平面OAM 的一个法向量为BB 1=()0,-1,3,所以cos < BB 1,n >=BB 1∙n || BB 1||n 所以平面OAM 与平面OPB 所成锐二面角的余弦值为.20.解:(1)由表中数据知x ˉ=3,y ˉ=100,所以b =1410-150055-45=-9,所以a =y ˉ-b x ˉ=127,故所求回归直线方程为y =-9x +127.(2)由(1)知,令x =9,则y =-9×9+127=46人.(3)假设H 0:“礼让行人”行为与驾龄无关,由表中数据得k 2=70×(24×14-16×16)240×30×40×30=1445≈0.311<2.706,所以没有97.5%的把握认为“礼让行人”行为与驾龄有关.21.(1)解:因为过椭圆E 的左、右焦点倾斜角为π3的两条直线间的距离为3,所以sin π3所以c =1.因为椭圆的离心率为12,所以a =2,所以b =3,故椭圆E 的标准方程为x 24+y 23=1.(2)证明:设A (x 1,y 1),B (x 2,y 2),直线l :x =my +1,则Q (x 1,-y 1).因为直线l 与坐标轴不垂直,所以直线QB :y +y 1=y 1+y 2x 2-x 1(x -x 1),所以y =y 1+y 2x 2-x 1x -x 2y 1+x 1y 2x 2-x 1=y 1+y 2m (y 2-y 1)x -2my 1y 2+y 1+y 2m (y 2-y 1),由得ìíîïïx 24+y 23=1,x =my +1,得(3m 2+4)y 2+6my -9=0,所以y 1+y 2=-6m 3m 2+4,y 1y 2=-93m 2+4,所以y =-6m(3m 2+4)(y 2-y 1)(x -4),所以直线QB 恒过定点(4,0).22.(1)证明:令F (x )=f (x )-g (x )=e x -1+sin x ,所以F ′(x )=e x +cos x .当x ∈(0,+∞)时,e x >1,cos x ≤1,所以F ′(x )>0.所以F (x )在[0,+∞)上单调递增.又x ∈[0,+∞),所以F (x )≥F (0)=0,所以f (x )≥g (x )在x ∈[0,+∞)上恒成立.(2)解:因为φ(x )=e x -1-a sin x (a ∈R ),所以φ′(x )=e x -a cos x .设h (x )=φ′(x ),h ′(x )=e x +a sin x ,①当a ≤0时,因为x ∈[0,π],所以-a sin x ≥0,而e x -1≥0,所以e x -1-a sin x ≥0,即φ(x )≥0恒成立,所以φ(x )零点个数为1个.②当0<a ≤1时,h ′(x )=e x +a sin x ≥0,所以φ′(x )在[0,π]上单调递增,而φ′(0)=1-a ≥0,所以φ′(x )≥φ′(0)=0,所以φ(x )在[0,π]上单调递增.因为φ(0)=0,所以x =0是唯一零点,此时φ(x )零点个数为1个.③当a >1时,h ′(x )=e x +a sin x ≥0,所以φ′(x )在[0,π]上单调递增,而φ′(0)=1-a <0,φ′(π2)=e π2>0,所以存在x 0∈[0,π],使φ′(x 0)=0,所以当0<x <x 0时,φ(x )单调递减,当x 0<x <π时,φ(x )单调递增,所以当x =x 0时,φ(x )取得最小值φ(x 0).而φ(x 0)<φ(0)=0,φ(π)=e π-1>0,又φ(x )图象是连续不间断的,由零点存在性定理知,φ(x )在(x 0,π)上有唯一零点.因为x =0也是零点,所以φ(x )在[0,π]上有2个零点.综上:当a ≤1时,φ(x )在[0,π]上有1个零点;当a >1时,φ(x )在[0,π]上有2个零点.高考链接56。