专题三 高考数列命题动向

聚焦数列本质,重视运算推理高考全国卷数列解答题命题动向分析ʏ广东省佛山市顺德区容山中学 潘敬贞 沈 健数列是高中数学的重要内容,也是每年高考必考的内容,历年高考全国卷中的数列解答题始终保持着 聚焦数列本质,重视运算推理 的特色,试题以基本知识㊁基本技能和基本思想方法为出发点,以数学素养为落脚点,对同学们进行全面考查㊂本文结合实例对全国卷中数列解答题的命题动向进行分析,目的是帮助同学们把握高考数列解答题的命题动向,提高备考的针对性与有效性㊂一㊁考查基本概念与基本思想方法例1 设公差不为0的等差数列{a n }的前n 项和为S n ,且a 4=2a 2+2,S 1,S 2,S 4成等比数列㊂(1)求数列{a n }的通项公式;(2)设b n =2n -a n +33,数列{b n }的前n 项和为T n ,若∀n ɪN *,都有T n <m 成立,求m 的取值范围㊂解析:(1)设数列{a n }的公差为d ,由a 4=2a 2+2,以及S 1,S 2,S 4成等比数列得,a 1(4a 1+6d )=(2a 1+d )2,a 1+3d =2(a 1+d )+2,解得a 1=2,d =4,所以a n =2+4(n -1)=4n -2㊂(2)由(1)知a n =4n -2,所以b n =2n -a n +33=35-2n ㊂所以T n =(33+35-2n )n 2=-n 2+34n=-(n -17)2+289,所以当n =17时,T n 取得最大值289㊂因为∀n ɪN *,都有T n <m 成立,所以m >289㊂评注:本题第一问聚焦等差㊁等比数列的基本概念与基本量的求解;第二问结合不等式考查等差数列的求和公式㊂试题着力考查同学们对数列基本知识㊁基本思想方法的掌握情况,考查同学们的运算求解能力,以及数学运算㊁逻辑推理等核心素养㊂试题凸显基础性与综合性,难度不大,属于基础题㊂例2 已知S n是数列{a n }的前n 项和,2S n =n a n ,a 2=3㊂(1)求数列{a n }的通项公式;(2)若b n =|16-a n |,求数列{b n }的前n 项和T n ㊂解析:(1)因为2S n =n a n ,所以2S n +1=(n +1)a n +1,两式相减得2a n +1=(n +1)a n +1-n a n ,整理得(n -1)a n +1=n a n ,即当n ȡ2时,a n +1a n=n n -1㊂所以当n ȡ2时,a n =a n a n -1㊃a n -1a n -2㊃ ㊃a 3a 2㊃a 2=n -1n -2㊃n -2n -3㊃ ㊃21㊃3=3(n -1)㊂又当n =1时,2a 1=a 1,得a 1=0,也满足上式,故a n =3(n -1)㊂(2)由(1)可知,b n =|16-a n |=|19-3n |㊂记C n =19-3n ,设数列{C n }的前n 项和为T n '㊂当n ɤ6时,T n =n (16+19-3n )2=-3n 2+35n2;当n >6时,T n =C 1+C 2+ +C 6-C 7- -C n =T 6'-(T n '-T 6')=2T 6'-T n '=102--3n 2+35n 2=3n 2-35n +2042㊂综上可得,T n =-3n 2+35n 2,n ɤ6,3n 2-35n +2042,n >6㊂评注:本题结合a n 与S n 的关系,考查累乘法求通项公式㊂当然,本题第一问还可以通过构造常数列来求数列的通项公式,即由(n -1)a n +1=n a n ,得a n +1n =a nn -1(n ȡ2),所9以a nn -1是常数列,但要注意检验首项是否满足;第二问需要分类讨论去掉绝对值,然后进行求和㊂本题是数列中典型的问题,求解过程中涉及的思想方法都是数列常用的思想方法,需要同学们掌握㊂例3 记数列a n的前n 项和为S n ,已知a 1=3,a n +1=S n +n +3㊂(1)求数列{a n }的通项公式;(2)令b n =1a n ,设数列{b n }的前n 项和为T n ,证明:T n <1㊂解析:(1)因为a n +1=S n +n +3,所以a n =S n -1+n +2(n ȡ2),两式相减得a n +1-a n =a n +1,即a n +1=2a n +1(n ȡ2),所以a n +1+1=2(a n +1)(n ȡ2),即a n +1+1a n +1=2(n ȡ2)㊂又因为a 2=S 1+1+3=7,所以a 2+1a 1+1=2,所以{a n +1}是以4为首项,2为公比的等比数列,故a n +1=4ˑ2n -1=2n +1,所以a n =2n +1-1㊂(2)由(1)知a n =2n +1-1,所以b n =1a n=12n +1-1<1+12n +1-1+1=12n ㊂所以T n =b 1+b 2+ +b n =122-1+123-1+ +12n +1-1<121+122+ +12n =12-12n ˑ121-12=1-12n <1㊂评注:本题的第一问是结合a n 与S n 的关系,进而构造等比数列来求相应数列的通项公式,这类问题同学们都比较熟悉,求解方法也很常见;第二问是利用 糖水不等式 进行放缩,最后用等比数列的求和公式进行求和㊂试题比较基础,但有一定的灵活性,需要同学们平时多积累基本活动经验,这对问题的求解会有很大的帮助㊂二㊁理解概念本质,重视运算推理例4 设数列{a n }的前n 项和为S n ,已知a 1=1,且数列3-2S n a n是公比为13的等比数列㊂(1)求数列{a n }的通项公式;(2)设b n =3n(a n +1-1)(a n +2-1),数列{b n }的前n 项和为T n ,证明:T n <14㊂解析:(1)因为S 1=a 1=1,所以3-2S 1a 1=1,所以数列3-2S na n是首项为1,公比为13的等比数列,所以3-2S n a n =13n -1,整理得2S n =3-13n -1a n,所以2S n +1=3-13 na n +1,两式作差得2(S n +1-S n)=2a n +1=3-13 na n +1-3-13 n -1a n,化简得(1-3-n )a n +1-3(1-3-n )a n =0,即(3n -1)(a n +1-3a n )=0,所以a n +1=3a n ,所以数列{a n }是以a 1=1为首项,3为公比的等比数列,故数列{a n }的通项公式为a n =3n -1㊂(2)由(1)知b n =3n(a n +1-1)(a n +2-1)=3n(3n -1)(3n +1-1)=1213n-1-13n +1-1㊂所以T n =12131-1-132-1+12㊃132-1-133-1++12㊃13n -1-13n +1-1 =1213-1-13n +1-1 =14-12(3n +1-1)㊂因为12(3n +1-1)>0,所以T n <14㊂评注:本题第一问的求解对推理能力有较高的要求,最关键的一点是通过对题目中的条件进行运算推理得(3n-1)㊃(a n +1-3a n )=0;第二问则是常见的裂项求和问题,大家都比较熟悉㊂例5 已知正项数列{a n }的前n 项和S n =A q n+B ,其中A ,B ,q 为常数㊂1(1)若A +B =0,证明:数列{a n }是等比数列;(2)若a 1=1,a n +2=4a n ,求数列n a n的前n 项和T n ㊂解析:(1)当n ȡ2时,S n -1=A q n -1+B ,则a n =S n -S n -1=A q n +B -(A q n -1+B )=A (q -1)q n -1㊂因为{a n }是正项数列,所以q >0且q ʂ1㊂当n =1时,a 1=S 1=A q +B ,又A +B =0,则a 1=A (q -1),也符合a n =A (q -1)㊃qn -1㊂所以a n =A (q -1)q n -1,a n +1=A (q -1)㊃q n,则a n +1a n =q ,故数列{a n }是以A (q -1)为首项,q 为公比的等比数列㊂(2)由(1)知,当n ȡ2时,a n =A (q -1)㊃qn -1,则a n +2=A (q -1)q n +1,由a n +2=4a n ,可得q 2=4㊂因为{a n }是正项数列,所以q >0,即q =2,所以a n =A ㊃2n -1(n ȡ2),则a 3=4A ㊂由a 1=1,a 3=4a 1,可得A =1,则a n =2n -1(n ȡ2)㊂当n =1时也符合,则a n =2n -1㊂所以T n =1ˑ20+2ˑ21+3ˑ22+ +n ㊃2n -1,2T n =1ˑ21+2ˑ22+3ˑ23+ +n ㊃2n ,两式相减得-T n =20+21+22+23++2n -1-n ㊃2n =1-2n1-2-n ㊃2n=(1-n )㊃2n-1,所以T n =1+(n -1)㊃2n㊂例6 已知数列{a n }满足a 1=2,a n +1=a n +1,n 为奇数,2a n ,n 为偶数㊂(1)记b n =a 2n +1,求证:{b n }为等比数列;(2)设数列{c n }的前n 项和为T n ,且c n ㊃(n +1)l o g 2(a 2n -1+2)=1,证明:T n <1㊂解析:(1)因为b n +1b n =a 2n +2+1a 2n +1=a 2n +1+1+1a 2n +1=2a 2n +2a 2n +1=2,所以{b n }为等比数列㊂(2)由(1)可知,{b n }是以2为公比的等比数列,又b 1=a 2+1=a 1+1+1=2+2=4,所以b n =4㊃2n -1=2n +1,即b n =2n +1=a 2n +1,所以a 2n =2n +1-1㊂因为a 2n =a 2n -1+1,所以a 2n -1=a 2n -1=2n +1-2㊂所以c n ㊃(n +1)l o g 2(a 2n -1+2)=c n ㊃(n +1)2=1,所以c n =1(n +1)2㊂因为c n =1(n +1)2<1n (n +1)=1n -1n +1,所以T n =c 1+c 2+ +c n =122+132++1(n +1)2<1-12+12-13+ +1n -1n +1=1-1n +1<1㊂评注:例5和例6的求解不仅需要对数列本质的深刻理解,还要有较强的推理能力,否则很难将问题解决,例6还需要掌握简单的放缩法㊂这是近年来高考全国卷命题专家比较青睐的问题,希望同学们能引起足够重视,并深化对数列本质的理解,提升自己的推理能力㊂三㊁聚焦基础性㊁综合性与创新性例7 已知正数数列{a n },{b n }满足:a 1=8,b 1=16,且a n ,b n ,a n +1成等差数列,b n ,a n +1,b n +1成等比数列㊂(1)求数列{a n },{b n }的通项公式;(2)求证:1a 1-1+1a 2-1+ +1a n -1<13㊂解析:(1)因为a n ,b n ,a n +1成等差数列,所以2b n =a n +a n +1㊂因为b n ,a n +1,b n +1成等比数列,所以a 2n +1=b n b n +1㊂因为数列{a n },{b n }为正数数列,所以a n +1=b n b n +1㊂当n ȡ2时,a n =b n -1b n ,所以2b n =b n b n +1+b n -1b n ,所以2b n =b n +1+b n -1,且b 1=16,则b 1=4㊂因为2b 1=a 1+a 2,所以a 2=24,又因为a 22=b 1b 2,所以b 2=36,所以b 2-b 1=6-4=2,所以数列{b n }是以4为首项,2为11公差的等差数列,所以b n =4+2(n -1)=2n +2,所以b n =4(n +1)2㊂当n =1时,b 1=16满足上式,所以b n =4n +12㊂当n ȡ2时,a n=b n -1b n =4n 2ˑ4(n +1)2=4n (n +1)㊂当n =1时,a 1=8满足上式,所以a n =4n (n +1)㊂(2)由(1)知1a n -1=14n (n +1)-1=14n 2+4n -1<14n 2+4n -3=1(2n -1)(2n +3)=1412n -1-12n +3㊂当n =1时,1a 1-1=17<13;当n =2时,1a 1-1+1a 2-1=17+123<17+121=421<13;当n ȡ3时,1a 1-1+1a 2-1+1a 3-1++1a n -1=17+123+ +14n 2+4n -1<17+123+1415-19 +17-111+ +12n -3-12n +1 +12n -1-12n +3=17+123+1415+17-12n +1-12n +3 <17+123+1415+17 =17+123+335=219805<13㊂综上所述,对一切正整数n ,有1a 1-1+1a 2-1+ +1a n -1<13成立㊂评注:本题的第一问是两个数列深度融合,体现很强的综合性,但求解过程都是涉及基本知识与基本思想方法,体现基础性;第二问需要灵活的放缩,然后用常见的裂项相消法求和㊂整道题有很强的基础性与综合性,问题的求解不仅要有扎实的基本知识与基本思想方法,还要有较强的运算推理能力㊂例8 已知各项均为正数的等比数列{a n },其前n 项和为S n ,满足2S n =a n +2-6㊂(1)求数列{a n }的通项公式;(2)记b m 为数列{S n }在区间(a m ,a m +2)中最大的项,求数列{b n }的前n 项和T n ㊂解析:(1)设{a n }的公比为q ,则q >0㊂又2S n =a n +2-6,当n =1时,2S 1=a 3-6;当n =2时,2S 2=a 4-6㊂两式相减得2a 2=a 4-a 3,所以2=q 2-q ,解得q =2或q =-1(舍去),所以2S 1=a 3-6=4a 1-6,即a 1=3㊂所以数列{a n }的通项公式为a n =3ˑ2n -1㊂(2)由a n =3ˑ2n -1,2S n =a n +2-6,可得S n =12a n +2-6 =12(3ˑ2n +1-6)=3ˑ2n-3,所以S n =a n +1-3<a n +1㊂又因为a n >0,所以S n ȡa n ,当且仅当n =1时等号成立,所以a m ɤS m <S m +1<a m +2<S m +2,所以b m =S m +1=3ˑ2m +1-3㊂所以T n =3(22+23+24+ +2n +1)-3n =3ˑ22-2n +21-2-3n =3ˑ2n +2-3n -12㊂评注:本题的第一问较为常规,第二问的情境较为新颖,很难让人读懂题意,问题的求解需要有敏锐的洞察力和较强的创新意识㊂如何寻找数列{S n }在区间(a m ,a m +2)中最大的项?数列{S n }与区间(a m ,a m +2)有什么关联怎样寻找关联?这些问题是解决该题的关键!聚焦数列本质,重视运算推理 是历年高考全国卷中数列解答题始终保持的特色,试题主要考查数列的基本知识㊁基本技能和基本思想方法㊂试题一般不会单独考查某个知识点,而是将多个知识点融入问题情境中进行考查,更加注重多个知识点交织融合,凸显基础性㊁综合性与创新性㊂因此,同学们在复习备考过程中,要学会透过问题表象,揭开问题的神秘面纱,深入问题的内核,看透问题的本质,深刻理解数列概念的本质内涵,平时要勤思考,多动手实践,在解决问题中深化对概念的理解,在动手实践中积累活动经验,在归纳总结中构建知识体系,从而提升自己的数学素养㊂(责任编辑 王福华)21。

【高考复习】高考数学题型分析：数列问题篇高考数学题型分析：数列问题篇数列是高中数学的重要内容，又是学习高等数学的基础。

高考对本章的考查比较全面，等差数列，等比数列的考查每年都不会遗漏。

有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起。

探索性问题是高考的热点，常在数列解答题中出现。

本章中还蕴含着丰富的数学思想，在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想，以及配方法、换元法、待定系数法等基本数学方法。

近几年来，高考关于数列方面的命题主要有以下三个方面;(1)数列本身的有关知识，其中有等差数列与等比数列的概念、性质、通项公式及求和公式。

(2)数列与其它知识的结合，其中有数列与函数、方程、不等式、三角、几何的结合。

(3)数列的应用问题，其中主要是以增长率问题为主。

试题的难度有三个层次，小题大都以基础题为主，解答题大都以基础题和中档题为主，只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题难度较大。

知识整合1.在掌握等差数列、等比数列的定义、性质、通项公式、前n项和公式的基础上，系统掌握解等差数列与等比数列综合题的规律，深化数学思想方法在解题实践中的指导作用，灵活地运用数列知识和方法解决数学和实际生活中的有关问题;2.在解决综合题和探索性问题实践中加深对基础知识、基本技能和基本数学思想方法的认识，沟通各类知识的联系，形成更完整的知识网络，提高分析问题和解决问题的能力，进一步培养学生阅读理解和创新能力，综合运用数学思想方法分析问题与解决问题的能力。

3.培养学生善于分析题意，富于联想，以适应新的背景，新的设问方式，提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法感谢您的阅读，祝您生活愉快。

近年的“数列”考了哪些内容？数列是高中数学的重要内容，又是学习高等数学的基础.高考对本章的考查比较全面，等差数列、等比数列的考查每年都不会遗漏.一般情况下都是一个客观题和一个解答题，分值占整个试卷的10%左右.从近三年各地高考试卷来看，高考关于数列方面的命题主要有以下两个方面：一、 数列本身的有关知识，考查数等差数列、等比数列的概念、性质、通项公式及求和公式. 【例1】 （2007年天津卷）设等差数列{}n a 的公差d 不为0，19a d =．若k a 是1a 与2k a 的等比中项，则k =（ ） Ａ．2 Ｂ．4 Ｃ．6Ｄ．8解答：B 由题意得，a n =（n +8）d ,a k k a a 212=, ∴（k +8）2d 2=9d (2k +8)d .∴k =4.【点评】 本题主要考查等差、等比数列的性质.【例2】 （2007年北京卷）数列{}n a 中，12a =，1n n a a cn +=+（c 是常数，123n =，，，），且123a a a ，，成公比不为1的等比数列． （I ）求c 的值；（II ）求{}n a 的通项公式．解：（I ）12a =，22a c =+，323a c =+， 因为1a ，2a ，3a 成等比数列， 所以2(2)2(23)c c +=+， 解得0c =或2c =．当0c =时，123a a a ==，不符合题意舍去，故2c =． （II ）当2n ≥时，由于21a a c -=， 322a a c -=，1(1)n n a a n c --=-，所以1(1)[12(1)]2n n n a a n c c --=+++-=．又12a =，2c =，故22(1)2(23)n a n n n n n =+-=-+=，，． 当1n =时，上式也成立， 所以22(12)n a n n n =-+=，，．【点评】 本题主要考查等比数列、等差数列的基本性质以及通项公式的求法，同时也考查了学生的基本运算能力.【例3】 （2007年全国卷Ⅰ）已知数列{}n a 中12a =，11)(2)n n a a +=+，123n =，，，…．（Ⅰ）求{}n a 的通项公式； （Ⅱ）若数列{}n b 中12b =，13423n n n b b b ++=+，123n =，，，…，43n n b a -<≤，123n =，，，…． 解：（Ⅰ）由题设：11)(2)n n a a +=+1)(1)(2n a =+1)(n a =11)(n n a a +=．所以，数列{n a -是首项为21的等比数列，1)n n a ，即n a的通项公式为1)1nn a ⎤=+⎦，123n =，，，…． （Ⅱ）用数学归纳法证明．（ⅰ）当1n =2，112b a ==，所以11b a <≤，结论成立．（ⅱ）假设当n k =43k k b a -≤，也即430k k b a -< 当1n k =+时，13423k k k b b b ++=+(3(423k k b b -+-=+(3023k k b b -=>+，又1323k b <=-+所以1(32)2)23k k k b b b +-=+2(3(k b <-4431)(k a -≤41k a +=也就是说，当1n k =+时，结论成立．43n n b a -<≤，123n =，，，…． 【点评】 本题考查等差、等比数列的基本运算和错位相减法求和的技巧以及方程意识在解题中的作用.属于中档题，是高考中常见类型.在数列求和中常见的方法有公式法、分组法、错位相减法、裂项相消法、倒序相加法等，方法的选择由数列通项公式的特点来决定.二、数列与其他知识的整合，其中包括数列与函数、方程、不等式、三角函数、几何的整合【例4】 （2007年重庆）已知各项均为正数的数列{}n a 的前n 项和n S 满足11S >，且6(1)(2)n n n S a a =++，n ∈N ．（Ⅰ）求{}n a 的通项公式；（Ⅱ）设数列{}n b 满足(21)1n bn a -=，并记n T 为{}n b 的前n 项和，求证：231log (3)n n T a n ->+∈N ，．解：（I ）解由11111(1)(2)6a S a a ==++，解得11a =或12a =， 由假设111a S =>，因此12a =，又由111111(1)(2)(1)(2)66n n n n n n n a S S a a a a ++++=-=++-++， 得11()(3)0n n n n a a a a +++--=，即130n n a a +--=或1n n a a +=-，因0n a >，故1n n a a +=-不成立，舍去．因此13n n a a +-=，从而{}n a 是公差为3，首项为2的等差数列，故{}n a 的通项为31n a n =-．（II ）证法一：由(21)1n bn a -=可解得22213log 1log 31n nb a n ⎛⎫=+= ⎪-⎝⎭； 从而⎪⎭⎫⎝⎛-⋅⋅=+++=1335623log 221n n b b b T n n因此2321335623log )3(log 13322+⋅⎪⎭⎫ ⎝⎛-⋅⋅=+-+n n n a T n n 令2321335623)(3+⎪⎭⎫ ⎝⎛-⋅⋅=n n n n f ， 则223)23)(53()33(23335323)()1(+++=⎪⎭⎫ ⎝⎛++∙++=+n n n n n n n n f n f ． 因32(33)(35)(32)970n n n n +-++=+>，故(1)()f n f n +>．特别地27()(1)120f n f =>≥，从而2231log (3)log ()0n n T a f n +-+=>． 即231log (3)n n T a +>+． 证法二：同证法一求得n b 及n T ，由二项式定理知，当0c >时，不等式3(1)13c c +>+成立．由此不等式有333211131log 21112531n T n ⎛⎫⎛⎫⎛⎫+=+++ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭2333log 21112531n ⎛⎫⎛⎫⎛⎫>+++ ⎪⎪⎪-⎝⎭⎝⎭⎝⎭2225832log 2log (32)log (3)2531n n n a n +==+=+-····．证法三：同证法一求得n b 及n T ．令36347312531363n n n n A B n n +==-，······，58324731n n C n +=+···．因3313231331n n n n n n ++>>-+． 因此23+22n n n n n A A B C >=．从而32322log 13356232log 13n n A n n T =⎪⎭⎫ ⎝⎛-⋅⋅⋅=+222log 2log (32)log (3)n n n n A B C n a >=+=+．证法四：同证法一求得n b 及n T ．下面用数学归纳法证明：231log (3)n n T a +>+． 当1n =时，122731log 4T +=，212log (3)log 5a +=， 因此12131log (3)T a +>+，结论成立．假设结论当n k =时成立，即231log (3)k k T a +>+． 则当1n k =+时，12112131log (3)313log (3)k k k k k T a T b a +++++-+=++-+2211log (3)log (3)3k k k a a b ++>+-++ 322(33)log (35)(32)k k k +=++ 因32(33)(35)(32)970k k k k +-++=+>．故322(33)log 0(35)(32)k k k +>++． 从而12131log (3)k k T a +++>+．这就是说，当1n k =+时结论也成立． 综上231log (3)n n T a +>+对任何n ∈+N 成立．【点评】 考查数列的相关知识，具有一定难度，与不等式的证明相结合，带有一定的技巧性.【例5】（2007年江苏）已知{}n a 是等差数列，{}n b 是公比为q 的等比数列，11221,a b a b a ==≠，记n S 为数列{}n b 的前n 项和，（1）若(,k m b a m k =是大于2的正整数)，求证：11(1)k S m a -=-；（4分）（2）若3(i b a i =是某一正整数)，求证：q 是整数，且数列{}n b 中每一项都是数列{}n a 中的项；（8分）（3）是否存在这样的正数q ，使等比数列{}n b 中有三项成等差数列？若存在，写出一个q 的值，并加以说明；若不存在，请说明理由；（4分）解：设{}n a 的公差为d ，由11221,a b a b a ==≠，知0,1d q ≠≠，()11d a q =-（10a ≠）（1）因为k m b a =，所以()()111111k a q a m a q -=+--，()()()111121k q m q m m q -=+--=-+-，所以()()()()1111111111k k a q a m m q S m a qq------===--（2）()()23111,11i b a q a a i a q ==+--，由3i b a =， 所以()()()()22111,120,q i q q i q i =+----+-=解得，1q =或2q i =-，但1q ≠，所以2q i =-，因为i 是正整数，所以2i -是整数，即q 是整数，设数列{}n b 中任意一项为()11n n b a qn N -+=∈，设数列{}n a 中的某一项m a ()m N +∈=()()1111a m a q +--现在只要证明存在正整数m ，使得n m b a =，即在方程()()111111n a q a m a q -=+--中m有正整数解即可，()()11221111,111n n n q qm q m q q q q ----=+---==+++-，所以222n m q q q -=+++， 若1i =，则1q =-，那么2111,222n n b b a b b a -====，当3i ≥时，因为1122,a b a b ==，只要考虑3n ≥的情况，因为3i b a =，所以3i ≥，因此q 是正整数，所以m 是正整数，因此数列{}n b 中任意一项为()11n n b a qn N -+=∈与数列{}n a 的第222n q q q -+++项相等，从而结论成立.（3）设数列{}n b 中有三项(),,,,,m n p b b b m n p m n p N +<<∈成等差数列，则有2111111,n m p a q a q a q ---=+设(),,,n m x p n y x y N +-=-=∈，所以21yx q q=+， 令1,2x y ==，则3210,q q -+=()()2110q q q -+-=，因为1q ≠，所以210q q +-=，所以)q =舍去负值，即存在q ={}n b 中有三项()13,,m m m b b b m N +++∈成等差数列.【点评】 本小题主要考查等差、等比数列的有关知识，考查运用方程、分类讨论等思想方法进行分析、探索及论证问题的能力.三、数列的综合应用 【例6】 （2007年湖南）已知()n n n A a b ，（n ∈N *）是曲线x y e =上的点，1a a =，nS 是数列{}n a 的前n 项和，且满足22213n n n S n a S -=+，0n a ≠，234n =，，，…． （I ）证明：数列2n n b b +⎧⎫⎨⎬⎩⎭（2n ≤）是常数数列； （II ）确定a 的取值集合M ，使a M ∈时，数列{}n a 是单调递增数列； （III ）证明：当a M ∈时，弦1n n A A +（n ∈N *）的斜率随n 单调递增．解：（I ）当2n ≥时，由已知得22213n n n S S n a --=．因为10n n n a S S -=-≠，所以213n n S S n -+=． …… ① 于是213(1)n n S S n ++=+． ……② 由②－①得163n n a a n ++=+． …… ③ 于是2169n n a a n +++=+． …… ④ 由④－③得26n n a a +-=， …… ⑤所以2262n n n n a a a n a n b e e e b e ++-+===，即数列2(2)n n b n b +⎧⎫⎨⎬⎩⎭≥是常数数列．（II ）由①有2112S S +=，所以2122a a =-．由③有3215a a +=，4321a a +=，所以332a a =+，4182a a =-．而 ⑤表明：数列2{}k a 和21{}k a +分别是以2a ，3a 为首项，6为公差的等差数列， 所以226(1)k a a k =+-，2136(1)k a a k +=+-，2246(1)()k a a k k +=+-∈N*， 数列{}n a 是单调递增数列12a a ⇔<且22122k k k a a a ++<<对任意的k ∈N *成立．12a a ⇔<且2346(1)6(1)6(1)a k a k a k +-<+-<+- 1234a a a a ⇔<<<9151223218244a a a a a ⇔<-<+<-⇔<<． 即所求a 的取值集合是91544M aa ⎧⎫=<<⎨⎬⎩⎭．（III ）解法一：弦1n n A A +的斜率为1111n na a n n n n n n nb b e e k a a a a ++++--==-- 任取0x ，设函数00()x x e e f x x x -=-，则0020()()()()x x x e x x e e f x x x ---=- 记00()()()xx x g x e x x e e =---，则00()()()x x x x g x e x x e e e x x '=-+-=-， 当0x x >时，()0g x '>，()g x 在0()x +∞，上为增函数， 当0x x <时，()0g x '<，()g x 在0()x -∞，上为减函数，所以0x x ≠时，0()()0g x g x >=，从而`()0f x '>，所以()f x 在0()x -∞，和0()x +∞，上都是增函数．由（II ）知，a M ∈时，数列{}n a 单调递增，取0n x a =，因为12n n n a a a ++<<，所以11n n a a n n n e e k a a ++-=-22n na a n n e e a a ++-<-． 取02n x a +=，因为12n n n a a a ++<<，所以12112n n a a n n n e e k a a +++++-=-22n n a a n n e e a a ++->-． 所以1n n k k +<，即弦1()n n A A n +∈N*的斜率随n 单调递增．解法二：设函数11()n a x n e e f x x a ++-=-，同解法一得，()f x 在1()n a +-∞，和1()n a ++∞，上都是增函数，所以111111lim n n n n n a a a x a n n a n n n e e e e k e a a x a +++-+++--=<=--→，211111211lim n n n n n a a a x a n n a n n n e e e e k e a a x a ++++++++++--=>=--→． 故1n n k k +<，即弦1()n n A A n +∈N*的斜率随n 单调递增．【点评】 本题以函数、解析几何知识为载体，第一问考查由S n 的递推关系推导出a n ；第二问通过a n +2-a n =6对数列{a n }分为两个子数列，来表达其单调递增是本题的一大特点；第三问将数列还原为函数来解体现了函数和数列的关系，显示出命题者的独具匠心.此类题目除了考查基础知识之外，还考查了我们对教材中各知识间的联系的理解与综合运用，难度较大.但题目一般以简单的设问开始，因此考生还是可以拿到该题的部分分数的.解这种题目的能力不是短期能培养出来的，要顺其自然，相信功到自然成.【例7】 某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金，数目为a 1，以后每年交纳的数目均比上一年增加d （d >0），因此，历年所交纳的储务金数目a 1，a 2，…是一个公差为d 的等差数列，与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利.这就是说，如果固定年利率为r （r >0），那么，在第n 年末，第一年所交纳的储备金就变为a 1（1＋r ）n -1，第二年所交纳的储备金就变为a 2（1＋r ）n -2，……，以T n 表示到第n 年末所累计的储备金总额.（Ⅰ）写出T n 与T n －1（n ≥2）的递推关系式；（Ⅱ）求证：T n ＝A n ＋B n ，其中｛A n ｝是一个等比数列，｛B n ｝是一个等差数列. 解：（Ⅰ）我们有1(1)(2)n n n T T r a n -=++≥． （Ⅱ）11T a =，对2n ≥反复使用上述关系式，得2121(1)(1)(1)n n n n n n T T r a T r a r a ---=++=++++=12121(1)(1)(1)n n n n a r a r a r a ---=+++++++，①在①式两端同乘1r +，得12121(1)(1)(1)(1)(1)n n n n n r T a r a r a r a r --+=++++++++②②-①，得121(1)[(1)(1)(1)]n n n n n rT a r d r r r a --=++++++++-1[(1)1](1)n n n dr r a r a r=+--++-． 即1122(1)nn a r d a r d d T r n r r r ++=+--．如果记12(1)nn a r d A r r +=+，12n a r d d B n r r+=--，则n n n T A B =+． 其中{}n A 是以12(1)a r dr r ++为首项，以1(0)r r +>为公比的等比数列；{}n B 是以12a r d d r r +--为首项，dr-为公差的等差数列．【点评】 本小题主要考查等差数列、等比数列的基本概念和基本方法，考查学生阅读资料、提取信息、建立数学模型的能力、考查应用所学知识分析和解决实际问题的能力．从以上分析可看出，数列的综合题难度都很大，甚至很多都是试卷的压轴题，它不仅考查函数与方程、转化与化归、分类讨论等重要思想，还涉及了配方法、换元法、待定系数法、放缩法等基本数学方法.其中的高考热点——探索性问题也出现在近年高考的数列解答题中.。

数列高考试题探源及复习建议南昌一中 喻瑞明数列题在高考试卷中出现非常有规律：两个选填题或一个大题．重视基础知识和基本技能的考查，重视数学思想方法考查．我们现在一起探索高考数列题的命题规律，及对今后数列命题、复习的一些思考．1、近几年全国高考数列试题统计统计了全国I 卷近五年、全国II 卷近五年、全国III 卷近三年文理共26份试卷．以大题形式考查，全部是在第17题，14年II 卷题考查了先放缩再求和，从而证明不等式，有一定难度，其它题均是基本题型，比较容易；以小题形式考查，有1题次出现在第12题（2017理科1卷，考查分组数列求和），2题次出现在16题（递推公式求通项，），其它题都是偏容易题型，以数列基本量的换算题型出现次数最多．重视转化与化归思想，无论是递推公式求通项，还是数列求和，都注重将一般数列转化为等差、等比数列解决；重视函数与方程思想，考查数列的函数特性，利用函数图像、性质等求数列的最大（小）项，数列基本量的换算体现的是设未知数、列方程、解方程的基本思想．2、数列基本量的换算等差、等比数列的基本量有首项、公差（比），项数、项、和，这些量之间的相互换算，是高考题中常见题型．例1（2017年I 卷理科第4题）记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A ．1B ．2C ．4D ．8【答案】C题目来源：课本例题和习题思想方法：设未知数、列方程、解方程的方程思想这类题大多数学生能比较快的做好，对这类题，我们还有哪些方面可以帮助同学，或者说高考这类题型还可以从哪些方面变化呢？2.1灵活应用等差、等比数列的性质要求同学特别熟悉等差、等比数列性质，特别注意关注数列项与和的下标联系，简化条件，尽量列出易解方程． 【例1】另解由6S 联想到17a a +，从而得到3416a a +=，两式相减得到28d =．2.2 熟悉设未知数的方法一般设1,()a d q ，也可以设为,()k a d q ，如果等差数列已知和未知都只与n S 有关，设2n S An Bn =+更好算，同样，如果等比数列已知和未知都只与n S 有关，可以设(1)(1)n n S a q q =-≠．【例1变式1】（2015年II 卷文科第9题）已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（ ）A.2B.1 1C.2 1D.8【答案】C该题如果设公比q ，解方程，运算稍微麻烦，结合性质，把4a 看成未知数，先求4a ，再求q ，运算量小．2.3 重视解方程消元技巧等比数列基本量换算题，经常会出现高次方程，需要同学有整体思想，经常将两个方程相减、相加、相除，从而实现消元．【例1变式2】（2017江苏，9）等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知3676344S S ==,,则8a = ．分析：当1q =时，显然不符合题意；当1q ≠时，设(1)n n S a q =-，则 367(1),463(1)4a q a q ⎧-=⎪⎪⎨⎪-=⎪⎩，两式相除解得142a q ⎧=-⎪⎨⎪=⎩，所以1(21)4n n S =-，因此8758871(22)2324a S S =-=-==． 答案：32．2.4 数列性质与函数性质结合【结论1】若奇函数()y f x =是R 上的单调函数，数列{}n a 是等差数列， 则12120()()()0n n a a a f a f a f a +++=⇔+++=．【结论2】若函数()y f x =在R 上单调，且图像关于点(,)a b 对称，数列{}n a 是等差数列， 则：123123()()()()n n a a a a na f a f a f a f a nb ++++=⇔++++=．【例1变式3】已知函数3()sin f x x x x =+-的定义域为R ，数列{}n a 是等差数列，若10100a =，则1232019()()()()f a f a f a f a ++++A ．恒为正B ．恒为负C ．等于0D ．可正可负简解： 33()()()sin()(sin )()f x x x x x x x f x -=-+---=-+-=-，函数()f x 是奇函数，又2()31cos 110f x x x '=+-≥-=，所以函数()f x 是R 上的单调递增函数，10100a =，得120191232019201902a a a a a a +++++=⨯=， 根据结论1，1232019()()()()0f a f a f a f a ++++=，选C ．【方法总结】（1）研究函数与数列综合问题，不好入手，可以先看函数的性质、图像等．（2）利用上述结论解题，对函数有两个要求：①是定义域内的单调函数；②图像关于点成中心对称．2.5 与解不定方程结合数列与不定方程结合题，通常以存在性问题出现，一般问是否存在三项满足条件．难点在解不定方程，通常有：由不等式求范围找整数解，由整除条件找约数，由奇偶性否定，由有理数、无理数否定等方法．【例1变式4】（武汉市2015届五月模考题理科18题）若{}n a 是各项均不为零的等差数列，公差为d，n S 为其前n 项和，且满足221n n a S -=，若数列{}n b 满足11n n n b a a +=，n T 为数列{}n b 满足11n n n b a a +=，n T 为数列{}n b 的前n 项和．（1）求n a 和n T ；（2）是否存在正整数,(1)m n m n <<，使得1,,m n T T T 成等比数列？若存在，求出所有,m n 的值；若不存在，说明理由．（1）21,21n n na n T n =-=+ （2）21(),21321m nm n =⋅++2232410m m n m -++⇒=>11m ⇒<<+ 2,3m n ==3、递推公式上述26份试卷中，递推公式题出现次数多，但主要以等差、等比数列的证明、判定为主，有两题是只要求前几项，只有两题是直接由递推公式求通项的，但这两题仍然是通过转化成等差、等比数列求通项，没有考查过累加、累乘等方法．3.1 由递推公式求前几项【例2】（2014年II 卷文科第16题） 数列}{n a 满足2,1181=-=+a a a nn ，则=1a ________． 题目来源：课本例题和习题思想方法：特殊与一般思想，字母n 的意义 【答案】12． 参考题：（北京高考题）已知12,0,2()11,12x x f x x x ⎧<<⎪⎪=⎨⎪-≤<⎪⎩，若数列{}n a 满足111,()7n n a a f a +==，则20a 等于______.重视周期数列，善于归纳推理。

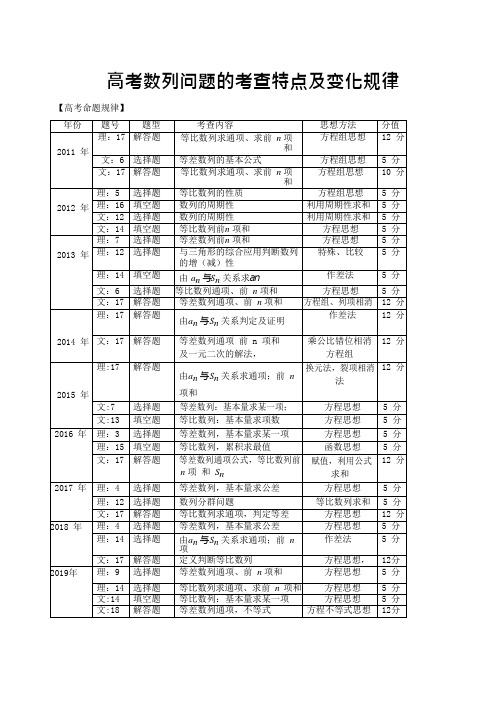
高考数列问题的考查特点及变化规律【高考命题规律】全国卷中的数列与三角基本上是交替考查，难度不大，题目多为常规题．从2011 年至2019 年，全国Ⅰ卷理科试题共考查了16 道数列题，文科试题共考查了 13 道数列题，都是标准的等差或等比数列，主要考查等差或等比数列的定义、性质、通项、前n 项和、某一项的值或某几项的和以及证明等差或等比数列等基础知识。

纵观全国Ⅰ卷的数列试题，我们可以发现，全国Ⅰ卷的数列题注重基础，强调双基，讲究解题的通性通法，从全国卷高考试题来看，本专题的热点题型有：一是等差、等比数列的基本运算；二是等差、等比数列的判定与证明；三是数列的求和问题(以裂项求和为主)，难度中等．但我们也注意到，2013 年，2017 年的12 题是数列题，2019 年的22 题概率题与数列结合，并且是累和求通项，也应引起我们注意。

下面我们看一下的热点题型。

高频热点一等差等比数列的基本运算问题【例1】(2017·全国卷Ⅱ)已知等差数列{a n}的前n 项和为S n，等比数列{b n}的前n 项和为T n，a1＝－1，b1＝1，a2＋b2＝2.(1)若a3＋b3＝5，求{b n}通项公式；(2)若T3＝21，求S3.【思维启迪】等差、等比数列的基本运算主要涉及两个数列的通项与求和公式，求解的关键是充分借助方程思想，代入数列的通项或和求公式，求公差d(或公比q)及首项a1，进而写出通项或和．【解析】[解] 设{a n}的公差为d，{b n}的公比为q，则a n＝－1＋(n－1)·d，b n＝q n－1.由a2＋b2＝2 得d＋q＝3.①(1)由a3＋b3＝5 得2d＋q2＝6.②联立①和②解得Error!(舍去)，Error!因此{b n}的通项公式为b n＝2n－1.(2)由b1＝1，T3＝21 得q2＋q－20＝0.解得q＝－5 或q＝4.当q＝－5 时，由①得d＝8，则S3＝21.当q＝4 时，由①得d＝－1，则S3＝－6.【思维升华】在求解数列基本量问题中主要使用的是方程思想，要注意公式使用时的准确性与合理性，更要注意运算的准确性．在遇到一些较复杂的方程组时，要注意运用整体代换思想，使运算更加便捷．【通性通法】解决等差、等比数列的综合问题，关键是理清两种数列的项之间的关系，并注重方程思想的应用，等差(比)数列共涉及五个量 a 1，a n ，S n ，d (q )，n ，“知三求二”．高频热点二 等比等差数列的定义判断与证明【例 2】 (2014·全国卷Ⅰ)已知数列{a n }的前 n 项和为 S n ，a 1＝1，a n ≠0，a n a n ＋1＝λS n －1，其中 λ 为常数．(1)证明：a n ＋2－a n ＝λ；(2) 是否存在 λ，使得{a n }为等差数列？并说明理由．【思维启迪】等差(比)数列的判定与证明是高考中的常见题型之一，其基本方法是利用等差(比)数a n ＋1列定义，即证明 a n ＋1－a n ＝常数( a n＝常数).难度不大．【解析】[解] (1)证明：由题设知a n a n ＋1＝λS n －1， a n ＋1a n ＋2＝λS n ＋1－1，两式相减得 a n ＋1(a n ＋2－a n )＝λa n ＋1， 由于 a n ＋1≠0，所以 a n ＋2－a n ＝λ.{a 2n }是首项为 3，公差为 4 的等差数列，a 2n ＝4n －1. 所以 a n ＝2n －1，a n ＋1－a n ＝2，因此存在 λ＝4，使得数列{a n }为等差数列．【思维升华】该类问题常以递推关系为载体，求解的关键是依据题目信息重新构造递推关系，并结合等差(比)数列的定义给予相应的证明．高频热点三 数列的通项求和问题数列的通项与求和是高考的必考题型，求通项属于基本问题，常涉及等差、等比数列的定义、性质、基本量的运算；求和问题关键在于分析通项的结构特征，选择适当的求和方法．常考的求和方法有： 公式法、错位相减法、裂项相消法、分组求和法等【例 3】（ 2015 年全国一 17） S 为数列{ a }的前 n 项和.已知 a ＞ 0， a2+ a=nn4S n + 3 .nnn（Ⅰ）求{ a n }的通项公式；（Ⅱ）设 n=1 a n a n +1,求数列{ b n }的 n 前项和.【思维启迪】（Ⅰ）用数列第 n 项与前 n 项和的关系求出数列{ a n }的递推公式，判断数列{ a n }是等b差数列，利用等差数列的通项公式即可写出数列{ a}的通项公式；（Ⅱ）nn 项和.根据（Ⅰ）数列{ b n }的通项公式，再用裂项消去法求其前【例4】(2016·全国卷Ⅱ)S n为等差数列{a n}的前n 项和，且a1＝1，S7＝28①.记b n＝[lg a n]②，其中[x]表示不超过x 的最大整数，如[0.9]＝0，[lg 99]＝1.(1)求b1，b11，b101；(2)求数列{b n}的前1 000项和③.【思维启迪】①等差数列的求和公式；②等差数列的通项公式及对数的运算性质；③数列的常见求和方法．【解析】[解](1)设{a n}的公差为d，S7＝7a4＝28，a4－a1所以a4＝4，·所以d＝＝1，3所以a n＝a1＋(n－1)d＝n. · 所以b1＝[lg a1]＝[lg 1]＝0，b11＝[lg a11]＝[lg 11]＝1，b101＝[lg a101]＝[lg 101]＝2.(2)记{b n}的前n 项和为T n，则T1000＝b1＋b2＋…＋b1000＝[lg a1]＋[lg a2]＋…＋[lg a1000]，当0≤lg a n＜1 时，n＝1,2，…，9；· 当1≤lg an＜2 时，n＝10，…，99；当2≤lg an＜3 时n＝100,…，999当lg an＝3 时，n＝1 000，所以T1 000＝0×9＋1×90＋2×900＋3×1＝1 893. ·【例5】在等差数列{a n}中，a10＝30，a20＝50.(1)求数列{an}的通项公式；(2)令bn＝2a n 10 ，证明：数列{bn}为等比数列；(3)求数列{nbn}的前n 项和Tn【思维升华】这几年全国一卷一直没有考成公比错位相减法，但今年考了累和求通项。

【高中数学】高考数学冲刺指导：数列问题
摘要：为大家带来高考数学冲刺指导，希望大家喜欢下文!
近几年来，
高考
关于数列方面的命题主要有以下三个方面;(1)数列本身的有关知识，其中有等差数列
与等比数列的概念、性质、通项公式及求和公式。

(2)数列与其它知识的结合，其中有数
列与函数、方程、不等式、三角、几何的结合。

(3)数列的应用问题，其中主要是以增长
率问题为主。

试题的难度有三个层次，小题大都以基础题为主，解答题大都以基础题和中
档题为主，只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题难度较大。

知识整合
1.在掌握等差数列、等比数列的定义、性质、通项公式、前n项和公式的基础上，系
统掌握解等差数列与等比数列综合题的规律，深化数学思想方法在解题实践中的指导作用，灵活地运用数列知识和方法解决数学和实际生活中的有关问题;
2.在解决综合题和探索性问题实践中加深对基础知识、基本技能和基本数学思想方法
的认识，沟通各类知识的联系，形成更完整的知识网络，提高分析问题和解决问题的能力，
进一步培养学生阅读理解和创新能力，综合运用数学思想方法分析问题与解决问题的
能力。

3.培养学生善于分析题意，富于联想，以适应新的背景，新的设问方式，提高学生用
函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的
思维方法.
总结：高考数学冲刺指导就介绍到这里了，希望能帮助同学们更好的复习本门课程，
更多精彩学习内容请继续关注!
感谢您的阅读，祝您生活愉快。

高考数学十大知识版块命题趋势及解题攻略（4）：数列与探索性新题型的解题技巧【命题趋向】从2007年高考题可见数列题命题有如下趋势：1.等差〔比〕数列的差不多知识是必考内容，这类咨询题既有选择题、填空题，也有解答题；难度易、中、难三类皆有.2.数列中a n与S n之间的互化关系也是高考的一个热点.3.函数思想、方程思想、分类讨论思想等数学思想方法在解决咨询题中常常用到，解答试题时要注意灵活应用.4.解答题的难度有逐年增大的趋势,还有一些新颖题型,如与导数和极限相结合等.因此复习中应注意：1.数列是一种专门的函数，学习时要善于利用函数的思想来解决.如通项公式、前n项和公式等.2.运用方程的思想解等差〔比〕数列，是常见题型，解决此类咨询题需要抓住差不多量a1、d〔或q〕，把握好设未知数、列出方程、解方程三个环节，常通过〝设而不求，整体代入〞来简化运算.3.分类讨论的思想在本章尤为突出.学习时考虑咨询题要全面，如等比数列求和要注意q=1和q≠1两种情形等等.4.等价转化是数学复习中常常运用的，数列也不例外.如a n与S n的转化；将一些数列转化成等差〔比〕数列来解决等.复习时，要及时总结归纳.5.深刻明白得等差〔比〕数列的定义，能正确使用定义和等差〔比〕数列的性质是学好本章的关键.6.解题要善于总结差不多数学方法.如观看法、类比法、错位相减法、待定系数法、归纳法、数形结合法，养成良好的学习适应，定能达到事半功倍的成效.7．数列应用题将是命题的热点，这类题关键在于建模及数列的一些相关知识的应用. 【考点透视】1．明白得数列的概念，了解数列通项公式的意义，了解递推公式是给出数列的一种方法，并能依照递推公式写出数列的前几项.2．明白得等差数列的概念，把握等差数列的通项公式与前n 项和公式，并能运用公式解答简单的咨询题.3．明白得等比数列的概念，把握等比数列的通项公式与前n 项和公式，并能运用公式解决简单的咨询题.4．数列是高中数学的重要内容，又是学习高等数学的基础，因此在高考中占有重要的地位.高考对本章的考查比较全面，等差数列，等比数列的考查每年都可不能遗漏.解答题多为中等以上难度的试题，突出考查考生的思维能力，解决咨询题的能力，试题大多有较好的区分度.有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起。