y 1
2 zy
1 2
xz
1 2
yz
z
且 (ij ) 为一二阶对称张量。
(3-2)
5
应用弹塑性力学
APPLIED ELASTO-PLASTICITY OF SOLIDS
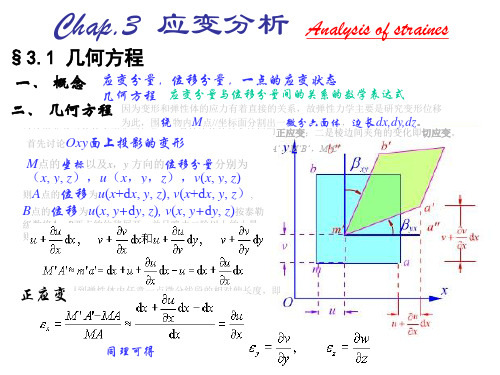
3-3、应变分量与位移分量之间的微分关系—几何方程:
应变是与位移有关的。物体中各质点相对位置的改变,则产生 变形。因此要分析物体的变形,就要研究各点的位置的变化。
v
xy
yx
v x
u y
x (3-5)
v(x, y) b
d
dy
yo
p
x
a
dx
p yx
a
v v(x dx, y)
u
dx u u
z u(x, y)
dx u
11
应用弹塑性力学
APPLIED ELASTO-PLASTICITY OF SOLIDS
x
y
z
v' v( x, y, z) v dx v dy v dz
x
y
z
w' w( x, y, z) w dx w dy w dz
x
y
z
14
应用弹塑性力学
APPLIED ELASTO-PLASTICITY OF SOLIDS
为了表示成应变分量的关系,对 u, v, w 作如下改写:
x
v v(x, y, z) v' v(x dx, y dy, z dz)
位移分量是坐标的函数 w w(x, y, z) w' w(x dx, y dy, z dz)