初中高中三角函数公式大全

初中三角函数公式有哪些
初中三角函数公式有三角函数半角公式，锐角三角函数公式，三角函数关系公式，三角函数两角和差公式等，下面是三角函数公式总结，供大家参考。

三角函数半角公式
1.正弦
sin(A/2)=√((1-cosA)/2)
sin(A/2)=-√((1-cosA)/2)
2.余弦
cos(A/2)=√((1+cosA)/2)
cos(A/2)=-√((1+cosA)/2)
3.正切
tan(A/2)=√((1-cosA)/((1+cosA))
tan(A/2)=-√((1-cosA)/((1+cosA))
锐角三角函数公式
sinα=∠α的对边/斜边
cosα=∠α的邻边/斜边
tanα=∠α的对边/∠α的邻边
cotα=∠α的邻边/∠α的对边
三角函数关系公式
1.倒数关系
tanαcotα=1
sinαcscα=1
cosαsecα=1
2.商数关系
tanα=sinα/cosα
cotα=cosα/sinα
3.平方关系
sin2α+cos2=1
1+tan2α=sec2α
1+cot2α=csc2α
三角函数两角和差公式
1.三角函数和角公式
sin(A+B)=sinAcosB+cosAsinB
cos(A+B)=cosAcosB-sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB)
2.三角函数差角公式
sin(A-B)=sinAcosB-cossinB
cos(A-B)=cosAcosB+sinAsinB
tan(A-B)=(tanA-tanB)/(1+tanAtanB)。

(完整版)三角函数公式表1. 正弦函数 (sin):定义：正弦函数是直角三角形中对边与斜边的比值。

公式：sin(θ) = 对边 / 斜边范围：1 ≤ sin(θ) ≤ 1特殊值：sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义：余弦函数是直角三角形中邻边与斜边的比值。

公式：cos(θ) = 邻边 / 斜边范围：1 ≤ cos(θ) ≤ 1特殊值：cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义：正切函数是直角三角形中对边与邻边的比值。

公式：tan(θ) = 对边 / 邻边范围：tan(θ) 可以取任意实数值特殊值：tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在（无穷大）4. 余切函数 (cot):定义：余切函数是直角三角形中邻边与对边的比值。

公式：cot(θ) = 邻边 / 对边范围：cot(θ) 可以取任意实数值特殊值：cot(0°) 不存在（无穷大）, cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义：正割函数是直角三角形中斜边与邻边的比值。

公式：sec(θ)= 1 / cos(θ)范围：sec(θ) 可以取任意实数值特殊值：sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在（无穷大）6. 余割函数 (csc):定义：余割函数是直角三角形中斜边与对边的比值。

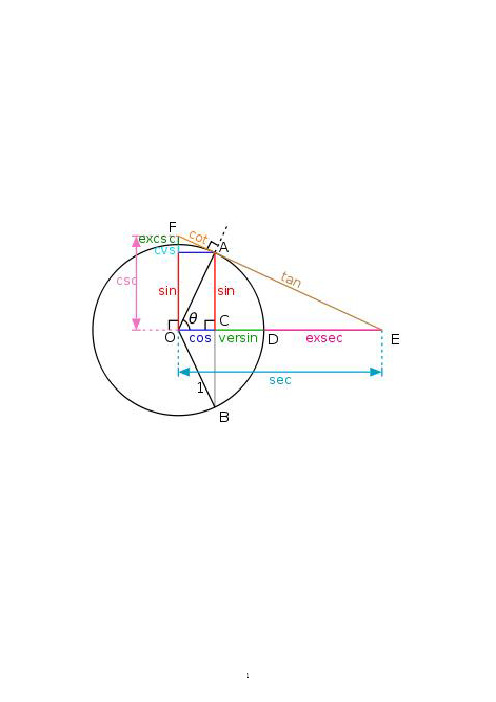
(完整版)初中三角函数公式表一、基本公式1. 正弦定理：在任意三角形ABC中，a/sinA = b/sinB = c/sinC，其中a、b、c分别为三角形ABC的边长，A、B、C分别为对应的角。

2. 余弦定理：在任意三角形ABC中，a² = b² + c² 2bccosA，b² = a² + c² 2accosB，c² = a² + b² 2abcosC。

3. 正切定理：在任意三角形ABC中，tanA = sinA/cosA，tanB = sinB/cosB，tanC = sinC/cosC。

4. 余切定理：在任意三角形ABC中，cotA = cosA/sinA，cotB = cosB/sinB，cotC = cosC/sinC。

5. 正割定理：在任意三角形ABC中，secA = 1/cosA，secB =1/cosB，secC = 1/cosC。

6. 余割定理：在任意三角形ABC中，cscA = 1/sinA，cscB =1/sinB，cscC = 1/sinC。

二、特殊角公式1. 30°、45°、60°的正弦、余弦、正切、余切、正割、余割值：sin30° = 1/2，cos30° = √3/2，tan30° = 1/√3，cot30° = √3，sec30° = 2/√3，csc30° = 2sin45° = cos45° = 1/√2，tan45° = 1，cot45° = 1，sec45° = √2，csc45° = √2sin60° = √3/2，cos60° = 1/2，tan60° = √3，cot60° = 1/√3，sec60° = 2，csc60° = 2/√32. 90°的正弦、余弦、正切、余切、正割、余割值：sin90° = 1，cos90° = 0，tan90° = 无穷大，cot90° = 0，sec90° = 无穷大，csc90° = 1三、三角函数的和差公式1. 正弦和差公式：sin(A±B) = sinAcosB ± cosAsinB2. 余弦和差公式：cos(A±B) = cosAcosB ∓ sinAsinB3. 正切和差公式：tan(A±B) = (tanA ± tanB) / (1 ∓tanAtanB)四、三角函数的倍角公式1. 正弦倍角公式：sin2A = 2sinAcosA2. 余弦倍角公式：cos2A = cos²A sin²A = 2cos²A 1 = 12sin²A3. 正切倍角公式：tan2A = 2tanA / (1 tan²A)五、三角函数的半角公式1. 正弦半角公式：sin(A/2) = ±√[(1 cosA)/2]2. 余弦半角公式：cos(A/2) = ±√[(1 + cosA)/2]3. 正切半角公式：tan(A/2) = ±√[(1 cosA)/(1 + cosA)] = ±(sinA)/(1 + cosA) = ±(1 cosA)/(sinA)六、三角函数的积化和差公式1. 正弦积化和差公式：sinAsinB = 1/2[cos(A B) cos(A + B)]2. 余弦积化和差公式：cosAcosB = 1/2[cos(A B) + cos(A +B)]3. 正切积化和差公式：tanAtanB = (sinAsinB) / (cosAcosB) = 1/2[sin(A + B) sin(A B)] / [cos(A + B) + cos(A B)]七、三角函数的和差化积公式1. 正弦和差化积公式：sinA + sinB = 2sin((A + B)/2)cos((AB)/2)，sinA sinB = 2cos((A + B)/2)sin((A B)/2)2. 余弦和差化积公式：cosA + cosB = 2cos((A + B)/2)cos((AB)/2)，cosA cosB = 2sin((A + B)/2)sin((A B)/2)3. 正切和差化积公式：tanA + tanB = (sin(A + B)) / (cosAcosB)，tanA tanB = (sin(A B)) / (cosAcosB)八、三角函数的倒角公式1. 正弦倒角公式：sin(π/2 A) = cosA，sin(π/2 + A) = cosA2. 余弦倒角公式：cos(π/2 A) = sinA，cos(π/2 + A) =sinA3. 正切倒角公式：tan(π/2 A) = cotA，tan(π/2 + A) =cotA九、三角函数的周期公式1. 正弦周期公式：sin(π + A) = sinA，sin(2π + A) = sinA2. 余弦周期公式：cos(π + A) = cosA，cos(2π + A) = cosA3. 正切周期公式：tan(π + A) = tanA，tan(2π + A) = tanA十、三角函数的辅助角公式1. 正弦辅助角公式：sin(A + B) = sinAcosB + cosAsinB，sin(A B) = sinAcosB cosAsinB2. 余弦辅助角公式：cos(A + B) = cosAcosB sinAsinB，cos(AB) = cosAcosB + sinAsinB3. 正切辅助角公式：tan(A + B) = (tanA + tanB) / (1 tanAtanB)，tan(A B) = (tanA tanB) / (1 + tanAtanB)十一、三角函数的恒等式1. 正弦平方加余弦平方等于1：sin²A + cos²A = 12. 正切平方加1等于正割平方：tan²A + 1 = sec²A3. 余切平方加1等于余割平方：cot²A + 1 = csc²A4. 正弦与余弦的乘积等于正弦与余弦的乘积：sinAcosA =1/2sin2A5. 正切与余切的乘积等于1：tanAcotA = 1十二、三角函数的积分公式1. 正弦积分公式：∫sinAdA = cosA + C2. 余弦积分公式：∫cosAdA = sinA + C3. 正切积分公式：∫tanAdA = ln|cosA| + C4. 余切积分公式：∫cotAdA = ln|sinA| + C5. 正割积分公式：∫secAdA = ln|secA + tanA| + C6. 余割积分公式：∫cscAdA = ln|cscA + cotA| + C(完整版)初中三角函数公式表一、基本公式1. 正弦定理：在任意三角形ABC中，a/sinA = b/sinB = c/sinC，其中a、b、c分别为三角形ABC的边长，A、B、C分别为对应的角。

数学三角函数公式大全一、基本关系式1. 正弦函数（sin）：正弦函数是一个周期为2π的周期函数，其基本关系式为：sin(x) = y2. 余弦函数（cos）：余弦函数是一个周期为2π的周期函数，其基本关系式为：cos(x) = y3. 正切函数（tan）：正切函数是一个周期为π的周期函数，其基本关系式为：tan(x) = y二、三角函数的性质1.基本性质：-正弦函数和余弦函数的值域在[-1,1]之间。

-正切函数的值域是实数集。

2.周期性质：-正弦函数和余弦函数的周期都是2π。

-正切函数的周期是π。

3.奇偶性质：- 正弦函数是奇函数，即sin(-x) = -sin(x)。

- 余弦函数是偶函数，即cos(-x) = cos(x)。

- 正切函数是奇函数，即tan(-x) = -tan(x)。

4.互余性质：- 正弦函数和余弦函数是互余的，即sin(x) = cos(π/2 - x)。

- 正切函数是其副函数的倒数，即tan(x) = 1/cot(x)。

三、三角函数的特殊值1.正弦函数和余弦函数的特殊值如下：- sin(0) = 0- sin(π/6) = 1/2- sin(π/4) = √2/2- sin(π/3) = √3/2- sin(π/2) = 1- cos(0) = 1- cos(π/6) = √3/2- cos(π/4) = √2/2- cos(π/3) = 1/2- cos(π/2) = 02.正切函数的特殊值如下：- tan(0) = 0- tan(π/6) = 1/√3- tan(π/4) = 1- tan(π/3) = √3- tan(π/2) = 无穷四、三角函数的基本运算1.四象限关系：-在第一象限，所有三角函数的值都是正的。

-在第二象限，只有正弦函数的值是正的。

-在第三象限，只有正切函数的值是正的。

-在第四象限，只有余弦函数的值是正的。

2.和差公式：- sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)- cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)- tan(x ± y) = (tan(x) ± tan(y))/(1 ∓ tan(x)tan(y)) 3.积化和差公式：- sin(x)sin(y) = (1/2)(cos(x-y) - cos(x+y))- cos(x)cos(y) = (1/2)(cos(x-y) + cos(x+y))- sin(x)cos(y) = (1/2)(sin(x-y) + sin(x+y))- sin(x)cos(y) = (1/2)(sin(x-y) - sin(x+y))五、倒数关系1.倒数关系：- csc(x) = 1/sin(x)- sec(x) = 1/cos(x),- cot(x) = 1/tan(x)六、复数表示1.复数形式：- sin(x) = (e^(ix) - e^(-ix))/(2i)- cos(x) = (e^(ix) + e^(-ix))/2- tan(x) = (e^(ix) - e^(-ix))/(e^(ix) + e^(-ix))。

第一部分三角函数公式·两角和差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sin α)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)csc(2α)=1/2*secα·cscαsec(2α)=sec^2α/(1-tan^2α)·三倍角公式：sin(3α) = 3sinα-4sin^3α= 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα= 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式：sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式：Asinα+Bcosα=√(A^2+B^2)sin(α+φ）（tanφ=B/A）Asinα+Bcosα=√(A^2+B^2)cos(α-φ）（tanφ=A/B）·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cos α·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sin α·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tan γ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sin α)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式：sin(3α) = 3sinα-4sin^3α= 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα= 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式：sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式：Asinα+Bcosα=√(A^2+B^2)sin(α+φ）（tanφ=B/A）Asinα+Bcosα=√(A^2+B^2)cos(α-φ）（tanφ=A/B）·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cos α·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sin α·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tan γ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^2 貌似就这么多了。

三角函数常用公式表格三角函数是数学中非常重要的一个部分，它在几何、物理、工程等多个领域都有广泛的应用。

为了更好地理解和运用三角函数，我们需要熟悉一些常用的公式。

以下是为大家整理的三角函数常用公式表格：一、基本关系1、平方关系sin²α ＋cos²α ＝ 11 ＋tan²α ＝sec²α1 ＋cot²α ＝csc²α2、商数关系tanα ＝sinα ／cosαcotα ＝cosα ／sinα3、倒数关系sinα · cscα ＝ 1cosα · secα ＝ 1tanα · cotα ＝ 1二、诱导公式1、终边相同的角的三角函数值相等sin(2kπ ＋α) ＝sinαcos(2kπ ＋α) ＝cosαtan(2kπ ＋α) ＝tanα2、关于 x 轴对称的角的三角函数值sin(α) ＝sinαcos(α) ＝cosαtan(α) ＝tanα3、关于 y 轴对称的角的三角函数值sin(π α) ＝sinαcos(π α) ＝cosαtan(π α) ＝tanα4、关于原点对称的角的三角函数值sin(π ＋α) ＝sinαcos(π ＋α) ＝cosαtan(π ＋α) ＝tanα5、函数名改变的诱导公式sin(π/2 α) ＝cosαcos(π/2 α) ＝sinαsin(π/2 ＋α) ＝cosαcos(π/2 ＋α) ＝sinα三、两角和与差的三角函数公式1、两角和的正弦公式sin(α ＋β) ＝sinαcosβ ＋cosαsinβ2、两角差的正弦公式sin(α β) ＝sinαcosβ cosαsinβ3、两角和的余弦公式cos(α ＋β) ＝cosαcosβ sinαsinβ4、两角差的余弦公式cos(α β) ＝cosαcosβ ＋sinαsinβ5、两角和的正切公式tan(α ＋β) ＝（tanα ＋tanβ) ／（1 tanαtanβ) 6、两角差的正切公式tan(α β) ＝（tanα tanβ) ／（1 ＋tanαtanβ)四、二倍角公式1、二倍角的正弦公式sin2α ＝2sinαcosα2、二倍角的余弦公式cos2α ＝cos²α sin²α ＝2cos²α 1 ＝1 2sin²α3、二倍角的正切公式tan2α ＝2tanα ／（1 tan²α)五、半角公式1、半角的正弦公式sin(α/2) ＝±√（1 cosα) ／ 22、半角的余弦公式cos(α/2) ＝±√（1 ＋cosα) ／ 23、半角的正切公式tan(α/2) ＝±√（1 cosα) ／（1 ＋cosα) ＝sinα ／（1 ＋cosα) ＝（1 cosα) ／sinα六、万能公式1、万能公式的正弦sinα ＝2tan(α/2) ／ 1 ＋tan²(α/2)2、万能公式的余弦cosα ＝1 tan²(α/2) ／ 1 ＋tan²(α/2)3、万能公式的正切tanα ＝2tan(α/2) ／1 tan²(α/2)七、积化和差公式1、sinαcosβ ＝（1/2)sin(α ＋β) ＋sin(α β)2、cosαsinβ ＝（1/2)sin(α ＋β) sin(α β)3、cosαcosβ ＝（1/2)cos(α ＋β) ＋cos(α β)4、sinαsinβ ＝（1/2)cos(α ＋β) cos(α β)八、和差化积公式1、sinα ＋sinβ ＝2sin(α ＋β) ／2cos(α β) ／ 22、sinα sinβ ＝2cos(α ＋β) ／2sin(α β) ／ 23、cosα ＋cosβ ＝2cos(α ＋β) ／2cos(α β) ／ 24、cosα cosβ ＝2sin(α ＋β) ／2sin(α β) ／ 2这些三角函数公式在解决各种数学问题和实际应用中都非常重要。

初高中三角函数公式大全三角函数公式倍角公式tan2A = 2 1 tan 2ASin2A=2SinA?CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA) 33cos3A = 4(cosA)3-3cosAtan3a = tana ·tan( 3 +a)·tan( 3 -a) 两角和公式 sin(A+B) = sin(A-B)=cos(A+B) sinAcosB+cosAsinBsinAcosB-cosAsinB = cosAcosB-sinAsinB cosAcosB+sinAsinBtan(A+B) = tanA tanB1- tanAtanBtan(A-B) = tanA tanB1 tanAtanBcot(A+B) cotAcotB -1 cotB cotAcot(A-B)=cotAcotB 1 cotB cotA半角公式cot( A )= 1 cosA2 1 cosAA 1 cosA sinA tan( )= = 2 sin A 1 cosAcos( 2A )= 1 cosA2 tan( 2A )= 1 cosA1 cosA和差化积a b a b sina+sinb=2sin cos 22a b a b sina-sinb=2cos sin 22 a b a b cosa+cosb = 2cos cos 22 a b a b cosa-cosb = -2sin sin 22 sin(a b) tana+tanb=cosa cosb积化和差sinasinb = 1- [cos(a+b)-cos(a-b)]cosacosb1= [cos(a+b)+cos(a-b)]sinacosb = 1[sin(a+b)+sin(a-b)]cosasinb = 1[sin(a+b)-sin(a-b)]诱导公式sin(-a) = - sina cos(-a) = cosasin( -a) = cosa cos( -a)2= sinasin( +a)2= cosa cos( +a) = -sinasin( -πa) = sinacos( π-a) = -cosasin( π +a)- s=i na cos( π +a) -=c osa sina tgA=tanA cosa万能公式sina= a 2 1 (tan ) 2 2a 21 (tan 2a )2 cosa= 21 (tan a ) 22 a 2tan2 tana= a 2 1 (tan )2 2其它公式b a?sina+b?cosa= (a 2b 2 ) ×sin(a+c) [其中 tanc= ] a2 2 a a?sin(a-)b?cos(a) = (a 2 b 2) ×cos(a-c) [其中 tan(c)= ] b a a 2 1+sin(a) =(sin +cos )2 a a 2 1-sin(a) = (sin -cos )2其他非重点三角函数双曲函数a -a sinh(a)= e - e2a -acosh(a)=e 2e tg h(a)=c s o in s h h ((a a ))三角函数公式证明（全部）公式表达式乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式 |a+b| ≤|a|+|b-|b ||a ≤|a|+|b| |a| -≤b ≤b<a=≤>b|a-b| ≥ |-a|b|| -|a| ≤ a ≤ |a|csc(a) = 1 sina sec(a) = cosa2tan a 2一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根ctg(A/2)= √((1+cosA)/(-(c1osA)) ctg(A/2)=- √ ((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n 项和1+2+3+4+5+6+7+8+9⋯+ +n=n(n+1)/21+3+5+7+9+11+13+15+⋯+(2n-1)=n22+4+6+8+10+12+14+⋯+(2n)=n(n+1)12+22+32+42+52+62+72+82+⋯+n2=n(n+1)(2n+1)/613+23+33+43+53+63+⋯n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+ ⋯+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注：角B 是边a 和边c 的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：( a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h' 圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2 圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l 弧长公式l=a*r a 是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h 斜棱柱体积V=S'L 注：其中,S'是直截面面积，L 是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-------------- 三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦：cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减，可以得到2组积化和差:相加：cosAcosB=[cos(A+B)+cos(A-B)]/2相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2 sin(A+B)=sinAcosB+sinBcosA sin(A-B)=sinAcosB-sinBcosA这两式相加或相减，可以得到2组积化和差: 相加：sinAcosB=[sin(A+B)+sin(A-B)]/2 相减：sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共 4 组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论：(不要求记忆)(1) anA+tanB+tanC=tanA ta·nB ·tanC(2) sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3) cosA+cosB+cosC=4sin(A/2) sin(·B/2) si·n(C/2)+1(4) sin2A+sin2B+sin2C=4sinA sin·B ·sinC(5) cos2A+cos2B+cos2C=-4cosAcosBcosC-1已知sin α=m sin( α+2β), |m求|＜证1, tan( α+β)=(1+m)-/(m1)tan β 解:sin α=m sin( α+2β)sin(a+ -β )=msin(a+ β +β )sin(a+ β )co-scoβs(a+ β)sin β =msin(a+ β)cos β +mcos(a+β )sin βsin(a+ β )cos-βm)(=1cos(a+ β)sin β (m+1)tan( α +β )=(1+m-)/m(1)tan β三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)= √(-(c1osA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)= √((1+cosA)/2) cos(A/2-)√= ((1+cosA)/2) tan(A/2)= √-(c(1osA)/((1+cosA)) tan(A/2)=- √((1-cosA)/((1+cosA))公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2k π＋α） cos （2k π＋α） tan （2k π＋α） cot （2k π＋α）= sin α= cos α= tan α= cot α公式二： 设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）= cos （π＋α）= -sin α-cosα tan （π＋α）= tan αcot （π＋α）= cot α 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sin α cos（- α）= cos α32tan （-α）= -tan α cot （-α）= -cot α 公式四： 利用公式二和公式三可以得到 π-α与α的三角函数值之间的关系： sin （ cos tan （ cot （ 公式五：利用公式 -和公式三可以得到 2π-α与α的三角函数值之间的关系： sin （2π-α）= -sin cos （2π-α） tan （2π-α） cot （2π-α） 公式六： ±α及32 π-α) π-α) π-α) π-α) = sin α = -cos α = -tan α = -cot α= cos = -tan = -cot α的三角函数值之间的关系： cot +α) = cos +α) = -sin +α) = -cot +α) = -tan-α)= cos-α) = sin -α) cot -α) tan ±α与 2 sin cos ( tan cotsin cos ( tan 2 2 2 2 2 2 2 sin cos ( tan cot2 3 +α)= -cos 2 3 +α)= sin 2 3 +α)= -cot 2 3 +α)= -tan 2 sin -α)= -cos α3 cos（-α）2tan（3 -α）2cot（3 -α）2 = -sin α= cot α= tan α(以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A?sin( ωt+θ)+ B?sin( ω t+A2φ )B =2 2 ABcos( )×t arcsin［（Asin Bsin ）sin2 2A2 B2 2ABcos（）。

初中常用三角函数公式这篇文章给大家分享初中常用三角函数公式以及同角三角函数的关系公式，接下来看一下具体内容。

常用三角函数公式三角函数半角公式sin(A/2)=±√((1-cosA)/2)cos(A/2)=±√((1+cosA)/2)tan(A/2)=±√((1-cosA)/((1+cosA))三角函数倍角公式Sin2A=2SinA*CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)三角函数两角和与差公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cossinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数积化和差sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数和差化积sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 三角函数的关系公式（一）倒数关系①tanαcotα=1②sinαcscα=1③cosαsecα=1(二）商数关系tanα=sinα/cosαcotα=cosα/sinα(三)平方关系①sin2α+cos2α=1②1+tan2α=se c2α③1+cot2α=csc2α。

初中三角函数公式初中三角函数公式有三角函数两角和差公式，三角函数半角公式，三角函数倍角公式，锐角三角函数公式等。

三角函数两角和差公式1.三角函数和角公式sin(A+B)=sinAcosB+cosAsinBcos(A+B)=cosAcosB-sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)2.三角函数差角公式sin(A-B)=sinAcosB-cossinBcos(A-B)=cosAcosB+sinAsinBtan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数半角公式1.正弦sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)2.余弦cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)3.正切tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))三角函数倍角公式1.三角函数倍角公式Sin2A=2SinA*CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)2.三角函数三倍角公式sin3A=4sinA*sin(π/3+A)sin(π/3-A)cos3A=4cosA*cos(π/3+A)cos(π/3-A)tan3A=tanA*tan(π/3+A)*tan(π/3-A)锐角三角函数公式si nα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边三角函数记忆口诀三角函数是函数，象限符号坐标注。

函数图像单位圆，周期奇偶增减现。

同角关系很重要，化简证明都需要。

正六边形顶点处，从上到下弦切割；中心记上数字一，连结顶点三角形。

向下三角平方和，倒数关系是对角，顶点任意一函数，等于后面两根除。