准双曲面锥齿轮传动计算

锥齿轮的轴向推力计算公式锥齿轮是一种常见的传动装置，其主要作用是将旋转运动转换为另一种旋转运动或者转动运动。

在实际应用中，锥齿轮的轴向推力是一个重要的参数，它直接影响着锥齿轮的使用寿命和传动效率。

因此，准确计算锥齿轮的轴向推力是非常重要的。

首先，我们需要了解一些基本的概念。

锥齿轮的轴向推力是指在齿轮轴向上产生的力，它的方向与齿轮轴线平行。

在实际应用中，轴向推力的大小和方向会影响齿轮的轴承和传动系统的设计。

因此，准确计算锥齿轮的轴向推力是非常重要的。

锥齿轮的轴向推力计算公式可以通过以下步骤来推导得到。

首先，我们需要知道锥齿轮的模数、齿数、齿轮的压力角、齿轮的齿宽等参数。

然后，我们可以通过以下公式来计算锥齿轮的轴向推力：Ft = 2T tan(α) / (d1 + d2)。

其中，Ft表示锥齿轮的轴向推力，T表示齿轮的传动力矩，α表示齿轮的压力角，d1和d2分别表示齿轮的基圆直径。

通过上述公式，我们可以看到锥齿轮的轴向推力与齿轮的传动力矩、压力角以及基圆直径等参数有关。

在实际应用中，我们可以根据具体的齿轮参数来计算锥齿轮的轴向推力，并进一步分析其对齿轮传动系统的影响。

在实际应用中，锥齿轮的轴向推力计算是一个复杂的问题，需要考虑多种因素的影响。

除了上述公式外，还可以通过有限元分析等方法来计算锥齿轮的轴向推力。

在进行锥齿轮的设计和选型时，我们需要充分考虑锥齿轮的轴向推力，并选择合适的齿轮参数来满足实际应用的需求。

总之，锥齿轮的轴向推力是一个重要的参数，它直接影响着锥齿轮的使用寿命和传动效率。

通过合适的计算方法和分析手段，我们可以准确计算锥齿轮的轴向推力，并进一步优化齿轮传动系统的设计。

希望通过本文的介绍，读者能够对锥齿轮的轴向推力有更深入的了解，并在实际应用中加以应用。

19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
准双曲面齿轮设计计算
小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数 大轮齿面宽 偏置距 29.2 38.6 锥度系数 压力角和 0.788532 38 大轮节径 刀盘半径 190.5 95.25 大轮齿顶高系数 齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向 小轮 大轮 左旋 右旋 偏置双曲面齿轮计算结果 称 小轮 16
大轮 41 4.646
齿数 模数 压力角 小轮偏置 外锥距 齿顶高 齿根高 工作齿高 全齿高 节锥定点到交错点的距离 面锥顶点到交错点的距离 根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径

15.51547 -4.812
23.86825 -1.819
89.93 50.973
60.46
25.63205 62.3573
29.79222 64.44521
23.63867 58.02087
54.49766 30.86347
0
右旋
190.5
0.20--0.30
190.5
120.7404 193.0721
压力角
19
小轮偏置 外锥距
下38.6 107.52
齿顶高 齿根高 工作齿高
2.7719 6.668 8.5281
全齿高
9.440
节锥定点到交错点的距离
-3.543
面锥顶点到交错点的距离
根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径
准双曲面齿轮设计计算
输入齿轮基本参数
小轮齿数 16
小轮螺旋角 54
大轮齿数 41
工作齿高系数 4.000
大轮齿面宽 29.2
锥度系数 0.788532
偏置距 38.6 压力角和 38
大轮节径 大轮1齿90顶.5高系
数 0.325 计算刀盘半径
准双曲面齿轮计算结果
名
称
小轮 大轮
齿数
16
41
模数
4.646
刀盘半径 95.25
齿侧间隙 0.20--0.30 95.24998171
旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250

锥齿轮传动设计1.设计参数1150150********=====d d z z u 式中：u ——锥齿轮齿数比；1z ——锥齿轮齿数；2z ——锥齿轮齿数；1d ——锥齿轮分度圆直径（mm ）； 2d ——锥齿轮分度圆直径（mm ）。

1.10621115021)2()2(2212221=+=+=+=u d d d R mm 25.125)33.05.01(150)5.01(11=⨯−⨯=−=R m d d φ mm同理 2m d =125.25 mm式中：1m d 、2m d ——锥齿轮平均分度圆直径（mm ）；R φ——锥齿轮传动齿宽比，最常用值为R φ=1/3，取R φ=0.33。

530150111===z d m 同理 2m =5式中：1m 、2m ——锥齿轮大端模数。

175.4)33.05.01(5)5.01(11=⨯−⨯=−=R m m m φ同理 2m m =4.175式中：m m 1、m m 2——锥齿轮平均模数。

2.锥齿轮受力分析因为锥齿轮1与锥齿轮2的传动比为1，且各项数据相同，则现以锥齿轮1为分析对象得：125015083.932211=⨯==m t d T F N 88.88345cos 45tan 1250cos tan 111=︒⨯︒⨯==δαt r F F N 88.88345cos 45tan 1250sin tan 111=︒⨯︒⨯==δαt a F F N 22.133020cos 1250cos 11=︒==αt n F F N 式中；1t F ——锥齿轮圆周力；1r F ——锥齿轮径向力；1a F ——锥齿轮轴向力；1n F ——锥齿轮法向载荷；α——锥齿轮啮合角；δ——锥齿轮分度角。

3.齿根弯曲疲劳强度计算(1) 确定公式内的各计算数值1) 由《机械设计》图10-20c 查得锥齿轮的弯曲疲劳强度极限=1FE σ580MPa2) 由《机械设计》图10-18取弯曲疲劳寿命系数=1FN K 13) 计算弯曲疲劳许用应力取弯曲疲劳安全系数S =1.4，由《机械设计》式（10-12）得=⨯==4.15801][111S K FE FN F σσ414.29 MPa 4) 计算载荷系数K23.235.111.15.1=⨯⨯⨯==βαF F v A K K K K K5) 查取齿形系数由《机械设计》表10-5查得8.21=Fa Y6) 查取应力校正系数由《机械设计》表10-5查得55.11=Sa Y7) 计算大、小齿轮的[]F Sa Fa Y Y σ并加以比较[]01048.029.41455.18.2111=⨯=F Sa Fa Y Y σ 由《机械设计》式（10-24）得弯曲强度的设计公式为 []27.029.4141130)33.05.01(33.055.18.283.9323.241)5.01(43222111221231=⨯+⨯⨯⨯−⨯⨯⨯⨯⨯=⨯+−≥F Sa Fa R R Y Y u z KT m σφφ 由m=5>0.27，则弯曲疲劳强度符合要求。

2023年第47卷第4期Journal of Mechanical Transmission准双曲面齿轮实际齿面接触分析与调整计算韩昆朋1杨建军2（1 新乡职业技术学院数控技术学院，河南新乡453000）（2 河南科技大学机电工程学院，河南洛阳471039）摘要为了对准双曲面齿轮实际齿面的接触区进行调整修正，基于齿面测量结果，对大、小轮齿面进行了双三次样条曲面拟合。

采用齿面点二维黄金分割加密方法，编制了离散齿面接触分析算法，获得了实际齿面的啮合信息和接触印痕调整参数，为机床加工参数的反调修正提供了依据。

对某车桥准双曲面齿轮副进行了实际齿面滚检试验，仿真分析与实际滚检结果基本一致，验证了所提出算法的可行性和正确性。

关键词准双曲面齿轮接触印痕齿面加密干涉Tooth Contact Analysis and Adjustment Calculation of Real ToothSurfaces of Hypoid GearsHan Kunpeng1Yang Jianjun2（1 School of Numerical Control Technology, Xinxiang Vocational and Technical College, Xinxiang 453000, China）（2 School of Mechatronics Engineering, Henan University of Science and Technology, Luoyang 471039, China）Abstract For the purpose of adjusting the calculation of the contact pattern of real hypoid gears, the double third-power spline surface is used for fitting tooth surfaces of pinions and gears accurately according to the measurement results of the gear surface. Based on the two-dimension golden section method for increasing the density of gear grid mesh points, the contact analysis algorithm for discrete real gear surface is established to carry out the contact information of real gear surface and adjust parameters of contact patterns, which is applied for adjusting of machining-tool settings conveniently. In the end, a hypoid gear pair of automobile driving axles is used to verify the feasibility and correctness of the proposed algorithm by rolling tests, which shows that the contact pattern by discrete tooth contact analysis is consistent with the real rolling test.Key words Hypoid gear Contact pattern Tooth surface refinement Interference0 引言准双曲面齿轮具有重合度大、传动平稳等特点，广泛应用于车辆驱动桥传动中。

圆锥齿轮传动设计计算首先，我们需要确定齿轮的模数。

模数是描述齿轮齿形和大小的重要参数，通常以m表示，计算公式为m=d/z，其中d为分度圆直径，z为齿数。

常用的模数有1，1.25，1.5，2等。

确定模数后，可以计算分度圆直径。

其次，根据齿轮的齿数，我们可以计算齿轮的轴间距。

轴间距是指两个相互啮合的齿轮轴线之间的距离。

轴间距的计算公式为：a=(z1+z2)/(2m*cosβ)，其中a为轴间距，z1和z2分别为齿轮1和齿轮2的齿数，m为模数，β为螺旋角。

确定了模数和轴间距后，我们可以计算齿轮的分度圆直径。

分度圆直径是齿轮表面上与齿轮齿数相对应的直径，是齿轮齿形和尺寸的基准。

分度圆直径的计算公式为：d=m*z，其中d为分度圆直径，m为模数，z为齿数。

接下来，我们需要计算齿轮的齿面角。

齿面角是指两个相互啮合的齿轮齿面上的角度。

齿面角的计算公式为：α=arctan(tanβ*cosγ)，其中α为齿面角，β为螺旋角，γ为压力角。

螺旋角和压力角是描述齿轮齿形的重要参数，具体计算方法可以根据具体情况进行选择。

最后，我们需要进行齿轮的强度校核。

齿轮的强度校核是为了确保齿轮传动在工作过程中不会出现失效的现象。

齿轮的强度校核主要包括弯曲强度和接触疲劳强度两个方面。

弯曲强度校核是为了确保齿轮在受到外力作用时不会发生弯曲变形或断裂。

接触疲劳强度校核则是为了确保齿轮在长期运行过程中不会发生疲劳断裂。

以上是圆锥齿轮传动设计计算的一些基本步骤和方法。

如果需要进行更加详细和精确的设计计算，还需要考虑材料的强度性能、表面质量要求等其他因素。

设计计算过程中还需要充分考虑安全系数以及实际应用情况，以确保齿轮传动的可靠性和稳定性。

标准圆锥齿轮传动的计算参数标准圆锥齿轮传动的计算参数一、引言在机械工程领域中，圆锥齿轮传动广泛应用于各种机械装置中，如汽车变速器、造船机械、起重机械等。

圆锥齿轮传动作为一种重要的动力传递方式，其计算参数的确定对于传动系统的工作性能具有重要影响。

在本文中，我们将探讨标准圆锥齿轮传动的计算参数，以便更好地了解其工作原理和设计方法。

二、标准圆锥齿轮传动的基本概念标准圆锥齿轮传动是由两个相互啮合的圆锥齿轮组成的传动系统，其中一个为主动齿轮，另一个为从动齿轮。

圆锥齿轮传动具有传递大扭矩、平稳传动、传动比变化范围广等特点。

其计算参数主要包括齿数、模数、齿面角、齿顶高、齿根径等。

三、标准圆锥齿轮传动计算参数的深度分析1. 齿数：齿轮的齿数直接影响传动比和传动性能。

在选择齿数时，需要考虑传动的速比和工作环境等因素。

2. 模数：模数是圆锥齿轮传动计算参数中非常重要的一个指标，其大小直接决定着齿轮的尺寸和传动能力。

在确定模数时，需要兼顾传动效率和传动扭矩。

3. 齿面角：齿面角是描述齿轮啮合面上齿廓曲线斜率的参数，其选择直接关系到齿轮的啮合性能和噪声水平。

4. 齿顶高和齿根径：齿顶高和齿根径分别影响齿轮的强度和韧性，其合理选择是保证齿轮传动系统可靠工作的重要保障。

四、标准圆锥齿轮传动计算参数的设计方法1. 确定传动比和速比；2. 选择合适的齿数，考虑齿数的变化范围；3. 根据传动比和齿数确定模数，兼顾传动效率和传动比变化范围；4. 选择合适的齿面角，控制齿轮啮合面的啮合性能和噪声水平；5. 确定齿顶高和齿根径，保证齿轮传动系统的可靠工作。

五、总结与展望通过本文对标准圆锥齿轮传动计算参数的深度分析和设计方法的介绍，我们可以更好地了解圆锥齿轮传动系统的工作原理和设计要点。

在未来的研究中，我们还可以进一步探讨圆锥齿轮传动系统的优化设计和应用实例，以期为相关领域的研究和工程实践提供更多的参考和借鉴。

个人观点：圆锥齿轮传动作为一种重要的动力传递方式，在工程实践中具有广泛的应用前景。

d f 1, 2 = d 1, 2 - q f 1 , 2
Ak 1, 2 = d 2,1 / 2 - ha1, 2 sin d 1, 2
s1 = m (p / 2 + 2 x 1 tan a / cos b + x t1 ) s 2 = pm - s1
____ s3 cos2 d ö æ s sin2b ö æ sn1,2 = ç1 - 1,2 ÷ · ç s1,2 - 1,2 2 1,2 ÷ · cosb 4R ø ç 6d1,2 ÷ è è ø ____ ö s12,2 æ s1,2 sin 2 b ö æ h1,2 = ç1 cos d 1,2 ÷ ÷ · ç ha1,2 + ç ÷ ç ÷ 4R ø è 4d1,2 è ø
u = z 2 / z1
GB12369-90 GB12369-90 GB12369-90
3 13 39
表14-3-8 高变位：x2 =-x 1 表14-3-9 高变位：x2 =-x 1
± å = 90°Ê £ ¦ 1 = arctan µ ±¬ Ä ± å < 90°Ê £ ¦ 1 = arctan µ ±¬ Ä z1 z2
cV 12 + cV 3
表；14-3-39
45 0 14 0.66 0.23
Fmt=2000× 9550P/(n1d1) KHβ =1.5KHβ be 表：14-3-30 表4-3-31 beH=0.85b uv = u cos d 1 / cos d 2
2448.717949 1.875 1.25 1.814107128 46.75 9
z1 z2
sin å u + cos å sin(180 - å ) ± å > 90°Ê £ ¦ 1 = arctan µ ±¬ Ä u - cos(180 - å )

锥齿轮的设计计算一. 锥齿轮尺寸计算根据检测设备的传动的要求，去传动比i=11.选择材料和精度等级1）小锥齿轮选用 45调制处理，HB 1=240 HBS ； 大锥齿轮选用 45 正火处理，HB 2=200HBS ；2）精度等级选为7级。

2.按齿面接触强度进行设计 2t 3124()[](10.5)E H HR R d Z Z K T σψψ≥⨯- 1） 确定载荷系数t K参照参考文献[1]得t K =1.30；2） 齿轮传递扭矩T由步进电机保持转矩8N/mm 得T=8000N mm;3） 齿宽系数查参考文献[1]表10-7，确定=0.3 4).区域系数Z H根据参考文献[1] 确定Z H =2.5；5).许用应力由参考文献[1]确定=522.5MPa; 6）材料弹性影响系数E Z由参考文献表10-6查得E Z =189.812a MP 综上计算得， 23124 1.38000189.8 2.5()522.50.3(10.50.3)d ⨯⨯⨯≥⨯⨯-⨯=59.1mm 3.确定齿数取Z 1=40，Z2= Z 1i=401=40；4.选大端模数m= d 1/Z 1=59.1/40=1.48圆整取m=2 ;5.计算分度圆锥角锥距 11240=arctan arctan 4540Z Z δ==21=90904545δδ-=-= 121mZ 1()56.572Z R mm Z =+=6.计算大端分度圆直径121d =d =m Z 24080mm ⨯=⨯= 7.确定齿宽=0.356.57=16.9R b R ψ=⋅⨯ b 1= b2=11 mm二. 齿根弯曲疲劳强度校核a 222214(10.5)u 1a F F S R R KT Y Y Z m σψψ=⋅⋅-+1. 查参考文献[1]10-5得 a F Y =2.4，a S Y =1.67 查阅参考文献[1]得[]=390 MPa;2.计算得 22224 1.38000 2.4 1.570.3(10.50.3)40211F σ⨯⨯=⨯⨯-⨯⨯⨯+ =79.9<[]=390 MPa;故所选齿轮满足齿根弯曲疲劳强度要求。

准双曲面齿轮和螺旋锥齿轮设计的统一算法准双曲面齿轮传动是锥齿轮传动中的普遍形式，螺旋锥齿轮是它的一种特殊情况.当准双曲面齿轮的偏置距E12=0时，就成为螺旋锥齿轮传动.在外形和加工方法上，准双曲面齿轮与螺旋锥齿轮无本质区别，切齿计算方法差别也不大［1，2］.在实际设计中，它们的几何计算方法却不相同.当偏置距E12趋近于零时，现行的准双曲面齿轮的几何计算公式误差增大，甚至失效.因此螺旋锥齿轮设计的几何计算不能采用准双曲面齿轮几何计算公式和计算方法.在CAD软件开发中必须对这两种锥齿轮分别进行处理. 作者提出一种适合于准双曲面齿轮和螺旋锥齿轮设计的统一几何计算方法，其特点是当偏置距E12较大时，它与准双曲面齿轮现行计算结果一致；当偏置距E12为零时，得到正确的螺旋锥齿轮几何参数；当E12较小时，计算误差很小.因此在锥齿轮CAD软件开发中，可将这两种锥齿轮甚至包括直齿锥齿轮统一处理.1 分度锥参数基本公式准双曲面齿轮与螺旋锥齿轮几何计算中最大的区别在于分度锥参数的确定方法.分析现行准双曲面齿轮几何计算公式可知，当偏置距E12趋近于零时，齿轮的偏置角η，ε，ε′也趋近于零，因而导致公式计算误差增大甚至失效.作者在分析过程中发现，虽然E12趋近于零时，齿轮的偏置角η，ε，ε′也趋近于零，但它们属于同阶无穷小.即极限和存在.令式中e1和e2为偏置角系数.根据偏置角系数，可给出分度锥参数基本公式为式中k为放大系数；上面这组基本公式不仅适合于准双曲面齿轮，也适合于螺旋锥齿轮，不会因E12=0而失效.2 分度锥参数的求解上面给出的基本公式是一组非线性方程组，其中有5个参数是在几何计算前确定的.根据传动和强度等要求先确定齿轮的偏置距E12，轴交角ζ=90°-Σ，齿轮齿数z1和z2，大齿轮中点端面模数mt2，小齿轮中点螺旋角β1.则上面基本公式中的已知参数为i12=z2/z1, r2=mt2z2/2,及E12，ζ，β1. 由于基本公式是非线性方程组，在此采用迭代法求解.即初选k和e1值，按下面步骤进行迭代：若｜k*-k｜≤ξ(由计算精度确定的某一小量)，则可进行下面的迭代；否则改变k初值重新迭代.式中rc为刀盘半径. 若｜k0-kc｜＞ξ，则改变e1初值重新迭代，直到｜k0-kc｜≤ξ为止.迭代完毕，便得到了所有的分度锥参数.然后根据齿宽、齿高系数、变位系数和齿根倾斜类型，按准双曲面齿轮的方法进行其它所有几何尺寸参数的计算.3 算例作者采用上面的统一公式和算法分别对准双曲面齿轮和螺旋锥齿轮两种情况进行了大量的计算分析.表1是偏置距E12=0的螺旋锥齿轮算例结果；表2是偏置距E12=30mm的准双曲面齿轮算例结果.大量的计算分析结果表明：当E12=0时，上面方法所确定的分度锥参数与现行螺旋锥齿轮几何计算结果一致；当E12≠0时，上面方法与现行准双曲面齿轮几何计算结果一致；特别是当E12非常小时，本方法所得结果比较精确.因此，可用上面方法将这两种锥齿轮的几何计算方法统一起来.这对CAD软件开发特别有利.表1 螺旋锥齿轮参数表2 准双曲面齿轮参数4 统一设计中的问题现行准双曲面齿轮和螺旋锥齿轮的标准参数，如模数、齿高系数、变位系数等都定义在大端.这对准双曲面齿轮会导致理论啮合节点偏离齿宽中点而与螺旋锥齿轮不同.因此建议将标准参数定义在齿宽中点，这样也可以与强度计算方法一致［3］.此外，现行准双曲面齿轮标准参数中的螺旋角是小齿轮螺旋角，而标准参数中的模数是大齿轮端面模数.建议标准参数取大齿轮螺旋角和法向模数，这样更合理.5 结论大量算例和实际应用表明，作者提出的几何计算方法是可行的.作者已经根据此原理开发了CAD应用软件，并用于实际设计中.这样就使准双曲面齿轮和螺旋锥齿轮甚至直齿锥齿轮设计中的几何计算方法的统一有了依据.结果也在一定程度上揭示了准双曲面齿轮和螺旋锥齿轮理论上的本质联系.对锥齿轮的标准化、系列化和CAD技术也有一定的意义.。

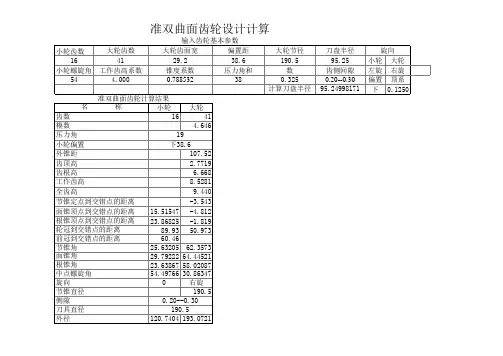
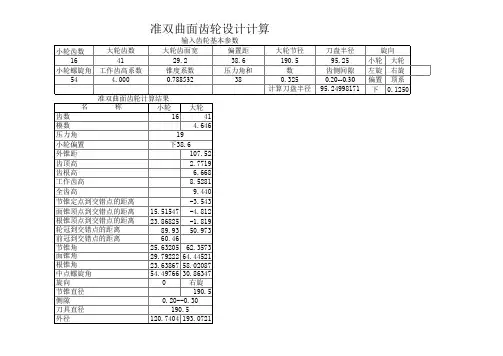
1小轮齿数Z1：6.00002大轮齿数Z2：38.00003齿数比的倒数Z1/Z2：0.4大轮齿面宽b2：62.00005偏置距E：35.00006大轮节圆直径de2：384.940007刀盘名义半径rb：152.400008初选小轮螺旋角βm1c：35.00009βm1c正切值tanβm1c：0.10初选大轮节锥角之余切值cotδ2c：0.11δ2c之正弦值sinδ2c：0.12初定大轮中点分圆半径rm2c：162.13大、小轮螺旋角差角正弦值sinΔβc：0.14Δβc之xx值cosΔβc：0.15初定小轮扩大系数Kc：1.16小轮中点分度圆半径换算值rm1H：25.17初定小轮中点分圆半径rm1c：28.18轮齿收缩系数H：1.1800019近似计算公法线K1K2在大轮轴线上的投影(截距)Q：883.20大轮轴线在小轮回转平面内偏置角正切tan纾?0.21偏置角余割sec纾?1.22偏置角正弦sin纾?0.03944723大轮轴线在小轮回转平面内偏置角纾? 2.24初算大轮回转平面内偏置角正弦sin錭：0.25an錭：0.26初算小轮节锥角正切tan?1c：0.27?1c角xxcos?1c：0.28第一次校正螺旋角差值拟'的正弦sin拟'：0.29拟'角xxcos拟'：0.30第一次校正小轮螺旋角正切tan?'m1：0.31扩大系数的xx量腒：0.32大轮扩大系数xx量的换算值腒H：0.00224133校正后大轮偏置角的正弦值sinxx?0.34anxx?0.35校正后小轮节锥角正切tan洌?0.36小轮节锥角?1：10.37?1角的xxcos?1：0.38第二次校正后的螺旋角差值的正弦sin拟：0.39拟值拟：12.40拟xxcos拟：0.41第二次校正后小轮螺旋角的正切值tan鈓1：0.42小轮中点螺旋角鈓1：35.00756743鈓1xxcos鈓1：0.44大轮中点螺旋角鈓2：22.45鈓2xxcos鈓2：0.46鈓2正切tan鈓2：0.41883247大轮节锥角余切cot?2：0.48大轮节锥角?2：79.49?2正弦sin?2：0.50?2xxcos?2：0.51 B1c：29.52 B2c：874.53两背锥之和B12：903.54大轮锥距在螺旋线中点切线方向投影T2：152.55小轮锥距在螺旋线中点切线方向投影T1：130.56极限齿形角正切负值-tana0：0.03881357极限齿形角负值-a0：1.58腶0的xxcos腶0：0.59 B59：0.60 B60：0.00145661 B61：19,795.62 B62：0.63 B63：64 B64：152.65齿线中点曲率半径r'0：152.66比较r'0与rb比值V：0.99894967 A67：0.68 A68：158.69 A69：1.70 rm2圆心至轴线交叉点距离Am2：28.71大轮节锥顶点至小轮轴线的距离A02，正数表示节锥顶点越过了小齿轮的轴线，负值表示节锥顶点在大轮与轴线之间：1.72大轮节锥上中点锥距Rm2：164.73大轮节锥上外锥距(节锥距)R2：74大轮节锥上齿宽之半0.5bm：30.75大轮在平均锥距上工作齿高h'm：13.76 A76：0.77 A77：0.78两侧压力角总和ac：20.000079 ac角正弦值sinac：0.34201480平均压力角a：10.000081 a角xxcosa：0.82 a角正弦tana：0.83 A83：84齿顶角与齿根角总和栌：16.85大轮齿顶高系数ha*2：0.1100086大轮齿根高系数hf*2：1.0400087大轮中点齿顶高ham2：1.88大轮中点齿根高hfm2：14.89大轮齿顶角鑑2：0.90鑑2角正弦sin鑑2：0.91大轮齿根角鑖2：4.92鑖2角正弦sin鑖2：0.93大轮大端齿顶高hae2：1.94大轮大端齿根高hfe2：17.95径向间隙c：2.96大轮大端齿全高he2：18.97大轮大端工作齿高h'e2：16.98大轮顶锥角(面锥角)鋋2：79.99鋋2角正弦sin鋋2：0.100鋋2角xxcos鋋2：0.101大轮根锥角鋐2：74.102鋐2角正弦sin鋐2：0.103鋐2角xxcos鋐2：0.104鋐2角余切cot鋐2：0.105大轮大端齿顶圆直径dae2：385.106大端节圆中心至轴线交叉点距离Akm2：34.107大轮轮冠至轴线交叉点距离Ake2：32.108大端顶圆齿顶与节圆处齿高之差膆am：-0.006485109大端节圆处与根圆处齿高之差膆mf：-0.110大轮面锥顶点到小轮轴线的距离Aoa2(参考71）：1.111大轮根锥顶点到小轮轴线的距离Aof2(参考71）：1.112 A112：170.113修正后小轮轴线在大轮回转平面内的偏置角正弦sin澹?0.114偏置角xxcosxx?0.115偏置角正切tanxx?0.116小轮顶锥角正弦sin鋋1：0.117小轮顶锥角(面锥角)鋋1：15.118顶锥角xxcos鋋1：0.119顶锥角正切tan鋋1：0.273884120 A120：13.121小轮顶锥顶点到轴线交叉点的距离Aoa1(参考71）：-6. 122 A122：0.123 A123：0.124 A124：11.125 A125：4.126 A126：-0.127 A127：1.128 A128：158.129 A129：0.130 A130：31.131小轮轮冠到轴线交叉点的距离Ake1：189.132：31.133小轮前轮冠到轴线交叉点的距离Aki1：123.134：182.135小轮大端齿顶圆直径dae1：99.136：167.137在大轮回转平面内偏置角正弦sin澹?138偏置角xx?12.139偏置角xxcosxx?0.140：21.141小轮根锥顶点到轴线交叉点的距离Aof1(参考71）：-14. 142：0.143小轮根锥角鋐1：9.144 cos鋐1：0.145 tan鋐1：0.146允许的最小侧隙jnmin：0.203200147允许的最大侧隙jnmax：0.279400148：149：12.150大轮内锥距Ri：133.。

准双曲面齿轮传动的动载荷计算中,由于小齿轮有一偏移距. 因此可采用双跨支承;并且小齿轮螺旋角增大,强度提高,最少齿数减小.这一系列优点显着提高了准双曲面齿轮的应用价值,尤其是为汽车底盘的布置提供了方便. 使其在汽车减速器中获得了广泛的应用. 随着汽车车速的不断提高, 作为传动环节的齿轮也达到了很高的工作转速, 高速下齿轮上的动载荷可能引起轮齿折断或齿轮结构破坏,因此, 以往传统的齿轮静态设计方法或齿轮动载荷的经验估算方法”0 都已不能满足当前汽车准双曲面齿轮的设计要求. 为此,本文作者首次建立了准双曲面齿轮传动系统的动力模型, 推导出动载荷的解析算法, 为准双曲面齿轮的动态计算与动态设计奠定了基础2准双曲面齿轮传动系统的动力学模型图1 所示, 是准双曲面齿轮传动系统动力学模型的简图. 如果忽略齿面摩擦力, 并假定两个齿轮问的啮合力的合力沿齿面法向作用在齿宽中部节点M 处, 该齿面法向力可以分解为周向力只,径向力和轴向力只（见图2）, 这里应注意到只t 和只在方向和大小上均不相同. 在这些力的作用下, 每个齿轮的自由度包括:.: 齿轮周向微角位移;一t:篓!曼!f）苎苎;图1准双曲面齿轮传动系统的动力学模型，：齿轮中心的径（一向位移; ''一•••’’ 一…一-,…一■原稿收到日期为 1 993年3月1 6日,修改稿收到日期为1993年5月12日1994年（第16卷）第2期汽车工程93k.: 齿轮中tk, 的轴向位移;I：下标,1,2分别表示小齿轮和太齿轮.上x与,,方向分别一致, 再考虑输入质量和输出质量的微角位移日, 日, 系统共有lO 个自由度以上x与只,,的方向分别一致，再考虑输A质量和输出质量的微角位移日,0, 系统共有lO 个自由度.齿轮问的啮合刚度为K,齿轮由于摩擦，搅油等产生的相对扭振阻尼为 c.K是齿轮啮合位置（齿轮转角）的函数,当齿轮匀速转动时,K是时间的周期函数.阻尼一般很小, 为计算方便起见，近似认为其性质为粘性阻尼，阻尼比取作常数0.1.每个齿轮上在rr,d 方向分别有支承刚度KT.Kr,K, 它们主要由轴和轴承的串联刷度构成,输入质量和输出质量由输入，输出轴的扭转刚度KK与小齿轮,大齿轮分别联接，构成了准双曲面齿轮传动系统的动力学模型3 齿轮系统的参数本文研究一对准双曲面齿轮传动系统,它们的几何参数列于表l 中.图2是齿轮系统的结构与支承简图,小齿轮和大齿轮均采用双跨支承方式.表 2 为齿轮系统的质量参数, 表3为齿轮系统的刚度参数.表 2 中m0=l,2) 为齿轮质量, 为齿轮惯性矩,.? 为输入, 输出质量的惯性矩. 表 1 齿轮几何参数齿数五=I1 三=43节圆直径 d.;205nma偏移距E;34mm平均压力角?州2:19e螺旋角=49993.2=2&amp;758.面锥角=22104=73211.节锥角. 分方程法向啮合力只沿,,r,a 三个方向分解, 得:=+.+(l,2)(1) 写成标量形式得:r. 只.oDs??o0s.{=只？COSC~.(tg-cos6,, —sinf1.?sin6,,)(il,2 】(2)IPo.=只？COSC~.?(我？sin6,,+shaft.. ' cosh 口.)式中分Y:Ih0:l, 齿轮驱动面和大齿轮被驱动面的压力角, 为小轮面锥角6o, 为大轮根锥角一齿轮在啮台力作用下, 轮齿齿面有法向位移x, 它在t,ra 三个方向的分量分别为+r_,XX(i=l,2】,为齿宽中点M至轴线的半径.两个齿轮间的法向弹性啮台力P 与齿轮相对位移成比例, 考虑啮合误差的影响, 得:mK ——？,(3)J式中m为同时啮台齿对数，K,为同时啮合的第，对齿的刚度，为同时啮合的第』对齿的综合误差. 两个齿轮间的阻尼力为:=c. 一)(4J将只和按(2)式分别在两个齿轮上沿t,r,a 三个方向分解,可以建立准双曲面齿轮传动系统的运动微分方程:1994年(第16卷】第2期汽车［程95r401+(+)?r,.?..cosflm1+KI(01 一)=0f 臼2 一(+).r_: ' ?s2' cos3.2+K?( —0 口)=0l1 茸1++)' ?s1(tgz1.cos 6.1 一sin8..sj1)+1x1=0lm22 一+).ms0~(tg2?cos6 —sin fl=2?sl n$iz)+Kt2=0lm,i(Pc+)?COS0~?COSf1..+Knxn=0【5Jlm 一(+ 只)？oosoh??s2+:2=0lm1 毫1++).?s1 ' (1.sin3+sin1?cos6.)+1x=0in3.).=x.?cos~zi(tg:c.?sin3.+sin.?eos6~.)将(6) 式,(3) 式和(4) 式代入(5) 式, 展开后可写成矩阵形式如下:f 釜｝+ 【c]f 叠｝+ 【K]fxj=fp｝(7)式中｛X｝—,02,xxr2lxxf2lxx0l 目?),【.K]是同期函数矩阵，它的周期就是啮合周期｛p｝中主要包括齿轮误差的激励,它的完整周期包括？个啮合周期,? 是z和z1 的最小公倍数, 在本文的算例中为473. 令【K]一【+【?K],(x 】=f｝+｝(8)?cos0~1??s1 —.？s.?s2=??s】(tgc~lsin6 】+sin1?cos6.l)=?COS0~2(tgjr2+sin2?~os6~2)=0其中…AK/+?,是静态弹性啮合力,即静态法向力,可由M算出,为常数, 重是平均啮合剐度, 中包括了刚度变化和误差的周期, 可以展为傅里叶级数.1994年(第16卷)第2期汽车工程卯?由关系式t=(60/n)(0/2) 转换成相应的时问坐标, 并得到相应的几0), 代人(9) 式中,可解出齿轮系统在转速 a 时的动态响应, 再由(3) 式求出齿轮上的动载荷. 图 4 所示是齿轮副在9000r/rain 时的动载波形定义最大的动载荷值与静载荷值之比为动载系数, 算出各种不同转速下的动载系数,示于图5中,表示了这对齿轮在负荷力矩M?乍用下的不同转速时的动载特性.由图5可以看到, 在4000r/min,7000r/min,13500r/min 附近分别有共振峰值, 这是支承振动引起的：在18000r,/rnin 有大幅值共振,这是齿轮副的相对扭振,也是齿轮副的主共振;在9000rtmin 附近的小峰值,是齿轮副相对扭振的1/2次共振,表现了齿轮传动的参数激励性质.目前国外轿车主减速器的输人转速已超过10000r/rain, 随着汽车技术的发展, 转速还将进一步提高. 图 5 为汽车准双曲面齿轮传动的设计提供了重要的参考依据.8 结论(1) 本文建立了准双曲面齿轮传动的动力学模型,包括每个齿轮在回转方向与各支承方向的振动自由度.(2) 本文推导出准双曲面齿轮传动系统的运动微分方程和动态响应的求解方法(3) 准双曲面齿轮传动在恒速恒载工作条件下的振动激励是齿轮副的传动误差系统振动具有参数激励性质.(4) 准双曲面齿轮传动的动载在齿轮副相对扭振时达到最大, 在支承共振时也有动载峰值.参考文献1 天津齿轮机床研究所, 西安交通大学, 北京机床J 等编译格里舞锥齿轮技术译文集(一),( 一),{ 三). 北京：机械工业出版杜,I9842 刘惟信圆锥齿轮与双曲面齿轮传动. 北京：人民变通出版社,I9803齿轮手册编委会.齿轮手册(上). 北京：机械工业出版社.19904何敬安译.在茕荷作用下螺旋锥齿轮及准双曲面齿轮轮齿接触分析.齿轮,1986;10 (5)TheCalculationofDynamicLoadinHypoidGearDriveFangZorlgdeAlastmetTakingintoaccountthevibrationDOFsofgearpairinbOttIdirectionsofrotati onandbearingsupports,adynarmcmodelofhypoidgearsetisbuiltup,thekinematicdi fferential equationsarederivedandthesolvingschemeforequationsetofexcitationpara metersispro.posedinthepaper.Inaddition,theexcitationcharacteristicsofthegeardriv eisstudiedandthedynamicloadsofgearsandtheirdynamicloadingcoefficientsunderdiffere ntrotationspeedafeaecuratelycalcttlatedKeywortlEG?rdriveOyaamleIoadCalaflalion。

锥齿轮传动设计计算说明：本程序适用于直齿锥齿轮及 GLEASON 齿制、小齿轮齿数大于或等于 12 的弧齿锥齿轮（包括零度锥齿轮）。

公差数值是按照中点法向模数 1至 10 毫米，中点分度圆直径 400 毫米以下，精度等级 5、6、7、8 级设定的。

弧齿锥齿轮的刀盘直径设定为3.5、6、7.5、9、12、18 英寸。

可进行几何参数计算和承载能力验算（工作条件原动机均匀平稳，从动机中等振动），并可对弧齿锥齿轮加工的可行性（刀盘选择）进行判断。

引用标准：GB11365--89 锥齿轮和准双曲面齿轮精度， GB10062--88 锥齿轮承载能力计算方法主要参考书目：《齿轮手册》上、下册，《机床设计手册》 2 上册，《复杂刀具设计手册》下册注意：本程序有“单变量求解”，应从工具--选项--重新计算中设置反复操作，最多迭代次数10000，最大误差0.0001。

说明：请在兰色框中输入已定或初定数据（黄色框中为判断或参考数据）。

输出数据在最后列表，可单独打印。

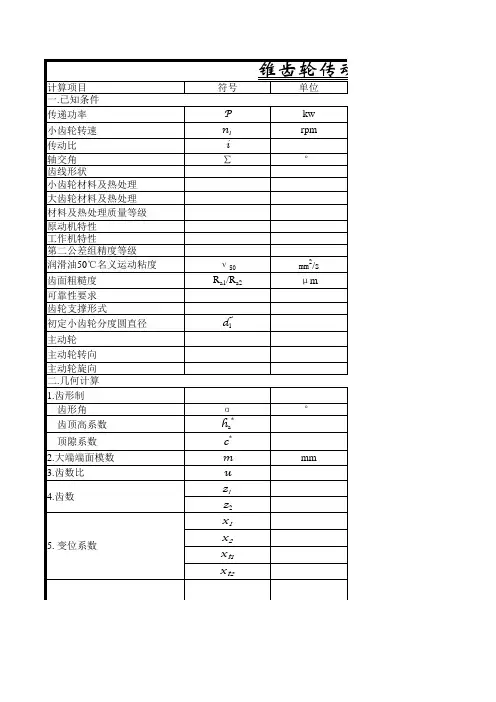
左旋小轮齿数Z1大轮齿数Z2大端端面模数m1018法向压力角αn轴交角Σ切向变位系数x s1齿宽参考值b0高度变位系数x h1齿宽实际值b第Ⅰ公差组精度等级全齿高系数x第Ⅱ公差组精度等级工作齿高系数x w第Ⅲ公差组精度等级全齿高h最小法向侧隙种类工作齿高hw法向侧隙公差种类齿数比u小轮基准端面直径极限值小轮基准端面直径大轮基准端面直径极限值大轮基准端面直径最小法向侧隙jn min最大法向侧隙jn max注：如果侧隙不合适，可重新选择最小法向侧隙种类、2—3—合金钢调质， 4—碳钢调质或正火，57—调质钢与1毫米大轮分度圆直径d2155.934516毫米外锥距Ra89.1913389毫米大端端面齿距p27.2157072毫米小轮齿顶高h a111.4178718毫米大轮齿顶高h a2 5.90818554毫米小轮齿根高h f17.64112824毫米大轮齿根高h f213.1508145毫米小轮分度圆锥角δ10.5070985弧度29.0546041度大轮分度圆锥角δ2 1.06369782弧度60.9453959度小轮顶锥角δa10.65348872弧度37.44214535度大轮顶锥角δa2 1.14916034弧度65.84203722度小轮根锥角δf10.42163599弧度24.15796278度大轮根锥角δf20.91730761弧度52.55785465度小轮齿根角γ10.08546251弧度 4.896641315度大轮齿根角γ20.14639021弧度8.387541249度小轮分度圆理论弧齿厚Sa115.9498152毫米大轮分度圆理论弧齿厚Sa211.2658919毫米小轮齿角δt10.12489965弧度7.156222524度大轮齿角δt 20.12422946弧度7.117823623度γ 1 + γ2797.1分0.23311616中点锥距Rm74.1913389内锥距Ri59.1913389D c0*毫米*K111K120K130.25K i115.949815211.26589196.330117910.89449140.766883844.935774035.055323820.321888510.0701730615.674382611.2566459测量小轮齿厚处的锥距L1L89.1913389测量大轮齿厚处的锥距L2L89.1913389110.641757790.09882026小轮大端法向弦齿厚Sx n115.6743826大轮大端法向弦齿厚S xn211.2566459小轮大端法向弦齿高H n112.0596295大轮大端法向弦齿高H n2 6.0070058公差值选取计算：中点法向模数m mn7.20609986中点分度圆直径d m172.0609986d m2中点分度圆弧长之半L m1/2113.193152L m2/2F P145F P24545*±f pt120±f pt22020*齿形相对误差的公差f c111f c21111*切向综合公差F'i158F'i2一齿切向综合公差f'i126f'i2齿圈跳动公差Fr145Fr24545*齿厚 公差Ts180Ts2808080***最小法向侧隙jn min7474齿厚上偏差系数xe747474*****Ess10-25Ess20*齿厚上偏差Ess1-68Ess2齿厚下偏差Esi1-148Esi2制造误差补偿EsΔ125EsΔ22525***最大法向侧隙jn max208最高精度等级7齿坯顶锥母线跳动公差40齿坯基准端面跳动公差250.8937417132323232323232*****轴交角极限偏差±EΣ28.599734628.59973456承载能力验算：当量圆柱齿轮端面参数：小轮齿数Zv111.439589Zv2齿数比u v 3.24分度圆直径d v182.434821d v2当量圆柱齿轮中心距a v174.76182齿顶圆直径d va1101.4301d va1齿宽中点齿顶高h am19.49763961h am2半齿宽高度变位系数x hm10.318x hm2半齿宽切向变位系数x sm10.00345x sm2基圆直径d vb176.1598439αvt0.392699082d vb2端面重合度εvα 1.40825269g vα29.45412216纵向重合度εvβ0总重合度εvγ 1.40825269当量圆柱齿轮法向参数：齿数Zvn111.439589βvb0Zvn2分度圆直径d vn182.434821d vn2齿顶圆直径d van1101.4301d van2基圆直径d vbn176.1598439d vbn2重合度εvαn 1.40825269刀具齿顶高h a07.47993165刀尖圆角半径ρa0名义切向力Fmt6938.56608N使用系数K A 1.5（工作条件原动机均匀平稳，从动机中等振动）m10.01877813m20.060841134m edN0.02804977ya 1.65cv1cv40.9cv50.47cv6动载系数K V 1.0193739亚临界 1.019373899主共振齿向载荷分布系数K Hβ 1.65K Fβ 1.65K Hα0-E162)/(C160*C164K Fα02-E162)/(C160*C164*K Hα0齿间载荷分布系数K Hα 1.40825269K Fα 1.277832999C ZLZ H 2.37841423Z B 1.08632448Z EZ K0.85Z L0.922403034Z V试验齿轮接触疲劳极限ζHmin1500N/mm2注：按合理的制造成本和中等质量考虑。

齿侧间隙 0.20--0.30 95.24998171
旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
准双曲面齿轮设计计算
输入齿轮基本参数
小轮齿数
大轮齿数
大轮齿面宽
偏置距
大轮节径
16
41
小轮螺旋角 工作齿高系数
54
4.000
29.2 锥度系数 0.788532
38.6 压力角和
38
大轮1齿90顶.5高系 数
0.325
计算刀盘半径
准双曲面齿轮计算结果
名
称
小轮 大轮
齿数
16
41
模数
4.646
压力角
19
小轮偏置
23.86825 -1.819
89.93 50.973
60.46
25.63205 62.3573
29.79222 64.44521
23.63867 58.02087
54.49766 30.86340--0.30 190.5
外径
120.7404 193.0721
刀盘半径 95.25
下38.6
外锥距
107.52
齿顶高
2.7719
齿根高 工作齿高
6.668 8.5281
全齿高
9.440
节锥定点到交错点的距离
-3.543
面锥顶点到交错点的距离 15.51547 -4.812
根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径

齿面接触疲劳强度计算 ※ 圆锥齿轮的接触强度计算是针对齿宽中点（dm）处的 当量齿轮（圆柱齿轮）进行的。 接触强度计算
校核公式
dm
H ZH ZE
4KT1
R (1 0.5R )2 d13u
H
d
设计公式
d1
3
(
ZH
ZE
H
)2
R
4KT1
(1 0.5R
)2 u
齿根弯曲疲劳强度计算
※ 圆锥齿轮的弯曲强度计算是针对齿宽中点（dm）处的 当量齿轮（圆柱齿轮）进行的。 弯曲强度计算
电动机驱动，载荷平稳
解：取Z1=24,Z2=77 R 0.3 Kt 1.3
按接触强度设计公式
d1t
3
(
ZH
Z
H
E
)2
R
(1
4KT1
0.5
R
)2
u
直接求得： d1t 84.97
dm1 d1t (1 0.5R ) 72.225
R d1t 2
1 u2
R
b R
b Rd1t u2 1 / 2 42.832
d1
R
b R
rv1
rm r
R 0.5b R
1 0.5R
1 2
dm2
rv 2
d2
0.5b
rm r
R 0.5b R
1 0.5R
rv1 rm1 / cos1
rv1 r1(1 0.5R )
1 u2 u
d1
cos1
u 1 u2
1 2
rv1
0.5b
rv 2
d2
u
z2 z1
rm2 rm1
d2 / 2R d1 / 2R

图6.1 螺旋锥齿轮切齿原理
2. 切齿原理
• 平面产形轮的刀盘轴线与摇台轴线是平行的，产形 轮的面锥角d0=900；锥形产形轮的刀盘轴线与摇 台轴线不平形，这是通过刀转体来实现的，产形轮 的面锥角d0不等于900
(a) 平面产形轮
(b) 锥形产形轮 图6.2 两种产形轮
2. 切齿原理
• 大轮的节锥角<650，大轮必须用展成法加工 • 大轮的节锥角>700，大轮用成形法加工 • HFT：大轮用成形法，小轮用锥形产形轮加工，
q tg1 V H
Sd H2 V2
三.刀倾法加工小轮
偏心角径向刀位S 摇台角Q1—角向刀位q1
sin S
2 K2
Q1
2
左旋 q1右旋
Y2280摇台结构
三.刀倾法加工小轮
4. 摇台角
切制左旋齿轮时，刀
Oe
Oc
K2/2 S
盘中心低于被切齿轮 中心；切制右旋齿轮 时，刀盘中心高于被 切齿轮中心。摇台角 Q 与 角 向 刀 位 q1 具 有 直接的关系。
M J刀转角 M'
图 6.5 刀倾刀转角的形成
三.刀倾法 加工小轮
• 径向刀位S1 • 角向刀位q1 • 刀倾角i
• 刀转角j
dM1轮坯安装角 • E01垂直轮位 • X1轴向轮位修正值 • XB1床位
• 滚比i01
OM
XB1
O01
机床平面
q1角向刀位
S1 机床水平面
E01
i刀倾
O1'
dM1
X1
具尺寸和小轮的安装距，三者之和即为机床实际的水 平轮位。可修正被切齿轮的压力角。
8.垂直轮位E01 —被切齿轮对于摇台中心偏置量。它对