绕流圆柱实验

目录1. 实验目的及原理 (2)1.1实验目的 (2)1.2 实验原理 (2)2. 物理现象描述 (3)3. 数值模型描述 (3)3.1计算域 (3)3.2 边界类型 (3)4.前处理 (3)4.1 Gambit软件介绍 (3)4.2网格绘制 (5)5.求解设置 (5)5.1 Fluent软件介绍 (5)5.2 计算过程 (7)6.后处理 (7)6.1 云图显示 (7)6.2 升力系数 (9)6.3 拖曳力系数 (10)6.4 斯托哈尔数 (10)7. 总结体会 (11)1. 实验目的及原理1.1实验目的（1）通过上机实验掌握计算流体力学中前处理、计算设置、后处理的基本流程，为后期船舶原理、船舶设计原理等课程的学习奠定基础。

（2）通过对单圆柱绕流的数值模拟，进一步理解流体力学理论课中的各项知识点，如边界层、湍流、圆柱绕流、卡门涡街、雷诺数、涡旋形式等。

1.2 实验原理对于静止圆柱绕流，本文研究对象为二维不可压缩流动。

在直角坐标系下，其运动规律可用 N-S 方程来描述，连续性方程和动量方程分别为:01()()i ii i i j ji j j u x u u P u u t x x x x νρ∂⎧=⎪∂⎪⎨∂∂∂∂∂⎪+=-+⎪∂∂∂∂∂⎩其中u i 为速度分量；p 为压力；ρ为流体的密度；ν为流体的动力黏性系数。

对于湍流情况，本文采用RNG k ⁃ε模型，RNG k ⁃ε模型是k ⁃ε模型的改进方案。

通过在大尺度运动和修正后的粘度项体现小尺度的影响， 而使这些小尺度运动有系统地从控制方程中去除。

所得到的 k 方程和ε方程，与标准k ⁃ε模型非常相似，其表达式如下：212()()()G ()()()G i k eff k i j ji eff k i j j ku k k t x x x u C C t x x x k k εεερραμρερεερεεεαμρ∂∂∂∂⎧+=++⎪∂∂∂∂⎪⎨∂∂∂∂⎪+=+-⎪∂∂∂∂⎩其中Gk 为由于平均速度梯度引起的湍动能的产生项，2efft t C k ρμμμμμε=+=， 经验常数1C ε=0.084 5，k α=εα=1.39，2C ε=1.68。

圆柱绕流的数值模拟一、问题简介我们考虑一个固定的无限长圆柱体，其直径为10mm，空气以均匀的速度由远处而来绕过圆柱，气流会在圆柱后发展为复杂的流动。

这是一个经典的流体力学问题，随雷诺数的增加，柱体后的流动形态会由对称向不对称转变，并产生卡门涡街。

我对不同雷诺数下的流动进行了数值模拟，并对计算所得流场进行了比较和分析。

二、文献综述圆柱绕流作为最为常见的钝体绕流现象，演绎出了大量的流体控制工程技术和理论研究课题。

这类问题常见的有风掠过建筑物，气流对电线的作用，海流冲击海底电缆，河水对桥墩的冲击，气流经过冷凝器中的排管、空中加油机的油管以及飞行器上的柱体等等，具有很高的工程实践意义。

同时圆柱绕流又是流体力学的经典问题，其蕴含了丰富的流动现象和深刻的物理机理，长久以来一直是众多理论分析、实验研究及数值模拟的研究对象。

流体绕圆柱体流动时，过流断面收缩，流速沿程增加，压强沿程减小，由于黏性力的存在，就会在柱体周围形成附面层的分离，形成圆柱绕流。

在圆柱绕流问题中，流体边界层的分离与脱落、剪切层的流动和变化、尾迹区域的分布和变动，以及它们三者之间的相互作用等因素，使得该问题成为了一项复杂的研究课题。

圆柱绕流的流动状态主要由雷诺数(Re)决定,根据不同的Re范围，流动会经历多种流动状态，在我们流体力学的教材上，就可以查到不同雷诺数下圆柱绕流的形态变化，而下表更加完整详细。

表一在使用CFD方法对圆柱绕流进行求解时，早期使用求解二维定常N-S方程的方法来模拟绕流流场。

然而，由于圆柱尾部涡脱落的存在，绕流流场随时间在不断改变，具有非定常特性，因此就需要求解非定常N-S方程。

目前，在低雷诺数层流条件下，多以求解二维非定常N-S方程来研究圆柱绕流。

但随着雷诺数的增加，绕流流场中沿展向的三维特性越来越显著，如果还使用二维计算模型求解流场，必然不能正确的解析流场结构，获得正确的流场参数。

所以在大雷诺数条件下就需要求解三维的N-S方程。

一个世纪以来，圆柱绕流一直是众多理论分析，实验研究及数值模拟的对象。

因为这种流动既有不固定的分离点，又有分离后的尾流和脱体涡。

随着雷诺数的增加,尾流性质，脱体涡的形态有很大的变化，具有丰富的流动现象。

应观察到的物理现象图圆柱体的St（Strouhal数）随Re(Reynolds数）变化曲线/ u0 q+ C以上数据是由A.Roshko、H。

s.Ribner、B。

Etkins和K.K.Nelly，E。

F.Relt和L。

F。

G.Simmons，以及G.W。

Jones等人测量得到。

注意观察圆柱体的St（Strouhal数）随Re（Reynolds数）的变化规律。

St与特征长度、特征速度和特征频率（圆柱绕流：涡脱落的频率)有关.圆柱体的阻力系数Cd随Reynolds数的变化曲线( l％ ~1 O0 l# ］, f/ e图中实曲线是由Wieselsberger,A.Roshko 测量数据绘制得到注意观察圆柱体的阻力系数Cd随Reynolds数的变化规律及阻力危机现象。

湍流模型的选取FLUENT是目前国际上比较流行的商用CFD软件包。

它具有丰富的物理模型，先进的数值方法和强大的前后处理功能，在航空航天，汽车设计,石油天然气，涡轮机设计等方面都有着广泛的运用。

FLUENT提供的湍流模型包括：单方程（Spalart-Allmaras）模型、双方程模型(标准κ—ε模型、重整化群κ—ε模型、可实现(Realizable）κ-ε模型）及雷诺应力模型和大涡模拟.湍流模型种类如图所示。

. f） y7 l， l8图湍流模型种类示意图# g3 Q, j2 p2 l+ b F0 u+ e9 D； S） c6 n7 d注意!二维平面模型显示的湍流模式.注意没有大涡模型（LES）三维平面模型显示的湍流模式。

注意出现大涡模型(LES）要使二维平面模型出现LES，需要如下操作。

在FLUENT屏幕上键入(rpsetvar 'les—2d?’#t）屏幕会出现les-2d?，然后回车即可特别注意！/ w/ ［7 n’ L＊ T" z- e( `% X3 j, |雷诺数大于100000后，二维平面模型,运用各种湍流模型（除LES外）计算,卡门涡街都将很难出现。

中山大学工学院计算流体力学实验报告实验名称：圆柱绕流问题的三种网格划分姓名：刘广参与组员：刘广学号：11309018任课教师：詹杰民学科专业：工学院理论与应用力学中山大学2014年04月05日图1对于四个面，如图2所示，参数interval count我们选择10，点击apply效果如图3所示。

图2Page 3 of 12图3下面我们对其划分的网格进行质量分析。

点击面板进入网格分析区域，就是Examine Mesh面板当中，Display Type我们选择Rang，2D Element，三角形网格类型，点击下方update 就可以看到如图4所示网格质量图。

图4Page 4 of 12我们继续看图5所示的网格质量分析数据，可以看到，三角形网格一共有1324个，其中在圆柱后方的若干区域网格质量最差。

图5最差质量的网格如图6所示。

图6接下来我们开始介绍矩形网格划分。

如下图7所示；我们首先画四段四分之一圆弧，其中圆弧对应的圆周半径为1.然后我们再绘制如图所示的矩形。

其中外部的矩形长32，宽22，并做如下图所示的划分。

其中详细作图步骤在上次实验报告中有详细叙述，这里不再赘述。

所示图7中有八个面，其中圆形上的点为对圆形进行45度划分。

现在我们选择矩形网格对Page 5 of 12其进行划分，图7对于八个面，如图8所示，参数interval count我们选择10，点击apply效果如图9所示。

图8Page 6 of 12图9下面我们对其划分的网格进行质量分析。

点击面板进入网格分析区域，就是Examine Mesh面板当中，Display Type我们选择Rang，2D Element，矩形网格类型，点击下方update就可以看到如图10所示网格质量图。

图10我们继续看图11所示的网格质量分析数据，可以看到，矩形网格一共有20000个，其中在Page 7 of 12圆柱上方、左方、右方、后方的若干区域网格质量最差。

圆柱表面低速气流压强分布测量实验指导书郑州航空工业管理学院航空工程实验中心一、实验目的1 •用皮托管测量低速实验段出口气流速度，掌握皮托管测速的基本原理和方法。

2.测量二维圆柱体表面不同位置气流的压强分布，加深理解圆柱体表面低速粘性绕流特性，掌握物体绕流表面压强分布测量的基本原理和方法。

二、实验通用规范1•按时按地点参加实验，实验分组进行，爱护实验室实验仪器和设备，不准碰撞或任意移动仪器或设备，不许乱跑乱动和大声喧哗。

2 •实验前，各组学生必须认真预习，阅读实验指导书和教材、书籍等有关资料，了解实验目的、原理方法、操作步骤及注意事项。

3 •实验开始前，服从实验指导教师的安排，认真听讲，仔细了解实验设备和仪器的操作方法和注意事项，确定组长及组内人员实验分工。

4 •实验中，严格按照相应实验操作规程，集中精力，有条不紊，认真操作，如实观察和记录各种实验数据和有关实验现象，初步进行一定数据处理和分析。

5•实验过程，如出现异常情况，应及时向指导教师汇报。

6 •实验后，实验记录数据交指导教师检查，并按要求将实验仪器设备装置复位。

7•在规定时间内，按要求编写完成并上交实验报告，注意报告除原始记录数据外，实验数据的处理和分析等内容不得相互抄袭。

三、实验装置与实验原理1物体表面压强分布测定的意义首先有了压强分布图，就知道了物体上各部分的载荷分布，这是强度设计时的基本数据；其次，这又有助于了解气流绕过物体时的物理特性，如何判断流动分离点位置等。

在某些风洞中（如在二维风洞中，模型紧夹在两壁间而不便装天平），全靠压强分布图来间接推算出作用在机翼上的升力或力矩。

测定压强分布的模型构造是：在物体表面上各测点垂直钻一小孔，小孔底与埋置在模型内部的细金属管相通，小管的一端伸出物体外，然后再通过细皮管与多管压力计上各测管相接，各测压孔与多管压力计上各测管都编有号码， 于是根据各测管内液柱液面的升降 高度，就可以处理得出各测点的压强值分布了。

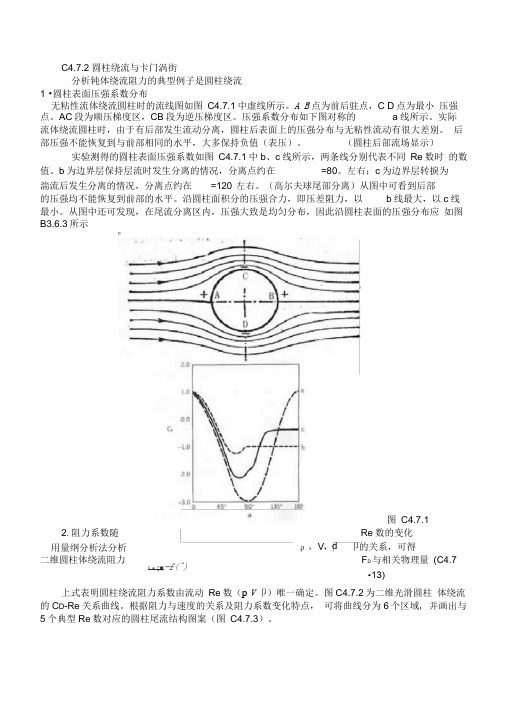
C4.7.2 圆柱绕流与卡门涡街分析钝体绕流阻力的典型例子是圆柱绕流1 •圆柱表面压强系数分布无粘性流体绕流圆柱时的流线图如图 C4.7.1中虚线所示。

A B 点为前后驻点，C D 点为最小 压强点。

AC 段为顺压梯度区，CB 段为逆压梯度区。

压强系数分布如下图对称的 a 线所示。

实际 流体绕流圆柱时，由于有后部发生流动分离，圆柱后表面上的压强分布与无粘性流动有很大差别。

后部压强不能恢复到与前部相同的水平，大多保持负值（表压）。

（圆柱后部流场显示）实验测得的圆柱表面压强系数如图 C4.7.1中b 、c 线所示，两条线分别代表不同 Re 数时 的数值。

b 为边界层保持层流时发生分离的情况，分离点约在 =80。

左右；c 为边界层转捩为 湍流后发生分离的情况，分离点约在 =120°左右。

（高尔夫球尾部分离）从图中可看到后部的压强均不能恢复到前部的水平。

沿圆柱面积分的压强合力，即压差阻力，以 b 线最大，以c 线 最小。

从图中还可发现，在尾流分离区内，压强大致是均匀分布，因此沿圆柱表面的压强分布应 如图B3.6.3所示2.阻力系数随Re 数的变化 用量纲分析法分析二维圆柱体绕流阻力F D 与相关物理量 (C4.7•13)上式表明圆柱绕流阻力系数由流动 Re 数（p V 卩）唯一确定。

图C4.7.2为二维光滑圆柱 体绕流的C D -Re 关系曲线。

根据阻力与速度的关系及阻力系数变化特点， 可将曲线分为6个区域, 并画出与5个典型Re 数对应的圆柱尾流结构图案（图 C4.7.3）。

图 C4.7.1 卩的关系，可得 d 、 6 =［車-f(^)C4.7.2（1） Re vv 1,称为低雷诺数流动或蠕动流。

几乎无流动分离，流动图案上下游对称（a ）。

阻力以摩擦阻力为主，且与速度一次方成比例。

（2） K Re < 500,有流动分离。

当Re=10，圆柱后部有一对驻涡（b ）。

当Re > 100时从圆柱后部交替释放出旋涡，组成卡门涡街（c ）。

试用环量的圆柱绕流原理说明乒乓球中的弧
度
1 弧度
乒乓球游戏中弧度占据了很大的重要地位，它控制着高低、左右
和旋转等飞行属性。

这些属性的变化是由四个维度的实际空间中的环
量圆柱绕流原理而控制的。

2 环量圆柱绕流原理
环量圆柱绕流是一种气流流动的基本原理，即气体的流动会产生
一圈的环状流场。

大量的乒乓球比赛中经常会发生环量圆柱绕流：圆
柱体的底面是乒乓球，上面包裹着绕流气囊，当气体从乒乓球一端流
出时，以非线性变幻的形式将卷向旁边。

如果两端都有气流，则两端
的气流会彼此相互缠绕。

3 受环量圆柱绕流影响的弧度
由于受到环量圆柱绕流的影响，乒乓球中的弧度会发生变化，这
也是乒乓球游戏中当球场上的双方攻击手未能准确猜测另一方行动时，造成乒乓球在舞台上飞行变化（高低、左右、旋转）的原因。

弧度的
变化使得技术竞技成为一种极具挑战性的游戏，也正是这种技术性和
挑战性使得乒乓球游戏在比赛中受到了认可和欢迎。

结论
从以上可以看出，环量圆柱绕流原理对乒乓球中弧度起着关键的作用，它控制着球的飞行高低、左右和旋转，使得比赛场上的双方攻击手未能准确猜测另一方行动，把乒乓球游戏变成了一种充满挑战性和技术性的游戏。

另外，乒乓球游戏在比赛中一直受到认可和欢迎，环量圆柱绕流原理也为其发展奠定了基础。

空气绕圆柱体流动压力分布测定空气绕圆柱体流动压力分布测定一 实验目的学习固体表面压力的测量方法结合流体力学,进一步了解平行无环流绕流圆柱体的特点*(较高要求) 与教材给出的理论压力分布比较,了解实际物体所受的形状阻力的来源 二 实验原理理想流体平行流绕流圆柱体作无环量流动时，圆柱表面速度分布θθsin 20∞-==u u u(1)圆柱表面任一点的压力p 根据Bernoulli 方程g u p g u p22220∞∞+=+γγ(2)引入无量纲压力系数 c p 来表征物体上任一点的压力分布221∞∞-=u p p c p ρ（3）实际流体具有粘性，Re 超过某数值，圆柱后产生涡流，出现尾涡区，破坏圆柱前后压力的对称分布，造成压差阻力。

流动动压∞-p p 0221∞=u ρ)(81.90∞-=h h(4)式中h 0h ∞分别为来流总压与静压水头。

圆柱表面一点的压力p)(81.9∞∞-=-h h p p(5)对应的压力系数 ∞∞∞∞--=--=h h h h p p p p c p00(6)实验中的空气发生比较低速的流动，可认为空气不可压，密度不变；又空气经过均流段后流经圆柱，可认为平行定常流。

实验流动的雷诺数νD u ∞=Re 式中D 为圆柱外直径。

三 实验设备实验系统仍利用箱式风洞，圆柱体置于实验段。

圆柱表面有一测压孔，压力信号从与圆柱体相垂直的方向上引出，圆柱能够绕自深轴线转动。

压力引出的位置由相对来流前驻点的角度θ表示。

从圆形刻度盘读数。

圆柱体的上游来流截面架设皮托管，以测量来流总压（流速）。

四实验步骤1 安装皮托管2 开启风机，测量来流总压p0与静压p∞之差p0 - p∞3 转动圆柱体，每隔10º记录一次圆柱表面压力与来流静压之差p-p∞4 调节来流速度，测量不同Re数时的压力分布（说明：本装置仅可测试Re≤5×105的亚临界流动）5 实验结束，停止风机图1 实验装置示意1 箱式风洞2 实验段3 圆柱体4 测压孔5 倾斜式微压计6 皮托管7 调节风门五 数据记录与处理室温t a 大气压强p a 空气运动粘度 m 2/s圆柱直径m D=48×10-3m 来流动压压头 来流静压压头 mmH 2Oaat p+=27346.0ρ h u ∆ρ81.92⨯=∞νD u ∞=Re填入下面的表格，画出压力系数随角度变化的图线，如图2所示。

圆柱绕流阻力实验一实验目的：1．熟悉多管压差计测量圆柱体压强分布的方法；2．了解利用压力传感器、数据采集系统测量绕流圆柱表面压强分布的方法；3 绘制压强分布图，并计算图柱体的阻力系数。

二实验装置：1. 小型风洞或气动台；2. 多管压差计；3. 压力传感器，数据采集模块及其系统。

三实验原理：1. 小型风洞或气动台经风机产生的气流经过稳压箱，收缩段，进入实验段。

圆柱体安装在实验段的中部。

气动台稳压箱的气流速度近似为零，其压强可认为是驻点压强p0。

小型风洞在试验段上部设置了一个正对来流方向的导管，为驻点压强p0。

实验段中分布比较均匀的气流，速度为V∞，压强为p∞。

气流绕圆柱体流动时，流动变得复杂起来。

本实验为了测量圆柱体表面各点的压强分布，在圆柱体表面开设一个测压孔，测压孔通过一个细针管接出与多管压差计或压力传感器相连，细针管垂直方向装有指针，当转动圆柱时其转角通过角度盘指针的读数来表示，因而随着测压孔位置的改变，即可将绕圆柱体整个壁面上的压强分布测出。

图2.2.1 圆柱表面压强分布实验装置2. 多管压差计的方法测量原理：在流体力学中，绕流阻力即流体绕物体流动而作用于物体上的阻力，由摩擦阻力f D 和压强阻力p D 构成，其f D 相对于p D 小得多，在本实验中可忽略不计。

其压强用无量纲的参数——压强系数C P 来表示：由伯努利方程2202121V p V p p ρρ+=+=∞∞推导得到各个不同角度测点的压强系数Cp∞∞∞∞∞--=--=-=l l l l p p p p V p p Cp 00221ρ ( 2-2-1 )式中p 为圆柱体不同测点压强。

0p 为稳压箱压强（或称驻点压强，总压），P ∞由收缩段出口测得(或来流压强，静压)，ρ为流体密度、V 为来流流速，l 为圆柱体测点在多管压差计上的读数， ∞l 为静压读数， 0l 为总压读数。

对无环量理想流体绕流圆柱体的压强阻力系数的理论解为θρsin 412120-=-=∞V p p C p ( 2-2-2 )对多管压差计实验装置，来流动压为e h p p V γρ∆=-=∞0221 ( 2-2-3 ) 式中0p 为稳压箱压强，∞p 为收缩段压强。