2019秋成才之路·人教B版数学·选修2-3习题：第2章 概率2.2 第3课时

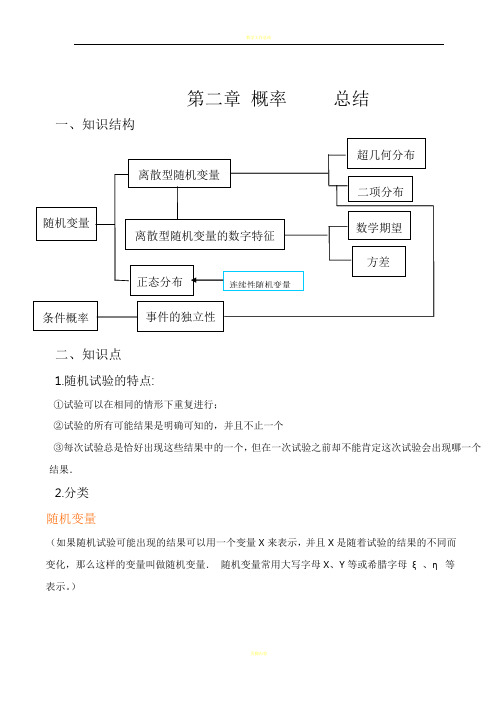
第二章概率总结一、知识结构二、知识点1.随机试验的特点:①试验可以在相同的情形下重复进行；②试验的所有可能结果是明确可知的，并且不止一个③每次试验总是恰好出现这些结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果．2.分类随机变量（如果随机试验可能出现的结果可以用一个变量X来表示，并且X是随着试验的结果的不同而变化，那么这样的变量叫做随机变量．随机变量常用大写字母X、Y等或希腊字母ξ、η等表示。

）离散型随机变量在上面的射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．连续型随机变量对于随机变量可能取的值，可以取某一区间内的一切值，这样的变量就叫做连续型随机变量.连续型随机变量的结果不可以一一列出.3.离散型随机变量的分布列一般的,设离散型随机变量X可能取的值为x1,x2, ,x i , ,x nX取每一个值xi(i=1,2,）的概率P(ξ=x i）＝P i，则称表为离散型随机变量X 的概率分布，简称分布列性质：①pi≥0, i =1，2，…；②p1 + p2 +…+p n= 1．③一般地，离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。

4.求离散型随机变量分布列的解题步骤例题：篮球运动员在比赛中每次罚球命中得1分，不中得0分，已知某运动员罚球命中的概率为0.7，求他罚球一次的得分的分布列.解：用随机变量X表示“每次罚球得的分值”，依题可知，X可能的取值为：1,0且P（X=1）=0.7，P（X=0）=0.3因此所求分布列为：引出超几何分布一般地, 设总数为N件的两类物品，其中一类有M件，从所有物品中任取n(n≤N)件,这n件中所含这类物品件数X是一个离散型随机变量，则它取值为k时的概率为()(0,1,2,,)k n kM N MnNC CP X k k mC--===，其中{}min,m M n=,且*,,,,n N M N n M N N∈≤≤则称随机变量X的分布列为超几何分布列,且称随机变量X服从参数N、M、n的超几何分布注意：二点分布如果随机变量X的分布列为：其中0<p<1，q=1-p，则称离散型随机变量X服从参数p的二点分布二点分布的应用：如抽取彩票是否中奖问题、新生婴儿的性别问题等.nNnMNMCCC-nNnMNMCCC11--nNmnMNmMCCC--（1）超几何分布的模型是不放回抽样；（2）超几何分布中的参数是N 、M 、n ，其意义分别是总体中的个体总数、N 中一类的总数、样本容量解题步骤：例题、在某年级的联欢会上设计了一个摸奖游戏，在一个口袋中装有10个红球和20个白球，这些球除颜色外完全相同.游戏者一次从中摸出5个球.至少摸到3个红球就中奖，求中奖的概率 解：设摸出红球的个数为X,则X 服从超几何分布,其中30,10,5N M n === X 可能的取值为0，1，2，3，4, 5. 由题目可知，至少摸到3个红球的概率为(3)(3)(4)(5)P X P X P X P X ==+=+=≥324150102010201020555303030C C C C C C C C C =++ ≈0.191答：中奖概率为0.191.条件概率1.定义：对任意事件A 和事件B ，在已知事件A 发生的条件下事件B 发生的概率，叫做条件概率.记作P 读作A 发生的条件下B 的概率2.事件的交（积）:由事件A 和事件B 同时发生所构成的事件D ，称为事件A 与事件B 的交（或积作D=A ∩B 或D=AB3.条件概率计算公式:P(B|A)相当于把A 看作新的基本事件空间,求Ａ∩Ｂ发生的概率:.0)(,)()()|(>=A P A P AB P A B P 发生的条件下样本点数在包含的样本点数发生的条件下在A B A )A |B (=P解题步骤：例题、10个产品中有7个正品、3个次品，从中不放回地抽取两个，已知第一个取到次品，求第二取到次品的概率.解：设 A = {第一个取到次品}， B = {第二个取到次品}，所以，P(B|A) = P(AB) / P(A)= 2/9 答：第二个又取到次品的概率为2/9.相互独立事件1.定义：事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事包含的样本点数包含的样本点数A AB =总数包含的样本点数总数包含的样本点数//AB A =)(P(AB)A P =.1)|(0)()|()(0)A (P ≤≤⋅=>A B P A P A B P AB P （乘法公式）；，则若.151)(21023==⇒C C AB P .103)(=A P2.相互独立事件同时发生的概率公式两个相互独立事件同时发生的概率，等于每个事件发生的概率的积。

高中数学学习材料马鸣风萧萧*整理制作与函数结合的概率问题1、A 、B 两个投资项目的利润率分别为随机变量X 1和X 2。

根据市场分析，X 1和X 2的分布列分别为X 15%10%X 22%8%12%P 0.8 0.2 P 0.2 0.5 0.3（1）在A 、B 两个项目上各投资100万元，Y 1和Y 2分别表示投资项目A 和B 所获得的利润，求方差DY 1、DY 2； （2）将x （0≤x≤100）万元投资A 项目，100－x 万元投资B 项目，f(x)表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和。

求f(x)的最小值，并指出x 为何值时，f(x)取到最小值。

（注：D(aX + b) = a 2DX ） 解：（Ⅰ）由题设可知1Y 和2Y 的分布列分别为Y 1 5 10 P0.80.2150.8100.26EY =⨯+⨯=，221(56)0.8(106)0.24DY =-⨯+-⨯=，220.280.5120.38EY =⨯+⨯+⨯=，2222(28)0.2(88)0.5(128)0.312DY =-⨯+-⨯+-⨯=．（Ⅱ）12100()100100x x f x D Y D Y -⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭2212100100100x x DY DY -⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭22243(100)100x x ⎡⎤=+-⎣⎦2224(46003100)100x x =-+⨯， 当6007524x ==⨯时，()3f x =为最小值． 2、函数f (x )＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点，B 为图象的最低点． (1)若φ＝π6，点P 的坐标为⎝⎛⎭⎫0，332，求ω；(2)若在曲线段ABC 与x 轴所围成的区域内随机取一点，求该点在△ABC 内的概率．解： (1)函数f (x )＝sin(ωx ＋φ)求导得，f ′(x )＝ωcos(ωx ＋φ)，把φ＝π6和点⎝⎛⎭⎫0，332代入得ωcos ⎝⎛⎭⎫0＋π6＝332解得ω Y 2 2 8 12 P0.20.50.3＝3.(2)取特殊情况，在(1)的条件下，导函数f ′(x )＝3cos ⎝⎛⎭⎫3x ＋π6，求得A ⎝⎛⎭⎫π9，0， B ⎝⎛⎭⎫5π18，－3，C ⎝⎛⎭⎫4π9，0，故△ABC 的面积为S △ABC ＝12×3π9×3＝π2，曲线段与x 轴所围成的区域的面积S ＝－⎪⎪⎪f x o(s\up7( ))4π9π9＝－sin ⎝⎛⎭⎫4π3＋π6＋sin ⎝⎛⎭⎫3π9＋π6＝2，所以该点在△ABC 内的概率为P ＝S △ABC S ＝π4. 3、某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花作垃圾处理．(1)若花店一天购进16枝玫瑰花，求当天的利润y (单位：元)关于当天需求量n (单位：枝，n ∈N )的函数解析式； (2)花店记录了100天玫瑰花的日需求量(单位：枝)，整理得下表：日需求量n 14 15 16 17 18 19 20 频数10201616151310以100天记录的各需求量的频率作为各需求量发生的概率．①若花店一天购进16枝玫瑰花，X 表示当天的利润(单位：元)，求X 的分布列、数学期望及方差； ②若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由． 解：(1)当日需求量n ≥16时，利润y ＝80. 当日需求量n <16时，利润y ＝10n －80.所以y 关于n 的函数解析式为y ＝⎩⎪⎨⎪⎧10n －80，n <16，80，n ≥16(n ∈N )．(2)①X 可能的取值为60,70,80，并且P (X ＝60)＝0.1，P (X ＝70)＝0.2，P (X ＝80)＝0.7. X 的分布列为X 60 70 80 P0.10.20.7X 的数学期望为EX ＝60×0.1＋70×0.2＋80×0.7＝76. X 的方差为DX ＝(60－76)2×0.1＋(70－76)2×0.2＋(80－76)2×0.7＝44. ②答案一：花店一天应购进16枝玫瑰花．理由如下：若花店一天购进17枝玫瑰花，Y 表示当天的利润(单位：元)，那么Y 的分布列为Y 55 65 75 85 P0.10.20.160.54Y 的数学期望为 EY ＝55×0.1＋65×0.2＋75×0.16＋85×0.54＝76.4. Y 的方差为DY ＝(55－76.4)2×0.1＋(65－76.4)2×0.2＋(75－76.4)2×0.16＋(85－76.4)2×0.54 ＝112.04.由以上的计算结果可以看出，DX <DY ，即购进16枝玫瑰花时利润波动相对较小． 另外，虽然EX <EY ，但两者相差不大．故花店一天应购进16枝玫瑰花． 答案二：花店一天应购进17枝玫瑰花．理由如下：若花店一天购进17枝玫瑰花，Y 表示当天的利润(单位：元)，那么Y 的分布列为Y 55 65 75 85 P0.10.20.160.54Y 的数学期望为 EY ＝55×0.1＋65×0.2＋75×0.16＋85×0.54＝76.4.由以上的计算结果可以看出，EX <EY ，即购进17枝玫瑰花时的平均利润大于购进16枝时的平均利润．故花店一天应购进17枝玫瑰花．4、经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t 该农产品,以X (单位:t,150100≤≤X)表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内销商该农产品的利润.(Ⅰ)将T 表示为X 的函数;(Ⅱ)根据直方图估计利润T 不少于57000元的概率;(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若[100,110)X ∈,则取105X =,且105X =的概率等于需求量落入[100,110)的概率),求利润T 的数学期望.【答案】5、/频率组距0.0100.0150.0200.0250.030100110120130140150需求量/x t。

其次章 2.3 第1课时一、选择题1．若随机变量X ～B (5,0.8)，则E (X )的值为( )导学号98570334 A ．0.8 B ．4 C ．5 D ．3[答案] B[解析] ∵X ～B (5,0.8)， ∴E (X )＝5×0.8＝4.2．样本(x 1，x 2，…，x n )的平均数为x ，样本(y 1，y 2，…，y n )的平均数为y (x ≠y )．若样本(x 1，x 2，…，x n ，y 1，y 2，…，y m )的平均数z ＝αx ＋(1－α)y ，其中0<α<12，则n ，m 的大小关系为( ) 导学号98570335A ．n <mB ．n >mC ．n ＝mD ．不能确定[答案] A[解析] 由题意，x 1＋x 2＋…＋x n ＝n x ，y 1＋y 2＋…＋y m ＝m y ， z ＝x 1＋x 2＋…＋x n ＋y 1＋y 2＋…＋y m m ＋n ＝n m ＋n x ＋m m ＋n y .∴n m ＋n ＝α，∴0<n m ＋n <12，∴m >n . 3．若随机变量ξ～B (n,0.6)，且E (ξ)＝3，则P (ξ＝1)的值是( 导学号98570336 A ．2×0.44 B ．2×0.45 C ．3×0.44 D ．3×0.64[答案] C[解析] ∵E (ξ)＝n ×0.6＝3，∴n ＝5.∴P (ξ＝1)＝C 15×0.6×(1－0.6)4＝3×0.44.故选C ．4．(2021·衡水高二检测)设随机变量ξ的分布列如下表所示且E (ξ)＝1.6，则a －b ＝( ) 导学号98570337ξ 0 1 2 3 P0.1ab0.1A ．0.2 C ．－0.2 D ．－0.4[答案] C[解析] 由0.1＋a ＋b ＋0.1＝1，得a ＋b ＝0.8①又由E (ξ)＝0×0.1＋1×a ＋2×b ＋3×0.1＝1.6，得a ＋2b ＝1.3②由①②解得a ＝0.3，b ＝0.5，∴a －b ＝－0.2.故选C ． 5．设E (X )＝10，则E (3X ＋5)等于( ) 导学号98570338 A ．35 B ．40 C ．30 D ．15[答案] A[解析] E (3X ＋5)＝3E (X )＋5＝3×10＋5＝35.6．一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c (a ，b ，c ∈(0,1))，已知他投篮一次得分的期值为1(不计其他得分状况)，则ab 的最大值为( 导学号98570339A ．148B ．124C ．112D ．16[答案] B[解析] 3a ＋2b ＋0×c ＝1，∴3a ＋2b ＝1， ∴ab ＝16×(3a ×2b )≤16×(3a ＋2b 2)2＝124.当且仅当3a ＝2b ，即a ＝16，b ＝14成立．7．(2021·长春高二检测)口袋中有5个球，编号为1,2,3,4,5，从中任取3球，以ξ表示取出的球的最大号码，则E (ξ)＝( ) 导学号98570340A ．4B ．5C ．92D ．154[答案] C[解析] ξ的可能取值为3,4,5，P (ξ＝3)＝1C 35＝110，P (ξ＝4)＝C 23C 35＝310，P (ξ＝5)＝C 24C 35＝610，故E (ξ)＝3×110＋4×310＋5×610＝92.二、填空题8．(2022·四川理，12)同时抛掷两枚质地均匀的硬币，当至少有一枚硬币正面对上时，就说这次试验成功，则在2次试验中成功次数X 的均值是________.导学号 98570341[答案] 32[解析] 由题意知，试验成功的概率p ＝34，故X ～B (2，34)，所以E (X )＝2×34＝32.9．已知某离散型随机变量ξ的数学期望E (ξ)＝76，ξ的分布列如下表：ξ 0 1 2 3 Pa1316b则a ＝________.导学号98570342 [答案] 13[解析] E (ξ)＝76＝0×a ＋1×13＋2×16＋3b ⇒b ＝16，又P (ξ＝0)＋P (ξ＝1)＋P (ξ＝2)＋P (ξ＝3)＝1⇒a ＋13＋16＋16＝1⇒a ＝13. 三、解答题10．某班联欢晚会玩飞镖投掷玩耍，规章如下：每人连续投掷5支飞镖，累积3支飞镖掷中目标即可获奖；否则不获奖．同时要求在以下两种状况下中止投掷：①累积3支飞镖掷中目标；②累积3支飞镖没有掷中目标．已知小明同学每支飞镖掷中目标的概率是常数p (p >0.5)，且掷完3支飞镖就中止投掷的概率为13.导学号98570343(1)求p 的值；(2)记小明结束玩耍时，投掷的飞镖支数为X ，求X 的分布列和数学期望． [解析] (1)由已知P (X ＝3)＝p 3＋(1－p )3＝13，解得p ＝13或p ＝23.∵p >0.5，∴p ＝23.(2)X 的全部可能取值为3,4,5.P (X ＝3)＝13，P (X ＝4)＝[C 23×(23)2×13]×23＋[C 23×(13)2×23]×13＝1027， P (X ＝5)＝C 24×(23)2×(13)2＝827(或P (X ＝5)＝1－P (X ＝3)－P (X ＝4)＝827)． X 的分布列为X345P13 1027 827∴X 的数学期望为E (X )＝3×13＋4×1027＋5×827＝10727.一、选择题1．如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的油漆面数为X ，则X 的均值E (X )＝( )导学号98570344A ．126125B ．65C ．168125D ．75[答案] B[解析] 题意知X ＝0、1、2、3，P (X ＝0)＝27125，P (X ＝1)＝54125，P (X ＝2)＝36125，P (X ＝3)＝8125，∴E (X )＝0×27125＋1×54125＋2×36125＋3×8125＝150125＝65.2．今有两台独立工作在两地的雷达，每台雷达发觉飞行目标的概率分别为0.9和0.85，设发觉目标的雷达台数为ξ，则E (ξ)＝( ) 导学号98570345A ．0.765B ．1.75C ．1.765D ．0.22 [答案] B[解析] 设A 、B 分别为每台雷达发觉飞行目标的大事，ξ的可能取值为0、1、2. P (ξ＝0)＝P (A ·B )＝P (A )·P (B )＝(1－0.9)×(1－0.85)＝0.015.P (ξ＝1)＝P (A ·B ＋A ·B )＝P (A )·P (B )＋P (A )·P (B )＝0.9×0.15＋0.1×0.85＝0.22. P (ξ＝2)＝P (AB )＝P (A )·P (B )＝0.9×0.85＝0.765. ∴E (ξ)＝0×0.015＋1×0.22＋2×0.765＝1.75.故选B. 3．已知随机变量p 的分布列为p －2 －1 0 1 2 3 P1/12mn1/121/61/12其中m ，n ∈[0,1)，且E (P )＝16，则m ，n 的值分别为( ) 导学号98570346A ．112，12B ．16，16C ．14，13D ．13，14[答案] D [解析] 由题意得⎩⎨⎧112＋m ＋n ＋112＋16＋112＝1，－2·112＋(－1)m ＋0·n ＋1·112＋2·16＋3·112＝16，即⎩⎨⎧m ＋n ＝712，12－m ＝16.∴⎩⎨⎧m ＝13，n ＝14.二、填空题4．马老师从课本上抄录一个随机变量ξ的概率分布列如下表：t 1 2 3 P (ξ＝t )？！？请小牛同学计算ξ的数学期望 ，尽管“！”处完全无法看清，且两个“？”处字迹模糊，但能确定这两个“？”处的数值相同．据此，小牛给出了正确答案E (ξ)＝________.导学号98570347 [答案] 2[解析] 设？处为x ，！处为y ，则由分布列的性质得2x ＋y ＝1，∴期望E (ξ)＝1×P (ξ＝1)＋2×P (ξ＝2)＋3×P (ξ＝3)＝4x ＋2y ＝2.5．设离散型随机变量ξ可能取的值为1、2、3、4.P (ξ＝k )＝ak ＋b (k ＝1、2、3、4)．又ξ的数学期望E (ξ)＝3，则a ＋b ＝________.导学号98570348[答案]110[解析] 由已知得，(a ×1＋b )＋(a ×2＋b )＋(a ×3＋b )＋(a ×4＋b )＝1，即10a ＋4b ＝1① 又E (ξ)＝3，故(a ＋b )×1＋(2a ＋b )×2＋(3a ＋b )×3＋(4a ＋b )×4＝3，即30a ＋10b ＝3② 联立①、②，解得b ＝0，a ＝110，∴a ＋b ＝110.三、解答题6．甲、乙等五名奥运志愿者被随机地分到A ，B ，C ，D 四个不同的岗位服务，每个岗位至少有一名志愿者．导学号98570349(1)求甲、乙两人同时参与A 岗位服务的概率；(2)设随机变量ξ为这五名志愿者中参与A 岗位服务的人数，求ξ的分布列． [解析] (1)记甲、乙两人同时参与A 岗位服务为大事E A ，那么P (E A )＝A 33C 25A 44＝140，即甲、乙两人同时参与A 岗位服务的概率是140.(2)随机变量ξ可能取的值为1,2，大事“ξ＝2”是指有两人同时参与A 岗位服务，则P (ξ＝2)＝C 25A 33C 25A 44＝14.所以P (ξ＝1)＝1－P (ξ＝2)＝34，ξ的分布列是ξ 1 2 P34147．(2022·全国卷Ⅰ，19)某公司方案购买2台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，假如备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：导学号 98570350以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X 表示2台机器三年内共需更换的易损零件数，n 表示购买2台机器的同时购买的易损零件数．(Ⅰ)求X 的分布列；(Ⅱ)若要求P (X ≤n )≥0.5，确定n 的最小值；(Ⅲ)以购买易损零件所需费用的期望值为决策依据，在n ＝19与n ＝20之中选其一，应选用哪个？ [解析] (Ⅰ)由柱状图并以频率代替概率可得，1台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2，0.4，0.2,0.2，从而P (X ＝16)＝0.2×0.2＝0.04； P (X ＝17)＝2×0.2×0.4＝0.16；P (X ＝18)＝2×0.2×0.2＋0.4×0.4＝0.24； P (X ＝19)＝2×0.2×0.2＋2×0.4×0.2＝0.24； P (X ＝20)＝2×0.2×0.4＋0.2×0.2＝0.2； P (X ＝21)＝2×0.2×0.2＝0.08； P (X ＝22)＝0.2×0.2＝0.04. 所以X 的分布列为(Ⅱ)由(Ⅰ)知P (X ≤18)＝0.44，P (X ≤19)＝0.68，故n 的最小值为19. (Ⅲ)记Y 表示2台机器在购买易损零件上所需的费用(单位：元)． 当n ＝19时，EY ＝19×200×0.68＋(19×200＋500)×0.2＋(19×200＋2×500)×0.08＋(19×200＋3×500)×0.04＝4 040.当n ＝20时，EY ＝20×200×0.88＋(20×200＋500)×0.08＋(20×200＋2×500)×0.04＝4 080. 可知当n ＝19时所需费用的期望值小于当n ＝20时所需费用的期望值，故应选n ＝19.8．已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分．现从该箱中任取(无放回，且每球取到的机会均等)3个球，记随机变量X 为取出此3(1)求X 的分布列； (2)求X 的数学期望E (X )．[解析] (1)由题意得X 取3,4,5,6，且 P (X ＝3)＝C 35C 39＝542；P (X ＝4)＝C 14·C 25C 39＝1021；P (X ＝5)＝C 24·C 15C 39＝514；P (X ＝6)＝C 34C 39＝121.所以X 的分布列为(2)由(1)知E (X )＝3·P (X ＝3)＋4·P (X ＝4)＋5·P (X ＝5)＋6·P (X ＝6)＝133.。

第二章 随机变量及其分布2.2 二项分布及其应用2.2.1 条件概率A 级 基础巩固一、选择题1．将两枚质地均匀的骰子各掷一次，设事件A ＝{两个点数互不相同}，B ＝{出现一个5点}，则P (B |A )＝( )A.13B.15C.16D.112解析：出现点数互不相同的共有6×5＝30(种)，出现一个5点共有5×2＝10(种)，所以P (B |A )＝1030＝13. 答案：A2．有一匹叫Harry 的马，参加了100场赛马比赛，赢了20场，输了80场．在这100场比赛中，有30场是下雨天，70场是晴天．在30场下雨天的比赛中，Harry 赢了15场．如果明天下雨，Harry 参加赛马的赢率是( )A.15B.12410解析：此为一个条件概率的问题，由于是在下雨天参加赛马，所以考查的应该是Harry 在下雨天的比赛中的胜率，即P ＝1530＝12. 答案：B3．在10个形状大小均相同的球中有6个红球和4个白球，不放回地依次摸出2个球，在第1次摸出红球的条件下，第2次也摸到红球的概率为( )A.35B.25C.110D.59解析：设第一次摸到的是红球为事件A ，则P (A )＝610＝35，设第二次摸得红球为事件B ，则P (AB )＝6×510×9＝13， 故在第一次摸得红球的条件下第二次也摸得红球的概率为P (B |A )＝P （AB ）P （A ）＝59. 答案：D4．某种电子元件用满3 000小时不坏的概率为34，用满8 000小时不坏的概率为12.现有一只此种电子元件，已经用满3 000小时不坏，还能用满8 000小时的概率是( )A.34B.2323解析：记事件A ：“用满3 000小时不坏”，P (A )＝34；记事件B ：“用满8 000小时不坏”，P (B )＝12.因为B ⊆A ，所以P (AB )＝P (B )＝12，P (B |A )＝P （AB ）P （A ）＝P （B ）P （A ）＝12÷34＝23. 答案：B5．有一批种子的发芽率为0.9，出芽后的幼苗成活率为0.8，在这批种子中，随机抽取一粒，则这粒种子能成长为幼苗的概率是( )A ．0.72B ．0.8C ．0.86D ．0.9解析：设“种子发芽”为事件A ， “种子成长为幼苗”为事件AB (发芽，并成活而成长为幼苗)，则P (A )＝0.9，又种子发芽后的幼苗成活率为P (B |A )＝0.8，所以P (AB )＝P (A )P (B |A )＝0.9×0.8＝0.72.答案：A二、填空题6．4张奖券中只有1张能中奖，现分别由4名同学无放回地抽取．若已知第一名同学没有抽到中奖券，则最后一名同学抽到中奖券的概率是________．解析：因为第一名同学没有抽到中奖券已知，所以问题变为3张奖券，1张能中奖，最后一名同学抽到中奖券的概率，显然是13. 答案：137．把一枚硬币任意抛掷两次，事件B 为“第一次出现反面”，事件A 为“第二次出现正面”，则P (A |B )为________．解析：事件B 包含的基本事件数有1×C 12＝2个，AB 包含的基本事件数为1，由条件概率公式P (A |B )＝n （AB ）n （B ）＝12. 答案：128．甲、乙两市都位于长江下游，根据一百多年来的气象记录，知道一年中下雨天的比例甲市占20%，乙市占18%，两地同时下雨占12%，记P (A )＝0.2，P (B )＝0.18，P (AB )＝0.12，则P (A |B )和P (B |A )分别等于________，________．解析：P (A |B )＝P （AB ）P （B ）＝0.120.18＝23，P (B |A )＝P （AB ）P （A ）＝0.120.2＝35. 答案：23 25三、解答题9．抛掷一枚骰子，观察出现的点数，若已知出现的点数不超过3，求出现的点数是奇数的概率．解：设事件A 表示“点数不超过3”，事件B 表示“点数为奇数”，所以P (A )＝36＝12，P (AB )＝26＝13. 所以P (B |A )＝P （AB ）P （A ）＝23. 10．某班级有学生40人，其中团员15人，全班分四个小组，第一小组10人，其中团员4人，如果要在班内任选一人当学生代表．(1)求这个代表恰好在第一小组内的概率；(2)现在要在班内任选一个团员代表，问这个代表恰好在第一小组内的概率是多少？解：设A ＝{在班内任选一个学生，该学生属于第一小组}，B ＝{在班内任选一个学生，该学生是团员}．(1)由古典概率知P (A )＝1040＝14. (2)法一 由古典概型知P (A |B )＝415. 法二 P (AB )＝440，P (B )＝1540， 由条件概率的公式，得P (A |B )＝415. B 级 能力提升1．从混有5张假钞的20张百元钞票中任意抽出2张，将其中1张放到验钞机上检验发现是假钞，则第2张也是假钞的概率为( )A.119B.1738C.419D.217解析：设事件A 表示“抽到2张都是假钞”，事件B 为“2张中至少有1张假钞”，所以所求概率为P (A |B )．而P (AB )＝C 25C 220，P (B )＝C 25＋C 15C 115C 220. 所以P (A |B )＝P （AB ）P （B ）＝217. 答案：D2．盒中装有6件产品，其中4件一等品，2件二等品，从中不放回地取产品，每次1件，取两次，已知第二次取得一等品，则第一次取得的是二等品的概率是________．解析：令第二次取得一等品为事件A ，第一次取得二等品为事件B ，则P (AB )＝C 12·C 14C 16·C 15＝415，P (A )＝C 14·C 13＋C 12C 14C 16·C 15＝23. 所以P (B |A )＝P （AB ）P （A ）＝415×32＝25. 答案：253．现有6个节目准备参加比赛，其中4个舞蹈节目，2个语言类节目，如果不放回地依次抽取2个节目，求：(1)第1次抽到舞蹈节目的概率；(2)第1次和第2次都抽到舞蹈节目的概率；(3)在第1次抽到舞蹈的条件下，第2次抽到舞蹈节目的概率． 解：设“第1次抽到舞蹈节目”为事件A ，“第2次抽到舞蹈节目”为事件B ，则“第1次和第2次都抽到舞蹈节目”为事件AB .(1)从6个节目中不放回地依次抽取2次的事件数为n (Ω)＝A 26＝30，根据分步计数原理n (A )＝A 14A 15＝20，于是P (A )＝n （A ）n （Ω）＝2030＝23. (2)因为n (AB )＝A 24＝12， 于是P (AB )＝n （AB ）n （Ω）＝1230＝25.(3)法一 由(1)(2)可得，在第1次抽到舞蹈节目的条件下，第2次抽到舞蹈节目的概率为P (B |A )＝P （AB ）P （A ）＝25÷23＝35. 法二 因为n (AB )＝12，n (A )＝20，所以P (B |A )＝n （AB ）n （A ）＝1220＝35.。

与统计相结合的概率问题1、为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：是否需要志愿性别男女需要40 30不需要160 270（1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；（2）能否有99％的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（3）根据（2）的结论，能否提供更好的调查方法来估计该地区老年人，需要志愿帮助的老年人的比例？说明理由附：解：（1）调查的500位老年人中有70位需要志愿者提供帮助，因此该地区老年人中，需要帮助的老年人的比例的估算值为7014%500=（2）22500(4027030160)9.96720030070430K⨯⨯-⨯==⨯⨯⨯。

由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关。

(III)由(II)的结论知，该地区老年人是否需要帮助与性别有关，并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异，因此在调查时，先确定该地区老年人中男、女的比例，再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好．2、某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测试了每件产品的质量指标值，得到下面试验结果：（Ⅰ）分别估计用A配方，B配方生产的产品的优质品率；（Ⅱ）已知用B配方生成的一件产品的利润y(单位：元)与其质量指标值t的关系式为从用B 配方生产的产品中任取一件，其利润记为X （单位：元），求X 的分布列及数学期望.（以实验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）. 解：（Ⅰ）由实验结果知，用A 配方生产的产品中优质的平率为228=0.3100+，所以用A 配方生产的产品的优质品率的估计值为0.3。

姓名，年级：时间：2。

2 概率1、已知箱中共有6个球,其中红球、黄球、蓝球各2 个,每次从该箱中取1个球(有放回，每球取到的机会均等)，共取三次。

设事件A: “第一次取到的球和第二次取到的球颜色相同”，事件B:“三次取到的球颜色都相同”,则(|)P B A （）A.16B.13C.23D.12、某地区空气质量监测资料表明，一天的空气质量为优良的概率是0。

75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是( ）A。

0。

8 B。

0。

75 C。

0.6 D。

0。

453、把一枚骰子连续掷两次，已知在第一次抛出的是偶数点的情况下，第二次抛出的也是偶数点的概率为( )A。

1B。

12C.13D。

144、在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球，在第一次摸出红球的条件下,第2次也摸到红球的概率为（)A. 35B。

25C.110D。

595、甲口袋内装有除颜色外完全相同的8个红球和4个白球,乙口袋内装有除颜色外完全相同的9个红球和3个白球，从两口袋内各摸出1个球,下列事件中概率为512的是( )A。

2个球都是白球 B.2个球中恰好有1个是白球C。

2个球都不是白球D。

2个球不都是红球6、某种子每粒发芽的概率都为0。

9，现播种1000粒,对于没有发芽的种子，每粒需再补种2粒，补种的种子数记X,则X的数学期望为（）A。

100 B.200 C.300 D。

4007、甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军,乙队需要再贏两局才能得冠军.若两队胜每局的概率相同，则甲队获得冠军的概率为（）A 。

12 B. 35C. 23D. 34 8、甲、乙二人争夺一场围棋比赛的冠军，若比赛为三局两胜制,甲在每局比赛中获胜的概率均为23，且各局比赛结果相互独立，则在甲获得冠军的情况下,比赛进行了三局的概率为( ）A 。

13B 。

25C. 23D. 45 9、某人射击一次,击中目标的概率为35，经过3次射击,此人至少有2次击中目标的概率为（ ) A.81125B 。

第二章 2.2 第2课时一、选择题1．若事件P 与Q 相互独立，则P 与Q 、P 与Q 、P 与Q 相互独立的对数是( ) A ．0 B ．1 C ．2 D ．3[答案] D2．甲、乙、丙3人投篮，投进的概率分别是13，25，12.现3人各投篮1次，求3人都没有投进的概率为( )A ．115B ．215C ．15D ．110[答案] C[解析] 记“甲投篮1次投进”为事件A 1，“乙投篮1次投进”为事件A 2，“丙投篮1次投进”为事件A 3，“3人都没有投进”为事件A ，则P (A 1)＝13，P (A 2)＝25，P (A 3)＝12，∴P (A )＝P (A 1 A 2 A 3)＝P (A 1)P (A 2)P (A 3)＝[1－P (A 1)]·[1－P (A 2)]·[1－P (A 3)]＝(1－13)(1－25)(1－12)＝15. ∴3人都没有投进的概率为15.3．甲、乙两水文站同时作水文预报，如果甲站、乙站各自预报的准确率为0.8和0.7，那么，在一次预报中，甲、乙预报都准确的概率为( )A ．0.7B ．0.56C ．0.64D ．0.8[答案] B[解析] 由题意可知，甲、乙两站的预报准确率是相互独立的，故所求事件的概率P ＝0.8×0.7＝0.56.4．在某道路A 、B 、C 三处设有交通灯，这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒，某辆车在这个道路上匀速行驶，则三处都不停车的概率为( )A ．35192B ．25192C ．35576D ．21192[答案] A[解析] 由题意知每个交通灯开放绿灯的概率分别为512、712、34.∴所求概率P ＝512×712×34＝35192.故选A ．5．甲、乙两人同时报考某一所大学，甲被录取的概率为0.6，乙被录取的概率为0.7，两人是否被录取互不影响，则其中至少有一人被录取的概率为( )A ．0.12B ．0.42C ．0.46D ．0.88[答案] D[解析] 由题意知，甲、乙都不被录取的概率为(1－0.6)(1－0.7)＝0.12. ∴至少有一人被录取的概率为1－0.12＝0.88.故选D.6．(2019·九江高二检测)甲射手击中靶心的概率为13，乙射手击中靶心的概率为12，甲、乙两人各射击一次，那么56等于( )A ．甲、乙都击中靶心的概率B ．甲、乙恰好有一人击中靶心的概率C ．甲、乙至少有1人击中靶心的概率D ．甲、乙不全击中靶心的概率 [答案] D[解析] 设“甲、乙两人都击中靶心”的事件为A ，则P (A )＝13×12＝16，P (A )＝1－P (A )＝56.而A 表示“甲、乙不全击中靶心”这一事件，故应选D.7．打靶时，甲每次打10次，可中靶8次；乙每次打10次，可中靶7次．若两人同时射击一个目标，则它们都中靶的概率是( )A ．35B.34 C ．1225D.1425[答案] D[解析] 由相互独立事件概率公式得P ＝0.8×0.7＝0.56＝1425.故选D.二、填空题8．加工某一零件需经过三道工序，设第一、二、三道工序的次品率分别为170、169、168，且各道工序互不影响，则加工出来的零件的次品率为__________．[答案]370[解析] 本题考查独立事件，对立事件有关概率的基本知识以及计算方法． 设加工出来的零件为次品为事件A ，则A 为加工出来的零件为正品． P (A )＝1－P (A )＝1－(1－170)(1－169)(1－168)＝370.9．有甲、乙、丙3批饮料，每批100箱，其中各有一箱是不合格的，从3批饮料中各抽出一箱，求：(1)恰有一箱不合格的概率____________； (2)至少有一箱不合格的概率____________． [答案] (1)0.029 (2)0.03[解析] 记抽出“甲饮料不合格”为事件A ，“乙饮料不合格”为事件B ，“丙饮料不合格”为事件C ，则P (A )＝0.01，P (B )＝0.01，P (C )＝0.01.(1)从3批饮料中，各抽取一箱，恰有一箱不合格的概率为 P ＝P (A BC )＋P (A B C )＋P (AB C )＝0.01×0.992＋0.01×0.992＋0.01×0.992≈0.029. (2)各抽出一箱都合格的概率为0.99×0.99×0.99≈0.97. 所以至少有一箱不合格的概率为1－0.97≈0.03. 三、解答题10．甲、乙两人轮流投篮，每人每次投一球．约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束．设甲每次投篮投中的概率为13，乙每次投篮投中的概率为12，且各次投篮互不影响． (1)求乙获胜的概率；(2)求投篮结束时乙只投了2个球的概率．[解析] 设A k ，B k 分别表示甲、乙在第k 次投篮投中，则P (A k )＝13，P (B k )＝12，(k ＝1,2,3)．(1)记“乙获胜”为事件C ，由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知P (C )＝P (A 1B 1)＋P (A1B1A 2B 2)＋P (A1B1A2B 2·A 3B 3)＝P (A 1)P (B 1)＋P (A 1)P (B 1)P (A 2)P (B 2)＋P (A 1)P (B 1)P (A 2)P (B 2)P (A 3)P (B 3) ＝23×12＋(23)2(12)2＋(23)3(12)3＝1327. (2)记“投篮结束时乙只投了2个球”为事件D ，则由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知P (D )＝P (A1B1A 2B 2)＋P (A1B1A2B 2A 3)＝P (A 1)P (B 1)P (A 2)P (B 2)＋P (A 1)P (B 1)P (A 2)·P (B 2)P (A 3) ＝(23)2(12)2＋(23)2(12)213＝427.一、选择题1．从甲口袋中摸出1个白球的概率为13，从乙口袋中摸出一个白球的概率为14，从两个口袋中各摸出一球，那么1112是( )A ．两个球都是白球的概率B ．两个球都不是白球的概率C ．两个球恰有一个是白球的概率D ．两个球至少有一个不是白球的概率 [答案] D2.(2019·德州高二检测)荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时，均从一片荷叶跳到另一个荷叶)，而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图所示．假设现在青蛙在A 荷叶上，则跳三次之后停在A 荷叶上的概率是( )A ．13B ．29C ．49D ．827[答案] A[解析] 由已知逆时针跳一次的概率为23，顺时针跳一次的概率为13.则逆时针跳三次停在A上的概率为P 1＝23×23×23＝827，顺时针跳三次停在A 上的概率为P 2＝13×13×13＝127.所以跳三次之后停在A 上的概率为P ＝P 1＋P 2＝827＋127＝13.3．如图，用K 、A 1、A 2三类不同的元件连接成一个系统．当K 正常工作且A 1、A 2至少有一个正常工作时，系统正常工作．已知K 、A 1、A 2正常工作的概率依次为0.9、0.8、0.8，则系统正常工作的概率为( )A ．0.960B ．0.864C ．0.720D ．0.576[答案] B[解析] 本题考查相互独立事件同时发生的概率计算．系统正常工作，则元件K 正常．A 1，A 2至少有一个正常．∴P ＝P (K ∩A 1∩A 2)＋P (K ∩A 1∩A －2)＋P (K ∩A －1∩A 2)＝0.9×0.8×0.8＋0.9×0.8×0.2＋0.9×0.2×0.8＝0.864.二、填空题4．甲、乙两门高射炮同时向一敌机开炮，已知甲击中敌机的概率为0.6，乙击中敌机的概率为0.8，敌机被击中的概率为________．[答案] 0.92[解析] 解法1：设“甲击中敌机”为事件A ，“乙击中敌机”为事件B ，由于事件A 、B 相互独立，所以所求的概率为P ＝P (A ∩B )＋P (A ∩B )＋P (A ∩B )＝P (A )·P (B )＋P (A )·P (B )＋P (A )·P (B )＝0.6×0.8＋0.4×0.8＋0.6×0.2＝0.92.解法2：利用对立事件的公式P ＝1－P (A ∩B )＝1－P (A )·P (B )＝1－(1－0.6)(1－0.8)＝0.92.解法3：敌机被击中为事件A ∪B ，∴P (A ∪B )＝P (A )＋P (B )－P (A ∩B )＝P (A )＋P (B )－P (A )·P (B )＝0.6＋0.8－0.6×0.8＝0.92.5．某班有4位同学住在同一个小区，上学路上要经过1个路口．假设每位同学在路口是否遇到红灯是相互独立的，且遇到红灯的概率都是13，则最多1名同学遇到红灯的概率是________．[答案]1627[解析] P ＝(23)4＋C 14·(13)·(23)3＝1627. 三、解答题6．在女子十米跳台比赛中，已知甲、乙两名选手发挥正常的概率分别为0.9,0.85，求(1)甲、乙两名选手发挥均正常的概率； (2)甲、乙两名选手至多有一名发挥正常的概率； (3)甲、乙两名选手均出现失误的概率．[解析] 令事件A ，B 分别表示甲、乙两名选手发挥正常，由题意可知，事件A ，B 相互独立，且P (A )＝0.9，P (B )＝0.85.(1)两名选手发挥均正常的概率P ＝P (AB )＝P (A )P (B )＝0.9×0.85＝0.765.(2)对立事件为“甲、乙两名选手发挥均正常”，故所求事件的概率P ＝1－P (AB )＝1－0.765＝0.235.(3)依题意可知，所求事件的概率P ＝P (A B )＝P (A )P (B )＝(1－P (A ))(1－P (B )) ＝(1－0.9)×(1－0.85)＝0.015.7．甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题．规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格．(1)分别求甲、乙两人考试合格的概率； (2)求甲、乙两人至少有一人考试合格的概率．[解析] (1)设甲、乙两人考试合格的事件分别为A 、B ，则P (A )＝C 26C 14＋C 36C 310＝60＋20120＝23，P (B )＝C 28C 12＋C 38C 310＝56＋56120＝1415. (2)解法1：因为事件A 、B 相互独立，所以甲、乙两人考试均不合格的概率为 P (A ·B )＝P (A )·P (B )＝⎝⎛⎭⎫1－23×⎝⎛⎭⎫1－1415＝145. 所以甲、乙两人至少有一人考试合格的概率为 P ＝1－P (A ·B )＝1－145＝4445.答：甲、乙两人至少有一人考试合格的概率为4445.解法2：因为事件A 、B 相互独立，所以甲、乙两人至少有一人考试合格的概率为 P ＝P (A ·B )＋P (A ·B )＋P (A ·B )＝P (A )·P (B )＋P (A )·P (B )＋P (A )·P (B )＝23×115＋13×1415＋23×1415＝4445. 8．甲、乙、丙三人分别独立解一道题，甲做对的概率是12，三人都做对的概率是124，三人全做错的概率是14.(1)分别求乙、丙两人各自做对这道题的概率； (2)求甲、乙、丙三人中恰有一人做对这道题的概率．[解析] (1)分别设甲、乙、丙三人各自全做对这道题分别为事件A 、B 、C 则P (A )＝12，由题意得⎩⎨⎧12·P (B )P (C )＝124，(1－12)(1－P (B ))(1－P (C ))＝14，解得P (B )＝13，P (C )＝14或P (B )＝14，P (C )＝13.所以乙、丙两人各自全做对这道题的概率分别为13和14，或14和13.(2)设“甲、乙、丙三人恰有一人做对这道题”为事件D ，则P (D )＝P (A )P (B )P (C )＋P (A )P (B )P (C )＋P (A )P (B )P (C )＝14＋18＋112＝1124. 所以甲、乙、丙三人中恰有一人做对这道题的概率为1124.。

2.4 正态分布 课时目标1.了解正态曲线的特点、意义.2.会用正态分布解决一些实际问题.3.理解3σ原则．1．正态分布：在生产、科研和日常生活中，经常会遇到这样一类随机现象，它们是由一些相互独立的偶然因素所引起的，而每一个这种偶然因素在总体的变化中都只是起着均匀、微小的作用，表示这类随机现象的随机变量的概率分布一般近似服从正态分布．__________________的随机变量叫做正态随机变量，简称正态变量．2．正态曲线：正态变量概率密度曲线的函数表达式为f (x )＝________________，x ∈R ，其中μ、σ是参数，且σ>0，μ∈R ，参数μ和σ分别为正态变量的数学期望和标准差．期望为μ、标准差为σ的正态分布通常记作N (μ，σ2)．________________________________的图象叫做正态曲线．3．3σ原则正态分布在三个特殊区间内取值的概率P (μ－σ<X <μ＋σ)＝________；P (μ－2σ<X <μ＋2σ)＝________；P (μ－3σ<X <μ＋3σ)＝________.一、选择题1．设有一正态总体，它的概率密度曲线是函数f (x )的图象，且f (x )＝18π·e －(x －10)28，则这个正态总体的平均数与标准差分别是( )A ．10与8B ．10与2C ．8与10D ．2与102．下列函数是正态分布密度函数的是( )A ．f (x )＝12πσe (x －μ)22σ2，μ、σ(σ>0)都是实数 B ．f (x )＝2π2π·e －x 22C ．f (x )＝122πe (x －1)2σ D ．f (x )＝12πe x 223．正态曲线关于y 轴对称，当且仅当它所对应的正态总体均值为( )A ．1B ．－1C ．0D ．不确定4．已知X ～N (0，σ2)，且P (－2≤X ≤0)＝0.4，则P (X >2)等于( )A ．0.1B ．0.2C ．0.3D ．0.45．已知随机变量ξ服从正态分布N (4，σ2)，则P (ξ>4)等于( )A.15B.14C.13D.12二、填空题6.如图所示是三个正态分布X ～N (0,0.25)，Y ～N (0,1)，Z ～N (0,4)的密度曲线，则三个随机变量X，Y，Z对应曲线分别是图中的______、______、______.7．在某项测量中，测量结果ξ服从正态分布N(1，σ2)(σ>0)，已知ξ在(0,1)内取值的概率为0.4，则ξ在(0,2)内取值的概率为________．8．工人生产的零件的半径ξ在正常情况下服从正态分布N(μ，σ2)．在正常情况下，取出1000个这样的零件，半径不属于(μ－3σ，μ＋3σ)这个范围的零件约有________个．三、解答题9．如图是一个正态曲线．试根据该图象写出其正态分布的概率密度函数的解析式，求出总体随机变量的期望和方差．10．在某次数学考试中，考生的成绩ξ服从一个正态分布，即ξ～N(90,100)．(1)试求考试成绩ξ位于区间(70,110)上的概率是多少？(2)若这次考试共有2000名考生，试估计考试成绩在(80,100)间的考生大约有多少人？能力提升11．若随机变量X～N(μ，σ2)，则P(X≤μ)＝________.12．某年级的一次信息技术测验成绩近似服从正态分布N(70,102)，如果规定低于60分为不及格，求：(1)成绩不及格的人数占多少？(2)成绩在80～90分之间的学生占多少？1．要求正态分布的概率密度函数式，关键是理解正态分布密度曲线的概念及解析式中各字母参数的意义．2．解正态分布的概率计算问题，一定要灵活把握3σ原则，将所求问题向P(μ－σ<ξ<μ＋σ)，P(μ－2σ<ξ<μ＋2σ)，P(μ－3σ<ξ<μ＋3σ)进行转化，然后利用特定值求出相应概率．同时要充分利用曲线的对称性和曲线与x轴之间的面积为1这一特殊性质．2．4正态分布答案知识梳理1．服从正态分布2.12πσe－(x－μ)22σ2正态变量的概率密度函数3．0.6830.9540.997 作业设计1．B[f(x)可以改写成f(x)＝12π×4e－(x－10)22×4，对照可知μ＝10，σ＝2.]2．B3．C[均值即为其对称轴，∴μ＝0.]4．A[∵X～N(0，σ2)，∴μ＝0，又P(－2≤X≤0)＝0.4，∴P(X>2)＝12(1－0.4×2)＝0.1.]5．D[由正态分布图象可知，μ＝4是该图象的对称轴，∴P(ξ<4)＝P(ξ>4)＝12.]6．①②③解析在密度曲线中，σ越大，曲线越“矮胖”；σ越小，曲线越“瘦高”．7．0.8解析正态曲线关于x＝1对称，∴ξ在(1,2)内取值的概率也为0.4.8．3解析半径属于(μ－3σ，μ＋3σ)的零件个数约有0.997×1000＝997，∴不属于这个范围的零件个数约有3个．9．解从给出的正态曲线可知，该正态曲线关于直线x＝20对称，最大值是12π，所以μ＝20，1 2π·σ＝12π，解得σ＝ 2.于是概率密度函数的解析式是f (x )＝12πe －(x －20)24，x ∈(－∞，＋∞)． 总体随机变量的期望是μ＝20，方差是σ2＝(2)2＝2.10．解 ∵ξ～N (90,100)，∴μ＝90，σ＝100＝10.(1)由于正态变量在区间(μ－2σ，μ＋2σ)内取值的概率是0.954，而该正态分布中，μ－2σ＝90－2×10＝70，μ＋2σ＝90＋2×10＝110，于是考试成绩ξ位于区间(70,110)内的概率就是0.954.(2)由μ＝90，σ＝10，得μ－σ＝80，μ＋σ＝100.由于正态变量在区间(μ－σ，μ＋σ)内取值的概率是0.683，所以考试成绩ξ位于区间(80,100)内的概率是0.683.一共有2000名考生，所以考试成绩在(80,100)内的考生大约有2000×0.683＝1366(人)．11.12解析 由于随机变量X ～N (μ，σ2)，其概率密度函数关于x ＝μ对称，故P (x ≤μ)＝12. 12．解 (1)设学生的得分情况为随机变量X ，X ～N (70,102)，则μ＝70，σ＝10.所以成绩在60～80之间的学生所占的比为P (70－10<X <70＋10)＝0.683，所以成绩不及格的学生的比为：12(1－0.683)＝0.1585，即成绩不及格的学生占15.85%. (2)成绩在80～90之间的学生的比为12[P (70－2×10<X <70＋2×10)－P (60<x <80)] ＝12(0.954－0.683)＝0.1355. 即成绩在80～90分之间的学生占13.55%.。