第一章 基本概念
- 格式:ppt
- 大小:69.00 KB
- 文档页数:38


概率论与数理统计复习第一章概率论的基本概念一.基本概念随机试验E:1可以在相同的条件下重复地进行;2每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;3进行一次试验之前不能确定哪一个结果会出现.样本空间S: E的所有可能结果组成的集合. 样本点基本事件:E的每个结果.随机事件事件:样本空间S的子集.必然事件S:每次试验中一定发生的事件. 不可能事件:每次试验中一定不会发生的事件.二. 事件间的关系和运算事件B包含事件A 事件A发生必然导致事件B发生.∪B和事件事件A与B至少有一个发生.3. A∩B=AB积事件事件A与B同时发生.4. A-B 差事件事件A 发生而B 不发生.5. AB= A 与B 互不相容或互斥事件A 与B 不能同时发生.6. AB=且A ∪B=S A 与B 互为逆事件或对立事件表示一次试验中A 与B 必有一个且仅有一个发生. B=A, A=B .运算规则 交换律 结合律 分配律 德摩根律 B A B A = B A B A =三. 概率的定义与性质1.定义 对于E 的每一事件A 赋予一个实数,记为PA,称为事件A 的概率.1非负性 PA ≥0 ; 2归一性或规范性 PS=1 ;3可列可加性 对于两两互不相容的事件A 1,A 2,…A i A j =φ, i ≠j, i,j=1,2,…,PA 1∪A 2∪…=P A 1+PA 2+…2.性质1 P = 0 , 注意: A 为不可能事件2有限可加性对于n个两两互不相容的事件A1,A2,…,An,PA1∪A2∪…∪An=PA1+PA2+…+PAn有限可加性与可列可加性合称加法定理3若A B, 则PA≤PB, PB-A=PB-PA .4对于任一事件A, PA≤1, PA=1-PA .5广义加法定理对于任意二事件A,B ,PA∪B=PA+PB-PAB .对于任意n个事件A1,A2,…,An…+-1n-1PA1A2…An四.等可能古典概型1.定义如果试验E满足:1样本空间的元素只有有限个,即S={e1,e2,…,en};2每一个基本事件的概率相等,即Pe1=Pe2=…= Pen.则称试验E所对应的概率模型为等可能古典概型.2.计算公式 PA=k / n 其中k是A中包含的基本事件数, n是S中包含的基本事件总数.五.条件概率1.定义 事件A 发生的条件下事件B 发生的条件概率PB|A=PAB / PA PA>0.2.乘法定理 PAB=PA P B|A PA>0; PAB=PB P A|B PB>0.PA 1A 2…A n =PA 1PA 2|A 1PA 3|A 1A 2…PA n |A 1A 2…A n-1 n ≥2, PA 1A 2…A n-1 > 03. B 1,B 2,…,B n 是样本空间S 的一个划分B i B j =φ,i ≠j,i,j=1,2,…,n, B 1∪B 2∪…∪B n =S ,则当PB i >0时,有全概率公式 PA=()()i ni i B A P B P ∑=1当PA>0, PB i>0时,有贝叶斯公式P B i|A=()()()()()()∑==ni i i i i i B A P B P B A P B P A P AB P 1. 六.事件的独立性1.两个事件A,B,满足PAB = PA PB 时,称A,B 为相互独立的事件.1两个事件A,B 相互独立 PB= P B|A .2若A 与B,A 与B ,A 与B, ,A 与B 中有一对相互独立,则另外三对也相互独立.2.三个事件A,B,C 满足PAB =PA PB, PAC= PA PC, PBC= PB PC,称A,B,C 三事件两两相互独立. 若再满足PABC =PA PB PC,则称A,B,C 三事件相互独立.个事件A 1,A 2,…,A n ,如果对任意k 1<k ≤n,任意1≤i 1<i 2<…<i k ≤n.有()()()()kki i i i i i A P A P A P A A A P 2121=,则称这n 个事件A 1,A 2,…,A n 相互独立.第二章 随机变量及其概率分布一.随机变量及其分布函数1.在随机试验E 的样本空间S={e}上定义的单值实值函数X=X e 称为随机变量.2.随机变量X 的分布函数Fx=P{X ≤x} , x 是任意实数. 其性质为:10≤Fx≤1 ,F -∞=0,F∞=1. 2Fx 单调不减,即若x 1<x 2 ,则 Fx 1≤Fx 2.3Fx 右连续,即Fx+0=Fx. 4P{x 1<X≤x 2}=Fx 2-Fx 1.二.离散型随机变量 只能取有限个或可列无限多个值的随机变量1.离散型随机变量的分布律 P{X= x k }= p k k=1,2,… 也可以列表表示. 其性质为:1非负性 0≤P k ≤1 ; 2归一性11=∑∞=k k p .2.离散型随机变量的分布函数 Fx=∑≤xX k k P 为阶梯函数,它在x=x kk=1,2,…处具有跳跃点,其跳跃值为p k =P{X=x k } .3.三种重要的离散型随机变量的分布1X~0-1分布 P{X=1}= p ,P{X=0}=1–p 0<p<1 .2X~bn,p 参数为n,p 的二项分布P{X=k}=()kn k p p k n --⎪⎪⎭⎫ ⎝⎛1k=0,1,2,…,n 0<p<1 3X~参数为的泊松分布 P{X=k}=λλ-e k k !k=0,1,2,… >0 三.连续型随机变量1.定义 如果随机变量X 的分布函数Fx 可以表示成某一非负函数fx 的积分Fx=()dt t f x⎰∞-,-∞< x <∞,则称X 为连续型随机变量,其中f x 称为X 的概率密度函数.2.概率密度的性质1非负性 fx ≥0 ; 2归一性 ⎰∞∞-dx x f )(=1 ;3 P{x 1<X ≤x 2}=⎰21)(xx dx x f ; 4若f x 在点x 处连续,则f x=F/x .注意:连续型随机变量X 取任一指定实数值a 的概率为零,即P{X= a}=0 .3.三种重要的连续型随机变量的分布1X ~U a,b 区间a,b 上的均匀分布⎩⎨⎧=-0)(1a b x f其它b x a << . 2X 服从参数为的指数分布.()⎩⎨⎧=-0/1θθx ex f 00≤>x x 若若 >0.3X~N ,2参数为,的正态分布222)(21)(σμσπ--=x e x f -<x<, >0.特别, =0, 2=1时,称X 服从标准正态分布,记为X~N 0,1,其概率密度2221)(x e x -=πϕ , 标准正态分布函数 ⎰=Φ∞--xt dt e x 2221)(π, -x=1-Φx .若X ~N ,2, 则Z=σμ-X ~N 0,1, P{x 1<X ≤x 2}=Φσμ-2x-Φσμ-1x .若P{Z>z }= P{Z<-z }= P{|Z|>z /2}= ,则点z ,-z , z / 2分别称为标准正态分布的上,下,双侧分位点. 注意:z =1- , z 1- = -z .四.随机变量X 的函数Y= g X 的分布1.离散型随机变量的函数若gx k k=1,2,…的值全不相等,则由上表立得Y=gX 的分布律.若gx k k=1,2,…的值有相等的,则应将相等的值的概率相加,才能得到Y=gX 的分布律.2.连续型随机变量的函数若X 的概率密度为f X x,则求其函数Y=gX 的概率密度f Y y 常用两种方法:1分布函数法 先求Y 的分布函数F Y y=P{Y ≤y}=P{gX ≤y}=()()dx x f ky Xk∑⎰∆其中Δk y 是与gX ≤y 对应的X 的可能值x 所在的区间可能不只一个,然后对y 求导即得f Y y=F Y/y .2公式法 若gx 处处可导,且恒有g /x>0 或g / x<0 ,则Y=g X 是连续型随机变量,其概率密度为()()()()⎩⎨⎧'=yhyhfyf XY其它βα<<y其中hy是gx的反函数 , = min g -,g = max g -,g .如果f x在有限区间a,b以外等于零,则 = min g a,g b = max g a,g b .第三章二维随机变量及其概率分布一.二维随机变量与联合分布函数1.定义若X和Y是定义在样本空间S上的两个随机变量,则由它们所组成的向量X,Y称为二维随机向量或二维随机变量.对任意实数x,y,二元函数Fx,y=P{X≤x,Y≤y}称为X,Y的X和Y的联合分布函数.2.分布函数的性质1Fx,y分别关于x和y单调不减.20≤Fx,y≤1 , Fx,- =0, F-,y=0, F-,-=0, F,=1 .3 Fx,y关于每个变量都是右连续的,即 Fx+0,y= Fx,y, Fx,y+0= Fx,y .4对于任意实数x 1<x 2 , y 1<y 2P{x 1<X ≤x 2 , y 1<Y ≤y 2}= Fx 2,y 2- Fx 2,y 1- Fx 1,y 2+ Fx 1,y 1二.二维离散型随机变量及其联合分布律1.定义 若随机变量X,Y 只能取有限对或可列无限多对值x i ,y j i ,j =1,2,… 称X,Y 为二维离散型随机变量.并称P{X= x i ,Y= y j }= p i j 为X,Y 的联合分布律.也可列表表示.2.性质 1非负性 0≤p i j ≤1 .2归一性 ∑∑=i jijp 1 .3. X,Y 的X 和Y 的联合分布函数Fx,y=∑∑≤≤x x yy ij i j p三.二维连续型随机变量及其联合概率密度1.定义 如果存在非负的函数f x,y,使对任意的x 和y,有Fx,y=⎰⎰∞-∞-y xdudv v u f ),(则称X,Y 为二维连续型随机变量,称fx,y 为X,Y 的X 和Y 的联合概率密度.2.性质 1非负性 f x,y ≥0 . 2归一性 1),(=⎰⎰∞∞-∞∞-dxdy y x f .3若f x,y 在点x,y 连续,则yx y x F y x f ∂∂∂=),(),(2 4若G 为xoy 平面上一个区域,则⎰⎰=∈Gdxdy y x f G y x P ),(}),{(.四.边缘分布1. X,Y 关于X 的边缘分布函数 F X x = P{X ≤x , Y<}= F x , .X,Y 关于Y 的边缘分布函数 F Y y = P{X<, Y ≤y}= F ,y2.二维离散型随机变量X,Y关于X 的边缘分布律 P{X= x i }=∑∞=1j ij p = p i · i =1,2,… 归一性 11=∑∞=•i i p .关于Y 的边缘分布律 P{Y= y j }=∑∞=1i ij p = p·jj =1,2,… 归一性11=∑∞=•j j p .3.二维连续型随机变量X,Y关于X 的边缘概率密度f X x=⎰∞∞-dy y x f ),( 归一性1)(=⎰∞∞-dx x f X关于Y 的边缘概率密度f Y y=x d y x f ⎰∞∞-),( 归一性1)(=⎰∞∞-dyy f Y五.相互独立的随机变量1.定义若对一切实数x,y,均有Fx,y= FX x FYy ,则称X和Y相互独立.2.离散型随机变量X和Y相互独立⇔p i j= p i··p·j i ,j =1,2,…对一切x i,y j成立.3.连续型随机变量X和Y相互独立⇔f x,y=f X xf Y y对X,Y所有可能取值x,y都成立.六.条件分布1.二维离散型随机变量的条件分布定义设X,Y是二维离散型随机变量,对于固定的j,若P{Y=yj}>0,则称P{X=xi |Y=yj}为在Y= yj条件下随机变量X的条件分布律.同样,对于固定的i,若P{X=xi}>0,则称P{Y=yj |X=xi}为在X=xi 条件下随机变量Y 的条件分布律.,}{},{jj ijjippyYPyYxXP•=====,}{},{•=====ij iijippxXPyYxXP第四章 随机变量的数字特征一.数学期望和方差的定义随机变量X 离散型随机变量连续型随机变量分布律P{X=x i }= p i i =1,2,… 概率密度f x数学期望均值EX∑∞=1i i i p x 级数绝对收敛⎰∞∞-dx x xf )(积分绝对收敛方差DX=E{X-EX 2}[]∑-∞=12)(i i i p X E x ⎰-∞∞-dx x f X E x )()]([2=EX 2-EX 2 级数绝对收敛 积分绝对收敛函数数学期望EY=EgXi i i p x g ∑∞=1)(级数绝对收敛 ⎰∞∞-dx x f x g )()(积分绝对收敛标准差X=√DX .二.数学期望与方差的性质1. c 为为任意常数时, Ec = c , EcX = cEX , Dc = 0 , D cX = c 2 DX .,Y为任意随机变量时, E X±Y=EX±EY .3. X与Y相互独立时, EXY=EXEY , DX±Y=DX+DY .4. DX = 0 P{X = C}=1 ,C为常数.三.六种重要分布的数学期望和方差 EX DX~ 0-1分布P{X=1}= p 0<p<1 p p 1- p ~ b n,p 0<p<1 n p n p 1- p ~~ Ua,b a+b/2 b-a 2/12服从参数为的指数分布2~ N ,22四.矩的概念随机变量X的k阶原点矩EX k k=1,2,…随机变量X 的k 阶中心矩E{X-EX k}随机变量X 和Y 的k+l 阶混合矩EX k Y l l=1,2,…随机变量X 和Y 的k+l 阶混合中心矩E{X-EX k Y-EY l }第六章 样本和抽样分布一.基本概念总体X 即随机变量X ; 样本X 1 ,X 2 ,…,X n 是与总体同分布且相互独立的随机变量;样本值x 1 ,x 2 ,…,x n 为实数;n 是样本容量.统计量是指样本的不含任何未知参数的连续函数.如:样本均值∑==n i i X n X 11 样本方差()∑--==n i i X X n S 12211 样本标准差S样本k 阶矩∑==n i k i k X n A 11 k=1,2,… 样本k 阶中心矩∑-==n i ki k X X n B 1)(1k=1,2,…二.抽样分布 即统计量的分布1.X 的分布 不论总体X 服从什么分布, E X = EX , D X = DX / n .特别,若X~ N ,2 ,则 X ~ N , 2 /n .分布 1定义 若X ~N 0,1,则Y =∑=ni i X 12~ 2n 自由度为n 的2分布.2性质 ①若Y~ 2n,则EY = n , DY = 2n .②若Y 1~ 2n 1 Y 2~ 2n 2 ,则Y 1+Y 2~ 2n 1 + n 2.③若X~ N ,2 , 则22)1(σS n -~ 2n-1,且X 与S 2相互独立.3分位点 若Y~ 2n,0< <1 ,则满足的点)()(),(),(22/122/212n n n n ααααχχχχ--和分别称为2分布的上、下、双侧分位点.3. t 分布1定义 若X~N 0,1 ,Y~ 2 n,且X,Y 相互独立,则t=nY X~tn 自由度为n 的t 分布. 2性质①n →∞时,t 分布的极限为标准正态分布.②X ~N ,2 时,nS X μ-~ t n-1 . ③两个正态总体相互独立的样本 样本均值 样本方差X~ N 1,12 且12=22=2 X 1 ,X 2 ,…,X n1 X S 12Y~ N 2,22 Y 1 ,Y 2 ,…,Y n2 Y S 22则 212111)()(n n S Y X w +---μμ~ t n 1+n 2-2 , 其中 2)1()1(212222112-+-+-=n n S n S n S w3分位点 若t ~ t n ,0 < <1 , 则满足的点)(),(),(2/n t n t n t ααα±-分别称t 分布的上、下、双侧分位点.注意: t 1- n = - t n.分布 1定义 若U~2n 1, V~ 2n 2, 且U,V 相互独立,则F =21n V n U ~Fn 1,n 2自由度为n 1,n 2的F 分布.2性质条件同3.2③22212221σσS S ~Fn 1-1,n 2-13分位点 若F~ Fn 1,n 2 ,0< <1,则满足的点),(),(),,(),,(212/1212/21121n n F n n F n n F n n F αααα--和分别称为F 分布的上、下、双侧分位点. 注意: .).(1),(12211n n F n n F αα=- 第七章 参数估计一.点估计 总体X 的分布中有k 个待估参数1, 2,…, k .X 1 ,X 2 ,…,X n 是X 的一个样本, x 1 ,x 2 ,…,x n 是样本值.1.矩估计法先求总体矩⎪⎩⎪⎨⎧===),,,(),,,(),,,(2121222111k k k k k θθθμμθθθμμθθθμμ 解此方程组,得到⎪⎩⎪⎨⎧===),,,(),,,(),,,(2121222111kk k k k μμμθθμμμθθμμμθθ ,以样本矩A l 取代总体矩 ll=1,2,…,k 得到矩估计量⎪⎪⎩⎪⎪⎨⎧===∧∧∧),,,(),,,(),,,(2121222111k k k k k A A A A A A A A A θθθθθθ,若代入样本值则得到矩估计值.2.最大似然估计法若总体分布形式可以是分布律或概率密度为px, 1, 2,…, k ,称样本X 1 ,X 2 ,…,X n 的联合分布∏==ni k i k x p L 12121),,,,(),,,(θθθθθθ 为似然函数.取使似然函数达到最大值的∧∧∧k θθθ,,,21 ,称为参数1, 2,…,k 的最大似然估计值,代入样本得到最大似然估计量.若L 1, 2,…, k 关于1, 2,…, k 可微,则一般可由似然方程组 0=∂∂i L θ 或 对数似然方程组 0ln =∂∂iLθ i =1,2,…,k 求出最大似然估计. 3.估计量的标准(1)无偏性 若E ∧θ=,则估计量∧θ称为参数的无偏估计量.不论总体X 服从什么分布, E X = EX , ES 2=DX, EA k =k =EX k ,即样本均值X , 样本方差S 2,样本k 阶矩A k 分别是总体均值EX,方差DX,总体k 阶矩k 的无偏估计,2有效性 若E ∧θ1 =E ∧θ2= , 而D ∧θ1< D ∧θ2, 则称估计量∧θ1比∧θ2有效.3一致性相合性 若n →∞时,θθP →∧,则称估计量∧θ是参数的相合估计量.二.区间估计1.求参数的置信水平为1-的双侧置信区间的步骤1寻找样本函数W=WX 1 ,X 2 ,…,X n ,,其中只有一个待估参数未知,且其分布完全确定.2利用双侧分位点找出W 的区间a,b,使P{a<W <b}=1-.3由不等式a<W<b 解出θθθ<<则区间θθ,为所求.2.单个正态总体待估参数 其它参数 W 及其分布 置信区间2已知 nX σμ-~N 0,1 2/ασz n X ±2未知 nS X μ-~ t n-1 )1((2/-±n t n S X α 2未知22)1(σS n -~ 2n-1 ))1()1(,)1()1((22/1222/2-----n S n n S n ααχχ 3.两个正态总体1均值差 1- 2其它参数 W 及其分布 置信区间已知2221,σσ22212121)(n n Y X σσμμ+--- ~ N0,1 )(2221212n n z Y Xσσα+±-未知22221σσσ==212111)(n n S Y X w +---μμ~tn 1+n 2-2)11)2((21212n n S n n t Y X w+-+±-α 其中S w 等符号的意义见第六章二. 3 2③.2 1, 2未知, W=22212221σσS S ~ Fn 1-1,n 2-1,方差比12/22的置信区间为注意:对于单侧置信区间,只需将以上所列的双侧置信区间中的上下限中的下标/2改为,另外的下上限取为- 即可.。


基本概念第一章数和数的运算一概念(一)整数1整数的意义:自然数和0都是整数。
2自然数:我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4数位:计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5数的整除整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说a 能被b整除,或者说b能整除a。
如果数a能被数b(b≠0)整除,a就叫做b的倍数,b就叫做a的约数(或a的因数)。
倍数和约数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的约数。
一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12……其中最小的倍数是3,没有最大的倍数。
个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
一个数各位数上的和能被9整除,这个数就能被9整除。
能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
一个数的末两位数能被4(或25)整除,这个数就能被4(或25)整除。
例如:16、404、1256都能被4整除,50、325、500、1675都能被25整除。
一个数的末三位数能被8(或125)整除,这个数就能被8(或125)整除。
例如:1168、4600、5000、12344都能被8整除,1125、13375、5000都能被125整除。

第一章基本概念一、单选题1.规定产品、过程或服务需要满足的要求以及用于判定其要求是否得到满足的证实方法的标准,是以下哪一类(C)。
A.指南标准B.标准化指导性技术文件C.规范标准D.规程标准2、(A)标准为服务业组织标准化工作提供了指南。
A.GB/T 24421-2009B.GB/T 19001-2016C.GB/T 24001-2016D.GB/T 45001-2020二、多选题1、以下属于国际标准化文件的有:(ACDE)。
A.标准B.标准化指导性技术文件C.技术规范(TS)D.可公开提供规范(PAS)E.技术报告(TR)2、按标准化对象划分,标准包括(BCD)。
A.指南标准B.产品标准C.过程标准D.服务标准3、我国标准化法中明确标准包括以下哪几类(ABCDE)。
A.国家标准B.行业标准C.地方标准D.团体标准E.企业标准F.联盟标准三、判断题1、地方标准可分为强制性标准和推荐性标准;(错)2、通过标准化活动制定的文件都是标准;(错)3、团体标准是由团体按照自行规定的标准制定程序制定并发布,供团体成员或社会自愿采用的标准;(对)4、服务业组织的服务规范可以严于国家标准、行业标准或地方标准。
(对)5、标准化是为了在既定范围内获得最佳秩序,促进共同效益,对现实问题或潜在问题确立共同使用和重复使用的条款以及编制、发布和应用文件的活动。
(对)第二章标准起草工作组基本要求一、多选题1、标准起草工作组应吸纳利益相关方参与,以下属于利益相关方的有(ABCD)。
A.业务主管部门B.行业协会C.服务机构D.客户二、判断题1、标准起草工作组应熟悉标准所属领域的基本情况,清楚该领域存在的主要问题,能够全面把握标准的技术内容。
(对)2、标准起草工作组成员必须是参加标准编写单位的领导;(对)3、标准起草工作组应具备相关研究成果、法律法规、相关国际及国内标准等文献检索的能力。
(对)第三章标准制定基本工作程序一、判断题1.认证认可行业标准(RB)制定不需要预审。




工程热力学与传热学第一章基本概念典型问题分析典型问题一.基本概念分析1闭口系统具有恒定的质量,但具有恒定质量的系统不一定就是闭口系统。
2孤立系统一定是闭口的,反之则不然。
3孤立系统一定是绝热系统,但绝热系统不一定都是孤立的。
4孤立系统的热力学状态不能发生变化。
5平衡状态的系统不一定是均匀的,均匀系统则一定处于平衡状态。
6摄氏温度的零点相当于热力学温度的273.15K。
7只有绝对压力才能表示工质所处的状态,才是状态参数。
8只有平衡状态,才能用状态参数坐标图上的一点来表示。
9非平衡状态,因为没有确定的状态参数,无法在状态参数坐标图中表示。
10不平衡过程,一定是不可逆过程;11不可逆过程就是指工质不能恢复原来状态的过程;12一个可逆过程必须同时也是一个准平衡过程,但准平衡过程不一定是可逆的。
13实际过程都是不可逆过程。
14功可以全部转变为热,但热不能全部转变为热15质量相同的物体A和B,若T A >T B,则物体A具有的热量比物体B多。
二.计算题分析1测得容器内气体的表压力为0.25MPa,当地大气压为755mmHg,求容器内气体的绝对压力p,并分别用(1)MPa(兆帕);(2)bar(巴);(3)atm(物理大气压);(4)at(工程大气压)表示。
2某种气体工质从状态1(p1,V1)可逆地膨胀到状态2。
膨胀过程中:(1)工质的压力服从p=a-bV,其中a,b为常数;(2)工质的pV保持恒定为p1V1。
试分别求两过程中气体的膨胀功。
3利用体积为2m3的储气罐中的压缩空气给气球充气,开始时气球内完全没有气体,呈扁平状,可忽略其内部容积。
设气球弹力可忽略不计,充气过程中气体温度维持不变,大气压力为0.9 ╳105Pa。
为使气球充到2m3,问气罐内气体最低初压力及气体所作的功是多少?已知空气满足状态方程式pV=mR g T。
分析解答一. 基本概念分析解答1 √;2 √;3 √;4 ╳;5 √;6 √;7 √;8 √;9 √;10 √;11 ╳;12 √;13 √;14 ╳;15 ╳;二. 计算题分析解答1 解:依据: Pa Pa Pa p Pa mmHg p p p b e 66107305.04322.1337551025.04332.1331,⨯=⨯+⨯==+=单位换算:at Pa Pa atm PaPa bar Pa Pa MPa PaPa 7575.35.06698107305.0)4(7460.3325101107305.0)3(057.310107305.0)2(7305.010107305.01665666=⨯=⨯=⨯=⨯)( 2 解:过程为可逆过程: 1211212121212221122121ln )2()(2)()(1V V V p V dV pV pdV W V V b V V a dV bV a pdV W ===---=-==⎰⎰⎰⎰--)( 分析:在上述两过程中,系统的初,终态相同,但中间途径不同,因而气体的膨胀功也不同。

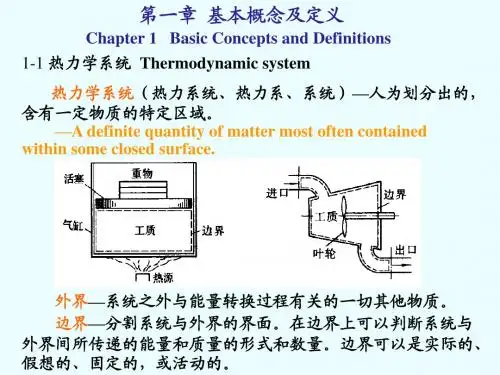
工程热力学概念第一章基本概念1.热力系:就是具体指定的研究对象。
(用界面将所要研究的对象将周围环境分开,这种人为分割的研究对象,称为热力系统。
)2.边界:分割系统与外界的分界面称为边界。
3.外界:与热力系有相互作用的周围物体称为外界。
4.根据热力系内部情况不同,热力系可分为:单元系:由单一化学成分组成。
多元系:由多种化学成分组成。
单相系:由单一的相组成。
复相系:由多种相组成。
均匀系:各部分性质均匀一致。
非均匀系:各部分性质不均匀。
5.根据热力系和外界相互作用情况不同,热力系可分为:闭口系:和外界无物质交换。
开口系:和外界有物质交换。
绝热系:和外界无热量交换。
孤立系:和外界无任何相互作用。
6.状态:是热力系在指定瞬间所呈现的全部宏观性质的总称。
7.状态参数:从各个不同方面描写宏观状态的物理量称为工质的状态参数。
8.基本状态参数:在工程热力学中常用的状态参数有6个,即压力、比体积、温度、热力学能、焓和熵。
其中压力、比体积、温度可以直接测量,也比较直观,称为基本状态参数。
9.真空度:当气体的绝对压强低于大气压力时,真空计所指示的是绝对压力低于大气压的部分,称为真空度。
10.热力学能:组成热力系的大量微观粒子本身所具有的能量(不包括热力系宏观运动的能量和外场作用的能量)。
11.比热力学能:单位质量物质的热力学能称为比热力学能。
12.平衡状态:是指热力系在没有外界作用的情况下宏观性质不随时间变化的状态。
13.简单热力系:和外界只有热能和机械能交换的热力系统称为简单热力系。
14.过程:是指热力系从一个状态向另一个状态变化时所经历的全部状态的总和。
15.内平衡过程:热力系从一个平衡(均匀)状态连续经历一系列(无数个)平衡的中间状态过渡到另一个平衡状态,这样的过程称为内平衡过程。
内平衡过程也称作准静态过程。
16.循环过程:热力系从某一状态开始,经过一系列中间状态后,有回复到原来状态。
17.做功量:热力系通过界面和外界进行的机械能的交换量称为做功量,简称功。