三角函数线

三角函数线
三角函数线是正弦线、余弦线、正切线、余切线、正割线和余割线的总称（有时还包括正矢线、余矢线等，是三角函数的几何表示。

如图：
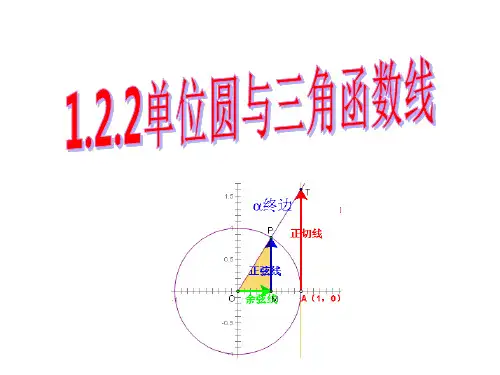
设任意角a的顶点在原点O（单位圆的圆心），始边与x轴的非负半轴重合，终边与单位圆相交于点P（x，y），过点P作x轴的垂线，，垂足为点M；过点A（1,0）作单位圆的切线，设它与角a的终边（当a位于第一、第四象限时）或其反向延长线（当a位于第二、第三象限是）相交于点T，于是有sin a=y=MP，cos a=x=OM，tan a=y/x=PM/OM=AT/OA=AT.
我们规定与坐标轴同向时，方向为正方向，与坐标轴反向时，方向为负向，则有向线段MP,OM,AT,分别叫做角a的正弦线、余弦线、正切线，他们统称三角函数线。

（1）三角函数线的意义是可以表示三角函数的值，其长度等于三角
函数值的绝对值，方向表示三角函数值的正负。

（2）因为三角函数线是与单位圆有关的有向线段，所以作角的三角函数线时，一定要先做单位圆。

（3）有向线段的书写：有向线段的起点字母写在前面，终点字母写在后面。

x OA
作三角函数线的步骤: 人教高中数学必修四.1三角函数线PPT课件
(1)以圆点为圆心画出单位圆，作出角的终边;
(2) 设α的终边与单位圆交于点P，作PM⊥x轴于M，则：
有向线段MP是正弦线, 有向线段OM是余弦线;
(3) 设单位圆与x轴的正半轴交于点A，过点A作x轴的垂线,
与角α的终边(或其反向延长线)交于点T，则：
α的
y
终边 P
MO
A(1,0)
x
T
(Ⅱ)
AT y tan, 有向线段AT叫角α的正切线
x
特别注意：正切线必须是： 以A为始点、T为终点
y
T
M
A(1,0)
O
x
α的 P
可以看出：正切线在第一三象限为正，第二四终边象限(Ⅲ为)负.
y T α的
终边
P
A(1,0)
OM x
(Ⅰ)
y
M A(1,0)
O
x
PT
α的
1
Ax
y=－1
T
4
题型四：利用三角函数线解三角不等式 人教高中数学必修四.1三角函数线PPT课件
例
写出满足条件
1 2
≤cosα＜
3 2
的角α的集合.
|2k
6
＜α≤
2k 2 ，或
3
2k 4 ≤α＜ 2k 11 ，k Z
3
6
x1 x 3
2
2
2
y
3
1
6
-1 O
4
-1
3
1
x
11
6
(2k
6
,2k
不查表，比较大小。
（２）cos 2

高考数学知识点：三角函数线（正弦线、余弦线、正切线）高考数学知识点：三角函数线（正弦线、余弦线、正切线）三角函数线的定义：设任意角α的顶点在原点O，始边与x轴的正半轴重合，终边与单位圆相交于点P（x，y），过P点作x轴的垂线，垂足为M，过点A（1，0）作单位圆的切线,高二，设它与角α的终边或其反向延长线相交于点T，则有向线段MP、OM，AT分别叫做角α的正弦线，余弦线，正切线，即：sinα=MP，cosα=OM，ta nα=AT，如下图：注：线段长度表示三角函数值大小，线段方向表示三角函数值正负。

关于三角函数线，要注意以下几点：（1）正弦线、余弦线、正切线都是有向线段，利用它们的数量来表示三角函数值，是数形结合的典型体现。

三角函数线表示三角的函数值的符号规定如下：正弦线MP、正切线AT方向与y轴平行，向上为正，向下为负；余弦线OM在x 轴上，向右为正，向左为负。

（2）作三角函数线时，所用字母一般都是固定的，书写顺序也不能颠倒。

特别要注意正切线必在过A（1，0）的单位圆的切线上（其中二、三象限角需作终边的反向延长线）。

（3）对于终边在坐标轴上的角，有时三角函数线退化为一个点，有时又为整个半径。

当角α的终边在y轴上时，角α的正切线不存在。

（4）当时，正弦线、余弦线、正切线与角α并不是一一对应的。

一般地，每一个确定的MP、OM、AT都对应两个α的值。

诱导公式：公式一公式二公式三公式四公式五公式六规律：奇变偶不变，符号看象限。

即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

诱导公式口诀“奇变偶不变，符号看象限”意义：的三角函数值．(1)当k为偶数时，等于α的同名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号；(2)当k为奇数时，等于α的异名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号。

单位圆中的三角函数线
圆心在原点，半径等于1的圆为单位圆．设角α的顶点在圆心O，始边与x轴正半轴重合，终边交单位圆于P，过P作PM垂直x轴于M，作PN垂直y轴于点N.以A为原点建立y'轴与y轴同向，与α的终边(或其反向延长线)相交于点T(或T')，则有向线段0M、0N、AT(或AT')分别叫作α的余弦线、正弦线、正切线，统称为三角函数线.有向线段：既有大小又有方向的线段.
要点诠释：
三条有向线段的位置：
正弦线为α的终边与单位圆的交点到x轴的垂直线段；
余弦线在x轴上；
正切线在过单位圆与x轴的正方向的交点的切线上；
三条有向线段中两条在单位圆内，一条在单位圆外.
第1 页共1 页。

P
T

O
M
A
S OPA SOPA S OAT 1 1 1 2 MP OA 1 AT OA 2 2 2 sin tan
4、比较sin11550与sin(-16540)的大小。
sin11550=sin750 sin(-16540)=sin1460
思考：
• 为了去掉上述等式中的绝对值符号，能否 给线段OM、MP、AT规定一个适当的方向， 使它们的取值与点P的坐标一致？
当角α的终边不在坐标轴上时，以O为始点、 M为终点，规定：
• 当线段OM与x轴同向时，OM的方向为正，且有 正值x； • 当线段OM与x轴反向时，OM的方向为负，且有 负值x。 • 这样，无论哪一种情况都有

75
P1 P2 M2 O M1

146
sin11550 >sin(-16540)
小结
• 1、 sin y MP
• 2、 • 3、
cos x OM
y tan AT x
• 4、有向线段：既有长度又有方向的线段
• 作业布置：课堂作业P10作业二
1、做出下列各角的三角函数线
• （1） 3
P T
O
M
A
2 • （2） 3
T
M
O
P
ቤተ መጻሕፍቲ ባይዱ
A
• 2、你能从单位圆中的三角函数线出发 得出三角函数的哪些性质吗?
y x
yx
O
3、已知 0， ，在单位圆中作出角 2
的正弦线、正切线，并证明： sin tan
• 当线段AT与y轴同向时，AT的方向为正，且有正 y • 值 ；

O
x
PT α的终边
应用举例:
例1.如图,α、β的终边分别与单位圆交于 点P、Q,过A(1,0)作切线AT交OP于T,交OQ的 反向延长线于T/,P、Q在x轴上的射影为M、N 指出α、β的三角函数线。 y
Q βP T α
NO M A x
T/
Hale Waihona Puke 例题2己知sin 1 ,求角的集合
2
练习
1) cos 3
y
α的终边
T
P
α
x
O
M A(1,0)
有向线段MP称为角的正弦线，即：sin MP 有向线段MP称为角的余弦线，即：cos OM 有向线段AT称为角的正切线，即：tan AT
y
α
sin MP
M A(1,0)
O
x cos OM
P T tan AT
α的终边
α的终边 P
M
y
sin MP
α
x cos OM
作业：
1 P17 2,3
O
A(1,0) tan AT
T
M
P α的终边
y
T
sin MP
α
x cos OM
O
A(1,0)
tan AT
α的终边 P
M
M
P α的终边
三角函数线
y
α
x
O A(1,0)
y α的终边 PT
α x sin MP
O M A(1,0)
T
y
T
α
x
O A(1,0)
cos OM
y
tan AT
α
M A(1,0)
同向时,数量为正;反向时,数量为负.

yr
-+
-o + x
tan y
yx
-+ +o - x
y
sin 全为+ tano cosx
心得:角定象限,象限定符号
记法： 一全正 二正弦
三正切 四余弦
练习
1. 角α的终边经过点P(0, b)则( D)
A.sin α=0
B.sin α=1
C.sin α=-1
D.sin α=± 1
2.若角600o的终边上有一点(-4, a),则a的值是( B)
知识 回顾
你记住了吗？
几个特殊角的三角函数值
角α 0o 角α
的弧 0
度数
sinα 0
cosα 1
tanα 0
30o 45o 60o 90o 180o 270o 360o

6 4 32
3 2
2
0 1 1 1
2
3
2
2
2
0
0 3
21
2
2
2
1 0 1
31
3
3 不存在 0 不存在 0
练习：求值
cos


11 3


sin


71 6


tan

19 3

解：cos


11 3


sin


71 6


tan

19 3


cos

4


3


sin

12

作业：
1 P17 2,3
练习
3 cos 2
拓展：三角函数的面积法定义
2002年，由中科院院士张 景中提出。他把边长为1， 夹角为 的菱形的面积定 义为 sin ，由此研 究正弦的性质，到处理余 弦，用面积的方法证明大 量几何问题，把三角学和 几何学打成一片。
小结：
1.有向线段的定义
2. 三角函数线 3. 三角函数线的应用
T/
例2：用三角函数线证明：
(1) sin cos 1
2 2
( 2) | sin | | cos | 1
你还能得到类似的其它结果吗？
例3. 已知α∈(0， )，试证明 2
sinα<α<tanα .
y N O P T x M A
α
例题4
1 己 知sin , 求 角的 集 合 2
α的终边 P
M
y α
三角 函 数 线 yα
的终边
P O y
T
T
x
A(1,0) T
α
O
M A(1,0)
x
sin MP
y
x
A(1,0)
cos OM
tan AT
M A(1,0)
M
α
O
α O
P
α的终边
x P
T
α终边
应用举例:
例1.如图,α、β的终边分别与单位圆交于 点P、Q,过A(1,0)作切线AT交OP于T,交OQ的 反向延长线于T/,P、Q在x轴上的射影为M、N 指出α、β的三角函数线。 y P T Q β α NO M A x
任意角的三角函数的单位圆定义：
sin y cos x y t an

y
tan y AT
T
x
AM
O Ax
P T
思考：当角α的终边在坐标轴上时，角α的正切线的含义如
何？
y
P
P
O
x
当角α的终边在x轴上时，角α的正切线是一个点；当角α的终 边在y轴上时，角α的正切线不存在.
思考：对于不等式 sin a < a < tan a（其中α为锐角），
你能用数形结合思想证明吗？
tan y AT
x
y
MA
O
x
P T
思考：若角α为第二象限角，其终边与单位圆的交点为P（x， y），则 tan y 是负数，此时用哪条有向线段表示角α 的正切值最合适？ x
y
tan y AT
x
TP
A
A MO
x
T
思考：若角α为第三象限角，其终边与单位圆的交点为P（x， y），则 tan y 是正数，此时用哪条有向线段表示角α 的正切值最合适？ x
y T
M O A(1,0) x
P
正弦线和余弦线
问题1：如图，设角α为第一象限角，其终边与单位圆的交点为P
（x，y），则 sin y ，cos x 都是正数，你能分别用一条
有向线段表示角α的正弦值和余弦值吗？ y
| MP | y sin
P（x，y）
| OM | x cos
OM x
正弦线和余弦线
问题2：若角α为第三象限角，其终边与单位圆的交点为P（x，
y），则 sin y ， cos x 都是负数，此时角α的正弦值
和余弦值分别用哪条线段表示？
y
| MP | y sin | OM | x cos
M
Ox

高考数学知识点：三角函数线（正弦线、余弦线、正切线）_知识点总结高考数学知识点：三角函数线（正弦线、余弦线、正切线）三角函数线的定义：设任意角α的顶点在原点O，始边与x轴的正半轴重合，终边与单位圆相交于点P（x，y），过P点作x轴的垂线，垂足为M，过点A（1，0）作单位圆的切线,高二，设它与角α的终边或其反向延长线相交于点T，则有向线段MP、OM，AT分别叫做角α的正弦线，余弦线，正切线，即：sinα=MP，cosα=OM，tanα=AT，如下图：注：线段长度表示三角函数值大小，线段方向表示三角函数值正负。

关于三角函数线，要注意以下几点：（1）正弦线、余弦线、正切线都是有向线段，利用它们的数量来表示三角函数值，是数形结合的典型体现。

三角函数线表示三角的函数值的符号规定如下：正弦线MP、正切线AT 方向与y轴平行，向上为正，向下为负；余弦线OM在x轴上，向右为正，向左为负。

（2）作三角函数线时，所用字母一般都是固定的，书写顺序也不能颠倒。

特别要注意正切线必在过A（1，0）的单位圆的切线上（其中二、三象限角需作终边的反向延长线）。

（3）对于终边在坐标轴上的角，有时三角函数线退化为一个点，有时又为整个半径。

当角α的终边在y轴上时，角α的正切线不存在。

（4）当时，正弦线、余弦线、正切线与角α并不是一一对应的。

一般地，每一个确定的MP、OM、AT都对应两个α的值。

诱导公式：公式一公式二公式三公式四公式五公式六规律：奇变偶不变，符号看象限。

即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

诱导公式口诀“奇变偶不变，符号看象限”意义：的三角函数值．(1)当k为偶数时，等于α的同名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号；(2)当k为奇数时，等于α的异名三角函数值，前面加上一个把α看作锐角时原三角函数值的符号。

练习1、作出下列各角的正弦线、余 弦线、正切线：
（1）π/3 （2）5 π
（3）-2 π/3 （4）- π/6 （5） π/2 （6） π
• 此题是一个基本题，要求学生独立 完成，尽管在提问（4）中已经涉及 A点变化问题，估计学生仍会有A点 随角α的变化而变化的情况，老师加
以引导，使学生走出这一误区，实 现知识目标C。
B、难点：三角函数线的应用
三角函数线可以看做是解三角函数 题的一种工具，所以本节课通过例 题、练习等途径，力图使难点得到 突破。
二、教学方法
本课采用：“自学辅导”和“启发探究 式”教学法，它符合辩证唯物主义内因和 外因相互作用的观点，符合教学论的主导 作用与学生主体作用相统一的原则，使学 生在获得感性知识的同时，为掌握理性知 识创造条件，从而培养学生的创新能力和 实践能力。
小结：（5分钟）
学生自结，教师补充，一结 知识，二结方法。
结束语：
本节课学习了三角函数的另一种定 义——三角函数线，利用三角函数线的 直观性，我们可以很方便地解决三角函 数的很多性质，那么它究竟有多大能力 呢，请同学们抱着极强的求知欲望往后 学习。
这样做的目的是：“承上启下、留下悬念”激 发学生的求知欲望，有利于养成课前预习的 习惯。
练习二、根据图象回答下列问题：
1、（口答）当角α的终边分别位于x 轴正半轴、y轴正半轴、x轴负半轴、 y轴负半轴时，角α的正弦、余弦、 正切值是多少？
2、根据（1）的结论，求出正弦、余 弦、正切函数的值域。
此题和练习一异曲同工，但涉
及了角在坐标轴上时的特殊情况， 引导学生不仅掌握事物的一般性， 更要熟悉事物的特殊性，求定义域 和值域，略高于课本要求，实现知 识目标D和能力目标A和C。

,������∈Z
=
������
������
=
������π
+
3π 4
,������∈Z
, 如图.
题型一 题型二 题型三
题型二
解简单的三角不等式
【例 2】 解不等式 sin α≥− 12.
解:如图,作直线
y=−
1 2
交单位圆于A,B
两点,则∠xOA=
76π,∠
xOB=− π6.
又
sin
α≥−
1 2
题型一 题型二 题型三
【变式训练 2】 已知 cos α≥12 , 试求出角������的集合. 解:
如图,在平面直角坐标系内作直线
x=
1 2
交单位圆于A,B
两点,当
α
的
终边落在阴影部分时,cos α≥12 , 所以角α 的集合为
������
2�����≤
2������π
2.三角函数线的方向:正弦线由垂足指向α的终边与单位圆的交 点;余弦线由原点指向垂足;正切线由切点指向切线与α的终边(或反 向延长线)的交点.
3.三角函数线的正负:三条有向线段凡与x轴的正方向或y轴的正 方向同向的为正值,与x轴的正方向或y轴的正方向反向的为负值.
4.三角函数线的书写:有向线段的起点字母在前,终点字母在后. 5.三角函数线的意义:三角函数线的方向表示三角函数值的符号; 三角函数线的长度等于所表示的三角函数值的绝对值.
x+ 3 > 0,
即
cos
x≥−
1 2
,
且sin
x>
−
23.
由
cos
x≥−
1 2
,

四个象限的三角函数线四个象限的三角函数线是数学中的重要概念，为各种复杂运算提供了可靠的理论框架，而且在日常生活中也有很多应用。

本文将从四个象限分别介绍三角函数线，让读者对三角函数线有更深刻的理解。

一、第一象限中的三角函数线第一象限也称为正象限，形成的三角函数线是正的，正的三角函数线是由“正角度”、“正比例常数”和“正比例因数”组成的，正角度即角度的绝对值小于180度。

正比例常数是对应于单位角的正y值的唯一定值，能够体现出上升或下降趋势。

正比例因数是和正比例常数一起确定每个角度上y值的定值，表明所给角度上y值是基于正比例常数进行改变的。

二、第二象限中的三角函数线第二象限是“负象限”，其形成的三角函数线是负的，所有的三角函数线的结构都是一样的，由“负角度”、“负比例常数”和“负比例因数”组成。

负角度即角度的绝对值大于180度；负比例常数是对应于单位角的负值y，体现出负趋势；负比例因数是和负比例常数一起决定每个角度上y值的定值，表明每个角度上y值是基于负比例常数进行改变的。

三、第三象限中的三角函数线第三象限也是“负象限”，所形成的三个象限的三角函数线是负的。

由于y的值已变为负，所以其结构是由“负角度”、正比例常数和“正比例因数”组成。

所以，正比例常数已改变其性质，用来表达下降趋势。

而正比例因数是和正比例常数一起确定每个角度上y值的定值，也可以体现出每个角度上y值是基于正比例常数的变换。

四、第四象限中的三角函数线第四象限也是“正象限”，由于y的值改变，所以其结构是由“正角度”、负比例常数和“负比例因数”组成的，正角度表示角度的绝对值小于180度；负比例常数是对应于单位角的负值y，表示上升性质；负比例因数是和负比例常数一起确定每个角度上y值的定值。

总之，四个象限中的三角函数线各不相同，由变换而产生，而每个象限都有自己各自定义的结构式，如正角度、正比例常数、负角度、正比例因数、负比例常数和负比例因数。

也就是说，只有识别出每个结构的独特性，读者才能深入理解三角函数线，进而使用它们在日常生活中，去做出正确的决策。

1 单位圆的定义：圆心在圆点，半径等于单位长的圆叫做单位圆。

2 三角函数的定义：如图,设是一个任意角,它的终边与单位圆交于点,那么得到六个三角函数
有向线段：有大小和方向的线段。

3，正弦线作法：
(1)设角的终边与单位圆交于点P(x,y),过点P作x轴的垂线,垂足M,
得有向线段MP叫做角的正弦线，当线段MP与y轴同向时，MP的方向为正向，且y有正值；当线段MP与y 轴反向时，MP的方向为负向，且y有负值。

同理可得余弦线等其它线。

正弦线的方向以上为正，且永远为从点P在x轴的投影点M指向终边与单位圆的交点P，
余弦线的方向以右为正，且永远为从原点O指向终边与单位圆的交点P在x轴的投影点M，
4. 正切线作法：
根据正切函数的定义与相似三角形的知识,借助有向线段,我们有
正切线的方向以上为正, 正切线的方向永远从（1，0）指向角终边所在直线，
且正切线永远在y轴右边，正切线在过单位圆与轴正方向的交点的切线上。

角终边落在1、3象限正切线为正，2、4象限时正切线为负，
常用的三种三角函数线的作法：
第一步：作出角的终边，与单位圆交于点P；
第二步：过点P作X轴的垂线，设垂足为M，得正弦线MP、余弦线OM；
第三步：过点A(1,0)作单位圆的切线，它与角的终边或其反向延长线的交点设为T，得角的正切线AT.
特别注意：三角函数线是有向线段，在用字母表示这些线段时，要注意它们的方向，分清起点和终点，书写时要带上方向符号。

五、三角函数线的应用。

3
5
解： 如图可知：
S2 S1
B
sin 2 sin 4
3
5
A o
T2
2
4
T1
tan tan
3
5
例5.求函数 f (a ) = 2 cos a - 1 的定义域.
y
P2 P
OM
x
cos a ³ 1 2
x
P1
=
1
2
p
p
a ? [ + 2kp, + 2kp](k ? Z )
3
3
练习
1.在(0, 2 )内使cos x sin x tan x成立的x的取值范围是(C )
O M Ax
sin tan.
例４.利用三角函数线比较下列各组数的大小：
sin 2 与sin 4
3
5
tan 2 与tan 4
3
5
解： 如图可知：
sin 2 sin 4
3
5
S2 S1 P1 B P2
A M2 M1 o
例４.利用三角函数线比较下列各组数的大小：
sin 2 与sin 4
3
5
tan 2 与tan 4
P Mo x
y=-x
y
o
y M
o P
小结sin cos的符号问题：
y
P
P
sin cos 1, (0, )
2
Mx
P MM o
0 sin cos 1, ( , 3 )
x
24
sin cos 0, (3 , )
y
y=-x
4
若
sin2kcos
403,2(k,43(2k)¢)

[解析] 要使函数 f(α)有意义，则 sinα≥12.如图所示， 画出单位圆，作直线 y＝12，交单位圆于 P1，P2 两点，连接 OP1，OP2，过点 P1，P2 作 x 轴的垂线，垂足分别为 M1， M2，易知正弦线 M1P1＝M2P2＝12.在[0,2π)范围内，sinπ6＝sin56π ＝12，则点 P1，P2 分别在56π，π6的终边上又 sinα≥12，结合图形可知，图中阴影部 分(包括边界)即满足 sinα≥12的角 α 的终边所在的范围，即当 α∈[0,2π)时，π6 ≤α≤56π，
故函数 f(α)的定义域为{α|2kπ＋π6≤α≤2kπ＋56π，k∈Z}．
利用三角函数线证明几何结论
典例 3
设α是锐角，利用单位圆和三角函数线证明：sinα<α<tanα．
[思路分析] sinα、tanα分别用正弦线、正切线表示出来，α用它所对的弧表示出来，从而使关系 式得证．
[证明] 如图所示，设角 α 的终边交单位圆于 P，过点 P 作 PM 垂直于 x 轴，垂足为 M.过点 A(1,0)作单位圆的切 线交 OP 于点 T，连接 PA，则 sinα＝MP，tanα＝AT，
[错因分析] 因两个不等式中的k各自独立，因此上述两集合是有公共部分 的，如图所示．
[思路分析] 解三角不等式组时，先解每个三角不等式，再取它们的交集．取交集时，要注意各自 解集中k的独立性．
[正解] 要使函数有意义，则需同时满足 1＋2cosx≥0 且 2sinx＋ 3>0， 即 cosx≥－12，且 sinx>－ 23． 由 cosx≥－12，知 2kπ－23π≤x≤2kπ＋23π，k∈Z． 由 sinx>－ 23，知 2nπ－π3<x<2nπ＋43π，n∈Z， ∴x 的取值范围是{x|2kπ－π3<x≤2kπ＋23π，k∈Z}．