第七章 桁架结构
- 格式:ppt
- 大小:5.61 MB
- 文档页数:58


桁架结构知识点总结归纳桁架结构是一种由多个杆件组成的支撑结构,它具有高强度、刚度和稳定性的特点,常用于建筑、桥梁和其他工程结构中。
桁架结构的设计和施工需要考虑多方面的因素,包括荷载、材料、连接方式等。
在本文中,我们将对桁架结构的基本知识点进行总结归纳,希望能够帮助读者更好地理解和应用桁架结构。
1.桁架结构的基本组成桁架结构由杆件、节点和连接件组成。
杆件是桁架结构的基本构件,它可以是直线型或曲线型的。
节点是杆件的连接点,通过节点将杆件连接在一起,形成桁架结构的整体。
连接件用于连接节点和杆件,常见的连接方式包括焊接、螺栓连接和销钉连接等。
2.桁架结构的类型桁架结构可以根据其构造形式分为平面桁架和空间桁架两种类型。
平面桁架是由一层平面构件组成的桁架结构,而空间桁架由多层平面构件组成的桁架结构。
根据杆件的形状和排列方式,桁架结构还可以分为平行桁架、交叉桁架、空间平行桁架等不同类型。
3.桁架结构的荷载特点桁架结构通常承受静载、动载和温度载荷等多种荷载。
静载是指桁架结构在静止状态下所承受的荷载,包括自重、外加荷载等;动载是指桁架结构在运动状态下所承受的荷载,包括风载、地震载等;温度载荷是指由于温度变化引起的结构变形和内力。
4.桁架结构的受力分析桁架结构的受力分析是设计和施工中的关键环节,它通过计算杆件和节点的内力、变形等参数,确定结构的稳定性和安全性。
在受力分析中需要考虑桁架结构的整体稳定性、节点的刚度和连接件的受力情况等。
5.桁架结构的设计要点桁架结构的设计需要考虑多方面的因素,包括结构的荷载、材料、构造形式等。
在设计中需要合理选择杆件的截面形状和尺寸、节点的连接形式和构造方法、连接件的选型和布局等。
此外,还需要考虑桁架结构的整体稳定性、杆件的疲劳寿命和变形控制等。
6.桁架结构的施工工艺桁架结构的施工包括杆件的加工、节点的装配和连接件的安装等多个环节。
在施工中需严格控制杆件的制作质量、节点的装配精度和连接件的安装工艺。



7桁架结构范文桁架结构是一种广泛应用在建筑和工程领域的结构形式。
它由多个横向和纵向的杆件组成,形成一个稳定的三维网格结构,能够有效地承载和分散荷载。
桁架结构的基本原理是通过将杆件的受力方向合理地设计和布置,使得整个结构能够在外部荷载的作用下保持平衡和稳定。
每个杆件都扮演着重要的角色,在整体结构中起着支撑和连接的作用。
桁架结构具有许多优点。
首先,它具有较高的强度和刚度,能够在不同荷载下保持结构的稳定性。
其次,桁架结构的重量相对较轻,可以提高建筑物的自重比,减少对地基的负荷。
此外,桁架结构还具有灵活性和可扩展性,可以根据需要进行设计和调整。
在建筑领域,桁架结构被广泛应用于大跨度的建筑物,如体育场馆、展览中心和机场候机楼等。
由于桁架结构的灵活性和可扩展性,在建筑设计中可以实现较大的空间自由度和创造性。
桁架结构还可以用于承载各种类型的荷载,甚至是动态荷载,如地震和风荷载。
在工程领域,桁架结构也有着广泛的应用。
特别是在大型机械设备和运输工具上,桁架结构能够提供良好的支撑和保护。
例如,大型起重机、桥梁和船舶都可以采用桁架结构。
此外,桁架结构还常用于搭建临时性的支撑结构,如脚手架和临时桥梁等。
桁架结构的设计和施工需要考虑多个因素。
首先是结构的稳定性和强度,需要根据设计荷载和材料性能来确定杆件的尺寸和连接方式。
其次是结构的可行性和经济性,需要综合考虑材料的成本、施工工艺和维护成本等因素。
最后是结构的美观性和环境影响,需要与整体建筑风格和环境要求相匹配。
总结起来,桁架结构是一种在建筑和工程领域广泛应用的结构形式。
它具有高强度、轻质、灵活性和可扩展性等优点,适用于大跨度建筑物和大型机械设备。
桁架结构的设计和施工需要综合考虑多个因素,以实现稳定、安全、经济和美观的结构。


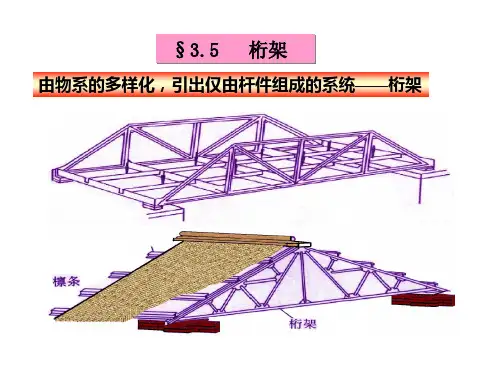
第七章结构力学的有限单元法一.桁架杆单元二.梁单元三.ANSYS桁架结构计算示例四.ANSYS刚架结构计算示例研究对象所研究的对象是细长的杆件,即轴线方向的尺寸远比其他二个方向的尺寸大的多;杆件系统可分为平面杆件系统和空间杆件系统,若组成结构物的杆件都在同一个平面内,外力也在这一平面内,则称为平面杆件系统;若组成结构物的杆件不在同一个平面内,则称为空间杆件系统;杆件系统中所用的单元主要为平面桁架杆单元,如果各杆件只受拉压作用则采用桁架单元。
LOGO1.杆单元一般规定位移函数单元在结点力作用下各点的位移叫内位移,描绘内位移的函数叫位移函数。
由材料力学知道:仅受轴向作用的二力杆,其应力及应变在轴线各点处均是恒定常数,因而位移沿杆子轴线呈线性变化,即12()u x a a x =+ (1)这就是二力杆单元的位移函数,式中1a ,2a 是两个待定常数,可由i ,j 两结点的位移唯一确定。
当()0,0,()ij x u u x l u l u ==== (2)将式(2)代入式(1)有:112i j u a u a a l ==+,,从而可得12ij ia u u u a l=−=(3)将式(3)中的12a a ,值代入式(1)得 ()1j ii i j u u x x u x u x u u ll l−⎛⎞=+=−+⎜⎟⎝⎠或写成[]{}()1ei i i j j j u u xx u x N N N u u u ll ⎧⎫⎧⎫⎡⎤⎡⎤=−==⎨⎬⎨⎬⎣⎦⎢⎥⎣⎦⎩⎭⎩⎭通常用{}u 代表单元内位移 {}[]{}ei i j j u N u N u N u ==+其中1i j x xN N l l=−=,在有限元法中,i j N N ,称为i 点、j 点的形状函数或插值函数,[]N 称为形状函数矩阵。
形状函数i N ,j N 如下图所示。
有了位移函数,就可以分析单元的应变和应力,根据应变定义x du dxε= 将位移函数代入有[]{}(){}[]{}1111eex edd x d x N u u dxdx l dx l u lεε⎡⎤⎛⎞⎛⎞===−⎜⎟⎜⎟⎢⎥⎝⎠⎝⎠⎣⎦=−或写成{}[]{}eB u ε=应变矩阵和应力矩阵其中[][]1/11B l =−称为应变矩阵。


平面桁架结构一、平面桁架的形式1.屋盖结构体系屋盖分为无檩屋盖有檩屋盖。
无檩屋盖一般用于预应力混凝土大型屋面板等重型屋面,将屋面板直接放在屋架上。
有檩屋盖常用于轻型屋面材料的情况。
2.屋架的形式屋架外形常用的有三角形、梯形、平行弦和人字形等。
桁架外形应尽可能与其弯矩图接近,这样弦杆受力均匀,腹杆受力较小。
腹杆的布置应尽量用长杆受拉、短杆受压,腹杆的数目宜少,总长度要短,斜腹杆的倾角一般在30°~60°之间,腹杆布置时应注意使荷载都作用在桁架的节点上。
(1)三角形桁架三角形桁架适用于陡坡屋面(i>1/3)的有檩屋盖体系,屋架通常与柱子只能铰接。
弯矩图与三角形的外形相差悬殊,弦杆受力不均,支座处内力较大,跨中内力较小,弦杆的截面不能充分发挥作用。
支座处上、下弦杆交角过小内力又较大,使支座节点构造复杂。
(2)梯形桁架梯形屋架适用于屋面坡度较为平缓的无檩屋盖体系,它与简支受弯构件的弯矩图形比较接近,弦杆受力较为均匀。
梯形屋架与柱的连接可以做成铰接也可以做成刚接。
梯形屋架的中部高度一般为(1/10~1/8)L,与柱刚接的梯形屋架,端部高度一般为(1/16~1/12)L,通常取为2.0~2.5m。
与柱铰接的梯形屋架,端部高度可按跨中经济高度和上弦坡度决定。
(3)人字形桁架人字形屋架的上、下弦可以是平行的,坡度为1/20~1/10,节点构造较为统一;也可以上、下弦具有不同坡度或者下弦有一部分水平段,以改善屋架受力情况。
人字形屋架因中高度一般为2.0~2.5m,跨度大于36m时可取较大高度但不宜超过3m;端部高度一般为跨度的1/18~1/12。
(4)平行弦桁架平行弦桁架在构造方面有突出的优点,弦杆及腹杆分别等长、节点形式相同、能保证桁架的杆件重复率最大,且可使节点构造形式统一,便于制作工业化。
3.托架形式支承中间屋架的桁架称为托架,托架一般采用平行弦桁架,其腹杆采用带竖杆的人字形体系。
托架高度般取跨度的1/5~1/10,托架的节间长度一般为2m或3m。
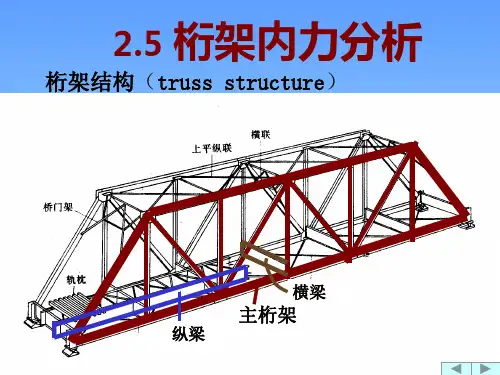
桁架结构
主要结构特点
各杆件受力均以单向拉、压为主,通过对上下弦杆和腹杆的合理布置,可适应结构内部的弯矩和剪力分布。
由于水平方向的拉、压内力实现了自身平衡,整个结构不对支座产生水平推力。
结构布置灵活,应用范围非常广。
桁架梁和实腹梁(即我们一般所见的梁)相比,在抗弯方面,由于将受拉与受压的截面集中布置在上下两端,增大了内力臂,使得以同样的材料用量,实现了更大的抗弯强度。
在抗剪方面,通过合理布置腹杆,能够将剪力逐步传递给支座。
这样无论是抗弯还是抗剪,桁架结构都能够使材料强度得到充分发挥,从而适用于各种跨度的建筑屋盖结构。
更重要的意义还在于,它将横弯作用下的实腹梁内部复杂的应力状态转化为桁架杆件内简单的拉压应力状态,使我们能够直观地了解力的分布和传递,便于结构的变化和组合。
一、根据桁架的外形分为:
1.平行弦桁架(便于布置双层结构;利于标准化生产,但杆力分布不够均匀);
2.折弦桁架(如抛物线形桁架梁,外形同均布荷载下简支梁的弯矩图,杆力分布均匀,材料使用经济,构造较复杂);
3.三角形桁架(杆力分布更不均匀,构造布置困难,但斜面符合屋顶排水需要)。
二、以桁架几何组成方式分:
1.简单桁架(由一个基本铰结三角形依次增加二元体组成);
2.联合桁架(由几个简单桁架按几何不变体系的简单组成规则联合组成);
3.复杂桁架(不同于前两种的其它静定桁架)。
桁架结构知识点归纳总结1. 桁架结构的基本组成桁架结构的基本组成包括杆件、节点和连接件。
杆件是构成桁架结构的主要构件,根据其形状和位置可分为立杆、弦杆和斜杆。
节点是连接杆件的位置,通常由连接件连接。
连接件是用于连接和固定杆件的构件,包括焊接、螺栓连接等。
2. 桁架结构的类型根据结构形式和用途,桁架结构可分为平面桁架和空间桁架。
平面桁架一般用在桥梁等跨度较小的地方,而空间桁架一般用在大跨度桥梁、建筑和大型工程中。
此外,桁架结构还可按构造形式分为金字塔式桁架、棱柱式桁架、网架式桁架等。
3. 桁架结构的受力特点桁架结构在受力时是受拉、受压和扭转力的作用。
弦杆主要受张力,斜杆和立杆主要受压力。
因此,在桁架结构的设计中,需要合理配置材料和截面形状,保证在结构受力时能够满足其受力要求。
4. 桁架结构的优点桁架结构具有结构轻、刚度大、变形小、施工方便等优点。
由于其结构轻,在大跨度结构中应用广泛。
另外,其刚度大使得桁架结构在承载荷载和抗震能力方面有很好的表现。
5. 桁架结构的设计原则桁架结构的设计需要考虑受力、变形和挠度等,其中设计原则包括合理布置和选择结构构件,使结构受力均匀分布,结构稳定可靠;合理选取结构截面形状和材料并确定连接方式,满足结构受力和挠度要求;合理布置连接件,确保结构连接牢固。
6. 桁架结构的施工技术桁架结构的施工需要考虑结构的装配和连接、受力稳定等问题。
施工技术包括预应力预紧、整体吊装等,这些技术能够保证桁架结构的安全施工和使用。
7. 桁架结构的工程应用桁架结构在工程项目中有着广泛的应用,包括桥梁、建筑和其他工程结构。
在大跨度桥梁结构中,桁架结构被广泛应用,如斜拉桥、悬索桥等;在建筑中,玻璃幕墙和屋顶结构常采用桁架结构。
桁架结构是一种重要的工程结构形式,它具有结构轻、刚度大、变形小、安装方便等优点,在工程领域中具有广泛的应用前景。
其设计、施工和应用需要深入理解其受力特点和设计原则,才能保证工程结构的安全可靠。