高等土力学土的强度

第三章 土的强度3.1 概述土与人类的关系十分密切。

在人类进化发展的上万年历史中，挖沟筑堤，疏河开渠，建造房屋殿宇、庙堂墓塔，首先涉及的是土的强度问题。

长期实践经验的积累，使人们对土的强度的重要性有了较深刻的理解。

土的强度理论研究甚至早于“土力学”学科的建立，亦即早在太沙基（Terzaghi ）1925年出版其著作《土力学》之前。

1776年，库仑（Coulomb ）就在试验的基础上提出了著名的库仑公式：ϕστtg c f += (3.1.1)1900年莫尔（Mohr ）提出：在土的破坏面上的抗剪强度是作用在该面上的正应力的单值函数：)(f f f στ= (3.1.2)这样，库仑公式（3.1.1）只是在一定应力水平下式（3.1.2）的线形特例。

从而建立了著名的莫尔－库仑强度理论。

在随后的许多年中，人们针对莫尔－库仑强度理论中抗剪强度与中主应力无关的假设，进行了大量的中主应力对土抗剪强度影响的研究，并且企图在土力学中引进广义密塞斯（Mises ）和广义屈雷斯卡（Tresca ）强度理论， 但它们与土的强度性质实在相差太大。

只有到了20世纪60年代以后，随着计算机技术的发展及大型土木工程的兴建，关于土的应力－应变－强度－时间关系即本构关系的研究广泛开展，人们才逐步认识到土的强度与土的应力－应变关系是密不可分的，它是土受力变形过程的一个阶段；并进一步认识到除剪切强度以外，还有拉伸强度、断裂及与孔隙水压力有关的土的破坏问题。

这样，一些与土的本构模型相应适应的土强度准则也相继被提出。

另一方面，人们也力图从微观机理上研究土的强度及建立强度理论；探索原状土、非饱和土、区域性土和老粘土等的强度问题。

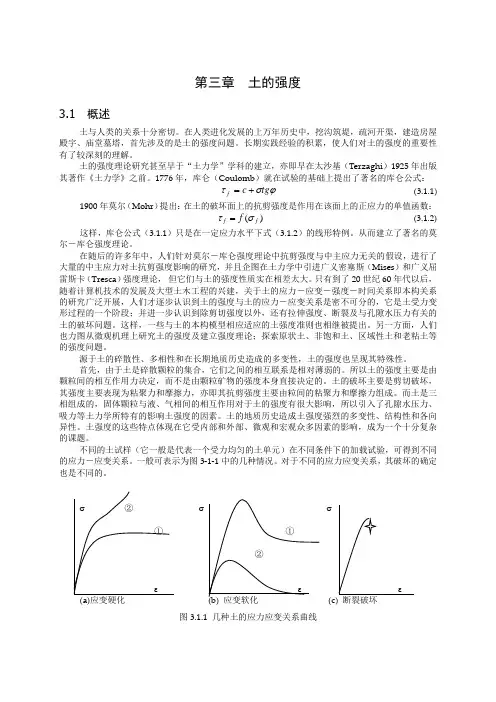
源于土的碎散性、多相性和在长期地质历史造成的多变性，土的强度也呈现其特殊性。

首先，由于土是碎散颗粒的集合，它们之间的相互联系是相对薄弱的。

所以土的强度主要是由颗粒间的相互作用力决定，而不是由颗粒矿物的强度本身直接决定的。

高等土力学考纲一、土质学 (1)知识点： (1)题目： (3)二、土的强度 (5)知识点： (5)题目： (8)三、本构理论 (9)知识点： (9)题目： (10)四、固结与流变 (12)知识点： (12)题目： (13)五、边坡稳定 (14)知识点： (14)题目： (15)一、土质学知识点：土的来源：土是母岩经过风化作用、搬运作用、沉积作用形成的松散堆积物质。

因此，土是由岩石风化而来的。

沉积岩是土经过成岩作用形成的岩石，因此，土和岩石实际上是互为物质来源，在地质历史时期是相互转化的。

举例：花岗岩风化作用，风力侵蚀（海蚀风、风蚀城堡、风蚀柱、风蚀蘑菇、风蚀洼地、戈壁滩），流水侵蚀（V形谷、沟谷、峡谷、瀑布），冰川侵蚀，海浪侵蚀。

成土作用：冰川堆积，风沙堆积，风力堆积（带有大量沙粒的气流，如果遇到灌丛或石块，风沙受阻堆积下来，就形成沙丘。

需利用植被阻滞），流水沉积。

土中矿物：原生矿物，次生矿物，水溶盐，有机质，次生氧化物和难容盐。

土的分类：按土堆积的地点与母岩关系分为残积土（母岩风化后未经搬运而与母岩处于同一地点的土叫残积土）、坡积土（母岩风化后经过重力短距离搬运的土）、运积土（岩石风化后经过搬运作用而存在于与母岩有一定距离的土），运积土按搬运力不同分为洪积土、冰渍土、冲积土、风积土；按土的沉积环境分残积土、动水沉积土（坡积土，洪积土，冲积土）、静水沉积土（湖相沉积土，海相沉积土）、风积土、冰渍土。

土的三相：指土矿物颗粒组成的固相，土孔隙中的水组成的液相和土孔隙中的气体组成的气相。

（三相之间的相互作用和三相比例的变化及各相的物质组成变化是土的性质变化的内因）土壤中的晶体粘土矿物是母岩在经受化学风化而成土过程中形成的层状硅酸盐晶体矿物粘土矿物具有可塑性、粘结性、膨胀性、阳离子交换与吸附特性等特殊性质，是土壤中最活跃的成分之一，因此成为土质学的主要研究对象（粘土矿物内部电荷经常处于不平衡状态，因此表面可吸附阳离子和水分子，在水中能分散成胶体悬浮状态）。

高等土力学——No.9 Advanced Soil Mechanics主讲老师：郭莹土木工程学院岩土工程研究所3. 6土的强度理论3.6.2 土的经典强度理论1. 特雷斯卡（Tresca）准则及其广义准则2. 米泽斯（Von Mises）准则及其广义准则3. 莫尔－库仑（Mohr-Coulomb）强度准则4. 三个强度准则的讨论1. 特雷斯卡（Tresca ）准则与广义特雷斯卡（Extended Tresca ）准则——单剪应力132kσσ−=02πsin 2=−⎟⎠⎞⎜⎝⎛+k J θ0212πsin 12=−−⎟⎠⎞⎜⎝⎛+I k J αθ()1231Ik ασσ+=−广义形式α、I 1反映平均主应力影响金属材料或或πsin =−⎟⎞⎜⎛+k J θ六棱柱的表面：π平面上的特雷斯卡与米泽斯准则两个破坏面交点，数学处理时有困难锥面——广义六棱柱面——特雷斯卡2. 米泽斯（Von Mises ）和广义米泽斯（extended Von Mises ）准则——三剪应力()()()22132322216k=−+−+−σσσσσσ22kJ =kJ =2kq 3=oct23kτ=或或12=−−k I J α0333=−−k p q α广义米泽斯——Drucker-Prager 准则α、I 1反映平均主应力影响σ1σ3σ2圆锥面——广义米泽斯准则圆柱面——米泽斯准则圆形应用起来更方便3. 莫尔－库仑强度准则——单剪切角()f f τσ=莫尔（Mohr ）单值函数1313sin 2c tan c σσϕσσϕ−=++f tan c τσϕ=+在一定的应力范围，线性关系－库仑公式莫尔－库仑强度准则（二维应力状态）0cos cos sin sin 31sin 321=+⎥⎦⎤⎢⎣⎡+−ϕθϕθϕc J I 0cos cos sin sin 3131sin =+⎥⎦⎤⎢⎣⎡+−ϕθϕθϕc q p 莫尔－库仑强度准则的应力不变量表达式三轴平面莫尔－库仑强度准则的破坏面与破坏轨迹三维空间π平面非规则六面体非规则六边形：拉压不等4. Tresca、Mises和Mohr-Coulomb三个强度准则的讨论1）Tresca和Mises都没有考虑平均主应力对土的抗剪强度的影响，不能反映土的摩擦特性；2）广义形式考虑了p，但没有考虑破坏面上正应力的影响；3）Tresca准则是最大剪应力准则；Mises是最大八面体剪应力准则，两者与土的摩擦强度不同；4）三轴压缩和伸长试验，用Tresca和Mises（拉压相等）预测的强度相同，显然与实际不符；三个准则在常规三轴压缩试验测得抗剪强度相等。

一、影响土的强度因素影响土强度的因素很多，土的抗剪强度及其影响因素的关系可以定性地用以下公式表示τf=f(e,ψ,C,σ’,c,H,T,ε,ε’,S)其中e为土的孔隙比，C为土的组成，H为应力历史，T为温度，ε和ε’分别为应变和应变率，S为土的结构，c和ψ分别为粘聚力和内摩擦角。

可分为两大类：内部因素（物理性质），外部因素（外界条件主要是应力应变条件）。

1、内部因素（1）影响土强度的一般物理性质：①颗粒矿物成分的影响。

不同矿物之间的滑动摩擦角是不同的②粗粒土颗粒的几何性质，当孔隙比相同及级配相似时，一方面大尺寸颗粒具有较强的咬合能力，可能增加土的剪胀，从而提高强度；另一方面，在单位体积中大尺寸颗粒间接触点少，接触点上应力加大，颗粒更容易破裂，从而减少剪胀，降低土的强度。

③土的组成的其他因素。

粗粒土的级配对于抗剪强度有较大影响，级配较好的砂，咬合作用也比较强，另一方面，单位体积中颗粒接触点多，接触应力小，颗粒破碎少，剪胀量加大，所以抗剪强度高④土的状态。

砂土的孔隙比和相对密度可能是影响其强度的最重要因素。

孔隙比小或者相对密度大的砂土有较高的抗剪强度。

孔隙比对黏土的影响通常变现为其应力历史的影响。

⑤土的结构。

土的结构对土的抗剪强度有很大影响，有时对于某些粘性土如区域土或特殊土，可以说是控制因素。

原状土的结构性使其强度高于重塑土或扰动土。

⑥剪切带的存在对土强度的影响。

剪切带处局部孔隙比很大，并且有很强烈的颗粒定向作用。

剪切带的生成会使土的强度降低。

（2）孔隙比与砂土抗剪强度的关系------临界孔隙比随着孔隙比减小，砂土的ψ将明显提高。

松砂与密砂在试验中的应力应变关系也有很大区别，松砂的应力应变曲线是应变硬化的，剪缩，孔隙比减小；密砂的应力应变曲线是应变软化的，剪胀，e增加。

两个式样加载到最后，其e接近相同，都达到临界孔隙比еcr，еcr是指在三轴试验加载过程中，轴向应力差几乎不变，轴向应变连续增加，最终式样体积几乎不变时的e。