DTCWT变换

基于Log-Polar和DT-CWT的旋转不变纹理分类算法
尚燕;练秋生
【期刊名称】《计算机工程与应用》
【年(卷),期】2007(043)011
【摘要】提出了一种基于对数-极坐标变换(Log-Polar)和双树复数小波变换(DT-CWT)的旋转不变纹理分类算法.该方法首先对纹理图像进行对教-极坐标变换将旋转转化为平移,再用具有平移不变性的双树复数小波对变换后的图像滤波并计算各子带的能量值组成旋转不变特征向量,最后利用支持向量机算法实现纹理图像的分类.将该方法与其它旋转不变纹理分类算法进行比较,实验结果表明,提出的算法能有效地提高正确分类率.
【总页数】3页(P48-50)
【作者】尚燕;练秋生
【作者单位】燕山大学,电子与通信工程系,河北,秦皇岛,066004;燕山大学,电子与通信工程系,河北,秦皇岛,066004
【正文语种】中文
【中图分类】TN911.7
【相关文献】
1.基于LBPV的旋转不变纹理分类算法 [J], 王楠楠;杨爱萍;寇志强;宋占杰;卜令勇
2.基于DT-CWT和SVM的纹理分类算法 [J], 练秋生;尚燕;陈书贞;王林
3.高效的光照、旋转、尺度不变纹理分类算法 [J], 樊养余;王军敏;余建明
4.基于局部特征多轴旋转不变特性的纹理图像分类算法 [J], 黄庆宇;章登义
5.基于DT-CWT和SVM的踏面旋转不变纹理提取算法 [J], 赵聪慧;冯庆胜
因版权原因，仅展示原文概要，查看原文内容请购买。

基于DTCWT方向信息的超声图像斑点噪声消除许慰玲;沈民奋;杨金耀【期刊名称】《数据采集与处理》【年(卷),期】2011(26)6【摘要】针对一般的小波去噪方法在去除超声图像斑点噪声时不能有效保持图像边缘信息的问题,本文提出基于双树复小波变换(Dual tree complex wavelet transform,DTCWT)方向信息的超声图像斑点噪声消除算法.利用双树复小波变换6个方向复小波系数的相对方差来确定该点是否位于边缘或纹理上,对低于门限的像素高频复系数置零以实现超声图像DTCWT域的自适应滤波.实验结果表明,与Lee,Frost,Kuan滤波方法相比,本文算法具有明显的优势；在图像平滑效果接近的情况下,本文算法边缘保持度略优于Yu提出的各向异性斑点噪声抑制(Speckle reducing anisotropic diffusion,SRAD)方法.%In general, the edge information of an image can not be effectively preserved when traditional wavelet de-noising methods are adopted to reduce the speckle in ultrasound images. In view of this problem, a novel speckle reducing algorithm for ultrasound images is proposed based on the dual tree complex wavelet transform (DD-DTCWT) direction information. The relative variance of the six directional complex detail coefficients about DTCWT is used to determine whether points are located at the edges or in the textures. Specifically, speckle is reduced by resetting complex detail coefficients to zero for the pixels beyond the threshold. Through such a way the adaptive filter in DTCWT domain is realized. Experimental resultsshow that the proposed method significantly outperforms the state-of-the-art competitors including Lee, Frost and Kuan filtering methods. Also, the degree of edge maintaining of the method is better than the speckle reducing anisotropic diffusion (SRAD) method proposed by Yu for images with similar smoothing effects.【总页数】5页(P671-675)【作者】许慰玲;沈民奋;杨金耀【作者单位】仲恺农业工程学院信息学院,广州,510225;汕头大学广东省数字信号与图像处理技术重点实验室,汕头,515063;汕头市超声仪器研究所有限公司,汕头,515041【正文语种】中文【中图分类】TP751【相关文献】1.基于颜色信息的改进NL法图像噪声消除算法初探 [J], 马瑞强;张丽霞2.基于复小波方向信息的SAR图像斑点噪声抑制 [J], 许慰玲;沈民奋;方若宇3.基于贝叶斯非局部平均滤波的超声图像斑点噪声抑制算法 [J], 方宏道;周颖玥;林茂松4.基于Fermi平台的双边滤波超声图像斑点噪声抑制并行处理算法 [J], 张霞;何兴无5.Fermi平台下基于直方图匹配的超声图像斑点噪声抑制 [J], 何兴无;周洪林;蒋蕙竹;雷静因版权原因，仅展示原文概要，查看原文内容请购买。

双树复小波变换
双树复小波变换（Dual-Tree Complex Wavelet Transforms, DT-CWT）是一种
为定位有用的（directional）信号分析中的关键技术，它利用相同的波形分解加
以微调，除了满足基于小波的特征分析需求外，还采取双树的结构，以确保理论预期的增益。

DT-CWT具有一种较强的完整性（coherence），可以有效地捕获复杂的
频率特征，即使是在低频域存在噪声的情况下仍可突出高频特征，因此受到了广泛的关注。

DT-CWT具有若干优势，如它有良好的分辨率，可以提取频带范围较窄的信号；具有几乎抗磁性的鲁棒性，能够具备良好的微弱信号抽取性能；另外它还具有优越的均衡性，可以很好地处理数据不均匀性，实现对复杂应用场景的有效建模；其次，它能够有效识别一时间周期分量，从而进一步提高定位能力。

作为一种基于实值小波变换的先进技术，DT-CWT非常适用于图像处理过程，
能够满足不同信号处理任务的要求，如图像压缩、图像分类、图像定位及图像剪裁等，为图像处理中高精度的实现奠定了基础。

DT-CWT在其他领域的应用也同样引
起了广泛的关注，如信号处理中定位低频信号、改善医学影像质量及构建语音自动识别系统等应用都能体现出其决定性的作用。

可以看出，DT-CWT不仅是一种简单有效的信号分析工具，而且对复杂信号处
理有着广泛的应用前景，未来估计可期预料其研究范围和领域的进一步扩大。

基于DT—CWT和PCA的唇部特征提取方法引言：唇部是人脸的重要组成部分之一，具有丰富的生物特征信息，如颜色、纹理、形状等。

因此，唇部特征在人脸识别、嘴唇表情识别等领域具有重要的应用价值。

本文提出了一种基于二维离散小波变换（DT-CWT）和主成分分析（PCA）的唇部特征提取方法，该方法能够有效地提取唇部的关键特征，提高唇部识别的准确率。

一、二维离散小波变换（DT-CWT）DT-CWT是一种基于小波变换的信号分析方法，具有良好的时频局部性和多分辨率特性。

它可以将一个二维离散信号分解为一组具有不同尺度和不同方向的子带信号，用于提取图像的局部特征。

在本方法中，我们采用DT-CWT对唇部图像进行变换，以获取唇部的局部特征信息。

首先，将彩色唇部图像转换为灰度图像，然后对灰度图像进行DT-CWT变换。

通过选择适当的小波滤波器和分解层数，可以得到一组具有不同方向和尺度的唇部子带图像。

二、主成分分析（PCA）PCA是一种常用的降维方法，它能够将高维数据映射到低维空间，保留最重要的特征。

本方法采用PCA对DT-CWT得到的唇部子带图像进行特征降维，以减少计算复杂度和提高唇部识别的准确率。

具体步骤如下：1.对输入的唇部图像进行预处理，包括图像的归一化、平滑处理等。

这样可以去除图像中的噪声和不必要的细节，提高后续处理的效果。

2.将预处理后的唇部图像转换为灰度图像。

3.对灰度图像进行DT-CWT变换，得到一组唇部子带图像。

选择适当的小波滤波器和分解层数，以获取唇部的局部特征信息。

4.对得到的唇部子带图像进行PCA降维。

将每个子带图像拉伸为一维向量，然后将所有子带图像的向量组合成矩阵，作为PCA的输入。

通过计算输入矩阵的协方差矩阵和特征值，可以得到特征向量。

选择最大的特征值对应的特征向量作为主成分，即提取的唇部特征。

5.对提取的唇部特征进行分类或识别。

可以使用支持向量机（SVM）等机器学习方法进行分类训练和识别。

实验结果：在实际的唇部识别任务中，我们采用了包含大量唇部图像的数据集进行实验，并与其他常用的特征提取方法进行了对比。

由双树复数小波变换的父系数及邻域系数实现图像去噪卢刚;闫敬文;寇业泉;张建中【期刊名称】《光学精密工程》【年(卷),期】2009(017)004【摘要】考虑二维双树复数小波变换(DTCWT) 有良好的平移不变性和方向选择性,基于当前系数与父系数及邻域系数间的关系,构造了DTCWT图像去噪阈值计算公式,提出了一种去噪方法,PNDTCWT.该方法在对图像进行二维DTCWT变换后,利用阈值公式,根据当前系数和父系数及相邻系数计算收缩阈值,对当前系数进行去噪处理.最后,经过二维DTCWT反变换,得到去噪结果.实验结果表明,PNDTCWT的噪声抑制效果明显优于各种基于DWT的去噪方法和其他DTCWT去噪方法.与基于父系数的DTCWT去噪方法相比,PNDTCW的峰值信噪比(PSNR)平均提高了0.5 dB左右.从视觉效果来看,PNDTCW能在去噪的同时较好地保留图像细节,物体轮廓显得比较平滑,不存在传统DWT算法中的混淆现象.【总页数】7页(P916-922)【作者】卢刚;闫敬文;寇业泉;张建中【作者单位】厦门大学,通信工程系,福建,厦门,361005;汕头大学电子工程系,广东,汕头,515063;厦门大学,通信工程系,福建,厦门,361005;厦门大学,通信工程系,福建,厦门,361005【正文语种】中文【中图分类】TP391.41【相关文献】1.基于尺度噪声水平估计的双树复数小波变换图像去噪方法 [J], 许慰玲;方若宇;闫敬文2.基于双密度双树复数小波变换的图像去噪 [J], 张春梅;张太镒;陆从德3.基于平稳小波变换邻域系数萎缩的图像去噪法 [J], 沈洋;陈文静4.基于平稳小波变换邻域系数萎缩的图像去噪法 [J], 沈洋;陈文静5.基于双树复数小波变换的图像去噪方法 [J], 罗鹏;高协平因版权原因，仅展示原文概要，查看原文内容请购买。

基于 DTCWT 和 Laplace 小波相关滤波的爆炸复合结构模态参数识别方法思悦;张周锁;成玮;何正嘉;孔垂青【摘要】精确提取结构模态参数是爆炸复合结构结合状态识别的重要基础，提出一种基于双树复小波变换（DTC-WT）和 Laplace 小波相关滤波相结合的爆炸复合结构模态参数识别方法。

利用 DTCWT 的抗频带混叠特性，对多模态混叠振动响应信号进行模态分离，得到一组单模态分量；将 DTCWT 与 Laplace 小波相关滤波提取模态参数法相结合，实现爆炸复合结构的模态参数提取。

将该方法应用于爆炸复合管的实验数据，精确提取了其固有频率和阻尼比，精度明显高于直接Laplace 小波相关滤波法。

将该方法应用于生产线上不同结合状态的爆炸复合管，有效提取了不同状态管道的模态参数。

%Accurate extraction of modal parameters is an important basis for identification of explosion composite structures'interface state.A new modal parameter identification method for explosion composite structures based on dual-tree complex wavelet transformation(DTCWT)and Laplace wavelet correlation filtering was proposed.With the resistance band aliasing effects of DTCWT,a multi-modal vibration response signal was decomposed into a set of single modal signals,and then the modal parameters of the explosion composite structures were extracted with Laplace wavelet correlation filtering method from the single modal signals.The proposed method was validated using the test data of an explosion composite pipe,and then its natural frequencies and damping ratios were extracted accurately.Furthermore,the precision of the proposed method was better than that of Laplace waveletcorrelation filtering method.The proposed method was applied to explosion composite pipes with different interface states on a production line,and their modal parameters were extracted effectively.【期刊名称】《振动与冲击》【年(卷),期】2014(000)017【总页数】6页(P191-196)【关键词】爆炸复合结构;DTCWT;Laplace 小波;模态参数识别【作者】思悦;张周锁;成玮;何正嘉;孔垂青【作者单位】西安交通大学机械制造系统工程国家重点实验室，西安 710049;西安交通大学机械制造系统工程国家重点实验室，西安 710049;西安交通大学机械制造系统工程国家重点实验室，西安 710049;西安交通大学机械制造系统工程国家重点实验室，西安 710049;中国重型机械研究院股份公司，西安 710032【正文语种】中文【中图分类】TN911;O237爆炸复合结构已广泛应用于化工、石油、天然气、航空航天、汽车等行业和领域［1］，并且有巨大的工程需求。

1、 基于DTCWT 变换的图像融合方法DWT 变换和Contourlet 变换都存在同样的缺陷，即不具备平移不变性。

这意味着信号的微小平移将导致各尺度上的小波系数的能量分布有较大变化。

一种实现平移不变性的方法是在小波分解时不进行下采样。

但是这样做不仅会导致计算量的增大，而且输出信息中有很大的冗余。

复小波变换虽然可以克服上面的问题，但是它存在另外一个问题。

由于超过一层分解的复小波变换的输入形式是复数形式,所以要构造它完整的重构滤波器非常困难.为了解决这个问题，1998年，Kingsbury 首先提出了一种新的解析小波变换的方法,叫做双树复小波变换(The Dual-Tree Complex Wavelet Transform ，DTCWT).它既满足完全重构条件，又保留了复小波的其它优点。

DTCWT 变换作为一种性能较优秀的多尺度几何分析工具,近几年来得到了国内外研究学者的广泛关注，并在图像处理领域取得了较为显著的研究成果。

DTCWT 使用解析的(analytical)复小波函数基设计一对小波函数()h t ψ和()g t ψ,使其满足Hilbert 变换对要求,则由这两个函数分别作为实部和虚部的复小波系数()()()h g t t j t ψψψ=+是近似解析的。

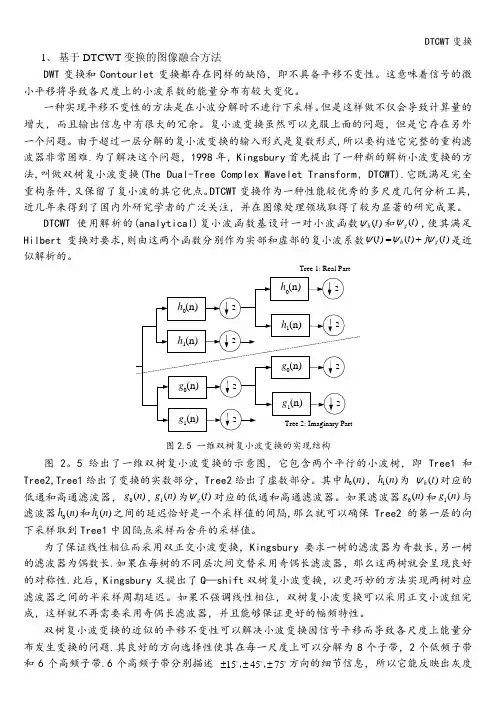
Tree 1: Real Part图2.5 一维双树复小波变换的实现结构图2。

5给出了一维双树复小波变换的示意图，它包含两个平行的小波树，即Tree1和Tree2,Tree1给出了变换的实数部分，Tree2给出了虚数部分。

其中0()h n ，1()h n 为 ()h t ψ对应的低通和高通滤波器，0()g n ,1()g n 为()g t ψ对应的低通和高通滤波器。

如果滤波器0()g n 和1()g n 与滤波器0()h n 和1()h n 之间的延迟恰好是一个采样值的间隔,那么就可以确保Tree2的第一层的向下采样取到Tree1中因隔点采样而舍弃的采样值。

双树复小波变换是一种常用的信号处理方法，可以用于信号压缩、去噪、特征提取等领域。

本文将介绍如何使用MATLAB实现双树复小波变换，并给出代码示例。

一、双树复小波变换简介双树复小波变换（Dual-Tree Complex Wavelet Transform，DTCWT）是由Kingsbury在2001年提出的一种小波变换方法。

与传统的小波变换不同，DTCWT采用了两棵树来进行分解，其中一棵树使用实数小波基，另一棵树使用虚数小波基，从而得到了更好的性能。

DTCWT的主要优点包括：1. 具有良好的时频局部性，可以更好地描述信号的时频特性。

2. 具有较高的压缩性能，可以用于信号压缩和去噪等应用。

3. 可以提取信号的多种特征，如边缘、纹理等。

二、MATLAB实现双树复小波变换在MATLAB中，我们可以使用WaveletToolbox中的函数dwt2和idwt2来实现DTCWT。

具体步骤如下：1. 定义一个信号x，可以是一维或二维的。

2. 使用dwt2函数进行双树复小波分解，得到分解系数cA、cH、cV和cD。

3. 对分解系数进行处理，如阈值处理、压缩等。

4. 使用idwt2函数进行反变换，得到重构信号。

下面给出一个简单的例子，演示如何使用MATLAB实现双树复小波变换。

% 定义一个信号xx = randn(256,256);% 使用dwt2函数进行双树复小波分解[cA,cH,cV,cD] = dwt2(x,'db2');% 对分解系数进行处理，如阈值处理、压缩等% 使用idwt2函数进行反变换，得到重构信号x_recon = idwt2(cA,cH,cV,cD,'db2');三、总结双树复小波变换是一种常用的信号处理方法，可以用于信号压缩、去噪、特征提取等领域。

在MATLAB中，我们可以使用Wavelet Toolbox中的函数dwt2和idwt2来实现DTCWT。

通过对分解系数的处理，可以实现信号的压缩、去噪等功能。

万向轴动不平衡检测的改进 DTCWT-SVD 方法何刘;林建辉;刘新厂;黄衍【摘要】针对经典小波和双树复小波（Dual-Tree Complex Wavelet Transform，DTCWT）频率泄露和混叠的根本缺陷，提出改进 DTCWT 算法，该算法解决了经典小波存在负频率以及经典小波和 DTCWT 滤波器频率不完全截止问题。

将改进DTCWT 算法和奇异值分解（Singular Value Decomposition，SVD）引入到万向轴动不平衡检测中，该方法的核心是：对万向节安装机座的振动信号进行改进DTCWT 变换得到不同尺度的分解信号，对低频近似信号进行奇异值分解，以奇异值关键叠层作为奇异值的选择准则对信号进行重构，应用重构信号的傅里叶谱来检测高速列车万向轴的动不平衡。

该方法在消除经典小波变换和 DTCWT 频率混叠的同时提高谱线清晰度，凸显故障特征。

应用万向轴动不平衡试验数据对该方法进行试验验证，结果表明：改进 DTCWT-SVD 能够很好提取出万向轴动不平衡故障特征频率的基频、倍频，与经典小波、DTCWT、纯改进 DTCWT 相比，该方法在谱的清晰度和故障表征力上得到了显著提高。

%A new improved algorithm of the dual tree complex wavelet transform (DTCWT)was proposed aiming at dealing with the leakage frequency and aliasing defect existing in classical wavelet transform and coventional DTCWT.The algorithm solves the problem of negative frequencies existing in classic wavelet and the problem of incomplete cut-off of filter frequency in classical wavelet transform and conventional DTCWT.The improved DTCWT and singular value decomposition (SVD)were introduced in the dynamic imbalance detection of cardan shaft.The vibration signals at the base installed with gimbal were decomposed through the improved DTCWT to get thedifferent scale decomposition signal. The low-frequency approximated signal was decomposed by the SVD and the key singular values were selected to reconstruct the vibration signal based on the key stack of singular values.The fourier spectrum of the reconstructed signal was applied to detect the dynamic imbalance of the cardan shaft.The method can eliminate the defects submerged in unbalanced fault signals and highlight the failure characteristics.The method was verified by test data in the condition of dynamic imbalance.The results show the improved DTCWT-SVD can effectively detect the fundamental frequency and frequency multiplication caused by the dynamic imbalance of cardan shaft and the clarity and failure characterization are significantly improved by using the improved DTCWT-SVD.【期刊名称】《振动与冲击》【年(卷),期】2016(035)022【总页数】10页(P142-151)【关键词】万向传动轴;改进 DTCWT;奇异值分解;动不平衡检测【作者】何刘;林建辉;刘新厂;黄衍【作者单位】西南交通大学牵引动力国家重点实验室，成都 610031;西南交通大学牵引动力国家重点实验室，成都 610031;西南交通大学牵引动力国家重点实验室，成都 610031;西南交通大学牵引动力国家重点实验室，成都 610031【正文语种】中文【中图分类】U211;U270高速列车万向轴是高速列车传动系统的核心部件，起到动力传递的关键作用。

技术平台基于LPT-DFT和DT-CWT变换的纹理图像检索张艳茹，张 莉，冯 芳（兰州工业学院电子信息工程学院，甘肃 兰州 730050）摘 要：基于纹理的图像检索技术是现在的研究热点。

文章提出了基于对数极坐标变换（LPT）、离散傅里叶变换（DFT）和（DT-CWT）结合方法来实现具有旋转、尺度不变性和抗噪性的图像检索。

该算法首先对图像进行极坐标变换、离散傅里叶变换。

然后，应用DT-CWT变换提取子带特征向量并对获得的特征向量进行高斯归一化。

最后，采用欧氏距离作为相似性度量方式。

实验验证了该方法的性能。

关键词：双树复小波变换；对数极坐标变换；离散傅立叶变换；图像检索0 引言随着科技的发展，数字图像的数量剧增，如何快速有效地检索出所需图像是现在的一个研究热点。

常用的图像检索方法有三类：基于文本的图像检索［1］、基于内容的图像检索（CBIR）［2，3］和基于语义的图像检索［4］。

由于CBIR通过提取图像的纹理、颜色、形状特征并进行相似性度量实现图像检索，简单易实现，所以应用于多个领域。

基于内容的图像检索，DT-CWT 的优势，然后介绍现在的纹理图像检索。

DT-CWT因具有良好的方向选择性、近似平移不变性和有限冗余度等优点，因此，DT-CWT被广泛应用于图像检索、图像去噪等领域中。

近几年多位研究学者提出了具备旋转不变性的纹理图像检索算法［5］，但检索效果需进一步提高。

对数极坐标变换（LPT）与离散傅里叶变换（DFT）相结合的方法（LPT-DFT）具有良好的旋转、尺度不变性。

文章将LPT-DFT与DT-CWT变换相结合的方法能够实现快速有效的图像检索。

1 LPT-DFT和DT-CWT结合算法对数极坐标变换（LPT）［6，7］将图像从笛卡尔坐标系映射到对数极坐标系中，能够将图像间旋转和尺度变化转化为图像间的平移变化。

DFT［8］具有平移不变性，因而，LPT与DFT相结合的方法LPT-DFT具有良好的旋转、尺度和平移不变性。