西工大高频课后习题部分答案教材
- 格式:ppt
- 大小:2.12 MB
- 文档页数:110


第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标,其定义为在不考虑摩擦的条件下机构的输出力(力矩)与输入力(力矩)之比值,即Δ=d r d r F F M M //=。
试求图示各机构在图示位置时的机械效益。
图a 所示为一铆钉机,图b 为一小型压力机,图c 为一剪刀。
计算所需各尺寸从图中量取。
(a ) (b) (c)解:(a)作铆钉机的机构运动简图及受力 见下图(a )由构件3的力平衡条件有:02343=++R R rF F F由构件1的力平衡条件有:04121=++d R R按上面两式作力的多边形见图(b )得θcot ==∆d r F F(b )作压力机的机构运动简图及受力图见(c )由滑块5的力平衡条件有:04565=++R R F F G由构件2的力平衡条件有:0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图(d ),得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。
tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中,设已知l AB=0.1m,l BC=0.33m,n1=1500r/min(为常数),活塞及其附件的重量G3=21N,连杆质量G2=25N,J S2=0.0425kg·m2,连杆质心S2至曲柄销B的距离l BS2=l BC/3。
试确定在图示位置时活塞的惯性力以及连杆的总惯性力。
解:1) 选定比例尺, mmml005.0=μ绘制机构运动简图。
(图(a) )2)运动分析:以比例尺vμ作速度多边形,如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3:)(37673333NagGamFCSI=-=-=方向与cp''相反。

机械原理第八版课后练习答案西工大版精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】<机械原理>第八版西工大教研室编第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答:参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答:机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,而且也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况?答:参考教材12~13页。
2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。
2-5 在计算平面机构的自由度时,应注意哪些事项?答:参考教材15~17页。
2-6 在图2-20所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗?为什么?答:不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答:参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答:参考教材20~21页。
2-9 任选三个你身边已有的或能观察到的下列常用装置(或其他装置),试画出其机构运动简图,并计算其自由度。
1)折叠桌或折叠椅;2)酒瓶软木塞开盖器;3)衣柜上的弹簧合页;4)可调臂台灯机构;5)剥线钳;6)磁带式录放音机功能键操纵机构;7)洗衣机定时器机构;8)轿车挡风玻璃雨刷机构;9)公共汽车自动开闭门机构;10)挖掘机机械臂机构;…。
2-10 请说出你自己身上腿部的髋关节、膝关节和踝关节分别可视为何种运动副?试画出仿腿部机构的机构运动简图,并计算其自由度。

工程材料习题 <习题一>1、抗拉强度是材料在破断前所能承受的最大应力。
屈服强度是材料开始产生明显塑性变形时的最低应力。
塑性是指材料在载荷作用下产生永久变形而不破坏的能力韧性材料变形时吸收变形力的能力硬度硬度是衡量材料软硬程度的指标材料表面抵抗更硬物体压入的能力。
刚度材料抵抗弹性变形的能力。
疲劳强度经无限次循环而不发生疲劳破坏的最大应力。
冲击韧性材料在冲击载荷作用下抵抗破坏的能力。
断裂韧性材料抵抗裂纹扩展的能力。
2 、材料的弹性模量与塑性无关。
3 、四种不同材料的应力应变曲线试比较抗拉强度屈服强度刚度和塑性。
由大到小的顺序抗拉强度 2 、 1 、 3 、 4 。
屈服强度 1 、 3 、 2 、 4 。
刚度 1 、 3 、 2 、 4 。
塑性 3 、 2 、 4 、 1 。
4、常用的硬度测试方法有几种这些方法测出的硬度值能否进行比较布氏、洛氏、维氏和显微硬度。
由于各种硬度测试方法的原理不同所以测出的硬度值不能直接进行比较。
5、以下工件应该采用何种硬度试验法测定其硬度1锉刀洛氏或维氏硬度2黄铜轴套布氏硬度3供应状态的各种碳钢钢材布氏硬度4硬质合金刀片洛氏或维氏硬度5耐磨工件的表面硬化层显微硬度6、反映材料承受冲击载荷的性能指标是什么不同条件下测得的这些指标能否进行比较怎样应用这些性能指标冲击功或冲击韧性。
由于冲击功或冲击韧性代表了在指定温度下材料在缺口和冲击载荷共同作用下脆化的趋势及其程度所以不同条件下测得的这种指标不能进行比较。
冲击韧性是一个对成分、组织、结构极敏感的参数在冲击试验中很容易揭示出材料中的某些物理现象如晶粒粗化、冷脆、热脆和回火脆性等故目前常用冲击试验来检验冶炼、热处理以及各种加工工艺的质量。
此外不同温度下的冲击试验可以测定材料的冷脆转变温度。
同时冲击韧性对某些零件如装甲板等抵抗少数几次大能量冲击的设计有一定的参考意义。
7、疲劳破坏时怎样形成的提高零件疲劳寿命的方法有哪些产生疲劳断裂的原因一般认为是由于在零件应力集中的部位或材料本身强度较低的部位如原有裂纹、软点、脱碳、夹杂、刀痕等缺陷在交变应力的作用下产生了疲劳裂纹随着应力循环周次的增加疲劳裂纹不断扩展使零件承受载荷的有效面积不断减小当减小到不能承受外加载荷的作用时零件即发生突然断裂。

第3章课后习题参考答案3—1何谓速度瞬心相对瞬心与绝对瞬心有何异同点答:参考教材30^31页。
3—2何谓三心定理何种情况下的瞬心需用三心定理来确定答:参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上) (a)答:3-4标出图示的齿轮一连杆纽合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比U)l/U)3o答:1)瞬新的数目:K 二N (N-1 )/2=6 (6T )/2=152)为求3(/33需求3个瞬心%、P%、P 竹的位置由构件J 3在K 点的速度方向相同,可知4与3同向。
3-6 在图示的四杆机构中,L AB 二60mm, LcD=90mm, L AD =L BC = 120mm, u)2=10rad/s,试用瞬心法求:1) 当 0=165°2) 当 0=165°2)求vc 定出瞬心"2的位置(图b) 因M 为构件3的绝对瞬心,则有 U )3=VB /IB PI 3=W2I JB / U=10X X78=(rad/s) v c = u c pi3U)a=X52X = (m/s)(2分)时,点的速度vc;吋,构件3的BC 线上速度最小的一点E 的位置及速度的大小:3i/3s= PadPu/PidPi^DK/AK(图b)C线上速度灵小的点必与p13点的距离3—11速度多边形和加速度多边彤有哪些特性试标出图中的方向。
答速度多边形和加速慶多边形特性参见下图,各速度方向在图中用箭头标出。
3T2在图示的机构中,设已知构件的尺寸及原动件1的角速度(顺时针),试用图解法求机构在图示位置吋C点的速厦和加速度。
V C3=V B+V C3B=V C2+V C3C2(2 分)aC3=aB+a n C3B+a C38=aC2+a C3C2+a”C3C2Vc2=0 3C2=0 (2 分)Vc30=O U) 3=0 a k C3C2=0(1分)(1分)答:(3分)答:(2分)V C2=V B+V C28=V O3+V G2C3U)3=W 2=0(2分)(2分)(1分)& f t k ra^+a C2B+3 C2B~3C3+3 C2C3+3 C2C3(3分)(c)(bj s bi iV B3=V B2B3B2(2分)(1分) a 阴+a B3_aB2+a B3B2+a B3B2 3- 13试判斷在图示的两机构中.B 点足否都存在哥氏加速度又在何位置哥氏加速度为零忤 出相应的机构位置图。

高频课后习题答案(部分)(总11页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\第一章何谓通信系统通信系统由哪几部分组成答:用电信号(或光信号)传输信息的系统称为通信系统。
它由输入变换器、发送设备、传输信道、接收设备、输出变换器等组成。
无线电通信为什么要采用调制技术常用的模拟调制方式有哪些答:采用调制技术可使低频基带信号装载在高频载波上,从而缩短天线尺寸,易于天线辐射,而且不同的发射台其载波频率不同,在接收端便于选择接收。
此外,采用调制可进行频分多路通信,实现信道的复用,提高信道利用率;还可以提高系统性能指标,提高抗干扰能力。
常用的模拟调制方式有振幅调制(AM )、频率调制(FM )和相位调制(PM )。
已知频率为3kHz 、1000kHz 、100MHz 的电磁波,试分别求出其波长并指出所在波段名称。
解:根据λ=c /f (其中c =3×108m/s )分别得出100km (为超长波)、300m (为中波)和3m (为超短波)。
画出无线广播调幅发射机组成框图,并用波形说明其发射过程。
答:参见图。
第二章二、选择题1.LC 串联回路谐振时阻抗最 ,且为纯电阻,失谐时阻抗变 ,当f <o f 回路呈 ,当f >o f 回路呈 。
A .容性B .感性C .大D .小2.LC 组成的并联谐振回路谐振时,阻抗为 ,谐振时电压为 ;电纳为 ,回路总导纳为 。
A .最大值B .最小值C .零D .不能确定3.把谐振频率为o f 的LC 并联谐振回路串联在电路中,它 的信号通过。
A .允许频率为o fB .阻止频率为o fC .使频率低于o fD .使频率高于o f4.在自测题1图所示电路中,1ω和2ω分别为其串联谐振频率和并联谐振频率。
它们之间的大小关系为 。
A .1ω等于2ωB .1ω大于2ωC .1ω小于2ωD .无法判断 5.强耦合时,耦合回路η越大,谐振曲线在谐振频率处的凹陷程度 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN M P a 3.324105.2105180946920112=⨯⨯⨯==--N N σσN M P a 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C012σσσΦσ-=- σΦσσ+=∴-1210 M P a 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。

第8章课后习题参考答案8-l 铰链四杆机构中,转动副成为周转副的条件是什么?在下图所示四杆机构ABCD 中哪些运动副为周转副?当其杆AB 与AD 重合时,该机构在运动上有何特点?并用作图法求出杆3上E 点的连杆曲线。
答:转动副成为周转副的条件是:(1)最短杆与最长杆的长度之和小于或等于其他两杆长度之和;(2)机构中最短杆上的两个转动副均为周转副。
图示ABCD 四杆机构中C 、D 为周转副。
当其杆AB 与AD 重合时,杆BE 与CD 也重合因此机构处于死点位置。
8-2曲柄摇杆机构中,当以曲柄为原动件时,机构是否一定存在急回运动,且一定无死点?为什么? 答:机构不一定存在急回运动,但一定无死点,因为:(1)当极位夹角等于零时,就不存在急回运动如图所示,(2)原动件能做连续回转运动,所以一定无死点。
8-3 四杆机构中的极位和死点有何异同?8-4图a 为偏心轮式容积泵;图b 为由四个四杆机构组成的转动翼板式容积泵。
试绘出两种泵的机构运动简图,并说明它们为何种四杆机构,为什么?解 机构运动简图如右图所示,ABCD 是双曲柄机构。
因为主动圆盘AB 绕固定轴A 作整周转动,而各翼板CD 绕固定轴D 转动,所以A 、D 为周转副,杆AB 、CD 都是曲柄。
8-5试画出图示两种机构的机构运动简图,并说明它们各为何种机构。
图a 曲柄摇杆机构图b 为导杆机构。
8-6如图所示,设己知四杆机构各构件的长度为240a mm =,600b =mm ,400,500c mm d mm ==。
试问:1)当取杆4为机架时,是否有曲柄存在?2)若各杆长度不变,能否以选不同杆为机架的办法获得双曲柄机构和双摇杆机构?如何获得?3)若a 、b ﹑c 三杆的长度不变,取杆4为机架,要获得曲柄摇杆机构,d 的取值范围为何值? :解 (1)因a+b=240+600=840≤900=400+500=c+d 且最短杆 1为连架轩.故当取杆4为机架时,有曲柄存在。

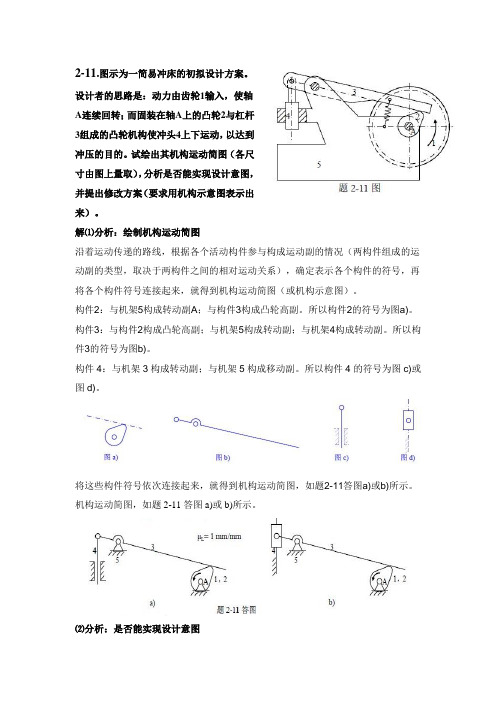
2-11.图示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案(要求用机构示意图表示出来)。
解⑴分析:绘制机构运动简图沿着运动传递的路线,根据各个活动构件参与构成运动副的情况(两构件组成的运动副的类型,取决于两构件之间的相对运动关系),确定表示各个构件的符号,再将各个构件符号连接起来,就得到机构运动简图(或机构示意图)。
构件2:与机架5构成转动副A;与构件3构成凸轮高副。
所以构件2的符号为图a)。
构件3:与构件2构成凸轮高副;与机架5构成转动副;与机架4构成转动副。
所以构件3的符号为图b)。
构件4:与机架3构成转动副;与机架5构成移动副。
所以构件4的符号为图c)或图d)。
将这些构件符号依次连接起来,就得到机构运动简图,如题2-11答图a)或b)所示。
机构运动简图,如题2-11答图a)或b)所示。
⑵分析:是否能实现设计意图在机构的结构分析中判断该方案否能实现设计意图,应该从以下两点考虑:①机构自由度是否大于零;②机构原动件的数目是否等于机构自由度的数目。
因此,必须计算该机构的自由度F=3n-(2p L+p H)=3×3-(2×4+1)=0。
因为机构的自由度为F=3n-(2p L+p H)=3×3-(2×4+1)=0可知,该机构不能运动,不能实现设计意图。
⑶分析修改方案因为原动件的数目为1,所以修改的思路为:将机构的自由度由0变为1。
因此,修改方案应有2种。
方案1:给机构增加1个构件(增加3个独立运动)和1个低副(增加2个约束),使机构自由度增加1,即由0变为1。
如题2-11答图c)、d)、e)所示。
方案2:将机构中的1个低副(2个约束)替换为1个高副(1个约束),使机构中的约束数减少1个,从而使机构自由度增加1,即由0变为1。


第七章 机械的运转及其速度波动的调节题7-7如图所示为一机床工作台的传动系统,设已知各齿轮的齿数,齿轮3的分度圆半径r 3,各齿轮的转动惯量J 1、J 2、J 2`、J 3,因为齿轮1直接装在电动机轴上,故J 1中包含了电动机转子的转动惯量,工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时,试求该机械系统的等效转动惯量J e 。
解:根据等效转动惯量的等效原则,有∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ni i Si Si i e J v m J 122ωωω 212133212221221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=''ωωωωωωωv g G J J J J J e 2322123232213221222121⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+='''Z Z Z Z r g G Z Z Z Z J Z Z J Z Z J J J e 题7-9已知某机械稳定运转时其主轴的角速度ωs =100rad/s ,机械的等效转动惯量J e =0.5Kg ·m 2,制动器的最大制动力矩M r =20N ·m (该制动器与机械主轴直接相联,并取主轴为等效构件)。
设要求制动时间不超过3s ,试检验该制动器是否能满足工作要求。
解:因此机械系统的等效转动惯量J e 及等效力矩M e 均为常数,故可利用力矩形式的机械运动方程式dtd J Me e ω= 其中:25.020m kg m N M M r e ⋅=⋅-=-= ωωωd d d M J dt r e 025.0205.0-=-=-= ()s t S S 5.2025.0025.0==--=∴ωωω由于 s s t 35.2<= 所以该制动器满足工作要求。
题7-11 在图a 所示的刨床机构中,已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P 1=367.7W 和P 2=3677W ,曲柄的平均转速n=100r/min ,空程中曲柄的转角φ1=120°。

西北工业大学POJ答案绝对是史上最全版(不止100题哦……按首字母排序)1.“1“的传奇2.A+B3.A+BⅡ4.AB5.ACKERMAN6.Arithmetic Progressions7.Bee8.Checksum algorithm9.Coin Test10.Dexter need help11.Double12.Easy problem13.Favorite number14.Graveyard15.Hailstone16.Hanoi Ⅱ17.Houseboat18.Music Composer19.Redistribute wealth20.Road trip21.Scoring22.Specialized Numbers23.Sticks24.Sum of Consecutive25.Symmetric Sort26.The Clock27.The Ratio of gainers to losers28.VOL大学乒乓球比赛29.毕业设计论文打印30.边沿与内芯的差31.不会吧,又是A+B32.不屈的小蜗33.操场训练34.插入链表节点35.插入排序36.插入字符37.成绩表计算38.成绩转换39.出租车费40.除法41.创建与遍历职工链表42.大数乘法43.大数除法44.大数加法45.单词频次46.迭代求根47.多项式的猜想48.二分查找49.二分求根50.发工资的日子51.方差52.分离单词53.分数拆分54.分数化小数55.分数加减法56.复数57.高低交换58.公园喷水器59.韩信点兵60.行程编码压缩算法61.合并字符串62.猴子分桃63.火车站64.获取指定二进制位65.积分计算66.级数和67.计算A+B68.计算PI69.计算π70.计算成绩71.计算完全数72.检测位图长宽73.检查图像文件格式74.奖金发放75.阶乘合计76.解不等式77.精确幂乘78.恐怖水母79.快速排序80.粒子裂变81.链表动态增长或缩短82.链表节点删除83.两个整数之间所有的素数84.路痴85.冒泡排序86.你会存钱吗87.逆序整数88.排列89.排列分析90.平均值函数91.奇特的分数数列92.求建筑高度93.区间内素数94.三点顺序95.山迪的麻烦96.删除字符97.是该年的第几天98.是该年的第几天?99.数据加密100.搜索字符101.所有素数102.探索合数世纪103.特殊要求的字符串104.特殊整数105.完全数106.王的对抗107.危险的组合108.文件比较109.文章统计110.五猴分桃111.小型数据库112.幸运儿113.幸运数字”7“114.选择排序115.寻找规律116.循环移位117.延伸的卡片118.羊羊聚会119.一维数组”赋值“120.一维数组”加法“121.勇闯天涯122.右上角123.右下角124.圆及圆球等的相关计算125.圆及圆球等相关计算126.程序员添加行号127.找出数字128.找幸运数129.找最大数130.整数位数131.重组字符串132.子序列的和133.子字符串替换134.自然数立方的乐趣135.字符串比较136.字符串复制137.字符串加密编码138.字符串逆序139.字符串排序140.字符串替换141.字符串左中右142.组合数143.最次方数144.最大乘积145.最大整数146.最小整数147.最长回文子串148.左上角149.左下角1.“1“的传奇#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){int n,i,j,k=0,x=1,y,z,m,p,q,a,s=0;scanf("%d",&n);m=n;for(i=1;i<12;i++){m=m/10;k++;if(m==0)break;}q=n;k=k-1;for(a=1;a<=k;a++){x=x*10;}y=q%x;z=q/x;p=q-y;if(z>=2)s=s+x+z*k*(x/10); elses=s+z*k*(x/10);for(j=p;j<=n;j++) {m=j;for(i=1;i<12;i++){x=m%10;if(x==1)s++;m=m/10;if(m==0)break;}}printf("%d",s);return 0;}2.A+B#include <stdio.h>int doubi(int n,int m){n=n+m;n=n%100;return n;}int main(){int t,i,a[100],n,m;scanf("%d",&t);for (i=0;i<=(t-1);i++){scanf("%d%d",&n,&m);a[i]=doubi(n,m);}for (i=0;i<=(t-1);i++)printf("%d\n",a[i]);return 0;}3.A+BⅡ#include <stdio.h>int main(){int A,B,sum;scanf("%d%d",&A,&B);sum=A+B;printf("%d\n",sum);return 0;}4.AB#include <stdio.h>#include <stdlib.h>#include <string.h>int main(){char s[100],q[100];double a,b,c;int n=0,i;scanf("%lf%lf",&a,&b);c=a*b;sprintf(s,"%.0lf",c);for(i=0;i<strlen(s);i++){n=n+s[i]-48;}while(n>=10){sprintf(q,"%d",n);n=0;for(i=0;i<strlen(q);i++)n=n+q[i]-48;}printf("%d",n);return 0;}5.ACKERMAN#include <stdio.h>#include <stdlib.h>int ack(int x,int y){int n;if (x==0) {n=y+1;return n;}else if (y==0) n=ack(x-1,1);else n=ack(x-1,ack(x,y-1));return n;}int main(){int m,b;scanf("%d%d",&m,&b);m=ack(m,b);printf("%d",m);return 0;}6.Arithmetic Progressions#include <stdio.h>#include <math.h>int g(int n){int i;if(n==1) return 0;if(n==2) return 1;if(n==3) return 1;for(i=2;i<=sqrt(n);i++) if(n%i==0) return 0;return 1;}int f(int a,int b,int c){int i=0,s=a-b;if(c==1&&g(a)==1) return a;if(b==0&&g(a)!=1) return -1;while(1){s=s+b;if(g(s)) i++;if(i>=c) break;}return s;int main(){int a,b,c,d[100],i=0,n;while(1){scanf("%d%d%d",&a,&b,&c);if(a==0&&b==0&&c==0) break;d[i]=f(a,b,c);i++;}n=i;for(i=0;i<n;i++)printf("%d\n",d[i]);return 0;}7.Bee#include <stdio.h>#include <stdlib.h>int main()int A[100],i=0,j,k,female=0,male=1,x;for(;;i++){scanf("%d",&A[i]);if(A[i]==-1)break;}for(j=0;j<i;j++){female=0,male=1;for(k=1;k<A[j];k++){x=female;female=male;male=x+male+1;}printf("%d %d\n",male,female+male+1);}return 0;}8.Checksum algorithm #include <stdio.h>#include <stdlib.h>#include <string.h>int main(){int i,n,t,j;char s[100][100];for(i=0;;i++){gets(s[i]);if(s[i][0]=='#') break;}n=i;for(i=0;i<n;i++){t=0;for(j=0;j<strlen(s[i]);j++)if(s[i][j]==32) t=t;else t=t+(j+1)*(s[i][j]-64);printf("%d\n",t);}return 0;}9.Coin Test#include <stdio.h>#include <stdlib.h>int main(){char A[100000];int n,i=0,a=0,b=0,j;double x;while(1){scanf("%c",&A[i]);if(A[i]=='\n')break;i++;}for(j=0;j<i;j++){if(A[j]=='S'){printf("WA");goto OH;}if(A[j]=='U')a++;if(A[j]=='D')b++;}x=a*1.0/(a+b)*1.0;if(x-0.5>0.003||x-0.5<-0.003) printf("Fail");elseprintf("%d/%d",a,a+b);OH:return 0;}10.Dexter need help#include <stdio.h>int fun(int a){if(a==1) return 1;elsereturn fun(a/2)+1;}int main(){int a,b[100],i=0,j; while(1){scanf("%d",&a);if(a==0)break;b[i]=fun(a);i++;}for(j=0;j<i;j++){printf("%d\n",b[j]); }return 0;}11.Double#include <stdio.h>#include <stdlib.h>int main(){int a[100],b[100],i,j,n,t=0;for(i=0;;i++){scanf("%d",&a[i]);if(a[i]==0) break;}n=i;for(i=0;i<n;i++)b[i]=2*a[i];for(i=0;i<n;i++)for(j=0;j<n;j++)if(a[i]==b[j]) t++;printf("%d",t);return 0;}12.Easy problem#include <stdio.h>#include <math.h>int main(){int N,i,n,j=0;scanf("%d",&N);for(i=2;i<N+1;i++){if((N+1)%i==0)j++;}printf("%d",j/2);return 0;}13.Favorite number #include <stdio.h>#include <string.h>#define MAXNUM 100000int prime_number = 0;int prime_list[MAXNUM]; bool is_prime[MAXNUM]; int ans[MAXNUM + 2];int dp[MAXNUM + 2];void set_prime() {int i, j;memset(is_prime, 0, sizeof(is_prime));for (i = 2; i < MAXNUM; i++) {if (is_prime[i] == 0) {prime_list[prime_number++] = i;if (i >= MAXNUM / i) continue;for (j = i * i; j < MAXNUM; j+=i) {is_prime[j] = 1;}}}}int main() {int i, j, k,o=0,d[100];memset(dp, -1, sizeof(dp));set_prime();ans[0] = 0;dp[1] = 0;for (i = 1; i <= MAXNUM; i++) {ans[i] = ans[i - 1] + dp[i];if (dp[i + 1] == -1 || dp[i + 1] > dp[i] + 1) { dp[i + 1] = dp[i] + 1;}for (j = 0; j < prime_number; j++) {if (i > MAXNUM / prime_list[j]) break;k = i * prime_list[j];if (dp[k] == -1 || dp[k] > dp[i] + 1) {dp[k] = dp[i] + 1;}}}while (scanf("%d%d", &i, &j) == 2 && (i || j)) { d[o]=ans[j] - ans[i - 1];o++;}for(i=0;i<o;i++)printf("%d\n",d[i]);}14.Graveyard#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){int a[100],b[100],n,i,j;double s,p,l,t;for(i=0;;i++){scanf("%d%d",&a[i],&b[i]);if(a[i]==0&&b[i]==0) break;}n=i;for(i=0;i<n;i++){p=10000;if(b[i]%a[i]==0){printf("0.0000\n");continue;};t=10000/((double)a[i]);for(j=1;j<a[i]+b[i];j++){l=10000/((double)(a[i]+b[i]));l=t-j*l;l=fabs(l);if(l<p) p=l;}s=(a[i]-1)*p;printf("%.4lf\n",s);}return 0;}15.Hailstone#include <stdio.h>#include <stdlib.h>#include <string.h>int f(int n){int s=1;while(1){if(n==1) return s;else if(n%2==0) n=n/2,s++;else n=3*n+1,s++;}}int main()int n,m,i,j=0,t;scanf("%d%d",&m,&n);printf("%d %d",m,n);if(m>n) t=m,m=n,n=t;for(i=m;i<=n;i++)if(f(i)>j) j=f(i);printf(" %d",j);return 0;}16.Hanoi Ⅱ#include <stdio.h>#include <stdlib.h>#define M 70int start[M], targe[M];long long f(int *p, int k, int fina){if(k==0) return 0;if(p[k]==fina) return f(p,k-1,fina); return f(p,k-1,6-fina-p[k])+(1LL<<(k-1));int main (){long long ans;int n;while(scanf("%d",&n),n){int i;for(i=1;i<=n;i++) scanf("%d",&start[i]);for(i=1;i<=n;i++) scanf("%d",&targe[i]);int c=n;for(;c>=1&&start[c]==targe[c];c--);if(c==0){printf("0\n"); continue;}int other=6-start[c]-targe[c];ans=f(start,c-1,other)+f(targe,c-1,other)+1;printf("%lld\n",ans);}return 0;}17.Houseboat#include <stdio.h>#include <stdlib.h>#include <math.h>#define pi 3.1415926int f(float x,float y){int i;for(i=0;;i++)if(50*i>sqrt(x*x+y*y)*sqrt(x*x+y*y)*pi/2) break;return i;}int main(){int n,i,a[100];float x,y;scanf("%d",&n);for(i=0;i<n;i++){scanf("%f%f",&x,&y);a[i]=f(x,y);}for(i=0;i<n;i++)printf("%d %d\n",i+1,a[i]);return 0;}18.Music Composer19.Redistribute wealth#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){int a[1000],b[1000],n,i,j,s,sum,t,m,mid,c[100],k=0;while(1){scanf("%d",&n);if(n==0) break;{s=0;for(i=1;i<=n;i++){scanf("%d",&a[i]);s=s+a[i];}m=s/n;b[1]=a[1]-m;b[0]=0;for(i=2;i<n;++i)b[i]=b[i-1]+a[i]-m;for(i=0;i<n;i++)for(j=0;j<n-1-i;j++)if(b[j]>b[j+1])t=b[j],b[j]=b[j+1],b[j+1]=t;mid=b[n/2];sum=0;for(i=0;i<=n-1;++i) sum=sum+fabs(mid-b[i]);c[k]=sum;k++;}}for(i=0;i<k;i++) printf("%d\n",c[i]);return 0;}20.Road trip#include <stdio.h>#include <stdlib.h>#include <math.h>int f(int n){int a[100],b[100],i,s;for(i=0;i<n;i++)scanf("%d%d",&a[i],&b[i]);s=a[0]*b[0];for(i=1;i<n;i++)s=s+a[i]*(b[i]-b[i-1]);return s;}int main(){int n,c[100],i=0;while(1){scanf("%d",&n);if(n==-1) break;c[i]=f(n);i++;}n=i;for(i=0;i<n;i++)printf("%d\n",c[i]);return 0;}21.Scoring#include <stdio.h>#include <stdlib.h>#include <string.h>int main(){int i,j,sum,min,c,count,n,a,b;char s1[50],s2[50];scanf("%d",&n);for(i=0;i<n;i++){count=sum=0;scanf("%s",s2);for(j=0;j<4;j++){scanf("%d%d",&a,&b);if(b!=0){sum+=(a-1)*20+b;count++;}}if(i==0){c=count,min=sum;strcpy(s1,s2);}else if(count>c||(count==c&&sum<min)){min=sum;c=count;strcpy(s1,s2);}}printf("%s %d %d\n",s1,c,min);return 0;}22.Specialized Numbers#include <stdio.h>#include <stdlib.h>int main(){int i,n,sum10,sum12,sum16;for(i=2992;i<3000;i++){n=i;sum10=0;while(n){sum10+=n%10;n/=10;}n=i;sum12=0;while(n){sum12+=n%12;n/=12;}n=i;sum16=0;while(n){sum16+=n%16;n/=16;}if(sum10==sum12&&sum12==sum16) printf("%d\n",i);}return 0;}23.Sticks#include <stdio.h>#include <string.h>#include <stdlib.h>int len[64], n, minlen, get;bool b[64];int cmp(const void *a, const void *b){return *(int *)a < *(int *)b ? 1 : -1;}bool dfs(int nowlen, int nowget, int cnt){if(cnt >= n) return false;if(get == nowget) return true;int i;bool f = false;if(nowlen == 0) f = true;for(i = cnt; i < n; i++){if(!b[i]){if(len[i] + nowlen == minlen){b[i] = true;if(dfs(0, nowget+1, nowget))return true;b[i] = false;return false;}else if(len[i] + nowlen < minlen){b[i] = true;if(dfs(nowlen+len[i], nowget, i+1))return true;b[i] = false;if(f) return false;while(i + 1 < n && len[i] == len[i+1]) i++;}}}return false;}int main(){int i, tollen;while(scanf("%d", &n), n){tollen = 0;int j = 0, p;for(i = 0; i < n; i++){scanf("%d", &p);if(p <= 50){len[j] = p;tollen += len[j];j++;}}n = j;if(n == 0){printf("0\n");continue;}qsort(len, n, sizeof(int), cmp);for(minlen = len[0]; ; minlen++) {if(tollen % minlen) continue;memset(b, 0, sizeof(b));get = tollen / minlen;if(dfs(0, 0, 0)){printf("%d\n", minlen);break;}}}return 0;}24.Sum of Consecutive#include <stdio.h>#include <stdlib.h>#include <string.h>int len[64],n,minlen,get;int b[64];int cmp(const void *a,const void *b) {return *(int *)a<*(int *)b?1:-1;}int dfs(int nowlen,int nowget,int cnt) {if(cnt>=n) return 0;if(get==nowget) return 1;int i,f=0;if(nowlen==0) f=1;for(i=cnt;i<n;i++){if(len[i]+nowlen==minlen){b[i]=1;if(dfs(0,nowget+1,nowget)) return 1;b[i]=0;return 0;}else if(len[i]+nowlen<minlen){b[i]=1;if(dfs(nowlen+len[i],nowget,i+1)) return 1;b[i]=0;if(f) return 0;while(i+1<n&&len[i]==len[i+1]) i++;}}return 0;}int main(){int i,tollen,q=0,c[100];while(scanf("%d",&n),n){tollen=0;int j=0,p;for(i=0;i<n;i++){scanf("%d",&p);if(p<=50){len[j]=p;tollen+=len[j];j++;}}n=j;if(n==0){printf("0\n");continue;}qsort(len,n,sizeof(int),cmp);for(minlen=len[0];;minlen++){if(tollen%minlen) continue;memset(b,0,sizeof(b));get=tollen/minlen;if(dfs(0,0,0)){c[q]=minlen;q++;break;}}}for(i=0;i<q;i++)printf("%d\n",c[i]);return 0;}25.Symmetric Sort#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double A[100];int i=0,j=0,k=0,l=0,sum=0;while(1){scanf("%lf",&A[i]);if(A[i]==0)break;i++;}for(j=0;j<i;j++){if(A[j]==2)printf("1\n");else{int B[10000],m=1,number=0;double n;B[0]=2;for(k=3;k<=A[j];k+=2){n=(double)k;for(l=2;l<=sqrt(n);l++){if(k%l==0)goto ai;}B[m]=k;m++;ai:;}for(k=0;k<m;k++){sum=0;for(l=k;l<m;l++){sum+=B[l];if(sum==A[j]){number++;break;}}}printf("%d\n",number);}}return 0;}26.The Clock#include <stdio.h>#include <stdlib.h>#include <string.h>int main(){char s[100][100],a[100];int i,j,n;scanf("%d",&n);for(i=0;i<n;i++) scanf("%s",s[i]);for(i=0;i<n-1;i++)for(j=0;j<n-1-i;j++)if(strlen(s[i])>strlen(s[i+1])) strcpy(a,s[i]),strcpy(s[i],s[i+1]),strcpy(s[i+1],a);if(n%2==0){for(i=0;i<n-1;i=i+2) printf("%s ",s[i]);printf("%s ",s[n-1]);for(i=i-3;i>0;i=i-2) printf("%s ",s[i]);}else{for(i=0;i<n-1;i=i+2) printf("%s ",s[i]);printf("%s ",s[n-1]);for(i=i-1;i>0;i=i-2) printf("%s ",s[i]);}return 0;}27.The Ratio of gainers to losers #include<stdio.h>int main(){char s[5];int i,sum=0;gets(s);for(i=0;s[i]!='\0';i++){switch(s[i]){case'I': sum+=1;break; case'V': sum=5-sum;break; case'X':sum=10-sum;break; }}printf("%d\n",sum);return 0;}28.VOL大学乒乓球比赛#include <stdio.h>#include <stdlib.h>int main(){printf("A=Z\nB=X\nC=Y\n");return 0;}29.毕业设计论文打印#include <stdio.h>#include <stdlib.h>int main(){int a[100],j=1,i,n,m;scanf("%d%d",&n,&m);for(i=0;i<n;i++)scanf("%d",&a[i]);for(i=0;i<n;i++)if(a[i]>a[m]) j++;printf("%d",j++);return 0;}30.边沿与内芯的差#include <stdio.h>#include <stdlib.h>int main(){int A[100][100],i,j,m,n,s=0,t=0;scanf("%d%d",&n,&m);for(i=1;i<=n;i++){for(j=1;j<=m;j++){scanf("%d",&A[i][j]);}}for(i=2;i<m;i++)s=s+A[1][i];for(i=2;i<m;i++)。



第6章课后习题参考答案6—1什么是静平衡?什么是动平衡?各至少需要几个平衡平面?静平衡、动平衡的力学条件各是什么?6—2动平衡的构件一定是静平衡的,反之亦然,对吗?为什么?在图示(a)(b)两根曲轴中,设各曲拐的偏心质径积均相等,且各曲拐均在同一轴平面上。
试说明两者各处于何种平衡状态?答:动平衡的构件一定是静平衡的,反之不一定。
因各偏心质量产生的合惯性力为零时,合惯性力偶不一定为零。
(a)图处于动平衡状态,(b)图处于静平衡状态。
6一3既然动平衡的构件一定是静平衡的,为什么一些制造精度不高的构件在作动平衡之前需先作静平衡?6—4为什么作往复运动的构件和作平面复合运动的构件不能在构件本身内获得平衡,而必须在基座上平衡?机构在基座上平衡的实质是什么?答由于机构中作往复运动的构件不论其质量如何分布,质心和加速度瞬心总是随着机械的运动周期各沿一条封闭曲线循环变化的,因此不可能在一个构件的内部通过调整其质量分布而达到平衡,但就整个机构而言.各构件产生的惯性力可合成为通过机构质心的的总惯性力和总惯性力偶矩,这个总惯性力和总惯性力偶矩全部由机座承受,所以必须在机座上平衡。
机构在基座上平衡的实质是平衡机构质心的总惯性力,同时平衡作用在基座上的总惯性力偶矩、驱动力矩和阻力矩。
6—5图示为一钢制圆盘,盘厚b=50 mm。
位置I处有一直径φ=50 inm的通孔,位置Ⅱ处有一质量m2=0.5 kg的重块。
为了使圆盘平衡,拟在圆盘上r=200 mm处制一通孔,试求此孔的直径与位置。
(钢的密度ρ=7.8 g/em3。
)解根据静平衡条件有:m1r I+m2rⅡ+m b r b=0m2rⅡ=0.5×20=10 kg.cmm1r1=ρ×(π/4) ×φ2×b×r1=7.8 ×10-3×(π/4)×52×5 ×l0=7.66 kg.cm 取μW=4(kg.cm)/cm,作质径积矢量多边形如图所示,所添质量为: m b=μw w b/r=4×2.7/20=0.54 kg,θb=72º,可在相反方向挖一通孔其直径为:6—6图示为一风扇叶轮。