线性谐振子量子力学课件
- 格式：ppt
- 大小：224.00 KB
- 文档页数：7
下载文档原格式
合集下载
量子力学2.7
当n = 0， 4， 偶数时，ψ n (− x ) = ψ n ( x )，偶函数 2， ⋯ 即 n = 1，5， 奇数时，ψ n (− x ) = −ψ n ( x )，奇函数 3， ⋯
ψ n (− x ) = (− 1)nψ n ( x )
偶函数量子状态——偶宇称态 偶宇称态 偶函数量子状态 奇函数量子状态——奇宇称态 奇宇称态 奇函数量子状态 作业： 作业：2-5
v=2 v =1 v =0
∞
∞
∞
或
(v + 2)(v + 1)av + 2ξ v − 2∑ vavξ v + (λ − 1)∑ avξ v ∑
v =0 v =0 v =0
∞
∞
∞
=0
(v + 2)(v + 1)av + 2 − 2vav + (λ − 1)a v = 0
8
U1
线性谐振子满足的定态薛定谔方程为
2 2
x
2 2
x
4α x =
2 2
2α 3
π
e
−α 2 x 2
x2
α −α w2 ( x ) = e 2 π
……
2 2
x
(2α 2 x 2 − 1) 2
17
下图是n ， ， ， ， ， 六个波函数图形 六个波函数图形。 下图是 =0，1，2，3，4，5六个波函数图形。
18
下图是n=0，1，2，3，4五个波函数的几率分布图。 ， ， ， ， 五个波函数的几率分布图 五个波函数的几率分布图。 下图是
一维线性谐振子.avi 一维线性谐振子
19
和经典振子对比： 和经典振子对比： 和微观谐振子能量相同的经典振子， 和微观谐振子能量相同的经典振子，其振幅为
ψ n (− x ) = (− 1)nψ n ( x )
偶函数量子状态——偶宇称态 偶宇称态 偶函数量子状态 奇函数量子状态——奇宇称态 奇宇称态 奇函数量子状态 作业： 作业：2-5
v=2 v =1 v =0
∞
∞
∞
或
(v + 2)(v + 1)av + 2ξ v − 2∑ vavξ v + (λ − 1)∑ avξ v ∑
v =0 v =0 v =0
∞
∞
∞
=0
(v + 2)(v + 1)av + 2 − 2vav + (λ − 1)a v = 0
8
U1
线性谐振子满足的定态薛定谔方程为
2 2
x
2 2
x
4α x =
2 2
2α 3
π
e
−α 2 x 2
x2
α −α w2 ( x ) = e 2 π
……
2 2
x
(2α 2 x 2 − 1) 2
17
下图是n ， ， ， ， ， 六个波函数图形 六个波函数图形。 下图是 =0，1，2，3，4，5六个波函数图形。
18
下图是n=0，1，2，3，4五个波函数的几率分布图。 ， ， ， ， 五个波函数的几率分布图 五个波函数的几率分布图。 下图是
一维线性谐振子.avi 一维线性谐振子
19
和经典振子对比： 和经典振子对比： 和微观谐振子能量相同的经典振子， 和微观谐振子能量相同的经典振子，其振幅为
3.5 线性谐振子
3.5 线性谐振子 (The Harmonic Oscillator)
在自然界中一维谐振子广泛存在,任何体系在平衡位置附近 的小振动,如分子的振动,晶格的振动,原子和表面振动以及辐 射场的振动等都可以分解成若干彼此独立的简谐振动 简谐振动.本节将应 简谐振动 用薛定谔方程来求出谐振子的能量本征值和本征函数. 假设一个一维谐振子,其势能按泰勒级数展开.
T /2
2π
π dx / dt
x=asinωt, 那么
dx = aω cos ωt = ωa 1 ( x / a ) 2 dt a 1 wcl ( x )dx = dx π 1 ( x / a )2
(31) (32)
振幅可以从能量得到 E = 1 mω 2 a 2 , a = 2 E / mω 2 2 相反, 对局域在x+dx中的粒子,量子力学中的几率为
∧ 1 (ξ + ) = a ξ 2
∧+
(48)
从这两个关系, 我们可以估算ψn的相邻函数ψn-1和ψn+1. 为了简便 起见,我们做如下替代
1 (ξ ) = a ξ 2
∧+
(49)
(48)式变为
aψ n = nψ n 1 ,
(6)
k2 k 2 E κ= = = 2 λ 2 m ω ω
为了解方程(6),我们设一个非对称试解
ψ ( y) = e
y/2
( y)
(7)
dψ 1 d y / 2 d 2ψ 1 d d 2 y / 2 = [ ( y ) + ]e and = [ ( y )- + 2 ]e (8) 2 dy 2 dy dy 4 dy dy
λ x, dx =
2
∫ ψ ( x)
在自然界中一维谐振子广泛存在,任何体系在平衡位置附近 的小振动,如分子的振动,晶格的振动,原子和表面振动以及辐 射场的振动等都可以分解成若干彼此独立的简谐振动 简谐振动.本节将应 简谐振动 用薛定谔方程来求出谐振子的能量本征值和本征函数. 假设一个一维谐振子,其势能按泰勒级数展开.
T /2
2π
π dx / dt
x=asinωt, 那么
dx = aω cos ωt = ωa 1 ( x / a ) 2 dt a 1 wcl ( x )dx = dx π 1 ( x / a )2
(31) (32)
振幅可以从能量得到 E = 1 mω 2 a 2 , a = 2 E / mω 2 2 相反, 对局域在x+dx中的粒子,量子力学中的几率为
∧ 1 (ξ + ) = a ξ 2
∧+
(48)
从这两个关系, 我们可以估算ψn的相邻函数ψn-1和ψn+1. 为了简便 起见,我们做如下替代
1 (ξ ) = a ξ 2
∧+
(49)
(48)式变为
aψ n = nψ n 1 ,
(6)
k2 k 2 E κ= = = 2 λ 2 m ω ω
为了解方程(6),我们设一个非对称试解
ψ ( y) = e
y/2
( y)
(7)
dψ 1 d y / 2 d 2ψ 1 d d 2 y / 2 = [ ( y ) + ]e and = [ ( y )- + 2 ]e (8) 2 dy 2 dy dy 4 dy dy
λ x, dx =
2
∫ ψ ( x)
经典力学和量子力学中的谐振子ppt课件
X=0处逗留时间最短，出现的几率最小。
11
2.量子力学中的谐振子
• 2.1一维谐振子 2.1.1哈密顿算符与能量本征态 2.1.2阶梯算符方法 2.1.3自然长度与自然能量
• 2.2三维谐振子 • 2.3谐振子的相干态
2.3.1降算符的本征态 2.3.2相干态的性质
12
2.1一维谐振子
2.1.1哈密顿算符和能量本征态
由牛顿第二定律，且加速度等于x对t的二次微分导数，
得： 若定义
02
k m
m
d2x dt 2
kx
，则方程可以写为：d 2 x dt 2
02 x
0
其一般解为：
x Acos(0t )
3
1.2受驱谐振子
一受驱谐振子满足如下非齐次二阶线性微分方程：
d2x dt 2
02 x
A0
证明等式： H (aˆ†aˆ 1 2)
aˆ, aˆ† 1
得：
Hˆ
n
(n 1) n
2
表示 n 态的能量本征值为：
En
(n 1) 2
14
2.1.3自然长度与自然能量
量子谐振子拥有自然长度与自然能量两个自然尺度，可以用来简
化问题。这可以透过无量纲化来实现。如果我们以 为单位来测量
a.容易看出其在x=0处 ，概率拥有最大值： ；而经
典谐振子中，由于在x=0处的速度最大，所以其出现几率
最小。
22
b.当经典谐振子的能量为 1 时，经典回转点 1 ，
经典振子只能处于
x
1
2
的区域中。应该在
量子力学2-3
2 2
ω=
k 对经典谐振子
它是角频率。 µ 它是角频率。
线性谐振子的定态薛定谔方程为： 线性谐振子的定态薛定谔方程为：
ℏ d 1 2 2 (− + µω x )ψ ( x) = Eψ ( x) 2 2µ dx 2
它是变系数二阶常微分方程，可解。 它是变系数二阶常微分方程，可解。
2.7-1
引进参量
ξ 和λ
∵ψ n ( x ) = ψ n ( − x )
为偶数时， 线性谐振子处于偶宇称。 可见当n为偶数时，称线性谐振子处于偶宇称。 n为奇数时 为奇数时
∵ψ n ( x ) = −ψ n ( − x )
为奇数时， 线性谐振子处于奇宇称。 可见当n为奇数时，称线性谐振子处于奇宇称。
例题： 例题：求基态微观线性谐振子在经典界限之外被发现 的几率。 的几率。 解：基态微观线性谐振子的波函数是
12
e
−ξ 2
dξ =
2
π
12
[∫
∞
0
e
−ξ 2
dξ − ∫0 e
1
−ξ 2
dξ
]
2 π π p= − × 0.84 = 0.16 2 π 2
• • • • • • • • •
小结） 第二章 波函数和薛定谔方程 （小结） 一.波函数统计解释 波函数统计解释 二.态迭加原理 态迭加原理 三.薛定谔方程 薛定谔方程 四.粒子流密度和粒子数守恒定律 粒子流密度和粒子数守恒定律 五.定态薛定谔方程 定态薛定谔方程 六.一维无限深势阱 一维无限深势阱 七.线性谐振子 线性谐振子 八.势垒贯穿 势垒贯穿
若选取线性谐振子平衡位置为坐标原点， 若选取线性谐振子平衡位置为坐标原点，并选取其为 势能的零点，则线性谐振子的势能表示为： 势能的零点，则线性谐振子的势能表示为：
ω=
k 对经典谐振子
它是角频率。 µ 它是角频率。
线性谐振子的定态薛定谔方程为： 线性谐振子的定态薛定谔方程为：
ℏ d 1 2 2 (− + µω x )ψ ( x) = Eψ ( x) 2 2µ dx 2
它是变系数二阶常微分方程，可解。 它是变系数二阶常微分方程，可解。
2.7-1
引进参量
ξ 和λ
∵ψ n ( x ) = ψ n ( − x )
为偶数时， 线性谐振子处于偶宇称。 可见当n为偶数时，称线性谐振子处于偶宇称。 n为奇数时 为奇数时
∵ψ n ( x ) = −ψ n ( − x )
为奇数时， 线性谐振子处于奇宇称。 可见当n为奇数时，称线性谐振子处于奇宇称。
例题： 例题：求基态微观线性谐振子在经典界限之外被发现 的几率。 的几率。 解：基态微观线性谐振子的波函数是
12
e
−ξ 2
dξ =
2
π
12
[∫
∞
0
e
−ξ 2
dξ − ∫0 e
1
−ξ 2
dξ
]
2 π π p= − × 0.84 = 0.16 2 π 2
• • • • • • • • •
小结） 第二章 波函数和薛定谔方程 （小结） 一.波函数统计解释 波函数统计解释 二.态迭加原理 态迭加原理 三.薛定谔方程 薛定谔方程 四.粒子流密度和粒子数守恒定律 粒子流密度和粒子数守恒定律 五.定态薛定谔方程 定态薛定谔方程 六.一维无限深势阱 一维无限深势阱 七.线性谐振子 线性谐振子 八.势垒贯穿 势垒贯穿
若选取线性谐振子平衡位置为坐标原点， 若选取线性谐振子平衡位置为坐标原点，并选取其为 势能的零点，则线性谐振子的势能表示为： 势能的零点，则线性谐振子的势能表示为：
量子力学线性谐振子（精品pdf）
６１§2.7线性谐振子(理想模型)重点：线性谐振子问题的本征解难点：结果讨论及其理解一、参考模型无论在经典物理还是在量子物理中线性谐振子都是很有用的模型。
任何体系在稳定平衡点附近的运动都可以近似地看作一维谐振子。
如双原子分子的振动，晶体结构中原子和离子的振动，核振动等等都使用了谐振子模型，辐射场也可以看作线性谐振子的集合。
以双原子分子为例： 双原子分子中两原子间的势能U 是两原子间距离x 的函数，其形状如图所示。
在a x =处势能有一极小值，这是一个稳定平衡点，在这点附近，)x (U 可以展为)a x (−的幂级数，且注意到 0x Ua x =∂∂= 则：....)a x )(a (''U !21)a (U )x (U 2+−+= 若忽略高次项，且令)a (''U k =， 则有：2)a x (k 21)a (U )x (U −+= 再令0)a (U =；a x 'x −=，则有2'kx 21)'x (U =，可以写成： 2kx 21)x (U =(1) 其中2k μω=。
６２ 凡是在势能为2kx 21)x (U =的场中运动的微观体系都称之为线性谐振子。
二、线性谐振子的本征问题1.体系的哈密顿及本征方程 22222x 21dx d 2H ˆμω+μ−=h )x (E )x (]x 21dx d 2[22222ψ=ψμω+μ−h 2.本征方程的求解 方程两边同乘以ωh 2得： ψω=ψμω+ψμω−h h h E 2x dx d 222 令hμω=α；x α=ξ；ω=λh E 2 (2) 得到：0)()()(d d 222=ξψξ−λ+ξψξ(3) 由于方程0)()()(d d 222=ξψξ−λ+ξψξ不能直接求解，可先求±∞→ξ的渐进解，此时由于λ与2ξ相比可以忽略，则方程退化为： 0d d 222=ψξ−ψξ—渐近方程 (4) 其渐进解为：221e )(ξ±∝ξψ 由波函数的有限性(满足0)(⎯⎯→⎯ξψ∞→ξ)知，只能取2/2e )(ξ−∝ξψ６３ 的解，于是可以令方程0)()()(d d 222=ξψξ−λ+ξψξ的一般解为： )(H e )(2/2ξ=ξψξ− (5) 其中待求函数)(H ξ应满足条件：a. 在ξ有限时)(H ξ应为有限；b. 当±∞→ξ时，)(H ξ也必须保证)(ξψ有限，即0)(→ξψ。
9 一维线性谐振子ppt
• 两端同除以 ( x) ( y) ( z ) ：
2 1 2 1 2 1 2 1 2 2 [ ( ) m x ] [ ( ) m 2 y 2 ] 2m x 2 2 2m y 2 2 2 1 2 1 [ ( ) m 2 z 2 ] E 2m z 2 2
H n ( ) 满足正交归一条件
H m ( )H n ( )e
2
d 2 n n! mn
• 据此可以得到归一化常数 cn ( 2 n n !) 1 2 • 还原到原来量纲的能量本征值和本征函数 •
En (n 1 ) 2
1 2 1 2 x2 n ( x) ( ) e 2 H n ( x) 2n n !
m ( x, t ) m ( x)e
m
• 如果初始时刻制备在某一个叠加态
( x)
1 2 [ 0 ( x) 1 ( x)]
• 那么t时刻它的状态是
( x, t )
1 2 [ 0 ( x)e
i E0t
1 ( x )e
i E1t
]
• 9.5 三维各向同性谐振子 • 1. 定态schrodinger方程 • Hamiltonian
• 上式三个方括号分别是三个独立坐标变量x, y, z的 函数，它们的和为一个常数E, 因此，三个方括号 必须分别是与坐标变量无关的常数：
•
2 1 2 1 ( ) m 2 x 2 E x 2m x 2 2
2 1 2 1 ( ) m 2 y 2 E y 2m y 2 2
d 2 (2 2 ) 0 d 2
• A)方程的渐进形式和渐进解 d 2 • 方程的渐进形式 2 • 渐进解 • 舍去 e
量子谐振子和谐振子的耦合PPT课件
第8页/共10页
作业
1.求一维谐振子处在第一激发态时几率最大的位置.
第9页/共10页
感谢您的观看！
第10页/共10页
§13-3 量子谐振子和谐振子的耦合
1、何为（一维）谐振子
经典力学中：质量m的粒子在弹性力F=-kx的作用下做往复 运动，称为谐振子；
经典力学中谐振子运动的弹性势能为 U 1 m；2x2
2
量子力学中的线性谐振子是指在 U 1 m的2势x2 场中做一维运动
的粒子。
2
第1页/共10页
2、一维谐振子的定态薛定谔方程
2
[ 2 U r ] (r ,t) E (r ,t)
2m
对一维谐振子，有：
则有：
U 1 m2x2
2
[ 2 d 2 1 m2x2 ] E
2m dx2 2
第2页/共10页
3、定态薛定谔方程的解(本征值和本征函数)
En
(n
1) 2
, n 0,1, 2,
厄米多项式
本征函数： n
x
1 2x2
Nne 2 Hn ( x)
1
其中：Nn
2n
n！
2
，
m
Hn ( )
(1)n
exp[
2
]
dn
d n
exp[ 2 ],
x
第3页/共10页
4、量子谐振子与经典谐振子的区别
(1)基态能量(最小能量)不同
经典谐振子:最小能量为0(经典粒子可停在原点)
量子谐振子:基态能量不为0,称为零点能.
1 E0 2
0
零点能是微观粒子波粒二相性的表现，是量子效应， .
即,经典谐振子被 局限在振幅范围内!
作业
1.求一维谐振子处在第一激发态时几率最大的位置.
第9页/共10页
感谢您的观看！
第10页/共10页
§13-3 量子谐振子和谐振子的耦合
1、何为（一维）谐振子
经典力学中：质量m的粒子在弹性力F=-kx的作用下做往复 运动，称为谐振子；
经典力学中谐振子运动的弹性势能为 U 1 m；2x2
2
量子力学中的线性谐振子是指在 U 1 m的2势x2 场中做一维运动
的粒子。
2
第1页/共10页
2、一维谐振子的定态薛定谔方程
2
[ 2 U r ] (r ,t) E (r ,t)
2m
对一维谐振子，有：
则有：
U 1 m2x2
2
[ 2 d 2 1 m2x2 ] E
2m dx2 2
第2页/共10页
3、定态薛定谔方程的解(本征值和本征函数)
En
(n
1) 2
, n 0,1, 2,
厄米多项式
本征函数： n
x
1 2x2
Nne 2 Hn ( x)
1
其中：Nn
2n
n！
2
，
m
Hn ( )
(1)n
exp[
2
]
dn
d n
exp[ 2 ],
x
第3页/共10页
4、量子谐振子与经典谐振子的区别
(1)基态能量(最小能量)不同
经典谐振子:最小能量为0(经典粒子可停在原点)
量子谐振子:基态能量不为0,称为零点能.
1 E0 2
0
零点能是微观粒子波粒二相性的表现，是量子效应， .
即,经典谐振子被 局限在振幅范围内!
ZJH_2-7_线性谐振子_33p
k ′= 0
令k=k’+2
k′
用 k 代替 k’
k
该式对任意ξ 该式对任意ξ都成立， 都成立， 故ξ同次幂前的系数均应为零， 同次幂前的系数均应为零， 2 d H dH bk +2 (k + 1)(k + 2) − bk 2k + bk (λ − 1) = 0 − 2ξ + ( λ − 1) H = 0 2 dξ dξ 2k + 1 − λ bk 方程 P30(2.7-6)式 系数bk的递推公式 bk + 2 = Hermite (k + 1)(k + 2) 9 线性谐振子
(2) ξ→±∞ 需考虑无穷级数H(ξ)的收敛性 H (ξ ) = bkξ k k =0 为此考察相邻两项之比 为此考察相邻两项之比： 两项之比： k +2 2k + 1 − λ bk + 2ξ 2 2 2 2k + 1 − λ bk + 2 = bk → ξ = ξ k→∞ k (k + 1)(k + 2) k ( k + 1)( k + 2) bξ
2 2
±
ξ
ξ
−
ξ
P30(2.7-6)式
线性谐振子
8
ψ (ξ ) = e
H ′′ = ∑bk k (k − 1)ξ
k =0
H (ξ ) P30(2.7-5)式 3). 解H(ξ)——级数解 k k −1 ′ 2ξ H = ∑ 2 bk k ξ H ′ = ∑ bk k ξ
2
k −2
−
ξ2
H(ξ)可表示 H (ξ ) = b ξ k ∑ k 为泰勒级数 k =0
h
α=
mω 2E ,λ = h hω
令k=k’+2
k′
用 k 代替 k’
k
该式对任意ξ 该式对任意ξ都成立， 都成立， 故ξ同次幂前的系数均应为零， 同次幂前的系数均应为零， 2 d H dH bk +2 (k + 1)(k + 2) − bk 2k + bk (λ − 1) = 0 − 2ξ + ( λ − 1) H = 0 2 dξ dξ 2k + 1 − λ bk 方程 P30(2.7-6)式 系数bk的递推公式 bk + 2 = Hermite (k + 1)(k + 2) 9 线性谐振子
(2) ξ→±∞ 需考虑无穷级数H(ξ)的收敛性 H (ξ ) = bkξ k k =0 为此考察相邻两项之比 为此考察相邻两项之比： 两项之比： k +2 2k + 1 − λ bk + 2ξ 2 2 2 2k + 1 − λ bk + 2 = bk → ξ = ξ k→∞ k (k + 1)(k + 2) k ( k + 1)( k + 2) bξ
2 2
±
ξ
ξ
−
ξ
P30(2.7-6)式
线性谐振子
8
ψ (ξ ) = e
H ′′ = ∑bk k (k − 1)ξ
k =0
H (ξ ) P30(2.7-5)式 3). 解H(ξ)——级数解 k k −1 ′ 2ξ H = ∑ 2 bk k ξ H ′ = ∑ bk k ξ
2
k −2
−
ξ2
H(ξ)可表示 H (ξ ) = b ξ k ∑ k 为泰勒级数 k =0
h
α=
mω 2E ,λ = h hω
2.7线性谐振子
Quantum mechanics
§2.7 线性谐振子
§2.7 线性谐振子 Linear harmonic oscillator
如果在一维空间运 动的粒子势能为
1 U ( x ) 2 x 2 2
U(x)
这系统称为线性谐 振子. 双原子分子中两原 子之间的势能为:
k U ( x) U 0 ( x a) 2 2
* ( x ) n ( x) dx 1 n
第二章 波函数和薛定谔方程
8/27
Quantum mechanics
§2.7 线性谐振子
1 En (n ) , (n 1, 2,...) 2 1 E0 , (零点能） 2
注:(1),能量量子化: 基态:
零点能:能量不等于零的最低的基态 能量称零点能 (2),n的奇偶性决定了谐振子波函数的奇偶性 n ( x) (1)n n ( x) n 奇数, n ( x） n ( x) 具有奇宇称 n 偶数, n ( x） n ( x) 具有偶宇称 (3),常用递推公式 x n ( x) 1 [ n n1 ( x) n 1 n1 ( x)]
2
3
11/27
第二章 波函数和薛定谔方程
Quantum mechanics
§2.7 线性谐振子
(5),概率密度分布 虚线表示经典线性谐振子的概率密度
n=3
-3
-2
-1
0
1 n=4
2
3
-4
-3
-2
-1
0
1
2
3
4
第二章 波函数和薛定谔方程
12/27
§2.7 线性谐振子 Quantum mechanics 19 18 17 n=10,线性谐振子的概率密度 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 第二章 波函数和薛定谔方程
§2.7 线性谐振子
§2.7 线性谐振子 Linear harmonic oscillator
如果在一维空间运 动的粒子势能为
1 U ( x ) 2 x 2 2
U(x)
这系统称为线性谐 振子. 双原子分子中两原 子之间的势能为:
k U ( x) U 0 ( x a) 2 2
* ( x ) n ( x) dx 1 n
第二章 波函数和薛定谔方程
8/27
Quantum mechanics
§2.7 线性谐振子
1 En (n ) , (n 1, 2,...) 2 1 E0 , (零点能） 2
注:(1),能量量子化: 基态:
零点能:能量不等于零的最低的基态 能量称零点能 (2),n的奇偶性决定了谐振子波函数的奇偶性 n ( x) (1)n n ( x) n 奇数, n ( x） n ( x) 具有奇宇称 n 偶数, n ( x） n ( x) 具有偶宇称 (3),常用递推公式 x n ( x) 1 [ n n1 ( x) n 1 n1 ( x)]
2
3
11/27
第二章 波函数和薛定谔方程
Quantum mechanics
§2.7 线性谐振子
(5),概率密度分布 虚线表示经典线性谐振子的概率密度
n=3
-3
-2
-1
0
1 n=4
2
3
-4
-3
-2
-1
0
1
2
3
4
第二章 波函数和薛定谔方程
12/27
§2.7 线性谐振子 Quantum mechanics 19 18 17 n=10,线性谐振子的概率密度 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 第二章 波函数和薛定谔方程
2.7 线性谐振子
§2.7 线性谐振子
一、参考模型
如果在一维空间内运动的粒子的势能为 x / 2 , 是常量，则这种体系就称为线性谐振子。无论是在
2 2
经典物理还是在量子物理中，线性谐振子都是很有用
的模型，其重要性不仅在于它是将来场量子化的基础，
而且许多体系都可以近似看作是线性谐振子。如双原 子分子的振动，晶体中原子和离子的振动，原子核表
面的振动，辐射场以及任何体系在平衡位置附近的小
振动都可以看着线性谐振子。同时，谐振子还是研究
复杂运动的基础，所以谐振子运动的研究，无论是理
论还是应用上都是很重要的。
思路：先求ψ在ξ→±∞时的渐近 解形式，再在渐近解基础上提出 一般解的形式，再求解。
该方程采用试探法求解 emx， xm， ax+b等试探
H av v
v oBiblioteka
一、参考模型
如果在一维空间内运动的粒子的势能为 x / 2 , 是常量，则这种体系就称为线性谐振子。无论是在
2 2
经典物理还是在量子物理中，线性谐振子都是很有用
的模型，其重要性不仅在于它是将来场量子化的基础，
而且许多体系都可以近似看作是线性谐振子。如双原 子分子的振动，晶体中原子和离子的振动，原子核表
面的振动，辐射场以及任何体系在平衡位置附近的小
振动都可以看着线性谐振子。同时，谐振子还是研究
复杂运动的基础，所以谐振子运动的研究，无论是理
论还是应用上都是很重要的。
思路：先求ψ在ξ→±∞时的渐近 解形式，再在渐近解基础上提出 一般解的形式，再求解。
该方程采用试探法求解 emx， xm， ax+b等试探
H av v
v oBiblioteka
线性谐振子
1
1
4
e2x2 / 2
1(x)
211!
e2x2 /2 H1( x)
2
e2x2 / 2 2 x
1
1
2 xe2x2 /2
4
2(x)
222!
e2x2 / 2 H2 ( x)
8
e2x2 /2 4 2 x2 2
其解为 x = Asin(ω t + δ)。这种运动称为 简谐振动,作这种运动的粒子叫谐振子。
因为
F dV dx
所以
因：k m2
V
kxdx
1 2
kx 2
V0
1 2
m 2 x2
V0
若取V0 = 0，即平衡位置处 于势 V = 0 点，则
V 1 m2 x2
2
量子力学中的线性谐振子就是指在该式所描述的势场中 运动的粒子。
e 2 / 2
为了使方程 d 2 d 2
[ 2 ] (x) 0的波函数
在无穷远处有 e 2 / 2渐近形式，我们自然会令：
( ) H( )e 2 / 2
(2.7-5)
• 其中 H(ξ) 必须满足波函数的单值、有限、连续的标准 条件。即：
ω0(ξ)
-1 0 1
ωn(ξ)
n=2
n=1 n=0
-1 1
|10|2
-4 -2
24
求
1
x
0
x
dx
0(x)
1
1
4
e 2x2 / 2
1(x)
3.5线性谐振子
2
2
d2
dx
2
d2 dy 2
d2 dz 2
1 2
2
(x2
y2
z2)
Hˆ x Hˆ y Hˆ z
其中
Hˆ
x
2
2
d2 dx2
1 2
2 x2
Hˆ
y
2
2
d2 dy 2
1 2
2
y2
Hˆ
z
2
2
d2 dz 2
1 2
2 z 2
38
24
（2）本征方程及其能量本征值
如果系统 Hamilton 量可以写成 则必有：
2
解：Schrodinger方程：
d2 dx 2
( x)
2
2
[E
V ( x)]
( x)
0
（1）解题思路
势V(x)是在谐振子势上叠加上-q x项，该项
是x 的一次项，而振子势是二次项。如果我们
能把这样的势场重新整理成坐标变量平方形式，
就有可能利用已知的线性谐振子的结果。
38
27
（2）改写 V(x)
1/
2
x
e
1 2
2
x
2
n 2,
第二激发态
E2
5 2
，
38
2(x)
2
1/
2
(2
2
x2
1 2x2
1)e 2
（偶宇称） （奇宇称） （偶宇称）
13
0
n0
线
x
性 谐
1
n 1
振 子
x
波
函
2
数 n2
x
§3.2线性谐振子
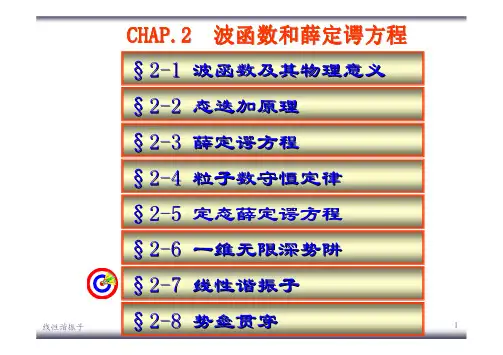
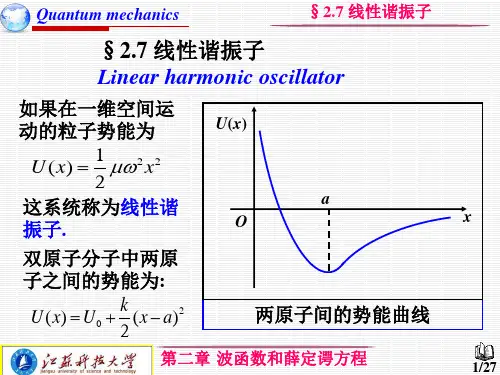
§3.2 线性谐振子重点：谐振子模型的意义能量波函数的特征与经典情况的区别(3.2-1)其中是弹性系数为k的谐振子作简谐振动的角频率。
经典力学中线性谐振子的哈密顿函数为（3.2-2）故在量子力学中，线性谐振子的哈密顿算符为由于U(x)与时间无关，故为定态。
线性谐振子的定态薛定谔方程为（3.2-4）为了简化，引入无量纲的变量（3.2-5）（3.2-6）（3.2-7）则方程（3.2-4）可改写成（3.2-8）我们令方程（3.2-8）的一般解为（3.2-9）所满足的方程得到H（3.2-10）（3.2-11）代入（3.2-7）中，可求得线性谐振子的能级（3.2-12）n=0, 1, 2,…，由此得下面结论：（1）线性谐振子能是只能取分立值（图3.4），好能量是量子化的，，这与普朗（2）谐振子的能级是均匀分布的，相邻两能级间隔克假设一致。
（3）谐振子的基态（n=0）能量为（3.2-13）称为零点能，零点能的存在，是量子力学的一个重要结果，这是旧量子论中所没有的。
对应于不同的n或不同的。
（3.2-14），它可以用下列式子表示方程（3.2-14）的解是厄密多项式（3.2-15）脚标n表示多项式的最高次幂。
下面列出前面n项厄密多项式：（3.2-16）由（3.2-9）式，对应能量E n的波函数是（3.2-17a）或（3.2-14b）这函数称厄密函数，式中N n为归一化常数。
由归一化条件经计算得（见附录1）（3.2-18）归一化后的前三个波函数如下：（3.2-19）等函数是x的偶函数，即从上面各式容易看出，我们称这些波函数具有偶宇称，而我们称这些波函数具有奇宇称。
（三）与经典比较经典和量子谐振子的能级与分布几率上图中横坐标代表振子的位置，抛物线代有势能曲线，En是量子化的能级，虚曲线代表波函数，实曲线代表几率分布，由图可以看出：当n=0时，波函数。
除了有n个节点，即有n个根。
类推，因此波函数只在于绕平均值迅速振荡而已。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对应的波函数是：
1 2
1 2x2
n (x) Nn H n ( ) e 2 Nn H n (x) e 2 .(
)
(3.2 9)
Nn是归一化常数，利用特殊积分
ex2 dx ,
可得
Nn
2n
n
. !
2.讨论 (1) 能级是等间隔的 ；(2)零点能是
E0
1
2
；(3)能级
的宇称偶奇相间，基态是偶宇称,即ψn(-x)=(-1)ψnn(x) (4)ψn(x)有
当ξ→±∞时，方程变为：
d 2 d 2
2 .
我们发现它有近似解：
12
() ~ e 2 .
但是 e 2 /2 应该舍去。
所以再进行变换：
12
() e 2 H(),
可得关于H(ξ)的如下方程：
d 2 H 2 dH ( 1)H 0. (3.2 4)
d 2
d
二. Hermitian多项式 可以用级数法求解H(ξ)的方程，结果发现：只要H(ξ)是“真”
§ 3.2线性谐振子
一维量子谐振子问题
在经典力学中，一维经典谐振子问题是个基本的问题，它 是物体在势（或势场）的稳定平衡位置附近作小振动这类常见 问题的普遍概括。在量子力学中，情况很类似。一维量子谐振 子问题也是个基本的问题，甚至更为基本。因为它不仅是微观 粒子在势场稳定平衡位置附近作小振动一类常见问题的普遍概 括，而且更是将来场量子化的基础。
d
dt
a
cos(t
)
a
(1
a
2 2
)
1 2
所以几率密度与 (1 2
/
a
2
)
1 2
成比例。
线性谐振子的势能函数是：
U (x) 1 2 x 2
2
(3.2 1)
其中ω是谐振子的固有圆频率。所以薛定谔方程是：
d 2
dx 2
2E
2
2 2
2
x2
0.
(3.2 2)
在方程中做如下的无量纲化变换：
x x,
则方程变成：
d 2 ( 2 ) ( ) 0. d 2
, 2E
(3.2 3)
无穷级数，那么在x→±∞的时候H(ξ)就→ eξ² ,仍然使ψ(ξ)发散。
能够避免这种情形出现的唯一出路是级数“中止” 或“退化”为多项式，而这就要求只能取一些特殊的值。 设要求H(ξ)是ξ的n次多项式，那么就必须让
λ=2n+1 n=0,1,2,3…
这样，我们首先得到了能量本征值：
En
n
1 , n
众所周知，当粒子在势场的平衡位置附近作小振动时，势 场V(x) 总可作泰勒展开并只取到最低阶不为零的项。设平衡位
置x0=0，并选取能量尺度的原点使V（0）=0，则
V (x)
1 2
V
(0)
x
2
这里，含V ′(0) 的一次项由于平衡位置V ′(0)=0而消失，
也由于是稳定振动而有V′ (0)＞0。除非振动的幅度较大，否则 不必考虑展开式中非简谐的高阶项。这类问题的物理例子比如， 原子核内核子（质子或中子）的简谐振动、原子和分子的简谐 振动、固体晶格上原子的简谐振动、甚至一个多自由度系统在 其平衡态附近的小涨落小振动，在通过引入简正坐标后也可以 化为一系列退耦的一维振子之和，即可近似为线性谐振动的迭 加。 一. 方程的化简
n个节点。
四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的
几率ω (ξ) dξ与质点在此区域内逗留的时间dt成
比例:
( )d dt
T
T是振动周期。因此有
( )
T
1
d
dt
1 vt
即几率密度与质点的速度成反比。对于经典的线性谐振子，ξ= a sin(ωt+δ ) ,在ξ点的速度为
v
2
0,1,2,3...
(3.2 5)
现在H(ξ)的方程成为：
d 2HnБайду номын сангаас
d 2
2
dH n
d
2nH n
0.
(3.2 6)
而不难验证下面的函数正满足这个方程:
H n ( ) (1) n e 2
dn
d n
e 2 .
(3.2 7)
它称为n次Hermitian多项式。
H0 1, H1 2 ,
头五个Hermitian多项式是:
H 2 4 2 2, H3 8 3 12 , H 4 16 4 48 2 12,
H5 32 5 160 3 120.
三. 线性谐振子的能级和波函数 1.我们把线性谐振子的能级和波函数总结如下。能级是：
En
n
1 , n
2
0,1,2,3,
(3.2 8)