杨浦五角场高一数学补习班恒高一对一两条直线的夹角

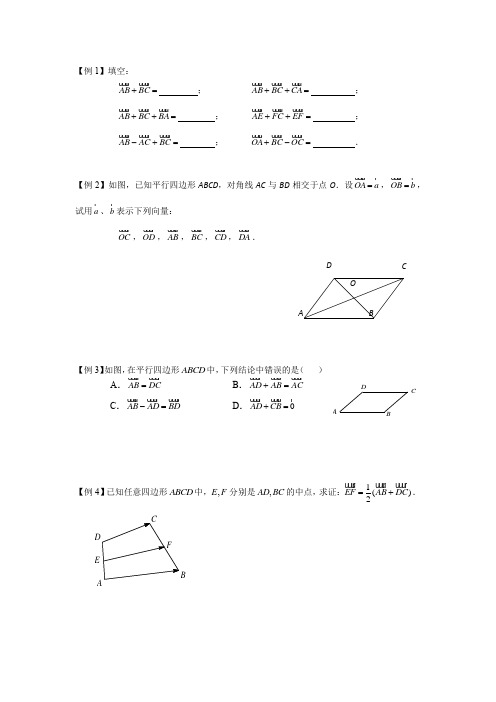
ABCDO【例1】填空：AB BC +=；AB BC CA ++=； AB BC BA ++=； AE FC EF ++=； AB AC BC -+=；OA BC OC +-=．【例2】如图，已知平行四边形ABCD ，对角线AC 与BD 相交于点O ．设OA a = ，OB b =，试用a 、b表示下列向量：OC ，OD ，AB ，BC ，CD ，DA．【例3】如图，在平行四边形ABCD 中，下列结论中错误的是（ ）A ．AB DC = B ．AD AB AC +=C ．AB AD BD -=D ．0AD CB +=【例4】已知任意四边形ABCD 中，,E F 分别是,AD BC 的中点，求证：1()2EF AB DC =+．E B DCBA【例5】（1）AB BC += ；OE EF +=； （2）AE FC EF ++=；（3）AB BC CD DE EF ++++=．【例6】如果5OA = ，3OB =，那么AB 的取值范围是．【例7】如图，多边形ABCDEF 是正六边形，设AB a = ，BC b = 。

试用向量a 和b表示向量OA ，OC ，OE．【例8】下列说法中正确的是（ ） A ．BC AC AB =-B ．对任意两个向量b a ，-，与-都是相反向量C ．在△ABC 中，-+D ．在四边形ABCD 中，0=+-+）（）（DA CD BC ABOFEDCBA。

模拟试卷：Part 2 Phonetics,Vocabulary and Grammar(第二部分语音、词汇和语法)II.Choose the best answer(选择最恰当的答案)（共20分）26.When I was young,I always read books at night.Which of the following is correct for the underlined word in the sentence?A)/ri:d/ B)/red/ C)/reid/ D)./rid/27.Which of the following underlined parts is different in pronunciation from others?A)He acts as a killer in the film. B)When did you arrive at the airport?C)Can you help me fix the chair? D)What did you think of the final exam?28._______man with black glasses is my host father in Britain.A)An B) A C)The D)/29.In our English class, the English teacher asked us to stand up and introduce__________.A)we B)us C)our D) ourselves30.Helen was too angry to say _________.A)nothing B)something C)anything D)everything31.We’ll have a________ holiday. Let’s go to the beach，shall we?A)three-day B)three days C)three-days D)three-days’32.An e-mail address consists _______letters and dots and the symbol‘@’.A)in B)of C)for D)with33.We felt very ______after we watched the ______ football matches in FIFA.A)exciting…excited B）exciting…excitingC）excited…exciting D）excited…excited34.It’s ______to send an e-mail than a regular mail.A)more quickly B)much quickly C)much quicker D)quick35.A lot of people will help you, so you _____________worry about the money.A)can’t B)needn’t C)mustn’t D)couldn’t36.A:Why do Chinese people like red?B:Because they think it can _____them good luck.A)carry B)bring C)take D)fetch37.I’m glad you’ve come back from the United States. Please tell me how long you ____there.A)have stayed B)had stayed C)have been staying D)stayed38.Some questions _______at their class meeting last week.A)raised B)rose C)were risen D)were raised39.My cousin was born in China, but ____in Australia.A)picked up B)gave up C)grew up D)took up40.What are you going to do when you finish ______the room?A)to clean B)cleaning C)clean D)cleaned41.We’ll make laws______ our environment.A)protected B)protecting C)to protect D)protect42.He didn’t tell us_________.A)if he will give us a lecture B)whether he would go with youC)when he was started D)when he will arrive43.________important computers are to everybody in a modern city!A)What B)How C)What an D)How an44.The weather there isn’t nice,____________?A)is there B)is it C)isn’t there D)isn’t it45.A:Woud you mind waiting outside for a moment?B:__________.A）Never mind B)So do I C)Certainly not D)You are welcomeplete the following passage with the words or phrases in the box.Each one can only be used once(将下列单词或词组填入空格。

第一章匀变速直线运动第2讲运动图象加速度一、位移—时间图象(s-t图象)知识梳理1．定义：以时间为横坐标，以位移为纵坐标，描述位移随时间变化情况的图象叫位移—时间图象．2．静止物体的s-t图象：是一条平行于时间轴的直线．3．匀速直线运动的s-t图象：是一条倾斜的的直线．4．匀变速直线运动的s-t关系为二次函数，故为曲线．想一想：如果质点的位移—时间图象是一条平行于时间轴的直线，但是在x的负半轴上，这表示质点做什么运动呢？答案只要是平行与时间轴的位移—时间图象即表示物体静止.考点突破1．几种常见的位移—时间图象，如图所示．(1)静止的物体的s-t图象是平行于时间轴的直线，如图a.(2)匀速直线运动的s-t图象是一条倾斜的直线，如图b.(3)匀变速直线运动的s-t图象是抛物线，如图c.2．对s-t图象的几点说明(1)纵坐标：初、末位置的纵坐标差的绝对值表示位移的大小；初、末位置纵坐标差的正负号表示位移的方向：正值表示位移沿正方向；负值表示位移沿负方向．(2)斜率：斜率的绝对值表示速度的大小；斜率的正负号表示速度的方向：斜率为正值，表示速度为正方向；斜率为负，表示速度为负方向．(3)截距：纵截距表示物体起始位置，横截距表示物体开始运动的时刻．(4)交点：交点表示两物体在同一时刻处于同一位置，即相遇．3．注意：①无论是s-t图象还是v-t图象都不是物体的运动轨迹．②s-t图象和v-t图象都只能描述直线运动，不能描述曲线运动．例1如图所示，是在同一条直线上运动的A、B两质点的位移—时间图象，由图可知()A．t＝0时，A在B后面B．B物体在t2秒末追上A并在此后跑在A的前面C．在0～t1时间内B的运动速度比A大D．A物体在0～t1做加速运动，之后做匀速运动【变式训练】1.一质点沿一条直线运动的位移—时间图象如图166所示，则()A．t＝0时刻，质点在坐标原点B．从t＝0时刻到t1时刻，质点位移是x0C．从t1时刻到t2时刻，质点位移大小等于路程D．质点在t1时刻的速度比t2时刻的速度大强化训练1．如图所示，是一辆汽车做直线运动的s-t图象，对线段OA、AB、BC、CD所表示的运动，下列说法正确的是()A．OA段运动速度最大B．AB段物体做匀速运动C．CD段的运动方向与初始运动方向相反D．运动4h汽车的位移大小为30km2．(多选)质点做直线运动，其s-t关系如图所示．关于质点的运动情况，下列说法正确的是()A．质点在0～20s内的平均速度为0.8m/sB．质点在0～20s内的平均速度为1m/sC．质点做单向直线运动D．质点做匀变速直线运动3．甲、乙两质点同时开始做直线运动，它们的位移s与时间t的图象如图所示，则() A．甲物体做匀加速直线运动，乙物体做曲线运动B．甲、乙两物体从同一地点出发C．当甲、乙两物体速度相同时，二者之间的距离为零D．甲、乙两物体有两次相遇4．龟兔赛跑的故事流传至今，按照龟兔赛跑的故事情节，兔子和乌龟的s-t图象如图所示，下列关于兔子和乌龟运动的说法中正确的是()A．兔子和乌龟是从同一地点出发的B．乌龟一直做匀加速运动，兔子先加速后匀速再加速C．骄傲的兔子在T4时刻发现落后奋力追赶，但由于跑得比乌龟慢，还是让乌龟先到达预定位置x3D．在T2～T4时间内，兔子比乌龟运动得快二、速度—时间图象(v-t图)知识梳理1．v-t图象以速度为纵轴，以时间为横轴，建立一个平面直角坐标系，在该坐标系中画出物体的速度随时间的变化关系，该图象就是速度—时间图象(v-t图象)，简称速度图象．2.速度—时间图象(v-t图象)理解(1)物理意义：反映了做直线运动的物体的速度随时间的变化关系.(2)图线斜率的意义①图线上某点切线的斜率大小表示物体运动的加速度的大小.②图线上某点切线的斜率正负表示加速度的方向.(3)两种特殊的v-t图象①匀速直线运动的v-t图象是与横轴平行的直线.②匀变速直线运动的v-t图象是一条倾斜的直线.(4)图象与时间轴围成的“面积”的意义①图象与时间轴围成的“面积”表示相应时间内的位移.②若此面积在时间轴的上方，表示这段时间内的位移方向为正方向；若此面积在时间轴的下方，表示这段时间内的位移方向为负方向.考点突破v-t图象中图线表示的物理规律①表示物体做匀加速直线运动(斜率表示加速度a)；②表示物体做匀速直线运动；③表示物体做匀减速直线运动；④交点的纵坐标表示三个运动质点的共同速度；⑤t1时刻物体速度为v1(图中阴影部分面积表示质点①在0～t1时间内的位移)例1如图所示，是某质点做直v-t图象中图线表示的物理规律线运动的v-t图象，试回答：(1)AB、BC、CD段质点分别做什么运动？(2)质点在4s末的速度多大？【变式训练】1.如图所示是甲、乙两个物体运动的v-t图象，至少从以下三个方面分别说明它们的速度是怎样变化的．(1)物体是从静止开始运动还是具有一定的初速度？(2)速度的大小是否变化？是加速还是减速？(3)运动的方向是否变化？强化训练1．某物体的v-t图象如图所示，则该物体()A．做往复运动B．做匀速直线运动C．朝某一方向做直线运动D．以上说法均不正确2．一同学从家中出发，沿平直的马路以一定的速率走到邮局．发信之后，沿原路以相同的速率返回．设出发时方向为正方向，则下图中能描述该同学运动情况的v-t图象是()三、加速度知识梳理一、加速度1．定义：加速度是速度的改变量与发生这一改变所用时间的比值．2．公式：a ＝ΔvΔt.3．单位：在国际单位制中，加速度的单位是米每二次方秒，符号是m/s 2.4．物理意义：描述物体速度变化的快慢．想一想：速度越大的物体，加速度一定越大吗？速度变化量越大的物体，加速度一定越大吗？答案加速度是描述物体速度变化快慢的物理量，加速度等于速度变化量与发生这一变化量所用时间的比值；速度越大，可能是匀速直线运动，所以加速度不一定越大；速度变化量很大，由于不知道时间长短，所以无法确定物体加速度的大小．二、加速度方向与速度方向的关系1．加速度是矢量(填“矢量”或“标量”)，它不仅有大小，也有方向．其方向与Δv 的方向一致．2．在直线运动中，建立一个坐标系后，可以用一个带正、负号的数值把加速度的大小和方向都表示出来．想一想：物体速度为正，加速度一定为正吗？答案加速度的方向与速度的方向无关，速度为正，加速度可以为正，也可以为负．三、从v-t 图象看加速度1．通过速度—时间(v-t)图象不但能够了解物体运动的速度随时间变化的规律，还能够知道物体的加速度．2．从速度—时间曲线的倾斜程度(即斜率大小)就能判断加速度的大小，倾斜程度越大，加速度越大．比值ΔvΔt表示加速度．想一想：v-t 图象中图线的“陡”和“缓”与加速度有什么关系？答案v-t 图象中图线的倾斜程度反映了物体加速度的大小，图线越“陡”，表明加速度越大；图线越“缓”表明加速度越小.三、从vt 图象看加速度1．通过速度—时间(vt)图象不但能够了解物体运动的速度随时间变化的规律，还能够知道物体的加速度．2．从速度—时间曲线的倾斜程度(即斜率大小)就能判断加速度的大小，倾斜程度越大，加速度越大．比值ΔvΔt表示加速度．想一想：vt 图象中图线的“陡”和“缓”与加速度有什么关系？答案vt 图象中图线的倾斜程度反映了物体加速度的大小，图线越“陡”，表明加速度越大；图线越“缓”表明加速度越小.考点突破一、对加速度的理解1．物理意义：加速度a 表示物体速度变化快慢，也叫速度对时间的变化率．2．对加速度概念的进一步理解：(1)a＝ΔvΔt是用比值定义法定义的物理量．加速度a的大小与Δv、Δt大小无关，因此不能说a 与Δv成正比，与Δt成反比．(2)加速度a与速度v无直接关系．①v大，a不一定大．比如：匀速飞行的飞机速度很大，但加速度却为零；v小，a也不一定小，如射击时火药爆炸瞬间，子弹的速度v可以看做零，这时加速度却很大．②速度变化Δv大，加速度a也不一定大，比如：列车由静止到高速行驶，速度变化量很大，但经历时间也长，所以加速度并不大．(3)速度变化得快，即ΔvΔt大，表示单位时间内速度变化大，加速度才大．3．加速度是矢量，它的方向总是与速度变化量Δv的方向一致，但与速度的方向没有必然联系．在加速直线运动中：v＞v0，Δv＝v－v0＞0，则a＞0，与初速度方向相同；在减速直线运动中：v＜v0，Δv＝v－v0＜0，则a＜0，与初速度方向相反．例1关于速度、速度改变量、加速度，正确的说法是()A．物体运动的速度改变量越大，加速度一定越大B．速度很大的物体，其加速度可能很小，但不能为零C．某时刻物体速度为零，其加速度可能很大D．加速度很大时，运动物体的速度一定很大借题发挥加速度大小反映了物体速度变化的快慢，而非速度变化的大小．例2（多选）一物体做速度均匀变化的直线运动，某时刻速度的大小为4m/s,1s后速度的大小变为10m/s，则在这1s内该物体的()A．速度变化的大小可能小于4m/sB．速度变化的大小可能大于10m/sC．加速度的大小可能小于4m/s2D．加速度的大小可能大于10m/s2借题发挥v0、v、a都是矢量，所以一定要考虑三者的方向，另外Δv＝v－v0也是矢量，与a的方向相同.加速度的正、负表示加速度的方向．若加速度的方向与规定的正方向相同，则加速度为正；若加速度的方向与规定的正方向相反，则加速度为负．【变式训练】1．下列关于加速度的描述中，正确的是()A．加速度在数值上等于单位时间内速度的变化B．加速度是标量，正负表示大小C．速度变化量的方向为正，加速度方向为负是可能的D．速度变化越来越快，加速度越来越小【变式训练】2．长征三号乙运载火箭搭载“嫦娥三号”点火升空时，如图所示，经过3s速度达到42m/s，设火箭上升可看做匀加速运动，则升空时的加速度为________m/s2；再经过________s，速度可以达到70m/s.二、加速度对运动的影响1．加速度的大小决定物体速度变化的快慢：2．加速度方向与速度方向的关系决定物体是加速还是减速：(1)加速度a与速度v0同向时，物体做加速运动；(2)加速度a与速度v0反向时物体做减速运动．例3（多选）根据给出的速度和加速度的正、负，对下列运动性质的判断正确的是() A．v0＞0，a＜0，物体做加速运动B．v0＜0，a＜0，物体做加速运动C．v0＜0，a＞0，物体做减速运动D．v0＞0，a＞0，物体做加速运动借题发挥物体存在加速度，表明物体在做变速运动，但是不一定是做加速运动；判断物体是加速还是减速的依据是看加速度与速度是同向还是反向．例4（多选）物体M的加速度是＋3m/s2，物体P的加速度为－5m/s2，下列说法正确的是()A．物体M的加速度比物体P的加速度大B．物体P的速度变化比物体M的速度变化快C．物体M的速度一定在增大D．物体P的速度可能在减小【变式训练】3．（多选）雨滴从高空由静止下落，由于受到空气阻力作用，其加速度逐渐减小，直到变为零，在此过程中雨滴的运动情况是()A．速度也减小，加速度为零时，速度最小B．速度继续增大，加速度为零时，速度最大C．速度的变化率越来越小D．速度与加速度的方向相反【变式训练】4．（多选）关于速度和加速度的说法正确的是()A．甲物体比乙物体速度大，则甲的加速度一定比乙的大B．甲物体的加速度比乙物体大，则甲一定比乙的速度变化快C．加速度逐渐减小，而速度逐渐增大是不可能的D．可能存在加速度方向不变，而速度方向改变的情况三、v-t图象的应用1．利用斜率求加速度如图所示的v-t图象中，图线的斜率在数值上等于质点运动的加速度．在v-t图象取两个点(t1，v1)、(t2，v2)，根据a＝ΔvΔt(即图象的斜率)可确定加速度．(1)斜率ΔvΔt的绝对值表示加速度的大小．同一坐标系中斜率越大，加速度越大；斜率越小，加速度越小．如图所示，甲物体a的加速度大于物体b的加速度．如图乙，v-t图象为曲线，切线的斜率表示那一时刻的加速度．乙图中切线斜率越来越小，表示加速度a越来越小，物体做加速度减小的加速直线运动．(2)加速度的方向：ΔvΔt的正、负可以表示加速度的方向．2．由v-t图象判断物体的运动性质随着时间的推移，若图线远离时间轴，v的数值在增大，说明物体做加速直线运动．若图线靠近时间轴，v的数值在减小，说明物体做减速运动．如图,0～t0内物体做减速直线运动，t>t0时，物体做加速直线运动．例5如图所示为某物体做直线运动的v-t图象，试求0～1s、1～3s、3～4s各段加速度的大小和方向，并分析各时间段内的运动性质．【变式训练】5．如图所示，是一个物体向东运动的速度图象．由图可知在0～10s内物体的加速度大小是________，方向________，物体做________运动；在10～40s内物体的加速度为________，物体做________运动；在40～60s内物体的加速度大小是________，方向________，物体做________运动．强化训练题组一对加速度的理解1．（多选）下列说法中的“快”，指加速度较大的是()A．小轿车比大卡车启动得快B．协和式客机能在两万米高空飞行得很快C．乘汽车从成都到济南，如果走高速公路能很快到达D．汽车在紧急刹车的情况下，能够很快地停下来2．一个做匀加速直线运动物体的加速度是3m/s2，这意味着()A．该物体在任1s末的速度是该秒初速度的3倍B．该物体在任1s末的速度比该秒的初速度大3m/sC．该物体在第1s末的速度为3m/sD．该物体在任1s初的速度比前1s末的速度大3m/s3．（多选）由a＝ΔvΔt可知()A．a与Δv成正比B．物体加速度大小由Δv决定C．a的方向与Δv的方向相同D．Δv/Δt叫速度变化率，就是加速度4．一辆汽车沿平直公路向东行驶，如图所示是该汽车的速度计，在汽车内的观察者观察速度计指针的变化，开始时指针指在如图甲所示的位置，经过8s后指针指示到如图乙所示的位置，那么它的加速度约为()A．11m/s2B．－5.0m/s2C．1.4m/s2D．－1.4m/s25．关于速度和加速度的关系，下列说法正确的是()A．物体的速度越大，加速度也越大B．物体的速度为零时，加速度也为零C．物体速度的变化量越大，加速度越大D．物体速度变化越快，加速度越大题组二加速度对运动的影响6．（多选）关于做直线运动的物体的加速度方向，下列判断正确的是()A．当物体做加速运动时，速度为正，加速度一定为正B．当物体做加速运动时，加速度的方向可以为负C．当物体做减速运动时，加速度的方向一定与速度方向相反D．当物体做减速运动时，加速度的方向与速度的方向相同7．（多选）在下面所说的物体运动情况中，可能出现的是()A．物体加速度不变，速度改变B．物体有加速度，速度一定增加C．物体加速度在减小，速度在增加D．物体加速度在增大，速度在减小题组三v-t图象的应用8．（多选）利用速度传感器与计算机结合，可以自动作出物体运动的图象．某同学在一次实验中得到的运动小车的速度—时间图象如图所示，以下说法正确的是()A．小车先做加速运动，后做减速运动B．小车运动的最大速度约为0.8m/sC．小车前10s朝正方向运动，10s后朝负方向运动D．小车做曲线运动9．如图所示的速度－时间图象中，质点A、B、C运动的加速度分别为a A＝________m/s2，a B＝________m/s2，a C＝________m/s2，其中________的加速度最大．在t＝0时________的速度最大，在t＝4s时________的速度最大，在t＝________s时，A、C的速度一样大．10．做直线运动的物体，其v-t图象如图所示，试根据v-t图象判断：(1)第1秒内，物体的加速度为多大？(2)第2秒内和第4秒内的加速度是否相同？(3)在第4秒内，物体做什么运动？题组四综合题组11．在世界杯比赛中，运动员在罚点球时，球获得20m/s的速度并做匀速直线运动．设脚与球作用时间为0.1s，球又在空中飞行0.2s后被守门员挡出，守门员双手与球接触时间为0.1s，且球被挡出后以20m/s沿原路反弹，求：(1)罚点球的瞬间，球的加速度的大小；(2)守门员接球瞬时，球的加速度的大小．12．某同学为了测定气垫导轨上滑块的加速度，他在滑块上安装了宽度d＝2cm的遮光板．然后他利用气垫导轨和数字毫秒计记录了遮光板通过第一个光电门所用的时间为Δt1＝0.1s，通过第二个光电门的时间Δt2＝0.05s，遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为t＝2.00s，请你根据上面他通过实验得到的数据，为他计算出滑块的加速度．。

变式1：如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；（1）若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；
（2）若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．
变式2：已知：CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，
则BE______CF；EF______|BE﹣AF|（填“＞”，“＜”或“=”）；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件______，使①中的两个结论仍然成立，并证明两个结论成立．
（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．。

浦东暑假一对一补习 高中物理 恒高1对1 运用比例法解题 利用初速度为0的匀变速直线运动的比例关系解题，使问题简单易求。

【例题】一物体从高处自由落下，在最后1s 内下落的距离是全程的一半，求下落全程所用时间及总高度。

★解析：利用比例式求解设总时间为t ，则有211=-t t 解得s t 22+=m gt h 22030212+== 【例题】一个质点从静止开始做匀加速直线运动，已知它在第4s 内的位移是14m ，求它前72m 所用的时间．★解析：质点第1s 内、第2s 内、……第n(s)内位移之比为s Ⅰ∶s Ⅱ∶s Ⅲ∶…＝1∶3∶5∶7…则第1s 内与第4s 内位移之比为s Ⅰ∶s Ⅳ＝1∶7s Ⅰ＝1147⨯m ＝2 m 质点前1s 内、前2s 内、……前n(s)内位移之比为s Ⅰ∶s Ⅱ∶s Ⅲ∶…＝1∶4∶9∶…2n21722t=t ＝6 s 即质点前72 m 的位移所用的时间为 6 s【例题】每隔一定时间，从车站以同一加速度沿一笔直的公路开出一辆汽车，当第五辆车开始起动时，第一辆车已离站320m ．此时第四辆车与第三辆车的距离是多大？ ★解析：作出5辆车的位置示意图如图所示此时第5辆车的速度为0，由于车出发的时间间隔均相等，所以可倒过来看，5、4车之间，4、3车之间，3、2车之间，2、1车之间的间隔为1∶3∶5∶7，按此比例关系，不难算得此时第四辆车与第三辆车的距离是（3/16）×320m=60m ．【例题】一列火车有n 节相同的车厢，一观察者站在第一节车厢的前端，当火车由静止开始做匀加速直线运动时（ B ）A ．每节车厢末端经过观察者时的速度之比是1∶2∶3∶…∶nB ．每节车厢经过观察者所用的时间之比是1∶(12-)∶(23-)∶…∶(1--n n )C ．在相等时间里，经过观察者的车厢节数之比是1∶2∶3∶…∶nD．如果最后一节车厢末端经过观察者时的速度为v，那么在整个列车经过观察者的过程中，平均速度为v/n。

浦东一对一数学辅导恒高1对1 高中直线与圆锥的复习1. 直线与圆锥曲线的位置关系常用研究方法是将曲线方程与直线方程联立，由所得方程组的解的个数来决定。

一般地，消元后所得一元二次方程的判别式记为△：△>0时，有两个公共点，△＝0时，有一个公共点，△<0时，没有公共点．但当直线方程与曲线方程联立的方程组只有一组解（即直线与曲线只有一个交点）时，直线与曲线未必相切，在判定此类情形时，应注意数形结合．（对于双曲线，重点注意与渐近线平行的直线，对于抛物线，重点注意与对称轴平行的直线）2. 直线与圆锥曲线相交产生的弦长公式设弦AB端点的坐标为A(x1，y1)，B(x2，y2),直线AB的斜率为k，则：1212AB x y y-=-利用这个公式求弦长时，要注意结合韦达定理（将直线方程代入圆锥曲线方程，消元后得到一个一元二次，利用韦达定理和中点公式建立等式求解）.3. 与弦的中点相关的问题主要有三类情况：①求平行弦的中点的轨迹方程；②求过定点的直线与圆锥曲线相交产生弦的中点的轨迹；③求过定点且被该定点平分的直线方程。

这三类问题除利用韦达定理外，也可以运用平方差法，但必须以直线与圆锥曲线相交为前提，否则不宜用此法。

如：设A(x1，y1)，B(x2，y2)是椭圆上不同的两点，且x1≠x2，x1＋x2≠0，M(x0，y0)为AB的中点，则两式相减可得4. 直线与圆锥曲线构成三角形面积若直线l经过x轴上的一定点D,与一圆锥曲线相交于A、B，C是x轴上不同于D点的定点，则12A B C A BS C D y y∆=-；若C、D在y轴上的两个不同定点，则12ABC A BS CD x x∆=-.12222=+byax22112222222211x ya bx ya b⎧+=⎪⎪⎨⎪+=⎪⎩2221212121abxxyyxxyy-=++⋅--。

指对数方程的有关应用【例1】已知关于x的方程：2log x-7·log a x+3=0有一个根是2，求a值及另一个根a=4或.【例2】若，（1）如果，求的值；（2）当为何值时，有最小值。

（1）（2）当时，有最小值为【例3】若为方程的两个实数解，则答案：【例4】解下列指数方程（1）；（2）；（3）．．或．【例6】解方程log4(3-x)+log(3+x)=log4(1-x)+log(2x+1)x=0为原方程解.【例7】解方程9x+6x=22x+1x=0.【例8】函数在上最大值比最小值大，则【例9】函数的最大值比最小值大，则【例10】解对数方程【例11】解指数方程令，得【例12】解对数方程【例13】若关于x的方程25-|x+1|－4·5-|x+1|－m=0有实根，求m的取值范围.［－3，0）.【例14】为何值时，方程有两解？一解？无解？时两解时一解时无解【例15】若关于的方程有实数解，求实数的范围。

由图像知：时有解【例16】方程x lgx·x2=1000的解集为_________。

【例17】求方程的解集。

【例18】方程log3(3x-1)log3(3x-1-)=2的解集为_________。

【例19】设方程lgx=10-x的根是α，方程10x=10-x的根是β，则α+β的值是（）A. 100 B. 10 C. 5 D. 4选B。

【例20】已知关于x的方程2a2x-2－7a x-1+3=0有一个根是2，求a的值和方程其余的根。

a=或a=3解得x=2或x=1－log23。

【例21】关于的方程有实数解，求实数的范围。

所以时原方程有实数解。

【例22】，（1）将表示为的函数，并求出的定义域；（2）若关于的方程有实数根，求的取值范围。

所以所以。

【例23】当a为何值时，关于x的方程4x-(2a+1)·2x+a2+2=0的根一个比另一个大1..。