2019年中考备战数学专题复习精品资料第十六讲《三角形与全等三角形》(含详细参考答案和教师用书)

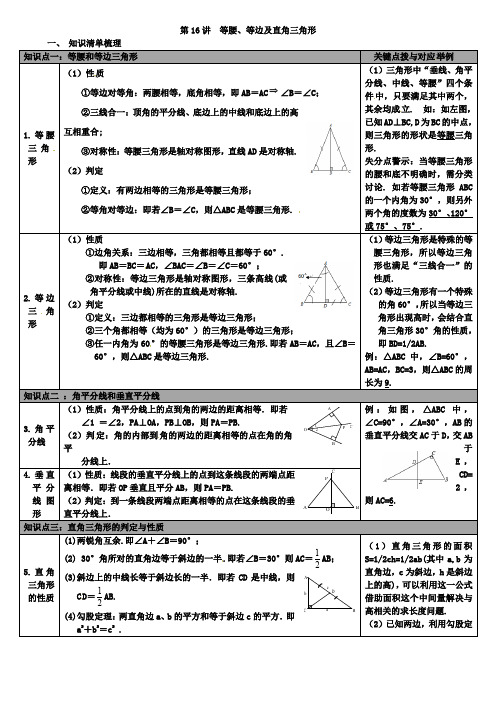
第16讲等腰、等边及直角三角形关键点拨与对应举例）性其余均成＝°的等腰三角形是等边三角形定：角的内部到角的两边的距离相等的点在角的角AC=6.30°角所对的直角边等于斜边的一半.cD DcDD2019-2020学年数学中考模拟试卷一、选择题1．二次函数y ＝x 2﹣6x+m 满足以下条件：当﹣2＜x ＜﹣1时，它的图象位于x 轴的下方；当8＜x ＜9时，它的图象位于x 轴的上方，则m 的值为（ ） A.27B.9C.﹣7D.﹣162．如图，在Rt △ABC 中，∠C ＝30°，AB ＝4，D ，F 分别是AC ，BC 的中点，等腰直角三角形DEH 的边DE 经过点F ，EH 交BC 于点G ，且DF ＝2EF ，则CG 的长为（ ）A ．B ． 1C ．52D 3．已知：如图，四边形ABCD 是⊙O 的内接正方形，点P 是劣弧上不同于点C 的任意一点，则∠BPC 的度数是（ ）A ．45°B ．60°C ．75°D ．90°4．下列运算中，结果正确的是（ ） A.235a a a +=B.236a a a =C.()236a a =D.623a a a ÷=5．浙江广厦篮球队5名场上队员的身高（单位：cm ）是：184，188，190，192，194．现用一名身高为170cm 的队员换下场上身高为190cm 的队员，与换人前相比，场上队员的身高（ ） A.平均数变小，方差变小 B.平均数变小，方差变大 C.平均数变大，方差变小D.平均数变大，方差变大6．用弹簧秤将一长方体铁块悬于没有盛水的水槽中，再向水槽匀速注入水，直至铁块完全浸没在水中（如图），则能反映弹簧秤的读数y （单位：N ）与水面高度x （单位：cm ）之间的函数关系的大致图象是（ ）A ．B ．C ．D ．7．如图，矩形ABCD 中，3AB =，5BC =，点P 是BC 边上的一个动点（点P 不与点B ，C 重合），现将PCD ∆沿直线PD 折叠，使点C 落到点'C 处；作'BPC ∠的平分线交AB 于点E 。

第16讲 三角形的基本知识及全等三角形考点1 三角形的概念及其分类⎧⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎧⎨⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎪⎨⎪⎧⎪⎪⎪⎪⎧⎨⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩⎪⎩⎩概念：由不在同一直线上的三条线段连接 所得到的图形叫做三角形.角三角形按角分类角三角形角三角形分类不等边三角形底与腰不相等的等腰三角形按边分类等腰三角形三角形①②③④⑤ 考点2 与三角形有关的线段高 ⑥ 三角形的三条高相交于三角形的内部；直角三角形的三条高相交于⑦ ；钝角三角形的三条高相交于三角形的外部.中线 三角形的三条中线相交于⑧ ，每一条中线都将三角形分成面积⑨ 的两部分.角平分线 三角形的三条角平分线相交于⑩ ，这个点是三角形的⑪ ，这个点到三边的距离⑫ . 三边关系 三角形的两边之和⑬ 第三边，三角形的两边之差⑭ 第三边. 稳定性三角形具有稳定性，四边形没有稳定性.三角形的中位线 定义连接三角形两边⑮ 的线段叫做三角形的中位线.性质三角形的中位线⑯ 第三边，并且等于第三边的○17 .考点3 与三角形有关的角定理 三角形三个内角的和等于○18 . 推论直角三角形的两个锐角○19 . 三角形的外角等于与它不相邻的两个内角的○20 . 考点4 全等三角形的性质与判定性质 全等三角形的对应边○21 ，对应角○22 . 判定判定1：三边分别相等的两个三角形全等(简写成“边边边”或“SSS ”)；判定2：两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS ”)；判定3：两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”);判定4：两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)；判定5：斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).【易错提示】“SSA”和“AAA”不能判定三角形全等.1.判断给定的三条线段能否组成三角形，只需判断两条较短线段的和是否大于最长线段即可.2.“截长法”和“补短法”是证明和差关系的重要方法，无论用哪一种方法都是要将线段的和差关系转化为证明线段相等的问题，因此添加辅助线构造全等三角形是通向结论的桥梁.命题点1 三角形中的线段例1 不一定在三角形内部的线段是( )A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线【思路点拨】不管是哪种类型的三角形，三角形的角平分线、中线和中位线都在三角形内部，但是锐角三角形的三条高在三角形内部，直角三角形的一条高在三角形内部，其余两条高与直角边重合，钝角三角形的一条高在三角形内部，其余两条高在三角形外部.方法归纳：解答本题的关键是熟练掌握三角形高、角平分线和中线的画法.1.(2013·温州)下列各组数可能是一个三角形的边长的是( )A.1,2,4B.4,5,9C.4,6,8D.5,5,112.如图，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C个数是( )A.2B.3C.4D.53.三角形的下列线段中能将三角形的面积分成相等的两部分的是( )A.中线B.角平分线C.高D.中位线命题点2 三角形中的角例2 (2013·海南改编)如图，AB∥CD，AE＝AF，CE交AB于点F，∠C＝110°，求∠A的度数.【思路点拨】根据“两直线平行，同位角相等”求出∠EFB的度数，进而求出∠AFE，根据“等边对等角”求出∠E的度数，根据三角形内角和定理求出∠A的度数.【解答】方法归纳：当问题中含有平行线时，可利用平行线的性质将其转化为其他角；当该角是一个三角形的外角或内角时，根据三角形外角的性质和三角形内角和定理进行计算.1.(2013·龙岩)如图，AB∥CD，BC与AD相交于点M，N是射线CD上的一点.若∠B＝65°，∠MDN＝135°，则∠AMB＝ .2.(2014·邵阳)如图，在△ABC中，∠B＝46°，∠C＝54°,AD平分∠BAC，交BC于D，DE ∥AB，交AC于E，则∠ADE的大小是( )A.45°B.54°C.40°D.50°3.(2014·威海)如图，在△ABC中，∠ABC＝50°，∠ACB＝60°，点E在BC的延长线上，∠ABC的平分线BC与∠ACE的平分线CD相交于点D，连接AD.下列结论不正确的是( ) A.∠BAC＝70° B.∠DOC＝90° C.∠BDC＝35° D.∠DAC＝55°命题点3 三角形的中位线例3 (2014·湘潭)如图，AB是池塘两端，设计一方法测量AB的距离，取点C，连接AC、BC，再取它们的中点D、E，测得DE=15米，则AB=( )A.7.5米B.15米C.22.5米D.30米【思路点拨】因为DE是△ABC的中位线，利用中位线定义求AB的长.方法归纳：解答本题的关键是要依据题目条件，活用中位线定理的结论.1.(2014·泸州)如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为( )A.30°B.60°C.120°D.150°2.如图，D是△ABC内一点，BD⊥CD,AD=6,BD=4,CD=3.E、F、G、H分别是AB、AC、CD、BD 的中点，则四边形EFGH的周长是( )A.7B.9C.10D.113.如图，在△ABC中，点D、E、F分别是AB、AC、BC的中点，若△ABC的周长为12 cm，则△DEF的周长是 cm.命题点4 全等三角形的性质与判定例4 (2014·福州)如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D.【思路点拨】∠A与∠D分别在△ABF和△DEC中，直接证明△ABF和△DCE全等即可.【解答】方法归纳：证明两条边或两个角相等时，若两条边或两个角分别在两个三角形当中，通常证明这两条边或两个角所在的三角形全等.1.(2014·南充)如图，AD、BC相交于O，OA=OC,∠OBD=∠ODB.求证：AB=CD.2.(2014·宜宾)如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC.求证：AD=BC.3.(2014·泸州)如图正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为G，求证：AE=BF.1.小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )2.(2013·襄阳)如图，在△ABC中，D是BC延长线上一点，∠B＝40°，∠ACD＝120°，则∠A等于( )A.60°B.70°C.80°D.90°3.(2014·枣庄)如图，AB∥CD，AE交CD于C，∠A=34°，∠DEC=90°，则∠D的度数为( )A.17°B.34°C.56°D.124°4.(2013·河池)一个三角形的周长是36 cm，则以这个三角形各边中点为顶点的三角形的周长是( )A.6 cmB.12 cmC.18 cmD.36 cm5.(2014·益阳)如图，平行四边形ABCD中，E,F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是( )A.AE=CFB.BE=FDC.BF=DED.∠1=∠26.(2014·广州)△ABC中，已知∠A=60°,∠B=80°,则∠C的外角的度数 .7.(2014·长沙)如图，点B，E，C，F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF= .8.(2014·温州)如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3= 度.9.(2013·娄底)如图，AB=AC，要使△ABE≌△ACD，应添加的条件是 .(添加一个条件即可)10.(2014·连云港)如图，AB∥CD，∠1=62°，FG平分∠EFD，则∠2= .11.(2013·威海)将一副直角三角板如图摆放,点C在EF上,AC经过点D,已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°,则∠CDF= .12.(2014·威海)如图，有一直角三角形纸片ABC，边BC＝6，AB＝10，∠ACB＝90°，将该直角三角形纸片沿DE折叠，使点A与点C重合，则四边形DBCE的周长为 .13.(2014·十堰)如图，点D在AB上，点E在AC上，AB=AC，AD=AE.求证：∠B=∠C.14.(2014·武汉)如图，AC和BD相交于点O，OA=OC，OB=OD.求证：DC∥AB.15.(2014·宜昌)如图，在Rt△ABC中，∠ACB=90°,∠B=30°,AD平分∠CAB.(1)求∠CAD的度数；(2)延长AC至E，使CE=AC,求证:DA=DE.16.(2014·杭州)在△ABC中，AB=AC，点E,F分别在AB,AC上，AE=AF，BF与CE相交于点P，求证：PB=PC，并请直接写出图中其他相等的线段.17.(2014·泰安)如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=13CD,过点B作BF∥DE，与AE的延长线交于点F.若AB=6，则BF的长为( )A.6B.7C.8D.1018.(2013·达州改编)如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2 014BC和∠A2 014CD的平分线交于点A2 015，则∠A2 015= 度.19.(2014·苏州)如图，在Rt△ABC中，∠ACB=90°,点D，F分别在AB，AC上，CF=CB.连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF.(1)求证：△BCD≌△FCE;(2)若EF∥CD，求∠BDC的度数.20.(2013·佛山)课本指出：公认的真命题称为公理，除了公理外，其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(1)叙述三角形全等的判定方法中的推论AAS；(2)证明推论AAS.要求：叙述推论用文字表达；用图形中的符号表达已知、求证，并证明，证明对各步骤要注明依据.21.(2014·内江)如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM＝CN，AM 交BN于点P.(1)求证：△ABM≌△BCN；(2)求∠APN的度数.参考答案考点解读①首尾顺次 ②锐 ③直 ④钝 ⑤等边 ⑥锐角 ⑦直角顶点 ⑧一点 ⑨相等⑩一点 ⑪内心 ⑫相等 ⑬大于 ⑭小于 ⑮中点 ⑯平行 ○17一半 ○18180° ○19互余 ○20和 ○21相等 ○22相等 各个击破例1 C题组训练 1.C 2.C 3.A例2 ∵AB ∥CD ，∴∠EFB ＝∠C ＝110°，∴∠AFE ＝180°-110°＝70°.又∵AE ＝AF ，∴∠E ＝∠AFE ＝70°，∴∠A ＝180°-∠E-∠AFE ＝180°-2×70°＝40°.题组训练 1.70° 2.C 3.B例3 D题组训练 1.C 2.D 3.6例4 证明：∵BE=CF ，∴BE+EF=CF+EF ，即BF=CE.在△ABF 和△DCE 中，,,AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩，∴△ABF ≌△DCE ，∴∠A=∠D.题组训练 1.证明：∵∠OBD=∠ODB ，∴OB=OD.在△AOB 和△COD 中，,,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOB ≌△COD(SAS)，∴AB=CD.2.证明：∵AE=CF ，∴AF=CE.∵AD ∥BC ，∴∠A=∠C.在△AFD 和△CEB 中，A CB D AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，，， ∴△AFD ≌△CEB(AAS),∴AD=BC.3.证明：∵四边形ABCD 是正方形，∴AB=BC ，∠ABC=∠BCF=90°，∴∠BAE+∠AEB=90°.又∵AE ⊥BF ，垂足为G ，∴∠CBF+∠AEB=90°,∴∠BAE=∠CBF.在△ABE 与△BCF 中，,,,BAE CBF AB BC ABE BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE ≌△BCF(ASA)，∴AE=BF.整合集训1.C2.C3.C4.C5.A6.140°7.68.809.∠C=∠B 或∠AEB=∠ADC 或∠CEB=∠BDC 或AE=AD 或CE=BE10.31° 11.25° 12.1813.证明：在△ABE 和△ACD 中，AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ABE ≌△ACD(SAS)，∴∠B=∠C.14.证明：∵在△ODC 和△OBA 中，∵,,,OD OB DOC BOA OC OA =⎧⎪∠=∠⎨⎪=⎩∴△ODC ≌△OBA(SAS)，∴∠C=∠A(或者∠D=∠B)(全等三角形对应角相等)，∴DC ∥AB(内错角相等，两直线平行).15.(1)∵∠ACB=90°,∴∠CAB+∠B=90°.又∵∠B=30°，∴∠CAB=60°.∵AD 平分∠CAB,∴∠CAD=12∠CAB,∴∠CAD=30°. (2)证明：∵∠ACB=90°,∴DC ⊥AE.又∵CE=AC ，∴DC 垂直平分AE.∴DA=DE.16.证明：∵AB ＝AC ，∴∠ABC ＝∠ACB.又∵AE ＝AF ，∠A ＝∠A ，∴△ABF ≌△ACE ，∴∠ABF ＝∠ACE ，∴∠PBC ＝∠PCB ，∴PB ＝PC.相等的线段还有BF ＝CE ，PF ＝PE ，BE ＝CF.17.C 18. 2 0152m19.(1)证明：∵CD 绕点C 顺时针方向旋转90°得CE,∴CD=CE,∠DCE=90°.∵∠ACB=90°,∴∠BCD=90°-∠ACD=∠FCE.在△BCD 和△FCE 中，,,,CB CF BCD FCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△FCE.(2)由△BCD ≌△FCE 得∠BDC=∠E.∵EF ∥CD,∴∠E=180°-∠DCE=90°,∴∠BDC=90°.20.(1)两个角和其中一个角的对边对应相等的两个三角形全等.(2)已知：在△ABC 与△DEF 中，∠A=∠D ，∠B=∠E ，BC=EF.求证：△ABC ≌△DEF.证明：在△ABC 中，∠A+∠B+∠C=180°，∴∠C=180°-∠A-∠B(三角形的内角和等于180°).同理：∠F=180°-∠D-∠E.又∵∠A=∠D ，∠B=∠E ，∴∠C=∠F(等式的性质).在△ABC 与△DEF 中，B E BC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩，，，∴△ABC ≌△DEF(ASA).21.(1)证明：∵五边形ABCDE 是正五边形，∴AB ＝BC ，∠ABM ＝∠BCN.在△ABM 和△BCN 中，,,,AB BC ABM BCN BM CN =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△BCN(SAS).(2)∵△ABM ≌△BCN ，∴∠MBP ＝∠BAP.∵∠MBP ＋∠BMP ＋∠BPM ＝180°，∠BAP ＋∠BMA ＋∠MBA ＝180°，∴∠BPM ＝∠MBA.∵∠BPM ＝∠APN ，∴∠APN ＝∠MBA ＝31805⨯︒＝108°.。

2019年中考数学三角形及全等知识点总结与解析三角形知识结构1、三角形的概念由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

组成三角形的线段叫做三角形的边；相邻两边的公共端点叫做三角形的顶点；相邻两边所组成的角叫做三角形的内角，简称三角形的角。

2、三角形中的主要线段（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。

（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。

（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。

3、三角形的稳定性三角形的形状是固定的，三角形的这个性质叫做三角形的稳定性。

三角形的这个性质在生产生活中应用很广，需要稳定的东西一般都制成三角形的形状。

4、三角形的特性与表示三角形有下面三个特性：（1）三角形有三条线段（2）三条线段不在同一直线上三角形是封闭图形（3）首尾顺次相接三角形用符号""表示，顶点是A、B、C的三角形记作"ABC"，读作"三角形ABC"。

5、三角形的分类三角形按边的关系分类如下：不等边三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形三角形按角的关系分类如下：直角三角形（有一个角为直角的三角形）三角形锐角三角形（三个角都是锐角的三角形）斜三角形钝角三角形（有一个角为钝角的三角形）把边和角联系在一起，我们又有一种特殊的三角形：等腰直角三角形。

它是两条直角边相等的直角三角形。

6、三角形的三边关系定理及推论（1）三角形三边关系定理：三角形的两边之和大于第三边。

推论：三角形的两边之差小于第三边。

（2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形②当已知两边时，可确定第三边的范围。

③证明线段不等关系。

7、三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°。

三角形与全等三角形【复习目标】1．掌握三角形的内角和定理及推论；掌握三角形三边之间的关系定理。

2．理解全等形、全等三角形的定义；掌握全等三角形的性质与判定方法。

3．能正确、恰当选用三角形全等的条件推证有全等、角相等、线段相等的问题．【直击考点】1．三角形三边关系定理：三角形任意两边的和大于第三边．2．三角形内角和定理：三角形的内角和是180°。

推论1：三角形的一个外等于与它不相邻的两个内角的和；推论2：三角形的一个外角大于与它不相邻的任何一个内角。

3．全等三角形的定义：能够完全重合的两个三角形叫做全等三角形 。

4．如图：（1），若BOD ∆≌C B COE ∠=∠∆,.指出这两个全等三角形的对应边。

OB 与OC ，OD 与OE ，BD 与CE ； （2）若ADO ∆≌AEO ∆,指出这两个三角形的对应角。

∠ADO 与∠AEO ，∠AOD 与∠AOE ，∠OAD 与∠OAE 。

5．全等三角形性质：（1）对应边相等 （2）对应角相等（3）周长相等 （4）面积相等6．全等三角形的判定方法：（1）SSS 是：三边对应相等的两个三角形全等； （2）SAS 是：两边和夹角对应相等的两个三角形全等； （3）ASA 是：两角和夹边对应相等的两个三角形全等 ； (4) AAS 是：两角和夹边对应相等的两个三角形全等 ；( 5)H L 是：一条直角边和斜边对应相等的两个直角三角形全等 。

【名题点拔】考点1 三角形三边关系定理例1三角形的最长边为10,另两边的长分别为x 和4,周长为c,求x 和c 的取值范围. 点拨：已知三角形的两边为10和4.那么第三边x 的范围应满足:410410+<<-x 即6<x <14.2420,41010641010610≤<++≤<++∴≤<∴c c c x 即的范围满足周长是最长边考点2 全等三角形的判定方法例2 如图所示，已知OA=OB ，点C 在OA 上，点D 在OB 上，OC=OD ， AD 与BC 相交于点E ，•那么图中全等的三角形共有________对．点拨：由OA=OB ，∠AOD=∠BOC ，OC=OD 得△AOD ≌△BOC （SAS ）． 由此得∠A=∠B ，∠ACE=∠BDE,因此可得△ACE ≌△BDE （ASA ）；△AOE ≌△BOE （SAS ）；△COE ≌△DOE 。

第16课时三角形与三角形全等三角形的基础知识1.（2019·百色中考）在△OAB中，∠O＝90°，∠A＝35°，则∠B＝（ B ）A.35°B.55°C.65°D.145°2.（2019·百色中考）下列图形中具有稳定性的是（ A ）A.正三角形B.正方形C.正五边形D.正六边形3.（2019·百色中考）顶角为30°的等腰三角形三条中线的交点是该三角形的（ A ）A.重心B.外心C.内心D.中心全等三角形的判定与性质4.（2019·百色中考）已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F.（1）求证：△ABF≌△CDE；（2）如图，若∠1＝65°，求∠B的大小.（1）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AD∥BC，∠B＝∠D，∴∠1＝∠ECB.∵AF∥CE，∴∠AFB＝∠ECB，∴∠AFB＝∠1.在△ABF和△CDE中，∵错误!∴△ABF≌△CDE（AAS）；（2）解：由（1）得∠1＝∠ECB.∵CE平分∠BCD，∴∠DCE＝∠ECB，∴∠1＝∠DCE＝65°，∴∠B＝∠D＝180°－2×65°＝50°.核心考点解读三角形的分类及边角关系1.三角形的分类（1）按边分类三角形eq \b\lc\{(\a\vs4\al\co1(不等边三角形（2）按角分类锐角三角形直角三角形钝角三角形2.三角形中的边角关系（1）三边关系三角形的任意两边的和大于第三边，任意两边的差小于第三边.（2）内角和定理三角形三个内角和等于180°.（3）内外角关系①三角形的任意一个外角等于与它不相邻的两个内角的和.②三角形的一个外角大于与它不相邻的任何一个内角.【温馨提示】（1）三角形具有稳定性；（2）大边对大角，小边对小角.三角形中的重要线段四线定义性质图示中线三角形中，连接一个顶点与它对边中点的线段BD＝DC高线从三角形一个顶点到它对边所在直线的垂线段AD⊥BC，即∠ADB＝∠ADC＝90°角平分线三角形中，一个角的平分线与这个角对边相交，顶点与交点之间的线段∠1＝∠2中位线连接三角形两边中点的线段DE∥BC且DE＝12BC全等三角形及其性质与判定3.全等三角形：能够完全重合的两个图形叫做全等形；能够完全重合的两个三角形叫做全等三角形Ｗ.4.全等三角形的性质（1）全等三角形的对应边、对应角相等；（2）全等三角形的周长相等、面积相等；（3）全等三角形对应的中线、高线、角平分线、中位线都相等.5.全等三角形的判定（1）全等三角形判定方法有SAS （基本事实），ASA （基本事实），SSS（基本事实），AAS；两个直角三角形全等的特定方法有HL Ｗ.（2）三角形全等的证明思路（已知边或角对应相等）⎩⎪⎪⎪⎨⎪⎪⎪⎧已知两边⎩⎪⎨⎪⎧找第三边（SSS ）找夹角（SAS ）找是否有直角（HL ）已知一边一角⎩⎪⎨⎪⎧已知一边和它的邻角⎩⎪⎨⎪⎧找这边的另一个邻角（ASA ）找这个角的另一条边（SAS ）找这边的对角（AAS ）已知一边和它的对角⎩⎪⎨⎪⎧找一角（AAS ）已知角是直角，找另一边（HL ）已知两角⎩⎪⎨⎪⎧找两角的夹边（ASA ）找夹边外的任意边（AAS ）（3）全等三角形模型平移模型 三垂直模型翻折轴对称模型旋转模型【温馨提示】（1）“SAS，ASA ，SSS ，AAS ”适用于所有三角形，而“HL”只适用于直角三角形全等的判定. （2）“SSA”和“AAA”不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与. （3）证明三角形全等时，对应顶点的字母必须写在对应位置上. （4）灵活运用“截长补短法”添加辅助线可以构造全等三角形.1.（2019·百色中考）三角形的内角和等于（ B ） A.90° B.180° C.300° D.360°2.（2019·河北中考）下列图形具有稳定性的是（ A ）3.（2019·河池中考）下列长度的三条线段不能组成三角形的是（ A ） A.5，5，10 B.4，5，6 C.4，4，4 D.3，4，54.如图，过△ABC 的顶点A ，作BC 边上的高，以下作法正确的是（ A ）A B C D5.（2019·河池中考）三角形的下列线段中能将三角形的面积分成相等两部分的是（ A ） A.中线 B.角平分线 C.高 D.中位线6.（2019·北部湾中考）如图，△ABC 中，∠A ＝60°，∠B ＝40°，则∠C 等于（ B ） A.100° B.80° C.60° D.40°,（第6题图）) ,（第7题图）)7.（2019·宿迁中考）如图，点D 在△ABC 边AB 的延长线上，DE ∥BC.若∠A＝35°，∠C ＝24°，则∠D 的度数是（ B ）A.24°B.59°C.60°D.69°8.（2019·梧州中考）如图，已知在△ABC 中，D ，E 分别是AB ，AC 的中点，BC ＝6 cm ，则DE 的长度是 3 cm.9.（2019·武汉中考）如图，点E ，F 在BC 上，BE ＝CF ，AB ＝DC ，∠B ＝∠C，AF 与DE 交于点G ，求证：GE ＝GF.证明：∵BE＝CF ， ∴BE ＋EF ＝CF ＋EF ， ∴BF ＝CE.在△ABF 和△DCE 中， ∵⎩⎪⎨⎪⎧AB ＝DC ，∠B ＝∠C，BF ＝CE ，∴△ABF ≌△DCE （SAS ）， ∴∠GEF ＝∠GFE， ∴GE ＝GF.典题精讲精练三角形中的边角关系例1 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（ C ） A.1 B.2 C.8 D.11【解析】根据三角形的三边关系求解即可.设三角形第三边的长为x ，由题意得7－3＜x ＜7＋3，即4＜x ＜10，由此选出满足条件的正确选项.例2 （2019·北部湾中考）如图，∠ACD 是△ABC 的外角，CE 平分∠ACD，若∠A＝60°，∠B ＝40°，则∠ECD 等于（ C ）A.40°B.45°C.50°D.55°【解析】根据三角形外角性质求出∠ACD 的度数，根据角的平分线定义即可求出∠ECD 的度数. ∵∠A ＝60°，∠B ＝40°， ∴∠ACD ＝∠A＋∠B＝100°.∵CE 平分∠ACD，∴∠ECD ＝12∠ACD＝50°.全等三角形的判定与性质例3 （2019·桂林中考）如图，点A ，D ，C ，F 在同一条直线上，AD ＝CF ，AB ＝DE ，BC ＝EF. （1）求证：△ABC≌△DEF；（2）若∠A ＝55°，∠B ＝88°，求∠F 的度数.【解析】（1）证出AC ＝DF ，结合已知条件根据SSS 就可以推出△ABC≌△DEF； （2）由（1）中结论利用全等三角形的性质得到∠F＝∠ACB，进而得出结果. 【解答】（1）证明：∵AC＝AD ＋DC ， DF ＝DC ＋CF ，且AD ＝CF ，∴AC ＝DF. 在△ABC 和△DEF 中， ∵⎩⎪⎨⎪⎧AB ＝DE ，BC ＝EF ，AC ＝DF ，∴△ABC ≌△DEF （SSS ）；（2）解：由（1）可知，∠F ＝∠ACB. ∵∠A ＝55°，∠B ＝88°，∴∠ACB ＝180°－（∠A ＋∠B）＝180°－（55°＋88°）＝37°， ∴∠F ＝∠ACB＝37°.1.（2019·来宾中考）如图，△ABC 中，∠A ＝40°，点D 为延长线上一点，且∠CBD＝120°，则∠C＝（ C ）A.40°B.60°C.80°D.100°2.（2019·泰州中考）已知三角形两边的长分别为1，5，第三边长为整数，则第三边的长为 5 Ｗ.3.（2019·百色中考）△ABC 的两条高的长度分别为4和12，若第三条高也为整数，则第三条高的长度是（ B ）A.4B.4或5C.5或6D.64.（2019·成都中考）如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB 的是（ C ）A.∠A ＝∠DB.∠ACB ＝∠DBCC.AC ＝DBD.AB ＝DC5.（2019·梧州中考）如图，在▱ABCD 中，对角线AC ，BD 相交于点O ，过点O 的一条直线分别交AD ，BC 于点E ，F.求证：AE ＝CF.证明：∵四边形ABCD 是平行四边形， ∴AD ∥BC ，OA ＝OC ， ∴∠OAE ＝∠OCF. 在△AOE 和△COF 中，∵⎩⎪⎨⎪⎧∠AOE＝∠COF，OA ＝OC ，∠OAE ＝∠OCF， ∴△AOE ≌△COF （ASA ）， ∴AE ＝CF.请完成精练本第27～28页作业2019-2020学年数学中考模拟试卷一、选择题1．已知关于x的不等式组314(1)x xx m--⎧⎨⎩无解，则m的取值范围是（）A．m≤3B．m＞3 C．m＜3 D．m≥32．一副学生用的三角板如图放置，则∠AOD的度数为（）A.75°B.100°C.105°D.120°3．3月30日，我区航空经济产业功能区2019年一季度重大项目集中开工仪式在电子科大产业园四期项目用地举行．参加此次集中开工仪式项目共计71个，总投资超过249亿元，未来随着这一波又一波项目的建成投产，必将为双流航空经济插上腾飞之翼，助力双流打造中国航空经济之都．用科学记数法表示249亿元为（）A．249×108元B．24.9×109元C．2.49×1010元D．0.249×1011元4．如图，嘉淇一家驾车从A地出发，沿着北偏东30°的方向行驶30公里到达B地游玩，之后打算去距离A地正东30公里处的C地，则他们行驶的方向是（）A．南偏东60°B．南偏东30°C．南偏西60°D．南偏西30°5．如图，已知直线MN：y＝kx+2交x轴负半轴于点A，交y轴于点B，∠BAO＝30°，点C是x轴上的一点，且OC＝2，则∠MBC的度数为（）A ．75°B ．165°C ．75°或45°D ．75°或165°6．如图，这是健健同学的小测试卷，他应该得到的分数是（ ）A ．40B ．60C ．80D ．1007．如图，点A （m ，1），B （2，n ）在双曲线ky x=（k≠0），连接OA ，OB ．若S △ABO ＝8，则k 的值是（ ）A ．﹣12B ．﹣8C ．﹣6D ．﹣48．已知抛物线223y x mx m =+-（m 是常数），且无论m 取何值，该抛物线都经过某定点H ，则点H 的坐标为A ．3,12⎛⎫-⎪⎝⎭B ．3,12⎛⎫-- ⎪⎝⎭C ．39,24⎛⎫⎪⎝⎭D ．39,24⎛⎫-⎪⎝⎭9．下列图案，既是轴对称图形又是中心对称图形的有( )A.1个B.2个C.3个D.4个10．在边长为2的正方形ABCD 中，对角线AC 与BD 相交于点O ，P 是BD 上一动点，过P 作EF ∥AC ，分别交正方形的两条边于点E ，F ．设BP=x ，△BEF 的面积为y ，则能反映y 与x 之间关系的图象为( )A ．B ．C ．D ．11．一个正多边形，它的每一个外角都等于40°，则该正多边形是（ ） A ．正六边形B ．正七边形C ．正八边形D ．正九边形12．如图，已知等腰梯形ABCD 中，AD ∥BC ，AB ＝DC ，AC 与BD 相交于点O ，则下列判断不正确的是（ ）A ．△ABC ≌△DCB B ．△AOD ≌△COBC ．△ABO ≌△DCOD ．△ADB ≌△DAC二、填空题13．某学校组织600名学生分别到野生动物园和植物园开展社会实践活动，到野生动物园的人数比到植物园人数的2倍少30人，若设到植物园的人数为x 人，依题意，可列方程为________________． 14．因式分解：222x x -+=______________。