最大频繁项集挖掘中搜索空间的剪枝策略

人工智能基础(试卷编号1201)1.[单选题]留一法是下列哪个函数？A)RepeatedKFoldB)KFoldC)LeaveOneOut答案:C解析:错题，答案为D2.[单选题]语音理解是指利用()等人工智能技术进行语句自动识别和语意理解。

A、声乐和心理A)合成和分析B)知识表达和组织C)字典和算法答案:C解析:3.[单选题]matpltlib中绘制图形,通过更改绘图框的尺寸来设置相等的缩放比例的参数是( )。

A)scaledB)equalC)autoD)normal答案:A解析:4.[单选题]设事件A、B相互独立，P(A)>0，P(B)>0，则（）。

A)P(AB)=0B)P(A|B)=0C)P(A)+P(B)=1D)P(A|B)=P(A)答案:D解析:5.[单选题]台区智能融合终端具备的接口资源不包含（ ）。

A)蓝牙接口B)RS-485接口C)以太网接口D)wifi接口答案:D解析:D)进化门答案:D解析:长短时记忆神经网络（LSTM）增加了三个门用来控制信息传递和最后的结果计 算，三个门分别为遗忘门、输入门、输出门。

7.[单选题]概率模型的训练过程就是（）过程。

A)分类B)聚类C)参数估计D)参数选择答案:C解析:8.[单选题]关于Sqoop的说法，不正确的是（）。

A)主要设计目的是在Hadoop与传统数据库之间进行数据的ETL操作B)数据导入导出通过MapReduce完成C)Sqoop具备MapReduce的并行化和容错性D)Sqoop的Reduce操作速度更快答案:D解析:Sqoop是一个强大的工具，主要用来处理大量的数据传输，并不会影响Reduce 的操作速度。

9.[单选题]以（）为中心是数据产品区别于其他类型产品的本质特征A)客户B)分析C)资源D)数据答案:D解析:10.[单选题]频繁项集、频繁闭项集、最大频繁项集之间的关系是：A)频繁项集->频繁闭项集->二最大频繁项集B)频繁项集->二频繁闭项集->最大频繁项集C)频繁项集->频繁闭项集->最大频繁项集D)频繁项集->二频繁闭项集->二最大频繁项集答案:C解析:11.[单选题]一个不能再分解的命题，是（）答案:A解析:12.[单选题]下列不在人工智能系统的知识包含的4个要素中A)事实B)规则C)控制和元知识D)关系答案:D解析:13.[单选题]根据数据管理计划，设计或选择具体方法实行计划中的工作内容，属于数据治理 的哪一步()0A)计划B)执行C)检查D)改进答案:B解析:数据治理并不是一次性工作，而是一种循序渐进的过程，主要包含计划、执行、 检查和改进等基本活动，即数据治理的PDCA模型，其中：①计划(Plan)：数据管理方 针和目标的确定，明确组织机构的数据管理的目的、边界和工作内容。

频繁项集挖掘算法 FP-GrowthApriori算法和FPTree算法都是数据挖掘中的关联规则挖掘算法，处理的都是最简单的单层单维布尔关联规则。

Apriori算法Apriori算法是⼀种最有影响的挖掘布尔关联规则频繁项集的算法。

是基于这样的事实：算法使⽤频繁项集性质的先验知识。

Apriori使⽤⼀种称作逐层搜索的迭代⽅法，k-项集⽤于探索(k+1)-项集。

⾸先，找出频繁1-项集的集合。

该集合记作L1。

L1⽤于找频繁2-项集的集合L2，⽽L2⽤于找L3，如此下去，直到不能找到频繁k-项集。

找每个L k需要⼀次数据库扫描。

这个算法的思路，简单的说就是如果集合I不是频繁项集，那么所有包含集合I的更⼤的集合也不可能是频繁项集。

算法原始数据如下：TID List of item_ID’sT100 T200 T300 T400 T500 T600 T700 T800 T900I1,I2,I5 I2,I4I2,I3I1,I2,I4 I1,I3I2,I3I1,I3I1,I2,I3,I5 I1,I2,I3算法的基本过程如下图：⾸先扫描所有事务，得到1-项集C1，根据⽀持度要求滤去不满⾜条件项集，得到频繁1-项集。

下⾯进⾏递归运算：已知频繁k-项集(频繁1-项集已知)，根据频繁k-项集中的项，连接得到所有可能的K+1_项，并进⾏剪枝（如果该k+1_项集的所有k项⼦集不都能满⾜⽀持度条件，那么该k+1_项集被剪掉），得到项集，然后滤去该项集中不满⾜⽀持度条件的项得到频繁k+1-项集。

如果得到的项集为空，则算法结束。

连接的⽅法：假设项集中的所有项都是按照相同的顺序排列的，那么如果[i]和[j]中的前k-1项都是完全相同的，⽽第k项不同，则[i]和[j]是可连接的。

⽐如中的{I1,I2}和{I1,I3}就是可连接的，连接之后得到{I1,I2,I3}，但是{I1,I2}和{I2,I3}是不可连接的，否则将导致项集中出现重复项。

Apriori算法的改进及实例【摘要】随着数据规模的不断增大，传统的Apriori算法在处理大规模数据集时性能较低。

为了解决这一问题，研究者们提出了多种改进策略。

本文针对Apriori算法的改进及实例进行了研究和探讨。

首先介绍了使用FP-growth算法替代Apriori算法的改进方法，其能够显著提高算法的效率。

其次讨论了剪枝策略的优化，通过精细化的剪枝方法可以减少计算时间。

对并行化处理进行了探讨，使得算法能够更好地应对大规模数据集。

通过实例分析，展示了基于FP-growth算法的关联规则挖掘和优化的剪枝策略在市场篮分析中的应用。

结论部分指出了不同场景下的改进策略对提高算法效率和精度的重要意义。

通过这些改进措施，Apriori算法在处理大规模数据集时将得到更好的应用和推广。

【关键词】关键词：Apriori算法、FP-growth算法、剪枝策略、并行化处理、关联规则挖掘、市场篮分析、大规模数据集、效率、精度1. 引言1.1 Apriori算法的改进及实例Apriori算法是一种经典的关联规则挖掘算法，它通过逐层扫描数据集来发现频繁项集，并基于频繁项集生成关联规则。

随着数据规模的不断增大，Apriori算法在处理大规模数据集时面临着一些效率和性能上的挑战。

为了克服这些挑战，研究者们提出了许多针对Apriori算法的改进方法。

一种常见的改进方法是使用FP-growth算法来替代Apriori算法。

FP-growth算法利用树结构存储数据集信息，减少了对数据集的多次扫描，从而提高了算法的效率。

剪枝策略的优化也是改进Apriori算法的一个重要方向。

通过优化剪枝策略，可以减少频繁项集的生成数量，进而提升算法的性能。

针对多核处理器的并行化处理也是一种改进Apriori算法的方法。

通过将数据集分割成更小的子集，可以实现并行处理，从而加快算法的运行速度。

在接下来的实例部分，我们将分别介绍基于FP-growth算法的关联规则挖掘实例以及优化的剪枝策略在市场篮分析中的应用实例，展示这些改进方法在实际应用中的效果和优势。

近几十年来，剪枝策略在博弈问题研究中变得越来越重要，它可以使得深层搜索更有效。

剪枝就是在搜索树中削减支路，以减少时间和空间的消耗。

剪枝策略主要用于搜索树，减少未决节点的数量，可以减少时间和内存的使用，使搜索更有效。

具体来说，剪枝策略会使算法中搜索一个节点时搜索它的后裔，以了解它是否应该从搜索树中剪去。

深层搜索（ Deep Search）是博弈问题研究中最常用的一种技术，它通过构建搜索树，来尝试穷举所有可能的局面，以了解处于某一局面的最佳行动。

然而，剪枝策略可以有效地削减搜索树中的衍生分支（descendant branch），使搜索变得更有效率，也能更快速地找到最优解。

基于动态规划的剪枝，对于具体的博弈问题可能都有不同的技术，但通常大致可以分为两种：最小值剪枝和最大值剪枝。

最小值剪枝是指，我们在当前局面中，把搜索空间中收益最低的分支剪枝；最大值剪枝是指，我们在当前局面中，把搜索空间中收益最高的分支剪枝。

举个例子，解决TicTacToe（井字棋）问题。

在每一步TicTacToe游戏中，玩家都会分析自己下一步的最佳走法，以获得比对方更多的胜算。

然而，由于游戏完全由玩家本身控制，因此每一步的搜索空间都非常大，常常需要分析很多层次的衍生分支，以了解自己最佳的走法，这就是深层搜索的原理。

剪枝策略可以使搜索更有效，通过应用最小值剪枝和最大值剪枝，可以在决定每步时，很容易削减决策树，节省时间和空间。

总之，剪枝策略可以起到减少搜索空间，提高搜索效率的作用，是博弈问题研究的重要策略。

它在不同的深层搜索算法中，都得到广泛的使用，被广泛应用于许多问题中，如棋类游戏，搜索引擎等。

apriori算法最大频繁项集介绍在数据挖掘领域，频繁项集是指在一个数据集中经常同时出现的项的集合。

频繁项集挖掘是一种常见的数据挖掘任务，可以用于发现数据中的关联规则。

apriori算法是一种用于发现频繁项集的经典算法，它通过利用数据中的Apriori原理，逐步生成候选项集，并使用支持度来筛选出频繁项集。

Apriori原理Apriori原理是指如果一个项集是频繁的，那么它的所有子集也是频繁的。

换句话说，如果一个项集不频繁，那么它的所有超集也不可能是频繁的。

Apriori算法基于这个原理，通过逐步生成候选项集来减少搜索空间，从而提高算法效率。

Apriori算法步骤Apriori算法的主要步骤如下：1.初始化：将每个单项作为候选项集，并计算其支持度。

2.生成候选项集：根据上一轮的频繁项集，生成下一轮的候选项集。

具体而言，对于k-1项的频繁项集，将其两两组合生成k项的候选项集。

3.剪枝：对于生成的候选项集，通过Apriori原理剪去不频繁的项集。

4.计算支持度：对剪枝后的候选项集，扫描数据集，计算每个候选项集的支持度。

5.筛选频繁项集：根据设定的最小支持度阈值，筛选出频繁项集。

6.生成关联规则：根据频繁项集，生成关联规则，并计算其置信度。

7.根据设定的最小置信度阈值，筛选出满足要求的关联规则。

生成候选项集在Apriori算法中，生成候选项集是一个重要的步骤。

候选项集的生成是通过对频繁项集的连接操作实现的。

具体而言，对于k-1项的频繁项集，将其两两组合生成k项的候选项集。

例如，对于频繁项集{A, B}和{B, C}，可以生成候选项集{A, B, C}。

剪枝剪枝是为了减少搜索空间，提高算法效率。

在Apriori算法中，剪枝操作是通过Apriori原理实现的。

具体而言，如果一个候选项集的某个子集不是频繁项集，那么该候选项集也不可能是频繁项集。

因此，在计算候选项集的支持度之前，需要对候选项集进行剪枝操作。

计算支持度在Apriori算法中，支持度是衡量项集在数据集中出现的频率的度量。

模式识别与数据挖掘期末总结第一章概述1.数据分析是指采用适当的统计分析方法对收集到的数据进行分析、概括和总结，对数据进行恰当地描述，提取出有用的信息的过程。

2.数据挖掘(Data Mining，DM) 是指从海量的数据中通过相关的算法来发现隐藏在数据中的规律和知识的过程。

3.数据挖掘技术的基本任务主要体现在：分类与回归、聚类、关联规则发现、时序模式、异常检测4.数据挖掘的方法：数据泛化、关联与相关分析、分类与回归、聚类分析、异常检测、离群点分析、5.数据挖掘流程：（1）明确问题：数据挖掘的首要工作是研究发现何种知识。

（2）数据准备（数据收集和数据预处理）：数据选取、确定操作对象，即目标数据，一般是从原始数据库中抽取的组数据；数据预处理一般包括：消除噪声、推导计算缺值数据、消除重复记录、完成数据类型转换。

（3）数据挖掘：确定数据挖掘的任务，例如：分类、聚类、关联规则发现或序列模式发现等。

确定了挖掘任务后，就要决定使用什么样的算法。

（4）结果解释和评估：对于数据挖掘出来的模式，要进行评估，删除冗余或无关的模式。

如果模式不满足要求，需要重复先前的过程。

6.分类（Classification）是构造一个分类函数(分类模型)，把具有某些特征的数据项映射到某个给定的类别上。

7.分类过程由两步构成：模型创建和模型使用。

8.分类典型方法：决策树，朴素贝叶斯分类，支持向量机，神经网络，规则分类器，基于模式的分类，逻辑回归9.聚类就是将数据划分或分割成相交或者不相交的群组的过程，通过确定数据之间在预先指定的属性上的相似性就可以完成聚类任务。

划分的原则是保持最大的组内相似性和最小的组间相似性10.机器学习主要包括监督学习、无监督学习、半监督学习等1.（1）标称属性(nominal attribute)：类别，状态或事物的名字（2）：布尔属性（3）序数属性(ordinal attribute)：尺寸={小，中，大}，军衔，职称【前面三种都是定性的】（4）数值属性(numeric attribute）: 定量度量，用整数或实数值表示●区间标度(interval-scaled)属性：温度●比率标度(ratio-scaled)属性：度量重量、高度、速度和货币量●离散属性●连续属性2.数据的基本统计描述三个主要方面：中心趋势度量、数据分散度量、基本统计图●中心趋势度量：均值、加权算数平均数、中位数、众数、中列数（最大和最小值的平均值）●数据分散度量：极差（最大值与最小值之间的差距）、分位数（小于x的数据值最多为k/q，而大于x的数据值最多为(q-k)/q）、说明（特征化，区分，关联，分类，聚类，趋势/跑偏，异常值分析等）、四分位数、五数概括、离群点、盒图、方差、标准差●基本统计图：五数概括、箱图、直方图、饼图、散点图3.数据的相似性与相异性相异性：●标称属性：d(i,j)=1−m【p为涉及属性个数，m:若两个对象匹配为1否则p为0】●二元属性：d(i,j)=p+nm+n+p+q●数值属性：欧几里得距离：曼哈顿距离：闵可夫斯基距离：切比雪夫距离：●序数属性：【r是排名的值，M是排序的最大值】●余弦相似性：第三章数据预处理1.噪声数据：数据中存在着错误或异常（偏离期望值），如：血压和身高为0就是明显的错误。

一种自底向上的最大频繁项集挖掘方法赵阳;吴廖丹【期刊名称】《计算机技术与发展》【年(卷),期】2017(027)008【摘要】频繁项集挖掘是关联规则挖掘中最关键的步骤.最大频繁项集是一种常用的频繁项集简化表示方法.自顶向下的最大频繁项集挖掘方法在最大频繁项集维度远小于频繁项数时往往会产生过多的候选频繁项集.已有的自底向上的最大频繁项集挖掘方法或者需多次遍历数据库,或者需递归生成条件频繁模式树,而预测剪枝策略有进一步提升的空间.为此,提出了基于最小非频繁项集的最大频繁项集挖掘算法(BNFIA),采用基于DFP-tree的存储结构,通过自底向上的方式挖掘出最小非频繁项集,利用最小非频繁项集的性质进行预测剪枝,以缩小搜索空间,再通过边界频繁项集快速挖掘出最大频繁项集.验证实验结果表明,提出算法的性能较同类算法有较为明显的提升.%Mining frequent itemsets is the most critical step in mining association rules.Maximum frequent itemsets is a common compressed representation of frequent itemsets.In mining maximum frequent itemsets,the top-down methods would produce lots of candidate itemsets when the dimensions of maximum frequent itemsets is smaller than the number of frequent itemsets.The existing bottom-up methods need either traversal in database many times or building FP-tree recursively,and the prediction pruning strategies have further room for improvement.The algorithm of discovering maximum frequent itemsets based on minimum non-frequent itemsets named BNFIA has been proposed,which usesstorage structure based on FP-tree and digs out the minimum non-frequent itemsets through a bottom-up approach first,then prunes with the minimum non-frequent itemsets to narrow search space for acquiring the maximum frequent itemsets fast through boundary frequent itemsets.Experimental results show that the proposed algorithm has performed better than the algorithm with same type.【总页数】5页(P57-60,65)【作者】赵阳;吴廖丹【作者单位】江南计算技术研究所,江苏无锡 214083;江南计算技术研究所,江苏无锡 214083【正文语种】中文【中图分类】TP311【相关文献】1.一种有效的负频繁项集挖掘方法 [J], 董祥军;马亮2.数据流上的最大频繁项集挖掘方法 [J], 李海峰;章宁3.MLFI:新的最大长度频繁项集挖掘方法 [J], 张忠平;郭静;韩丽霞4.一种不确定性数据中最大频繁项集挖掘方法 [J], 汪金苗;张龙波;闫光辉;王凤英5.一种基于倒排索引的频繁项集挖掘方法 [J], 贾丽波;姜晓明;叶青;陈占芳因版权原因，仅展示原文概要，查看原文内容请购买。

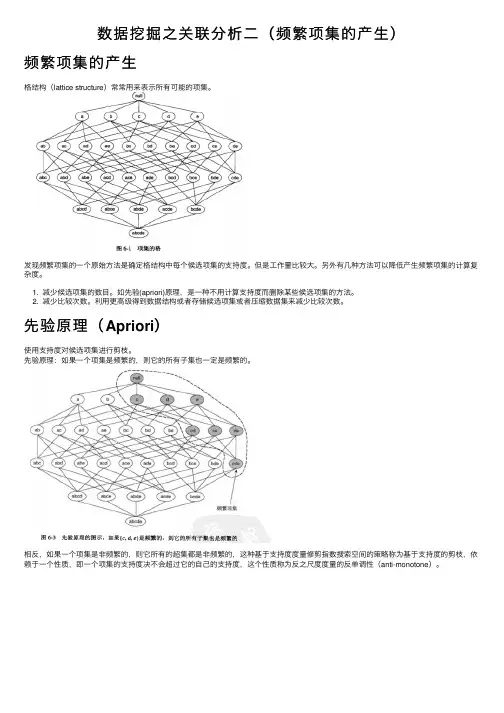
数据挖掘之关联分析⼆（频繁项集的产⽣）频繁项集的产⽣格结构（lattice structure）常常⽤来表⽰所有可能的项集。

发现频繁项集的⼀个原始⽅法是确定格结构中每个候选项集的⽀持度。

但是⼯作量⽐较⼤。

另外有⼏种⽅法可以降低产⽣频繁项集的计算复杂度。

1. 减少候选项集的数⽬。

如先验(apriori)原理，是⼀种不⽤计算⽀持度⽽删除某些候选项集的⽅法。

2. 减少⽐较次数。

利⽤更⾼级得到数据结构或者存储候选项集或者压缩数据集来减少⽐较次数。

先验原理（Apriori）使⽤⽀持度对候选项集进⾏剪枝。

先验原理：如果⼀个项集是频繁的，则它的所有⼦集也⼀定是频繁的。

相反，如果⼀个项集是⾮频繁的，则它所有的超集都是⾮频繁的，这种基于⽀持度度量修剪指数搜索空间的策略称为基于⽀持度的剪枝，依赖于⼀个性质，即⼀个项集的⽀持度决不会超过它的⾃⼰的⽀持度，这个性质称为反之尺度度量的反单调性（anti-monotone）。

Apriori算法的频繁项集产⽣Apriori算法是第⼀个关联规则挖掘算法，它开创性地使⽤基于⽀持度的剪枝技术，系统地控制候选项集指数增长。

算法：1. 初始通过单遍扫描数据集，确定每个项的⽀持度，得到所有频繁1-项集的集合F1.2. 迭代地使⽤上⼀步得到的k-1项集，产⽣新的候选k项集。

3. 为了对候选项的⽀持度技术，算法需要再次扫描⼀遍数据集。

4. 计算候选项的⽀持度，⼭区⽀持度⼩于minsup的左右后选集。

5. 当没有新的频繁项集产⽣，算法结束。

Apriori算法的频繁项集产⽣的部分有两个重要的特点：（1）逐层算法，从频繁1-项集到最长的项集，每次遍历项集格中的⼀层。

（2）它使⽤产⽣-测试（generate-and-test）策略来发现频繁项集，每次迭代后的候选项集都由上⼀次迭代发现的频繁项集产⽣。

算法总迭代次数为k_{max+1}，其中k_{max}为频繁项集最⼤长度。

候选的产⽣与剪枝剪枝：考虑候选k项集X={i_1,i_2,i_3……}，如果X的⼀个真⼦集⾮频繁，则X将会被剪枝。

数据挖掘算法数据挖掘是一门涉及从大量数据中提取信息和知识的学科，而数据挖掘算法则是实现这一目标的核心工具。

本文将介绍常用的数据挖掘算法，包括分类、聚类、关联规则挖掘和异常检测。

一、分类算法分类算法是数据挖掘中最常见的算法之一，主要用于将数据样本分为不同的类别。

以下是几种常用的分类算法：1. 决策树算法：基于树的数据结构，通过划分特征空间来实现分类。

决策树算法的优点是易于理解和实现，但对于数据的变化和噪声敏感。

2. 朴素贝叶斯算法：基于贝叶斯理论，假设特征之间相互独立，通过计算概率来进行分类。

朴素贝叶斯算法的优点是计算速度快，但对于特征之间的相关性要求较低。

3. 逻辑回归算法：基于线性回归模型，通过逻辑函数将线性回归结果转化为分类结果。

逻辑回归算法的优点是模型简单，但对于特征之间的非线性关系较难处理。

二、聚类算法聚类算法是将数据样本划分为若干个组（簇），使同一组内的样本相似度较高，而不同组之间的样本相似度较低。

以下是几种常用的聚类算法：1. K均值算法：将数据样本划分为K个簇，使每个样本与所属簇的中心点距离最小化。

K均值算法的优点是简单、高效，但对于异常点较敏感。

2. 层次聚类算法：通过计算样本之间的相似度或距离来构建层次化的簇结构。

层次聚类算法的优点是不需要预先指定簇的数量，但计算复杂度较高。

3. 密度聚类算法：基于样本点的密度来划分簇，通过定义样本点的领域和密度来进行聚类。

密度聚类算法的优点是可以发现任意形状的簇，但对于参数的选择较为敏感。

三、关联规则挖掘关联规则挖掘是从大规模数据集中发现事物之间的关联关系。

以下是几种常用的关联规则挖掘算法：1. Apriori算法：基于频繁项集的性质，逐层生成候选项集，并通过剪枝策略减少搜索空间。

Apriori算法的优点是简单、易于实现，但对于大规模数据集计算速度较慢。

2. FP-Growth算法：通过构建FP树（频繁模式树）来挖掘频繁项集，通过路径压缩和条件模式基的计数来加速挖掘过程。

ｏ ｔ ｉ ｅ ｏ ａ ｌｔ ａ ｓ ｃｉ ｎ ａ ｓ ｏ ｏ ｄ ｎ ｉ ｇ ｉ ｒ ｔ ｅ ｙ ｔ ｅ ｔａ ａ ｔｏ ｔ ｘ ｈ ｅ ｔａ ｓ ｃｉ ｅ ｔ ｒ ｎ ｅ ｓ ｃｉ ｎｓ ａ ｅ ａ ｑ ｉｅ ｏ ｂ ａ ｎ ｄ ｆ ｍ ｌ ｈｅ ｔ ｎ ａ ｔｏ ｓ ｂｙ ｍｅ ｎ ｆ ｃ ｎ ｅ ｓｎ ｔ ａｉ ｌ ｒ ｎｓ ｃ ｉ ｎ ｍａｒ ，ｔ ｒ ｎ ａ ｔ ｒ ｒ ｅ ｖ ｈ ｉ ｏｎ ｖ ｃ ｏ ｉ ｔｒ ｅ ｔｏ ｃ ｕ ｒ ｄ ｔ ｒ ｒｄ ｃ ｅ ｒｎ ｅ ｏ ｅ ｈ ｅ ｕ ｅ ｔ ａ ｇ ｆ ｓ ￣ｃ ．Ｌｏ ｉ ａ ｐ ｒ ｔｏ ｓ ａ ｄ ｐ ｕ ｉ ｇ ｍ ｅ ｏ ｓ ａ ｅ ａ ｏ ｔ ｄ ｔ ｍｐｒ ｖ ｈ ｆｉｉ ｎ ｙ ｏ ｅ ｍｉ ｉ ｇ． ｓ ｄ ｏ Ｍ Ｉ ｌ ｈ ｇ ｃ ｌｏ ｅ ａｉ ｎ ｎ ｒ ｎ ｎ ｔ ｄ ｒ ｄ ｐ ｅ ｏ ｉ ｈ ｏ ｅ ｔ ｅ ｅ ｆｃ ｅ ｃ ｆ ｔ ｎ ｎ Ｂａ ｅ ｎ ＡＦ ，ａｌ ｈ
据 挖 掘 研 究 的深 入 ，数 据 流 中 的最 大 频 繁 项 集 挖 掘 算法 也 陆 续 被提 出 ，如 ＤＳ ＭＦ 【、ｅｔ ｅ＋５ Ｆ ＭＦ— ＋６ 。本 Ｍ— Ｉ ｓ ｃ 【、 Ｐ Ｉ ４ Ｊ Ｄ Ｊ ＤＳ ｌ等
１ 概 述
频 繁 项 集 的 挖 掘 是关 联 规 则 挖 掘 的基 本任 务 ， 由于 最 大
务 ６个 项 目对 应 的关 联 矩事务数据库 Ｄ
事 务 ＴＤ Ｉ
１ ００
频 繁项集数据相对较少且 已隐含所有的频 繁项集 ，因此最大
项 目集
频繁项集的挖掘对于数据挖掘具有重要的意义 。相关算法也 陆续被提出 ，如 Ｆ ＭＡ 【、Ｔ － ｐｉｒ 】 Ａ３ 。随着数 ｐ ｘＪ ＴＡ ｒ ｉ 、ＤＩ ［等 Ｊ ｏ ］

Key w ords: G I L y ; ho sub-classing; w s U ibrar ok; indow
procedure
长春工程学院学报( 自然科学版)
2007 ,8( 1)
(Null) 的根; (2) 作为根的子女的项 目前缀子树集 合; (3)频繁项目 头表( head - table) 。其中项目 前缀 子树中的每个节点包含 3 个域: ( 1) 项 目名( item( name) ; ( 2 ) 支 持计 数 ( count ) ; ( 3 ) 节 点链 ( node 一 link) ， 它指向 FP - tree 中下一个具有相同项 目名的 节点。频繁项 目头表中的每个条 目也包含 3 个域 : ( 1)项目名( item - name) ; (2) 项 目的总支持度计数 (item- count) ; (3)节点链的头指针( head 一 link) ， 指
中 个事 每 务ti(j 二 } - ,n)包含 个 I 2T 一 惟一的 标 事务 识TID和一个项目 子集item set;模式(项集)PCI 被 事务t 所包含， 果pg t;T对P的 如 支持度sup(p,T) 是T 中 包含P 的事务数。 是频繁 p 模式， 如果对于
预先指定的最小支持度阂 m 值 in-sup， 有sup(p,T) ::,
[4] 李光明.Visual C+ + 6.0 经典实例大制作[M .北京: 中 ]
国 事出 社， 人 版 2000.
other techniques such as GDI pr gramming, message pr o o cessing mechanism, windows class，hook, sub-classing and etc . in one word it' s a complex of many technologies.

基于FP树的最大频繁项集挖掘【摘要】频繁项集的挖掘是数据挖掘中的一个基础和核心问题，具有广泛的应用领域。

而频繁项集挖掘可分为完全频繁项集挖掘、频繁闭项集挖掘和最大频繁项集挖掘三类，其中，最大频繁项集的数目最少。

频繁项集的挖掘是一个搜索问题，剪枝优化技术是提高频繁项集挖掘效率的一个重要手段。

对于最大频繁项集的挖掘可以从宽度优先和深度优先两个角度来考虑，而基于FP树的深度优先算法比宽度优先算法扫描数据集的次数要少很多，因此，具有较好的性能。

本文主要分析宽度优先的最大频繁项集挖掘算法和基于FP树的深度优先最大频繁项集挖掘算法。

【关键词】关联规则;频繁项集;最大频繁项集;FP树1.引言数据挖掘技术能从数据库中智能地获取有价值的知识和信息，是人工智能和数据库等多个学科的重要研究内容。

数据挖掘发展到现在，出现了许多技术分支和研究方向。

应用不同的挖掘技术可以从数据库中挖掘出不同类型的知识，根据挖掘出的知识不同的形式，可以把数据挖掘分为通用关联规则挖掘、特征规则挖掘、分类挖掘、聚类挖掘、序列模式分析、时间序列分析、趋势分析和偏差分析等类别。

其中关联规则挖掘及频繁项集的挖掘是数据挖掘研究的核心内容之一，频繁项集的挖掘效果对数据挖掘算法的性能和效率有重要的作用。

关联规则是数据中一种简单规则，这些规则能反映出实际的需求，是大量数据中项集之间相关联系。

关联规则的挖掘算法是无监督学习的方法，其中，频繁项集挖掘是关联规则挖掘的第一步，也是关联规则挖掘的关键步骤，是影响数据挖掘效率的关键问题。

本文主要分析频繁项集与最大频繁项集的概念，然后分析关联规则中的最大频繁项集挖掘的常用算法，并探讨算法的优劣。

2.频繁项集和最大频繁项集关联规则挖掘的主要目的是确定数据集中不同属性之间的联系，从这种联系中找出有价值的多个属性之间的依赖关系，通过这种依赖关系给出决策支持。

关联规则的挖掘可以分成两步来完成。

第一步是按照用户给定的最低阈值，识别出数据集中的所有频繁项目集，第二步是从频繁项目集中构造规则，要求构造的规则的可信度大于等于用户设定的最低值。

NB-MAFIA：基于N-List的最长频繁项集挖掘算法
沈戈晖;刘沛东;邓志鸿
【期刊名称】《北京大学学报：自然科学版》
【年(卷),期】2016(0)2
【摘要】本文在深度优先搜索的框架上,引入基于项集前缀树节点链表的项集表示方法 N-List,提出一个高效的最长频繁项集挖掘算法NB-MAFIA。

N-List的高压缩率和高效的求交集方法可以实现项集支持度的快速计算,同时采用对搜索空间的剪枝策略和超集检测策略来提高算法效率。

在多个真实和仿真数据集上,通过实验评估了NB-MAFIA和两个经典算法。

实验结果表明NB-MAFIA在多数情况下优于其他算法,尤其在真实和稠密数据集上优势更为明显。

【总页数】11页(P199-209)
【关键词】数据挖掘;频繁项集挖掘;最长项集;N-List;算法
【作者】沈戈晖;刘沛东;邓志鸿
【作者单位】北京大学信息科学技术学院计算机科学技术系;北京大学信息科学技术学院智能科学系;北京大学机器感知与智能教育部重点实验室
【正文语种】中文
【中图分类】TP302
【相关文献】
1.基于遗传粒子群算法的频繁项集挖掘算法 [J], 程灿;梁军;张超英
2.一种改进的基于N-List的频繁项集挖掘算法 [J], 翟悦;王璨;孙建言
3.基于Spark框架的大数据局部频繁项集挖掘算法设计 [J], 王黎;吕殿基
4.基于N-list的并行频繁项集挖掘算法 [J], 陈奇;张曦煌
5.采用N-list结构的混合并行频繁项集挖掘算法 [J], 刘卫明;张弛;毛伊敏
因版权原因，仅展示原文概要，查看原文内容请购买。

Apriori算法的改进及实例全文共四篇示例，供读者参考第一篇示例：Apriori算法是一种经典的关联规则挖掘算法，它通过扫描数据集来发现频繁项集，并利用频繁项集生成候选关联规则。

Apriori算法在处理大规模数据集时存在效率低下的问题。

研究者们在Apriori算法的基础上进行了一系列改进，以提高算法的效率和准确性。

本文将对Apriori算法的改进以及实例进行详细探讨。

一、Apriori算法的原理Apriori算法基于频繁项集的概念来挖掘数据中的关联规则。

频繁项集是指在数据集中频繁出现的项的集合，而关联规则是指两个项集之间的关系。

Apriori算法的工作流程大致分为两个步骤：对数据集进行扫描，得出频繁一项集；然后，利用频繁一项集生成候选二项集，再对候选二项集进行扫描，得出频繁二项集；以此类推，直到得出所有频繁项集为止。

1. FP-Growth算法FP-Growth算法是一种基于树形数据结构的频繁项集挖掘算法，它采用了一种称为FP树的紧凑数据结构来表示数据集。

与Apriori算法相比，FP-Growth算法不需要生成候选项集，从而提高了算法的效率。

通过压缩数据集和利用树形结构，FP-Growth算法能够在较短的时间内发现频繁项集，特别适用于大规模数据集的挖掘工作。

2. Eclat算法Eclat算法是一种基于垂直数据格式的频繁项集挖掘算法，它在数据集中以垂直的方式存储交易信息。

Eclat算法通过迭代挖掘的方式，从频繁一项集开始，逐步生成更高阶的频繁项集。

与Apriori算法相比，Eclat算法在挖掘频繁项集时能够更快速地完成工作，并且占用更少的内存空间。

3. 基于采样的改进基于采样的改进方法是一种在大规模数据集上提高Apriori算法效率的有效途径。

该方法通过对原始数据集进行采样，从而减少了算法所需的计算资源和时间。

基于采样的改进方法还能够在一定程度上保证挖掘结果的准确性，因此在实际应用中具有一定的实用性。

（
子集 非频 繁剪枝 （ｕ ｓ ｏ Ｆｅｕｎ ｐ ｒｉ ） 山频繁 项集 的Ｊ Ｓ ｂｅ Ｎ ｎ ｒ ｅ ｔ ｕｎ ｇ ｔ ｑ ｎ是 ｕ ， Ｊ 上闭包性质得来 ，当用户使 用深度优 先策略搜索树时 ，一旦达到某个 节 点ｎ ，就 要对该 结点 尾项集 中每个项 ｘ 汁算 ｓ ｃｕ ｔ ｌ ） （ ｝ ｕ ｏｎ Ｈ（ Ｕ Ｘ） ｐ （ ｎ 的 值 ，如果该值小 于最 低阂埴 ，贝 Ｈ （） ｘ 不是频繁项集 。根据 前面 ０ห้องสมุดไป่ตู้】 ｕ｛ ） ｎ 提到的性质 ，项集Ｈ （ ｕ（ 】 何超集也都不是频繁项集 凶此 ， Ｉ ） ｘ 的任 ｎ 我们可 以在该项 处进行剪枝 （ 该项从尾项 集Ｔ 中去掉 ，从而不产生 将 Ｉ
此 ，没有必要得到含在Ｐｈ ａ 但不包含Ｘ ． ｄ ｅ 的节点 。 此可 以把Ｘ 直接从 Ｐｔｉ 移 至 Ｐｈａ 中 ， 即 ｈａ ＝ ．ｅｄ ｘ ，’ａ ＝ ．ｉ 【 这 ．ｌ ａ中 ．ｅｄ ｅｄ Ｐｈａ １ ｆ ｝ ．ｉ Ｐｔ ｌ ｘ 。 ３ Ｐ ｔｌ ａ 一 Ｊ 样 ，在整个搜索树的扩展过程 ，可以删除部分不必要的计算节点 ，因 为像刚才那样的ｘ 项就不用再进 行扩展了 。 图ｌ 显示了父等价剪枝 的情况 ，从图 中可以看出 ，若ｓｐ ｆ） ｓｐ ｕ（ ） ｕ ａ＝ （ ，）， 以把图 中的节点 【 ，】 ａ ｛，ｄ ） 掉 ，在算法执 行的 （ ｂ） 可 Ａ ｆ ｃ， ， ， Ｃ １ ａ （ｄ ａ ． 剪 Ｊ
｛ ．ｉ Ｐｔ ｌ｛ ） ／ ｊｉ ．ｉ Ｐｔ ｌ ．ｉ ａ ： ／ ：从Ｐ ａ 中删除 ａ＝ ａ 一 ｉ ＃ａ ｔｌ
Ｐ．ｅｄ＝ ．ｅｄ ｉ： ’ ａ Ｐｈａ ｆ ） ｈ Ｕ ａ
ｆ ｒｉ ｔ Ｐ ｔｉｌ ｏ ｏ ＝ｌ ＯＩ ． ｌｄ ａ
（． ａ １ｘ，则表 示任何 包含Ｐｈａ的事务 ，肯 定包含项 Ｘ Ｐｈ ｄ３ ） ｅ ． ｄ ｅ 。也就 是 说，如果一个频繁项集ｚ 包含了Ｐ ｅｄ ． ａ 但是不包含ｘ ｈ ，那么我们 可以判 定ｚＵ｛ ｝ 是一个频繁 项 。由于我们 只需 要得到 最大频繁项 集 ，因 Ｘ也

大数据分析中的关联规则挖掘方法及异常检测技巧摘要：随着大数据时代的到来，大数据的分析与挖掘成为了重要的研究领域。

关联规则挖掘作为其中的一个重要方法，具有广泛的应用前景。

本文将介绍大数据分析中的关联规则挖掘方法，并探讨异常检测技巧在该领域的应用。

1.引言在大数据时代，数据的规模和复杂性呈现爆发式增长，传统的数据分析方法已经无法满足对庞大数据集进行有效分析和挖掘的需求。

关联规则挖掘作为一种有效的数据分析和挖掘方法，可以从大型数据集中发现不同项之间的关联关系，帮助人们理解数据中的规律和特征。

2.关联规则挖掘方法2.1 Apriori算法Apriori算法是一种常用的关联规则挖掘算法。

该算法通过逐层搜索频繁项集，并使用候选项集的剪枝策略，有效减少搜索空间，提高挖掘效率。

它基于以下两个重要概念：支持度和置信度。

支持度表示一个项集在数据集中出现的频率，置信度表示关联规则的可靠性。

Apriori算法的优点是简单易懂，容易实现，但它也存在一些问题，如对内存消耗较大，计算速度较慢等。

2.2 FP-Growth算法FP-Growth算法是一种通过构建FP树来挖掘频繁项集的方法。

FP 树是一种用于存储和表示频繁项集的数据结构，通过压缩数据中的冗余信息，有效地减少存储空间。

FP-Growth算法通过构建FP树，从而避免了Apriori算法中的大量扫描和候选项集的生成过程，提高了挖掘效率。

相比于Apriori算法，FP-Growth算法具有更高的挖掘效率和更低的内存消耗，但对于大型数据集来说，构建FP树可能会占用较大的内存空间。

3.异常检测技巧在关联规则挖掘中的应用异常检测是大数据分析中的一个重要任务，它可以帮助用户发现不符合正常规律的数据点。

在关联规则挖掘中，异常检测可以用于发现不符合最常见规则的项集，并通过对异常项集进行分析，得出新的关联规则。

常见的异常检测技巧包括基于统计的方法、基于机器学习的方法和基于图论的方法。

apriori剪枝的原理理论说明1. 引言1.1 概述本文主要介绍了Apriori剪枝的原理及其在数据挖掘中的应用。

Apriori算法是一种常用的关联规则挖掘算法，它通过寻找频繁项集（即经常出现在数据集中的item组合）来发现数据集中的规律和关联性。

而剪枝作为提高Apriori算法效率的一种方法，通过减少候选项集中无意义和不可能成为频繁项集的候选项，从而减小计算量。

1.2 文章结构本文共分为五个部分进行讨论。

首先，在引言部分对Apriori剪枝的原理进行简要概述，并介绍了文章整体结构。

接着，在第二部分“Apriori剪枝的原理”中，我们将对Apriori算法进行简单介绍，并解释支持度和置信度的概念。

然后，我们将详细阐述Apriori剪枝策略及其实现方式。

在第三部分“理论说明”中，我们将深入解析Apriori剪枝的原理，并介绍基于先验知识的剪枝方法以及剪枝对算法性能的影响。

接下来，在第四部分“应用实例分析”中，我们将选择合适的数据集，并进行数据准备工作。

然后，通过实例演示和结果分析，展示Apriori 剪枝在真实数据集上的应用效果。

最后，在第五部分“结论与展望”中，我们将对全文进行总结，并提出未来进一步研究方向。

1.3 目的本文的目的是帮助读者更好地理解Apriori剪枝的原理及其在数据挖掘中的应用。

通过系统介绍Apriori算法、支持度和置信度的概念以及剪枝策略，读者能够了解Apriori剪枝背后的原理。

同时，通过实例分析和比较评估，读者可以更清晰地认识到剪枝策略对Apriori算法性能的影响。

最终，本文旨在为读者提供一个全面且深入的认识Apriori剪枝方法的指南，并为相关领域研究提供参考依据。

2. Apriori剪枝的原理：2.1 Apriori算法简介：Apriori算法是一种用于数据挖掘中频繁项集挖掘的经典算法。

它基于集合论中的先验知识，通过扫描事务数据库来发现频繁项集，并生成关联规则。