各类边界条件
- 格式:doc
- 大小:317.50 KB
- 文档页数:69

边界条件的类型一、边界条件的类型嘿,小伙伴们!今天咱们来唠唠边界条件的类型这个事儿哈。
那啥是边界条件呢?简单来说,就是在解决一些物理、数学或者工程问题的时候,在研究区域的边界上所需要满足的一些条件啦。
咱先说说第一类边界条件,这也叫狄利克雷边界条件哦。
想象一下,就像是在一个大的区域里面,边界上的值是给定好的。
比如说,在研究热传导问题的时候,在物体的边界上,温度是已经知道的数值,这个数值就像是一个固定的标准,不管里面怎么变,边界上就是这个数,是不是很神奇呢?接着呢,就是第二类边界条件啦,也被称为诺伊曼边界条件。
这个条件就有点不同咯,它规定的不是边界上的值,而是边界上值的变化率。
就好比在流体流动的问题里,在边界上流体的流速的变化率是给定的。
这就像是在一个游戏里,不是告诉你边界上的具体状态,而是告诉你这个状态的变化速度呢。
还有第三类边界条件,这可就更有趣了。
它是前两种边界条件的一种混合形式呢。
比如说在一些热交换的问题里,边界上的热量交换既和边界上的温度有关,也和温度的变化率有关。
这就像是把两个规则混合起来玩一个更复杂的游戏。
然后呢,还有周期性边界条件。
这个在研究一些具有周期性结构的问题里特别有用。
比如说晶体结构,它的边界就像是循环的一样,一边的边界和另一边的边界在某种意义上是一样的。
就像一个无限循环的图案,这边的边界和那边的边界就像双胞胎一样有着相同的性质。
最后呀,还有混合边界条件。
这个就比较复杂啦,它是把好几种不同的规则组合在一起,根据具体的问题来设定边界上的各种条件。
就像是一个超级复杂的拼图,每一块都有自己的规则,但是组合起来就能解决那些特别难搞的问题。
哈哈,边界条件的类型是不是很有趣呢?它们就像是一把把钥匙,能帮我们打开解决各种问题的大门哦。

fluent中边界条件的类型Fluent中边界条件的类型在Fluent中,边界条件是指在仿真模拟过程中,用于限定模型的边界或区域范围的条件。
这些边界条件的设置对于模拟结果的准确性和可靠性具有重要作用。
在Fluent中,常见的边界条件类型包括:入口边界条件、出口边界条件、壁面边界条件、对称边界条件和周期性边界条件。
一、入口边界条件入口边界条件是指流体进入仿真模型的边界条件。
在Fluent中,常见的入口边界条件类型有:速度入口、质量流入口和压力入口。
速度入口边界条件是通过指定流体的速度矢量来定义的,可以根据实际情况指定不同方向的速度分量。
质量流入口边界条件是通过指定流体的质量流率来定义的,常用于气体或液体进入模型的情况。
压力入口边界条件是通过指定流体的压力值来定义的,适用于流体进入模型时压力已知的情况。
二、出口边界条件出口边界条件是指流体离开仿真模型的边界条件。
在Fluent中,常见的出口边界条件类型有:压力出口和速度出口。
压力出口边界条件是通过指定流体的压力值来定义的,适用于流体离开模型时压力已知的情况。
速度出口边界条件是通过指定流体的速度矢量来定义的,可以根据实际情况指定不同方向的速度分量。
三、壁面边界条件壁面边界条件是指模型中的实体表面,通过设置壁面边界条件来模拟流体与实体表面的相互作用。
在Fluent中,常见的壁面边界条件类型有:壁面摩擦和壁面热传导。
壁面摩擦边界条件用于模拟流体与实体表面间的摩擦作用,可以通过设置壁面摩擦系数来定义。
壁面热传导边界条件用于模拟流体与实体表面间的热传导作用,可以通过设置壁面热传导系数来定义。
四、对称边界条件对称边界条件是指模型中的对称面,通过设置对称边界条件来模拟流体在对称面上的行为。
在Fluent中,常见的对称边界条件类型有:对称面和对称压力。
对称面边界条件要求流体在对称面上的速度和温度分量与对称面的法向分量相等。
对称压力边界条件要求流体在对称面上的压力与对称面的压力相等。

定义边界条件概述边界条件包括流动变量和热变量在边界处的值。
它是FLUENT分析得很关键的一部分,设定边界条件必须小心谨慎。
边界条件的分类:进出口边界条件:压力、速度、质量进口、进风口、进气扇、压力出口、压力远场边界条件、质量出口、通风口、排气扇;壁面、repeating, and pole boundaries:壁面,对称,周期,轴;内部单元区域:流体、固体(多孔是一种流动区域类型) ;内部表面边界:风扇、散热器、多孔跳跃、壁面、内部。
(内部表面边界条件定义在单元表面,这意味着它们没有有限厚度,并提供了流场性质的每一步的变化。
这些边界条件用来补充描述排气扇、细孔薄膜以及散热器的物理模型。
内部表面区域的内部类型不需要你输入任何东西。
)下面一节将详细介绍上面所叙述边界条件,并详细介绍了它们的设定方法以及设定的具体合适条件。
周期性边界条件在本章中介绍,模拟完全发展的周期性流动将在周期性流动和热传导一章中介绍。
使用边界条件面板边界条件(Figure 1)对于特定边界允许你改变边界条件区域类型,并且打开其他的面板以设定每一区域的边界条件参数菜单:Define/Boundary Conditions...Figure 1: 边界条件面板改变边界区域类型设定任何边界条件之前,必须检查所有边界区域的区域类型,如有必要就作适当的修改。
比方说:如果你的网格是压力入口,但是你想要使用速度入口,你就要把压力入口改为速度入口之后再设定。
改变类型的步骤如下::1.在区域下拉列表中选定所要修改的区域2.在类型列表中选择正确的区域类型3.当问题提示菜单出现时,点击确认确认改变之后,区域类型将会改变,名字也将自动改变(如果初始名字时缺省的请参阅边界条件区域名字一节),设定区域边界条件的面板也将自动打开。
!注意:这个方法不能用于改变周期性类型,因为该边界类型已经存在了附加限制。
创建边界条件一节解释了如何创建和分开周期性区域。
需要注意的是,只能在图一中每一个类别中改变边界类型(注意:双边区域表面是分离的不同单元区域.)Figure 1: 区域类型的分类列表设定边界条件在FLUENT中,边界条件和区域有关而与个别表面或者单元无关。

导热问题的三类边界条件
第一类边界条件(或称为Dirichlet边界条件):指定了系统中某些区域的温度或者某些点的温度值。
例如,一个金属板的两端分别与不同温度的热源接触,可以指定板的两端温度分别为T1和T2,这便是一个第一类边界条件。
第二类边界条件(或称为Neumann边界条件):指定了系统中某些区域的热流量或者某些点的热流密度值。
例如,在一个金属板表面,可以指定表面的热流密度为q,这便是一个第二类边界条件。
第三类边界条件(或称为Robin边界条件):又称混合边界条件,指定了系统某些区域的温度和热流量之间的关系。
例如,一个金属板表面受到风的吹拂而产生冷却,这个过程既受到金属板表面温度的影响,也受到风速的影响,因此需要同时考虑温度和热流量。
这便是一个第三类边界条件。
这三类边界条件是导热问题求解中非常重要的概念,也是理解和解决导热问题的基础。

Fluent技巧边界条件定义边界条件概述边界条件包括流动变量和热变量在边界处的值。
它是FLUENT分析得很关键的一部分,设定边界条件必须小心谨慎。
边界条件的分类:进出口边界条件:压力、速度、质量进口、进风口、进气扇、压力出口、压力远场边界条件、质量出口、通风口、排气扇;壁面、repeating, and pole boundaries:壁面,对称,周期,轴;内部单元区域:流体、固体(多孔是一种流动区域类型) ;内部表面边界:风扇、散热器、多孔跳跃、壁面、内部。
(内部表面边界条件定义在单元表面,这意味着它们没有有限厚度,并提供了流场性质的每一步的变化。
这些边界条件用来补充描述排气扇、细孔薄膜以及散热器的物理模型。
内部表面区域的内部类型不需要你输入任何东西。
)下面一节将详细介绍上面所叙述边界条件,并详细介绍了它们的设定方法以及设定的具体合适条件。
周期性边界条件在本章中介绍,模拟完全发展的周期性流动将在周期性流动和热传导一章中介绍。
使用边界条件面板边界条件(Figure 1)对于特定边界允许你改变边界条件区域类型,并且打开其他的面板以设定每一区域的边界条件参数菜单:Define/Boundary Conditions...Figure 1: 边界条件面板改变边界区域类型设定任何边界条件之前,必须检查所有边界区域的区域类型,如有必要就作适当的修改。
比方说:如果你的网格是压力入口,但是你想要使用速度入口,你就要把压力入口改为速度入口之后再设定。
改变类型的步骤如下::1.在区域下拉列表中选定所要修改的区域2.在类型列表中选择正确的区域类型3.当问题提示菜单出现时,点击确认确认改变之后,区域类型将会改变,名字也将自动改变 (如果初始名字时缺省的请参阅边界条件区域名字一节),设定区域边界条件的面板也将自动打开。
!注意:这个方法不能用于改变周期性类型,因为该边界类型已经存在了附加限制。
创建边界条件一节解释了如何创建和分开周期性区域。


有限元4类边界条件有限元方法是一种重要的工程分析方法,通常用于求解结构的应力、变形、振动等问题。
在有限元分析中,边界条件是非常重要的,它直接影响到分析结果的准确性和可靠性。
在本文中,我们将介绍四类常见的边界条件:位移边界条件、力边界条件、自由边界条件和周期边界条件。
一、位移边界条件位移边界条件是最常见的边界条件之一,通常用于限定结构的位移或变形。
在有限元分析中,位移边界条件可以分为以下两种情况:1.固定边界条件:在这种情况下,结构的某些部分被固定,禁止其发生位移或变形。
例如,固定梁端的边界条件可以表示为:u(x=0)=0,其中u为梁的位移。
2.位移边界条件:在这种情况下,结构的某些部分需要满足一定的位移或变形。
例如,梁的支座边界条件可以表示为:u(x=L)=u0,其中u0为支座的位移。
二、力边界条件力边界条件是指在有限元分析中,结构受到一定的外力作用。
力边界条件可以分为以下两种情况:1.集中力边界条件:在这种情况下,结构的某些部分受到集中的力。
例如,悬臂梁的端部受到集中力的边界条件可以表示为:F(x=L)=F0,其中F0为集中力的大小。
2.分布力边界条件:在这种情况下,结构的某些部分受到分布的力。
例如,梁受到均布载荷的边界条件可以表示为:q(x)=q0,其中q0为载荷的大小。
三、自由边界条件自由边界条件是指在有限元分析中,结构某些部分不受任何边界条件的限制。
例如,在轴对称模型中,通常假设模型的顶部和底部为自由边界条件。
四、周期边界条件周期边界条件是指在有限元分析中,结构的某些部分需要满足周期性的限制条件。
例如,在周期性结构中,周期边界条件可以表示为:u(0,t)=u(L,t),其中u表示结构的位移。
边界条件在有限元分析中起着非常重要的作用。
通过合理的选择和使用边界条件,可以获得准确、可靠的分析结果。
在实际工程应用中,需要根据具体的问题和分析要求选择合适的边界条件,以确保分析结果的正确性和可靠性。

一.边界条件(Boundry Conditions)1.理想电边界(Perfect-E)理想电边界即理想电导体边界.电荷可在其中自由移动.边界内电场为0,边界上可存在面电荷,面电流,从而使外界电场分量垂直与边界,磁场方向平行与边界. 在HFSS design中任何与背景相邻接的部分会被默认为Perfect-E边界(outer)对于矩形波导,若将波导终端端面设置为Perfect-E, 由于波导内电场平行于端面,在边界处被置0,即入射波与反射波在端面处摸值相等,相位相反,叠加为0,由于电压V是对电场强度的积分,因为边界处电场强度为0,则端面处电压为0,相当于终端短路(阻抗值Z=0,在阻抗圆图上表示短路点),VSWR趋于无穷大.(反射系数为1)H模截止频率为以下是对这一过程的仿真,其中矩形波导a=1.5mm, b=1mm,10λ=4.52267mm.取波导长度为100Ghz 取f=120Ghz 满足单模传输。
gλ,将端面设置为Perfect-E 进行测试。
18.09068mm=4*g图1-1 矩形波导主模传输终端设为Perfect-E时电场分布从图1-1可见在端面处电场切向方向为0,电场垂直于端面图1-2矩形波导主模传输终端设为Perfect-E时输入端Smith Chart可见负载端阻抗接近于开路。
L=1/4*g2.理想磁边界(Perfect-H)理想磁边界即理想磁导体,用电磁场理论中的磁荷模型进行分析即磁荷可以在理想磁导体自由移动,理想磁导体中磁场为0,边界上可聚集面磁荷,面磁流,从而使磁场方向垂直于边界。
电场方向与边界相切。
对应于矩形波导终端Perfect-H边界使得磁场垂直于边界,置切向磁场为0,由于电流Z趋向于是切向磁场的积分,故边界使电流为0,而切向电场存在,负载处电压不为0。
故L无穷,VSWR趋向于无穷,相当于终端开路。
以下是对这一过程仿真。
波导参数与上例中完全相同。
端面边界设置为Perfect-H.从图2-1中可看出端面处磁场垂直于端面,切向磁场分量为0。

材料力学边界条件边界条件在材料力学中起到非常重要的作用,它们是物理现象或力学问题的解决方案的关键要素之一、边界条件确定了在研究区域边界上发生的物理过程和影响。
在材料力学中,常见的边界条件包括:1.位移边界条件:位移边界条件是指物体在边界上的位移情况。
常见的位移边界条件有固定边界条件、自由边界条件和摩擦边界条件等。
固定边界条件是指物体在其中一边界上的位移被限制为零,即该边界上的点不能发生位移。
自由边界条件是指物体在其中一边界上的位移没有任何限制,即该边界上的点可以自由运动。
摩擦边界条件是指物体在其中一边界上的位移受到边界面上的摩擦力所限制。
2.力边界条件:力边界条件是指物体在边界上受到的外力情况。
常见的力边界条件有固定力边界条件和自由力边界条件等。
固定力边界条件是指物体在其中一边界上受到的外力为零,即该边界上没有外力作用。
自由力边界条件是指物体在其中一边界上受到的外力没有任何限制,即该边界上的外力可以自由作用。
3.应力边界条件:应力边界条件是指物体在边界上的应力情况。
常见的应力边界条件有固定应力边界条件和自由应力边界条件等。
固定应力边界条件是指物体在其中一边界上的应力被固定为其中一个值,即该边界上的应力受到限制。
自由应力边界条件是指物体在其中一边界上的应力没有任何限制,即该边界上的应力可以自由变化。
边界条件的选择需要根据具体问题的要求和实际情况进行确定。
通常情况下,边界条件需要满足力学平衡条件、位移连续条件和应力连续条件等。
同时,边界条件的选择也需要考虑到物体的边界特性,比如是否有固定边界、自由边界或者摩擦边界等。
边界条件的正确选择对于力学问题的解决至关重要。
不恰当的边界条件会导致计算结果的不准确甚至错误。
因此,在进行模拟和计算时,需要仔细分析和确定边界条件,并考虑到实际问题的特点和要求。
总之,材料力学边界条件是研究区域边界上发生的物理过程和影响的要素,其正确选择对于解决力学问题具有重要作用。
在选择边界条件时,需要考虑到力学平衡、位移连续和应力连续等方面,以获得准确的计算结果。

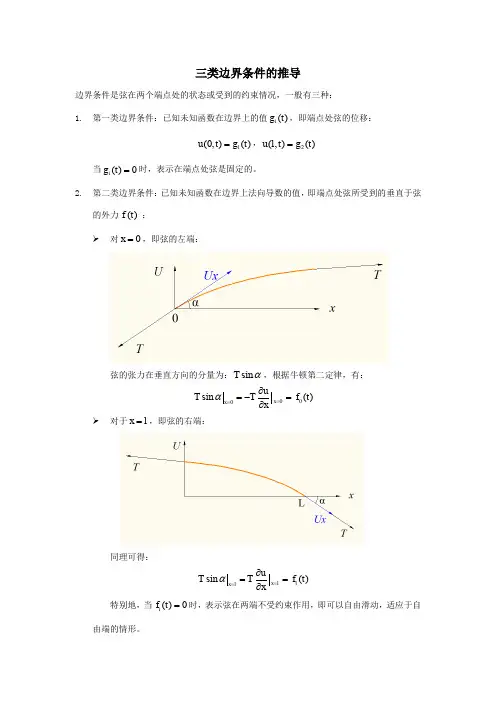
数学物理方法三类边界条件
在数学物理中,常常会遇到需要考虑边界条件的问题。
根据不同的情况,可以将数学物理方法中的边界条件分为三类,第一类边界条件、第二类边界条件和第三类边界条件。
1. 第一类边界条件(Dirichlet边界条件):
第一类边界条件是指在边界上给定了物理量的具体值。
例如,在一个热传导问题中,可以给定边界上的温度值。
在一个波动方程中,可以给定边界上的振幅值。
这类边界条件可以用数学上的等式或函数来表示。
2. 第二类边界条件(Neumann边界条件):
第二类边界条件是指在边界上给定了物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度(即温度梯度)。
在一个波动方程中,可以给定边界上的振幅的导数。
这类边界条件可以用数学上的导数来表示。
3. 第三类边界条件(Robin边界条件):
第三类边界条件是指在边界上给定了物理量的线性组合,其中既包括物理量的值,也包括物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度和温度的线性组合。
这类边界条件可以用数学上的线性组合来表示。
需要注意的是,以上分类只是一种常见的方式,具体问题中的边界条件可能会有其他形式。
此外,边界条件的选择和应用也取决于所研究的具体物理问题和数学模型。
在实际问题中,根据边界条件的具体形式,可以选择合适的数学方法和技巧来求解。
边界条件类型5.1 惯性边界条件5.1.1 加速度1.简介加速度以长度比上时间的平方为单位作用在整个模型上。
由于加速度施加到系统上,惯性将阻止加速度所产生的变化,因此惯性力的方向与所施加的加速度的方向相反。
加速度可以通过定义部件或者矢量进行施加。
该边界条件支持显示动力学分析,谐响应分析,刚体动力学分析,静态结构分析和瞬态结构动力学分析。
该边界条件支持二维模型和三维模型,并且支持矢量和分量定义。
2.定义方法在支持的求解环境中,右击求解类型,选择Insert>Acceleration,则在细窗口出现定义加速度设置面板,该面板包括两个选项:模型范围选择(Scope)和定义方法(Definition)。
(1)范围选择对于该边界条件条件,程序会默认的选择所有模型,并且不能进行人工选择。
(2)定义方法1)矢量定义将Define By设置为Vector,则细节窗口出现如图5-1所示的定义加速度矢量设置面板,用户需要输入加速度的幅值(Magnitude)和指定加速度的方向(Direction),通过拾取模型的表面来定义方向。
图5-1 定义加速度矢量设置面板2)分量定义将Define By设置为Components,则细节窗口出现如图5-2所示的定义加速度分量设置面板,用户需要选择坐标系(Coordinate System)和输入三个方向的幅值。
简明教程• 2 •图5-2 定义加速度分量设置面板5.1.2 标准的地球重力1.简介可以作为一个载荷施加。
其值为9.80665 m/s2 (在国际单位制中),标准的地球重力载荷方向可以沿总体坐标轴的任何一个轴。
不需要定义与其实际相反的方向得到重力的作用力。
该边界条件适用于显示动力学,刚体动力学,静力学分析和瞬态结构动力学分析的二维或三维模型。
2.定义方法在支持的求解环境中,右击求解类型,选择Insert>Standard Earth Gravity,则在细窗口出现如图5-3所示的定义重力加速度设置面板,该面板包括两个选项:模型范围选择(Scope)和定义方法(Definition)。
流体力学三类边界条件
流体力学作为力学的一个重要分支,研究的是流体在运动中的力学性质。
在流体运动过程中,存在着三类不同的边界条件,分别是壁面边界条件、开放边界条件和封闭边界条件。
壁面边界条件是指流体与固体壁面接触时的边界条件。
在这种情况下,流体的速度与固体壁面的速度相同,并且流体的法向速度分量为零。
这意味着流体在与固体壁面接触时会发生粘滞效应,使得流体在壁面附近的速度较低,流线较为密集。
这种边界条件在实际工程应用中非常常见,例如在管道内部流体运动中,壁面边界条件对流体的流动状态有着重要影响。
开放边界条件是指流体与自由表面接触时的边界条件。
在这种情况下,流体在自由表面处的法向速度分量为零,且流体的速度与自由表面的速度相同。
这种边界条件通常用于研究液体在自由表面上的运动,例如瀑布的水流、湖泊中的波浪等。
开放边界条件的研究对于水文学、海洋学等领域具有重要意义。
封闭边界条件是指流体在封闭容器内部流动时的边界条件。
在这种情况下,流体与容器壁面接触时的速度分量为零,且流体在容器内部流动时受到容器壁面的约束。
封闭边界条件在工程实践中也是十分常见的,例如在液压系统中液体在管道内部的流动、气体在容器内部的压缩等。
封闭边界条件的研究有助于优化系统设计,提高系统效率。
流体力学中的三类边界条件分别是壁面边界条件、开放边界条件和封闭边界条件。
这些边界条件在不同的流体运动场景中发挥着重要作用,对于工程实践和科学研究具有重要意义。
通过深入研究和理解这些边界条件,可以更好地掌握流体运动规律,为工程设计和科学研究提供有效的理论支持。
传热学三类边界条件公式热力学第一定律指出:热量是一种不可摧毁的能量形式,只能从一处转移到另一处,不可能消失也不可能自行产生。
在热传导、对流、辐射等传热方式中,边界条件关系到传热效率的高低。
按照边界条件的不同,传热学分为三类:第一类边界条件、第二类边界条件以及第三类边界条件。
第一类边界条件第一类边界条件又称为Dirichlet 边界条件,其中边界的温度值保持不变。
在一维传热的情况下,边界条件通常设定为温度值在 $x=0$ 和$x=L$ 处分别为 $T_0$ 和 $T_L$ 。
在这种情况下,温度分布可以表示为如下式子:$$T=T_0+\frac{T_L-T_0}{L}x$$由此式子可知,第一类边界条件下的温度分布是线性的。
这类边界条件应用于一些特殊装置的分析中,如热插入的分析。
第二类边界条件第二类边界条件又称为Neumann边界条件,其中边界的热通量值保持不变。
在一维传热的情况下,设定一端的热通量为 $q_0$ ,另一端的热通量为 $q_L$ 。
这类边界条件通常应用于热轧、淬火、熔炼等过程中的热传导分析。
设定 $q_0$ 时,温度分布可以表示为如下式子:$$T(x)=\frac{q_0}{2k}x^2+\frac{T_0-T_L}{L}x+T_L$$在这里, $k$ 是热导率, $T_0$ 是 $x=0$ 时的温度值, $T_L$ 是$x=L$ 时的温度值。
同样地,设定 $q_L$ 得到的温度分布式子与此类似。
在对流传热分析中,常常将这类边界条件与热对流导致的边界传热耦合在一起。
例如,在车厢内部空气对容器表面的冷凝现象中,汽车内部环境的温度分布会被相应的表面冷凝热通量所影响。
第三类边界条件第三类边界条件又称为Robin边界条件,可以用于热通量或温度的同时指定边界条件。
这种类型的边界条件可应用于实际问题中,比如计算机芯片和半导体器件中的散热、热泵等。
自然对流中的平板,把温度和热通量应用于Robin边界条件,可以得到如下式子:$$h(T(x)-T_\infty)=-k\frac{dT}{dx}\bigg|_{x=0}$$其中, $h$ 是热传递系数, $T_\infty$ 是远离边界的环境温度。
电磁场三类边界条件电磁场三类边界条件电磁场的边界条件是指在介质边界处,电场和磁场的变化情况。
根据边界条件的不同,可以将其分为三类:第一类边界条件、第二类边界条件和第三类边界条件。
下面将详细介绍这三类边界条件。
一、第一类边界条件第一类边界条件也称为零法向电场和零切向磁场边界条件。
它是指在介质表面上,法向于表面的电场强度和切向于表面的磁感应强度均为零。
1. 零法向电场在介质表面上,由于介质内部和外部存在不同的电荷分布情况,因此会产生一个法向于表面方向的电场。
而当这个电场穿过介质表面时,就会发生反射和折射现象。
为了描述这种现象,我们需要引入一个重要的物理量——法向于表面方向上的电通量密度。
根据高斯定理可知,在任意一个闭合曲面内部,通过该曲面的总电通量等于该曲面所包围空间内部所有自由电荷之代数和。
因此,在介质表面附近,我们可以将其看作一个微小的闭合曲面。
则在该曲面上的电通量密度可以表示为:$$\vec{D_1}\cdot\vec{n}=\rho_s$$其中,$\vec{D_1}$表示介质1内部的电位移矢量,$\vec{n}$表示介质表面法向矢量,$\rho_s$表示表面自由电荷密度。
当我们将这个式子应用于介质表面时,可以得到:$$D_{1n}=\rho_s$$其中,$D_{1n}$表示介质1内部法向于表面方向上的电场强度。
由于介质表面上不存在自由电荷,因此$\rho_s=0$。
因此,在第一类边界条件下,法向于介质表面方向上的电场强度为零。
2. 零切向磁场在介质表面上,由于介质内部和外部存在不同的磁场分布情况,因此会产生一个切向于表面方向的磁感应强度。
而当这个磁场穿过介质表面时,就会发生反射和折射现象。
为了描述这种现象,我们需要引入一个重要的物理量——切向于表面方向上的磁通量密度。
根据安培环路定理可知,在任意一个闭合回路上,通过该回路的总磁通量等于该回路所包围空间内部所有电流之代数和。
因此,在介质表面附近,我们可以将其看作一个微小的闭合回路。
力学边界条件类型一、力学边界条件类型有哪些呢?(一)固定边界条件这就好比把东西死死地钉在那儿一样。
比如说,一根柱子插在地上,它底部的边界就是固定的,不能移动也不能转动。
在很多建筑结构里,像高楼大厦的地基部分,就会有这种类似的固定边界情况。
就像是一个超级固执的家伙,坚决不让步。
(二)简支边界条件想象一下,一个梁架在两个支座上,支座只提供竖向的支撑力,梁可以在这个支撑上自由转动。
就像跷跷板一样,中间有个支撑点,两边可以上下晃悠。
这种边界条件在一些桥梁结构的设计中经常会用到呢。
(三)滑动边界条件这就像是在冰面上滑动的物体,它只能沿着某个方向滑动,其他方向的运动是被限制的。
比如一些机械结构里,有滑块在导轨上滑动的情况,滑块的边界就是滑动边界条件。
(四)弹性边界条件这个就有点复杂啦。
就像是一个弹簧连接着物体,物体在边界上会受到一个与位移成比例的力。
就好像物体被一个有弹性的东西拉扯着,动一下就会有相应的拉力或者推力回来。
在一些地质结构的分析中,岩石和土壤之间的相互作用有时候就可以用弹性边界条件来近似模拟。
(五)自由边界条件这是最自由的啦,没有任何约束。
就像在空中飞行的小鸟,没有东西限制它的边界。
在一些有限元分析中,如果我们只关注物体内部的力学情况,而把物体的边缘当作自由边界,就可以简化计算呢。
(六)对称边界条件这种边界条件是利用结构的对称性来简化分析的。
比如说一个圆形的盘子,如果它受到的力也是对称分布的,我们就可以只分析它的一部分,然后利用对称边界条件得到整个盘子的力学情况。
这就像是照镜子一样,一边的情况可以反映出另一边的情况。
(七)反对称边界条件和对称边界条件有点相反。
如果结构有反对称的特性,那么在边界上就会有反对称的约束。
比如一个结构关于某个轴对称,但是受到的力是反对称的,那么在对称轴上就会有反对称边界条件。
(八)周期性边界条件这种边界条件常见于一些具有周期性结构的物体。
比如说晶体结构,它的原子排列是有周期性的。
定义边界条件概述边界条件包括流动变量和热变量在边界处的值。
它是FLUENT分析得很关键的一部分,设定边界条件必须小心谨慎。
边界条件的分类:进出口边界条件:压力、速度、质量进口、进风口、进气扇、压力出口、压力远场边界条件、质量出口、通风口、排气扇;壁面、repeating, and pole boundaries:壁面,对称,周期,轴;内部单元区域:流体、固体(多孔是一种流动区域类型) ;内部表面边界:风扇、散热器、多孔跳跃、壁面、内部。
(内部表面边界条件定义在单元表面,这意味着它们没有有限厚度,并提供了流场性质的每一步的变化。
这些边界条件用来补充描述排气扇、细孔薄膜以及散热器的物理模型。
内部表面区域的内部类型不需要你输入任何东西。
)下面一节将详细介绍上面所叙述边界条件,并详细介绍了它们的设定方法以及设定的具体合适条件。
周期性边界条件在本章中介绍,模拟完全发展的周期性流动将在周期性流动和热传导一章中介绍。
使用边界条件面板边界条件(Figure 1)对于特定边界允许你改变边界条件区域类型,并且打开其他的面板以设定每一区域的边界条件参数菜单:Define/Boundary Conditions...Figure 1: 边界条件面板改变边界区域类型设定任何边界条件之前,必须检查所有边界区域的区域类型,如有必要就作适当的修改。
比方说:如果你的网格是压力入口,但是你想要使用速度入口,你就要把压力入口改为速度入口之后再设定。
改变类型的步骤如下::1.在区域下拉列表中选定所要修改的区域2.在类型列表中选择正确的区域类型3.当问题提示菜单出现时,点击确认确认改变之后,区域类型将会改变,名字也将自动改变(如果初始名字时缺省的请参阅边界条件区域名字一节),设定区域边界条件的面板也将自动打开。
!注意:这个方法不能用于改变周期性类型,因为该边界类型已经存在了附加限制。
创建边界条件一节解释了如何创建和分开周期性区域。
需要注意的是,只能在图一中每一个类别中改变边界类型(注意:双边区域表面是分离的不同单元区域.)Figure 1: 区域类型的分类列表设定边界条件在FLUENT中,边界条件和区域有关而与个别表面或者单元无关。
如果要结合具有相同边界条件的两个或更多区域请参阅合并区域一节。
设定每一特定区域的边界条件,请遵循下面的步骤:1.在边界条件区域的下拉列表中选择区域。
2. 点击Set...按钮。
或者,1.在区域下拉列表中选择区域。
2.在类型列表中点击所要选择的类型。
或者在区域列表中双击所需区域.,选择边界条件区域将会打开,并且你可以指定适当的边界条件在图像显示方面选择边界区域在边界条件中不论你合适需要选择区域,你都能用鼠标在图形窗口选择适当的区域。
如果你是第一次设定问题这一功能尤其有用,如果你有两个或者更多的具有相同类型的区域而且你想要确定区域的标号(也就是画出哪一区域是哪个)这一功能也很有用。
要使用该功能请按下述步骤做:1.用网格显示面板显示网格。
2.用鼠标指针(默认是鼠标右键--参阅控制鼠标键函数以改变鼠标键的功能)在图形窗口中点击边界区域。
在图形显示中选择的区域将会自动被选入在边界条件面板中的区域列表中,它的名字和编号也会自动在控制窗口中显示改变边界条件名字每一边界的名字是它的类型加标号数(比如pressure-inlet-7)。
在某些情况下你可能想要对边界区域分配更多的描述名。
如果你有两个压力入口区域,比方说,你可能想重名名它们为small-inlet和large-inlet。
(改变边界的名字不会改变相应的类型)重名名区域,遵循如下步骤:1.在边界条件的区域下拉列表选择所要重名名的区域。
2.点击Set...打开所选区域的面板。
3.在区域名字中输入新的名字4.点击OK按钮。
注意:如果你指定区域的新名字然后改变它的类型,你所改的名字将会被保留,如果区域名字是类型加标号,名字将会自动改变。
边界条件的非一致输入每一类型的边界区域的大多数条件定义为轮廓函数而不是常值。
你可以使用外部产生的边界轮廓文件的轮廓,或者用自定义函数(UDF)来创建。
具体情况清参阅相关内容流动入口和出口FLUENT有很多的边界条件允许流动进入或者流出解域。
下面一节描述了每一种边界条件的类型的使用以及所需要的信息,这样就帮助你适当的选择边界条件。
下面还提供了湍流参数的入口值的确定方法。
使用流动边界条件下面对流动边界条件的使用作一概述对于流动的出入口,FLUENT提供了十种边界单元类型:速度入口、压力入口、质量入口、压力出口、压力远场、质量出口,进风口,进气扇,出风口以及排气扇。
下面是FLUENT中的进出口边界条件选项:l 速度入口边界条件用于定义流动入口边界的速度和标量l 压力入口边界条件用来定义流动入口边界的总压和其它标量。
l 质量流动入口边界条件用于可压流规定入口的质量流速。
在不可压流中不必指定入口的质量流,因为当密度是常数时,速度入口边界条件就确定了质量流条件。
l 压力出口边界条件用于定义流动出口的静压(在回流中还包括其它的标量)。
当出现回流时,使用压力出口边界条件来代替质量出口条件常常有更好的收敛速度。
l 压力远场条件用于模拟无穷远处的自由可压流动,该流动的自由流马赫数以及静态条件已经指定了。
这一边界类型只用于可压流。
l 质量出口边界条件用于在解决流动问题之前,所模拟的流动出口的流速和压力的详细情况还未知的情况。
在流动出口是完全发展的时候这一条件是适合的,这是因为质量出口边界条件假定出了压力之外的所有流动变量正法向梯度为零。
对于可压流计算,这一条件是不适合的。
l 进风口边界条件用于模拟具有指定的损失系数,流动方向以及周围(入口)环境总压和总温的进风口。
l 进气扇边界条件用于模拟外部进气扇,它具有指定的压力跳跃,流动方向以及周围(进口)总压和总温。
l 通风口边界条件用于模拟通风口,它具有指定的损失系数以及周围环境(排放处)的静压和静温。
l 排气扇边界条件用于模拟外部排气扇,它具有指定的压力跳跃以及周围环境(排放处)的静压。
决定湍流参数在入口、出口或远场边界流入流域的流动,FLUENT需要指定输运标量的值。
本节描述了对于特定模型需要哪些量,并且该如何指定它们。
也为确定流入边界值最为合适的方法提供了指导方针。
使用轮廓指定湍流参量在入口处要准确的描述边界层和完全发展的湍流流动,你应该通过实验数据和经验公式创建边界轮廓文件来完美的设定湍流量。
如果你有轮廓的分析描述而不是数据点,你也可以用这个分析描述来创建边界轮廓文件,或者创建用户自定义函数来提供入口边界的信息。
一旦你创建了轮廓函数,你就可以使用如下的方法:l Spalart-Allmaras模型:在湍流指定方法下拉菜单中指定湍流粘性比,并在在湍流粘性比之后的下拉菜单中选择适当的轮廓名。
通过将m_t/m和密度与分子粘性的适当结合,FLUENT为修改后的湍流粘性计算边界值。
l k-e模型:在湍流指定方法下拉菜单中选择K和Epsilon并在湍动能(Turb. Kinetic Energy)和湍流扩散速度(Turb. Dissipation Rate)之后的下拉菜单中选择适当的轮廓名。
l 雷诺应力模型:在湍流指定方法下拉菜单中选择K和Epsilon并在湍动能(Turb. Kinetic Energy)和湍流扩散速度(Turb. Dissipation Rate)之后的下拉菜单中选择适当的轮廓名。
在湍流指定方法下拉菜单中选择雷诺应力部分,并在每一个单独的雷诺应力部分之后的下拉菜单中选择适当的轮廓名。
湍流量的统一说明在某些情况下流动流入开始时,将边界处的所有湍流量指定为统一值是适当的。
比如说,在进入管道的流体,远场边界,甚至完全发展的管流中,湍流量的精确轮廓是未知的。
在大多数湍流流动中,湍流的更高层次产生于边界层而不是流动边界进入流域的地方,因此这就导致了计算结果对流入边界值相对来说不敏感。
然而必须注意的是要保证边界值不是非物理边界。
非物理边界会导致你的解不准确或者不收敛。
对于外部流来说这一特点尤其突出,如果自由流的有效粘性系数具有非物理性的大值,边界层就会找不到了。
你可以在使用轮廓指定湍流量一节中描述的湍流指定方法,来输入同一数值取代轮廓。
你也可以选择用更为方便的量来指定湍流量,如湍流强度,湍流粘性比,水力直径以及湍流特征尺度,下面将会对这些内容作一详细叙述。
湍流强度I定义为相对于平均速度u_avg的脉动速度u^'的均方根。
小于或等于1%的湍流强度通常被认为低强度湍流,大于10%被认为是高强度湍流。
从外界,测量数据的入口边界,你可以很好的估计湍流强度。
例如:如果你模拟风洞试验,自由流的湍流强度通常可以从风洞指标中得到。
在现代低湍流风洞中自由流湍流强度通常低到0.05%。
.对于内部流动,入口的湍流强度完全依赖于上游流动的历史,如果上游流动没有完全发展或者没有被扰动,你就可以使用低湍流强度。
如果流动完全发展,湍流强度可能就达到了百分之几。
完全发展的管流的核心的湍流强度可以用下面的经验公式计算:例如,在雷诺数为50000是湍流强度为4%湍流尺度l是和携带湍流能量的大涡的尺度有关的物理量。
在完全发展的管流中,l被管道的尺寸所限制,因为大涡不能大于管道的尺寸。
L和管的物理尺寸之间的计算关系如下:其中L为管道的相关尺寸。
因子0.07是基于完全发展湍流流动混合长度的最大值的,对于非圆形截面的管道,你可以用水力学直径取代L。
如果湍流的产生是由于管道中的障碍物等特征,你最好用该特征长度作为湍流长度L而不是用管道尺寸。
注意:公式并不是适用于所有的情况。
它只是在大多数情况下得很好的近似。
对于特定流动,选择L和l的原则如下:l 对于完全发展的内部流动,选择强度和水力学直径指定方法,并在水力学直径流场中指定L=D_H。
l 对于旋转叶片的下游流动,穿孔圆盘等,选择强度和水力学直径指定方法,并在水力学直径流场中指定流动的特征长度为Ll 对于壁面限制的流动,入口流动包含了湍流边界层。
选择湍流强度和长度尺度方法并使用边界层厚度d_99来计算湍流长度尺度l,在湍流长度尺度流场中输入l=0.4 d_99这个值湍流粘性比m_t/m直接与湍流雷诺数成比例(Re_t ?k^2/(e n))。
Re_t在高湍流数的边界层,剪切层和完全发展的管流中是较大的(100到1000)。
然而,在大多数外流的自由流边界层中m_t/m相当的小。
湍流参数的典型设定为1<m_t/m <10。
要根据湍流粘性比来指定量,你可以选择湍流粘性比(对于Spalart-Allmaras模型)或者强度和粘性比(对于k-e模型或者RSM)。
推导湍流量的关系式要获得更方便的湍流量的输运值,如:I, L,或者m_t/m,你必须求助于经验公式,下面是FLUENT中常用的几个有用的关系式。