x
x
4
k,
k
Z.
最小值为-3.
三角函数单调性
例3(课本p206).不计算,比较下列函数值的大小
(1)sin( )和sin( )
18
10
(2)cos( 23 )和cos( 17 )
5
4
解(1)因为 0,
2 10 18
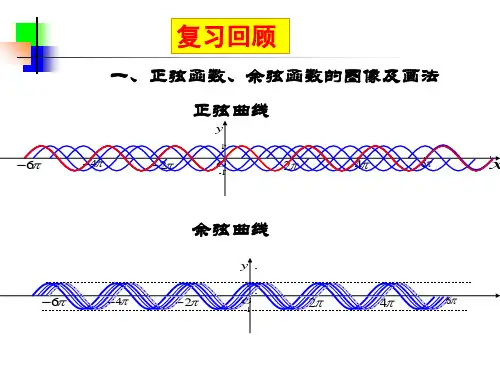
正弦函数 y = sin x 在区间
2
,0
上单调递增。所以
(2) y 3sin 2x, x R
解:这两个函数都有最大值、最小值. (1)使函数 y cos x 取1得, x最 R大值的 的集合为x
x x 2k,k Z, 最大值为 11 2.
使函数 y cos x 取1得, x最小R 值的 的集合为x
x x 2k, k Z, 最小值为 11 0.
三角函数的最值
解:(2)令z ,2x 使函数 y 3sin z, z R取得最大值的
z 的集合是
z
z
2
2k,
k
Z,
由 2x z 2k,得 x k.
2
4
因此使函数 y 3sin 2取x, 得x 最R大值的 的集合为x
x
x
4
k, k Z.
最大值为3.
同理使函数 y 3sin 2取x, 得x 最R小值的 的集合为x
人教202XA版
5.4.2 正弦函数、余弦函数的性质(2)
÷
目录
01
学习目标
CONTENTS
03
教学过程
02
复习回顾
04
学以致用
01
学习目标
1.掌握正余弦函数一个周期上的单调性 和整个定义域上的单调性.