当前位置：文档之家 › 勾股定理第一课时PPT课件

勾股定理第一课时PPT课件

  • 格式：ppt
  • 大小：798.00 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

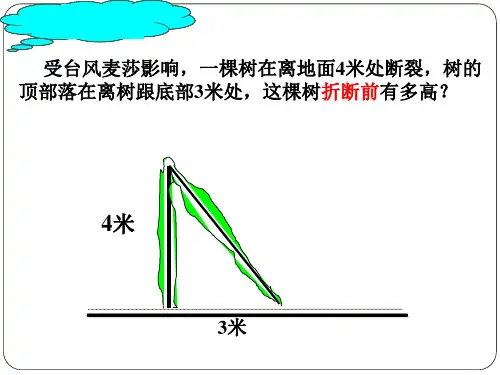
初中数学《勾股定理》课件

初中数学《勾股定理》课件

（图中每个小方格代表一个单位面积）
你是怎样得到正方形c 的面积。
P
Q CR
P
Q CR
用了“补”的方法
用了“(1)你能求出正方形R的面积吗？
C A
（2）在图1-2中，正方 形A，B，C中各含有多 少个小方格？它们的面 积各是多少？
B
图1-1
C A
B
图1-2
（3）你能发现图1-1中 三个正方形A，B，C的 面积之间有什么关系吗？ 图1-2中呢？
小明妈妈买了一部29英寸（74厘米）的 电视机.小明量了电视机的屏幕后，发现屏幕 只有58厘米长和46厘米宽，他觉得一定是售 货员搞错了.你同意他的想法吗？你能解释这 是为什么吗？
1、小明家住在18层的高楼，一天，他与妈妈去买竹竿。
买最 长的 吧！
快点回家， 好用它凉衣
服。
糟糕，太 长了，放 不进去。
国我家国之是一。最早早在三了千解多勾年前股，定理的 国国家家之之一。一早。在早三千在多三年前千，多年前，周 朝国家数之学一。家早商在高三千就多提年前出，，将一根直 尺国家折之成一。一早个在直三千角多，年前如，果勾等于三， 股国家等之于一。四早，在那三千么多弦年前就，等于五，即 “国家勾之三一。、早股在四三千、多弦年前五，”，它被记 载国家于之我一。国早古在代三千著多名年前的，数学著作 《国家周之髀一。算早经在》三千中多。年前
SA+SB=SC
即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积
C A
B
C
图1-1 A
（1）你能用三角 形的边长表示正方 形的面积吗？
（2）你能发现直 角三角形三边长度 之间存在什么关系 吗？与同伴进行交 流。
B
直角三角形两直角边的

勾股定理(第1课时)精选教学PPT课件

勾股定理(第1课时)精选教学PPT课件
“你走吧。”他说。 她简直不敢相信自己的耳朵。 “快走，不要让我后悔，也许我一分钟之后就后悔了！” 她下了车，走了几步，居然又回头看了他一眼。她永远不知道，是她那个家常电话救了她，那个电话，唤醒了劫匪心中最后仅存的善良，那仅有的一点善良，救了她的命！ 她刚走到安全地带，便听到一声枪响，回过头去，她看到他倒在方向盘上。
b
a
证明结y论=0得到定理
勾股定理:
如果直角三角形两直角边分别 为a、b,斜边为c，那么
a2 b2 c2
即 直角三角形两直角边 的平方和等于斜边的平方。
ac
b
勾
弦
股
勾 股
在中国古代，人们把弯曲成直角的手臂的上半部分称为 "勾"，下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”，较长的直角边称为“股”， 斜边称为“弦”.
清晨，当欢快的小鸟把我从睡中唤醒，我推开窗户，放眼蓝蓝的天，绿绿的草，晶莹的露珠，清清爽爽的早晨，我感恩上天又给予我一个美好的一天。 入夜，夜幕中的天空繁星点点，我打开日记，用笨拙的笔描画着一天的生活感受，月光展露着温柔的笑容，四周笼罩着夜的温馨，我充满了感恩，感谢大地赋予的安宁。
朋友相聚，酒甜歌美，情浓意深，我感恩上苍，给了我这么多的好朋友，我享受着朋友的温暖，生活的香醇，如歌的友情。 走出家门，我走向自然。放眼花红草绿，我感恩大自然的无尽美好，感恩上天的无私给予，感恩大地的宽容浩博。生活的每一天，我都充满着感恩情怀，我学会了宽容，学会了承接，学会了付出，学会了感动，懂得了回报。用微笑去对待每一天，用微笑去对待世界，对待人生，对待朋友，对待困难。所以，每天，我都有一个好心情，我幸福的生活着每一天。
1 = (a2+2ab+b2)

北师大版八年级数学上册1.1 第1课时 勾股定理的认识 课件(共23张PPT)

北师大版八年级数学上册1.1 第1课时 勾股定理的认识 课件(共23张PPT)

探究新知
1.在纸上画若干个直角三角形，分别测量它们的
三条边，看看三边长的平方之间有怎么样的关系？
c
a
b
直角三角形的两直角边的平方和等于斜边的平方，这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b，斜边为c，那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾，较长的直角
求 的长.
解：因为 ⊥ ，
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中， 2 = 2 − 2 = 102 − 82 = 36 ，
所以 = 6 .
设 = = ，则 = − 6 .
在 Rt △ 中， 2 = 2 + 2 ，
所以 △ =
1

2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图，直线 上有三个正方形 ， ， .若 ， 的面积分别
为 5 和 11 ，则 的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图，在 △ 中， = ， = 10 ， ⊥ ，垂足为 ， = 8 .
（2） 已知 = 12 ， = 16 ，求 .
【解】在 Rt △ 中， ∠ = 90∘ ， = 12 ， = 16 ，
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图，在 △ 中， ⊥ 于点 ，且 + = 32 ，
因为 ∠ = 90∘ ，所以 2 + 2 = 2 .

《勾股定理》PPT(第1课时)

《勾股定理》PPT(第1课时)
由上面的例子，我们猜想：
命题1 如果直角三角形的两条直角边长分别为a,b，斜边 长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
ac
b
课程讲授
1 勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c b a
b-a
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4S三角形＋S小正方形，
课程讲授 2 勾股定理与图形面积
归纳：与直角三角形三边相连的正方形、半圆及 正多边形、圆都具有相同的结论：两直角边上图 形面积的和等于斜边上图形的面积．本例考查了 勾股定理及半圆面积的求法，解答此类题目的关 键是仔细观察所给图形，面积与边长、直径有平 方关系，就很容易联想到勾股定理．
课程讲授Biblioteka 2 勾股定理与图形面积定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
课程讲授
1 勾股定理
几何语言： ∵在Rt△ABC中 ，∠C=90°，
B ac
∟
∴a2+b2=c2（勾股定理）.
C
勾股定理揭示了直角三角形三边之间的关系.
bA
课程讲授 1 勾股定理
例 在Rt△ABC中，∠C＝90°，AB＝10 cm， BC＝8 cm，求AC的长．
（1）正方形P的面积是 1 平方厘米； （2）正方形Q的面积是 1 平方厘米； （3）正方形R的面积是 2 平方厘米.
AR P
CQ B
上面三个正方形的面积之间有什么关系？ SP+SQ=SR
（图中每一格代表一平方厘米）
课程讲授 1 勾股定理
直角三角形ABC三边长度之间存在什么关系吗？ SP=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2

《探索勾股定理》勾股定理PPT课件(第1课时)

《探索勾股定理》勾股定理PPT课件(第1课时)
解：利用勾股定理 a2 + b2 = c2 可以得到c²=100， c=10m
巩固新知
1.求下列直角三角形中未知边的长:
常见整数的平方 （大于10）
12
112 = 121 242 = 576
8
17
5
122 = 144 252 = 625 132 = 169 302 = 900
x
142 = 196 402 =
历史课件： . /kejian/lishi/
c
数是根据圆形和方形的数学道理计算得来的。 圆来自方，而方来自直角三角形，直角三角形是根 据乘法九九表算出来的。如果将一线段折成三段围 成直角三角形，一直角边（勾）为三，另外一直角
边（股）为四，则斜边（弦）就是五。
勾股定理是关于什么图形的定理？
答：关于直角三角形三边的关系
解:∵在Rt△ADC中,AD=12,AC=13（已知）, ∴由勾股定理,得CD2=AC2-AD2=132-122=52, ∵CD=5.BC=14（已知）, ∴BD=14-5=Hale Waihona Puke . 在Rt△ABD中,由勾股定理,得
AB2=AD2+BD2=122+92=152, ∴AB=15.
课堂小结
如果直角三角形两直角边长分别为a，b，
《周髀算经》曾记载记录着商高和周公的一段对话。
我早就听说您是擅长数 学的人，请问古代伏羲测量天文 制定历法，可没有登天的台阶，又 不能测量大地的尺寸，这数据是
怎么来的呢？
ppt模板： . /moban/
ppt素材： . /sucai/
ppt背景： . /beijing/
ppt图表： . /tubiao/
（2）△ABC的a=6,b=8,则c=10.

《勾股定理》PPT优质课件(第1课时)

《勾股定理》PPT优质课件(第1课时)

A． 3
B．3
C． 5
D．5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的
长为（ C）
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则
另一直角边长为（ A ）
A.8
B.40
C.50
D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则 a= _6_0___，b = __8_0___.
课堂检测
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角 形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面 积之和为_____4_9_____cm2 ．
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：
当AB为斜边时，如图，BC 42 32 7;
形，拼成一个新的正方形.
探究新知 剪、拼过程展示：
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
探究新知
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图 示进行拼图，然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152，

1勾股定理(第1课时)(教学PPT课件(华师大版))28张

正方形中小方格的个数，你有什么猜想？
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
（1）正方形P的面积是
1
（2）正方形Q的面积是
1
平方厘米；
（3）正方形R的面积是
2
平方厘米.
平方厘米；
上面三个正方形的面积之间有什么关系？
等腰直角三角形ABC三边长度之间存在什么关系吗？
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明：大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2，
a
c
化简可得a2+b2=c2.
我们利用拼图的方法，将形的问题
与数的问题结合起来，再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系？
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现：对于任意的直角三角形，如果它的两
数学（华东师大版）
八年级 上册
第14章 勾股定理

冀教版初中八年级数学上册17-3勾股定理第一课时勾股定理课件


11.(2024江苏扬州邗江期末,16,★★☆)如图,在Rt△ABC中,
AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则DC的长
3
是2.
解析 在Rt△ABC中,AC=4,AB=5,∠C=90°,∴BC=
A=B2 =3A,C如2图,过52 D 作42 DE⊥AB于点E,∵BD平
分∠ABC,DC⊥BC,∴DC=DE,设DC=DE=x,∵S△BCD+S△ABD=S△ABC,
2
2ab+b2-2ab=a2+b2,∵中间小正方形的边长为c,∴小正方形的
面积为c2,∴a2+b2=c2,∴甲能利用面积验证勾股定理.乙中直
角梯形的面积为 (a =b)(aa2+b) b12+ab1,两个直角三角形
2
22
的面积和为2× 1 ab=ab,则中间等腰直角三角形的面积为1 a2+
2
2
1 b2+ab-ab=1 a12+ b2,∵中间等腰直角三角形的两条直角边
7.(2024四川成都龙泉驿期末)如图,△ABC中,AB=AC,BD⊥AC于 点D,∠BDF=∠BAF=∠C,BD=3,CD=1. (1)求证:∠CBD=∠EDA. (2)求AB的长.
解析 (1)证明:∵BD⊥AC, ∴∠C+∠CBD=∠EDA+∠BDF=90°, ∵∠BDF=∠C,∴∠CBD=∠EDA. (2)设AD=x,则AB=AC=AD+CD=x+1, ∵BD=3,AD2+BD2=AB2,∴x2+32=(x+1)2, 解得x=4,∴AB=x+1=5.
∴1 BC·DC+1 AB·DE1=222解33

北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT)


例1 高为2.5 m的木梯，架在高为2.4 m的墙上(如图)，
这时梯脚与墙的距离是多少?
A
解：在Rt△ABC中，根据勾股定理，得：
BC2=AB2-AC2=2.52-2.42=0.49，
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三 角形的另一边长.
正方形C的面积应该怎么计算呢？
C A
B
图①
➢ 分“割”成若干个直角边为整数的三角形 SC=12×2×3×4+1×1=13；
➢ 把C“补”成边长为5的正方形 SC=5×5-12×2×3×4=13.
观察：
C A
B
图①
正方形A中含有__4__个小正方形，即A的 面积是___4__. 正方形B中含有__9__个小正方形，即B的 面积是___9__. 正方形C中含有_1_3__个小正方形，即C的 面积是__1_3__.
第一章 勾股定理
1.1 探索勾股定理
第1课时 勾股定理
学习目标
1.经历探索勾股定理的过程，了解勾股定理的探 究方法；
2.掌握勾股定理，并能运用勾股定理解决一些简 单问题.
新知引入
一个直角三角形的两条直角边长分别是3和4，你 知道它的第三边长吗？
实际上，利用勾股定理我们可以很容易地解决这个问题. 勾股定理是一个古老的定理，人类很早就发现了这个定理.
观察：
A＇
C＇
B＇
图②
正方形A＇中含有__1_6_个小正方形，即 A＇的面积是__1_6__.
正方形B＇中含有__9__个小正方形，即 B＇的面积是__9___.
正方形C＇中含有__2_5_个小正方形，即 C＇的面积是__2_5__.

苏科版初中八年级数学上册3-1勾股定理第一课时勾股定理课件


圆的面积S2= 9 π,以BC为直径的半圆的面积S3=25 π,S△ABC=6,
8
8
∴S阴影=S1+S2+S△ABC-S3=6,故选A.
13.(2023江苏南京中考,5,★☆☆)我国南宋数学家秦九韶的 著作《数书九章》中有一道问题:“问沙田一段,有三斜,其 小斜一十三里,中斜一十四里,大斜一十五里.里法三百步,欲 知为田几何?”问题大意:在△ABC中,AB=13里,BC=14里,AC =15里,则△ABC的面积是 ( C ) A.80平方里 B.82平方里 C.84平方里 D.86平方里
解析 (1)证明:∵BD⊥AC, ∴∠C+∠CBD=90°=∠EDA+∠BDF, ∵∠BDF=∠C,∴∠CBD=∠EDA. (2)设AD=x,则AB=AC=AD+CD=x+1, ∵BD=3,AD2+BD2=AB2,∴x2+32=(x+1)2, 解得x=4,∴AB=x+1=5.
能力提升全练
11.(情境题·中华优秀传统文化)(2023江苏苏州姑苏期中,5,★ ★☆)勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》中早有记载.如图1,以直角三角形的各边为边 分别向外作正方形,再把较小的两个正方形按如图2所示的 方式放置在最大正方形内.若知道图中阴影部分的面积,则一 定能求出 ( C )
8.(2022江苏盐城校级期末)若一个直角三角形的两边长分别 为4和5,则第三条边长的平方为 9或41 . 解析 当5为直角边长时,第三条边长的平方为42+52=41;当5 为斜边长时,第三条边长的平方为52-42=9.故答案为9或41.
9.如图,在由边长为1的小正方形组成的网格中,A、B、C均 在格点上,求AB2-CA2的值.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AB = AC2 BC2 5.4122.162 4.96（米）
答：梯子上端A到墙的底端B的距离AB长约4.96米。
试一试:
１、如图:一个高3 米,宽4 米的大门,需在相对角
的顶点间加一个加固木板,则木板的长为 ( C )
A.3 米 B.4 米 C.5米 D.6米
３
４
试一试:
２、隔湖有两点A、Ｂ，从与ＢA方向成直
角 的BC方向上的点C测得CA=13米,CB=12
米,则AB为
(A)
A.5米 B.12米 C.10米 D.13米
A
13
?
C 12 B
试一试:
３、一个直角三角形的三边长为三个连续
偶数,则它的三边长分别为
( B)
A 2、4、6
Ｂ 6、8、10
Ｃ 4、6、8
Ｄ 8、10、12
试一试:
4、求下列2个三角形中的第三条边的长。
a =
B
c b
a
A
D
c2
证法（三） 总统证法
a
伽菲尔德的证明方法．1881年， 伽菲尔德就任美国第二十任总统后， 人们为了纪念他对勾股定理的证明， 就称这一证法称为“总统”证法。
∟
bc
½(a + b)(b + a) = ½c2 + 2(½ab) ½a2 + ab + ½b2 = ½c2 + ab
a2 + b2 = c2
同学们，我们也来 观察图中的地面， 看看你能发现什么？ 是否和大哲学家有 同样的发现呢？
你能发 现图中 的等腰 直角三 角形有 什么性 质吗？
A
B
C
观察 & 发现
C A
B
（1）观察图形
正方形A中含有 __9_个小方格即A的 面积是位面积--9----
正方形B中含有 个小方格，即B的 面积是__9 个单位 面积---9---
正方形C中含 有18 个小方格， 即C的面积是_1_8__ 个单位面积。
是不是所有的直角三角形都有两直边的平方和等于斜边的平方
B
A C
A的面 B的面积 C的面 积(单位 (单位长 积(单位 长度) 度) 长度)
图2 4 9 13
图2
C
图3 9 25 34
A
A、B、 C面积 关系
sA+sB=sC
B 图3
３、学了本节课后我们有什么感想？
很多的数学结论存在于平常的生活中，需要我们用数学 的眼光去观察、思考、发现，这节课我们还受到了数学文化 辉煌历史的教育。
即直角三角形两直角边的平方和等于斜边的平方.
a2 c2 c2
+ -
b2 b2 a2
=c2
=a2 =b2
勾a
弦
c
股b
在西方又称毕达哥拉斯定理！
通过探究我们得到这样的结论 a
c
如果直角三角形的两直角边长分 别为ａ、ｂ，斜边为ｃ，那么ａ2+b2=c2. b
这个命题如何证明呢?
试一试,用直角边分别为a b,斜边为c的直角三角
a
c b
图１
ca b
图２
证明：如图１ S大正方形=2ab+c2
S大正方形=(a+b)2
即(a+b)2=2ab+c2 ∴a2+b2=c2 第二种证法
证明：如图２
S大正方形=c2 S大正方形=2ab+(a－b)2
2ab+(a－b)2 =c2
∴a2+
b a2+ b2
D
C
B
A
2、 蚂蚁沿图中的折线从A点爬到D点，一共
爬了多少厘米？（小方格的边长为1厘米）
A
G
B
E
C
F
D
回顾与思考
１、本节课我们经历了怎样的过程？
经历了从实际问题引入数学问题然后发现定理，再到探 索定理，最后学会验证定理及应用定理解决实际问题的过程。
２、本节课我们学到了什么？
通过本节课的学习我们不但知道了著名的勾股定理，还 知道从特殊到一般的探索方法及借助于图形的面积来探索、 验证数学结论的数形结合思想。
直角三 两直角边的平方和
角形三 边关系
等于斜边的平方
勾 股
在中国古代，人们把弯曲成直角的手臂的上半部分称为 "勾"，下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”，较长的直角边称为“股”， 斜边称为“弦”.
勾股定理
如果直角三角形两直角边分别为a，b，斜边
为c，那么 a2 + b2 = c2
形能拼成哪些图形?
ba
a bc
c bc a
a
我们用下面的图形的来证明直角三角形的三边关系
a2+b2=c2
a
证明：S大正方形=a2+b2+2ab
bc
S大正方形=2ab+c2 ∵S大正方形= S大正方形
a bc
∴a2+b2+2ab =2ab+c2 ∴a2+b2=c2 毕达哥拉斯证法 经过证明被确认为正确的命题叫做 定理.我们把它称为勾股定理.
18.1.1 勾股定理
相传2500年前，古希腊著名数学家毕达哥拉斯 从朋友家的地砖铺成的地面上找到了答案，同学们 看看图中有没有等腰直角三角形，从中你能找到答 案吗？
A
B
C
A
B
C
A、B、C的面积有什么关系？ 等腰直角三角形三边有什么 特殊关系？ 以等腰直角三角形两直角边为边长的小正方形的面积 的和,等于以斜边为边长的正方形的面积.即SA+SB=SC 两直边的平方和等于斜边的平方
c=？ b=2
a=1
c=17
a=15
b=?
已知△ABC中，∠C=Rt ∠,AB=c,
BC=a,AC=b.
B
⑴如果a=12，c=13，求b;
a
c
⑵如果c=34, a∶b=8∶15，
求a,b.
C┓ b
A
考一考：
1、 在我国古代数学著作 《九章算术》中记载了一道 有趣的问题，这个问题的意 思是：有一个水池，水面是 一个边长为10尺的正方形，在 水池的中央有一根新生的芦 苇，它高出水面1尺，如果把 这根芦苇垂直拉向岸边，它 的顶端恰好到达岸边的水面， 请问这个水池的深度和这根 芦苇的长度各是多少？
∟
c a
b
你还有其他证明 方法吗？
想一想：
1、已知：a＝3， b＝4，求c 2、已知： c ＝10，a＝6，求b
c
ba
3、已知： c ＝13，a＝5，求阴影总分面积
4 、小明妈妈买了一部29英寸
c
（74厘米）的电视机.小明量了电 a
视机的屏幕后，发现屏幕只有58
厘米长和46厘米宽，他觉得一定
是售货员搞错了.你同意他的想法
吗？你能解释这是为什么吗？ 46厘米
58厘米
5、如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)
分析：先把实际问题转化成数学问题。
已知：AC = 5.41 , BC = 2.16 且 ∠B =
求：AB的长。
90º
解：在Rt⊿ABC中，∠ABC = 90º ， BC = 2.16 ， CA = 5.41 根据勾股定理得：