(3)速度—位移关系式:v2-v02=-2gh (4)上升的最大高度 H=v20g2
(5)上升到最大高度用时:t=vg0
2.对推论Δx=aT2的拓展 (1)公式的适用条件:
①匀变速直线运动; ②Δx为连续相等的时间间隔T内的位移差. (2)进一步的推论:xm-xn=(m-n)aT2 要注意此式的适用条件及m、n、T的含义. (3)此公式常用来研究打点计时器纸带上的加速度.
一道题可能有多种不同的解题方法,但采用不同的 方法,繁简程度不同,因此在处理问题时,要分析题目 特点,判断利用哪种方法更合适.
(2)弄清研究对象,明确哪些量已知,哪些 量未知,根据公式特点恰当选用公式.
(3)利用匀变速直线运动的两个推论和初速 度为零的匀加速直线运动的特点,往往能 够使解题过程简化.
例1.做匀变速直线运动的物体,初速度为10 m/s,方向沿x轴正
方向,经过2 s,末速度为10 m/s,方向沿x轴负方向,则其加速
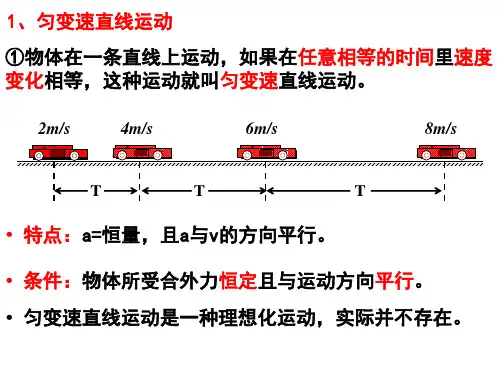
一、匀变速直线运动 1.定义:沿着一条直线,且加速度不变的运动. 2.种类 (1)匀加速直线运动:物体的速度随时间均匀增加,加速度的
方向与速度的方向相同. (2)匀减速直线运动:物体的速度随时间均匀减小,加速度的
方向与速度的方向相反.
二、匀变速直线运动的规律
1.基本公式 (1)速度公式: v=v0+at (2)位移公式:x=v0t+12at2 (3)速度—位移关系式:v2-v02=2ax
方法
分析说明
逆向 把运动过程的“末态”作为“初态”的反向研究
思维法 问题的方法,一般用于末态已知的情况
应用v-t图象,可把较复杂的问题转变为较为简
图象法 单的数学问题解决,尤其是用图象定性分析,可
躲开纷杂的计算,快速得出答案