人教版九年级数学《二次函数》知识点梳理与总结(超经典)---副本

函数是初中数学知识的主线，而二次函数是这条主线上的高潮.我们通过探索二次函数与方程的关系，让我们领悟到事物之间相互联系的辨证关系.我们能够利用二次函数解决实际问题，培养数学建模的能力. 【知识结构】【知识梳理】1、定义：形如 c bx ax y ++=2（a 、b 、c 是常数，a≠0）的函数叫做x 的二次函数. 二次函数的一般形式是c bx ax y ++=2（a≠0），还可以用配方法化为k h x a y +-=2)(的形式，它可直接看出其顶点坐标为（k h ,），故把k h x a y +-=2)(叫做二次函数的顶点式.2、图象：二次函数的图象是抛物线，它是轴对称图形，其对称轴平行于y 轴. 注意：二次函数c bx ax y ++=2的图象的形状、大小、开口方向只与a 有关，所以，c bx ax y ++=2的图象可通过2ax y =的 图象平移得到．平移可按照如下口诀进行：上加下减，左加右减，即向上或向左用加，向下或向右用减.例如，将22x y =向左平移1个单位为()212+=x y ，再向下平移3个单位为()3122-+=x y ．3、性质注意：二次函数的性质要结合图象，认真理解，灵活应用，不要死记硬背． 4、二次函数与一元二次方程的关系对于二次函数c bx ax y ++=2（a≠0），当y =0时，就变成了一元二次方程02=++c bx ax ．二次函数c bx ax y ++=2（a≠0）的图象与x 轴的交点有三种情况： 当ac b 42-﹥0时，有两个交点； 当ac b 42-=0时，有一个交点； 当ac b 42-﹤0时，无交点.当二次函数c bx ax y ++=2（a≠0）的图象与x 轴的有交点时，其交点横坐标就是方程02=++c bx ax 的根． 【易错点剖析】一、忽略二次项系数不等于0例1已知二次函数263y kx x =-+的图象与x 轴有交点，则k 的取值范围 是（ ）（A ）k ＜3 (B) k ＜3 且k ≠0 (C) k ≤3 (D) k ≤3 且k ≠0 错解:选C.由题意,得△=()26-－4 k ×3≥0,解得k ≤3,故选C.错解分析:当k =0时,二次项系数为0,此时原函数不是二次函数.欲求k 的取值范围,须同时满足:①函数是二次函数;②图象与x 轴有交点,上面的解法只注重了△≥0而忽略了二次项系数不等于0的条件.正解: 选D.由题意,得△=()26-－4 k ×3≥0且k ≠0,即k ≤3 且k ≠0,故应选D. 二、忽略隐含条件例2如图,已知二次函数2y x bx c =++的图象与y 轴交于点A, 与x 轴正半轴交于B,C 两点,且BC ＝2,ABC S ∆ ＝3,则b 的值为( )（A ）-5 (B)4或-4 (C) 4 (D)-4错解: 选 B.依题意BC ＝2,ABC S ∆ ＝3,得点A(0,3),即c ＝3.又BC ＝2,得方程20x bx c ++=的两根之差为2,2-=,解得b =±4.故选B.错解分析:上面的解法忽略了“抛物线的对称轴x ＝-2b在y 轴的右侧”这一隐含条件,正确的解法应是同时考虑-2b＞0,得b ＜0,∴b =4应舍去,故应选D. 正解: 选D.例3 若y 关于x 的函数y =(a -2)x 2-(2a -1)x +a 的图象与坐标轴有两个交点，则a 可取的值是多少？错解：因为函数y =(a -2)x 2-(2a -1)x +a 的图象与坐标轴有两个交点，而其中与y 轴有一个交点(0,a )，则与x 轴就只有一个交点，所以关于x 的一元二次方程y =(a -2)x 2-(2a -1)x +a有两个相等的实数根，所以判别式[-(2a-1)]2-4×(a-2)a=0，解得a=-14.错解分析：本题关于函数的描述是“y关于x的函数”，并没有指明是二次函数，所以需要分“y关于x的一次函数”和“y关于x的二次函数”两种情况进行讨论.当函数y是关于x的二次函数时，函数y=(a-2)x2-(2a-1)x+a的图象与y轴有一个交点(0,a)，与坐标轴三、忽略数形结合思想方法的应用例4 求二次函数y=2x+4x+5(-3≤x≤0)的最大值和最小值.错解:当x=-3时,y=2; 当x=0时,y=5;所以，-3≤x≤0时,y最小=2,y最大=5.错解分析:上面的解法错在忽略了数形结合思想方法的应用,误以为端点的值就是这段函数的最值.解决此类问题,画出函数图象,借助图象的直观性求解即可.四、求顶点坐标时混淆符号例5 求二次函数y =-x 2+2x -2的顶点坐标. 错解1 用配方法y =-x 2+2x -2=-(x 2-2x )-2=-(x 2-2x +1-1)-2=-(x 2-2x +1) -1=-(x -1) 2-1所以二次函数y =-x 2+2x -2的顶点坐标为(-1,-1).错解2 用公式法 在二次函数y =-x 2+2x -2中，a =-1，b =2，c =-2，则2122(1)b a ==-⨯-，22424(1)(2)142(1)b ac a --⨯-⨯-==⨯- 所以二次函数y =-x 2+2x -2的顶点坐标为(-1,1).错解分析：二次函数y =a (x -h )2+k 的顶点坐标为(h ,k ),即横坐标与配方后完全平方式中的常数项互为相反数，而非相等，也就是说不是(-h ,k ).二次函数y =ax 2+bx +c (a ≠0)的顶点坐标为(-2b a ,244b ac a-)，横坐标前面带“-”，纵坐标的分子为4ac -b 2,不要与一元二次方程根的判别式b 2-4ac 混淆.另外，把一般式转化为顶点式，常用配方法，如果二次项系数是1，则常数项为一次项系数一半的平方；如果二次项系数不是1，则先提出二次项系数（注意：不能像解方程一样把二次项系数消去），使括号中的二次项系数变为1，再对括号中进行配方.五、忽视根的判别式的作用例6 已知抛物线y=-12x2)x+m-3与x轴有两个交点A，B，且A，B关于y轴对称，求此抛物线解析式.错解：因为A与B关于y轴对称，所以抛物线对称轴为y轴，即直线x=-02ba==.解得m=6或m=-6.当m=6时，方程抛物线解析式为y=-12x2+3.错解分析：抛物线与x轴有两个交点为A，B，等价于：相应的一元二次方程有两个不相等的实数根，所以b2-4ac>0.如果忽视根的判别式在解题中的作用，就不能排除不符合题意的解，扩大了解的范围，导致错误.。

九年级二次函数知识点总结一、二次函数的基本形式二次函数一般写为y=ax^2+bx+c（a≠0），其中a、b、c为常数，x为自变量，y为因变量。

其中a决定了抛物线开口的方向，当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

b决定了抛物线的位置，c决定了抛物线与y轴的交点。

二、二次函数的图像1. 抛物线的开口方向：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

2. 抛物线的顶点：抛物线的顶点坐标为（-b/2a, f(-b/2a)），其中f(x)=ax^2+bx+c。

3. 抛物线的对称轴：抛物线的对称轴方程为x=-b/2a。

4. 抛物线的焦点：抛物线没有焦点。

5. 抛物线的焦距：抛物线没有焦距。

三、二次函数的性质1. 零点：二次函数的零点即为其实根，求零点的方法可以通过求解二次方程ax^2+bx+c=0来得到。

2. 正负性：当a>0时，抛物线上方为正区间，下方为负区间；当a<0时，抛物线上方为负区间，下方为正区间。

3. 单调性：当a>0时，函数单调递增；当a<0时，函数单调递减。

4. 极值：当a>0时，抛物线的最小值为f(-b/2a)；当a<0时，抛物线的最大值为f(-b/2a)。

四、二次函数的相关应用1. 最值问题：通过求解二次函数的极值来解决相关的最值问题，如求解最大值、最小值等。

2. 零点问题：通过求解二次函数的零点来解决相关的方程问题，如求解方程ax^2+bx+c=0的解。

3. 切线问题：通过求解二次函数的导数来得到其切线的斜率，从而解决相关的切线问题。

4. 抛物线运动问题：通过二次函数的图像特点，解决相关的抛物线运动问题，如抛体的运动轨迹、最大高度、飞行时间等。

五、二次函数的解题方法1. 求解零点：通过求解二次方程ax^2+bx+c=0来得到函数的零点。

2. 求解极值：通过求解函数的导数来得到函数的极值点，并求解其极值。

新人教版九年级上二次函数知识点总结知识点一：二次函数的定义1．二次函数的定义：一般地，形如 y ax2bx c 〔 a ，b ，c 是常数，a 0〕的函数，叫做二次函数．其中 a 是二次项系数， b 是一次项系数，c是常数项．知识点二：二次函数的图象与性质抛物线的三要素：张口、对称轴、极点2. 二次函数y a x h 2k 的图象与性质〔1〕二次函数根本形式 y ax2的图象与性质： a 的绝对值越大，抛物线的张口越小〔2〕 y ax2 c 的图象与性质：上加下减2〔3〕 y a x h的图象与性质：左加右减〔4〕二次函数 y a x h2k 的图象与性质3. 二次函数 yax 2 bx c 的图像与性质〔 1〕当 a 0 时，抛物线张口向上，对称轴为xb，极点坐标为b ，4ac b 2 ．2a2a 4a当 xb 时， y 随 x 的增大而减小；当 xb 时， y 随 x 的增大而增大；当xb 时，2a2 a2ay 有最小值4 ac b 2．4a〔 2〕当 a 0 时，抛物线张口向下，对称轴为xb，极点坐标为b ，4ac b 2 ．2 a2a 4a当 xb 时， y 随 x 的增大而增大；当 x b 时， y 随 x 的增大而减小；当xb 时，2a2 a2a2y 有最大值 4 ac b．4a4. 二次函数常有方法指导（ 1〕二次函数 y ax 2 bx c 图象的画法①画精确图五点画图法〔列表 -描点 -连线〕利用配方法将二次函数y ax 2 bx c 化为极点式 y a(x h) 2 k ，确定其张口方向、 对称轴及极点坐标， 尔后在对称轴两侧，左右对称地描点画图.②画草图抓住以下几点：张口方向，对称轴，与 y 轴的交点，极点 .（ 2〕二次函数图象的平移平移步骤：① 将抛物线解析式转变为极点式y a x h2h ，k ；k ，确定其极点坐标 ② 可以由抛物线 ax 2 经过合适的平移获取详尽平移方法以下：y=ax2向上 (k>0)【或向下 (k<0)】平移 |k |个单位y=ax 2+k向右 (h>0)【或左 ( h<0)】 向右 (h>0) 【或左 (h<0) 】 向右 (h>0)【或左 (h<0)】 平移 |k|个单位平移 |k|个单位平移 |k|个单位向上 (k>0) 【或下 (k<0) 】平移 |k|个单位y=a(x-h)2向上 (k>0) 【或下 (k<0)】平移 |k|个单位y=a(x-h)2+k平移规律：概括成八个字“左加右减，上加下减〞 ．〔 3〕用待定系数法求二次函数的解析式①一般式：. 图象上三点或三对 、 的值，平时选择一般式 .②极点式：. 图象的极点或对称轴，平时选择极点式.③交点式：. 图象与轴的交点坐标、，平时选择交点式 .〔 4〕求抛物线的极点、对称轴的方法24ac b2b 4ac b2①公式法：2bx c a xby ax2a，∴极点是〔2a，〕，对称轴4a4a是直线 xb.2a②配方法：运用配方的方法，将抛物线的解析式化为 y a xh 2k 的形式，获取极点为( h , k ) ，对称轴是直线x h .③运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，因此对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是极点.〔 5〕抛物线y ax2bx c 中， a,b, c 的作用① a 决定张口方向及张口大小，这与y ax 2中的a完满相同.② b和 a 共同决定抛物线对称轴的地址由于抛物线 y ax 2bx c 的对称轴是直线x b，故2a若是 b0 时，对称轴为y 轴；若是b0 〔即a、b同号〕时，对称轴在y 轴左侧；a若是b0 〔即a、b异号〕时，对称轴在y 轴右侧. a③ c 的大小决定抛物线y ax 2bx c 与y轴交点的地址当 x0 时， y c ，因此抛物线y ax 2bx c 与y轴有且只有一个交点〔0，c〕，故若是 c0 ，抛物线经过原点；若是 c0 ,与 y 轴交于正半轴；若是 c0 ,与 y 轴交于负半轴.知识点三：二次函数与一元二次方程的关系5.函数 y ax 2bx c ，当 y 0 时，获取一元二次方程ax2bx c 0 ，那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标，因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况 .(1)当二次函数的图象与x 轴有两个交点，这时，那么方程有两个不相等实根；(2)当二次函数的图象与x 轴有且只有一个交点，这时，那么方程有两个相等实根；(3)当二次函数的图象与x 轴没有交点，这时，那么方程没有实根 .经过下面表格可以直观地观察到二次函数图象和一元二次方程的关系：的图象方程有两个相等实数解方程有两个不等实数解方程没有实数解的解6.拓展：关于直线与抛物线的交点知识〔1〕y轴与抛物线y ax 2bx c 得交点为 (0, c) .〔 2 〕与y轴平行的直线x h 与抛物线y ax 2 bx c 有且只有一个交点( h , ah2bh c ).〔 3〕抛物线与x 轴的交点二次函数 y ax 2bx c 的图像与 x 轴的两个交点的横坐标x1、 x2，是对应一元二次方程 ax 2bx c0 的两个实数根.抛物线与 x 轴的交点情况可以由对应的一元二次方程的根的鉴识式判断：①有两个交点0抛物线与 x 轴订交；②有一个交点〔极点在 x 轴上〕0 抛物线与x轴相切；③没有交点0抛物线与x 轴相离.〔 4〕平行于x轴的直线与抛物线的交点同〔 3〕相同可能有0 个交点、 1 个交点、 2 个交点 . 当有 2 个交点时，两交点的纵坐标相等，设纵坐标为k ，那么横坐标是ax2bx c k 的两个实数根.〔 5〕一次函数y kx n k 0的图像 l 与二次函数y ax 2bx c a 0 的图像G的y kx n 交点，由方程组ax2的解的数目来确定：y bx c②方程组只有一组解时l 与 G 只有一个交点；③方程组无解时l 与 G 没有交点.〔 6 〕抛物线与x 轴两交点之间的距离：假设抛物线y ax 2bx c 与 x 轴两交点为A x ，，B x ，，由于x1、 x2是方程 ax 2bx c0 的两个根，故1 020x1x2b, x1 x2ca ab2b24acAB x1 x2x12x1 x224x1 x24cx2a a a a知识点四：利用二次函数解决实责问题7.利用二次函数解决实责问题，要建立数学模型，即把实责问题转变为二次函数问题，利用题中存在的公式、内含的规律等相等关系，建立函数关系式，再利用函数的图象及性质去研究问题 . 在研究实责问题时要注意自变量的取值范围应拥有实质意义.利用二次函数解决实责问题的一般步骤是：(1)建立合适的平面直角坐标系；(2)把实责问题中的一些数据与点的坐标联系起来；(3)用待定系数法求出抛物线的关系式；(4)利用二次函数的图象及其性质去解析问题、解决问题.。

人教版九年级数学二次函数知识点梳理与总结超副本Jenny was compiled in January 2021《二次函数》单元知识梳理与总结一、二次函数的概念1、定义：一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数.2、注意点：（1）二次函数是关于自变量x 的二次式，二次项系数a 必须为非零实数，即a ≠0，而b 、c 为任意实数。

（2）当b=c=0时，二次函数2ax y =是最简单的二次函数。

（3）二次函数c b a c bx ax y ,,(2++=是常数，)0≠a 自变量的取值为全体实数（c bx ax ++2为整式）3、三种函数解析式：（1）一般式： y=ax 2+bx+c （a ≠0），对称轴：直线x=ab2- 顶点坐标：( a b ac a b 4422--， )（2）顶点式：()k h x a y +-=2（a ≠0）， 对称轴：直线x=h 顶点坐标为（h ,k ）（3）交点式：y=a （x-x 1）（x-x 2）（a ≠0）, 对称轴:直线x=22x1x + (其中x 1、x 2是二次函数与x 轴的两个交点的横坐标). 二、二次函数的图象1、二次函数 c bx ax y ++=2的图像是对称轴平行于（包括重合）y 轴的抛物线.2、二次函数由特殊到一般，可分为以下几种形式：①2ax y =；②k ax y +=2；③()2h x a y -=；④()k h x a y +-=2；⑤c bx ax y ++=2.注：二次函数的图象可以通过抛物线的平移得到 3、二次函数c bx ax y ++=2的图像的画法因为二次函数的图像是抛物线，是轴对称图形，所以作图时常用简化的描点法和五点法，其步骤是： (1)先找出顶点坐标，画出对称轴； (2)找出抛物线上关于对称轴的四个点(如与坐标轴的交点等)； (3)把上述五个点按从左到右的顺序用平滑曲线连结起来.三、二次函数的性质注：常用性质： 1、增减性：当a>0时，在对称轴左侧，y 随着x 的增大而减少；在对称轴右侧，y 随着x 的增大而增大；当a<0时，在对称轴左侧，y 随着x 的增大而增大；在对称轴右侧，y 随着x 的增大而减少； 2、最大或最小值：当a>0时，函数有最小值，并且当x=a b2- ， y 最小 ＝a b ac 442-当a<0时，函数有最大值，并且当x=ab2- ， y 最大 ＝a b ac 442-四、.抛物线的三要素：开口方向、对称轴、顶点坐标。

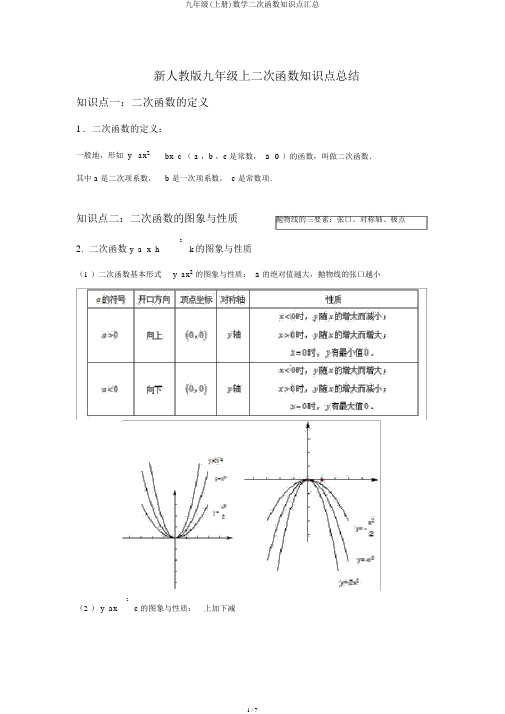
新人教版九年级上二次函数知识点总结知识点一：二次函数的定义1．二次函数的定义：一般地，形如 y ax2bx c （ a ，b ，c 是常数，a 0）的函数，叫做二次函数．其中 a 是二次项系数， b 是一次项系数， c 是常数项．知识点二：二次函数的图象与性质抛物线的三要素：张口、对称轴、极点2. 二次函数y a x h2的图象与性质k（1 ）二次函数基本形式y ax2的图象与性质：a的绝对值越大，抛物线的张口越小（2 ） y ax 2c 的图象与性质：上加下减2（3 ） y a x h的图象与性质：左加右减（4 ）二次函数 y a x h 2k 的图象与性质3.二次函数 y ax 2bx c 的图像与性质（ 1 ）当a 0时，抛物线张口向上，对称轴为x b ，极点坐标为 b ，4ac b2．2a 2 a4a当 x b时， y 随x的增大而减小；当x b时， y 随x的增大而增大；当x b时，2a 2 a2ay有最小值 4 ac b 2．4a（ 2 ）当a 0时，抛物线张口向下，对称轴为x b ，极点坐标为 b ，4acb2．2a2a4a当 x b时， y 随x的增大而增大；当x b时， y 随x的增大而减小；当x b时，2a 2 a2a 2y 有最大值4 ac b．4a4. 二次函数常有方法指导（ 1 ）二次函数 y ax 2 bx c 图象的画法①画精确图五点画图法（列表 - 描点 -连线）利用配方法将二次函数y ax 2 bx c 化为极点式 y a(x h) 2 k ，确定其张口方向、 对称轴及极点坐标， 今后在对称轴两侧，左右对称地描点画图.②画草图抓住以下几点：张口方向，对称轴，与 y 轴的交点，极点 .（ 2 ）二次函数图象的平移平移步骤：① 将抛物线剖析式转变为极点式y a x h2h ，k ；k ，确定其极点坐标② 可以由抛物线 ax 2 经过合适的平移获取详尽平移方法以下：y=ax2向上 (k>0)【或向下 (k<0)】平移 |k |个单位y=ax 2+k向右 (h>0)【或左 ( h<0)】 向右 (h>0) 【或左 (h<0) 】 向右 (h>0)【或左 (h<0)】 平移 |k|个单位平移 |k|个单位平移 |k|个单位向上 (k>0) 【或下 (k<0) 】平移 |k|个单位y=a(x-h)2向上 (k>0) 【或下 (k<0)】平移 |k|个单位y=a(x-h)2+k平移规律：概括成八个字“左加右减，上加下减” ．（ 3 ）用待定系数法求二次函数的剖析式①一般式： .已知图象上三点或三对、的值，平时选择一般式.②极点式： .已知图象的极点或对称轴，平时选择极点式.③交点式： . 已知图象与轴的交点坐标、，平时选择交点式.（ 4 ）求抛物线的极点、对称轴的方法b 2b2b 4ac b 2①公式法： y24acax bx ca x4a，∴极点是（，），对称轴2a2a4ab .是直线 x2a②配方法： 运用配方的方法， 将抛物线的剖析式化为 ya x h 2k 的形式，获取极点为 ( h , k )，对称轴是直线 xh .③运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，因此对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是极点.（ 5 ）抛物线y ax2bx c 中， a,b,c 的作用① a 决定张口方向及张口大小，这与y ax 2中的a圆满相同.② b和 a 共同决定抛物线对称轴的地址由于抛物线 y ax 2bx c 的对称轴是直线x b，故2a若是 b0 时，对称轴为y 轴；b0（即 a 、 b 同号）时，对称轴在y 轴左侧；若是ab0（即 a 、 b 异号）时，对称轴在y 轴右侧.若是a③ c 的大小决定抛物线y ax 2bx c 与y轴交点的地址当 x0 时， y c ，因此抛物线y ax 2bx c 与y轴有且只有一个交点（0 ，c），故若是 c0 ，抛物线经过原点；若是 c0 ,与 y 轴交于正半轴；若是 c0 ,与 y 轴交于负半轴.知识点三：二次函数与一元二次方程的关系5. 函数y ax2bx c ，当 y 0 时，获取一元二次方程 ax2bx c 0 ，那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标，因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况 .(1)当二次函数的图象与 x 轴有两个交点，这时，则方程有两个不相等实根；(2) 当二次函数的图象与x 轴有且只有一个交点，这时，则方程有两个相等实根；(3) 当二次函数的图象与 x 轴没有交点，这时，则方程没有实根.经过下面表格可以直观地观察到二次函数图象和一元二次方程的关系：的图象方程有两个相等实数解方程有两个不等实数解方程没有实数解的解6. 拓展：关于直线与抛物线的交点知识（1 ）y 轴与抛物线yax 2bxc 得交点为(0, c) .（ 2 ） 与y轴 平 行 的 直 线xh 与 抛 物 线yax 2bxc 有 且 只 有 一 个 交 点( h , ah 2bh c ).（ 3 ）抛物线与 x 轴的交点二次函数yax 2bx c 的图像与x 轴的两个交点的横坐标x 1 、 x 2 ，是对应一元二次方程ax 2bxc0 的两个实数根. 抛物线与 x 轴的交点情况可以由对应的一元二次方程的根的鉴识式判断：①有两个交点抛物线与 x 轴订交；②有一个交点（极点在x 轴上）抛物线与 x 轴相切；③没有交点抛物线与x 轴相离 .（ 4 ）平行于 x 轴的直线与抛物线的交点同（ 3 ）相同可能有 0 个交点、 1 个交点、 2 个交点 .当有 2 个交点时，两交点的纵坐标相等，设纵坐标为k ，则横坐标是 ax 2bx c k 的两个实数根 .（ 5 ）一次函数 ykx n k0 的图像 l 与二次函数 y ax 2 bx c a 0 的图像 Gykx n的交点，由方程组 y ax 2的解的数目来确定：bx c①方程组有两组不一样样的解时l 与 G 有两个交点 ;②方程组只有一组解时l 与 G 只有一个交点；③方程组无解时l 与 G 没有交点 .（ 6 ）抛物线与 x 轴两交点之间的距离：若抛物线yax 2 bx c 与 x 轴两交点为A x ，，B x ， ，由于x 1、 x 2 是方程 ax 2bx c 0 的两个根，故12x1x2b, x1 x2ca ab2b24acAB x1 x22x1x224cx1 x2 4 x1x2a a a a知识点四：利用二次函数解决实诘责题7.利用二次函数解决实诘责题，要建立数学模型，即把实诘责题转变为二次函数问题，利用题中存在的公式、内含的规律等相等关系，建立函数关系式，再利用函数的图象及性质去研究问题 .在研究实诘责题时要注意自变量的取值范围应拥有本质意义.利用二次函数解决实诘责题的一般步骤是：(1)建立合适的平面直角坐标系；(2)把实诘责题中的一些数据与点的坐标联系起来；(3)用待定系数法求出抛物线的关系式；(4)利用二次函数的图象及其性质去剖析问题、解决问题.。

《二次函数》单元知识梳理与总结一、二次函数的概念1、定义：一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数.2、注意点：（1）二次函数是关于自变量x 的二次式，二次项系数a 必须为非零实数，即a ≠0，而b 、c 为任意实数。

（2）当b=c=0时，二次函数2ax y =是最简单的二次函数。

（3）二次函数c b a c bx ax y ,,(2++=是常数，)0≠a 自变量的取值为全体实数 （c bx ax ++2为整式）3、三种函数解析式：（1）一般式： y=ax 2+bx+c （a ≠0），对称轴：直线x=ab2- 顶点坐标：( a b ac a b 4422--， ) （2）顶点式：()k h x a y +-=2（a ≠0），对称轴：直线x=h 顶点坐标为（h ,k ）（3）交点式：y=a （x-x 1）（x-x 2）（a ≠0）, 对称轴:直线x=22x1x + (其中x 1、x 2是二次函数与x 轴的两个交点的横坐标).二、二次函数的图象1、二次函数 c bx ax y ++=2的图像是对称轴平行于（包括重合）y 轴的抛物线.2、二次函数由特殊到一般，可分为以下几种形式：①2ax y =；②k ax y +=2；③()2h x a y -=；④()k h x a y +-=2；⑤c bx ax y ++=2.注：二次函数的图象可以通过抛物线的平移得到 3、二次函数c bx ax y ++=2的图像的画法因为二次函数的图像是抛物线，是轴对称图形，所以作图时常用简化的描点法和五点法，其步骤是：(1)先找出顶点坐标，画出对称轴；(2)找出抛物线上关于对称轴的四个点(如与坐标轴的交点等)； (3)把上述五个点按从左到右的顺序用平滑曲线连结起来.1、增减性：当a>0时，在对称轴左侧，y 随着x 的增大而减少；在对称轴右侧，y 随着x 的增大而增大； 当a<0时，在对称轴左侧，y 随着x 的增大而增大；在对称轴右侧，y 随着x 的增大而减少； 2、最大或最小值：当a>0时，函数有最小值，并且当x=a b2- ， y 最小 ＝a b ac 442-当a<0时，函数有最大值，并且当x=ab2- ， y 最大 ＝a b ac 442-四、.抛物线的三要素：开口方向、对称轴、顶点坐标。

二次函数知识点一、基本概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：（上加下减）3. ()2y a x h =-的性质：（左加右减）4. ()2y a x h k =-+的性质：三、二次函数图象的平移1. 平移步骤：方法1：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法2：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k=-+与2y axbx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小．2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba -<，即抛物线的对称轴在y 轴左侧；当0b =时，02ba -=，即抛物线的对称轴就是y 轴；当0b <时，02ba->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即当0b >时，02ba ->，即抛物线的对称轴在y 轴右侧；当0b =时，02ba -=，即抛物线的对称轴就是y 轴；当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧．总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．九、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．这两点间的距离21AB x x =-=.② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2' 当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；3. 二次函数常用解题方法总结：⑴ 求二次函数的图象与x 轴的交点坐标，需转化为一元二次方程；⑵ 求二次函数的最大（小）值需要利用配方法将二次函数由一般式转化为顶点式；⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ，b ，c 的符号，或由二次函数中a ，b ，c 的符号判断图象的位置，要数形结合；⑷ 二次函数的图象关于对称轴对称，可利用这一性质，求和已知一点对称的点坐标，或已知与x 轴的一个交点坐标，可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式，二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数；下面以0a >时为例，揭示二次函数、二次三项式和一元二次方程之间的内在联系：二次函数考查重点与常见题型1． 考查二次函数的定义、性质，有关试题常出现在选择题中，如：已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点， 则m 的值是2． 综合考查正比例、反比例、一次函数、二次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题，如： 如图，如果函数b kx y +=的图像在第一、二、三象限内，那么函数12-+=bx kx y 的图像大致是（ ）y y y y1 10 x o-1 x 0 x 0 -1 x A B C D3． 考查用待定系数法求二次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题，如： 已知一条抛物线经过(0,3)，(4,6)两点，对称轴为35=x ，求这条抛物线的解析式。

九年级上二次函数知识点归纳总结二次函数是初中数学中比较重要的一个内容，也是高中数学的重点。

在九年级上学期，我们学习了关于二次函数的各种知识点，包括定义、性质、图像和应用等方面。

在本文中，我们将对这些知识点进行归纳总结，以便加深对二次函数的理解和掌握。

一、二次函数的定义二次函数是形如 y = ax^2 + bx + c（其中a ≠ 0，a、b、c为常数）的函数，它的图像是一个抛物线。

在定义中，a决定了抛物线的开口方向和大小，b决定了抛物线在x轴方向上的平移，c决定了抛物线在y轴方向上的平移。

二、二次函数的性质1. 对称性：二次函数的图像以抛物线的开口处为对称轴对称。

对于 y = ax^2 + bx + c，对称轴的方程为 x = -b/2a。

2. 零点：二次函数的零点即为方程 y = ax^2 + bx + c 的解，可以通过求根公式或配方法得到。

零点的个数与二次函数与x轴的交点个数相同。

3. 最值：当 a > 0 时，二次函数的最小值为（-b/2a, f(-b/2a))；当 a < 0 时，二次函数的最大值为（-b/2a, f(-b/2a)）。

4. 单调性：当a > 0 时，二次函数在（-∞，-b/2a）上单调递增，在（-b/2a，+∞）上单调递减；当 a < 0 时，二次函数在（-∞，-b/2a）上单调递减，在（-b/2a，+∞）上单调递增。

三、二次函数的图像特征1. 开口方向：当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。

2. 平移：二次函数 y = ax^2 + bx + c 的图像在 x 方向上的平移量为 -b/2a，即向左平移 -b/2a 个单位；在 y 方向上的平移量为 c，即向上平移 c 个单位。

3. 顶点坐标：二次函数的顶点坐标为抛物线对称轴上的点，即（-b/2a, f(-b/2a)）。

四、二次函数的应用1. 求解问题：利用二次函数的模型，可以求解与日常生活和实际问题相关的各种数学问题，如求解最值、零点等。

点新人教版九年级上二次函数知识点总结知识点一：二次函数的定义1. 二次函数的定义：一般地，形如 y = ax 2 + bx + c （ a ，， b c 是常数， a ≠ 0 ）的函数，叫做二次函数． 其中 a 是二次项系数， b 是一次项系数， c 是常数项．知识点二：二次函数的图象与性质⇒⇒ 2. 二次函数 y = a (x - h )2+ k 的图象与性质（1） 二次函数基本形式 y = ax 2 的图象与性质：a 的绝对值越大，抛物线的开口越小（2） y = ax 2 + c 的图象与性质：上加下减抛物线的三要素：开口、对称轴、顶（3）y =a (x -h)2 的图象与性质：左加右减⎝⎭ ⎝ ⎭（4） 二次函数 y = a (x - h )2+ k 的图象与性质3. 二次函数 y = ax 2 + bx + c 的图像与性质b⎛ b 4ac - b 2 ⎪⎫ ． （1）当 a > 0 时，抛物线开口向上，对称轴为 x = - 2a ，顶点坐标为 - 2a， 4a当 x < - b 时， y 随 x 的增大而减小；当 x > - b 时， y 随 x 的增大而增大；当 x = - b时，2a 2a 2a4ac - b 2y 有最小值 ．4ab⎛ b 4ac - b 2 ⎪⎫． （2）当 a < 0 时，抛物线开口向下，对称轴为 x = - 2a ，顶点坐标为 - 2a， 4a当 x < - b 时， y 随 x 的增大而增大；当 x > - b时， y 随 x 的增大而减小；当 x = - b 时，2a 2a2a 4ac - b 2y 有最大值 ．4ab4. 二次函数常见方法指导（1） 二次函数 y = ax 2 + bx + c 图象的画法①画精确图 五点绘图法（列表-描点-连线）利用配方法将二次函数 y = ax 2 + bx + c 化为顶点式 y = a (x - h )2 + k ，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.②画草图 抓住以下几点：开口方向，对称轴，与 y 轴的交点，顶点. （2） 二次函数图象的平移 平移步骤：① 将抛物线解析式转化成顶点式 y = a (x - h )2+ k ，确定其顶点坐标(h ， ② 可以由抛物线 ax 2 经过适当的平移得到具体平移方法如下：k )；【【(k >0)【【【【(k <0)【【【 |k |【【【【 【( h >0)【【【( h <0【【 【 |k|【【【【 【( h >0)【【【( h <0) 【 【 |k|【【【【 【( k >0)【【【( k <0)【 【 【 |k |【【【【 【( h >0)【【【( h <0)【 【 【 |k|【【【y=a (x-h )2【【(k >0)【【【(k <0)【【【 |k |【【【平移规律：概括成八个字“左加右减，上加下减”．（3） 用待定系数法求二次函数的解析式y=a (x-h )2+k①一般式： .已知图象上三点或三对 、 的值，通常选择一般式.②顶点式：.已知图象的顶点或对称轴，通常选择顶点式.③交点式：.已知图象与 轴的交点坐标 、 ，通常选择交点式.（4） 求抛物线的顶点、对称轴的方法①公式法： y = ax 2 + bx + c = ⎛ +b⎫2 4ac - b 2 b 4ac - b 2a x⎪ + ，∴顶点是（- ， ），对称轴是直线 x = - .2a⎝ 2a ⎭4a 2a 4a ②配方法：运用配方的方法，将抛物线的解析式化为 y = a (x - h )2+ k 的形式，得到顶点为( h ,k )，对称轴是直线 x = h .y=ax 2y=ax 2+k③运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，所以对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是顶点.（5）抛物线y =ax 2 +bx +c 中，a, b, c 的作用① a 决定开口方向及开口大小，这与y =ax 2 中的a 完全一样.② b 和a 共同决定抛物线对称轴的位置由于抛物线y =ax 2 +bx +c 的对称轴是直线x =-b，故2a如果b = 0 时，对称轴为y 轴；b如果> 0 （即a 、b 同号）时，对称轴在y 轴左侧；a b如果< 0 （即a 、b 异号）时，对称轴在y 轴右侧.a③ c 的大小决定抛物线y =ax 2 +bx +c 与y 轴交点的位置当x=0时，y =c ，所以抛物线y =ax 2+bx +c 与y轴有且只有一个交点（0，c ），故如果c = 0 ，抛物线经过原点；如果c > 0 ,与y 轴交于正半轴；如果c < 0 ,与y 轴交于负半轴.知识点三：二次函数与一元二次方程的关系5.函数y =ax 2 +bx +c ，当y = 0 时，得到一元二次方程ax2 +bx +c = 0 ，那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标，因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(1)当二次函数的图象与x 轴有两个交点，这时，则方程有两个不相等实根；(2)当二次函数的图象与x 轴有且只有一个交点，这时，则方程有两个相等实根；(3)当二次函数的图象与x 轴没有交点，这时，则方程没有实根.通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系：⎩的图象的解方程有两个不等实数解方程有两个相等实数解方程没有实数解6. 拓展：关于直线与抛物线的交点知识（1） y 轴与抛物线 y = ax 2 + bx + c 得交点为(0, c ) .（2）与 y 轴平行的直线 x = h 与抛物线 y = ax 2 + bx + c 有且只有一个交点( h ,ah 2 + bh + c ).（3） 抛物线与 x 轴的交点二次函数 y = ax 2 + bx + c 的图像与 x 轴的两个交点的横坐标 x 1 、 x 2 ，是对应一元二次方程 ax 2 + bx + c = 0 的两个实数根.抛物线与 x 轴的交点情况可以由对应的一元二次方程的根的判别式判定：①有两个交点⇔ ∆ > 0 ⇔ 抛物线与 x 轴相交；②有一个交点（顶点在 x 轴上） ⇔ ∆ = 0 ⇔ 抛物线与 x 轴相切； ③没有交点⇔ ∆ < 0 ⇔ 抛物线与 x 轴相离. （4）平行于 x 轴的直线与抛物线的交点同（3）一样可能有 0 个交点、1 个交点、2 个交点.当有 2 个交点时，两交点的纵坐标相等，设纵坐标为 k ，则横坐标是 ax 2 + bx + c = k 的两个实数根.（5）一次函数 y = kx + n (k ≠ 0)的图像l 与二次函数 y = ax 2 + bx + c (a ≠ 0)的图像⎧ y = kx + nG 的交点，由方程组⎨ y = ax 2+ bx + c的解的数目来确定： ①方程组有两组不同的解时⇔ l 与G 有两个交点;( x + x ) - 4x x 21 2 1 2⎛ - ⎪ - b ⎫24c ⎝ a ⎭ ab 2 - 4ac a ( x - x )21 2 ②方程组只有一组解时⇔ l 与G 只有一个交点； ③方程组无解时⇔ l 与G 没有交点.（6）抛物线与 x 轴两交点之间的距离：若抛物线 y = ax 2 + bx + c 与 x 轴两交点为A (x ，0)，B (x ，0)，由于 x 、 x 是方程 ax 2 + bx + c = 0 的两个根，故1212x + x = - b , x ⋅ x = c 1 2a 1 2 aAB = x 1 - x 2 == = = =知识点四：利用二次函数解决实际问题7. 利用二次函数解决实际问题，要建立数学模型，即把实际问题转化为二次函数问题，利用题中存在的公式、内含的规律等相等关系，建立函数关系式，再利用函数的图象及性 质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义.利用二次函数解决实际问题的一般步骤是：(1) 建立适当的平面直角坐标系；(2) 把实际问题中的一些数据与点的坐标联系起来；(3)用待定系数法求出抛物线的关系式；(4)利用二次函数的图象及其性质去分析问题、解决问题.∆a“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。