弹簧选材及计算公式

弹簧参数尺寸及计算公式弹簧是一种用来储存和释放机械能的装置，应用广泛于机械、汽车、电器等领域。

弹簧的参数、尺寸以及计算公式对于设计和选择弹簧十分重要。

1.弹簧的参数：- 预压力（Preload）：弹簧在未加载之前的初始压力。

- 弹性系数（Spring Constant）：弹簧在单位变形下的恢复力。

- 卸载长度（Unloaded Length）：未加载时的弹簧长度。

- 动载荷（Dynamic Load）：弹簧所承受的变动力。

- 疲劳寿命（Fatigue Life）：弹簧能够承受的循环加载次数。

2.弹簧的尺寸：- 线径（Wire Diameter）：弹簧材料的直径，决定着弹簧的承载能力。

- 外径（Outer Diameter）：弹簧的最大直径。

- 内径（Inner Diameter）：弹簧的最小直径。

- 组件高度（Solid Height）：弹簧在最大压缩状态下的高度。

- 活动齿数（Active Coils）：弹簧上具有弹性的齿数。

- 紧齿数（Total Coils）：弹簧上总共的齿数。

3.弹簧的计算公式：-弹性系数（K）的计算公式：K=Gd^4/(8Na^3)其中，G为剪切模量，d为线径，N为齿数，a为活动齿数。

-预压力（P）的计算公式：P=K*δ其中，δ为弹簧的压缩/拉伸变形量。

-力（F）的计算公式：F=K*δ弹簧所受的力正比于弹性系数与变形量之积。

-弹簧的伸长（δ）计算公式：δ=(F*L)/(K*Gd^4)其中，L为弹簧的长度。

-弹簧的疲劳寿命（Nf）计算公式：Nf=(C*S^b)/(F^b)其中，C为常数，S为应力幅值（一般为弹簧的最大变形量）。

以上公式仅为常见的弹簧计算公式，实际应用中可能还需要考虑更多的因素，如安全系数、材料的疲劳强度等。

总结起来，弹簧的参数、尺寸和计算公式对于弹簧的设计和选择至关重要。

具体的参数和尺寸根据实际应用需求和弹簧类型来确定，而计算公式则是根据力学原理和材料特性推导得出的。

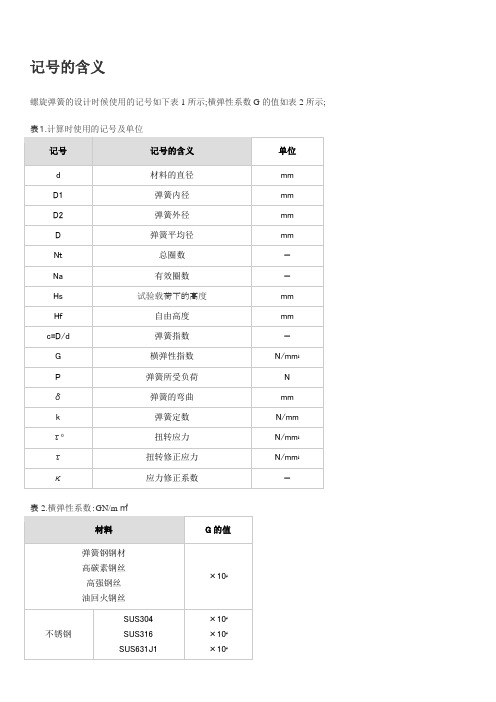
记号的含义螺旋弹簧的设计时候使用的记号如下表1所示;横弹性系数G的值如表2所示; 表１.计算时使用的记号及单位表2.横弹性系数：GN/m㎡螺旋弹簧的设计用基本计算公式螺旋弹簧的负荷和弹簧定数弯曲的关系具有线性特征弹簧的负荷和弯曲是成比例的;从螺旋弹簧的尺寸求弹簧的定数压缩螺旋弹簧的素线径因扭转而产生弯曲的弹簧定数K螺旋弹簧的扭转应力螺旋弹簧的扭转修正应力螺旋弹簧试验载荷下高度端面磨削的情况下螺旋弹簧两端的各厚度之和不同材质螺旋弹簧在高温时的机械特性表3. 不同温度下弹簧的横弹性定数N/mm2表4. 不同温度下弹簧的容许应力N/mm2组合弹簧的计算公式螺旋弹簧的直列和并列弹簧在设计的时候,虽然应该尽可能设计一根弹簧,但是一根弹簧无法满足的情况下,也会对多根弹簧进行组合以满足设计要求;弹簧的组合有纵向排列的直列法和横向排列的并列法两种模式;这样的分类,不仅和螺旋弹簧有关,盘形弹簧等其他种类的弹簧也是一样,也会进行直列和并列组合来使用;从负荷的观点来考虑的话,对各个弹簧作用相等的力的组合方式叫直列,各个弹簧变位相等的组合方式叫并列;图1. 螺旋弹簧的直列组合和并列组合图示显示的是使用了3个弹簧的情况;n个弹簧的各个定数就是k1 , k2 ,, kn弹簧并列和直列组合时全部的定数K公式参照下列;式1. 并列的弹簧定数计算公式式2. 直列的弹簧定数计算公式并列组合的螺旋弹簧的个数增加会导致全体弹簧定数变大,直列组合个数的增加会导致弹簧定数变小;図2. 亲子弹簧并列的字面意思就是横向排列,但是单纯的排列空间上不好安排,所以像图3那样弹簧的内侧和弹簧组合,同心相排的情况下很多;这样的排列一般被称作亲子弹簧;但是,同心组合的情况下,为了弹簧不互相缠绕在一起,交替的改变弹簧卷的方向,或者确保弹簧和弹簧之间有一定的间隙是很有必要的;另外,对弹簧的组合进行下功夫的话,像下图a,b那样,可以制作出不是直线的弹簧特性;例如需要像图4那样特性弹簧的时候,需要对自由长或者不同密着负荷的弹簧进行组合;图5的弹簧特性是在图6那样结构中加入弹簧,事先加上负荷,就会得到〔上段弹簧定数〕＜〔下段弹簧定数〕这样的组合;図5.得到特殊弹簧特性的结构弹性能量的计算公式弹簧内积蓄的能量弹簧加上负荷的话,弹簧内就会被积蓄能量;弹簧内积蓄的能量U,和图6中荷重Ｐ―変位δ曲线围成的面积相同図6. 弹簧内积蓄的能量用公式3来表示;一般常见的弹簧积蓄能量的公式;公式4适用场合为像上图a那样存在线性关系的时候,也就是公式5另外,说到能量的积蓄和释放,一般会像图6的a,b,c所表示的那样, 增加负荷的时候和去除负荷的时候,是相同的负荷-变位曲线,增加负荷积蓄能量,一旦去除负荷能量就会完全释放,但是像图6d那样具有滞后循环特性的弹簧,被曲线围起来的面积的能量,从增加负荷到去除负荷就会消耗一个周期;螺旋弹簧的振动计算公式螺旋弹簧有固有的振动数弹簧加上负荷,使其变形,加上力,去除力的时候弹簧会发生振动,这个振动数会因不同的弹簧而不同,但是每种弹簧都有其固有的振动数;弹簧自身的质量为m的时候,其固有振动数f就为式6来表示;这里的α ,根据弹簧的固定条件和振动的方向为一定的定数;另外,像图7,8,9,10所表示的那样质量为ms 的弹簧用质量为m 的物体来固定,物体振动时候的固有振动数f0就为 公式7来表示;这里也结合了板簧来进行说明螺旋弹簧-质量系单侧板簧-质量系两端销支撑板簧-质量系两端固定支撑板簧-质量系弹簧的质量ms和物体的质量m相比,一般情况下都比较小,所以一般β看作β＝０的情况比较多, 但是必须考虑到弹簧质量的时候,近似图9中β＝,图10中β＝来进行计算;进行弹簧设计的时候,虽然弹簧的定数很重要,但是这个固有振动数也是必须要考虑到的;弹簧碰撞的计算公式弹簧是为了缓和冲击力碰撞时为了冲击力降低,比较有效果的手段就是使用弹簧;为了评价缓和冲击的能力,像下面那样用缓冲效率η来定义;公式8这里的M为碰撞侧的质量、v0 为碰撞时的速度、Pmax为最大冲击力、δmax为被碰撞侧的最变位; η的值一般为0以上1以下,虽然理想的情况下为1,一定弹簧定数弹簧的碰撞效率η就会变为1/2;1-1 长方形断面的单侧支撑弹簧薄板弹簧最简单的就是长方形断面的单侧支撑弹簧,A为固定端,B为自由端,在B点加上负荷P的情况下的计算公式为这里的Ｉ表示2次力矩;来表示,较大的情况下来表示;因此, 较大情况的计算公式为;ν为泊松比、钢的情况下、ν≒;应力在固定端为最大时来表示;这里薄板弹簧材料的纵弹性系数E的值在表2表示;表１. 计算用记号及单位表2.纵弹性系数：EN/m㎡1-2 梯形单侧支撑薄板弹簧计算公式図2像图2那样,薄板弹簧的板厚一定的时候,板幅为直线式变化的情况下,自由端的弯曲为公式4公式中B的计算,根据板厚不同分为下列2种板厚较厚的情况下板厚非常薄厚的情况下、另外,公式中的值,根据β=b1/b可以从图3中求出;图31-3板幅带台阶的薄板弹簧计算公式图4像图4那样,当板厚一定时,板幅带台阶的薄板弹簧的自由端弯曲为,公式5这里,是由P而产生的台阶部位A的弯曲和弯曲角,的长度为,表示板幅的单边弹性的自由端的弯曲;1-4圆环状单侧支撑的薄板弹簧计算公式图5像图5这样,板厚的中心为直线,板幅的中心线为圆弧状,垂直负荷P在自由端作用的时候,任意位置φ的弯曲δφ为这里的C表示板的扭转强度;1-5圆弧状单侧支撑的薄板弹簧计算公式图6板厚的中心线为圆弧状的单侧支撑弹簧,求其在负荷作用下的弯曲,一般利用卡氏定律来求解;以下就是利用该定律的计算结果;如图6表示在圆弧状薄板上,垂直负荷P,水平负荷W各自在中心角的位置上作用的时候,中心角的位置Y方向的弯曲为,X方向的弯曲为;因P产生的弯曲,的时候、公式7的时候、公式8因W产生的弯曲的时候、公式9的时候、公式10图7图7中, 、各自公式如下;公式11公式12图8如图8 的时候,公式13公式14因P产生的最大应力已经在固定端发生,公式15因W产生的最大应力,的时候再图8的A点产生, 的时候在固定端产生,公式161-6 圆轮状的薄板弹簧计算公式图9像图9那样圆轮状的弹簧,因为是上下对称,它的弯曲就是图8的2倍;公式171-7 半圆和1/4圆组合成的薄板弹簧的计算公式图10图10的弯曲为公式18最大应力在固定端产生,公式191-8 圆弧的薄板弹簧的计算公式图11图11左侧所显示的形状自由端的弯曲为公式20如图11右侧形状所示,水平方向被约束的圆弧的弯曲为公式21这两种情况,无论是哪一种,最大应力都为公式221-9 圆弧和带有直线部分的薄板弹簧的计算公式1-9-1其1图12如图12,由直线部分AB和圆弧部分BD组合而成,一端D被固定,另一端A在垂直负荷P或者水平负荷W的作用下,,如以下表示;公式23公式24的时候,公式25W作用的时候,公式26公式27这里,公式中的,为另外,最大应力的时候在固定端产生, 的时候在C点产生;1-9-2 圆弧和带有直线部分的薄板弹簧的计算公式其2图13图13中的弹簧,为2个图12中的弹簧组合在一起,在负荷作用下的弯曲为公式23中得到的倍;公式28图14如图14所示,直线部分和带有圆弧部分弹簧在A端的弯曲为公式29这里、、;最大弯曲应力,在C点产生公式30、的时候,最大应力在固定端发生,,的时候,公式311-9-3 圆弧和带有直线部分的薄板弹簧的计算公式其3图15如图5的情况时,分割AC部分和CD部分,对公式25弯曲的2倍和以下公式的弯曲进行各自的计算,然后结合之后算出A部分的弯曲;公式321-9-4 圆弧和带有直线部分的薄板弹簧的计算公式其4图16如图16所示,直线部分被固定,圆弧部分的A端受到负荷的作用,A端的垂直弯曲和水平弯曲,,受到负荷P作用的时候,公式33公式34受到负荷W作用的时候,公式35公式36图17如图17的形状,受到负荷P作用的时候,公式37公式38受到负荷W作用的时候,公式39公式40这里, ;1-9-5 圆弧和带有直线部分的薄板弹簧的计算公式其5图18如图18所示,曲率半径比较小的圆弧和直线的组合而成的弹簧,忽视圆弧部分的半径之后的弯曲如下所示;公式41最大应力,的时候,在BC部分产生公式42的时候,在固定端产生,公式431-9-6 圆弧和直线部分结合的比较复杂的薄板弹簧的计算公式薄板弹簧的形状,实际上圆弧部分和直线部分复杂结合的情况比较多,可以利用以上介绍的各种公式;以下展示的形状和计算公式都是利用以上所介绍的内容而进行的实际应用;图19图19的形状为2 个图13的组合,可以利用公式28的2倍来求其弯曲;图20图20的形状,两端部分和图10是相同的,应力的公式可以利用公式19来计算;对称轴单侧的弯曲就是公式18加上部分,因此单侧的弯曲就是公式44公式45２．特性不同用途的薄板弹簧计算公式2-1 非线性特征的薄板弹簧的计算公式图21非线形特性的薄板弹簧,像图21那样,公式如下显示;式462-2 受到轴负荷和横负荷的薄板弹簧计算公式図22薄板弹簧像图22那样的负荷一般是用来测定机器的;一端被固定,另一端虽然可以横方向运动但是不能旋转;这种情况时,轴负荷P和压弯负荷相比较小,横负荷Q的弯曲及应力为以下公式表示;公式47公式48P比座面负荷大的时候,根据上面公式中的来决定系数以及;这里为,这里的系数,为以下公式;公式49公式502-3 弯曲较大的薄板弹簧的计算公式2-3-1 长方形断面的薄板弹簧图23弯曲较大的情况下,变化到,加上其他影响的计算结果如图24所示;图24图的横轴由表示,纵轴由,表示,表示板的弯曲刚度,比较大的话, ;看图24就可以明白,的值较小的话,也就是负荷P较小的时候,和与1比较相近,的时候,,;因此,这种程度的变形,实际运用中也许并不被采用;2-3-2 梯形单侧支撑薄板弹簧图25图26梯形单侧支撑薄板弹簧的弯曲较大的时候近似值如图25,26所示;横轴为,以为参数,纵轴展示的是弯曲和应力的减少率,这个适用于公式;记号的含义弹簧的设计用记号如下记表1所示,横弹性系数G的值如表2所示;表１. 计算用记号及单位表2.横弹性系数：GN/m㎡线圈部分的弯曲及应力线圈部分弯曲的基本公式是利用压缩弹簧的公式来进行计算的;但是,对于负荷,要考虑到初张力,这个初张力为Pi,任意负荷为P根据公式1,弯曲δ就为另外,剪切应力τ0τ 和压缩弹簧相同,公式如上;钩子部分的应力钩子部分,根据弯曲力矩和扭转力矩会发生拉伸应力以及剪断应力,正确的计算是非常复杂的;这里就对半圆钩子,U 型钩子进行简单的近似计算;i半圆钩子的时候图1中,拉伸应力的最大值在A部分的内侧,剪切应力的最大值在B部分的内侧发生;A部分内侧的最大拉伸应力是弯曲力矩M和轴负荷P的拉伸应力的和,这里的K1是基于曲率的应力集中系数, 代入下列公式;整理公式7,得到但是K1为这里,C为线圈部分的弹簧指数;B部分内侧的最大剪断应力和扭转力矩M相关,得到这里的K2是基于曲率的应力集中系数, 代入下列公式;iiU型钩子的时候图2中,拉伸应力的最大值在A部内侧,剪切应力的最大值在B部的内侧发生;A部分内侧的最大拉伸应力是弯曲力矩M和轴负荷P的拉伸应力的和,公式为这里K3是基于曲率的应力集中系数, 代入下列公式;整理公式13,得到但是Ｋ′3 为B部分的最大剪切应力,和半圆钩子相同代入公式11;另外,其他形状的钩子也是同样的考虑方法;。

各种弹簧计算范文弹簧是一种常见的机械零件，具有储存和释放机械能的能力。

在工程设计和力学分析中，弹簧的计算是一个重要的问题。

本文将介绍各种弹簧计算的方法和技巧。

1.弹簧刚度计算：弹簧的刚度是指弹簧单位变形所产生的反作用力。

刚度可以用力学公式计算，公式为：k=F/x其中，k为弹簧刚度，单位为牛顿/米（N/m）；F为施加在弹簧上的力，单位为牛顿（N）；x为弹簧的变形量，单位为米（m）。

2.弹簧的长度计算：弹簧的长度可以通过材料弹性模量和簧片的几何尺寸计算。

通常采用钢材制作的弹簧，长度计算公式如下：L=(8*n*t*R)/(π*d³*E)+d其中，L为弹簧的总长度，单位为米（m）；n为簧片的数量；t为簧片的厚度，单位为米（m）；R为簧片弧度，单位为米（m）；d为簧片的宽度，单位为米（m）；E为材料的弹性模量，单位为帕斯卡（Pa）。

3.弹簧的应变能计算：弹簧的应变能是指弹簧储存的机械能。

弹簧的应变能可以通过弹簧刚度和变形量计算，公式为：U=(1/2)*k*x²其中，U为应变能，单位为焦耳（J）；k为弹簧刚度，单位为牛顿/米（N/m）；x为弹簧的变形量，单位为米（m）。

4.弹簧的最大变形量计算：弹簧的最大变形量是指弹簧在受到最大外力作用时的变形量。

最大变形量可以通过弹簧刚度和作用力的比较计算，公式为：x_max = F_max / k其中，x_max为弹簧的最大变形量，单位为米（m）；F_max为施加在弹簧上的最大力，单位为牛顿（N）；k为弹簧刚度，单位为牛顿/米（N/m）。

5.弹簧的材料选取：弹簧的材料选取需要考虑加载条件、工作环境和弹簧的工作寿命等因素。

一般情况下，选取材料时需要考虑弹簧的刚度、强度和耐磨性等性能指标，常用材料有高碳钢、合金钢和不锈钢等。

在选取材料时，还需要根据具体需求进行试验和验证。

综上所述，弹簧的计算涉及弹簧刚度、长度、应变能、最大变形量和材料选取等方面。

计算弹簧需要考虑材料的弹性模量、弹簧的几何尺寸和施加在弹簧上的外力。

压簧、拉簧、扭簧弹力计算公式压力弹簧压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；·弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；·弹簧常数公式（单位：kgf/mm）：G=线材的钢性模数：琴钢丝G=8000，不锈钢丝G=7300，磷青铜线G=4500 ，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

·初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）·弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm).·弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

弹簧计算公式范文弹簧是一种常用的机械弹性元件，主要用于储存能量、缓冲震动、调节压力和支撑重物等多种应用。

弹簧的计算公式主要包括弹性力、弹簧刚度、变形量和共振频率等。

1.弹性力的计算公式：弹簧的弹性力是指弹簧所受的恢复力，即外力消失后，弹簧产生的力。

弹性力与弹簧的变形量成正比。

F=k*x其中，F为弹性力，k为弹簧的刚度系数，x为弹簧的变形量。

2.弹簧刚度的计算公式：弹簧的刚度是指单位变形量产生的弹性力。

刚度系数越大，弹簧刚度越高。

k=(G*d^4)/(8*n*D^3)其中，k为弹簧刚度，G为弹簧材料的剪切模量，d为弹簧丝径，n为弹簧的圈数，D为弹簧的平均直径。

3.弹簧变形量的计算公式：弹簧的变形量是指弹簧在受力后的长度变化。

x=F/k其中，x为变形量，F为外力，k为弹簧刚度。

4.弹簧的共振频率计算公式：共振频率是指弹簧在一定条件下形成共振的频率。

f=1/(2*π)*√(k/m)其中，f为共振频率，k为弹簧刚度，m为弹簧的质量。

此外，还有一些特殊情况下的弹簧计算公式：5.扭簧的刚度计算公式：扭簧的刚度是指扭簧所受的力矩与其转角之间的比值。

k=(G*d^4)/(10.4*n*D^3)其中，k为扭簧刚度，G为扭簧材料的剪切模量，d为扭簧丝径，n为扭簧的圈数，D为扭簧的平均直径。

6.悬挂式弹簧的刚度计算公式：悬挂式弹簧是指一端固定，另一端受力，通常用于汽车悬挂系统等。

k=(G*d^4)/(8*n*D^3)其中，k为悬挂式弹簧刚度，G为弹簧材料的剪切模量，d为弹簧丝径，n为弹簧的圈数，D为弹簧的平均直径。

综上所述，弹簧的计算公式涵盖了弹性力、弹簧刚度、变形量和共振频率等多个方面，可根据实际需求选择相应的计算公式进行弹簧的设计和分析工作。

弹簧参数、尺寸及计算公式弹簧参数及尺寸一、小型圆柱螺旋拉伸弹簧尺寸及参数1、弹簧的工作图及形式1.1 工作图样的绘制按GB4459、4规定。

1.2 弹簧的形式分为A型和B型两种。

2、材料弹簧材料直径为0.16~0.45mm，并规定使用GB4357中B组钢丝或YB(T)11中B组钢丝。

采用YB(T)11中B组钢丝时，需在标记中注明代号“S”。

3、制造精度弹簧的刚度、外径、自由长度按GB1973规定的3级精度制造。

如需按2级精度制造时，加注符号“2”，但钩环开口尺寸均按3级精度制造。

4、旋向弹簧的旋向规定为右旋。

如需左旋应在标记中注明“左”。

5、钩环开口弹簧钩环开口宽度a为0.25D~0.35D。

注：D为弹簧中径。

6、表面处理6.1采用碳素弹簧钢丝制造的弹簧，表面一般进行氧化处理，但也可进行镀锌、镀镉、磷化等金属镀层及化学处理。

其标记方法应按GB1238的规定。

6.2采用弹簧用不锈钢丝制造的弹簧，必要时可对表面进行清洗处理，不加任何标记。

7、标记7.1标记的组成弹簧的标记由名称、型式、尺寸、标准编号、材料代号(材料为弹簧用不锈钢丝时)以及表面处理组成。

规定如下：7.2标记示例例1:A型弹簧，材料直径0.20mm，弹簧中径3.20mm，自由长度8.80mm，左旋，刚度、外径和自由长度的精度为2级，材料为碳素弹簧钢丝B组，表面镀锌处理。

标记:拉簧A0.20*3.20*8.80-2左GB1973.2——89-D-Zn例2：B型弹簧，材料直径0.40mm，弹簧中径5.00mm，自由长度17.50mm，右旋，刚度、外径和自由长度的精度为3级，材料为弹簧用不锈钢丝B组。

标记：拉簧B0.40*5.00*17.50 GB1973.2--89-S8、计算依据标准中的计算采用如下基本公式：切应力(N/mm²)：τ=(8PDK)/(πd³)变形量(mm)：F=(8PD³n)/ Gd4弹簧钢度(N/mm):P′=P/ F=(Gd4)/(8D³n)曲度系数：K =(4C-1)/(4C-4)+ (0.615)/C旋转比：C =D/d 自由长度(mm)：H。

弹簧的计算公式范文弹簧是一种常见的弹性元件，广泛应用于工业、交通、家居等领域。

弹簧的计算公式是根据弹簧的材料、构造参数以及受力情况等因素来确定的，下面将分别介绍弹簧的计算公式。

1.弹簧的刚度计算公式：弹簧的刚度描述了弹簧的抗弯刚度。

弹簧刚度的计算公式可以根据材料的弹性模量、截面形状、长度等参数来计算。

弹簧的刚度公式为：k=(G*d^4)/(8*n*D^3)其中，k表示弹簧的刚度（单位为N/m），G表示弹簧材料的剪切模量（单位为N/m^2），d表示弹簧线直径（单位为m），n表示弹簧的圈数，D表示弹簧的平均直径（单位为m）。

2.弹簧的变形计算公式：弹簧在受力时会发生变形，弹簧的变形计算公式可以根据受力情况、材料性质、几何形状等参数来计算。

弹簧的变形公式根据受力情况的不同可分为拉伸弹簧和扭转弹簧的变形公式。

拉伸弹簧的变形公式为：δ=(F*L)/(k*n)（单位为N），L表示弹簧的长度（单位为m），k表示弹簧的刚度（单位为N/m），n表示弹簧的圈数。

扭转弹簧的变形公式为：θ=(M*L)/(k*n)其中，θ 表示弹簧的扭转角（单位为rad），M 表示施加于弹簧上的弯矩（单位为N·m），L 表示弹簧的长度（单位为m），k 表示弹簧的刚度（单位为N/m），n 表示弹簧的圈数。

3.弹簧的应力计算公式：弹簧在受力时会发生应力，弹簧的应力计算公式可以根据受力情况、材料性质、几何形状等参数来计算。

弹簧的应力公式根据受力情况的不同可分为拉伸弹簧和扭转弹簧的应力公式。

拉伸弹簧的应力公式为：σ=(F*d)/(4*n*D^2)其中，σ表示弹簧的应力（单位为N/m^2），F表示施加于弹簧上的力（单位为N），d表示弹簧线直径（单位为m），n表示弹簧的圈数，D 表示弹簧的平均直径（单位为m）。

扭转弹簧的应力公式为：τ=(T*r)/(J*n)扭矩（单位为N·m），r表示弹簧的平均半径（单位为m），J表示弹簧的截面转动惯量（单位为m^4），n表示弹簧的圈数。

弹簧计算公式弹簧计算公式是用来计算弹簧的弹力的数学公式。

弹簧是一种用来存储和释放能量的弹性元件，广泛应用于各种机械装置和工具中。

根据弹簧的形状和用途，可以分为压簧、拉簧和扭簧。

下面将分别介绍这三种弹簧的弹力计算公式。

1.压簧弹力计算公式压簧是一种用于承受压缩力的弹簧，通常由钢丝绕成螺旋形。

压簧的弹力与其形状、材料的物理性质以及受到的压缩力有关。

压簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为簧系数，x是压簧的变形量。

压簧的弹力与其变形量呈线性关系，即弹簧的弹力与其压缩或拉伸的距离成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

2.拉簧弹力计算公式拉簧是一种用于承受拉力的弹簧，通常由钢丝绕成螺旋形。

拉簧的弹力与其形状、材料的物理性质以及受到的拉力有关。

拉簧的弹力计算公式如下：F=k*x其中，F表示弹簧的弹力，k是一个常数，称为拉簧的刚度系数或簧系数，x是拉簧的变形量。

拉簧的弹力与其变形量呈线性关系，即弹簧的弹力与其拉伸或压缩的长度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

3.扭簧弹力计算公式扭簧是一种用于承受扭转力的弹簧，通常由钢丝绕成螺旋形。

扭簧的弹力与其形状、材料的物理性质以及受到的扭转力矩有关。

扭簧的弹力计算公式如下：T=k*φ其中，T表示弹簧的扭力，k是弹簧的刚度系数或簧系数，φ是弹簧的扭转角度。

扭簧的弹力与其扭转角度成正比。

簧系数k的大小取决于弹簧的材料和几何形状。

需要注意的是，以上的公式都是基于线性弹性假设的情况下推导出来的。

实际上，弹簧的变形行为通常是非线性的，因此在计算弹力时需要考虑非线性效应，例如在变形量较大或载荷较高的情况下。

除了弹力的计算公式，还可以根据实际需要计算弹簧的弹性系数、刚度系数、临界长度等参数。

这些参数对于设计和选择弹簧具有重要意义，可以保证弹簧在工作过程中具有足够的弹性和耐力。

弹簧参数弹簧参数⑴弹簧丝直径d：制造弹簧的钢丝直径。

⑵弹簧外径D2：弹簧的最⼤外径。

⑶弹簧内径D1：弹簧的最⼩外径。

⑷弹簧中径D：弹簧的平均直径。

它们的计算公式为：D=（D2+D1）÷2=D1+d=D2－d⑸t：除⽀撑圈外，弹簧相邻两圈对应点在中径上的轴向距离成为节距，⽤t表⽰。

⑹有效圈数n：弹簧能保持相同节距的圈数。

⑺⽀撑圈数n2：为了使弹簧在⼯作时受⼒均匀，保证轴线垂直端⾯、制造时，常将弹簧两端并紧。

并紧的圈数仅起⽀撑作⽤，称为⽀撑圈。

⼀般有1.5T、2T、2.5T，常⽤的是2T。

⑻总圈数n1:有效圈数与⽀撑圈的和。

即n1=n+n2.⑼⾃由⾼H0：弹簧在未受外⼒作⽤下的⾼度。

由下式计算：H0=nt+(n2-0.5）d=nt+1.5d(n2=2时）⑽弹簧展开长度L：绕制弹簧时所需钢丝的长度。

L≈n1（ЛD2）2+n2（压簧）L=ЛD2n+钩部展开长度（拉簧）⑾螺旋⽅向：有左右旋之分，常⽤右旋，图纸没注明的⼀般⽤右旋。

⑿弹簧旋绕⽐：中径D与钢丝直径d之⽐。

符号单位A——弹簧材料截⾯⾯积（mm2）；当量弯曲刚度（N/mm）；系数a——距形截⾯材料垂直于弹簧轴线的边长（mm）；系数B——平板的弯曲刚度（N/mm）；系数b——⾼径⽐；距形截⾯材料平⾏于弹簧轴线的边长（mm）；系数C——螺旋弹簧旋绕⽐；碟簧直径⽐；系数D——弹簧中径（mm）D1——弹簧内径（mm）D2——弹簧外径（mm）d——弹簧材料直径（mm）E——弹簧模量（MPa）F——弹簧的载荷（N）F’——弹簧的刚度Fj——弹簧的⼯作极限载荷（N）Fo——圆柱拉伸弹簧的初拉⼒（N）Fr——弹簧的径向载荷（N）F’r——弹簧的径向刚度（N/mm）Fs——弹簧的试验载荷（N）f——弹簧的变形量（mm）fj——⼯作极限载荷Fj下的变形量（mm）fr——弹簧的静变形量（mm)fs——试验载荷Fs下弹簧的变形量（mm）；线性静变形量（mm）fo——拉伸弹簧对应于处拉⼒Fo的假设变形量（mm）；膜⽚的中⼼变形量（mm）G——材料的切变模量（MPa）g——重⼒加速度，g=9800mm/s2H——弹簧的⼯作⾼（长）度（mm）Ho——弹簧的⾃由⾼（长）度（mm)Hs——弹簧试验载荷下的⾼（长）度（mm）h——碟形弹簧的内载锥⾼度（mm）I——惯性矩（mm4）Ip——极惯性矩（mm4）K——曲度系数；系数Kt——温度修正系数σ——弹簧⼯作时的正应⼒（Mpa）σb——材料抗拉强度（Mpa）σj——材料的⼯作极限应⼒（Mpa）σs——材料的抗拉屈服点（Mpa）τ——弹簧⼯作时的切应⼒（Mpa）k——系数L——弹簧材料的展开长度（mm）l——弹簧材料有效⼯作圈展开长度（mm）；板弹簧的⾃由弦长（mm）M——弯曲⼒矩（N·mm）m——作⽤于弹簧上物体的质量（kg）ms——弹簧的质量（kg）N——变载荷循环次数n——弹簧的⼯作圈数nz——弹簧的⽀承圈数n1——弹簧的总圈数pˊ——弹簧单圈的刚度（N/mm）R——弹簧圈的中半径（mm）R1——弹簧圈的内半径（mm）R2——弹簧圈的外半径（mm）r——阻尼系数S——安全系数T——扭矩；转矩（N·mm）Tˊ——扭转刚度（N·mm/（º；））t——弹簧的节矩tc——钢索节距（mm）U——变形能（N·mm）；（N·mm·rad）V——弹簧的体积（mm³；）v——冲击体的速度（mm/s）Zm——抗弯截⾯系数（mm³；）Zt——抗扭截⾯系数（mm³；）α——螺旋⾓（º；）；系数β——钢索拧⾓（º；）；圆锥半⾓（º；）；系数δ——弹簧圈的轴向间隙（mm）δr——组合弹簧圈的径向间隙（mm）ζ——系数η——系数θ——扭杆单位长度的扭转⾓（rad）κ——系数µ——泊松⽐；长度系数ν——弹簧的⾃振频率（Hz）Vr——弹簧所受变载荷的激励频率（Hz）τb——材料的抗剪强度（Mpa）τj——弹簧的⼯作极限切应⼒（Mpa）τo——材料的脉动扭转疲劳极限（Mpa）τs——材料的抗扭屈服点（Mpa）τ-1——材料的对称循环扭转疲劳极限（Mpa）υ——扭转变形⾓（º；）；（rad）规定画法⑴在平⾏螺旋弹簧线的视图上，各圈的轮廓线画成直线。