2013年中考数学复习冲刺预测卷 抽样与数据分析

32013年中考数学统计与概率模拟试题及答案一、选择题（本题共10小题，每小题4分，满分40分） 1.若一组数据1，2，3，x 的极差为6,贝U x 的值是（）。

A. 7B. 8C. 9D . 7 或一3X 4的平均数是X ，方差是S 2,则样本X 1+3, X 2+3, X B +3, X 4+3的平均数和方差分别是（）。

B. 明天本市70%勺地区下雨，30%勺地区不下雨C. 明天本市一定下雨D. 明天本市下雨的可能性是 70% 7.某校男生中，若随机抽取若干名同学做“是否喜欢足球”的问卷调查，抽到喜欢足球的3 3同学的概率是3，这个3的含义是（）。

55A. 只发出5份调查卷，其中三份是喜欢足球的答卷B. 在答卷中，喜欢足球的答卷与总问卷的比为3 ：8C.在答卷中，喜欢足球的答卷占总答卷的 -5D. 发出100份问卷，有60份答卷是不喜欢足球2个黄球和2个红球，任意摸出一个球后放回，再任意摸出一个球，则两次都摸到红球的概率为（ ）。

A.2.样本X 、人、％、2A . x +3, S+3 B2 2x +3, S C . x , S+3 D3.刘翔在出征北京奥运会前刻苦进行110米跨栏训练, 教练对他20次的训练成绩进行统计分析，判断他的成绩是否稳定，则教练需要知道刘翔这20次成绩的（ ）。

A 、方差B•平均数C.频数D.众数4•盒中装有5个大小相同的球，其中一个红球和一个白球的概率是（3个白球，2个红球，从中任意取两个球，恰好取到 ）。

A. 425 5.如图所示的两个圆盘中， 指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是（ ）。

191065A.; B . ; C . ; D .— 25 ' 25 ' 25 ' 256.其市气象局预报称：明天本市的降水概率为 70%这句话指的是（A .明天本市70%勺时间下雨, 30%勺时间不下雨 &一个袋中装有D.9.袋中有5个红球, 有m个白球，从中任意取一个球,2恰为白球的机会是，则m为（A . 10B 16C . 20D 1810. 现有A、B两枚均匀的小立方体小莉掷A立方体朝上的数字为（立方体的每个面上分别标有数字x、小明掷B立方体朝上的数字为1, 2, 3, 4, 5, 6).用y来确定点P ( x, y),3那么它们各掷一次所确定的点P 落在已知抛物线 y = _x 2 • 4x 上的概率为（11. 袋中有红、黄、蓝3球，从中摸出一个，放回，共摸3次，摸到二黄一蓝的机会是 _________________ 。

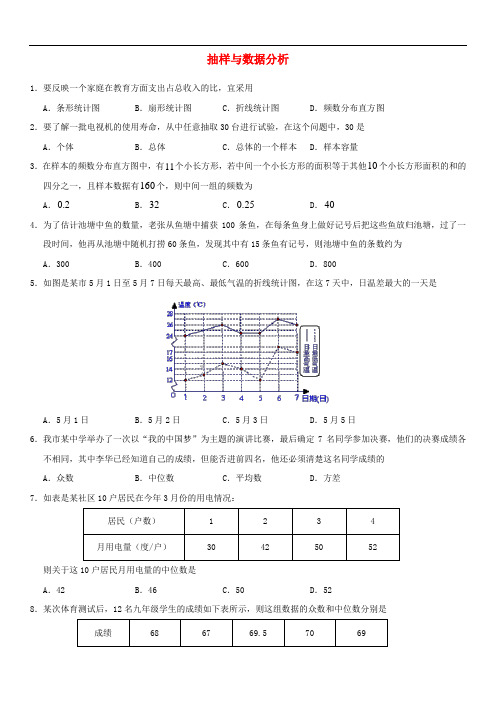
抽样与数据分析1．要反映一个家庭在教育方面支出占总收入的比，宜采用A．条形统计图B．扇形统计图C．折线统计图D．频数分布直方图2．要了解一批电视机的使用寿命，从中任意抽取30台进行试验，在这个问题中，30是A．个体B．总体C．总体的一个样本D．样本容量3．在样本的频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其他10个小长方形面积的和的四分之一，且样本数据有160个，则中间一组的频数为A．0.2B．32C．0.25D．404．为了估计池塘中鱼的数量，老张从鱼塘中捕获100条鱼，在每条鱼身上做好记号后把这些鱼放归池塘，过了一段时间，他再从池塘中随机打捞60条鱼，发现其中有15条鱼有记号，则池塘中鱼的条数约为A．300 B．400 C．600 D．8005．如图是某市5月1日至5月7日每天最高、最低气温的折线统计图，在这7天中，日温差最大的一天是A．5月1日B．5月2日C．5月3日D．5月5日6．我市某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定7名同学参加决赛，他们的决赛成绩各不相同，其中李华已经知道自己的成绩，但能否进前四名，他还必须清楚这名同学成绩的A．众数B．中位数C．平均数D．方差7．如表是某社区10户居民在今年3月份的用电情况：则关于这10户居民月用电量的中位数是A．42 B．46 C．50 D．528．某次体育测试后，12名九年级学生的成绩如下表所示，则这组数据的众数和中位数分别是A．69，69.5 B．70，69 C．69，69 D．69，709．某校四个绿化小组一天植树的棵数如下：10，x，10，8，已知这组数据的众数与平均数相等，则这组数据的中位数是A．8 B．9 C．10 D．1210．某科普小组有5名成员，身高分别为（单位：cm）160，165，170，163，167，增加1名身高为165 cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是A．平均数不变，方差不变B．平均数不变，方差变小C．平均数变小，方差不变D．平均数不变，方差变大11．某中学开展“阳光体育活动”，七年级一班全体同学分别参加了巴山舞、乒乓球、篮球三个项目的活动，陈老师统计了该班参加这三项活动的人数，并绘制了如图所示的条形统计图和扇形统计图，根据这两个统计图，可以知道该班参加乒乓球活动的有__________人．12．老师在计算学期平均分的时候按照如下标准，作业占10%，测验占20%，期中考试占30%，期末考试占40%，小丽的成绩如表所示，则小丽的平均分是__________分．13．某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛．在选拔赛中，每人射击10次，他们10次成绩的平均数及方差如下表所示．请你根据表中数据选一人参加比赛，最合适的人选是__________．14．随着2018年两会的隆重召开，中学校园掀起了关注时事政治的热潮，我区及时开展“做一个关心国家大事的中学生”主题活动．为了了解我区中学生获取时事新闻的主要途径，分别从电脑上网、手机上网、听广播、看电视、看报纸五个方面，在全区范围内随机抽取了若干名中学生进行问卷调查（每名中学生只选一种主要途径），根据调查结果绘制了如图所示的不完整的统计图，请根据统计图的信息回答下列问题：（1）本次调查共抽取了中学生多少人？（2）求本次调查中，以听广播获取时事新闻为主要途径的人数并补全条形统计图；（3）若本区共有中学生7000人，请你估计我区以看电视获取时事新闻为主要途径的中学生有多少人？15．为了了解某水库养殖鱼的有关情况，从该水库多个不同位置捕捞出200条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，绘制了直方图．（1）根据直方图提供的信息，这组数据的中位数落在__________范围内；（2）估计数据落在1.00~1.15中的频率是__________；（3）将上面捕捞的200条鱼分别作一记号后再放回水库.几天后再从水库的多处不同的位置捕捞150条鱼，其中带有记号的鱼有10条，请根据这一情况估算该水库中鱼的总条数．参考答案1．【答案】B2．【答案】D3．【答案】B4．【答案】B5．【答案】D6．【答案】B7．【答案】C8．【答案】C9．【答案】C10．【答案】B11．【答案】1512．【答案】8013．【答案】丁14．【解析】（1）120÷40%=300（人），∴本次抽样调查共抽取了中学生300人．（2）300-90-120-45-15=30（人），∴被调查的中学生中以听广播作为主要途径获取时事新闻主要途径有30人，补全条形统计图：（3）7000×45300=1050（人），∴由样本估计总体全区以看电视作为获取时事新闻主要途径的中学生有1050人．15．【解析】（1）1.10~1.15．从直方图可得出这组数据的中位数位于1.10~1.15范围内．（2）0.53．（10+40+56）÷200=0.53，频率是0.53．（3）200÷（10÷150）=3000，故水库中的鱼大约有3000条．。

俯视最新2012-2013年中考冲刺预测模拟试卷(5)数 学 试 题（总分120分 考试时间120分钟）注意事项：1． 本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷3页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共11页．2． 答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．3． 第Ⅰ卷每题选出答案后，都必须用2B 铅笔把答题卡上对应题目的答案标号【ABCD 】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．4． 考试时，不允许使用科学计算器．第Ⅰ卷（选择题 共36分）一、选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来．每小题选对得3分,选错、不选或选出的答案超过一个均记零分． 1．计算(ab 2)3的结果是 ( ) A ．ab 5B ．ab6C ．a 3b 5D ．a 3b 62．若实数a 、b 满足5a b +=，2210a b ab +=-，则ab 的值是( )A. -2B. 2C. -50D. 503．一个几何体及它的主视图和俯视图如图所示， 那么它的左视图正确的是________4. 小明调查了本班同学最喜欢的课外活动项目，并作出如图1所示的扇形统计图，则从图中可以直接看出的信息是( )A. 全班总人数B. 喜欢篮球活动的人数最多C. 喜欢各种课外活动的具体人数D. 喜欢各种课外活动的人数占本班总人数的百分比A B C D图15．某青年排球队12名队员的年龄情况如下：则这个队队员年龄的众数和中位数是________ A ______A 、19，20B 、19，19C 、19，20.5D 、20，196．已知半径分别为5cm 和8cm 的两圆相交，则它们的圆心距可能是 ( ) A ．1cm B ．3cm C ．10cm D ．15cm7．为缓解考试前的紧张情绪，某校九年级举行了“猪八戒背媳妇”的趣味接力比赛. 比赛要求每位选手在50米跑道上进行折返跑，其中有50米必须“背媳妇”. 假设某同学先跑步后“背媳妇”，且该同学跑步、“背媳妇”均匀速前进，他与起点的距离为s ，所用时间为t ，则s 与t 的函数关系用图象可表示为( )A.B.C.D.8． 在同一平面内，如果两个多边形(含内部)有除边界以外的公共点，则称两多边形有“公共部分”. 如图，若正方形ABCD 由9个边长为1的小正方形镶嵌而成，另有一个边长为1的正方形与这9个小正方形中的n 个有“公共部分”，则n 的最大值为( )A. 4B. 5C. 6D. 79． 方程0411)1(2=+---x k x k 有两个实数根，则k 的取值范围是（ ）． A ． k ≥1B ． k ≤1C ． k >1D ． k <110．楠溪江某景点门票价格：成人票每张70元，儿童票每张35元。

上海市初中数学教学质量抽样分析试卷 (2013.5.18)一、选择题：（本大题共6题，每题4分，满分24分） 【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．如果点P 与点Q （-2,3）关于x 轴对称，那么点P 的坐标是 （ ） （A ）（2,3）； （B ）（-2,3）； （C ）（2,-3）； （D ）（-2,-3）． 2．在下列二次根式中，与a 同为同类二次根式的是 （ ） （A ）a 2； （B ）23a ； （C ）3a ； （D ）4a ．3．如果从1、2、3这三个数字中任意选取两个数字，组成一个两位数，那么这个两位数是素数的概率等于（ ） （A ）21； （B ）31； （C ）41； （D ）61． 4．已知某班学生上学时乘车、步行、骑车的人数分布条形图和扇形图如图所示（两图都不完整），那么下列结论中错误的是（ ） （A ）该班总人数为40人； （B ）骑车人数占总人数的20%； （C ）步行人数为30人； （D ）乘车人数是骑车人数的2.5倍．5．如图，如果在高为2m ，坡度为1∶2的楼梯上铺地毯，那么地毯的长度至少应截取（ ） （A ）2m ； （B ）6m ； （C ）52m ； （D ）()526+m ．6．已知：⊙O 1、⊙O 2的半径分别是3和4，那么下列叙述中，一定正确的是（ ）（A ）当123O O =时，⊙O 1与⊙O 2相交； （B ）当121O O =时，⊙O 1与⊙O 2内含；（C ）当122O O <时，⊙O 1与⊙O 2没有公共点； （D ）当126O O >时，⊙O 1与⊙O 2有两个公共点．二、填空题：（本大题共12题，每题4分，满分48分） 【请将结果直接填入答题纸的相应位置上】 7．计算：32a a ⋅= ．8．在实数范围内分解因式：822-x = ．9．不等式组12,2(2)32x x x ->-⎧⎨+>+⎩的解集是 ．10．如果x =6是方程12)(23=--t x x 的根，那么t = ． 11．已知函数12)(+=x x f ，那么=)2(f ． 12．已知一次函数y =kx +b （k ≠0）的图像经过点（0,1），且y 随x 的增大而增大，请你写出一个符合上述条件的一次函数解析式，这个解析式可以是 ．13．面积为300平方米的一块长方形绿地，长比宽多10米．如果设长方形绿地的宽为x 米，（第5题图）骑车步行30% 乘车50%（第4题图）那么可列方程为 ．14．已知一组数据24、27、19、13、x 、12的中位数是21，那么x 的值等于 ． 15．正八边形的中心角等于 度．16．如图，已知在△ABC 中，点D 在边BC 上，且BD ︰DC =1︰2．如果AB a =，AC b =，那么AD = （结果用含a 、b 的式子表示）．17．已知点E 在面积为4的平行四边形ABCD 的边上运动，那么使△ABE 的面积为1的点E 共有 个．18．已知直线l 经过正方形ABCD 的顶点A ，过点B 和点D 分别作直线l 的垂线BM 和DN ，垂足分别为点M 、点N ，如果BM =5，DN =3，那么MN = ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）计算：232)31(23)3(21+++----π．20．（本题满分10分）解方程：121442--=-x x ． 21．（本题满分10分，其中第（1）小题4分，第（2）小题6分）已知：如图，⊙O 的半径为5，弦AB 的长等于8，OD ⊥AB ，垂足为点D ，DO 的延长线与⊙O 相交于点C ，点E 在弦AB 的延长线上，CE 与⊙O 相交于点F ，54cos =C ． 求：（1）CD 的长； （2）EF 的长．ABCD（第16题图）（第21题图）22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）我们知道：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零．由此可得：如果ax +b =0，其中a 、b 为有理数，x 为无理数，那么a =0且b =0．运用上述知识，解决下列问题： （1）如果032)2(=++-b a ，其中a 、b 为有理数，那么a = ，b = ； （2）如果5)21()22(=--+b a ，其中a 、b 为有理数，求a +2b 的值． 23．（本题满分12分，其中第（1）小题4分，第（2）小题8分）已知：如图，在梯形ABCD 中，AD ∥BC ，点E 、F 分别是边BC 、CD 的中点，直线EF 交边AD 的延长线于点M ，交边AB 的延长线于点N ，联结BD ．（1）求证：四边形DBEM 是平行四边形；（2）联结CM ，当四边形ABCM 为平行四边形时， 求证：MN =2DB ．24．（本题满分12分，其中第（1）小题5分，第（2）小题7分）已知在直角坐标系xOy 中，二次函数c bx x y ++-=2的图像经过点A （-2,3）和点B （0,-5）．（1）求这个二次函数的解析式；（2）将这个函数的图像向右平移，使它再次经过点B ，并记此时函数图像的顶点为M ．如果点P 在x 轴的正半轴上，且∠MPO =∠MBO ，求∠BPM 的正弦值．AB C D EFMN （第23题图）25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）已知：在Rt △ABC 中，∠C =90°，AC =4，∠A =60°，CD 是边AB 上的中线，直线BM ∥AC ，E 是边CA 延长线上一点，ED 交直线BM 于点F ，将△EDC 沿CD 翻折得△DC E '，射线E D '交直线BM 于点G ． （1）如图1，当CD ⊥EF 时，求BF 的值； （2）如图2，当点G 在点F 的右侧时；①求证：△BDF ∽△BGD ； ②设AE =x ，△DFG 的面积为y ，求y 关于x 的函数解析式，并写出x 的取值范围； （3）如果△DFG 的面积为36，求AE 的长．（第25题图1）M（第25题图2）（第25题备用图）M上海市初中数学教学质量抽样分析试卷参考答案及评分说明一、选择题：1．D ； 2．C ； 3．A ； 4．C ； 5．B ； 6．A ． 二、填空题：7．a 5； 8．2(x +2)(x -2)； 9．-1<x <2； 10．3； 11．5； 12．y =x +1等； 13．x (x +10)=300； 14．23；15．45；16．3132+； 17．2； 18．2或8． 三、解答题：19．解：原式=）（3223231-++-+……………………………………………（各2分） =3．……………………………………………………………………………（2分）20．解：去分母，得4242+-+=x x ．…………………………………………………（3分）整理，得 022=--x x ．………………………………………………………（2分）解得 x 1=-1，x 2=2．………………………………………………………（4分）经检验：x 1=-1是原方程的根，x 2=2是增根．…………………………………（1分） ∴原方程的根为x =-1．21．解：（1）联结OA ．∵OD ⊥AB ，AB =8，∴AD =4．…………………………………………………（2分） ∵OA =5，∴OD =3．………………………………………………………………（1分） ∵OC =5，∴CD =8．………………………………………………………………（1分） （2）作OH ⊥CE ，垂足为点H ．∵OC =5，54cos =C ，∴CH =4．…………………………………………………（2分） ∵OH ⊥CE ，∴CF =2CH =8．……………………………………………………（1分） 又∵CD =8，54cos =C ，∴CE =10．……………………………………………（2分） ∴EF =2．……………………………………………………………………………（1分）22．解：（1）2，-3；……………………………………………………………………（各2分）（2）整理，得0)52(2)(=--++b a b a ．……………………………………（2分）∵a 、b 为有理数，∴⎩⎨⎧=--=+.052,0b a b a …………………………………………（2分）解得⎪⎩⎪⎨⎧-==.35,35b a ……………………………………………………………………（1分）∴352-=+b a ．…………………………………………………………………（1分）23．证明：（1）∵CE =BE ，CF =DF ，∴EF ∥BD ．………………………………………（2分）又∵AD ∥BC ，∴四边形DBEM 是平行四边形．……………………………（2分） （2）∵四边形ABCM 为平行四边形，∴AB =CM ，AB ∥CM ．………………（2分）∴CEBECM BN =．…………………………………………………………………（1分） ∵BE =CE ，∴BN =CM ．…………………………………………………………（1分） ∴AB =BN ．………………………………………………………………………（1分） ∵EF ∥BD ，∴ANABMN DB =．……………………………………………………（2分） ∴MN =2DB ．……………………………………………………………………（1分）24．解：（1）由题意，得⎩⎨⎧=-+--=.5,243c c b ………………………………………………（2分）解得⎩⎨⎧-=-=.5,6c b ……………………………………………………………………（2分）∴所求二次函数的解析式为562---=x x y ．………………………………（1分） （2）二次函数562---=x x y 图像的顶点坐标为（-3,4）．……………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分） 由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°． 设点P 的坐标为（x ,0）． ∴2222225934)3(+=+++-x x ．…………………………………………（1分） 解得x =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分） ∴53sin =∠BPM ．………………………………………………………………（1分） 另解：二次函数562---=x x y 图像的顶点坐标为（-3,4）．………………（1分） ∴图像平移后顶点M 的坐标为（3,4）．………………………………………（1分） 由题意∠MPO =∠MBO ，可得∠PMB =∠POB =90°． 过M 点作x 轴、y 轴的垂线，垂足分别为点H 、K ． 在Rt △BKM 中，由题意，得tan ∠MBK =1∶3．在Rt △MPH 中，tan ∠MPH =tan ∠MBK =1∶3．………………………………（1分） ∴PH =12．∴OP =15．………………………………………………………………………（1分） ∴点P 的坐标为（15,0）．………………………………………………………（1分） ∴103=BM ，105=PB ．………………………………………………（1分）∴53sin =∠BPM ．………………………………………………………………（1分） 25．（1）解：∵∠ACB =90°，AD =BD ，∴CD =AD =BD ．………………………………（1分）∵∠BAC =60°，∴∠ADC =∠ACD =60°，∠ABC =30°，AD =BD =AC ． ∵AC =4，∴AD =BD =AC =4．……………………………………………………（1分）∵BM ∥AC ，∴∠MBC =∠ACB =90°．又∵CD ⊥EF ，∴∠CDF =90°． ∴∠BDF =30°． ∴∠BFD =30°． ∴∠BDF =∠BFD ．∴BF =BD =4．……………………………………………………………………（2分）（2）①证明：由翻折，得CD E '∠=∠ACD =60°，∴∠ADC =CD E '∠．∴E C '∥AB ．∴D E C '∠=∠BDG ．……………………………………………………………（1分） ∵BM ∥AC ，∴∠CED =∠BFD ．又∵D E C '∠=∠CED ，∴∠BDG =∠BFD ．……………………………………（1分）∵∠DBF =∠GBD ，∴△BDF ∽△BGD ．………………………………………（1分） ②解：由△BDF ∽△BGD ，得BGBDBD BF =． 由AE =x ，可得BF =x ．∴BGx 44=． ∴xBG 16=．……………………………………………………………………（1分）又∵点D 到直线BM 的距离为32， ∴32)16(21⋅-=x xy ，即x x y 3316-=．………………………………（1分） 定义域为0<x <4．………………………………………………………………（1分）（3）解：（i ）当点G 在点F 的右侧时，由题意，得x x331636-=． 整理，得01662=-+x x ．解得x 1=2，x 2=-8（不合题意，舍去）．………………………………………（2分） （ii ）当点G 在点F 的左侧时， 由题意，得xx 316336-=． 整理，得01662=--x x ．解得x 3=8，x 4=-2（不合题意，舍去）．………………………………………（2分）综上所述AE的值为2或8．。

2013年中考数学模拟复习调研考试题五一、选择题（本大题共6小题，每小题2分，共计12分．在每小题所给出的四个选项中，恰有一项．．．．是符合题目要求的，请将正确选项的序号填涂在答题卡上） 1．函数y =x 的取值范围是（ ▲ ）A ．2x >-B ．2x -≥C ．2x ≠-D ．2x -≤2．我市统计局发布的统计公报显示，2004年到2008年，我市GDP 增长率分别为9.6%、10.2%、10.4%、10.6%、10.3%. 经济学家评论说，这5年的年度GDP 增长率相当平稳，从统计学的角度看，“增长率相当平稳”说明这组数据的（ ▲ ）比较小.A ．中位数B ．平均数C ．众数D ．方差 3．△ABC 中，∠C=90°，AC=8，BC=6，则cosA 的值是（ ▲ ）A ．45B ．35C ．43D ．344．已知Rt ΔABC 中，∠ACB =90°，AC = 4，BC=3，以AB 边所在的直线为轴，将ΔABC 旋转一周，则所得几何体的表面积是（ ▲ ） A ．π5168 B ．π24 C ．π584D ．π12 5．如图，△ABC 内接于⊙O ，AD 是⊙O 的直径，∠ABC ＝25°，则∠CAD 的度数是（ ▲ ） A ．25°B ．60°C ．65°D ．75°6．如图，正三角形ABC 的边长为1，E 、F 、G 分别是AB 、BC 、CA 上的点，且AE ＝BF ＝CG ，设△EFG 的面积为y ，AE 的长为x ，则y 关于x 的函数的图象大致是（ ▲ ）二、填空题（本大题共10小题，每小题2分，共计20分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 7. 比较大小：215- ▲ 21． 8. 计算：=-⨯263_ _▲___．（第5题）9.已知命题“如果一个平行四边形的两条对角线互相垂直，那么这个平行四边形是菱形”，写出它的逆命题：_____________▲ ________________10.方程062=++k x x 有两个不相等的实数根，则k 的取值范围是 ____▲____ 11. 已知1O ⊙的半径为3cm ，2O ⊙的半径为4cm ，两圆的圆心距12O O 为7cm ，则1O ⊙与2O ⊙的位置关系是 ____▲____．12. 在Rt △ABC 中，∠C=90°，AC=6，BC=8，则其外接圆的半径为 __▲____ 13.有五张卡片，每张卡片上分别写有1，2，3，4，5，洗匀后从中任取一张，放回后再抽一张，抽到和大于8的概率为 ▲ 。

2013年中考数学复习冲刺预测卷 综合全卷分A 卷和B 卷，A 卷满分100分，B 卷满分50分；考试时间l20分钟。

A 卷(共100分)一、选择题（本大题共1０个小题，每小题3分，共3０分在每小题给出的四个选项中，有且仅有一项是符合题目要求的．）1.2009年初甲型H1N1流感在墨西哥暴发并在全球蔓延，我们应通过注意个人卫生加强防范．研究表明，甲型H1N1流感球形病毒细胞的直径约为0.00000156 m ，用科学记数法表示这个数是（ ）A ．0.156×10－5B ．0.156×105C ．1.56×10－6D ．1.56×1062．下列计算错误的是（ ）A ．－（－2）=2 B．= C ．22x +32x =52x D ．235()a a = 3．按如图所示的方式摆放在一起，其左视图是（ ）4．下列说法正确的是（ ）A ．抛一枚硬币，正面一定朝上；B ．掷一颗骰子，点数一定不大于6；C ．为了解一种灯泡的使用寿命，宜采用普查的方法；6．若△ABC ∽△DEF, △ABC 与△DEF 的相似比为１∶2，则△ABC 与△DEF 的周长比为（ ）A ．1∶4B ．1∶2C ．2∶1D 7． 如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A=70o ，∠C=50o ，那么sin ∠AEB 的值为( ) A. 21 B.33 C.22 D.238．如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根，那么k 的取（第3题）A ．B ．Ｃ．Ｄ．值范围是（ ） A.k ＞14-B.k ＞14-且0k ≠ C.k ＜14-D.14k ≥-且0k ≠9．如图，在平面直角坐标系中，点A 在第一象限，⊙A 与轴相切于B ，与轴交于C （0，1），D （0，4）两点，则点A 的坐标是 （ ）A.35(,)22B.3(,2)2C.5(2,)2D.53(,)2210．“只要人人都献出一点爱，世界将变成美好的人间”．在今年的慈善一日捐活动中，成都市某中学九年级三班50名学生自发组织献爱心捐款活动．班长将捐款情况进行了统计，并绘制成了统计图．根据右图提供的信息，捐款金额．．的众数和中位数分别是（ ） A ．20、20 B ．30、20 C ．30、30 D ．20、30二、填空题（本大题共４个小题，每小题4分，共16分．把答案直接填在题目中的横线上.） 11．分解因式33222ax y axy ax y +-= ．12．若x ＝1是一元二次方程x 2＋x ＋c ＝0的一个解，则=2c ．13．在A B C △中，5A B A C ==，3cos 5B =．如果圆O 且经过点B C ，，那么线段A O 的长等于 ．14．如图，A B C △与A B C '''△是位似图形，且顶点都在格点上，则位似中心的坐标是 ．三、（第15题每小题6分，第16题6分，共18分） 15.解答下列各题： （1）计算：()60sin 623183101+-+-⎪⎭⎫⎝⎛--（2）先化简，再求值：32444)1225(222+=++-÷+++-a a a a a a a ，其中16.解不等式组205121123x x x ->⎧⎪+-⎨+⎪⎩，≥，并把解集在数轴上表示出来,并写出该不等式组的最大整数解。

最新2012-2013年中考冲刺预测模拟试卷(4)数学试题（总分120分考试时间120分钟）注意事项：1．本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷3页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共11页．2．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．3．第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．4．考试时，不允许使用科学计算器．第Ⅰ卷（选择题共36分）一、选择题：本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来．每小题选对得3分,选错、不选或选出的答案超过一个均记零分．1．﹣2012的相反数是（）A．﹣2012 B． 2012 C．D．2．某市在一次扶贫助残活动中，共捐款3185800元，将3185800元用科学记数法表示（保留两个有效数字）为（故选C ）3．下列图形中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.4．直角三角形两直角边和为7，面积为6，则斜边长为（）A. 5B. C. 7D.5．已知：如图，CF平分∠DCE，点C在BD上，CE∥AB．若∠ECF=55°，则∠ABD的度数为（）A．55°B．100°C．110°D．125°F DE CBA6．东营市2009年平均房价为每平方米4000元．连续两年增长后，2011年平均房价达到每平方米5500元，设这两年平均房价年平均增长率为x，根据题意，下面所列方程正确的是（）ABCD FOG HE图7BOA C O ACBA ．5500（1+x ）2=4000B ．5500（1﹣x ）2=4000 C ．4000（1﹣x ）2=5500 D ．4000（1+x ）2=55007．如图，在⊙O 中，OA ＝AB ，OC ⊥AB ，则下列结论正确的是（ ） ①．弦AB 的长等于圆内接正六边形的边长 ②．弦AC 的长等于圆内接正十二边形的边长 ③．弧AC=弧AB④．∠BAC =30°A ．①②④B ．①③④C ．②③④D ．①②③8．使代数式x x --87有意义的自变量x 的取值范围是 （ ）A.7≥xB. 87≠>x x 且C. 87≠≥x x 且D. 7>x9．关于x 、y 的方程组3,x y m x my n -=⎧⎨+=⎩的解是1,1,x y =⎧⎨=⎩则m n -的值是（ ）故选D ．10．如图，在矩形ABCD 中，BC=8，AB=6，经过点B 和点D 的两个动圆均与AC 相切，且与AB 、BC 、AD 、DC分别交于点G 、H 、E 、F ，则EF+GH 的最小值是（ ）A ．6B ．8C ．9.6D ．1011．如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S （阴影部分），则S 与t 的大致图象为（ ）12．如图，点O 为正方形ABCD 的中心，BE 平分∠DBC 交DC 于点E ，延长BC 到点F ，使FC ＝EC ，连结DF 交BE 的延长线于点H ，连结OH 交DC 于点G ，连结HC ．则以下四个结论中正确结论的个数为（ ） ①OH ＝21BF ； ②∠CHF ＝45°； ③GH ＝41BC ；④DH2＝HE ·HBA. 1个B. 2个C. 3个D. 4个stO A stOB stO C stOD 图4A G BHC FDE第10题数学试题第Ⅱ卷（非选择题共84分）注意事项：1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．2．答卷前将密封线内的项目填写清楚．二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．13．地球的表面积约为5.1亿Km2，其中陆地面积约为地球表面积的0.29，则地球上陆地面积约为14．分解因式：a2b－2ab2＋b3＝．15．如图，在半圆O中，直径AE=10，四边形ABCD是平行四边形，且顶点A、B、C在半圆上，点D在直径AE上，连接CE，若AD=8，则CE长为．16．某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是cm．17在x轴正半轴上，斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲线xy=(x＞0)的图像经过点A，若8=∆EBCS则k=_____________三、解答题：本大题共7小题，共64得分评卷人18． (本题满分7分，第⑴题3分，第⑵题4分)（1）计算：()122160tan 33101+-+︒-⎪⎭⎫⎝⎛--；（2）(本小题满分4分)解不等式组：3265212x x x x -<+⎧⎪⎨-+>⎪⎩，并把解集在数轴上表示出来.得 分 评 卷 人19． （本题满分9分）某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的(一次只能摸一个)，顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元.(1)每摸一次球所获购物卷金额的平均值是多少？(2)你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？得 分评 卷 人20． （本题满分9分）如图，AB 是⊙O 的直径，AM 和BN 是它的两条切线，DE 切⊙O 于点E ，交AM 于点D ，交BN 于点C ，（1）求证：OD ∥BE ；（2）如果OD =6cm ，OC =8cm ，求CD 的长．得 分评 卷 人（第20题图）A D NEC OM得分评卷人21．（本题满分9分）小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤．妈妈：“今天买这两样菜共花了45元，上月买同重量的这两样菜只要36元”；爸爸：“报纸上说了萝卜的单价上涨50%，排骨单价上涨20%”；小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少？”请你通过列方程（组）求解这天萝卜、排骨的单价（单位：元/斤）．得分评卷人22．（本题满分9分）青青草原上，灰太狼每天都想着如何抓羊，而且是屡败屡试，永不言弃.（如图7所示）一天，灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°，然后下到城堡的C处，测得B处的俯角为30°.已知AC=50米，若灰太狼以5m/s的速度从城堡底部D处出发，懒羊羊以3m/s沿DB延长线方向逃跑，灰太狼几秒钟后能抓到懒羊羊？B23．（本题满分10分）如图(1)，在直角梯形OABC中，BC∥OA，∠OCB＝90°，OA＝6，AB＝5，cos∠OAB＝35．(1)写出顶点A、B、C的坐标；(2)如图(2)，点P为AB边上的动点（P与A、B不重合），PM⊥OA，PN⊥OC，垂足分别为M，N．设PM ＝x，四边形OMPN的面积为y．①求出y与x之间的函数关系式，并写出自变量x的取值范围；②是否存在一点P，使得四边形OMPN的面积恰好等于梯形OABC的面积的一半？如果存在，求出点P 的坐标；如果不存在，说明理由．得分评卷人24．（本题满分11分）如图1，在平面直角坐标系xOy 中，抛物线的解析式是y ＝2114x +，点C 的坐标为(–4，0)，平行四边形OABC 的顶点A ，B 在抛物线上，AB 与y 轴交于点M ，已知点Q (x ，y )在抛物线上，点P (t ，0)在x 轴上．(1) 写出点M 的坐标；(2) 当四边形CMQP 是以MQ ，PC 为腰的梯形时． ① 求t 关于x 的函数解析式和自变量x 的取值范围；② 当梯形CMQP 的两底的长度之比为1∶2时，求t 的值．（第24题图1）参考答案： 一、选择题BCCACDDCCBB二、二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分． 13．28105.1km ⨯14． b(a-b)215．1016． 20 cm ． 17.16三、解答题： （2）解：由（1）得：4<x得 分 评 卷 人…… 1′由（2）得：0>x不等式组的解为：40<<x 在数轴上表示为：19．解：（1） ∵P(摸到红球)= 202 ， P(摸到兰球)= 203，P(摸到黄球) = 205 ， P(摸到白球)= 2010，∴每摸一次球所获购物卷金额的平均值为：80×202+30×203+10×205=15(元)（2）∵15＞10，∴两种方式中我会选择摸球这种方式，此时较合算。