工程流体力学习题解析_(夏泰淳_着)_上海交通大学出版社

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？ 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P pdV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆tp V V ，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

(完整版)工程流体力学习题集及答案（一）选择题1. 下列哪项不是流体的基本特性？（）A. 连续性B. 压缩性C. 粘性D. 不可压缩性答案：D2. 在流体的伯努利方程中，下列哪个物理量保持不变？（）A. 动能B. 势能C. 总能量D. 静压能答案：C3. 下列哪种流动状态是稳定的？（）A. 层流B. 紊流C. 涡流D. 粘性流动答案：A（二）填空题1. 流体的连续性方程是______。

答案：质量守恒方程2. 在流体的伯努利方程中，流速和压强的关系是______。

答案：流速越大，压强越小3. 流体力学中的雷诺数用于判断______。

答案：流动状态（三）计算题1. 已知一水平管道，直径为0.2m，流速为1.5m/s，流体密度为1000kg/m³，求管道中的流量。

答案：流量Q = π * d² * v = π * (0.2m)² * 1.5m/s = 0.0942m³/s2. 一管道中的流体在某一截面处的流速为2m/s，压强为1.5×10⁵Pa，流体密度为1000kg/m³，求该截面处的动能。

答案：动能 = 0.5 * ρ * v² = 0.5 *1000kg/m³ * (2m/s)² = 2000J/m³3. 已知一圆柱形油桶，直径为1m，高为2m，油桶内装有密度为800kg/m³的油，求油桶内油的体积。

答案：油桶内油的体积V = π * d² * h / 4 =π * (1m)² * 2m / 4 = 1.5708m³（四）论述题1. 请简述层流和紊流的区别。

答案：层流是指流体流动时各层流体之间没有交换，流动稳定，速度分布呈抛物线状。

紊流是指流体流动时各层流体之间发生交换，流动不稳定，速度分布呈锯齿状。

2. 请解释伯努利方程的物理意义。

答案：伯努利方程描述了理想流体在流动过程中，流速、压强和高度之间的关系。

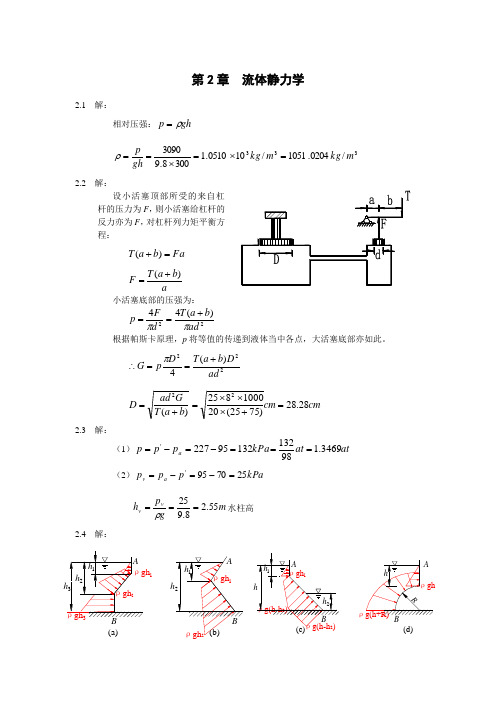
第2章 流体静力学2.1 解：相对压强：gh p ρ=333/0204.1051/100510.13008.93090m kg m kg gh p =⨯=⨯==ρ 2.2 解：设小活塞顶部所受的来自杠杆的压力为F ，则小活塞给杠杆的反力亦为F ，对杠杆列力矩平衡方程：Fa b a T =+)(a b a T F )(+=小活塞底部的压强为：22)(44ad b a T d F p ππ+==根据帕斯卡原理，p 将等值的传递到液体当中各点，大活塞底部亦如此。

222)(4ad D b a T D p G +==∴π cm cm b a T Gad D 28.28)7525(201000825)(22=+⨯⨯⨯=+=2.3 解：（1）at at kPa p p p a 3469.19813213295227'===-=-= （2）kPa p p p a v 257095'=-=-=m g p h v v 55.28.925===ρ水柱高 2.4 解：ρgh 2 ρgh 1ρgh 3ρgh 2ρgh 1h 2h 1 h 1 h 2h 3 (b)(a)BAA Bρg(h-h 2)ρg(h+R)ρghρg(h-h 2) ρgh 1Rhh 2h 1h(d)(c)B AAB2.5 解：1－1为等压面：gh p gH p a ρρ+=+0kPa m N m N m N H h g p p a 94.100/100940/)2.15.1(8.91000/108.9)('22240==-⨯⨯+⨯=-+=ρ kPa p 94.20=2.6 解: kPa gL p c 45.230sin 5.08.9sin =⨯⨯==αρ 2.7 解：如图所示，过1、2、3点的水平面是等压面。

)()()(322341121z z g z z g gh p z z g gh p B B A A ---++=--+ρρρρρ[])()()()(32212341z z g z z z z g h h g p p A B B A ---+-+-=-ρρρ[])()()()(3221234141z z g z z z z g z z g ---+-+-=ρρρ[]{}310)3262(8.0)1862()3253(6.13)5318(8.9-⨯---+-+-⨯=Pa 8085=2.8 解：gh gh p gh p p B B A A ρρρ+-=- ()gh h h g p p p B A B A ρρ+-=-＝()[]gh h g p ρρ++-1＝()[]31036.08.96.13136.08.9-⨯⨯⨯++-＝34.6528kPa2.9 解：如图所示，A 、B 、C 点水平面是等压面。

第一章 绪论1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。

试求m h 5.0=时渠底（y =0）处的切应力。

[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τ Pa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。

[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律yud d μτ=，定性绘出切应力沿y 方向的分布图。

[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。

= 0.257L[1-4]用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa o 封闭后由于温度变化升高了 20°C,此时汽油的蒸汽压力为17640Pa o 若汽油的膨胀 系数为0.0006KL 弹性系数为13.72Xl （）6pa, （1）试计算由于压力温度变化所增 加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由/3=-^ = ~可得，由于压力改变而减少的体积为 Vdp E1 dV t^V~dT =明=彼"= 0.0006x200x20 = 2.40L（2）因为△（? △匕，相比之下可以忽略由压力变化引起的体积改变，则r + r/?/r = 200L__ = = ______ : _____ = 98 8% 200 一 1 + "T ~ 1 + 0.0006x20 一 ,[1-5]图中表示浮在油面上的平板，其水平 运动速度为$ = 10mm,油品的粘度〃 =0. 9807Pa - s,求作用在平板单位面积上的阻力。

【解】根据牛顿内摩擦定律则丁 二 〃 凶=（）.9807 X-!— = 98.07 N/n?8 0.01[2-1]容器中装有水和空气,求力、B 、。

和〃各点的表压力?【解】空气各点压力相同，与空气接触的液面压力即为空气的压力，另外相 互连通的同种液体同一高度压力相同，即等压面PMA=Pgg+2P MB = P MA - pg （佑 + 九 + 力2）= 一Pgh?P MD = P MC - Pgh + 处）=一Pg （勾 +匹）Pmc=Pmd+P g （hl+h2+h3） Pmd= -pg （hl+2h2+h3）【2-5】图示两水管以U 形压力计相连， A.^V p =-dV p =200x17640 13.72乂10厂A =习题1-5题2-5图题= 0.1m两点高差Im, U 形管内装有水银，若读数A/i=O. 5m,求4、8两点的压力差为多少?【解】选取U 形管内水银最低液面为等压面，设①点到水银最高液面的垂 直高度为x ，则P A + Z\g （l + x ） + P 〃ghh = P B + p“.g （x + 醐）得P B - P A = P 、、g +（P H - Pw ）gM= 1000x9.8 + （13600-1000） x9.8x 0.5 = 7.154x10, Pa[2-7]图示一个安全闸门，宽为0.6m,高 为1. 0m o 距底边0. 4m 处装有闸门转轴，使之仅 可以绕转轴顺时针方向旋转。

(完整版)工程流体力学习题及答案一、习题1. 一个直径为0.2米的管道，输送密度为800kg/m³的水，流速为2 m/s。

求管道中的流量和动能。

2. 一管道突然扩大，进口直径为0.1米，出口直径为0.2米。

若进口处流速为3 m/s，求出口处的流速。

3. 一水平管道，直径为0.5米，输送20℃的水。

已知进口处的压力为0.2 MPa，流速为1 m/s。

求管道出口处的压力。

4. 一管道中的流体在收缩段突然减小，进口直径为0.3米，出口直径为0.2米。

已知进口处流速为2m/s，求收缩段处的流速。

5. 一管道系统中有两个测压点，分别为A和B。

测得A点的压力为0.1 MPa，流速为1 m/s；B点的压力为0.08 MPa，流速为1.5 m/s。

求管道两点的能量损失。

二、答案1. ：根据流量公式 Q = A * v，其中A为管道截面积，v为流速。

管道截面积 A = π * (d/2)²，其中d为管道直径。

管道截面积 A = π * (0.2/2)² = 0.0314 m²流量 Q = A * v = 0.0314 * 2 = 0.0628 m³/s动能 E = 1/2 * ρ * v² * A，其中ρ为流体密度。

动能 E = 1/2 * 800 * (2)² * 0.0314 = 100.48 J答案：流量为0.0628 m³/s，动能为100.48 J。

2. ：根据连续方程，流量在管道中保持不变，即进口流量等于出口流量。

进口流量 Q1 = A1 * v1，出口流量 Q2 = A2 * v2A1 = π * (d1/2)²，A2 = π * (d2/2)²0.1 * 3 = 0.2 * v2v2 = 1.5 m/s答案：出口处的流速为1.5 m/s。

3. ：根据伯努利方程，管道中任一截面的总能量保持不变，即进口总能量等于出口总能量。

工程流体力学课后单选题100道及答案解析1. 流体的粘性与流体的（）无关。

A. 分子内聚力B. 分子动量交换C. 温度D. 压强答案：D解析：流体的粘性主要与分子内聚力、分子动量交换和温度有关，与压强无关。

2. 理想流体是指（）的流体。

A. 无粘性B. 不可压缩C. 无粘性且不可压缩D. 符合牛顿内摩擦定律答案：C解析：理想流体是指无粘性且不可压缩的流体。

3. 液体的压缩性比气体的压缩性（）。

A. 大B. 小C. 相等D. 无法比较答案：B解析：液体的压缩性很小，气体的压缩性较大。

4. 下列关于流线的描述错误的是（）。

A. 流线不能相交B. 流线是光滑的曲线C. 稳定流动时流线与迹线重合D. 流线可以是折线答案：D解析：流线是光滑的曲线，不能是折线。

5. 连续性方程是根据（）原理推导出来的。

A. 质量守恒B. 能量守恒C. 动量守恒D. 牛顿第二定律答案：A解析：连续性方程基于质量守恒原理。

6. 伯努利方程适用于（）。

A. 理想流体B. 粘性流体C. 可压缩流体D. 不可压缩流体的定常流动答案：D解析：伯努利方程适用于不可压缩流体的定常流动。

7. 沿程阻力损失与（）成正比。

A. 流速的平方B. 管长C. 管径D. 流体的密度答案：B解析：沿程阻力损失与管长成正比。

8. 局部阻力损失产生的主要原因是（）。

A. 流体的粘性B. 流速的变化C. 管道的粗糙度D. 流体的压缩性答案：B解析：局部阻力损失主要由流速的变化引起。

9. 圆管层流的平均流速是最大流速的（）倍。

A. 0.5B. 1/2C. 1/4D. 2答案：A解析：圆管层流的平均流速是最大流速的0.5 倍。

10. 圆管紊流的速度分布呈（）。

A. 抛物线分布B. 对数分布C. 均匀分布D. 线性分布答案：B解析：圆管紊流的速度分布呈对数分布。

11. 雷诺数的物理意义是（）。

A. 惯性力与粘性力之比B. 压力与粘性力之比C. 重力与粘性力之比D. 惯性力与重力之比答案：A解析：雷诺数表示惯性力与粘性力之比。

第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。

又，0.2m 3此种油的质量和重量各为多少？已已知知：：γ＝7800N/m 3；V ＝0.2m 3。

解解析析：：(1) 油的密度为 3kg/m 79581.97800===gγρ； 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。

已已知知：：V ＝300L ，m ＝4080kg 。

解解析析：：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv1－3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ，温度由20℃升高到78℃，空气的气体常数为287.06J/k g ·K 。

问每kg 空气的体积将比原有体积减少多少？减少的百分比又为多少？已已知知：：p 1＝101325Pa ，p 2＝607950Pa ，t 1＝20℃，t 2＝78℃，R ＝287.06J/k g ·K 。

解解析析：：由理想气体状态方程(1－12)式，得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3；减少的百分比为80％。

工程流体力学习题解析(夏泰淳_著)_上海交通大学出版社第1章 绪论选择题【1.1】 按连续介质的概念，流体质点是指：（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

解：流体质点是指体积小到可以看作一个几何点，但它又含有大量的分子，且具有诸如速度、密度及压强等物理量的流体微团。

（d ）【1.2】 与牛顿内摩擦定律直接相关的因素是：（a ）切应力和压强；（b ）切应力和剪切变形速度；（c ）切应力和剪切变形；（d ）切应力和流速。

解：牛顿内摩擦定律是d d v y τμ=，而且速度梯度d d vy 是流体微团的剪切变形速度d d t γ，故d d t γτμ=。

（b ）【1.3】 流体运动黏度υ的国际单位是：（a ）m 2/s ；（b ）N/m 2；（c ）kg/m ；（d ）N·s/m 2。

解：流体的运动黏度υ的国际单位是/s m 2。

（a ）【1.4】 理想流体的特征是：（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RTp =ρ。

解：不考虑黏性的流体称为理想流体。

（c ）【1.5】 当水的压强增加一个大气压时，水的密度增大约为：（a ）1/20 000；（b ）1/1 000；（c ）1/4 000；（d ）1/2 000。

解：当水的压强增加一个大气压时，其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。

（a ）【1.6】 从力学的角度分析，一般流体和固体的区别在于流体：（a ）能承受拉力，平衡时不能承受切应力；（b ）不能承受拉力，平衡时能承受切应力；（c ）不能承受拉力，平衡时不能承受切应力；（d ）能承受拉力，平衡时也能承受切应力。

解：流体的特性是既不能承受拉力，同时具有很大的流动性，即平衡时不能承受切应力。

（c ）【1.7】 下列流体哪个属牛顿流体：（a ）汽油；（b ）纸浆；（c ）血液；（d ）沥青。