立体图形的练习题

一年级立体图形练习题一、选择题1. 下列哪个图形是长方体？A. 圆形B. 正方体C. 长方体D. 三角形2. 一个正方体有几个面？A. 4个B. 6个C. 8个D. 10个3. 圆柱体的侧面展开是什么形状？A. 圆形B. 三角形C. 长方形D. 正方形4. 一个球体有几个面？A. 1个B. 2个C. 3个D. 无数个5. 下列哪个图形不是立体图形？A. 长方体B. 正方体C. 圆柱体D. 长方形二、填空题6. 一个长方体有____个顶点。

7. 一个正方体的每个面都是____形。

8. 圆柱体的底面是____形。

9. 球体是一个____面体。

10. 当你从不同方向看一个正方体时，你看到的都是____形。

三、判断题11. 长方体的每个面都是长方形。

（）12. 正方体的每个面都是正方形。

（）13. 圆柱体有两个底面和一个侧面。

（）14. 球体的每个方向看起来都是一样的。

（）15. 长方体和正方体都有12条边。

（）四、简答题16. 描述一下长方体的特征。

17. 描述一下正方体的特征。

18. 描述一下圆柱体的特征。

19. 描述一下球体的特征。

20. 为什么说球体是一个单面体？五、操作题21. 请画出一个长方体，并标注出它的长、宽、高。

22. 请画出一个正方体，并标注出它的边长。

23. 请画出一个圆柱体，并标注出它的底面半径和高。

24. 请画出一个球体，并描述它的特性。

25. 请用橡皮泥或纸制作一个正方体，并描述制作过程。

六、综合应用题26. 如果你有一个长方体的盒子，它的长是10厘米，宽是8厘米，高是5厘米，请计算它的体积。

27. 假设你有一个正方体的骰子，它的边长是2厘米，请计算它的表面积。

28. 如果你有一个圆柱形的杯子，它的底面直径是8厘米，高是10厘米，请计算它的容积。

29. 假设你有一个球形的气球，它的直径是20厘米，请计算它的表面积。

30. 请描述一下如何用积木搭建一个长方体的房子，并说明需要多少块积木。

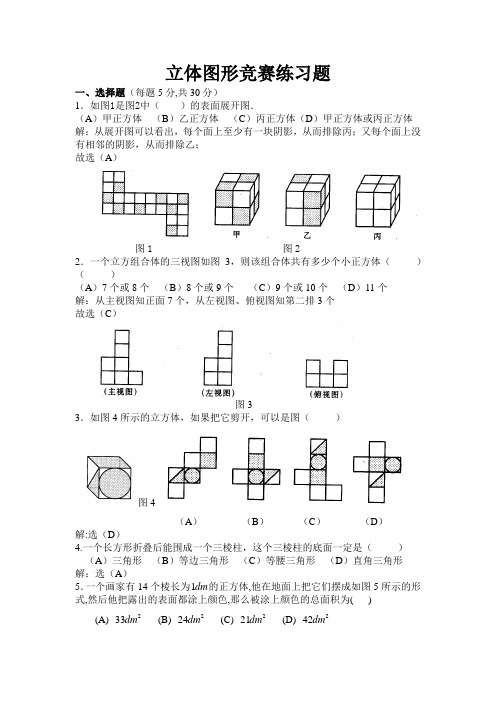
立体图形竞赛练习题一、选择题（每题5分,共30分）1．如图1是图2中（ ）的表面展开图．（A ）甲正方体 （B ）乙正方体 （C ）丙正方体（D ）甲正方体或丙正方体 解：从展开图可以看出，每个面上至少有一块阴影，从而排除丙；又每个面上没有相邻的阴影，从而排除乙；故选（A ）图1 图22．一个立方组合体的三视图如图3，则该组合体共有多少个小正方体（ ）（ ）（A ）7个或8个 （B ）8个或9个 （C ）9个或10个 （D ）11个 解：从主视图知正面7个，从左视图、俯视图知第二排3个故选（C ）图33．如图4所示的立方体，如果把它剪开，可以是图（ ）图4（A ） （B ） （C ） （D ） 解:选（D ）4.一个长方形折叠后能围成一个三棱柱，这个三棱柱的底面一定是（ ）（A ）三角形 （B ）等边三角形 （C ）等腰三角形 （D ）直角三角形 解：选（A ）5．一个画家有14个棱长为dm 1的正方体,他在地面上把它们摆成如图5所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )(A) 233dm (B) 224dm (C) 221dm (D) 242dm图5 图6 图7解：:这个模型的主视图如图6,它的面积是26dm ,其它的三个侧面的视图和它一样,故侧面积是222446dm dm =⨯; 这个模型的俯视图如图7, 它的面积是2933dm dm dm =⨯.所以涂上颜色的总面积是22233924dm dm dm =+.故选(A).二、填空题（每题5分,共30分）6．如图8，是标有1，2，3，4，5，6六个数字的一个正方体的三种不同摆法。

问三个正方体朝左的一面的数字之和是______. 图8解：有三个正方体中的已知数字可判断数字1与4相对，2与6相对，3与5相对，故三个正方体朝左的一面的数字和为5+1+4=107． 如图9，是一个大正立方体，把它的每个面都划分为9个小正方形，这个大正方体中共有多少个正方体。

第三单元认识立体图形注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．注意保持卷面整洁一、选择题1．这个图形至少还要用（）个，才能拼成一个大正方体。

A．1B．2C．32．下面（）号图形搭得稳．A．B．C．3．下面（）物体可以画出。

A．B．C．4．下面物体的形状是正方体的是（）。

A．B．C．5．能向任意方向滚动的图形是（）。

A．B．C．6．下面的物品是正方体的有（）．A．铅笔笔盒B．魔方C．书二、填空题7．我会数。

( )个，( )个，( )个，( )个。

8．在长方体的下面写“C”，在正方体的下面写“Z”．9．拼成的形状需要( )个。

10．长方体有( )个，正方体有( )个，圆柱有( )个，球有( )个；一共有( )个图形；( )最多，( )最少，( )和( )同样多。

11．数一数。

有( )个，有( )个，有( )个，有( )个。

12．长方体有( )个，圆柱有( )个，正方体有( )个，球有( )个。

三、判断题13．“七巧板”是由7块板组成，拼出来的图案变化万千。

( ) 14．数学课本是长方体，算术本是长方形。

( )15．我的数学课本是正方体。

( )16．用手摸一摸，圆柱上下两个面，它们的大小相同．( ) 17．长方体的六个面允许有两个面是一样大小的正方形。

( )四、解答题18．照样子把下列图形分成我们学过的图形．19．右面哪个图形是用左面两个图形拼起来的？圈一圈。

20．（1）左边有（）个图形，右边有（）个图形。

（2）把左边3个图形圈起来，从右边数第3个图形涂上你喜欢的颜色。

21．第一行摆第二行摆从第一行拿几个放到第二行，两行一样多？参考答案：1．B【分析】由题意可知，用8个小正方体能拼成一个大正方体，图中的图形用了6个小正方体，还差2个小正方体就能拼成一个大正方体了，据此解答即可。

【详解】这个图形至少还要用（2）个，才能拼成一个大正方体。

故答案为：B2．A【详解】略3．A【详解】略4．B【详解】略5．B【解析】略6．B【详解】略7． 4 2 1 4【分析】长方体是长长方方的有平平的面；正方体是正正方方的有平平的面；圆柱上下是圆且上下一样粗；球没有平面可以任意方向滚动的；根据立体图形的特征，先数一数，再填空即可。

立体图形的练习题一、选择题（每题2分，共20分）1. 一个正方体的体积是27立方厘米，其棱长是：A. 3厘米B. 6厘米C. 9厘米D. 12厘米2. 一个长方体的长、宽、高分别是5厘米、4厘米和3厘米，其表面积是：A. 94平方厘米B. 114平方厘米C. 134平方厘米D. 154平方厘米3. 一个圆柱的底面半径为2厘米，高为5厘米，其体积是：A. 12π立方厘米B. 20π立方厘米C. 36π立方厘米D. 50π立方厘米4. 一个圆锥的底面半径为3厘米，高为4厘米，其体积是：A. 9π立方厘米B. 12π立方厘米C. 15π立方厘米D. 18π立方厘米5. 若一个球的体积是4/3π立方厘米，其半径是：A. 1厘米B. 2厘米C. 3厘米D. 4厘米二、填空题（每题2分，共20分）6. 一个长方体的长、宽、高分别是a厘米、b厘米和c厘米，其体积公式为：_________立方厘米。

7. 圆柱的体积公式为：底面积乘以_________。

8. 圆锥的体积公式为：1/3乘以底面积乘以_________。

9. 球的体积公式为：4/3π乘以_________的立方。

10. 若一个正方体的棱长为x厘米，其表面积公式为：_________平方厘米。

三、计算题（每题10分，共30分）11. 一个长方体的长为10厘米，宽为8厘米，高为6厘米，求其体积和表面积。

12. 一个圆柱的底面半径为4厘米，高为9厘米，求其体积和表面积。

13. 一个圆锥的底面半径为5厘米，高为12厘米，求其体积。

四、解答题（每题15分，共30分）14. 一个正方体的棱长为7厘米，求其对角线的长度。

15. 一个球的半径为8厘米，求其表面积和体积。

五、附加题（10分）16. 一个正四面体的棱长为a厘米，求其表面积和体积。

答案：1-5：A B C B A6-10：abc，高，高，半径，6x^211：体积=480立方厘米，表面积=596平方厘米12：体积=452π立方厘米，表面积=226π平方厘米13：体积=60π立方厘米14：对角线长度=7√3厘米15：表面积=502.4π平方厘米，体积=2048π立方厘米16：表面积=√3a^2平方厘米，体积=√2/12a^3立方厘米。

2024年数学七年级上册立体几何基础练习题（含答案）试题部分一、选择题：1. 下列哪个图形是正方体？（）A. 长方体B. 正六面体C. 圆柱体D. 球体2. 一个长方体的长、宽、高分别为2cm、3cm、4cm，它的对角线长度是多少cm？（）A. 5cmB. 6cmC. 7cmD. 9cm3. 下列哪个图形的表面积最小？（）A. 正方体B. 长方体C. 球体D. 圆柱体4. 一个正方体的体积是64立方厘米，它的棱长是多少厘米？（）A. 2cmB. 4cmC. 6cmD. 8cm5. 下列哪个图形有6个面？（）A. 三棱锥B. 四棱锥C. 圆锥D. 球体6. 一个圆柱的底面半径为3cm，高为5cm，它的侧面积是多少平方厘米？（）A. 45πcm²B. 54πcm²C. 75πcm²D. 90πcm²7. 下列哪个图形的体积最大？（）A. 长方体（长、宽、高分别为2cm、3cm、4cm）B. 正方体（棱长为3cm）C. 球体（半径为2cm）D. 圆柱体（底面半径为2cm，高为3cm）8. 一个圆锥的底面半径为4cm，高为3cm，它的体积是多少立方厘米？（）A. 48πcm³B. 64πcm³C. 72πcm³D. 96πcm³9. 下列哪个图形可以展开成一个长方形？（）A. 正方体B. 球体C. 圆锥D. 圆柱体10. 一个正方体的棱长为x，它的表面积是多少？（）A. 6x²B. 8x²C. 12x²D. 24x²二、判断题：1. 正方体的六个面都是正方形。

（）2. 圆柱体的底面和顶面都是圆形。

（）3. 球体的表面积和体积相等。

（）4. 长方体的对角线长度等于其长、宽、高的和。

（）5. 圆锥的体积等于底面积乘以高。

（）6. 正方体的体积是棱长的三次方。

（）7. 两个相同体积的正方体，它们的表面积也相同。

初一立体图形练习题一、选择题（每题2分，共20分）1. 下列哪个选项不是立体图形？A. 立方体B. 圆柱C. 圆锥D. 长方形2. 一个长方体的长、宽、高分别为3cm、2cm和4cm，其体积是：A. 12cm³B. 24cm³C. 36cm³D. 48cm³3. 圆柱的底面半径为2cm，高为6cm，其体积是：A. 12πcm³B. 24πcm³C. 36πcm³D. 48πcm³4. 圆锥的底面半径为3cm，高为5cm，其体积是：A. 15πcm³B. 22.5πcm³C. 30πcm³D. 45πcm³5. 一个正方体的棱长为4cm，其表面积是：A. 64cm²B. 96cm²C. 128cm²D. 196cm²6. 一个球的半径为5cm，其体积是：A. 125πcm³B. 250πcm³C. 500πcm³D. 1000πcm³7. 一个棱锥的底面是正方形，边长为4cm，高为6cm，其体积是：A. 24cm³B. 32cm³C. 48cm³D. 64cm³8. 一个棱柱的底面是正六边形，边长为3cm，高为4cm，其体积是：A. 54cm³B. 72cm³C. 90cm³D. 108cm³9. 一个圆锥的底面直径为6cm，高为8cm，其体积是：A. 24πcm³B. 36πcm³C. 48πcm³D. 60πcm³10. 一个圆柱的底面直径为8cm，高为10cm，其体积是：A. 251.2πcm³B. 502.4πcm³C. 1004.8πcm³D.2009.6πcm³二、填空题（每题2分，共20分）11. 一个长方体的长、宽、高分别为a、b、c，其体积公式为________。

小学数学毕业考试立体图形真题练习一、选择题1．将一个正方体木块加工成一个最大的圆柱形木块，圆柱形木块上的底面直径是二、图形计算11．求表面积。

12．求下面组合图形的体积。

（单位：厘米，取3.14）=13．一个零件的形状如下图所示，求这个零件的体积。

三、解答题14．吴老师买了一套新房，客厅长6米，宽4米，高3米。

请同学们帮吴老师算一算装修所需要的部分材料。

（1）客厅准备用边长5分米的方砖铺地面，需要多少块？（2）准备粉刷客厅的四周墙壁和顶面，门窗、电视墙等10平方米不粉刷，实际粉刷的面积是多少平方米？15．神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱，将三名航天员运送至中国空间站。

神舟十三号乘组人员在空间站工作和生活六个月，创造了我国航天员在太空驻留天数的新纪录。

飞船主体由轨道舱、返回舱和推进舱构成。

轨道脑主体为圆柱形，集工作、吃饭和睡觉等诸多功能于一体，总长度为2.8米，直径约2.2米（如图）它的体积大约是多少？（得数保留一位小数）16．求瓶子的体积。

（单位：cm）17．一只底面半径为40厘米的圆柱形水桶内盛有80厘米深的水，将一个高8厘米的圆锥形铁块沉没水中，水没有溢出，水面上升1.5厘米，铁块的底面积是多少平方厘米？18．毕业啦！同学们用卡纸做了一顶“博士帽”（如图），帽子上面是边长为30厘米的正方形，下面是底面直径为20厘米、高为8厘米的无盖无底圆筒，做这顶帽子的上、下部分，分别用卡纸多少平方厘米？（连接处不计）18．一个圆锥形的沙堆，底面面积是28.26平方米，高是6米。

用这堆沙在20米宽的公路上铺2厘米厚的路面，能铺多少米？20．一块蛋糕如下图，在它的表面涂上奶油，需要涂多少平方厘米的奶油？这块蛋糕体积多大？21．一根长2米，横截面直径是20厘米的木头浮在水面上，它正好是一半露出水面。

（1）这根木头的体积是多少立方厘米？（2）这根木头与水接触的面积是多少平方厘米？22．如图是一个粮囤的示意图，它是由圆锥和圆柱两部分组成的。

一、基础概念题1. 请列举出三种常见的立体图形。

2. 立体图形的体积和表面积分别是什么？3. 立体图形的三视图分别是什么？4. 简述长方体、正方体、圆柱体、圆锥体的特征。

二、计算题1. 已知长方体的长、宽、高分别为10cm、6cm、4cm，求其体积和表面积。

2. 一个正方体的边长为8cm，求其体积和表面积。

3. 圆柱体的底面半径为5cm，高为10cm，求其体积和表面积。

4. 圆锥体的底面半径为3cm，高为4cm，求其体积和表面积。

三、应用题1. 一个长方体木块，长、宽、高分别为15cm、10cm、6cm，将其切割成最大的正方体，求正方体的边长。

2. 一个圆柱体水池，底面直径为10m，深为2m，求水池的容积。

3. 一个圆锥形帐篷，底面半径为6m，高为10m，求帐篷的占地面积。

4. 一块长方体铁块，长、宽、高分别为20cm、15cm、10cm，将其熔铸成一个球体，求球体的半径。

四、作图题1. 请画出长方体的三视图。

2. 请画出正方体的三视图。

3. 请画出圆柱体的三视图。

4. 请画出圆锥体的三视图。

五、判断题1. 立体图形的体积和表面积都是固定的。

（）2. 长方体和正方体都是特殊的立方体。

（）3. 圆柱体的底面一定是圆形。

（）4. 圆锥体的侧面展开是一个扇形。

（）六、选择题1. 下列哪个立体图形的体积公式是V = πr²h？A. 长方体B. 正方体C. 圆柱体D. 圆锥体2. 下列哪个立体图形的表面积公式是S = 2πrh + 2πr²？A. 长方体B. 正方体C. 圆柱体D. 圆锥体3. 一个正方体的边长为2cm，其体积为多少？A. 4cm³B. 8cm³C. 12cm³D. 16cm³4. 一个圆锥体的底面半径为3cm，高为4cm，其体积为多少？A. 12πcm³B. 36πcm³C. 48πcm³D. 144πcm³七、填空题1. 一个立方体的边长为5cm，其体积是______cm³，表面积是______cm²。

立体图形拼组练习题一、基础题型1. 请用4个相同的小正方体拼成一个长方体。

2. 用6个相同的小正方体拼成一个正方体。

3. 用8个相同的小正方体拼成一个长方体。

4. 请用10个相同的小正方体拼成一个长方体。

5. 用12个相同的小正方体拼成一个长方体。

二、进阶题型6. 用5个小正方体拼成一个十字形立体图形。

7. 请用7个小正方体拼成一个“L”形立体图形。

8. 用8个小正方体拼成一个“T”形立体图形。

9. 请用9个小正方体拼成一个“E”形立体图形。

10. 用10个小正方体拼成一个“Z”形立体图形。

三、综合题型11. 用6个小正方体和2个大正方体拼成一个长方体。

12. 请用8个小正方体和4个大正方体拼成一个更大的正方体。

13. 用10个小正方体和5个大正方体拼成一个长方体。

14. 请用12个小正方体和6个大正方体拼成一个更大的长方体。

15. 用15个小正方体和5个大正方体拼成一个“十”字形立体图形。

四、创意题型16. 请用7个小正方体拼成一个你喜欢的动物形状。

17. 用8个小正方体拼成一个你喜欢的植物形状。

18. 请用9个小正方体拼成一个你喜欢的交通工具。

19. 用10个小正方体拼成一个你喜欢的建筑物。

20. 请用12个小正方体拼成一个你喜欢的动漫角色。

五、挑战题型21. 用20个小正方体拼成一个2x2x2的大正方体。

22. 请用30个小正方体拼成一个2x3x2的长方体。

23. 用40个小正方体拼成一个2x4x2的长方体。

24. 请用50个小正方体拼成一个3x3x2的长方体。

25. 用60个小正方体拼成一个3x4x2的长方体。

六、空间想象题型26. 设想你面前有一个由小正方体组成的大正方体，如果每个面上都缺少了一个小正方体，请描述这个大正方体的可能形状。

27. 如何用小正方体拼成一个中空的正方体框架？28. 请用小正方体拼出一个立方体，其中一个角上缺少一个小正方体。

29. 设计一个由小正方体拼成的立体图形，使得从不同方向看都是不同的形状。

立体图形练习题一、选择题1. 一个立方体的边长为a，那么它的体积是：A. a^2B. a^3C. 3aD. a2. 一个长方体的长、宽、高分别为l、w、h，那么它的表面积是：A. 2(lw + lh + wh)B. lwhC. 2(l + w + h)D. lw + lh + wh3. 如果一个正四面体的边长为s，那么它的表面积是：A. √3s^2B. 2√3s^2C. 3√3s^2D. 4√3s^24. 一个圆锥的底面半径为r，高为h，它的体积是：A. πr^2hB. 1/3πr^2hC. πr^2D. 1/3πr^35. 一个球的体积公式是：A. V = 4/3πr^3B. V = πr^2C. V = 2πr^2D. V = 2πr^3二、填空题6. 一个圆柱的底面半径为2厘米，高为5厘米，它的体积是______立方厘米。

7. 如果一个正方体的体积是64立方厘米，那么它的边长是______厘米。

8. 一个长方体的长为10厘米，宽为8厘米，高为5厘米，它的表面积是______平方厘米。

9. 一个正十二面体的每个面的边长为1厘米，它的表面积是______平方厘米。

10. 一个球的直径为4厘米，它的体积是______立方厘米。

三、计算题11. 一个棱柱的底面是一个边长为5厘米的正方形，高为10厘米，求它的体积。

12. 一个正二十面体的每个面的边长为2厘米，求它的表面积和体积。

13. 一个圆锥的底面半径为3厘米，高为12厘米，求它的体积。

14. 一个球的半径为7厘米，求它的表面积和体积。

15. 一个圆柱的底面直径为8厘米，高为15厘米，求它的表面积。

四、解答题16. 一个长方体的长、宽、高分别为15厘米、10厘米、8厘米，求它的对角线长度。

17. 一个正方体的体积是125立方厘米，求它的对角线长度。

18. 一个球的表面积是150π平方厘米，求它的半径。

19. 一个圆锥的底面直径为6厘米，高为9厘米，求它的表面积。