下载文档原格式
第二章2．1已知x 是一平稳随机信号，取1、0、-1三个值的概率相等。
用x 对载波)(n c 进行调制后在噪声信道中传输。
接受信号为M n n v n xc n y ,,1,0 ),()()( =+=式中)(n v 是方差为σ2v的零均值白色高斯噪声，与x 相互独立。
上式用矢量表示为v c x y +=（1） 求条件概率函数)/()/(x y f y x f和。
（2） 由y求x 的四种估计：最大后验概率估计x MAP ˆ，最大似然估计x ML ˆ，最小均方误差估计x MS ˆ，最小线性均方误差估计xLMSˆ。
并用图形对它们进行比较。
解：（1）先求)/(x y f ，显然在这种情况下，y是一个1+M 的正态随机矢量，,][/c x v c x E mxy =+=I m m M v T T Txy x y xy v v E c x v c x c x v c x E y y E 12///][ ]))([( ]))([(+==-+-+=--=∑σ)]()(1exp[)2( )](1)(21exp[][)2(1)/(222/)1(21221)1(221c x y c x y c x y c x y vx y f T vM v M vT M M I---=---=+-+++σσσσππ求)/(y x f。
)/(y x P =)()()/()(),(y f x P x y f y f y x f= 已知)1(31)(31)1(31)(-+++=x x x x P δδδ简记)/()/(a y f a x y f ==根据全概率公式，得：)]1/()0/()1/([31 )1()1/( )0()0/()1()1/()()(=≤+=≤+-=≤===≤+==≤+-=-=≤=≤=∴x y Y P x y Y P x y Y P x P x y Y P x P x y Y P x P x y Y P y Y P y F)]1/()0/()1/([31)()(-++==y f y f y f y d y dF y f记)1/()0/()1/(ˆ-++=y f y f y f A，则 Ay f y x P A y f y x P Ay f A y f y x P )1/()/1(,)0/()/0()1/(31)1/(31)/1(====-=-=-=同理： 由)/(y x P 的分布律，我们可以容易得到)/(y x fA x y f x y f x y f y x f /)]1()1/()()0/()1()1/([)/(-+++-=δδδ（2） 求最大似然估计xMLˆ已知：0ˆ)/(ln(=∂∂=x x x y f M Lxy cc yc c c x y c c c x y c x y c xc x y c x y xc x y c x y T T ML T T vT T v T vT vM vx ===-=-----=∂---∂=∂---∂∴+-ˆ0)(1])()([21)]()(21[)]}()(21exp[)2ln{(ˆ2222212解得：σσσσσπ求最小均方误差估计xMSˆ)2(2)2(2]2exp[]2exp[]exp[]2exp[]2exp[2,2, ]exp[]exp[]exp[]exp[]exp[ ]21exp[ )]2(21exp[)]2(21exp[)]2(21exp[)]2(21exp[ )]2(21exp[1 )]2(21exp[1)]1/()1/([1 )]1()1/()()0/()1()1/([)/(22222222222222y a ch y a sh y a y a a y a y a y a yc c c a c c y c y c c y c y c y c y c y y y c c c y y y c c c y y y c c c y y y c c c y y A y c c c y y A y c c c y y A y f y f A A x y f x y f x y f x dx y x xf exav T vT T T vT vT vT vT vT T v TT T v T T T v T T T vTT T v T T T vT T T vML +=-++--====++-=-+++-+-+-++---+-++---+-=--=-+++-==⎰⎰∞∞=∞∞=则原式则令代入将σσσσσσσσσσσσσσδδδ求线性均方误差最小估计xLMSˆ已知)]([)])[var(,cov()(1ˆy E y y y x x E xLMS-+=-① 0)(=x E ， ②Tx T T T T T cv x c x x E y E x E y x E y E y x E x E y x σ2)]([ )()()(]))())(([(),cov(=+=-=--= ③I M v T x T T T T c c v c x v c x E y y E y E y y E y E y 122)])([( )(]))())(([()var(++=++==--=σσ 将I IM =+ˆ1σσσσσσσσσσσ212221121][ ])1[()][var(vT x x vT x x vvT x x vI c I c I c c IIc I c I y----+-=+=利用矩阵反演公式④ y y E y=-)(∴yc c cc c c y c c c c y c c c c c c y c c c c c c y c c cc c y E y y y x x E xvT T TvTxv vxTvTxvTxvTx xTTvTxvvxvTxvT x vTvx vT x LMSxσσσσσσσσσσσσσσσσσσσσσσσσσσσσ22222222224222222222222242221 )( )(][ ][ ]1[ )]([)])[var(,cov()(ˆ+=+=+-+=+-=+-=-+=-题2。
1．用冲激响应不变法将以下 )(s H a 变换为 )(z H ，抽样周期为T。
为任意正整数 ,)()( )2()()( )1(022n s s As H b a s a s s H na a -=+++=分析：①冲激响应不变法满足)()()(nT h t h n h a nT t a ===，T 为抽样间隔。
这种变换法必须)(s H a 先用部分分式展开。
②第（2）小题要复习拉普拉斯变换公式1!][+=n n S n t L ,n a n t s a S S As H t u n t Ae t h )()()()!1()(010-=⇔-=-，可求出)()()(kT Th t Th k h a kT t a ===，又dz z dX zk kx )()(-⇔，则可递推求解。
解: (1)22111()()2a s a H s s a b s a jb s a jb ⎡⎤+==+⎢⎥+++++-⎣⎦[])( 21)()()(t u e e t h tjb a t jb a a --+-+=由冲激响应不变法可得：[]()()()() ()2a jb nTa jb nT a T h n Th nT ee u n -+--==+ 11011() () 211n aT jbT aT jbT n T H z h n z e e z e e z ∞------=⎡⎤==+⎢⎥--⎣⎦∑2211cos 21cos 1 ------+--⋅=ze bT z e bTz e T aT aT aT(2) 先引用拉氏变换的结论[]1!+=n n sn t L可得： na s s As H )()(0-=)()!1()(10t u n t Ae t h n t s a -=-则)()!1()()()(10k u n kT Ae T Tk Th k h n kT s a -⋅==-dzz dX zk kx azk u a ZZk )()( , 11)( 1-−→←-−→←-且按)11()()!1( )()!1( )()(111111000--∞=---∞=----=-==∑∑ze dz d z n AT e z k n T TA z k h z H T s n n k kT s n n k k可得⎪⎪⎩⎪⎪⎨⎧=-=-=•••---,3,2)1(1,1)(111000n z e z e AT n z e AT z H n T s T S n T s ，可以递推求得：2. 已知模拟二阶巴特沃思低通滤波器的归一化系统函数为：2'4142136.111)(ss s H a ++=而3dB 截止频率为50Hz 的模拟滤波器，需将归一化的)('s H a 中的s 变量用502⨯πs来代替424'108696044.928830.444108696044.9)100()(⨯++⨯==s s s H s H a a π 设系统抽样频率为Hz f s 500=，要求从这一低通模拟滤波器设计一个低通数字滤波器，采用阶跃响应不变法。
数字信号处理（姚天任江太辉）第三版课后习题答案第二章2.1判断下列序列是否是周期序列。
若是，请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n )，得出5。
因此82 16是有理数，所以是周期序列。
5 最小周期等于N=^k 16(k取5)。
5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。
因此2168是无理数，所以不是周期序列。
(3)对照正弦型序列的般公式x(n)二 Acos( 3n )，又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄)，得出3。
因此2 8是有理数，所以2 434 6 4 3是周期序列。
最小周期等于N=-k38(k 取3)2.2在图2.2中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。
解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k)：n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解：(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联，已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法，求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。
6.2 教材第六章习题解答1. 设计一个巴特沃斯低通滤波器，要求通带截止频率6p f kHz =，通带最大衰减3p a dB =，阻带截止频率12s f kHz =，阻带最小衰减3s a dB =。
求出滤波器归一化传输函数()a H p 以及实际的()a H s 。
解：（1）求阶数N 。
lg lg sp spk N λ=-0.10.30.1 2.51011010.0562101101p s asp a k --==≈--332121022610s sp p πλπΩ⨯⨯===Ω⨯⨯将sp k 和sp λ值代入N 的计算公式得lg 0.05624.15lg 2N =-=所以取N=5（实际应用中，根据具体要求，也可能取N=4，指标稍微差一点，但阶数低一阶，使系统实现电路得到简化。
） （2）求归一化系统函数()a H p ，由阶数N=5直接查表得到5阶巴特沃斯归一化低通滤波器系统函数()a H p 为54321() 3.2361 5.2361 5.2361 3.23611a H p p p p p p =+++++或 221()(0.6181)( 1.6181)(1)a H p p p p p p =+++++ 当然，也可以按（6.12）式计算出极点:121()22,0,1,2,3,4k j Nk p ek π++==按（6.11）式写出()a H p 表达式41()()a k k H p p p ==-代入k p 值并进行分母展开得到与查表相同的结果。
（3）去归一化（即LP-LP 频率变换），由归一化系统函数()a H p 得到实际滤波器系统函数()a H s 。
由于本题中3p a dB =，即32610/c p rad s πΩ=Ω=⨯⨯，因此()()a a cH s H p s p ==Ω5542332453.2361 5.2361 5.2361 3.2361c c c cc cs s ss s Ω=+Ω+Ω+Ω+Ω+Ω对分母因式形式，则有()()a a cH s H p s p ==Ω52222(0.6180)( 1.6180)()c c c c cc s s s s s Ω=+Ω-Ω+Ω-Ω+Ω如上结果中，c Ω的值未代入相乘，这样使读者能清楚地看到去归一化后，3dB 截止频率对归一化系统函数的改变作用。
数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理（姚天任江太辉）第三版课后习题答案第二章判断下列序列是否是周期序列。
若是，请确定它的最小周期。
（1）x(n)=Acos(685ππ+n )（2）x(n)=)8(π-ne j（3）x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，得出=ω85π。
因此5162=ωπ是有理数，所以是周期序列。
最小周期等于N=)5(16516取k k =。
（2）对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数，所以不是周期序列。
（3）对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，又x(n)=Asin(343ππ+n )＝Acos(-2π343ππ-n )＝Acos(6143-n π)，得出=ω43π。
因此382=ωπ是有理数，所以是周期序列。
最小周期等于N=)3(838取k k =在图中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解：(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联，已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法，求系统的单位阶跃响应。
习题二1、求证：,()(,)x i j x i j xi xj R t t C t t m m =+。
证明：(,)(,)(,,,)x i j i j iji j i j i j R t t E x x x xp x x t t dx dx ==⎰⎰(,)[(),()](),()(,,,)()(,,,)(,)(,)i j i j j i i j i j j i i j i jx i j i x j x i x j x i j i j i ji j i x j x x x i j i j i j x i j x x x x x x x i j x x C t t E x m x m x m x m p x x t t dx dx x x x m x m m m p x x t t dx dx R t t m m m m m m R t t m m =--=--=--+=--+=-⎰⎰⎰⎰ 2、令()x n 和()y n 不是相关的随机信号，试证：若()()()w n x n y n =+，则w x y m m m=+和222w x y σσσ=+。
证明：(1)[()][()()][()][()]x ym E n E x n y n E x n E y n m m ωω==+=+=+ (2)2222222222[(())]{[()()()]}[(())(())][(())][(())]2[(())(())]2[]x y x y x y x y x y x y x y x y x y x yE n m E x n y n m m E x n m y n m E x n m E y n m E x n m y n m m m m m m m m m ωωσωσσσσ=-=+-+=-+-=-+-+--=++--+=+即222x y ωσσσ=+3、试证明平稳随机信号自相关函数的极限性质，即证明： ①当0τ=时，2(0),(0)x x x x R D C σ==； ②当τ=∞时,2(),()0x x x R m C ∞=∞=。
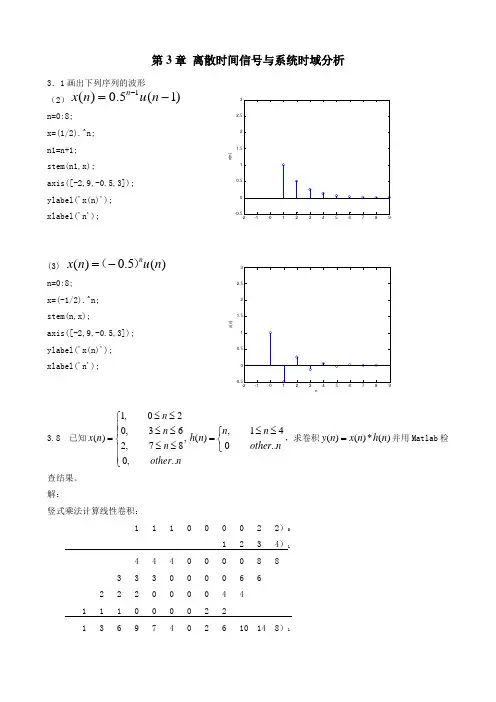
第3章 离散时间信号与系统时域分析3．1画出下列序列的波形（2）1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-（）n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩，求卷积()()*()y n x n h n =并用Matlab 检查结果。
解：竖式乘法计算线性卷积： 1 1 1 0 0 0 0 2 2）01 2 3 4）14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8）1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果：x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx （n ）=5sin(n) 解：2214337w πππ==，所以N=14 (2) 326n ππ-x （n ）=sin()-sin(n)解：22211213322212,2122612T N w T N w N ππππππ=========，所以(6) 3228n π-x （n ）=5sin()-cos(n) 解：22161116313822222()T N w T w x n ππππππ=======，为无理数，所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=，()4()nx n u n -=，(1)4y -=，(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应，并画出图形。
