函数的基本性质

f(x1) f(x1) f(x2) f(x2) x1 x2o x2 x1 x
例1. 如图是定义在区间[-5, 5]上的函数 y=f(x), 根据图象说出函数的单调区间, 以及在每一单调区间 上, 它是增函数还是减函数? y
解: 函数的单调区
间有 [-5, -2), [-2, 1). [1, 3), [3, 5].
例题(补充). 如图是函数 y=f(x) 的图象, 其定义域 为[-p, p], x0 为何值时, 有f(x)≥f(x0), 或 f(x)≤f(x0)? 函数的最大值是多少? 最小值是多少? 解: (1) 当 x0 = - p 时, f(x)≥f(x0),
2
-p y
-p 2
1
这时函数取得最小值
o
-1
[解析] 任取 x1、x2，使得－1<x1<x2<1， 则 Δx＝x2－x1>0. ax1x2＋1x1－x2 Δy＝f(x2)－f(x1)＝ ， 2 x2 － 1 x － 1 1 2
∵－1<x1<x2<1，
2 ∴x1x2＋1>0，x2 1－1<0，x2－1<0，
Байду номын сангаас
x1x2＋1x1－x2 ∴ 2 <0， x1－1x2 － 1 2 ∴当 a>0 时，f(x2)－f(x1)<0， 故此时函数 f(x)在(－1,1)上是减函数， 当 a<0 时，f(x2)－f(x1)>0， 故此时 f(x)在(－1,1)上是增函数． 综上所述，当 a>0 时，f(x)在(－1,1)上为减函数， 当 a<0 时，f(x)在(－1,1)上为增函数．
• 3．函数单调性在图象上的反映：若f(x)是区间A上的单调增 函数，则图象在A上的部分从左向右是逐渐________ 的，若 上升 f(x)是单调减函数，则图象在相应区间上从左向右是逐渐 下降 的． ________ 取值 作差 ， • 4．用定义证明单调性的步骤：__________ ，________ 变形 ，________ 定号 ，________. 结论 ________

题型二 求函数的单调区间 【典例 2】 求下列函数的单调区间： (1)f(x)＝x－1 1； (2)f(x)＝|x2－3x＋2|. [思路导引] (1)先求出函数的定义域，再利用定义求解；(2) 作出函数 y＝x2－3x＋2 的图象，再将 x 轴下方的图象翻折到 x 轴 上方，结合图象写出 f(x)的单调区间．
2．函数的单调区间 如果函数 y＝f(x)在区间 D 上 单调递增 或 单调递减 ，
那么就说函数 y＝f(x)在这一区间上具有(严格的)单调性，区间 D 叫做函数 y＝f(x)的 单调区间．
温馨提示：(1)函数的单调性是对定义域内某个区间而言的，
它是函数的一个局部性质．
(2)函数 f(x)在定义域的某个区间 D 上单调，不一定在定义域 上单调．如 f(x)＝x2 等．
[变式] (1)若本例(1)条件改为“函数 f(x)＝x2－2(1－a)x＋2 的单调递增区间为[4，＋∞)”，其他条件不变，如何求解？
(2) 若 本 例 (2) 中 “ 定 义 域 ( － ∞ ， ＋ ∞)” 改 为 “ 定 义 域 ( － 1,1)”，其他条件不变，如何求解？
[解] (1)∵f(x)＝x2－2(1－a)x＋2＝[x－(1－a)]2＋2－(1－ a)2，
题型三 函数单调性的应用 【典例 3】 (1)已知函数 f(x)＝x2－2(1－a)x＋2 在[4，＋∞) 上是增函数，求实数 a 的取值范围． (2)已知 y＝f(x)在定义域(－∞，＋∞)上是减函数，且 f(1－ a)<f(2a－1)，求 a 的取值范围． [思路导引] 二次函数的单调性由开口方向及对称轴确定， 与函数值有关的不等式问题依据单调性转化为自变量的不等关 系．
数 M 满足：
①∀x∈I，都有 f(x)≤M

y轴 对称
奇函数 一般地,如果对于函数f(x)的定义域内任意一个x,都有 关于 f(-x)=-f(x) ,那么函数f(x)就叫做奇函数
2.奇、偶函数的性质
原点 对称
(1)奇函数在关于原点对称的区间上的单调性 相同 ,偶函数在关于原
点对称的区间上的单调性 (2)在公共定义域内,
相反 .
(i)两个奇函数的和是奇函数,两个奇函数的积是偶函数;
例3 求函数f(x)=log1 (-x2-2x+3)的单调区间.
2
解题导引 先求定义域,然后拆分函数式为y=log1 u,u=-x2-2x+3,判断单调性
2
得单调区间.
解析 由已知得-x2-2x+3>0,∴-3<x<1. ∴f(x)的定义域为{x|-3<x<1}.令u=-x2-2x+3.
∵u=-x2-2x+3在区间(-3,-1)上单调递增,在区间(-1,1)上单调递减,y=log1 u为
§3.2 函数的基本性质 (讲解部分)
考点清单
考点一 函数的单调性及最值
1.函数的单调性
(1)单调函数的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I.区间D⊆I,如果对于任意x1,x2∈D,且x1<x2
都有① f(x1)<f(x2)
都有② f(x1)>f(x2)
函数f(x)在区间D上是③ 增函数
2
(2)∵f(x)在R上单调递减,
a-1 0,
∴0 a 1,
∴
loga 2 (a-1) 2-2a,
2 ≤a<1.
2
∴a的取值范围为
2 2

第四讲 函数的基本性质.函数的单调性概念（1）增函数和减函数的概念如果函数y ＝f (x )在区间D 上是增函数或减函数，那么就说函数y ＝f (x )在这一区间具有(严格的)单调性．区间D 叫做函数y ＝f (x )的单调区间． （3）函数的单调性等价变形 设[]2121,,x x b a x x ≠∈，那么 ①[]1212()()()0x x f x f x --> ⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数；②[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数.2.运算法则：如果函数)(x f 和)(x g 在相同区间上是单调函数,则（1）增函数+增函数是增函数；（2）减函数+减函数是减函数；（3)增函数-减函数是增函数；（4）减函数-增函数是减函数；3.常见函数的单调性：（1）一次函数b kx y +=，当0>k 时，在区间),(+∞-∞上是增函数，当0<k 时，在区间),(+∞-∞上是减函数；（2）反比例函数xky =，当0>k 时，在区间)0,(-∞和区间),0(+∞上是减函数，当0<k 时，在区间)0,(-∞和区间),0(+∞上是增函数（3）二次函数c bx ax y ++=2，当0>a 时，在区间)2,(ab--∞是减函数，在区间),2(+∞-a b 是增函数，当0<a 时，在区间)2,(a b --∞是增函数，在区间),2(+∞-ab是减函数.4.函数单调性判定方法①定义法：取值、作差、变形、定号、下结论 ②运算法则法④图像法，利用图像研究函数的单调性.1.根据函数的单调性的定义，证明函数1)(3+-=x x f 在),(+∞-∞上是减函数。

2.判断函数)0()(>+=p xpx x f 的单调性3.根据函数的单调性的定义，证明函数x x x f -+=1)(2在),(+∞-∞上是减函数。

函数的基本性质(函数的单调性、奇偶性、周期性)一、函数单调性 1、可以从三个方面理解（1）图形刻画：对于给定区间上的函数()f x ，函数图象如从左向右连续上升，则称函数在该区间上单调递增；函数图象如从左向右连续下降，则称函数在该区间上单调递减。

（2）定性刻画：对于给定区间上的函数()f x ，如函数值随自变量的增大而增大，则称函数在该区间上单调递增；如函数值随自变量的增大而减小，则称函数在该区间上单调递减。

（3）定量刻画，即定义。

2、判断增函数、减函数的方法：①定义法：一般地，对于给定区间上的函数()f x ，如果对于属于这个区间的任意两个自变量的值1x 、2x ，当21x x <时，都有()()21x f x f <〔或都有()()21x f x f >〕，那么就说()f x 在这个区间上是增函数（或减函数）。

与之相等价的定义： ⑴()()02121>--x x x f x f ，〔或都有()()02121<--x x x f x f 〕则说()f x 在这个区间上是增函数（或减函数）。

其几何意义为：增（减）函数图象上的任意两点()()()()2211,,,x f x x f x 连线的斜率都大于（或小于）0。

⑵()()()[]02121>--x f x f x x ，〔或都有()()()[]02121<--x f x f x x 〕则说()f x 在这个区间上是增函数（或减函数）。

②导数法：一般地，对于给定区间上的函数()f x ，如果()0`>x f 那么就说()f x 在这个区间上是增函数；如果()0`<x f 那么就说()f x 在这个区间上是减函数；如果函数()x f y =在某个区间上是增函数（或减函数），就说()f x 在这一区间上具有（严格的）单调性，这一区间叫做()f x 的单调区间。

如函数是增函数则称区间为增区间，如函数为减函数则称区间为减区间。

• 当 > 时， − < ，则
• − ＝ −

− ＝ − ＝ − ()．
• 综上，对 ∈ (−∞，) ∪ (，＋∞)，
• ∴ ()为奇函数．
都有 − ＝ − ()．
奇偶性判定
• 【解析】 (4) =
−
−
• 定义域为 −， 关于原点对称
• ③一个奇函数，一个偶函数的积是 奇函数 ．
函数的奇偶性
• 判断函数的奇偶性
• 1、首先分析函数的定义域，在分析时，不要把函数化简，而要根据
原来的结构去求解定义域，如果定义域不关于原点对称，则一定是非
奇非偶函数．
• 2、如果满足定义域对称，则计算(−)，看与()是否有相等或互为
相反数的关系.
−
−−
+
++
−+
• 即
= 恒成立，
• 则2(＋)2＋2＝0对任意的实数恒成立．
• ∴ ＝＝0.
函数的单调性

+
•
(2)∵ =
∈ 是奇函数, 只需研究(, ＋∞)上()的单调区间即可．
•
任取， ∈ (，＋∞)，且 < ，则
应值，故函数取得最值时，一定有相应的x的值．
抽象函数的单调性
• 函数()对任意的、 ∈ ，都有 ＋ ＝ ＋ − ，并且当
> 时，() > .
• (1)求证：()是上的增函数；
• (2)若()＝，解不等式( − − ) < .
抽象函数的单调性
• ∴ ()＝， ∴原不等式可化为( − − ) < ()，
• ∵ ()是上的增函数，

函数的基本性质⏹1。

函数的奇偶性⏹（1）函数的奇偶性的定义。

⏹（2）函数的奇偶性的判断与证明。

⏹（3）奇、偶函数图象的特征。

⏹2。

函数的单调性⏹（1）函数的单调性的定义。

⏹（2）函数的单调性的判断与证明。

⏹复合函数的单调性⏹（3）求函数的单调区间。

3．函数的周期性(1)定义:设函数的定义域是D，若存在非零常数T，使得对任何x∈D，都有x+T ∈D且f(x+T)=f(x)，则函数f(x)为周期函数，T为f(x)的一个周期。

定理:设函数的定义域是D，a,b为不相等的常数，若对任何x∈D，都有x+a∈D,x+b∈D,且f(x+a)=f(x+b)，则函数f(x)为周期函数，a-b为f(x)的一个周期。

(2)最小正周期:(3)定理:若T是函数f(X)的一个周期,则nT也是函数f(x)的一个周期.(n为非零整数.)4．函数图象的对称性⏹一·中心对称：⏹(1) 奇函数的图象关于原点对称；⏹一般地，如果方程f(x,y)=0满足f(x,y)=f(-x,-y)，则曲线f(x,y)=0关于原点对称（2）函数y=f(x)的图象关于点（a,b）对称的充要条件为：对函数定义域中的任意x均满足2b-y=f(2a-x)(3)函数的图象关于点(a,0)对称的充要条件为: f(x) =- f(2a-x) ⇔f(a+x)=- f(a-x)(4)设函数f(x)对其定义域中的任意值x均满足f(a+x)=-f(b-x),则f(x)的图象关于点((a+b)/2,0)成中心对称.二．轴对称：（1）偶函数的图象关于Y轴对称；一般地，如果方程f(x,y)=0满足f(x,y)=f(-x,y)，则曲线f(x,y)=0关于Y轴对称（2）设a是非零常数，如果对函数定义域中的任意值x均满足f(x)=f(2a-x)⇔f(a+x)=f(a-x)，则函数y=f(x)的图象关于直线x=a对称。

一般地，如果方程f(x,y)=0满足f(x,y)=f(2a-x,y)，则曲线f(x,y)=0关于直线x=a对称设函数f(x)对其定义域中的任意值x均满足f(a+x)=f(b-x),则f(x)的图象关于直线x=(a+b)/2对称．(3)反函数的图象⏹函数y=f(x)的图象与y=f -1(x)的图象关于直线y=x对称；⏹函数y=f(x)的图象与y=-f-1 (-x)的图象关于直线y= - x对称；⏹设函数y=f(x)有反函数y=f– 1(x)，则其图象关于直线y=X对称的充要条件是：f(x)=f– 1(x).5．函数图象的对称性与函数的周期性有着密切的内在联系，我们有下面的结论：⏹命题1：如果函数的图象关于直线x=a和直线x=b(a ≠b)对称，那么函数是以2(a-b)为周期的周期函数。

函数的基本性质知识梳理1) 函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数y f[g(x)]，令u g(x)，若y f(u)为增，u g(x)为增，则y f [ g(x)]为增；若y f(u)为减，u g(x)为减，则y f[g(x)]为增；若y f(u)为增，u g(x)为减，则y f[g(x)]为减；若 y f （u ）为减， u g （x ）为增，则 y f [ g （x ）]为减．f （x ） （2）打“√”函数 ax (a 0)x的图象与性质yf(x) 分别在( , a]、[ a,）上为增函数，分别在[ a,0) 、(0, a]上为减函数．（3）最大（小）值定义ox①一般地，设函数 yf （x ）的定义域为 I ，如果存在实数M满足：（1 ）对于任意的 x I ，都有 f（x ）M；（2）存在 x 0 I ，使得 f（x0） M．那么，我们称M 是函数f （x ）的最大值，记作 f max（x ） M②一般地，设函数 y f （x ）的定义域为 I ，如果存在实数 m 满足：（1）对于任意的 x I ，都有 f（x ） m（2）存在 x 0 I ，使得 f （x 0）m ．那么，我们称 m是函数f（x ）的最小值，记作fmax （x ） m．2）函数的奇偶性①定义及判定方法②若函数 f （x ）为奇函数，且在x 0处有定义，则f （0） 0．③奇函数在 y 轴两侧相对称的区间增减性相同，偶函数在y轴两侧相对称的区间增减性相反．④ 在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数） ，两个偶函数（或奇函数） 的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．3) 函数的周期性定义】若T为非零常数，对于定义域内的任一x，使 f (x T) f ( x)恒成立则f(x)叫做周期函数，T叫做这个函数的一个周期。

函数是数学中一种重要的概念，它具有一些重要的性质。

常见的函数性质包括：
1.单调性：函数在定义域内单调递增或递减。

2.可导性：函数在定义域内可导。

3.可积性：函数在定义域内可积。

4.可逆性：函数在定义域内可逆。

5.可微性：函数在定义域内可微。

6.可解析性：函数在定义域内可解析。

7.持久性：函数在定义域内持久，即函数的值在定义域内不会突然变化。

8. 函数的值域：函数的值域是函数在定义域内所有可能取到的值的集合。

9. 函数的导函数：函数在定义域内可导，那么它就有导函数，并且导函数是唯一的。

10. 函数的导数：函数的导数描述了函数在某一点处的变化率。

这些性质对于理解和分析函数具有重要的意义。

不同的函数具有不同的性质，因此在研究和使用函数时需要结合具体情况来考虑这些性质。

高中数学必修1函数的基本性质1．奇偶性（1）定义：如果对于函数f (x )定义域内的任意x 都有f (－x )=－f (x )，则称f (x )为奇函数；如果对于函数f (x )定义域内的任意x 都有f (－x )=f (x )，则称f (x )为偶函数。

如果函数f (x )不具有上述性质，则f (x )不具有奇偶性.如果函数同时具有上述两条性质，则f (x )既是奇函数，又是偶函数。

注意：○1 函数是奇函数或是偶函数称为函数的奇偶性，函数的奇偶性是函数的整体性质； ○2 由函数的奇偶性定义可知，函数具有奇偶性的一个必要条件是，对于定义域内的任意一个x ，则－x 也一定是定义域内的一个自变量（即定义域关于原点对称）。

（2）利用定义判断函数奇偶性的格式步骤：○1 首先确定函数的定义域，并判断其定义域是否关于原点对称； ○2 确定f (－x )与f (x )的关系； ○3 作出相应结论： 若f (－x ) = f (x ) 或 f (－x )－f (x ) = 0，则f (x )是偶函数；若f (－x ) =－f (x ) 或 f (－x )＋f (x ) = 0，则f (x )是奇函数。

（3）简单性质：①图象的对称性质：一个函数是奇函数的充要条件是它的图象关于原点对称；一个函数是偶函数的充要条件是它的图象关于y 轴对称；②设()f x ，()g x 的定义域分别是12,D D ，那么在它们的公共定义域上：奇+奇=奇，奇⨯奇=偶，偶+偶=偶，偶⨯偶=偶，奇⨯偶=奇2．单调性（1）定义：一般地，设函数y =f (x )的定义域为I ， 如果对于定义域I 内的某个区间D 内的任意两个自变量x 1，x 2，当x 1<x 2时，都有f (x 1)<f (x 2)（f (x 1)>f (x 2)），那么就说f (x )在区间D 上是增函数（减函数）；注意：○1 函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质； ○2 必须是对于区间D 内的任意两个自变量x 1，x 2；当x 1<x 2时，总有f (x 1)<f (x 2) （2）如果函数y =f (x )在某个区间上是增函数或是减函数，那么就说函数y =f (x )在这一区间具有（严格的）单调性，区间D 叫做y =f (x )的单调区间。

答案 [－2，＋∞)
►单调性的两个易错点：单调性；单调区间.
（2）函数的单调递增(减)区间有多个时，不能用并集表示， 可以用逗号或“和”。
例如 函数 f(x)＝x＋1x的单调递增区间为________.
解析 由f(x)图象易知递增区间为(－∞，－1]，[1，＋∞). 答案 (－∞，－1]，[1，＋∞)
变式训练：
已知奇函数f (x)的定义域为- 2,2，且在区间 - 2,0上递减，则满足f (1 m) f (1 m2) 0的 实数m的取值范围是-1,1
题型五、函数的周期性解题方略
1.有关函数周期性的常用结论 (1)若 f(x＋a)＝f(x－a)，则函数的周期为 2|a|； (2)若 f(x＋a)＝－f(x)，则函数的周期为 2|a|； (3)若 f(x＋a)＝f（1x），则函数的周期为 2|a|； (4)若 f(x＋a)＝－f（1x），则函数的周期为 2|a|.
叫做f(x)的最小正周期.
题型归纳
题型一 判断函数的单调性 判断函数的单调性或求单调区间的方法 (1)利用已知函数的单调性. (2)定义法：先求定义域，再利用单调性定义.
(3) 图 象 法 ： 如 果 f(x) 是 以 图 象 形 式 给 出 的 ， 或 者 f(x)的图象易作出，可由图象的直观性写出它的单
域为[a－1，2a]，则a＝________，b＝________.
解析 由定义域关于原点对称得 a－1＋2a＝0，解得 a＝13，即
f(x)＝13x2＋bx＋b＋1，又 f(x)为偶函数，由 f(－x)＝f(x)得 b＝0.
答案
1 3
0
（2）若函数 f(x)为奇函数且在原点有意义，则 f(0)＝0
[点评] 解题(1)的关键是会判断复合函数的单调性；解题(2) 的关键是利用奇偶性和单调性的性质画出草图.

−

1
即函数f（x）＝x＋ 为奇函数．

函数的基本性质
例1 判断下列函数的奇偶性：
（3）f（x）＝0；
（2）f（x）＝ ；
解：（1）函数f（x）的定义域为R．
∀x∈R，都有－x∈R，且f（－x）＝0＝-f(x)＝f（x），
函数f（x）既是奇函数，又是偶函数．
1
（2）函数f（x）＝x＋ 的定义域I为[0，＋∞）．
(1)若函数f(x)在区间[a，b]上是增(减)函数，则f(x)在区间
[a，b]上的最小(大)值是f(a)，最大(小)值是f(b)．
(2)若函数f(x)在区间[a，b]上是增(减)函数，在区间[b，c]
上是减(增)函数，则f(x)在区间[a，c]上的最大(小)值是f(b)，
最小(大)值是f(a)与f(c)中较小(大)的一个．
当 > 0时,(1 ) − (2 )<0，即(1 ) < (2 )
所以函数() = + 在R上单调递增，即函数() = + 是增函数。
当 < 0时,(1 ) − (2 )>0，即(1 ) > (2 )
所以函数() = + 在R上单调递减，即函数() = + 是减函数。
1
（2）f（x）＝x＋

；
解：（1）函数f（x）＝x4的定义域为R．
∀x∈R，都有－x∈R，且f（－x）＝（－x）4＝x4＝f（x），
函数f（x）＝x4为偶函数．
1
（2）函数f（x）＝x＋ 的定义域I为（－∞，0）∪（0，＋∞）．

1
1
∀x∈I，都有－x∈I，且f（－x）＝－x＋ ＝－（x＋ ）＝－f（x），

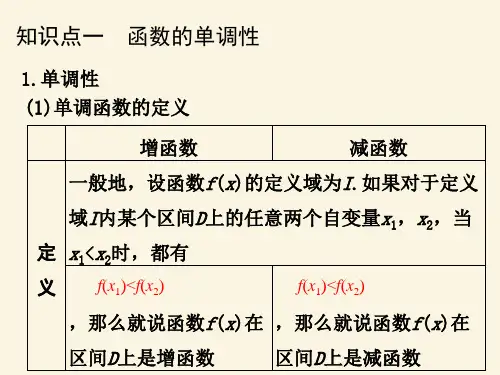
函数的基本性质一．函数的单调性：1. 定义：设D 为函数)(x f 定义域的子集。

对任意的D ,21∈x x 且21x x <时，都有⇔>--⇔>--⇔<0)](()([0)()()()(1212121221）x x x f x f x x x f x f x f x f 函数)(x f y =在D 上是增加的。

对任意的D ,21∈x x 且21x x <时，都有⇔<--⇔<--⇔>0)](()([0)()()()(1212121221）x x x f x f x x x f x f x f x f 函数)(x f y =在D 上是减少的。

2. 图像特点：自左向右看图像是上升的。

（图像在此区间上是增加的） 自左向右看图像是下降的。

（图像在此区间上是减少的）3.判断函数单调性的方法：（1）图像法：作出函数图像，由图像直观判断求解，只能用于判断。

（数形结合） 解题程序：解析式-----图像-----单调区间（2）性质法：需要先记清基本初等函数的单调性。

高中基本初等函数：一次函数：)0(≠+=k b kx y ，二次函数：)0(2≠++=a c bc ax y 反比例函数：)0(≠=k x k y ，简单幂函数：3,2,21,1,1)(-=∈=αααR x y 指数函数：)10(≠>=a a a y x 且，对数函数：)10(log ≠>=a a x y a 且， “对勾”函数：)0(>+=a x ax y①a x f y +=)(与)(x f y =的单调性相同。

②当0>a 时，函数)(x af y =与)(x f y =的单调性相同；当0<a 时，函数)(x af y =与)(x f y =的单调性相反；③在公共定义域内，增函数)(x f +增函数)(x g 是增函数， 减函数)(x f +减函数)(x g 是减函数；增函数)(x f －减函数)(x g 是增函数，减函数)(x f －增函数)(x g是减函数；④两函数积的单调性：当)(x f ，)(x g 在公共区间上都是增（减）函数。

函数的基本性质（奇偶性、单调性、周期性、对称性）函数的性质（奇偶性、单调性、周期性、对称性）“定义域优先”的思想是研究函数的前提，在求值域、奇偶性、单调性、周期性、换元时易忽略定义域，所以必须先考虑函数的定义域，离开函数的定义域去研究函数的性质没有任何意义。

1. 奇偶性f(-x)与f(x)之间的关系：①f(-x)=f(x)为偶函数；f(-x)=-f(x)为奇函数；②f(-x)-f(x)=0为偶；f(x)+f(-x)=0为奇；③f(-x)÷f(x)=1是偶；f(x)÷f(-x)=-1为奇函数. （1）若定义域关于原点对称（2）若定义域不关于原点对称⾮奇⾮偶例如：3x y =在)1,1[-上不是奇函数常⽤性质：1．0)(=x f 是既奇⼜偶函数；2．奇函数若在0=x 处有定义，则必有0)0(=f ； 3．偶函数满⾜)()()(x f x f x f =-=；4．奇函数图象关于原点对称，偶函数图象关于y 轴对称；5．0)(=x f 除外的所有函数的奇偶性满⾜：（1）奇函数±奇函数=奇函数偶函数±偶函数=偶函数奇函数±偶函数=⾮奇⾮偶（2）奇函数×奇函数=偶函数偶函数×偶函数=偶函数奇函数×偶函数=奇函数 6．任何函数)(x f 可以写成⼀个奇函数2)()()(x f x f x --=和⼀个偶函数2)()()(x f x f x -+=ψ的和。

2. 单调性定义：函数定义域为A ，区间，若对任意且①总有则称在区间M 上单调递增②总有则称在区间M 上单调递减应⽤：（⼀）常⽤定义法来证明⼀个函数的单调性⼀般步骤：（1）设值（2）作差（3）变形（4）定号（5）结论（⼆）求函数的单调区间定义法、图象法、复合函数法、导数法(以后学) 注：常⽤结论（1）奇函数在对称区间上的单调性相同（2）偶函数在对称区间上的单调性相反（3）复合函数单调性-------同增异减3. 周期性（1）⼀般地对于函数内⼀切值时总有，那么叫做周期函数，T 叫做周期，kT （T 的整数倍）也是它的周期（2）如果周期函数在所有周期中存在⼀个最⼩正数，就把这个最⼩正数叫最⼩正周期。

函数的基本性质与变换函数是数学中的一个重要概念，它描述了两个数集之间的对应关系。

在数学分析中，函数的基本性质及其变换是需要深入了解和掌握的。

一、函数的基本性质1. 定义域和值域：函数的定义域是指函数的自变量可能取值的范围，值域是函数的因变量可能取值的范围。

在函数表示中，我们常用f(x)来表示函数y与自变量x的对应关系。

2. 单调性：函数的单调性指函数在其定义域内的变化趋势。

当函数的自变量增加时，如果函数值也增加，则称函数是递增的；当自变量减小时，函数值也减少，则称函数是递减的。

3. 极值：函数的极大值和极小值统称为极值。

极大值是指函数在某一区间内取得的最大值，极小值是指函数在某一区间内取得的最小值。

极值点是函数曲线上的特殊点，处于极大值或极小值的位置。

4. 奇偶性：函数的奇偶性指函数在定义域内的对称性。

如果对于定义域内任意一点x，都有f(-x) = -f(x)，则函数是奇函数；如果对于定义域内任意一点x，都有f(-x) = f(x)，则函数是偶函数。

二、函数的变换函数的变换是指通过一系列变换操作，得到函数图像在坐标平面上的移动、伸缩和翻转等变化。

1. 平移变换：平移变换是指将函数图像在坐标平面上沿着横轴或纵轴方向移动的操作。

平移变换可以分为水平平移和垂直平移两种情况。

- 水平平移：将函数图像在横轴方向上左右移动。

当平移量为a时，函数图像的横坐标x变为x-a，纵坐标y不变。

- 垂直平移：将函数图像在纵轴方向上上下移动。

当平移量为b时，函数图像的横坐标x不变，纵坐标y变为y-b。

2. 伸缩变换：伸缩变换是指通过改变函数的自变量和因变量的尺度，改变函数图像的形状和大小。

伸缩变换可以分为水平方向和垂直方向的伸缩。

- 水平伸缩：将函数图像在横轴方向上拉伸或压缩。

当伸缩比例为k 时，函数图像的横坐标x变为x/k，纵坐标y不变。

- 垂直伸缩：将函数图像在纵轴方向上拉伸或压缩。

当伸缩比例为k 时，函数图像的横坐标x不变，纵坐标y变为y/k。

§2函数的基本性质【知识精要】 一、函数的奇偶性1、定义：如果对于函数)(x f 定义域内的任意x 都有)()(x f x f -=-，则称)(x f 为奇函数；如果对于函数)(x f 定义域内的任意x 都有)()(x f x f =-，则称)(x f 为偶函数.【注意】（1）函数的奇偶性是函数的整体性质，函数的奇偶性要求：对于函数)(x f 定义域内的任意x 都有)()(x f x f -=-（或)()(x f x f =-），即要求“全票通过”；若有例外，则可“一票否决”.判断函数奇偶性首先判断函数定义域是否关于原点对称。

（2）由函数的奇偶性定义可知，函数具有奇偶性的一个必要（前提）条件是，对于定义域内的任意一个x ，则x -也一定是定义域内的一个实数（即定义域关于原点对称）.【例1】（1）已知f (x )＝ax 2＋bx 是定义在[a －1,2a ]上的偶函数，那么a ＋b 的值是( )A. －13B.13C.12 D ．－12（2）已知函数2x ay +=的图象关于y 轴对称，则实数a 的值是__________；2、简单性质：（1）图象的对称性质：一个函数是奇函数的充要条件是它的图象关于原点对称；一个函数是偶函数的充要条件是它的图象关于y 轴对称；（2）若奇函数)(x f 在0=x 处有意义，则必有0)0(=f ；（3）若函数)(x f 既是奇函数，又是偶函数，则解析式为0)(=x f ，由于定义域（可以是任意一个关于原点对称的集合）不确定，这样的函数仍有无穷多. （4）)(x f 是偶函数，则)()(x f x f =． 【例2】（1）函数)12lg()(xa x f ++=为奇函数，则实数=a _________； （2）若1()21x f x a =+-是奇函数，则a =_________； （3）设定义在[]2,2-上的偶函数)(x f 在区间[]2,0上单调递减，若)()1(m f m f <-，求实数m 的取值范围． 【例3】函数x x y ln cos ⋅=的部分图象大致是下图中的（ ）A.B. C. D.【例4】设)(x f 是连续的偶函数，且当0>x 时，)(x f 是单调的函数，则满足)43()(++=x x f x f 的所有的x 的和为____________．（5）设)(x f ，)(x g 的定义域分别是21,D D ，φ≠⋂=21D D D ，那么在它们的公共定义域D 上：①奇函数±)(x f 奇函数)(x g 是奇函数；②奇函数⨯)(x f 奇函数)(x g 是偶函数；③偶函数±)(x f 偶函数)(x g 是偶函数；④奇函数⨯)(x f 偶函数)(x g 是奇函数. 二、函数的单调性1、定义：一般地，设函数)(x f y =的定义域为I ，如果对于定义域I 内的某个区间D 内的任意两个自变量的值21,x x ，当21x x <时，都有)()(21x f x f <（)()(21x f x f >），那么就说)(x f 在区间D 上是增函数（减函数）；如果函数)(x f y =在某个区间上是增函数或是减函数，那么就说函数)(x f y =在这一区间具有（严格的）单调性，区间D 叫做)(x f y =的单调区间.【注意】（1）函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质，因此，函数的单调区间一定是函数定义域的子集，因此求函数单调区间应先确定函数定义域。

函数的基本性质知识点归纳与题型总结0＝x2＝f(x)，所以f(x)为偶函数．4)因为f(x)有意义，则x＞0，所以f(x)的定义域不关于原点对称。

所以f(x)为非奇非偶函数．二、知识归纳1．函数的单调性1)单调递增对于函数f(x)，如果对于定义域内的任意两个数x1和x2，当x1＜x2时，有f(x1)＜f(x2)，那么函数f(x)就叫做单调递增函数．2)单调递减对于函数f(x)，如果对于定义域内的任意两个数x1和x2，当x1＜x2时，有f(x1)＞f(x2)，那么函数f(x)就叫做单调递减函数．3)严格单调性如果对于定义域内的任意两个不相等的数x1和x2，有f(x1)＜f(x2)或f(x1)＞f(x2)，那么函数f(x)就叫做严格单调函数．4)单调性判定设函数f(x)在区间[a，b]上连续，在(a，b)内可导，则①当f'(x)＞0时，函数f(x)在(a，b)上单调递增；②当f'(x)＜0时，函数f(x)在(a，b)上单调递减；③当f'(x)＝0时，函数f(x)在x处取极值．2．函数的极值1)极值定义设函数f(x)在点x0的某个去心邻域内有定义，如果对于x0的任何一个邻域内的x值，都有f(x)≤f(x0)(或f(x)≥f(x0))，那么就称f(x0)是函数f(x)的一个极大值(或极小值)，而x0就称为函数f(x)的一个极值点．2)判别极值的方法①一阶导数法设函数f(x)在点x0处可导，且f'(x0)＝0，则1)当f''(x0)＞0时，f(x0)是函数f(x)的一个极小值；2)当f''(x0)＜0时，f(x0)是函数f(x)的一个极大值；3)当f''(x0)＝0时，判别困难，需用其他方法．②二阶导数法设函数f(x)在点x0处二阶可导，则1)当f''(x0)＞0时，f(x0)是函数f(x)的一个极小值；2)当f''(x0)＜0时，f(x0)是函数f(x)的一个极大值；3)当f''(x0)＝0时，判别困难，需用其他方法．3．函数的凹凸性1)凹函数对于函数f(x)，如果对于定义域内的任意两个数x1和x2，以及任意实数λ(0＜λ＜1)，都有f(λx1＋(1－λ)x2)≤λf(x1)＋(1－λ)f(x2)，那么函数f(x)就叫做凹函数．2)凸函数对于函数f(x)，如果对于定义域内的任意两个数x1和x2，以及任意实数λ(0＜λ＜1)，都有f(λx1＋(1－λ)x2)≥λf(x1)＋(1－λ)f(x2)，那么函数f(x)就叫做凸函数．3)严格凹凸性如果对于定义域内的任意两个不相等的数x1和x2，以及任意实数λ(0＜λ＜1)，都有f(λx1＋(1－λ)x2)λf(x1)+(1－λ)f(x2)，那么函数f(x)就叫做严格凹函数或严格凸函数．4)凹凸性判定设函数f(x)在区间[a，b]上具有二阶导数，则①当f''(x)＞0时，函数f(x)在(a，b)上是凹函数；②当f''(x)＜0时，函数f(x)在(a，b)上是凸函数；③当f''(x)＝0时，函数f(x)在x处可能是拐点．解题提醒：①判定函数的单调性时，要注意定义域的连续性和可导性．②判定函数的极值和拐点时，要注意函数的可导性和二阶导数的符号．题型二函数单调性、极值和凹凸性的判定典型例题：求函数f(x)＝x3－3x2＋3的单调性、极值和凹凸性．解：(1)单调性f'(x)＝3x2－6x，令f'(x)＝0，得x＝0或x＝2。