六杆机构加速度分析

2000t，行程 1100mm 的多连杆机构。为满足用户使用要求和最小化生产厂家变更引起费用，此机 构必须满足下列条件： 驱动臂 R＝250～280mm；支撑点变化范围 X＝1100～1300，Y＝150～350mm； 曲柄中心到下死点距离 2800～3150；公称压力 2400T，公称压力行程 30mm； 滑块拉伸行程为 400mm，拉伸行程内速度小于 21m/s，最大小于 23m/s，为保证冲压质量， 在拉伸行程内拉伸曲线要接近直线，如图 3 示； 连杆压力角小于 45 度； 摆杆与摇杆之间传动角大于 55 度； 连杆最大应力小于 60MPa。 对应的冲头的位移、速度、加速度曲线如图示：
1 机构性能设计
在机构设计中，用户最关心的整机性能设计，而目前机构运动分析的方法有图解法、解析法 和实测法等。图解法特点是形象直观、方法简单、但精度不高，且在对机构的一系列位置进行分 析时，需反复作图而显得繁琐，设计周期过于冗长。实测法以物理样机为基础，在设计多用于检 验和校核。解析法的特点是精度高、比较抽象，计算量大。随着电子计算机硬件资源和各种专业 软件的发展和普及而日益得到广泛应用。 其中代表的仿真软件 Recurdyn 等。 在机构详细设计阶段， 则利用有限元对具体的机构尺寸参数进行强度、刚度、稳定性校核，常用的校核工具有 Simulia 的 Abaqus 等软件，而进行网格划分使用 Abaqus CAE 等工具。
- 262 -
第六届中国 CAE 工程分析技术年会论文集
图 6：Isight 集成 Recurdyn、Abaqus 试验设计流程
粒子群算法(particle swarm optimization，PSO)由 Kennedy 和 Eberhart 在 1995 年提出，该算法 模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的，是一种基于 Swarm Intelligence 的优化方法。同遗传算法类似，也是一种基于群体叠代的，但并没有遗传算法用的交 叉以及变异，而是粒子在解空间追随最优的粒子进行搜索。PSO 的优势在于简单容易实现同时又 有深刻的智能背景，既适合科学研究，又特别适合工程应用，并且没有许多参数需要调整。目前， 已有的群智能理论和应用研究证明群智能方法是一种能够有效解决大多数优化问题的新方法，更 重要是,群智能潜在的并行性和分布式特点为处理大量的以数据库形式存在的数据提供了技术保 证。无论是从理论研究还是应用研究的角度分析,群智能理论及应用研究都是具有重要学术意义和 现实价值的。 粒子群算法(particle swarm optimization，PSO)搜索方向按照下式更新。

l
1
φ θ
2
l
x
a2 x 2l cos al sin a2 y 2l sin al cos
已知：构件的长度L及运动参数角位置θ 、角速度ω 、 角加速度ε ，1点的运动参量。
求： 3点的运动参量。
解： P 3x P 1 x l cos( ) v3 x v1 x l sin( ) P v3 y v1 y l cos( ) 3y P 1 y l sin( )
运 动 副 点 号
要求赋值
构 件 号
构 件 长 度
角位置角速度角加速 度，位置 速度 加速 度 n1
r1
m>0——实线 M<=0——虚线
不赋值
已知： 外运动副N1的位置P、速度v、加速度a，导路上任意参考点 N2的位置P、 速度v、加速度a，构件1的长度及导路的角位置、角速度、角加速度。 求：内运动副N3的运动参量、构件①的运动参量、 r2、vr2、ar2
P 3x P 1x l1 cos 1 P 3y P 1 y l1 sin 1
P 3y P 2y 2 arctan P P 2x 3x
rrrk(m,n1,n2,n3,k1,k2,r1,r2,t,w,e,p,vp,ap)
装 配 模 式
n3 k1 k2 r2 n2 N3’
}
y
3
l
1
φ
l
2
θ
x
bark(n1,n2,n3,k,r1,r2,gam,t,w,e,p,vp,ap)
关 键 点 号 构 n n 件 1 1 号 n n ∠ n3 n1 2 3 间 间 n2 距 距 离 离 角位置角速度 角加速度，位 置 速度 加速度

一·机构简介·1.1牛头刨床的组成牛头刨床主要由床身、滑枕、刀架、工作台、横梁、进给机构和变速机构等组成。

(1)床身床身内部有变速机构和曲柄摇杆机构。

床身的顶面有水平导轨,滑枕沿水平导轨作往复直线运动。

在床身前面有垂宜导轨,横梁带动工作台沿垂直导轨升降。

2)滑枕滑枕的前端有环状T形槽,用来安装刀架和调节刀架的偏转角度:滑枕的内部装有调整滑枕行程位置的机构,它是由一对锥齿轮和丝杠组成。

滑枕的下部有两条燕尾型导轨,它与床身上部的水平导轨配合。

在曲柄摇杆机构的带动下,滑枕在床身水平导轨上作往复直线运动。

(3)横梁与工作台校梁安装在床身前部垂直导轨上。

横梁的底部装有升降丝杠,使校梁能沿着床身前部的垂直导轨作上下移动。

工作台和滑板连接在一起,安装在横梁水平导轨上,转动安装在校梁凹框内的横向进给丝杠,工作台就沿着横梁的水平导轨作横向移动。

工作台的前部底下装有支架,以防止工作台在刨削过程中产生向下倾斜和振动现象。

工作台的上平面和两侧面均制有T形槽、v 形槽和圆孔,用来固定不同形状的工件或夹具。

(4)刀架刀架用于装夹刨刀,并使刨刀沿着垂直方向和倾斜方向移动。

刀架由手柄、丝杠、刻度转盘、夹刀座、拍板、拍板座、滑板等组成。

刻度转盘6用T形职栓5紧固在滑枕前端的“环”状T形槽内。

可按加工的需要作160’的回转。

刻度转盘6与滑板13通过导轨相配合,只要摇动丝杠3上端的手柄1,就可使滑板13沿着刻度转盘6上的导轨移动,通过刻度环2来控制背吃刀量的大小。

拍板10与拍板座11的凹槽相配合,用铰链销7连接。

在拍板10的孔内装有夹刀座8刨刀就装在它的槽孔内,拍板10可以绕铰链销7向前上方拾起,这样可避免滑枕回程时刨刀与工件已加工。

(5)进给机构进给机构主要用来控制工作台横向进给运动的大小。

(6)变速机构操纵变速机构的手柄,可以把各种不同的转速传递到曲柄摆杆机构而改变格杆在相同时间间隔内的摆动次数。

(7)曲柄摇杆机构主要作用是把电动机的旋转运动转换为滑枕的往复直线运动。

70.试在图上标出机构各构件间的瞬心位置，并用瞬心法说明当构件1等速转动时，构件3与机架间夹角 为多大时，构件3的 与 相等。
71.在图示的四杆机构中， mm， mm， mm， 。当构件1以等角速度 rad/s逆时针方向转动时，用瞬心法求C点的速度。
72.图示机构运动简图取比例尺 m/mm。已知 rad/s，试用速度瞬心法求杆3的角速度 。
51.图示为按比例尺绘制的牛头刨床机构运动简图和速度矢量多边形。试由图中的比例尺计算导杆3的角速度 和滑块2的角速度 ，并指出其方向。(提示： 为构件3上特殊点，据 、 求得，作题时不必去研究 如何求得。)
(取 m/mm， (m/s)/mm。)
52.试求图示机构的速度瞬心数目、各瞬心位置、各构件角速度的大小和方向、杆2上点M的速度大小和方向。(机构尺寸如图： mm， mm， mm， mm， ， mm， m/mm。)已知 rad/s。
9.当两构件组成转动副时，其速度瞬心在处；组成移动副时，其速度瞬心在处；组成兼有相对滚动和滑动的平面高副时，其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心，其中个是绝对瞬心，个是相对瞬心。
12.速度影像的相似原理只能应用于的各点，而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
86.图示机构的运动简图取长度比例尺 m/mm，其中 m， m， m，构件1以 rad/s等角速度顺时针方向转动，试用相对运动图解法求图示位置：
（1） 、 、 和 的大小和方向；
（2） 、3、4和5的大小和方向；
（3）在机构运动简图上标注出构件2上速度为零的点 ，在加速度多边形图上标注出构件2上点 的加速度矢量 ，并算出点 的加速度 的大小。在画速度图及加速度图时的比例尺分别为： =0.02 (m/s)/mm， (m/s2)/mm。

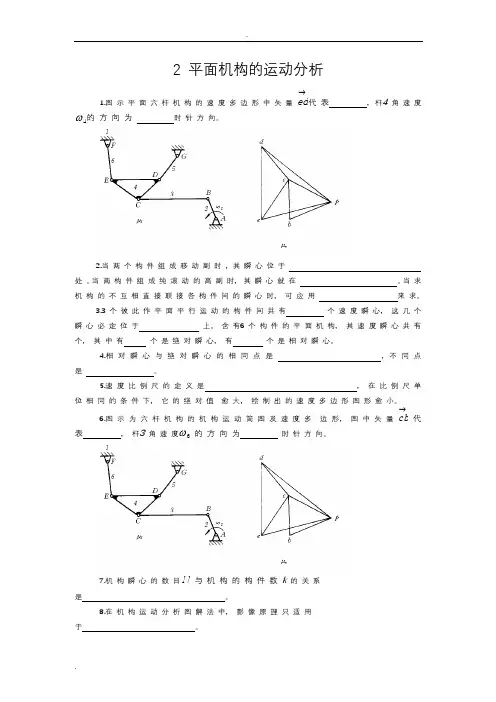
基于UG/CAE的平面六杆机构的运动分析1、题目说明如上图所示平面六杆机构，试用计算机完成其运动分析。

已知其尺寸参数如下表所示：题目要求：两人一组计算出原动件从0到360时（计算点数37）所要求的各运动变量的大小，并绘出运动曲线图及轨迹曲线。

注：为了使计算的结果更好的拟合运动的实际情况，同时考虑到UG在运动仿真分析计算方面的快速性，我们决定在绘制曲线时将计算点由37点增加到600点。

数据输出到Excel表格时计算点取100点。

建模及其分析方法附后！2、建模及其运动分析软件介绍：UG NX是集CAD\CAE\CAM于一体的三维参数化软件，也是当今世界最先进的设计软件，它广泛应用于航空航天、汽车制造、机械电子等工程领域。

还有在系统创新、工业设计造型、无约束设计、装配设计、钣金设计、工程图设计等方面的功能。

运动仿真是UG/CAE（Computer Aided Engineering）模块中的主要部分，它能对任何二维或三维机构进行复杂的运动学分析、动力分析和设计仿真。

通过UG/Modeling的功能建立一个三维实体模型，利用UG/Motion的功能给三维实体模型的各个部件赋予一定的运动学特性，再在各个部件之间设立一定的连接关系既可建立一个运动仿真模型。

UG/Motion的功能可以对运动机构进行大量的装配分析工作、运动合理性分析工作，诸如干涉检查、轨迹包络等，得到大量运动机构的运动参数。

通过对这个运动仿真模型进行运动学或动力学运动分析就可以验证该运动机构设计的合理性，并且可以利用图形输出各个部件的位移、坐标、加速度、速度和力的变化情况，对运动机构进行优化。

我们通过学习UG，通过建立平面六杆机构模型，通过UG/CAE模块对平面连杆的运动进行分析。

3.六连杆机构的三维造型连杆L1连杆L2连杆L3连杆L5连杆L6六杆机构装配示意图机构装配后运动演示见附件—平面六杆运动演示.avi （本报告相同目录下）3. 运动分析数据计算结果在附件的Excel表格中。

六连杆铰链机构的运动仿真分析运用CATIA DMU运动仿真模块对六连杆铰链机构进行运动仿真，分析六连杆铰链机构的运动特性。

根据分析结论，对六连杆铰链机构进行改善设计。

标签：CATIA DMU；六连杆铰链；运动仿真六连杆铰链因其结构强度高，占用空间小、开启角度大等优点被广泛应用于大型客车的侧围行李舱门上。

如图1所示为六连杆铰链的基本结构：支座AB（可视为杆AB），杆AC，杆CD，杆EF，杆BE，支座DF（可视为杆DF）通过7个转动副（A、B、C、D、E、F、O）组合成一个统一的整体。

其中杆CD通过转动副O与杆BE连结，孔G为气弹簧固定点。

支座AB固定在车身上，侧围行李舱门锁付于支座DF上。

由于六连杆铰链输出的是六根连杆的组合运动，其运动特性比较复杂，单靠二维CAD绘图很难绘制出其完整的运动轨迹，从而无法对侧舱门的运动过程进行完整的校核。

而CATIA DMU运动机构模块[1]提供了一个非常直观的分析工具。

应用该模块，我们能对运动机构进行运动仿真，能绘制指定机构的运动轨迹，还能测量指定位置的速度、加速度等运动参数。

通过模拟运动过程，我们可以更加直观、准确的对侧舱门进行运动校核，防止干涉的产生。

1 运动仿真分析1.1 建立仿真模型切换到CATIA DMU运动机构模块，对六连杆机构的7个转动销轴添加转动副[2]。

由于支座AB与车身相连接，因此对支座AB添加一个固定副，由此来观察其余杆的运动特性。

正常情况下，六连杆机构运动的驱动外力是由锁付于G 点的气弹簧提供。

模拟时，可把杆AC当成驱动构件，因此对杆AC施加一个转动命令。

至此，仿真模型建立完成。

因为仓门锁付于支座DF上，与其相对静止，运动状况一致，因此仿真时对支座DF的运动状况进行分析并进行轨迹绘制。

通常仓门的开启角度达到120度[3]时（与铅垂面夹角）即可满足存取货物的需求，因此，对支座DF在0到120时的运动状况进行仿真分析，如图3所示。

1.2 运动分析2 结论验证及运用初步分析完六连杆铰链机构的运动特性，还需将铰链装配到整车环境下进行验证结论是否正确。

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构，按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。

许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量，运动参数又是机械动力学分析的依据，所以机构的运动分析是机械设计过程中必不可少的重要环节。

以计算机为手段的解析方法，由于解算速度快，精确度高，程序有一定的通用性，已成为机构运动分析的主要方法。

连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式，同其他型式机构特别是凸轮机构相比具有很多优点。

连杆机构采用低副连接，结构简单，易于加工、安装并能保证精度要求。

连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件，实现间歇运动，满足给定的运动要求，完成机器的工艺操作。

牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。

工作台的纵向往复运动是机床的主运动，实现工件的切削。

工作台的横向运动即是进给运动，实现对切削精度的控制。

本文中只分析纵向运动的运动特性。

牛头刨床有很多机构组成，其中实现刨头切削运动的六连杆机构是一个关键机构。

刨床工作时，通过六杆机构驱动刨刀作往复移动。

刨刀右行时，当刨刀处于工作行程时;要求刨刀的速度较低且平稳，以减小原动机的容量和提高切削质量。

当刨刀处于返回行程时，刨刀不工作，称为空行程，此时要求刨刀的速度较高以提高生产率。

由此可见，牛头刨床的纵向运动特性对机床的性能有决定性的影响。

1 牛头刨床的六连杆机构牛头刨床有很多机构组成，其中实现刨头切削运动的六杆机构是一个关键机构。

图1所示的为一牛头刨床的六连杆机构。

杆1为原动件，刨刀装在C点上。

假设已知各构件的尺寸如表1所示，原动件1以等角速度ω1=1rad/s沿着逆时针方向回转，要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。

（ ． ａ ｃＪ ｎ ｘ ３ ０ ６ ， ｈｎ ； ． ａ ｃ ａ ｇ Ｕ ｉ ｒ ｔ ， ａ ｃ ａ ｇ，ｉ ｇ ｉ ３ ０ １ Ｃ ｉａ １ Ｎ ｎｈ ｎ ａ ｇ ｏ ｇ Ｕ ｉ ｒ ｔ Ｎ ｎ ｈ ｎ ，ｉ ｇ ｉ ３ ０ ３ Ｃ ｉ ２ Ｎ ｎ ｈ ｎ ｎｖ ｓ ｙ Ｎ ｎ ｈ ｎ Ｊ ｎ ｘ ３ ０ ３ ， ｈｎ ） ｖ ｓｙ ａ ａ ｅｉ ａ
机构 的运动 分 析 ， 要是 获 得 机 构 中某 些 构件 的动态 仿真 。采用 ＭＡ Ｌ Ｂ对 机构 进 行仿 真 ， 乎 主 ＴＡ 几
的位 移 、 角速 度 和 加速 度 ， 以及 某 些 点 的轨 迹 ， 速度 所 有 的构件 运 动 参 数 都 在 仿 真 模 型 的数 据 线 上 传 和加 速度 。它是机 械设计 及评 价机 械运 动和动 力性 输 ， 只要将该 数 据 线 上 的 信 息 引入 Ｓｍ ｕ 模 块 ， ｉｏｔ 就
柄 、Ｒ Ｒ ＲⅡ级 杆组 、 Ｒ Ｒ ＰⅡ级 杆 组 三 个 基 本 模 组 的 运 动 学 数 学 模 型 ， 用 其 组 成 机 构 杆 组 并 搭 建 平 面 连 杆 机 构 的 运 动 学 仿 真 利
模型 ， 充分利用 ＭＡ Ｌ Ｂ的 Ｓｍ ｌ ｋ ＴＡ ｉ ｕｉ 仿真模型数据可视化的特点， ｎ 观察和分析其运动参数的变化 。 ［ 中图分类号 ］Ｔ ３ １９ Ｐ ９ ． ［ 文献标志码 ］Ａ ［ 文章编号］１０ ４ ２ （００）４— ０ ６— ５ ０ １— ９ ６ ２ １ ０ ０４ ０
能 的基础 ， 是 分析 现 有 机械 优 化 综合 新 机 械 的基 可 以观察 到该 运 动 参 数 是 如 何 变 化 的及 相 应 的数 也
本手段 。
一
据， 并可 以 图形 的形 式直 观地 表现 出来 。 为 了利用 Ｍａ ａ ｔ ｂ仿 真 软 件 包 的数 值 积 分 算 法 ｌ

表3平面六杆机构中预设的部分构件初始参数
3.2平面六杆机构motion运动分析
本部分介绍了利用SolidWorks中的motion插件
进行运动仿真分析以输出平面六杆机构中构件5的
运动图像。首先，利用SolidWorks中的motion功能，将
电机加装在杆*上，设定电机转速恒定为10 r=d・s>#
，X motion 分析中，对构件 5 进行运动分析
终端
发
至
，
回 入库
旧管
系统，
资 的用 ，
本:
Research and Design "0 Fixed Network Terminal Inventory Management
U*#=)-
bang bing
(Chongbo Information Technology Researph Institute Ko・HLtd・，Nanjing Jiangs. 211500)
，
输出平面六杆机构中构件 5 的位移、速度、加速度运
动图像⑷(构件5运动图像如图4所示)。
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>1
Ie
>FG
0.00 0.72 1.44 2.16 2.88 3.60 4.32 5.04 5.76 6.48 7.20
Js
4>2滑块I方
-速度
@
50 100 150 200 250 300 350 400
角度JM
图!平面六杆机构构件4的运动图像
' (" " 789:;<FG*H

第6期2021年2月No.6February ，2021六自由度机器人运动学及主要构件的有限元分析摘要：文章以六自由度机器人为研究对象，根据实际的作业情况，对机器人进行运动学分析以及主要构件的有限元分析。

运动学分析分为正运动学分析和逆运动学分析，解决的是机器人的手臂转向何方，分析的是手部的速度、加速度和位移。

有限元分析主要是机械系统静力学分析。

对主要构件建立模型、模型简化、网格划分，根据危险工况的受力情况，分析了各构件的应力、形变等性能，确保结构设计合理。

对于工业机器人机械结构、传动等方面，运动学和有限元分析能够判断整机设计是否达到设计目标，对结构件的优化设计具有重要的意义。

关键词：六自由度；机器人；运动学；有限元分析中图分类号：TP242.2文献标志码：A 程锴（南京以禾电子科技有限公司，江苏南京210039）作者简介：程锴（1981—），男，江苏南京人，工程师，硕士；研究方向：电子产品总体结构设计。

江苏科技信息Jiangsu Science &Technology Information引言在当前科学技术不断进步和快速发展的背景下，很多先进的技术手段被广泛应用在各个领域中［1］。

特别是机器人在工业中得到广泛的应用，在实际运行过程中，类似于码垛搬运的六自由度机器人在搬运货物中节省大量劳动力，但安全性与可靠性一直备受考验。

因此，本文主要对六自由度机器人进行运动学和静力学分析［2］。

机器人运动学研究解决的是机器人的手臂转向何方，分析的是手部的速度、加速度和位移。

运动学方程是进行机器人位移分析的基本方程，也称为位姿方程。

机器人运动学分为正运动学分析和逆运动学分析。

正运动学是机器人运用各个关节角度、各个构件车长度等已知条件来判断末端执行器在三维空间中的位置；而逆运动学正好相反，它解决的是机器人需要如何运动才能使得末端执行器到达指定位置这一问题。

静力学分析用来分析结构在给定静力载荷作用下的响应。

铰链六杆机构的运动分析1.题目：铰链六杆机构的运动分析如图所示，已知铰链六杆机构各构件的尺寸为:AB=100mm,BC=370mm, CD=150mm,DE=150mm,EF=250mm,a=120mm,b=360mm,c=90mm,=45°及原动件1以转速n=1000npm逆时针转动，计算杆2，3，4及滑块5的角位移，角速度，角加速度及位移，速度和加速度，并绘制出运动线图。

2.数学模型（1）位置分析由图知：,即：由几何关系：(2)速度分析对（1）中式子关于时间t求导得：对应矩阵：(3)加速度分析对（2）中式子关于时间t求导，得：对应矩阵：+=3、程序设计主程序文件%1.输入已知数据clear;l1=100;l2=370;lcd=150;lde=150;l4=250;;a=120;b=360;c=90;n=1000;du=180/pi;hd=pi/180;omega1=2*pi*n/60;alpha1=0;%2.调用子函数计算机构位移、速度、加速度、角位移、角速度、角加速度for n1=1:361theta1=(n1-1)*hd;[theta,omega,OMEGA,alpha,ALPHA,s5(n1),v5(n1),a5(n1)]=crank_rock er(theta1,omega1,alpha1,l1,l2,lcd,lde,l4,a,b,c);theta2(n1)=theta(2);theta3(n1)=theta(3);theta4(n1)=theta(4);omega2(n1)=omega(1);omega3(n1)=omega(2);omega4(n1)=OMEGA(1);alpha2(n1)=alpha(1);alpha3(n1)=alpha(2);alpha4(n1)=ALPHA(1);end%3.角位移、角速度、角加速度和滑块的位移、速度、加速度输出figure(1);n1=1:361;subplot(2,3,1); %绘角位移线图plot(n1,theta2*du,n1,theta3*du,n1,theta4*du);title('角位移线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;text(200,150,'\theta_2')text(100,100,'\theta_3')text(200,300,'\theta_4')subplot(2,3,2); %绘角速度线图plot(n1,omega2,n1,omega3,n1,omega4);title('角速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')grid on;hold on;text(200,-50,'\omega_2')text(200,75,'\omega_3')text(200,0,'\omega_4')subplot(2,3,3); %绘角加速度线图plot(n1,alpha2,n1,alpha3,n1,alpha4);title('角加速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')grid on;hold on;text(200,-2*10^4,'\alpha_2')text(200,-10*10^4,'\alpha_3')text(200,5*10^4,'\alpha_4')subplot(2,3,4); %绘滑块位移线图plot(n1,s5);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ')ylabel('滑块位移/mm')grid on;hold on;text(150,300,'s_5')subplot(2,3,5); %绘滑块速度线图plot(n1,v5);title('滑块速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;text(200,-0.5*10^4,'v_5')subplot(2,3,6) %绘滑块加速度图plot(n1,a5);title('滑块加速度线图');xlabel('曲柄转角\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;text(200,10*10^6,'a_5')%4.机构图形输出figure(2);x(1)=0;y(1)=0;x(2)=l1*cos(45*hd);y(2)=l1*sin(45*hd);x(3)=x(2)+l2*cos(theta2(45));y(3)=y(2)+l2*sin(theta2(45));x(4)=-a;y(4)=b;x(5)=2*x(4)-x(3);y(5)=2*y(4)-y(3);x(6)=x(5)+l4*cos(theta4(45));y(6)=b+c;x(7)=x(6)+40;y(7)=y(6)+20;x(8)=x(6)+40;y(8)=y(6)-20;x(9)=x(6)-40;x(10)=x(6)-40;y(10)=y(6)+20;x(11)=x(6)+40;y(11)=y(6)+20;i=1:6;plot(x(i),y(i));grid on;hold on;i=7:11;plot(x(i),y(i));plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(3),y(3),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(6),y(6),'o');title('曲柄滑块机构');grid on;hold on;xlabel('mm')ylabel('mm')axis([-400 500 -100 600]);%5.曲柄滑块机构运动仿真figure(3)m=moviein(20);j=0;for n1=1:5:360j=j+1;clf;x(1)=0;y(1)=0;x(2)=l1*cos(n1*hd);y(2)=l1*sin(n1*hd);x(3)=x(2)+l2*cos(theta2(n1)); y(3)=y(2)+l2*sin(theta2(n1)); x(4)=-a;y(4)=b;x(5)=2*x(4)-x(3);y(5)=2*y(4)-y(3);x(6)=x(5)+l4*cos(theta4(45)); y(6)=b+c;x(7)=x(6)+40;y(7)=y(6)+20;x(8)=x(6)+40;y(8)=y(6)-20;y(9)=y(6)-20;x(10)=x(6)-40;y(10)=y(6)+20;x(11)=x(6)+40;y(11)=y(6)+20;i=1:6;plot(x(i),y(i));grid on;hold on;i=7:11;plot(x(i),y(i));plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(3),y(3),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(6),y(6),'o');axis([-400 500 -100 600]);title('曲柄滑块机构仿真');xlabel('mm');ylabel('mm');m(j)=getframe;endmovie(m);子程序文件function[theta,omega,OMEGA,alpha,ALPHA,s5,v5,a5]=crank_rocker(theta1, omega1,alpha1,l1,l2,lcd,lde,l4,a,b,c)%1.计算从动件的角位移和滑块5的位移L1=sqrt((a+l1*cos(theta1))*(a+l1*cos(theta1))+(b-l1*sin(theta1))*(b-l 1*sin(theta1)));beta1=acos((L1*L1+l2*l2-lcd*lcd)/(2*L1*l2));beta2=atan((a+l1*cos(theta1))/(b-l1*sin(theta1)));theta2=pi/2+beta1+beta2;theta3=atan(-b/(a-(-l2*cos(theta2)-l1*cos(theta1))));theta4=asin((c-lde*sin(theta3))/l4);theta=[theta1;theta2;theta3;theta4];s5=l4*cos(theta4)+lde*cos(theta3);%2.计算从动件的角速度和滑块5的线速度A=[-l2*sin(theta2),-lcd*sin(theta3);-l2*cos(theta2),-lcd*cos(theta3)] ;B=[l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);omega3=omega(2);C=[l4*sin(theta4),1;-l4*cos(theta4),0];D=[-lde*sin(theta3);lde*cos(theta3)];OMEGA=C\(omega3*D);omega4=OMEGA(1);v5=OMEGA(2);%3.计算从动件的角加速度和滑块5的加速度A=[-l2*sin(theta2),lcd*sin(theta3);l2*cos(theta2),lcd*cos(theta3)];At=[omega2*l2*cos(theta2),omega3*lcd*cos(theta3); omega2*l2*sin(theta2),omega3*lcd*sin(theta3)]; B=[omega1*l1*cos(theta1);omega1*l1*sin(theta1)];alpha=A\(At*omega+omega1*B);alpha2=alpha(1);alpha3=alpha(2);C=[l4*sin(theta4),1;-l4*cos(theta4),0];D=[-lde*sin(theta3),-omega3*lde*cos(theta3);lde*cos(theta3),-omega3*lde*sin(theta3)];Ct=[omega4*l4*cos(theta4),0;omega4*l4*sin(theta4),0];Dt=[alpha3;omega3];ALPHA=C\(D*Dt-Ct*OMEGA);alpha4=ALPHA(1);a5=ALPHA(2);4、计算结果下图为六杆机构的运动线图：。

毕业设计（论文）-牛头刨床六杆机构运动分析河南理工大学本科毕业设计,论文,摘要在工程技术领域，经常会遇到一些需要反复操作，重复性很高的工作，如果能有一个供反复操作且操作简单的专用工具，图形用户界面就是最好的选择。

如在本设计中对于牛头刨床平面六杆机构来说，为了保证结构参数与运动参数不同的牛头刨床的运动特性，即刨刀在切削过程中接近于等速运动从而保证加工质量和延长刀具寿命，以及刀具的急回性能从而提高生产率，这样的问题如果能够通过设计一个模型平台，之后只需改变参量就可以解决预期的问题，这将大大的提高设计效率。

设计本设计中正是通过建立牛头刨床六杆机构的数学模型，然后用MATLAB程序出一个友好的人机交互的图形界面，并将数学模型参数化，使用户只需改变牛头刨床的参数就可以方便的实现运动分析和运动仿真，用户可以形象直观地观察到牛头刨床的运动轨迹、速度变化及加速度变化规律。

关键词:牛头刨床六杆机构 MATLAB 运动仿真程序开发1河南理工大学本科毕业设计,论文,AbstractIn the engineering area, often repeatedly encountered some operational needs, repetitive highly, and if the operation can be repeated for a simple operation and dedicated tool graphical user interface is the best choice. As in the planer graphic design for six pole bodies, and campaigns to ensure the structural parameters of different parameters planer movement characteristics, planning tool inthe process of cutting close to equal campaign to ensure processing quality and extended life cutlery and cutlery rush back to the performance enhancing productivity, If such issues can be adopted to design a model platform parameter can be changed only after the expected settlement, which will greatly enhance the efficiency of the design. It is through the establishment of this design planer six pole bodies mathematical model, and then use MATLAB to devise procedures of a friendly aircraft in the world graphics interface, and mathematical models of the parameters, so that users only need to change the parameters planer can facilitate the realization of movement analysis and sports simulation, Users can visual image observed in planer movement trajectories, speed changes and acceleration changes.Keywords:Planer 6 pole bodies MATLAB Campaign simulation Procedure development.2河南理工大学本科毕业设计,论文,目录1 绪论 (4)2牛头刨床六杆机构运动分析程序设计2.1 MATLAB介绍 (5)2.2 MATLAB的特点 (6)2.3 用MATLAB处理工程问题优缺点................................7 3牛头刨床运动分析的模型3.1 基本概念与原理 (9)3.2 牛头刨床六杆机构的数学模型 .................................9 4图形用户界面GUI4.1界面设计的原则 (13)4.2 功能要求 (16)4.3界面结构设计 (17)4.4 程序框图的设计 .............................................19 5运动仿真程序界面设计与编程实现5.1 句柄图形体系 (21)5.1.1 图形对象、对象句柄和句柄图形树结构 (22)5.1.2 对象属性 (23)5.1.3 对象句柄的获取方法 (23)5.1.4 对象句柄的获取和设置 (25)5.2 主界面参数含义 (27)5.3 界面制作步骤 (27)6总结 (49)7致谢 (50)8参考书目 (51)9附录程序源代码 (52)3河南理工大学本科毕业设计,论文,1 绪论1.1本课题的意义机构运动分析是不考虑引起机构运动的外力的影响，而仅从几何角度出发，根据已知的原动件的运动规律(通常假设为匀速运动)，确定机构其它构件上各点的位移、速度、加速度，或构件的角位移、角速度、角加速度等运动参数。

平面六杆机构运动分析平面六杆机构的结构由六个连杆组成，其中包括三个固定连杆和三个可动连杆。

固定连杆通常被称为定态杆，可动连杆则被称为转动杆。

根据转动杆的数量和连杆相互连接的方式，平面六杆机构可以分为多种类型，如四杆机构、多杆机构等。

在运动分析中，首先需要确定平面六杆机构的运动副，即确定机构中的可动部分和约束部分。

在平面六杆机构中，三个固定连杆固定在轴上，不发生相对运动，因此构成了三个约束副。

而另外三个可动连杆可以沿着其中一方向进行平移或转动，从而实现不同的运动形式。

平面六杆机构的运动是通过连杆相互连接而实现的。

连杆之间的连接点称为铰链，铰链的位置确定了连杆之间的运动关系。

根据铰链的位置不同，连杆之间可以形成不同的树状结构，如三杆树状结构、四杆树状结构等。

通过这些连杆和铰链的组合，平面六杆机构可以实现复杂的运动路径和运动轨迹。

在几何分析中，可以利用连杆的长度和连接点位置来确定连杆的运动范围和运动路径。

通过使用向量和矩阵的运算，可以推导出连杆的运动方程和运动状态方程。

这些方程可以用来描述连杆的位移、速度和加速度，并进一步分析机构的运动性能和稳定性。

在力学分析中，可以应用牛顿定律和动力学原理来分析连杆之间的力学关系和力学性能。

通过建立连杆之间的功率传递和力矩平衡方程，可以计算出机构的输入功率和输出功率，并进一步分析机构的能量转换和运动效率。

平面六杆机构的运动分析在工程设计中具有广泛的应用。

它可以用来实现复杂的运动路径和运动轨迹，广泛应用于各种机械设备和机器人的设计中。

例如，在运动控制领域，平面六杆机构可以用来控制机械臂的运动轨迹和末端位置，实现精确的定位和操作。

在工业自动化领域，平面六杆机构可以用来控制机器人的运动路径和运动速度，实现灵活的操作和自动化生产。

总而言之，平面六杆机构是一种重要的机械结构，它可以实现复杂的运动功能和运动轨迹。

通过几何分析和力学分析，可以对平面六杆机构的运动进行详细的分析和研究。

机械原理课程设计说明书设计题目：六杆机构运动分析学院：工程机械学院专业：机械设计制造及其自动化班级：25041004设计者：25041004指导老师：张老师日期：2013年01月07日目录1.课程设计题目以及要求————————————————————32.运用辅助软件对结构进行结构分析———————————————43.数据收集以及作图———————————————————————114.总结————————————————————————————17六杆机构运动分析1、分析题目对如图5所示的六杆机构进行运动与动力分析，各构件长度、滑块5的质量G 、构件1转速n1、不均匀系数δ的已知数据如表5所示。

2、分析内容（1）对机构进行结构分析：（2）绘制滑块D 的运动线图（即位移、速度和加速度线图）：（3）绘制构件3和4的运动线图（即角位移、角速度和角加速度线图）： （4）绘制S4点的运动轨迹。

图5表5方案号L CDmmL ECmmymm L AB mm L CS4 mm n 1r/mi n1 975 360 50 250 400 23.52 975 325 50 225 350 33.53 9003005020030035（一）对机构进行结构分析选取方案三方案号L CDmm L ECmmymmL ABmmL CS4mmn 1r/mi n3 900 300 50 200 300 35对六杆机构进行运动分析：（1）原始数据的输入：（2）基本单元的选取及分析：（3）各点运动参数:（4）长度变化参数（5）各构件角运动参数：（二）滑块D的运动线图（位移-速度-加速度线图）：（三）构件3的运动线图（角位移-角速度-角加速度线图）：（四）构件4的运动线图（角位移-角速度-角加速度线图）：（五）S4点的运动轨迹：（六）数据收集以及作图（1）滑块D 点x 、y 方向的运动参数如表6.1所示表6..1由上表可以得到D 点运动线图如图6.1所示图6.1位置 0123456789101112位 移X 1188.097 1187.376 1058.394 848.5281 680.2758 607.9142 606.0113 651.5314 734.6896 848.5281 980.0058 1105.089 1188.097 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 速 度X 332.4289 -434.0533 7293.698 -1466.08 -831.5157 -222.7902 169.5616 457.6898 699.4701 879.648 933.0263 776.3062 332.4289 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 加 速度X -4255.382 -6281.231 -4679198 2533.081 4920.073 3387.318 2265.425 1834.254 1530.378 911.9092 -264.7796 -2020.469 -4255.382 y 0（2）构件3的运动参数如表6.2所示表6.2位置0 1 2 3 4 5 6 7 8 9 10 11 12角位移φ14.03624 -16.10211 -50.93532 -90 230.9353 196.1021 165.9638 139.1066 114.1333 90 65.86674 40.89339 14.03624角速度ω-3.4496 -3.947138 -4.561904 -4.886933 -4.561904 -3.947138 -3.4496 -3.1416 -2.981412 -2.93216 -2.981412 -3.1416 -3.4496角加速度ɛ-2.789002 -4.130385 -3.972855 -6.092957 3.972855 4.130385 2.789002 1.582846 0.7038764 2.368942 -0.703876 -1.582846 -2.789002由上表得构件3的运动线图如图6.2所示图6.2（3）构件4的运动参数如表6.3所示表6.3位置0 1 2 3 4 5 6 7 8 9 10 11 12 φ-4.63715 5.304571 14.99956 19.471122 14.99956 5.304571 -4.63715 -12.60438 -17.70998 -19.47122 -17.70998 -12.60438 -4.63715 角位移ω 1.119198 1.269533 0.992103 1.253846 -0.9921031 -1.269533 -1.119198 -0.8111576 -0.4265414 -1.775216 0.4265414 0.1811158 1.119198 角速度ɛ 1.768468 0.031558 -4.448388 -8.443604 -4.448388 0.031558 1.768468 2.468482 2.88811092 3.039697 2.881092 2.468482 1.768468 角加速度由表6.3参数可得构件4的运动线图如图6.3所示图6.3（4）S4点x、y方向的运动参数如表6.4所示表6.4位置0 1 2 3 4 5 6 7 8 9 10 11 12位移X 590.0608 586.9459 478.8375 282.8427 100.7192 10.48452 7.975251 65.99134 163.1245 282.8427 408.4406 519.5487 590.0608 Y 48.50713 -55.47002 755.287 -200 -155.287 -55.47002 48.50713 130.9307 182.5194 200 182.5194 130.9307 48.50713速度X 278.1398 -363.6323 -1139.637 -1466.08 -985.5764 -293.2113 223.8507 563.8953 777.3222 879.648 855.1742 670.1007 278.1398 Y -669.3207 -758.4576 -574.98 -8.42273 574.98 758.4576 669.3207 474.9653 243.7962 7.905602 -243.7962 -474.9653 -669.3207加速度X -3592.063 -5316.593 -4799.736 844.3604 4920.073 4351.956 2928.744 1896.326 1108.512 303.9697 -686.6455 -1958.397 -3592.063 y -1118.368 70.54837 2730.937 4776.623 2730.937 70.54837 -1118.368 -1531.544 -1679.939 -1719.512 -1679.939 -1531.544 -1118.368（七）总结：六杆机构的运动分析相比课本上的平面四杆机构来说难度大些，而且是用辅助软件进行运动分析，这看起来似乎难度更大。

《机械原理》复习第二章机构的结构分析内容：1．掌握运动副的概念和各种平面运动副的一般表示方法，能较熟练地看懂一般的平面结构运动简图，初步掌握平面机构运动简图的绘制方法。

2．掌握平面移动副、转动副和高副及其约束数。

能够识别机构简图中的复合铰链、局部自由度和虚约束，并在自由度计算时加以适当处理。

3．熟练掌握平面机构自由度的计算公式，正确应用该公式对给定的平面机构进行自由度计算，并判断机构运动是否确定。

4．平面机构的组成原理，拆分基本杆组，机构的结构分类重点：1、平面高副、平面低副2、自由度的计算（公式、复合铰链、局部自由度、虚约束）3、机构有确定运动的条件4、拆分基本杆组，机构的结构分类内容：1．速度瞬心的定义，速度瞬心的个数，速度瞬心位置的确定；2．用速度瞬心法作机构的速度分析；3．用矢量方程图解法作机构的速度及加速度分析，具体包括：（1）同一构件上两点间的速度、加速度（2）两构件重合点间的速度、加速度建立矢量方程、绘制速度多边形、加速度多边形，求解未知量，会用速度影像和加速度影像。

重点：1、用矢量图解法对机构进行速度分析和加速度分析。

内容：1、移动副、转动副、平面高副摩擦力的确定；2、考虑摩擦时机构的受力分析。

重点：1、考虑摩擦时机构的受力分析。

第五章机械的效率和自锁内容：1、机械效率的三种计算方法（注意力的表示方法）；2、并联、串联、混联机械系统效率的计算；3、什么是机械的自锁，产生的根本原因是什么；4、计算机械发生自锁的条件（有四种方法），建立力平衡矢量方程，绘制力多边形，力之间的函数关系；重点：1、建立力平衡矢量方程，绘制力多边形，力之间的函数关系，计算机械发生自锁的条件第八章平面连杆机构及其设计内容：1．了解平面连杆机构的特点、应用和分类。

2．掌握铰链四杆机构的组成和三种基本类型，了解它们的应用。

了解含有一个移动副的平面四杆机构的类型及其应用，知道它们是怎样演化而来的。

3．熟练掌握铰键四杆机构中曲柄存在的条件，并能应用该条件确定机构中某构件的取值范围和机构类型。

---------------------------------------------------------------最新资料推荐------------------------------------------------------压床主体机构分析与设计压床主体机构分析与设计设计题目：压床主体机构分析与设计一、机构简介与设计数据 1. 1. 机构简介图示为压床机构简图，其中六杆机构为主体机构。

图中电动机经联轴器带动三对齿轮将转速降低，然后带动曲柄1 转动，再经六杆机构使滑块 5 克服工作阻力 Fr 而运动。

为了减少主轴的速度波动，在曲柄轴 A 上装有大齿轮 z6 并起飞轮的作用。

在曲柄轴的另一端装有油泵凸轮，驱动油泵向连杆机构的供油。

（a）压床机构及传动系统 1. 2 机构的动态静力分析已知：各构件的重量 G 及其对质心轴的转动惯量 Js(曲柄 1 和连杆4 的重力和转动惯量（略去不计) ，阻力线图(图 97) 以及连杆机构设计和运动分析中所得的结果。

要求：确定机构一个位置的各运动副中的反作用力及加于曲柄上的平衡力矩。

作图部分亦画在运动分析的图样上。

1. 3 凸轮机构构设计已知：从动件冲程 H，许用压力角[ ]．推程角。

1 / 13，远休止角ı，回程角‘ ，从动件的运动规律见表9-5，凸轮与曲柄共轴。

要求：按[ ]确定凸轮机构的基本尺寸．求出理论廓线外凸曲线的最小曲率半径。

选取滚子半径 r，绘制凸轮实际廓线。

以上内容作在 2 号图纸上 1. 4. 设计数据 1 二、压床机构的设计 2. 1. 传动方案设计 2. 1. 1. 基于摆杆的传动方案 2 优点：结构紧凑，在Ｃ点处，力的方向与速度方向相同，所以传动角，传动效果最好；满足急回运动要求；缺点：有死点，造成运动的不确定，需要加飞轮，用惯性通过； 2. 1. 2. 六杆机构 A 优点：能满足要求，以小的力获得很好的效果；缺点：结构过于分散：2. 1.3. 六杆机构 B 优点：结构紧凑，满足急回运动要求；缺点：机械本身不可避免的问题存在。

2.3 试题精解和答题技巧例2-1 如例2-1图所示，已知四杆机构各构件长度：a =240mm ，b =600mm ，c =400mm ，d =500mm 。

试问：1． 当取构件4为机架时，是否存在曲柄？如存在则哪一构件为曲柄？2． 如选取别的构件为机架时，能否获得双曲柄或双摇杆机构？如果可以，应如何得到？ 解题要点：根据铰链四杆机构曲柄存在条件进行分析。

在铰链四杆机构中，其杆长条件是机构有曲柄的根本条件。

即最短杆与最长杆长度之和小于或等于其他两杆长度之和；这时如满足杆长条件，以最短或与最短杆相邻的杆为机架，机构则有曲柄；否则无曲柄；如不满足杆长条件，无论取那个构件为机架，机构均无曲柄，机构为双摇杆机构。

解： 1. 现在a+b =840mm<c+d =900mm 条件成立。

取构件4为机架时，最短杆a 为曲柄。

2. 当取最短杆a 为机架时，得双曲柄机构；若选最短杆的对杆c 为机架时，则得双摇杆机构。

例2-1图例2-2图 例2-2 试根据铰链四杆机构的演化原理，由曲柄存在条件推导如例2-2图所示偏置导杆机构成为转动导杆机构的条件。

解题要点：如例2-2图所示机构是由铰链四杆机构演化而来，本题关键在于铰链四杆机构曲柄存在条件的灵活运用。

解：因为导杆与滑块组成移动副，所以转动副中心D 在无穷远处，即： ∞→CD l ， ∞→AD l 并且 AD l ＞CD l 要使机构成为转动导杆机构，则各杆长度应满足下列条件： AB l +AD l ≤BC l +CD l AB l +(AD l -CD l )≤BC l b e a ≤+例2-3如例2-3图所示铰链四杆机构中，已知mm l BC 500=，mm l CD 350=，mm l AD 300=，AD 为机架。

试问：1．若此机构为曲柄摇杆机构，且AB 为曲柄，求AB l 的最大值； 2． 若此机构为双曲柄机构，求AB l 的最小值； 3． 若此机构为双摇杆机构，求AB l 的的取值范围。