数学和台球的问题(数学问题在台球中的应用)

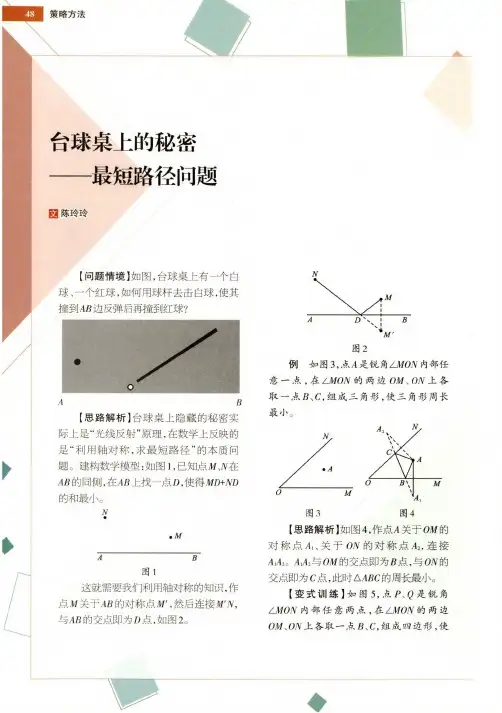
台球运动中的数学原理摘要：在现实生活中，台球作为一种娱常见的乐消遣活动，因为娱乐方式很简单，几乎所有人都接触过，首先提出本文的目的是为了更好的帮助桌球初学者提高桌球技术，本文主要是利用数学原理及物理原理找到击球角度与击球后目标球运动的方向问题，最后给出与击球角度有关的数学公式。

关键词：数学原理；击打一、问题重述现实生活中，台球作为一种常见的消遣活动，因其娱乐方式很简单，几乎所有的朋友都接触过这种运动，当然，对于大部分人来说，所谓高手就是打得次数很多，经过了大量的练习；而普通选手或者说菜鸟之所以不能够准确打进球，是因为不具备专业球手那种指哪打哪的能力。

本文讨论的是在近距离击球时，击球的角度与击球后目标球的运动方向的关系问题，本文需要解决的问题是球在目标球，白球及袋口位置确定后假设球球心与目标球球心的连线和BA的延长线的夹角的公式，如图1所示。

D图1二、问题分析首先进行一些简单的定义，把需要打进的球定义为目标球，击打目标球的球称之为白球，进球口称为袋口。

因为本文阐述的问题与具体球袋(一个球台有四个角袋和两个中袋)的位置没有关系，因此下文，主要以中袋作为研究的切入点。

而且本文只考虑传统的击球方式，即采用球杆击打白球的中心去碰撞目标球，因此这里所说的击球点仅指得是白球碰到目标球的点位，而非球杆击打白球时的点位。

而且下文所涉及到的进球仅指直接进球，通过反弹方式进球不在本文考虑之内。

图2 中最上部是中袋的一个示意图，其中心为P 点，假设有一目标球位于距中袋一定距离的垂直正下方某点(除掉袋口球，这种球与击球点已无关系)，用 C 点表示其几何中心，MN 是和球台侧壁相平行的一条假想直线，A 表示任意白球球心所在方位，首先，总的来讲，A点只有位于MN 虚线以下的任何一点才有可能把目标球打进中袋，因为，假设白球和目标球的接触点为O 点，根据力学中的碰撞原理[1]，只有白球去撞击了O 点，目标球才有可能进袋(从理论上来说，因为袋口的宽度要比球的直径稍大，如果白球不是正好撞击在O 点，而是撞击在距离O 点极小距离的左右某一点上，也有进球可能，但是为了说明问题的方便性，本文只考虑球袋中心进球情况)。

台球桌上的数学问题（最新版）目录1.引言：介绍台球桌上的数学问题2.台球桌上的物理学原理3.台球桌上的数学应用4.结论：总结台球桌上的数学问题正文【引言】台球是一种广泛流行的娱乐运动，它不仅需要精准的打击技巧，还蕴含着丰富的物理学和数学原理。

在台球桌上，我们可以通过运用物理学和数学知识来预测球路的走势，从而更好地掌握比赛。

本文将探讨台球桌上的数学问题，包括物理学原理和数学应用。

【台球桌上的物理学原理】在台球桌上，球之间的碰撞是物理学中的弹性碰撞问题。

当两个球碰撞时，它们之间的动能会发生转换。

根据物理学原理，我们可以通过计算球之间的碰撞角度和速度来预测球路的走势。

此外，台球桌的表面也对球的运动产生了影响。

球在台球桌上的运动是一种受到摩擦力影响的滚动运动，因此我们需要考虑摩擦力对球路走势的影响。

【台球桌上的数学应用】在台球桌上，数学应用主要体现在以下几个方面：1.几何学：在打击台球时，我们需要考虑球的旋转方向和角度。

通过运用几何学知识，我们可以计算出球在台球桌上的运动轨迹。

2.概率论：在台球比赛中，我们需要根据对手的打击技巧和球的运动规律来预测球路的走势。

概率论可以帮助我们计算出各种可能的结果，从而做出更加明智的决策。

3.微积分：微积分在台球运动中的应用主要体现在对球路走势的精确预测。

通过计算球的速度、摩擦力和碰撞角度，我们可以运用微积分原理来预测球在台球桌上的运动轨迹。

【结论】总之，台球桌上蕴含着丰富的数学和物理学原理。

了解这些原理和应用可以帮助我们更好地掌握台球技巧，提高比赛水平。

情况一当母球与彩球的中心及球袋中心在一条直线上时，只要瞄准彩球的中心，这样撞击后彩球可以运动到球袋的中心，进入球袋。

情况二当母球与彩球的中心及球袋中心不在一条直线上时，则下杆时要偏移一定的角度，瞄准点在彩球中心附近一点，确定该点方法如下：彩球位于B点，母球在A点，球袋中心为P。

为了让彩球B沿直线BP运行到P处，瞄准点应在直线BP的反向延长线上的某一点。

以B为圆心，台球直径为半径做一个圆，延长BP和圆交于点O，O就是所求的瞄准点。

（球杆的击打方向与参照直线ＡＢ形成∠BAO=α,调整α使∠OBA=β理想。

）在△ABO中,用余弦定理∣AO∣２=∣AB∣2+∣BO∣2−2∣AB∣∣BO∣cosβ求得:∣AO∣=√∣AB∣2+∣BO∣2−2∣AB∣∣BO∣cosβ用正弦定理∣AO∣sinβ=∣BO∣sinα求出的α的理论值。

α=arc sin√∣AB∣2+∣BO∣2−2∣AB∣∣BO∣cosβ（0°≤β≤90°）⑴（在实际中已知︱AB︱,︱BO︱,β取理想值，可计算α的大小）角度大小估计与长度距离的估计的转化我们在一定条件下已计算了的理论值，然而人的眼睛与手不容易打出这个理论值α，因为在人们的日常生活中，对长度的估计比对角度的估计相对准确，所以我们可以把对角度的估计转化为对长度的估计。

以球杆长为腰，构造等腰三角形，得到D=2L sinα2即球杆以母球为顶点，以AB为参照，球杆向彩球同侧转动，球杆末端移动D，即获得α角，这是最佳击球位置。

D误差角度分析与计算误差分析在打球时实际的偏角α与理想的β的取值是允许有误差的，这是因为球袋口的入口比台球的直径要大，只要经过球杆与母球的撞击、母球与彩球的撞击，把偏角α的误差传到β的误差，使其误差范围不超过球袋入口的直径即可，这个误差也是可以估计的。

如上图所示，当彩球被击到O或O’时可以进袋，O和O’是彩球进袋的“临界位置”，如果彩球球心的运动轨迹处在O和O’之间就可以保证能进球袋，所以我们就可以考虑球心在这两点时的β角，算出临界角度β1和β2，只要撞击后的角度在[β1,β2]之间，就可以使得彩球的球心轨迹在O和O’之间。

台球数学原理
嘿，朋友们！咱今儿来聊聊台球里那藏着的数学原理。

你想啊，台球桌上那一颗颗球，可不只是简单的碰撞和滚动。

这里
面的数学，就像一个神秘的宝藏，等着咱们去发掘。

比如说角度，每次击球的时候，你得算好球与球撞击的角度。

这就
好像你走在迷宫里，要找对方向才能走出去。

要是角度没算好，那球
可就跑偏啦！这难道不像你迷路的时候，明明想去东边，结果却走到
了西边？
还有力度的控制，轻了重了都不行。

力度小了，球到不了预定的位置；力度大了，说不定直接把球打飞出去。

这跟咱们做饭放盐似的，
放少了没味道，放多了齁得慌，得恰到好处才行，不是吗？
再说说路线的规划。

打台球可不是随便乱打，你得想好让球怎么走。

就像你出门旅行，得规划好路线，先去哪再去哪。

一个不小心规划错了，那这台球局可就乱套喽！
而且，台球里的数学还讲究个概率。

有时候，你得猜猜这球撞击后
的走向，有几种可能。

这就跟抽奖似的，你不知道会抽到啥，但可以
猜猜哪个可能性大。

想想看，要是没有这些数学原理在里头，台球不就成了乱撞一气的
游戏？那多没意思！
咱们平常玩台球，要是能把这些数学原理搞明白，那水平肯定蹭蹭往上涨。

说不定还能在朋友面前露一手，让他们对你刮目相看呢！
所以啊，别小看了这小小的台球桌，里面的数学世界可丰富着呢！咱们可得好好琢磨琢磨，把这门学问给弄清楚，让台球玩得更带劲！。

数学应用于台球教学的原理1. 引言台球是一种非常受欢迎的室内运动，它不仅需要运动员具备良好的技术和策略，还需要掌握一定的数学知识。

数学在台球教学中起到了重要的作用，它不仅可以帮助学生更好地理解击球的原理，还可以提高他们的技术水平。

本文将介绍数学在台球教学中的应用原理。

2. 几何知识在击球方向选择中的应用在台球教学中，运动员需要选择合适的击球方向来达到预期的效果。

几何知识可以帮助运动员准确地判断球的位置和轨迹，从而选择最佳的击球方向。

•利用直线的几何性质，可以判断球的运动轨迹是否符合预期路径。

•利用角度的概念，可以确定击球的角度和进球的角度。

•利用直线和角度的关系，可以计算击球时所需要施加的力度。

3. 物理学知识在击球力度控制中的应用在击球过程中，运动员需要掌握合适的力度，以达到预期的效果。

物理学知识可以帮助运动员理解力度和速度之间的关系，并控制好击球的力度。

•利用质量、加速度和速度的关系，可以计算出运动员需要施加的力量。

•利用摩擦力和弹性碰撞的原理，可以控制球的速度和旋转。

4. 数学模型在击球技术分析中的应用数学模型在击球技术分析中起到了重要的作用。

通过建立数学模型，可以对击球技术进行分析和预测。

•利用数学模型，可以分析球的运动轨迹和碰撞的过程，以帮助运动员更好地控制球的位置。

•利用数学模型，可以预测球的弹性变形和运动过程，以帮助运动员提高击球的精准度。

5. 数学知识在战术安排中的应用台球比赛中的战术安排也需要运用数学知识。

通过数学知识的帮助，运动员可以优化战术策略，并提高胜率。

•利用概率和统计的知识，可以分析对手的击球特点和偏向，从而选择合适的对策。

•利用游戏论的知识，可以分析比赛中的策略选择和最优解。

6. 结论数学在台球教学中担任着重要的角色。

通过运用几何知识、物理学知识、数学模型和数学战术，可以帮助运动员更好地理解击球的原理，并提高他们的技术水平。

因此，台球教学中应注重培养学生的数学能力，并将数学运用于实际的击球过程中。

台球翻袋数学证明
台球翻袋数学证明是一个在台球运动中的数学问题，主要涉及到台球在撞击后能否将其它球打入袋中的概率计算。

这个问题可以通过概率论和几何学的知识进行分析和证明。

首先，我们需要确定一些前提条件：
1. 台球桌是标准的矩形桌面，袋口是圆形的，并且袋口大小和台球直径相同。

2. 台球之间的碰撞是完全弹性碰撞，即没有能量损失。

3. 台球的轨迹是直线，没有滚动和旋转的影响。

接下来，我们可以从简单情况开始，考虑只有两颗球的情况。

假设我们有一颗球A和另一颗球B，球A撞击球B后尝试将球B 打入袋中。

我们可以通过分析球A和球B的初始位置、速度和角度等因素，以及袋口的位置和大小，来计算球B进袋的概率。

对于更复杂的情况，比如有多个球和多个袋口的情况，我们可以应用相似的原理进行分析。

通过考虑每个球与其它球的碰撞以及与袋口的关系，我们可以计算出每个球进袋的概率，并将它们相加得到最终结果。

总之，台球翻袋数学证明是一个涉及到概率论和几何学的复杂问题，需要考虑多个因素如球的初始位置、速度和角度，袋口的位置和大小等。

对于简单情况，可以通过数学计算得出结果；而对于更复杂的情况，可能需要借助计算机模拟或其他数值方法来求解。

台球与数学如何利用几何原理提高击球准确性在台球运动中，击球的准确性是取得成功的关键之一。

而要提高准确性，数学中的几何原理可以给我们很大的帮助。

本文将介绍如何运用几何原理来提高台球击球的准确性。

一、角度的选择在击球时，选取合适的击球角度是决定击球准确性的重要因素之一。

几何学中的角度概念可以帮助我们正确地选择击球角度。

几何学中的垂直线和水平线是决定角度的基本工具。

首先，需要观察球杆和目标球的相对位置，利用几何原理，找出垂直于目标球的直线。

然后，以目标球为圆心，画出合适的圆弧，找出水平线。

击球角度就是两者交汇点与目标球的连线所形成的角度。

而具体选择何种角度需要根据实际情况来决定，不同的击球距离、目标球位置等都会对角度起到影响。

因此，通过几何原理来提供合适的击球角度是至关重要的。

二、碰撞角度的计算在台球运动中，当白球和目标球相撞时，了解碰撞角度的计算能够帮助我们预测和控制球的移动轨迹。

在几何学中，我们可以利用碰撞角度和入射角度之间的关系来计算碰撞后球的运动情况。

当白球撞击目标球时，入射角度等于出射角度。

通过利用几何原理，可以计算出初始碰撞角度和速度，从而帮助我们预测球的运动轨迹。

此外，还可以使用几何原理来计算不同碰撞角度下球杆对白球和目标球施加的力。

通过合适的施力计算，可以使得球的运动更加精准和准确。

三、球的旋转问题球的旋转是台球运动中一个重要而复杂的问题。

不同的旋转方式会对球的运动轨迹产生不同的影响。

利用几何原理可以帮助我们更好地理解和控制球的旋转情况。

在几何学中，我们可以通过观察球的形状和旋转轨迹，利用旋转的几何原理来计算球的旋转速度和转动方向。

这样，我们就可以通过调整球杆的击球方式和力度来达到控制球旋转的目的，从而使球的移动更加准确和可控。

四、距离和击球力度的控制除了角度的选择和球的旋转控制外，了解几何原理还可以帮助我们在击球过程中控制击球力度和距离。

几何学中的直线距离概念可以帮助我们计算白球和目标球的距离，并据此调整击球力度。

台球桌上的数学问题
在台球桌上，当我们挑战好友进行友谊赛时，除了需要技巧和策略外，还有许
多数学问题融入其中。

这些数学问题能够帮助我们预测球的移动轨迹、角度和速度，从而更好地规划我们的击球策略。

首先，一个重要的数学问题是如何计算球的反射角度。

当我们击打一只球时，
球会与被击球的球杆接触，并反弹到台球桌的另一个位置。

在这个过程中，我们需要考虑到入射角度和反射角度之间的关系。

根据光的反射定律，入射角等于反射角。

这意味着，如果我们以45度的角度击打球，球会以45度的角度反弹。

这种数学问题帮助我们预测球的移动轨迹，并决定如何击打下一个球。

其次，我们还需要考虑球的速度和距离问题。

在击打球时，我们需要根据球的
速度和距离来调整击球的力度和方向。

在数学中，我们可以使用速度、时间和距离的公式来帮助我们计算这些问题。

例如，如果我们想要将球推向远处的一个特定位置，我们需要估计所需的力度，这可以通过计算球的速度和时间来实现。

最后，我们还可以应用一些几何学的概念来解决一些与球的击打和碰撞相关的
数学问题。

例如，当两个球碰撞时，我们可以使用几何学中的交叉点概念来预测碰撞点的位置。

通过理解几何学中的角度和距离，我们可以更好地规划我们的战略，以便在游戏中取得更好的成绩。

总而言之，在台球桌上玩台球不仅仅是一项技巧和策略的运动，还与数学紧密
相关。

通过理解和应用这些数学问题，我们可以更好地理解球的移动轨迹、角度和速度，从而提高我们的台球技巧，并在游戏中取得更好的表现。

台球桌上的数学问题摘要：I.引言- 台球运动的普及- 台球桌上的数学问题II.台球桌的几何形状- 椭圆形桌面的特点- 不同种类台球的尺寸和形状III.球的运动与碰撞- 球在桌面上的运动- 碰撞的物理原理- 计算角度与力度IV.策略与技巧- 瞄准与打击的技巧- 球杆与球的角度计算- 实际比赛中策略的应用V.总结- 台球运动中的数学问题- 数学在台球运动中的重要性正文：台球，一项在全球范围内极受欢迎的运动，其普及程度堪比足球、篮球等运动。

人们在享受台球带来的愉悦时，可能没有意识到台球桌上其实存在着许多有趣的数学问题。

本文将探讨台球桌的几何形状、球的运动与碰撞以及策略与技巧等方面的数学问题。

首先，我们来关注台球桌的几何形状。

台球桌通常采用椭圆形设计，这种形状可以确保球在桌面上的运动更为稳定。

此外，根据不同种类台球的规则，桌面的尺寸和形状也会有所不同。

例如，标准的美式台球桌面尺寸为12.5 英尺长、6 英尺宽，而英式台球的桌面则稍小，为11 英尺长、5 英尺宽。

椭圆形桌面使得台球运动具有独特的魅力，同时也为球手带来了一定的挑战。

其次，我们来探讨球的运动与碰撞。

在台球运动中，球在桌面上的运动遵循着物理学中的碰撞原理。

当球杆击打球时，球会受到一定的力度和角度，从而改变其运动状态。

为了准确打击目标球，球手需要计算好角度与力度，以便让球顺利撞击到目标球。

在这个过程中，数学知识在计算角度与力度方面发挥了关键作用。

最后，我们来关注台球运动的策略与技巧。

在实际比赛中，球手需要运用各种策略和技巧来赢得比赛。

例如，瞄准与打击的技巧、球杆与球的角度计算等。

通过对这些数学问题的掌握，球手可以更好地发挥自己的实力，提高比赛胜率。

总之，台球运动中蕴含着丰富的数学问题。

从台球桌的几何形状、球的运动与碰撞到策略与技巧，数学知识在每一个环节都发挥着重要作用。

用轴对称知识解决打台球一题
山东于秀坤
题目:小强和小勇利用课本上学过的知识来进行台球比
赛(
(1)小强把白球放在如图1所示的位置，想通过击打白
球撞击黑球，使黑球撞AC边后反弹进F洞;想想看小强
这样击打，黑球能进F洞吗,请画图的方法验证你的判
断，并说明理由(
图1 (2)小勇想通过击打白球撞击黑球，使黑球至多撞台球桌边一次后进A
洞，请你猜想小勇有几种方案,并分别在下面的台球桌上画出示意图，解释你的理由(
分析:本题是一道操作型探究题，主要根据轴对称的知识的有关进行探究(第(1)题可以通过击打AC边使球反弹进F洞(第(2)题有多种方法(击球入洞需要对每一杆的角度进行适当的估算，实质上等同于几何角度的计算，二者有着密切的关系(要想至多撞台球桌边一次击黑球于F洞(方案可以有以下情况:(1)不击台球桌边，直接用白球撞击黑球;(2)通过白球击CF边反弹再撞击黑球进A洞;(3)用白球撞击DF
边反弹撞击黑球进F洞(要想准确撞击黑球，必须找准击球的方向角度，准确估算击球的方向(在数学上，可以借助轴对称的知识来解决问题(
解: (1)如图2，将白球与黑球视为两点，过这两点画直线交台球桌边AC于M，过点M作法线MN?AC，在MN右侧?F′MN=?PMN，由于射线MF′过F洞，知黑球经过一次反弹后必进入F洞(
图2
(2)方案1:如图3，视白球、黑球为两点P，G，使A、G、P在同一直线上(
方案2:如图4，延长AC到H点，使AC=CH，连接GH交FC于点K，根据轴对称的知识可知，用白球沿GK方向撞击边CF反弹后可进行A洞(
方案3:如图5，延长AD到M点，使MD=AD，连结GM交DF于N，根据轴对称知识可知，沿GN方向用白球撞击黑球经反弹后可进入A洞(
图3 图4
图5。

生活中的数学--台球问题1 问题的提出我们平时经常接触数学的理论知识，其实走出书本，在生活中也有许许多多关于数学的问题值得我们去接触去学习。

今天，我们小组准备就台球问题进行研究，以下是我们小组研究的成果。

台球运动在我国已十分流行，从城市到乡村，到处可见，成为中国人健身娱乐的项目之一.优秀台球手的技术能给人深刻的印象，他们能从各种距离和各个角度击球入袋.初学者应不断地努力训练，学会如何操杆撞击球，使母球与彩球相撞，将彩球以合适的角度和速度送进袋中.我们试着对台球技术问题建立数学模型，帮助提高技艺.台球的网口虽然很小，但有较小的余地，即使你不是瞄得很准球也能入网.人的误差总是存在的，所以一个有趣的问题是在一次击球中允许多大的偏差，仍能保证彩球进入球网.这里考虑台球桌上只有母球和一个彩球.2 模型的假设台球桌面绝对平滑，不存在凹凸；没有撞击的台球运动轨迹是一条直线；两个台球的运动速度不受摩擦的影响；两个台球的形状质量完全一样；碰撞轨迹与母球的初始速度无关.3 模型的准备、撞击后台球的运动轨迹(母球碰撞前瞬间的速度为V，彩球静止0v=)母球和彩球位于同一直线上母球和彩球位于同一直线，即彩球的球心在母球的运动轨迹所在直线上.当母球以速度V撞击彩球，撞击瞬间，母球的动量全部传递给彩球，母球立刻停止运动.根据动量守恒：''mv MV mv MV +=+，即有'0V =，'v V =.母球和彩球不在同一直线上母球和彩球不是在同一直线，即彩球的球心不在母球的运动方向上.母球撞击彩球，撞击瞬间后，两球的速度符合以原母球速度为对角线的“矩形定则”，碰撞后的母球和彩球运动方向互相垂直，瞬间的母球与彩球的速度夹角成九十度，构成了矩形的两个边，这个矩形对角线，就是原母球的速度.4.瞄准点的确定母球和彩球的球心与球袋中心在同一直线上当母球和彩球的球心与球袋中心三者在同一条直线上时，只要瞄准彩球的球心，这样碰撞后彩球便可以运动到球袋的中心，进入球袋.母球和彩球的球心与球袋中心不在同一直线上设彩球在台面上A处，母球在O处，为了让彩球A可以沿直线AP运行到球袋开口中点P处，我们的瞄准点应该在直线AP的反向延长线上的某一点.具体的做法如下:以A为圆心,台球的直径为半径作一个圆.延长AP和圆相交于点'OO就是母球的理想轨迹.O,'O就是所求的瞄准点.而'模型的建立5.三角关系模型的建立为了简化问题，便于分析，我们把台球桌上的状态简化如下：A是母球原位置，B是彩球的位置，C是瞄准点.母球原位置A与彩球原位置B决定一条有向直线AB；母球运动方向决定一条有向直线AC；彩球碰撞后运动方向决定一条有向直线CB.这样就构成一个三角形ABC.根据瞄准点的确定，知道碰撞点在BC中点，所以|BC|=2d ,在某一个特定的状态下||BC 也是一个定值.所以在ABC ∆中我们在击球时能控制调整的是BAC ∠，通过控制调整BAC ∠使ABC ∠达到理想值，进而使彩球能顺利入袋.βα为为记ABC BAC ∠∠,.在ABC ∆中，由余弦定理得βcos ||||2||||||222BC AB BC AB AC -+=βcos ||||2||||||22BC AB BC AB AC -+= ……………… (1) 由正弦定理得：αβsin ||sin ||BC AC = ……………… (2) 于是αββsin ||sin cos ||||2||||22BC BC AB BC AB =-+ ……………… (3) 分析一个特定例子在某一个已知的状态中，可以视|AB|和|BC|为已知的值，α与β为变量，那么该方程反应了变量α与β的必然联系.击球时就可以通过控制和调整α的大小，来决定β的大小.在实际中，已知|AB|,|BC|,β取为理想值，便可以计算α的大小.由(3)式可得)900()cos ||||2||||sin ||arcsin(0022≤≤-+=βββαBC AB BC AB BC (4)我们假设某一个状态中，台球半径d=2.5cm ，彩球与母球的球心距离为5Ocm ，β的理想角度为045，这时候才能使彩球落进球袋中心.我们可以计算出α的值.把已知代入上述公式得：002204.4)076.0arcsin())45cos(5502550)45sin(5arcsin(==⨯⨯-+=α.也就是说，当球杆的击打方向与参照线AB 形成04.4夹角，可把彩球准确打入球袋.角度大小估计与长度距离的估计的转化利用上面的模型，我们在给定某一个条件下已计算出了α的理论值，然而人的眼睛与手是不容易打出这个理论值(04.4)的.也就是说：我们怎么做才能更好的打出和参照线||AB 成04.4的夹角呢? 因为人的生活经验对长度数量的直观估计比对角度数值的估计要相对准确，所以我们可以把对角度的估计转化为数值长度的估计.假设顶角为α，以球杆长度为腰，构造一个等腰三角形，得到:2sin()2D l a = ………………(5) 所以利用这个公式来把握a 要好一些.在上面一个状态里，假设球杆长150cm ，那么cm d 5.11)2.2sin(15020=⨯⨯=即，当用150cm 长的球杆打球时，只要将球杆以母球为顶点，以AB 为参照线，将球杆向与彩球同侧稍加转动，使球杆未端移动约11.5cm ，即可获得04.4的角度，这是最佳击球位置.6.考虑实际的误差的情况误差的大小分析在打球时，实际的偏角α与理想的β取值是允许有误差的.这是因为球袋口的入口直径比台球直径要大.只要经过球杆与母球击打、母球与彩球碰撞，把偏角α的误差传到β的误差范围不超过球袋口的直径即可.这个误差也是可以估计的.如上图所示，当彩球被击到O O '或者时还可以进球袋，O O '和是彩球能进球袋的“临界位置”，如果彩球球心的运动轨迹处在O O '和之间就可以保证能进球袋.所以我们就可以考虑球心在这两点时的β角，算出临界角度l r ββ和，只要撞击后的角度在[]l r ββ,之间，就可以使彩球球心的运动轨迹在O O '和之间了.误差角度计算由基本的几何知识知道：OCB CA O r l ∠-=∠+=ββββ,'.BCBO OCB =∠)tan( )arctan(BC BO OCB =∠ ………………(6) 同理)arctan(''AC AO CA O =∠ ………………(7) 由（4）式可以计算出[,]l r a a :)cos ||||2||||sin ||arcsin(22lll BC AB BC AB BC ββα-+= ………………(8) )cos ||||2||||sin ||arcsin(22rrr BC AB BC AB BC ββα-+= (9)5.3 误差对下杆影响在某一状态下，只要击球的角度偏差不要太大，范围在l r αα和之间，就可以保证彩球可以进球袋.与上面相同的情况下，假设'1.5, 1.5,40BO cm AO cm BC cm ===，038.0)tan(==∠BCBO OCB ,即是02.2=∠OCB ，同理得到0'2.2=∠CA O . 0000045 2.242.8,l r b b =-=0=45+2.2=47.2,分别代入（8）式和（9）式得到004.68, 4.15l r a a ==.同样地，可以把角度转化为对距离的估计：cm d cm d 86.10)215.4sin(1502,25.12)268.4sin(150221=⨯==⨯= 以AB 为参照线，下杆时只要距离估计范围在[10.86,12.25]cm cm 之间，就可以把彩球打入球袋.7.参考文献[1] 李钧.台球撞击的偏角方程[J].中学数学杂志(高中).20OO 年.第2期.30-31[2] 戴俊, 傅怀梁,等.一个边界振荡的台球模型[J]. 扬州大学学报(自然科学版).2004年11月第7卷第4期.27－31[3] 李东升.台球桌上的物理问题.中学物理教学参考.2002年.第31卷.第1～2期.28[4] 刘宗良.台球桌上的数学.数学教学.2005年.第5期.238.活动心得我们小组的成员都在这次的数学研究活动中受益匪浅，我们把数学融入到生活中，体验到了不同于课堂中理论知识的乐趣，我们共同希望在以后的生活中，多接触数学，体验其中的乐趣.。

台球涉及的数学知识嘿，朋友们！你们可别小瞧了台球这项运动，这里面藏着的数学知识那可多了去啦！你想想看，台球桌上的那些球，它们的排列不就像是一个个等待解开的数学谜题吗？当你准备击球的时候，你得考虑角度问题吧，这可不是随便乱打的哟！这就好比是一道几何题，你要找到那个最精准的角度，才能让球乖乖地按照你的想法滚动。

比如说，你要打一个直线球，那是不是得清楚球和目标洞之间的距离，然后计算出要用多大的力量去击打它呢？这就是简单的数学计算呀！要是遇到更复杂的局面，几个球挡在那里，你就得像个解题高手一样，分析各种可能的路线，这不就是在运用数学思维嘛。

还有啊，台球中的碰撞也充满了学问呢。

当球与球碰撞的时候，会发生能量的传递和方向的改变，这就像是物理课上学的动量守恒定律在起作用。

你得了解这些规律，才能更好地控制球的走向。

再看看那些高手们，他们为什么能那么厉害？不就是因为他们对这些数学知识掌握得炉火纯青嘛！他们能在瞬间判断出角度、力度和路线，这可不是光靠感觉就能做到的呀。

就好像解方程一样，你得一步一步地找到那个正确的答案。

打台球也是如此，你要通过不断地尝试和计算，才能找到最佳的击球方式。

而且，台球还能锻炼你的空间想象力呢！你要在脑海中构想出球的运动轨迹，这可不是一件容易的事儿。

想象一下，要是没有这些数学知识，那打台球岂不是乱打一气，哪还有什么乐趣可言呢？所以啊，可别再觉得数学只是在课堂上有用啦，在台球桌上它也能大显身手呢！台球就像是一个充满挑战的数学考场，每一次击球都是一次测试。

你要运用你的智慧和技巧，才能在这个考场中取得好成绩。

朋友们，下次再去打台球的时候，可别忘了好好感受一下其中的数学魅力哟！说不定你还能从中发现更多有趣的数学现象呢！让我们一起在台球桌上探索数学的奥秘吧！这多有意思呀，不是吗？。

台球中的数学原理嘿，大家好呀！我是你们的小伙伴。

嘿，你们知道吗？我最近发现了台球中的数学原理，可有趣啦！有一天，我和小伙伴们一起去台球馆玩。

台球桌上铺着绿色的台布，上面放着各种颜色的台球，看起来可漂亮啦。

我们拿着球杆，准备来一场激烈的比赛。

可我忽然想起了平时学的数学知识，心想：“台球运动中是不是也有数学的影子呢？”我开始仔细观察，发现每次球被击打后，它们都会沿着特定的方向运动。

球的运动轨迹让我想到了一些几何图形，尤其是直线和角度。

我用球杆轻轻地击打白球，白球沿着一条直线滚动，撞到一颗红球后，它们的运动方向发生了变化。

这让我联想到数学中的反射定律——入射角等于反射角。

接着，我继续实验。

我试着用不同的角度去击打白球，观察它与其他球碰撞后的反应。

我发现，如果我能够准确地计算出入射角，我就能预测白球碰撞后的运动方向。

这样，我就可以通过精确的击球，让球顺利地滚进洞里。

这不是很像在解一道几何题吗？不光是角度，我还发现了力和速度在台球中的重要性。

每次击球的力度不同，球的速度也会有所不同。

如果击球力度很大，球就会快速滚动；反之，如果力度小，球滚动的速度也会变慢。

这让我想到了物理中的速度公式：速度等于距离除以时间。

通过调整我的击球力度，我可以控制球的速度，让它准确地停在我想要的位置。

除了几何和物理，我还发现台球桌上的球与球之间的碰撞让我想起了数学中的概率论。

每次我击打白球，它可能会碰撞到其他不同的球。

每次碰撞后，球的运动方向和结果都是不确定的，但如果我能够精确地控制击球角度和力度，我就可以增加击球成功的概率。

在一次比赛中，我和小伙伴们决定比比谁能最快把球打进洞里。

我运用之前学到的数学原理，计算好每次击球的角度和力度。

第一次，我稍稍失误，白球没有按照预想的方向滚动，但我没有灰心，马上调整了击球的角度和力度。

这一次，白球碰到红球后，红球顺利地滚进了洞里。

我高兴得跳了起来，小伙伴们也为我鼓掌。

我越玩越发现台球中的数学原理是多么有趣。

台球桌上的数学问题摘要：一、台球运动的起源与发展1.台球的起源2.台球在我国的发展3.台球在国际上的影响力二、台球桌上的数学问题1.介绍台球桌的基本参数2.探讨台球运动中的几何关系3.实际案例分析：解决台球比赛中遇到的数学问题三、台球运动中的策略与技巧1.数学在制定台球策略中的重要性2.运用几何知识提高台球技巧3.结合实际情况，分析著名台球选手如何运用数学技巧获得胜利四、台球运动与数学教育的结合1.将台球运动引入数学教育，提高学生学习兴趣2.通过台球运动培养学生的几何直观能力3.总结：台球运动在数学教育中的积极作用正文：台球，一项起源于15世纪的英国的运动，经过数百年的发展，已经成为世界上最受欢迎的体育项目之一。

在我国，台球运动同样具有广泛的影响力，不仅拥有众多的爱好者，还培养出了许多世界级的台球选手。

台球运动看似轻松简单，实际上却蕴含着丰富的数学原理。

今天，我们就来探讨一下台球桌上的数学问题。

首先，我们来了解一下台球桌的基本参数。

一张标准的台球桌长为2.54米，宽为1.27米，桌面四周设有6条长边和6条短边，共12条边。

此外，桌面上还分布着15个球洞，其中1个为母球洞，14个为彩色球洞。

了解了这些基本参数，我们就可以开始探讨台球运动中的几何关系。

在实际的台球比赛中，选手们需要根据球桌上的几何关系来制定击球策略。

例如，在击打目标球时，选手需要考虑母球与目标球之间的角度、距离以及速度，以保证目标球顺利撞到库边并弹入球袋。

此外，选手还需要根据台球桌的形状和球洞的分布，来判断自己的击球是否能够成功将球送入球袋。

在著名的台球比赛中，许多选手都运用了数学技巧来获得胜利。

例如，我国台球选手丁俊晖在比赛中，经常运用几何知识来判断球的走势，从而制定出精妙的击球策略。

这充分说明，在台球运动中，数学知识的重要性不容忽视。

将台球运动引入数学教育，可以提高学生的学习兴趣。

通过实际操作，学生可以直观地感受到几何知识在实际生活中的应用，从而激发他们对数学的兴趣。

1、在标准的斯诺克台球桌上，从开球点到黑球之间的直线距离大约是多少？A. 12英尺B. 22英尺C. 32英尺D. 42英尺（答案：A）2、在九球比赛中，如果一名选手在击打1号球时不慎将9号球打入袋口，这一行为如何计分？A. 仅计算1号球的分数B. 同时计算1号球和9号球的分数，并赢得比赛C. 犯规，不计分D. 重新击打1号球（答案：B）3、在美式8球比赛中，当桌上只剩下8号球和黑球时，选手应如何击打才能合法获胜？A. 先击打黑球，再击打8号球入袋B. 只能直接击打8号球入指定袋口C. 可以选择任意顺序，但8号球必须最后入袋D. 必须同时击打两球入袋（答案：B）4、在台球比赛中，如果选手的球杆意外触碰到桌面上的其他球，这通常被视为：A. 有效击球B. 犯规C. 自由球机会D. 重新摆球（答案：B）5、在斯诺克比赛中，当白球被击打后未能触碰到任何目标球而直接落入袋口，这种情况称为：A. 自由球B. 失误入袋C. 犯规击球D. 有效进球（答案：B）6、在台球术语中，“香蕉球”通常指的是：A. 球以曲线轨迹运动进球B. 球以极高速度进球C. 球以极低速度滚动进球D. 球直接碰撞袋口边缘进球（答案：A）7、在九球比赛中，若选手击打的是非目标球（如击打2号球而非当前应击的1号球），且该球意外入袋，应如何处理？A. 计入2号球的分数，继续击打1号球B. 犯规，对手获得自由球机会C. 重新击打当前应击的目标球D. 视为有效击球，继续下一球（答案：B）8、在斯诺克比赛中，当选手击打白球后，白球跳跃离开桌面再落回，这是否合法？A. 合法，只要白球最终落回桌面B. 合法，但需扣除相应分数C. 犯规，对手获得自由球D. 犯规，且当前轮次得分无效（答案：D）9、在台球比赛中，如果选手在击打时球杆断裂，且不是因为故意或不当使用造成的，通常应如何处理？A. 选手自动输掉比赛B. 给予选手一次更换球杆的机会，继续比赛C. 对手获得一次自由球机会D. 比赛重新开始，双方重新摆球（答案：B）10、在美式8球比赛中，如果选手在击打时未声明要打入的袋口，但球仍然进入了某个袋口，这是否有效？A. 有效，只要球进入袋口即可B. 无效，必须事先声明袋口C. 由裁判决定是否有效D. 双方选手协商决定是否有效（答案：A）。

台球技巧问题的数学模型吴琛11级电气学院本科2班摘要利用物理学碰撞原理,分析台球碰撞后的运动轨迹,确定了理想的瞄准点.当母球和彩球的位置确定后,通过建立三角关系式,得出了瞄准时球杆的偏移角度,使下杆时有了理论的依据,解决了下杆时如何瞄准的问题.通过角度和距离的转化, 把不容易用眼睛估计的角度变换为对距离的估计.然后再根据实际情况,引入误差分析,在某一个误差范围内都可以把彩球打入球袋里.使得瞄准后知道如何更好下杆.还分析了一个状态,下杆时球杆和参照线角度在015.468.4和之间(相应的估计距离在cmcm25.1286.10和之间)就可以入球，研究台球模型意义在于用科学的角度解析台球，使台球的技术和美观完美的的搭配，更好的打好台球。

关键词：台球模型;瞄准点;角度估计;距离估计1 问题的提出台球运动场地小，是室内运动，不受季节、天气、时间等因素影响；台球的运动量不大，不会耗费大的体力，适合任何人；台球是一种智力的体育活动，趣味性很强.台球运动在我国已十分普及，从城市到乡村，到处可见，成为中国人健身娱乐的项目之一.优秀台球手的技术能给人深刻的印象，他们能从各种距离和各个角度击球入袋.初学者应不断地努力训练，学会如何操杆撞击球，使母球与彩球相撞，将彩球以合适的角度和速度送进袋中.试对台球技术问题建立数学模型，指导初学者，帮助他们提高技艺.台球的网口虽然很小，但有较小的余地，即使你不是瞄得很准球也能入网.人的误差总是存在的，所以一个有趣的问题是在一次击球中允许多大的偏差，仍能保证彩球进入球网.这里考虑台球桌上只有母球和一个彩球.2 模型的假设2.1台球桌面绝对平滑，不存在凹凸；2.2没有撞击的台球运动轨迹是一条直线；2.3两个台球碰撞等同于物理上两个刚体的碰撞；2.4两个台球的运动速度不受摩擦的影响；2.5两个台球的形状质量完全一样；2.6碰撞轨迹与母球的初始速度无关.3 模型的准备3.1撞击后台球的运动轨迹(母球碰撞前瞬间的速度为V ，彩球静止0v =) 3.1.1 母球和彩球位于同一直线上母球和彩球位于同一直线，即彩球的球心在母球的运动轨迹所在直线上.当母球以速度V 撞击彩球，撞击瞬间，母球的动量全部传递给彩球，母球立刻停止运动.根据动量守恒：''mv MV mv MV +=+，即有'0V =，'v V=.3.1.2母球和彩球不在同一直线上母球和彩球不是在同一直线，即彩球的球心不在母球的运动方向上.母球撞击彩球，撞击瞬间后，两球的速度符合以原母球速度为对角线的“矩形定则”，碰撞后的母球和彩球运动方向互相垂直，瞬间的母球与彩球的速度夹角成九十度，构成了矩形的两个边，这个矩形对角线，就是原母球的速度.3.2 瞄准点的确定3.2.1 母球和彩球的球心与球袋中心在同一直线上当母球和彩球的球心与球袋中心三者在同一条直线上时，只要瞄准彩球的球心，这样碰撞后彩球便可以运动到球袋的中心，进入球袋.3.2.2 母球和彩球的球心与球袋中心不在同一直线上当母球和彩球的球心与球袋中心三者不在同一条直线上时，则下杆时要偏移一定的角度，这时瞄准点不是彩球的中心点，而是在这个中心点附近的某一点.具体确定该点可以按如下的方法：假想彩球球心与球袋中心上有一条连结二者的直线，而你向彩球击出母球时，如果碰撞时母球与彩球的接触点正好在这一条想像的连线上时，彩球就会朝球袋中心前进.而在接触瞬间时母球的中心点就是假想中心点.说得更清楚一点，我们可以在彩球球心与球袋中心连线上假想有一颗球与彩球正好紧密地靠在一起，而这颗假想球的中心必须是在这条假想的连线上.当你击球的时候，就是要把母球击向这一颗假想球的位置上.当母球被击出而能运动到在这个位置上，然后再碰触到彩球时，彩球就会顺利入袋.因为在碰触的那一瞬间，母球和彩球的球心与球袋中心正好在一直线上.设彩球在台面上A 处，母球在O 处，为了让彩球A 可以沿直线AP 运行到球袋开口中点P 处，我们的瞄准点应该在直线AP 的反向延长线上的某一点.具体的做法如下:以A 为圆心,台球的直径为半径作一个圆.延长AP 和圆相交于点'O ,'O就是所求的瞄准点.而'OO 就是母球的理想轨迹.4 模型的建立4.1 三角关系模型的建立为了简化问题，便于分析，我们把台球桌上的状态简化如下：A 是母球原位置，B 是彩球的位置，C 是瞄准点.母球原位置A 与彩球原位置B 决定一条有向直线AB ；母球运动方向决定一条有向直线AC ；彩球碰撞后运动方向决定一条有向直线CB .这样就构成一个三角形ABC .根据瞄准点的确定，知道碰撞点在BC 中点，所以|BC|=2d ,在某一个特定的状态下||BC 也是一个定值.所以在ABC ∆中我们在击球时能控制调整的是BAC ∠，通过控制调整BAC ∠使ABC∠达到理想值，进而使彩球能顺利入袋.βα为为记ABC BAC ∠∠,.在ABC ∆中，由余弦定理得βcos ||||2||||||222BC AB BC AB AC -+=βcos ||||2||||||22BC AB BC AB AC -+= (1)由正弦定理得：αβsin ||sin ||BC AC = ……………… (2) 于是αββsin ||sin cos ||||2||||22BC BC AB BC AB =-+ ……………… (3) 4.2 分析一个特定例子在某一个已知的状态中，可以视|AB|和|BC|为已知的值，α与β为变量，那么该方程反应了变量α与β的必然联系.击球时就可以通过控制和调整α的大小，来决定β的大小.在实际中，已知|AB|,|BC|,β取为理想值，便可以计算α的大小.由(3)式可得)900()cos ||||2||||sin ||arcsin(0022≤≤-+=βββαBC AB BC AB BC (4)我们假设某一个状态中，台球半径d=2.5cm ，彩球与母球的球心距离为5Ocm ，β的理想角度为45，这时候才能使彩球落进球袋中心.我们可以计算出α的值.把已知代入上述公式得：002204.4)076.0arcsin())45cos(5502550)45sin(5arcsin(==⨯⨯-+=α.也就是说，当球杆的击打方向与参照线AB 形成4.4夹角，可把彩球准确打入球袋.4.3 角度大小估计与长度距离的估计的转化利用上面的模型，我们在给定某一个条件下已计算出了α的理论值，然而人的眼睛与手是不容易打出这个理论值(4.4)的.也就是说：我们怎么做才能更好的打出和参照线||AB 成04.4的夹角呢?因为人的生活经验对长度数量的直观估计比对角度数值的估计要相对准确，所以我们可以把对角度的估计转化为数值长度的估计.假设顶角为α，以球杆长度为腰，构造一个等腰三角形，得到:2sin()2D l a= ………………(5) 所以利用这个公式来把握a 要好一些.在上面一个状态里，假设球杆长150cm ，那么cmd 5.11)2.2sin(15020=⨯⨯=即，当用150cm 长的球杆打球时，只要将球杆以母球为顶点，以AB 为参照线，将球杆向与彩球同侧稍加转动，使球杆未端移动约11.5cm ，即可获得4.4的角度，这是最佳击球位置.5 考虑实际的误差的情况5.1 误差的大小分析在打球时，实际的偏角α与理想的β取值是允许有误差的.这是因为球袋口的入口直径比台球直径要太.只要经过球杆与母球击打、母球与彩球碰撞，把偏角α的误差传到β的误差范围不超过球袋口的直径即可.这个误差也是可以估计的.如上图所示，当彩球被击到O O '或者时还可以进球袋，O O '和是彩球能进球袋的“临界位置”，如果彩球球心的运动轨迹处在O O '和之间就可以保证能进球袋.所以我们就可以考虑球心在这两点时的β角，算出临界角度l rββ和，只要撞击后的角度在[]l r ββ,之间，就可以使彩球球心的运动轨迹在O O '和之间了.5.2 误差角度计算 由基本的几何知识知道：OCBCA O r l ∠-=∠+=ββββ,'.BCBOOCB =∠)tan()arctan(BC BOOCB =∠ ………………(6) 同理)arctan(''AC AO CA O =∠ (7)由（4）式可以计算出[,]l r a a :)cos ||||2||||sin ||arcsin(22lll BC AB BC AB BC ββα-+= (8))cos ||||2||||sin ||arcsin(22rrr BC AB BC AB BC ββα-+= (9)5.3 误差对下杆影响在某一状态下，只要击球的角度偏差不要太大，范围在l rαα和之间，就可以保证彩球可以进球袋.与上面相同的情况下，假设'1.5, 1.5,40BO cm AO cm BC cm===，038.0)tan(==∠BCBOOCB ,即是02.2=∠OCB ，同理得到0'2.2=∠CA O . 0000045 2.242.8,l r b b =-=0=45+2.2=47.2,分别代入（8）式和（9）式得到004.68, 4.15l r a a ==.同样地，可以把角度转化为对距离的估计：cm d cm d 86.10)215.4sin(1502,25.12)268.4sin(150221=⨯==⨯= 以AB 为参照线，下杆时只要距离估计范围在[10.86,12.25]cm cm 之间，就可以把彩球打入球袋.6 模型的应用及推广6.1 在实际的台球技术中，文章可以对初学者有一定的指导作用.可以避免初学者盲目的练习.可以有针对性的练习和提高对角度和距离的估计，这样对入球会有明显的提高.6.2 台球游戏的开发中，编程设计时可以借鉴本文的一些结果.6.3 对物理学上的粒子碰撞和碰撞后的粒子轨迹的研究，也有一定的参考价值.７参考文献[1] 李钧.台球撞击的偏角方程[J].中学数学杂志(高中).20OO年.第2期.30-31[2] 戴俊, 傅怀梁,等.一个边界振荡的台球模型[J]. 扬州大学学报(自然科学版).2004年11月第7卷第4期.27－31[3] 李东升.台球桌上的物理问题.中学物理教学参考.2002年.第31卷.第1～2期.28[4] 刘宗良.台球桌上的数学.数学教学.2005年.第5期.23。

台球桌上的数学问题
（原创实用版）
目录
1.引言：介绍台球桌上的数学问题
2.目标球和袋口的角度问题
3.球的反弹和旋转问题
4.结论：总结台球桌上的数学问题
正文
在台球比赛中，选手们经常需要解决一些数学问题，以便更好地控制球的走向和力度。

今天我们就来探讨一下台球桌上的数学问题。

首先，我们来看目标球和袋口的角度问题。

在打台球时，选手需要准确地判断目标球和袋口之间的角度，以便更好地掌握击球方向。

这就需要选手对几何学有一定的了解，能够快速计算出角度的大小。

此外，选手还需要考虑球杆的倾斜程度，以及球在滚动过程中可能发生的偏移，这些都会影响到目标球最终是否能够顺利进入袋口。

其次，我们来看球的反弹和旋转问题。

在台球比赛中，球的反弹和旋转是非常重要的因素。

选手需要掌握球的反弹规律，以便更好地控制球的落点。

这就需要选手对物理学有一定的了解，能够准确地判断球的反弹方向和力度。

同时，选手还需要掌握球的旋转技巧，通过旋转来控制球的走向。

这需要选手对力学和几何学都有一定的了解，能够准确地判断球的旋转方向和力度。

总的来说，台球桌上的数学问题主要包括目标球和袋口的角度问题、球的反弹问题和球的旋转问题。

第1页共1页。