2012北京中考数学一模几何压轴题汇总
- 格式:pdf
- 大小:767.10 KB
- 文档页数:12

2012年各地中考数学压轴题精选21~30_解析版【21.2012上海】24.如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=,EF⊥OD,垂足为F.(1)求这个二次函数的解析式;(2)求线段EF、OF的长(用含t的代数式表示);(3)当∠ECA=∠OAC时,求t的值.考点:相似三角形的判定与性质;待定系数法求二次函数解析式;全等三角形的判定与性质;勾股定理。
解答:解:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),∴,解得,∴这个二次函数的解析式为:y=﹣2x2+6x+8;(2)∵∠EFD=∠EDA=90°∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°,∴∠DEF=∠ODA∴△EDF∽△DAO∴.∵,∴=,∴,∴EF=t.同理,∴DF=2,∴OF=t﹣2.(3)∵抛物线的解析式为:y=﹣2x2+6x+8,∴C(0,8),OC=8.如图,连接EC、AC,过A作EC的垂线交CE于G点.∵∠ECA=∠OAC,∴∠OAC=∠GCA(等角的余角相等);在△CAG与△OCA中,,∴△CAG≌△OCA,∴CG=4,AG=OC=8.如图,过E点作EM⊥x轴于点M,则在Rt△AEM中,∴EM=OF=t﹣2,AM=OA+AM=OA+EF=4+t,由勾股定理得:∵AE2=AM2+EM2=;在Rt△AEG中,由勾股定理得:∴EG===∵在Rt△ECF中,EF=t,CF=OC﹣OF=10﹣t,CE=CG+EG=+4由勾股定理得:EF2+CF2=CE2,即,解得t1=10(不合题意,舍去),t2=6,∴t=6.【22. 2012广东】22.如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).考点:二次函数综合题。
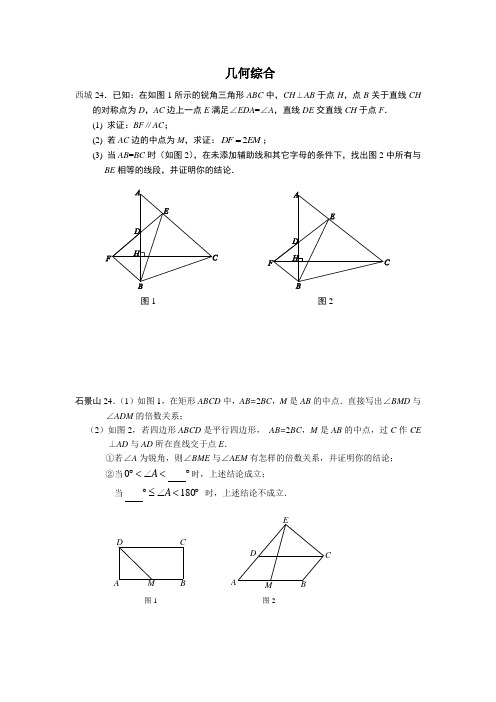
几何综合西城24.已知:在如图1所示的锐角三角形ABC 中,CH ⊥AB 于点H ,点B 关于直线CH的对称点为D ,AC 边上一点E 满足∠EDA =∠A ,直线DE 交直线CH 于点F . (1) 求证:BF ∥AC ;(2) 若AC 边的中点为M ,求证:2DF EM =;(3) 当AB =BC 时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE 相等的线段,并证明你的结论.图1 图2石景山24.(1)如图1,在矩形ABCD 中,AB=2BC ,M 是AB 的中点.直接写出∠BMD 与∠ADM 的倍数关系;(2)如图2,若四边形ABCD 是平行四边形, AB=2BC ,M 是AB 的中点,过C 作CE⊥AD 与AD 所在直线交于点E .①若∠A 为锐角,则∠BME 与∠AEM 有怎样的倍数关系,并证明你的结论; ②当︒<∠<︒A 0时,上述结论成立;当︒<∠≤︒180A 时,上述结论不成立.M D BA CEADMBC图1 图2平谷25.两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D =30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的DBE△绕点B按顺时针方向旋转角α,且060α<<°°,其它条件不变,请在图②中画出变换后的图形,并直接写出⑴中的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60180β<<°°,其它条件不变,如图③.你认为⑴中的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.解:(1)证明:(2)结论:AF+EF=DE .(填成立还是不成立)门头沟24.已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.(1)如图l,当∠ACB=90°时,直接写出线段DE、CE之间的数量关系;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG 和△DBG关于直线DG对称(点B的对称点是点K),延长DK交AB于点H.若BH=10,求CE的长.图 1EDACB图 2EDACB FGKH图 3EDACB图1A B C 图2D A C B P 丰台24.已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是 ;(2)将图1中的△ADE 绕点A 旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.房山25.如图1,在△ABC 中,∠ACB =90°,AC =BC =5,以点B 为圆心,以2为半径作圆.⑴设点P 为☉B 上的一个动点,线段CP 绕着点C 顺时针旋转90°,得到线段CD ,联结DA ,DB ,PB ,如图2.求证:AD =BP ;⑵在⑴的条件下,若∠CPB =135°,则BD =___________; ⑶在⑴的条件下,当∠PBC =_______° 时,BD 有最大值,且最大值为__________;当∠PBC =_________° 时,BD 有最小值,且最小值为__________.DCB AEMMEABCD昌平25. 如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,直线MN 经过点O ,设锐角∠DOC =∠α,将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’,直线A D ’、B C ’相交于点P .(1)当四边形ABCD 是矩形时,如图1,请猜想A D ’、B C ’的数量关系以及∠APB 与∠α的大小关系;(2)当四边形ABCD 是平行四边形时,如图2,(1)中的结论还成立吗?(3)当四边形ABCD 是等腰梯形时,如图3,∠APB 与∠α有怎样的等量关系?请证明.图3图2图1D CBANC'OMPD'D CBAN C'O MPD'D'PM OC'N A BCD顺义25.问题:如图1, 在Rt △ABC 中,90C ∠=︒,30ABC ∠=︒,点D 是射线CB 上任意一点,△ADE 是等边三角形,且点D 在ACB ∠的内部,连接BE .探究线段BE 与DE 之间的数量关系. 请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.(1) 当点D 与点C 重合时(如图2),请你补全图形.由BAC ∠的度数为 ,点E落在 ,容易得出BE 与DE 之间的数量关系为 ; (2) 当点D 在如图3的位置时,请你画出图形,研究线段BE 与DE 之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.DB CAABC (D )图3图2图1D EBCA延庆24.如图1,已知:已知:等边△ABC ,点D 是边BC 上一点(点D 不与点B 、点C重合),求证:BD+DC > AD 下面的证法供你参考:把ACD ∆绕点A 瞬时间针旋转60得到ABE ∆,连接ED , 则有ABE ACD ∆≅∆,DC=EB ∵AD=AE,60=∠DAE∴ADE ∆是等边三角形 ∴AD=DE在DBE ∆中,BD+EB > DE 即:BD+DC >AD 实践探索:(1)请你仿照上面的思路,探索解决下面的问题:如图2,点D 是等腰直角三角形△ABC 边上的点(点D 不与B 、C 重合),求证:BD+DC>2AD(2)如果点D 运动到等腰直角三角形△ABC 外或内时,BD 、DC 和AD 之间又存在怎样的数量关系? 直接写出结论.创新应用:(3)已知:如图3,等腰△ABC 中, AB=AC ,且∠BAC=α(α为钝角), D 是等腰△ABC 外一点,且∠BDC+∠BAC =180º, BD 、DC 与AD 之间存在怎样的数量关系?写出你的猜想,并证明.CAB D 图2 CA BD图1C D AB 图3海淀24. 在□ABCD 中,∠A =∠DBC , 过点D 作DE =DF , 且∠EDF=∠ABD , 连接EF 、 EC ,N 、P 分别为EC 、BC 的中点,连接NP .(1)如图1,若点E 在DP 上, EF 与DC 交于点M , 试探究线段NP 与线段NM 的数量关系及∠ABD 与∠MNP 满足的等量关系,请直接写出你的结论;(2)如图2,若点M 在线段EF 上, 当点M 在何位置时,你在(1)中得到的结论仍然成立,写出你确定的点M 的位置,并证明(1)中的结论.图1 图2密云24.已知:正方形ABCD 中,45MAN ∠=,绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于点M 、N .(1)如图1,当M AN ∠绕点A 旋转到BM DN =时,有BM DN MN +=.当MAN ∠绕点A 旋转到BM DN ≠时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间有怎样的等量关系?请写出你的猜想,并证明.MBDCFEANPPNA E FCDB通州25.已知四边形ABCD ,点E 是射线BC 上的一个动点(点E 不与B 、C两点重合),线段BE 的垂直平分线交射线AC 于点P ,联结DP ,PE. (1)若四边形ABCD 是正方形,猜想PD 与PE 的关系,并证明你的结论.(2)若四边形ABCD 是矩形,(1)中的PD 与PE 的关系还成立吗?(填:成立或不成立).(3)若四边形ABCD 是矩形,AB =6,cos ∠ACD =35,设AP=x ,△PCE 的面积为y ,当AP>12AC 时,求y 与x 之间的函数关系式.东城24. 已知∠ABC =90°,点P 为射线BC 上任意一点(点P 与点B 不重合),分别以AB 、AP 为边在∠ABC 的内部作等边△ABE 和△APQ ,连结QE 并延长交BP 于点F . (1)如图1,若AB =32,点A 、E 、P 恰好在一条直线上时,求此时EF 的长(直接写出结果);(2)如图2,当点P 为射线BC 上任意一点时,猜想EF 与图中的哪条线段相等(不能添加辅助线产生新的线段),并加以证明;(3)若AB =32,设BP =x ,以QF 为边的等边三角形的面积y ,求y 关于x 的函数关系式.B CA D A DB C朝阳25. 在矩形ABCD 中,点P 在AD 上,AB =2,AP =1,将三角板的直角顶点放在点P 处,三角板的两直角边分别能与AB 、BC 边相交于点E 、F ,连接EF .(1)如图,当点E 与点B 重合时,点F 恰好与点C 重合,求此时PC 的长;(2)将三角板从(1)中的位置开始,绕点P 顺时针旋转,当点E 与点A 重合时停止,在这个过程中,请你观察、探究并解答:① ∠PEF 的大小是否发生变化?请说明理由;② 直接写出从开始到停止,线段EF 的中点所经过的路线长.P D C(F)A B(E)F P D C A B E。

2012年北京市中考数学模拟试卷(三)2012年北京市中考数学模拟试卷(三)一、精心选(每题的四个选项中只有一个是符合题意的,请将符合题意的选项字母填在相应的答题栏内,每小题3分,共30分) ± D2.(3分)(2008•点军区一模)如图所示是由一些相同的小正方体构成的立体图形的三视图,这些相同的小正方体的个数是( ).CD .5.(3分)(2012•衢州模拟)如图,折叠直角三角形纸片的直角,使点C 落在斜边AB 上的点E 处,已知AB=8,∠B=30°,则DE 的长为( )6.(3分)如图,是某人骑自行车的行驶路程S (千米)与行驶时间t (时)的函数图象,下列说法错误的是( )7.(3分)(2009•鄂尔多斯)某闭合电路中,电源的电压为定值,电流I (A )与电阻R (Ω)成反比例.如图所示的是该电路中电流I 与电阻R 之间的函数关系的图象,则用电阻R 表示电流I 的函数解析式为( )2.CD .9.(3分)如图,在同心圆中,大圆的弦AB 切小圆于点C ,AB=8,则圆环的面积是( )10.(3分)(2003•苏州)如图,A ,B ,C ,D 四点在⊙O 上,四边形ABCD 的一条外角∠DCE=70°,则∠BOD 等于( )二、耐心填(请将你认为符合题意的答案直接写在题中的横线上,填不完整不能得分.每小题4分,共24分) 11.(4分)(2008•包头)不等式组的整数解共有 _________ 个.12.(4分)将直线y=﹣2x 平移且过点(2,0)的直线的函数的解析式是 _________ .13.(4分)已知x=,则x﹣2x+3=_________.14.(4分)(2005•苏州)如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为_________.15.(4分)(2012•东莞)分解因式:2x2﹣10x=_________.16.(4分)(2011•桂林模拟)如图,在正方形ABCD的边AB上连接等腰直角三角形,然后在等腰直角三角形的直角边上连接正方形,无限重复上述过程,如果第一个正方形ABCD的边长为1,那么第n个正方形的面积为_________.三、认真做(请认真审题,按要求进行解答,并写出详细解答过程.相信你能做的很好.共96分)17.(8分)(2013•宛城区一模)先化简,然后选取一个合适的a的值代入求值.18.(8分)(2006•大连)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是.(1)试写出y与x的函数关系式.(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为,求x和y的值.19.(8分)(2004•日照)如图,等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,AE=BE.BF⊥AE于F.判断线段BF与图中的哪条线段相等.先写出猜想,再加以证明.(1)猜想:BF=_________;(2)证明.20.(10分)计划建造乌海黄河大坝,需要测量黄河宽度,河边有笔直的滨河大道MN,路两侧是平坦地带,要求测量河的宽度.C是对岸河边的一棵树,A、B分别是滨河大道上的两点,测量结果如图所示:∠BAC=30°,∠NBC=60°,AB=600米.请你帮助计算河的宽度(结果保留根号).21.(10分)解决数学问题时经常用到平移.如图,要在一段水平宽为8米,高为4米的阶梯上铺地毯,需要购买多长的地毯?我们可以把所有水平线段向下平移,竖直方向线段向右平移.得到所需地毯长度为8米+4米=12米.请你按照这个思路解决下面问题:如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图2中阴影部分),余下的部分种草坪,要使草坪的面积为540m2,求道路的宽.22.(10分)(2006•徐州)如图,已知AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连接AC.(1)求证:△ABC∽△POA;(2)若AB=2,PA=,求BC的长.(结果保留根号)23.(10分)某工程队要招聘甲、乙两种工种的工人150名,甲、乙两种工种的工人的月工资分别为600元和1000元.现要求乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?最少工资是多少?24.(10分)(2007•茂名)某学校为了学生的身体健康,每天开展体育活动一小时,开设排球、篮球、羽毛球、体操四项体育活动课.学生可根据自己的爱好任选其中一项,老师根据学生报名情况进行了统计,并绘制了下面尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:(1)该校学生报名总人数有多少人?(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?(3)频数分布直方图补充完整.25.(10分)(2006•苏州)今年,苏州市政府的一项实事工程就是由政府投入1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户)试估计该社区需要对水龙头、马桶进行改造的家庭共有_________户;(2)改造后一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水?(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?26.(12分)(2007•安顺)如图,已知二次函数y=ax2﹣2ax+3的图象与x轴交于点A,点B,与y轴交于点C,其顶点为D,直线DC的函数关系式为y=kx+b,又tan∠OBC=1.(1)求二次函数的解析式和直线DC的函数关系式;(2)求△ABC的面积.2012年北京市中考数学模拟试卷(三)参考答案与试题解析一、精心选(每题的四个选项中只有一个是符合题意的,请将符合题意的选项字母填在相应的答题栏内,每小题3分,共30分)±D解:∵=22.(3分)(2008•点军区一模)如图所示是由一些相同的小正方体构成的立体图形的三视图,这些相同的小正方体的个数是().C D.,5.(3分)(2012•衢州模拟)如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知AB=8,∠B=30°,则DE的长为()AE=BE=AB=46.(3分)如图,是某人骑自行车的行驶路程S(千米)与行驶时间t(时)的函数图象,下列说法错误的是()7.(3分)(2009•鄂尔多斯)某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为()观察图象,函数经过一定点,将此点坐标代入函数解析式解:设反比例函数的解析式为2=,得.2.C D.>>9.(3分)如图,在同心圆中,大圆的弦AB切小圆于点C,AB=8,则圆环的面积是()AB10.(3分)(2003•苏州)如图,A,B,C,D四点在⊙O上,四边形ABCD的一条外角∠DCE=70°,则∠BOD等于()二、耐心填(请将你认为符合题意的答案直接写在题中的横线上,填不完整不能得分.每小题4分,共24分)11.(4分)(2008•包头)不等式组的整数解共有5个.的整数解为﹣12.(4分)将直线y=﹣2x平移且过点(2,0)的直线的函数的解析式是y=﹣2x+4(答案不唯一).13.(4分)已知x=,则x2﹣2x+3=5.+1(﹣﹣+114.(4分)(2005•苏州)如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为(2,0).15.(4分)(2012•东莞)分解因式:2x2﹣10x=2x(x﹣5).16.(4分)(2011•桂林模拟)如图,在正方形ABCD的边AB上连接等腰直角三角形,然后在等腰直角三角形的直角边上连接正方形,无限重复上述过程,如果第一个正方形ABCD的边长为1,那么第n个正方形的面积为.),),))=倍,及正方形的面积公式求解.找到第)三、认真做(请认真审题,按要求进行解答,并写出详细解答过程.相信你能做的很好.共96分)17.(8分)(2013•宛城区一模)先化简,然后选取一个合适的a的值代入求值.﹣]×(18.(8分)(2006•大连)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是.(1)试写出y与x的函数关系式.(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为,求x和y的值.,有成立.化简可得颗棋子,则取得黑色棋子的概率变为)根据题意得:,∴;)解法一:根据题意,得)根据题意,可得,.=19.(8分)(2004•日照)如图,等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,AE=BE.BF⊥AE于F.判断线段BF与图中的哪条线段相等.先写出猜想,再加以证明.(1)猜想:BF=DE;(2)证明.20.(10分)计划建造乌海黄河大坝,需要测量黄河宽度,河边有笔直的滨河大道MN,路两侧是平坦地带,要求测量河的宽度.C是对岸河边的一棵树,A、B分别是滨河大道上的两点,测量结果如图所示:∠BAC=30°,∠NBC=60°,AB=600米.请你帮助计算河的宽度(结果保留根号).NBC=×=300.21.(10分)解决数学问题时经常用到平移.如图,要在一段水平宽为8米,高为4米的阶梯上铺地毯,需要购买多长的地毯?我们可以把所有水平线段向下平移,竖直方向线段向右平移.得到所需地毯长度为8米+4米=12米.请你按照这个思路解决下面问题:如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图2中阴影部分),余下的部分种草坪,要使草坪的面积为540m2,求道路的宽.22.(10分)(2006•徐州)如图,已知AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连接AC.(1)求证:△ABC∽△POA;(2)若AB=2,PA=,求BC的长.(结果保留根号)PA=∴∴23.(10分)某工程队要招聘甲、乙两种工种的工人150名,甲、乙两种工种的工人的月工资分别为600元和1000元.现要求乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?最少工资是多少?24.(10分)(2007•茂名)某学校为了学生的身体健康,每天开展体育活动一小时,开设排球、篮球、羽毛球、体操四项体育活动课.学生可根据自己的爱好任选其中一项,老师根据学生报名情况进行了统计,并绘制了下面尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:(1)该校学生报名总人数有多少人?(2)从表中可知选羽毛球的学生有多少人?选排球和篮球的人数分别占报名总人数的百分之几?(3)频数分布直方图补充完整.)由两个统计图可知该校报名总人数是人,所以,人,所以,25.(10分)(2006•苏州)今年,苏州市政府的一项实事工程就是由政府投入1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户)试估计该社区需要对水龙头、马桶进行改造的家庭共有1000户;(2)改造后一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水?(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?×=1000×26.(12分)(2007•安顺)如图,已知二次函数y=ax2﹣2ax+3的图象与x轴交于点A,点B,与y轴交于点C,其顶点为D,直线DC的函数关系式为y=kx+b,又tan∠OBC=1.(1)求二次函数的解析式和直线DC的函数关系式;(2)求△ABC的面积.参与本试卷答题和审题的老师有:心若在;yangwy;fuaisu;wdxwzk;sks;zhehe;zzz;蓝月梦;MMCH;py168;zhjh;zhangCF;张长洪;sjzx;lbz;lantin;lanchong;leikun;ln_86;kuaile;CJX;ZJX;星期八;sd2011;zcx;自由人;HJJ;wenming(排名不分先后)菁优网2014年2月27日。

中考数学---几何选择填空压轴题精选1一.选择题:1.如下图1,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为()①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HE•HB.A. 1个B. 2个C. 3个D. 4个2、如上图2,梯形ABCD中,AD∥BC,,∠ABC=45°,AE⊥BC于点E,BF⊥AC于点F,交AE于点G,AD=BE,连接DG、CG.以下结论:①△BEG≌△AEC;②∠GAC=∠GCA;③DG=DC;④G为AE中点时,△AGC的面积有最大值.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个3.如上图3,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论:①EC=2DG;②∠GDH=∠GHD;③S△CDG=S▭DHGE;④图中有8个等腰三角形.其中正确的是()A.①③ B.②④ C.①④ D.②③4.如下图1,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交BD于点02,同样以AB,AO2为两邻边作平行四边形ABC2O2.…,依此类推,则平行四边形ABC2009O2009的面积为()A.B. C. D.5、如上图2,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,BN=PC.其中正确的个数是()A.1个 B.2个 C.3个 D.4个6.Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下图1,下列结论:①(BE+CF)=BC;②S△AEF ≤S△ABC;③S四边形AEDF=AD•EF;④AD≥EF;⑤AD与EF可能互相平分,其中正确结论的个数是()A.1个B.2个C.3个D.4个7.如上图2,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连接GF.下列结论①∠ADG=22.5°;②tan∠AED=2;③S△AGD =S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有()A.①④⑤B.①②④C.③④⑤D.②③④8.如上图3,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE 交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤.其中正确的结论是()A.①②③B.①②④C.①②⑤D.②④⑤9.如下图1,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有()A.①②③B.①②④C.①③④D.①②③④10.正方形ABCD、正方形BEFG和正方形RKPF的位置如上图2所示,点G在线段DK上,正方形BEFG 的边长为4,则△DEK的面积为()A. 10B. 12C. 14D. 16二.填空题1.如下图1,观察图中菱形的个数:图1中有1个菱形,图2中有5个菱形,图3中有14个菱形, 图4中有30个菱形…,则第6个图中菱形的个数是 个.2.如下图2,在△ABC 中,∠A=α.∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1; ∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2; …;∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012,得∠A 2012,则∠A 2012= .3.如下图1,已知Rt △ABC 中,AC=3,BC=4,过直角顶点C 作CA 1⊥AB ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去,得到了一组线段CA 1,A 1C 1,C 1A 2,…,则CA 1= ,= .4、如上图2,点A 1,A 2,A 3,A 4,…,A n 在射线OA 上,点B 1,B 2,B 3,…,B n ﹣1在射线OB 上, 且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ﹣1B n ﹣1,A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n ﹣1,△A 1A 2B 1,△A 2A 3B 2,…,△A n ﹣1A n B n ﹣1为阴影三角形,若△A 2B 1B 2,△A 3B 2B 3的面积分别为1、4,则△A 1A 2B 1的面为 ; 面积小于2011的阴影三角形共有 个. 5、如下图1,已知点A 1(a ,1)在直线l :上,以点A 1为圆心,以为半径画弧,交x 轴于点B 1、B 2,过点B 2作A 1B 1的平行线交直线l 于点A 2,在x 轴上取一点B 3,使得A 2B 3=A 2B 2,再过点B 3作A 2B 2的平行线交直线l 于点A 3,在x 轴上取一点B 4,使得A 3B 4=A 3B 3,按此规律继续作下去, 则①a= ;②△A 4B 4B 5的面积是 .6、如下图,在梯形ABCD中,AD∥BC,EA⊥AD,M是AE上一点,F、G分别是AB、CM的中点,且∠BAE=∠MCE,∠MBE=45°,则给出以下五个结论:①AB=CM;②A E⊥BC;③∠BMC=90°;④EF=EG;⑤△BMC是等腰直角三角形.上述结论中始终正确的序号有.7、如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为.8、如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于.9.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD =15cm2,S△BQC=25cm2,则阴影部分的面积为cm2.中考数学---几何选择填空压轴题精选1答案一.选择题:1、解:作EJ⊥BD于J,连接EF①∵BE平分∠DBC ∴EC=EJ,∴△DJE≌△ECF ∴DE=FE∴∠HEF=45°+22.5°=67.5°∴∠HFE==22.5°∴∠EHF=180°﹣67.5°﹣22.5°=90°∵DH=HF,OH是△DBF的中位线∴OH∥BF ∴OH=BF②∵四边形ABCD是正方形,BE是∠DBC的平分线,∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,∵CE=CF,∴Rt△BCE≌Rt△DCF,∴∠EBC=∠CDF=22.5°,∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,∵OH是△DBF的中位线,CD⊥AF,∴OH是CD的垂直平分线,∴DH=CH,∴∠CDF=∠DCH=22.5°,∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故②正确;③∵OH是△BFD的中位线,∴DG=CG=BC,GH=CF,∵CE=CF,∴GH=CF=CE∵CE<CG=BC,∴GH<BC,故此结论不成立;④∵∠DBE=45°,BE是∠DBF的平分线,∴∠DBH=22.5°,由②知∠HBC=∠CDF=22.5°,∴∠DBH=∠CDF,∵∠BHD=∠BHD,∴△DHE∽△BHD,∴=∴DH=HE•HB,故④成立;所以①②④正确.故选C.(第5题图)2、解:根据BE=AE,∠GBE=∠CAE,∠BEG=∠CEA可判定①△BEG≌△AEC;用反证法证明②∠GAC≠∠GCA,假设∠GAC=∠GCA,则有△AGC为等腰三角形,F为AC的中点,又BF⊥AC,可证得AB=BC,与题设不符;由①知△BEG≌△AEC 所以GE=CE 连接ED、四边形ABED为平行四边形,∵∠ABC=45°,AE⊥BC于点E,∴∠GED=∠CED=45°,∴△GED≌△CED,∴DG=DC;④设AG为X,则易求出GE=EC=2﹣X 因此,S△AGC =SAEC﹣SGEC=﹣+x=﹣(x2﹣2x)=﹣(x2﹣2x+1﹣1)=﹣(x﹣1)2+,当X取1时,面积最大,所以AG等于1,所以G是AE中点,故G为AE中点时,GF最长,故此时△AGC的面积有最大值.故正确的个数有3个.故选C.3、解:∵DF=BD,∴∠DFB=∠DBF,∵AD∥BC,DE=BC,∴∠DEC=∠DBC=45°,∴∠DEC=2∠EFB,∴∠EFB=22.5°,∠CGB=∠CBG=22.5°,∴CG=BC=DE,∵DE=DC,∴∠DEG=∠DCE,∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°,∠DGE=180°﹣(∠BGD+∠EGF)=180°﹣(∠BGD+∠BGC),=180°﹣(180°﹣∠DCG)÷2=180°﹣(180°﹣45°)÷2=112.5°,∴∠GHC=∠DGE,∴△CHG≌△EGD,∴∠EDG=∠CGB=∠CBF,∴∠GDH=∠GHD,∴S△CDG =S▭DHGE.故选D.4、解:∵矩形ABCD的对角线互相平分,面积为5,∴平行四边形ABC1O1的面积为,∵平行四边形ABC1O1的对角线互相平分,∴平行四边形ABC2O2的面积为×=,…,依此类推,平行四边形ABC2009O2009的面积为.故选B.5、解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,∴PM=BC,PN=BC,∴PM=PN,正确;②在△ABM与△ACN中,∵∠A=∠A,∠AMB=∠ANC=90°,∴△ABM∽△ACN,∴,正确;③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,∴∠ABM=∠ACN=30°,在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°,∵点P是BC的中点,BM⊥AC,CN⊥AB,∴PM=PN=PB=PC,∴∠BPN=2∠BCN,∠CPM=2∠CBM,∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,∴∠MPN=60°,∴△PMN是等边三角形,正确;(见上图)④当∠ABC=45°时,∵CN⊥AB于点N,∴∠BNC=90°,∠BCN=45°,∴BN=CN,∵P为BC边的中点,∴PN⊥BC,△BPN为等腰直角三角形;∴BN=PB=PC,正确.故选D.6、解:∵Rt△ABC中,AB=AC,点D为BC中点,∴∠C=∠BAD=45°,AD=BD=CD,∵∠MDN=90°,∴∠ADE+∠ADF=∠ADF+∠CDF=90°,∴∠ADE=∠CDF.在△AED与△CFD中,∵,∴△AED≌△CFD(ASA),∴AE=CF,在Rt△ABD中,BE+CF=BE+AE=AB==BD=BC.故①正确;设AB=AC=a,AE=CF=x,则AF=a﹣x.∵S△AEF =AE•AF=x(a﹣x)=﹣(x﹣a)2+a2,∴当x=a时,S△AEF有最大值a2,又∵S△ABC =×a2=a2,∴S△AEF≤S△ABC.故②正确;EF2=AE2+AF2=x2+(a﹣x)2=2(x﹣a)2+a2,∴当x=a时,EF2取得最小值a2,∴EF≥a(等号当且仅当x=a时成立),而AD=a,∴EF≥AD.故④错误;由①的证明知△AED≌△CFD,∴S四边形AEDF =S△AED+S△ADF=S△CFD+S△ADF=S△ADC=AD2,∵EF≥AD,∴AD•EF≥AD2,∴AD•EF>S四边形AEDF故③错误;当E、F分别为AB、AC的中点时,四边形AEDF为正方形,此时AD与EF互相平分.故⑤正确.综上所述,正确的有:①②⑤,共3个.故选C.7、解:∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG=∠ADO=22.5°,故①正确.∵tan∠AED=,由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE<AB,∴tan∠AED=>2,故②错误.∵∠AOB=90°,∴AG=FG>OG,△AGD与△OGD同高,∴S△AGD >S△OGD,故③错误.∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF=OG,∴BE=EF=×OG=2OG.故⑤正确.∴其中正确结论的序号是:①④⑤.故选:A.8、解:①由∠ABC=90°,△BEC为等边三角形,△ABE为等腰三角形,∠AEB+∠BEC+∠CEH=180°,可求得∠CEH=45°,此结论正确;②由△EGD≌△DFE,EF=GD,再由△HDE为等腰三角形,∠DEH=30°,得出△HGF为等腰三角形,∠HFG=30°,可求得GF∥DE,此结论正确;③由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD此结论不正确;④如图,过点G作GM⊥CD垂足为M,GN⊥BC垂足为N,设GM=x,则GN=x,进一步利用勾股定理求得GD=x,BG=x,得出BG=GD,此结论不正确;⑤由图可知△BCE和△BCG同底不等高,它们的面积比即是两个三角形的高之比,由④可知△BCE的高为(x+x)和△BCG的高为x,因此S△BCE :S△BCG=(x+x):x=,此结论正确;故正确的结论有①②⑤.故选C.9、解:(1)连接FC,延长HF交AD于点L,∵BD为正方形ABCD的对角线,∴∠ADB=∠CDF=45°.∵AD=CD,DF=DF,∴△ADF≌△CDF.∴FC=AF,∠ECF=∠DAF.∵∠ALH+∠LAF=90°,∴∠LHC+∠DAF=90°.∵∠ECF=∠DAF,∴∠FHC=∠FCH,∴FH=FC.∴FH=AF.(上图2)(2)∵FH⊥AE,FH=AF,∴∠HAE=45°.(3)连接AC交BD于点O,可知:BD=2OA,(上图3)∵∠AFO+∠GFH=∠GHF+∠GFH,∴∠AFO=∠GHF.∵AF=HF,∠AOF=∠FGH=90°,∴△AOF≌△FGH.∴OA=GF.∵BD=2OA,∴BD=2FG.(4)延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,根据△MEC≌△CIM,(见下图2)可得:CE=IM,同理,可得:AL=HE,∴HE+HC+EC=AL+LI+IM=AM=8.∴△CEH的周长为8,为定值.故(1)(2)(3)(4)结论都正确.故选D.10、解:如下图1,连DB,GE,FK,则DB∥GE∥FK,在梯形GDBE中,S△DGE =S△GEB(同底等高的两三角形面积相等),同理S△GKE=S△GFE.∴S阴影=S△DGE+S△GKE=S△GEB+S△GEF=S正方形GBEF=4×4=16 故选D.二.填空题:1、解:观察图形,发现规律:图1中有1个菱形,图2中有1+22=5个菱形,图3中有5+32=14个菱形,图4中有14+42=30个菱形,则第5个图中菱形的个数是30+52=55,第6个图中菱形的个数是55+62=91个.故答案为91.2、解:∵∠ABC与∠ACD的平分线交于点A1,∴∠A1BC=∠ABC,∠A1CD=∠ACD,根据三角形的外角性质,∠A+∠ABC=∠ACD,∠A1+∠A1BC=∠A1CD,∴∠A1+∠A1BC=∠A1+∠ABC=(∠A+∠ABC),整理得,∠A1=∠A=,同理可得,∠A2=∠A1=×=,…,∠A2012=.故答案为:.3、解:在Rt△ABC中,AC=3,BC=4,∴AB=,又因为CA1⊥AB,∴AB•CA1=AC•BC,即CA1===.∵C4A5⊥AB,∴△BA5C4∽△BCA,∴,∴==.所以应填和.4、解:由题意得,△A2B1B2∽△A3B2B3,∴==,==,又∵A1B1∥A2B2∥A3B3,∴===,==,∴OA1=A1A2,B1B2=B2B3继而可得出规律:A1A2=A2A3=A3A4…;B1B2=B2B3=B3B4…又△A2B1B2,△A3B2B3的面积分别为1、4,∴S△A1B1A2=,S△A2B2A3=2,继而可推出S△A3B3A4=8,S△A4B4A5=32,S△A5B5A6=128,S△A6B6A7=512,S△A7B7A8=2048,故可得小于2011的阴影三角形的有:△A1B1A2,△A2B2A3,△A3B3A4,△A4B4A5,△A5B5A6,△A6B6A7,共6个.故答案是:;6.5、解:如图所示:①将点A1(a,1)代入直线1中,可得,所以a=.②△A1B1B2的面积为:S==;因为△OA1B1∽△OA2B2,所以2A1B1=A2B2,又因为两线段平行,可知△A1B1B2∽△A2B2B3,所以△A2B2B3的面积为S1=4S;以此类推,△A4B4B5的面积等于64S=.6、解:∵梯形ABCD中,AD∥BC,EA⊥AD,∴AE⊥BC,即②正确.∵∠MBE=45°,∴BE=ME.在△ABE与△CME中,∵∠BAE=∠MCE,∠AEB=∠CEM=90°,BE=ME,∴△ABE≌△CME,∴AB=CM,即①正确.∵∠MCE=∠BAE=90°﹣∠ABE<90°﹣∠MBE=45°,∴∠MCE+∠MBC<90°,∴∠BMC>90°,即③⑤错误.∵∠AEB=∠CEM=90°,F、G分别是AB、CM的中点,∴EF=AB,EG=CM.又∵AB=CM,∴EF=EG,即④正确.故正确的是①②④.7、解:连接DB,∵四边形ABCD是菱形,∴AD=AB.AC⊥DB,∵∠DAB=60°,∴△ADB是等边三角形,∴DB=AD=1,∴BM=,∴AM==,∴AC=,同理可得AC1=AC=()2,AC2=AC1=3=()3,按此规律所作的第n个菱形的边长为()n﹣1故答案为()n﹣1.8、解:∵∠1=∠2,∠3=∠4,∴∠2+∠3=90°,∴∠HEF=90°,(见上图3)同理四边形EFGH的其它内角都是90°,∴四边形EFGH是矩形.∴EH=FG(矩形的对边相等);又∵∠1+∠4=90°,∠4+∠5=90°,∴∠1=∠5(等量代换),同理∠5=∠7=∠8,∴∠1=∠8,∴Rt△AHE≌Rt△CFG,∴AH=CF=FN,又∵HD=HN,∴AD=HF,在Rt△HEF中,EH=3,EF=4,根据勾股定理得HF=,∴HF=5,又∵HE•EF=HF•EM,∴EM=,又∵AE=EM=EB(折叠后A、B都落在M点上),∴AB=2EM=,∴AD:AB=5:=.故答案为:.9、解:如图,连接EF;∵△ADF与△DEF同底等高,∴S△ADF =S△DEF即S△ADF﹣S△DPF=S△DEF﹣S△DPF,即S△APD =S△EPF=15cm2,同理可得S△BQC=S△EFQ=25cm2,∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2.故答案为40.。

2011-2012学年北京市海淀区中考数学模拟试卷2011-2012学年北京市海淀区中考数学模拟试卷一、选择题(本题共8个小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的.D2.(4分)(2010•平谷区一模)温家宝总理在2010年3月5日的十一届全国人大第三次会议的政府工作报告中指出,3.(4分)(2011•内江)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是()4.(4分)(2012•武鸣县一模)一个几何体的三视图如图所示,这个几何体是()5.(4分)(2013•武侯区一模)小明要给刚结识的朋友小林打电话,他只记住了电话号码的前5位的顺序,后3位.C D.6.(4分)(2007•韶关)2007年5月份,某市市区一周空气质量报告中某项污染指数的数据是:31 35 31 34 30 32 31,7.(4分)(2010•福州)已知反比例函数y=(k≠0)的图象经过点(1,3),则此反比例函数的图象在()8.(4分)(2008•丽水)如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是()≤≤二、填空题(本题共16分,每小题4分)9.(4分)(2013•普洱)函数y=中,自变量x的取值范围是_________.10.(4分)(2008•无锡)如图,CD⊥AB于E,若∠B=60°,则∠A=_________度.11.(4分)(2011•石景山区二模)分解因式:8a3﹣8a2+2a=_________.12.(4分)(2012•宿迁模拟)如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11…的点作OA 的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4…则第一个黑色梯形的面积S1= _________;观察图中的规律,第n(n为正整数)个黑色梯形的面积S n=_________.三、解答题(本题共25分,每小题5分)13.(5分)(2009•黄石)求值:|﹣2|+20090﹣(﹣)﹣1+3tan30°.14.(5分)(2013•湖北模拟)解分式方程:.15.(5分)(2013•东城区二模)已知:如图,点E、F分别为▱ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.16.(5分)(2010•平谷区一模)已知x2﹣4x+3=0,求(x﹣1)2﹣2(1+x)的值.17.(5分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)求b的值;(2)不解关于x,y的方程组,,请你直接写出它的解;(3)直线l3:y=nx+m是否也经过点P?请说明理由._________.四、解答题(本题共10分,每小题5分)18.(5分)(2009•金华)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.(1)求梯形ABCD面积;(2)求图中阴影部分的面积.19.(5分)(2013•兰州)已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.五、解答题(本题共6分)20.(6分)(2009•本溪)初中生对待学习的态度一直是教育工作者关注的问题之一.为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了_________名学生;(2)将图①补充完整;(3)求出图②中C级所占的圆心角的度数;(4)根据抽样调查结果,请你估计该市近20 000名初中生中大约有多少名学生学习态度达标?(达标包括A级和B级)六、解答题(本题共9分,21小题5分,22小题4分)21.(5分)(2012•合浦县模拟)某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?22.(4分)如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α,且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.(1)在图(2)正方形ABCD内画一个半等角点P,且满足α≠β;(2)在图(3)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法).七、解答题(共22分,其中23题7分、24题8分,25题7分)23.(7分)(2013•密云县二模)已知:关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0(m为实数)(1)若方程有两个不相等的实数根,求m的取值范围;(2)在(1)的条件下,求证:无论m取何值,抛物线y=(m﹣1)x2+(m﹣2)x﹣1总过x轴上的一个固定点;(3)关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0有两个不相等的整数根,把抛物线y=(m﹣1)x2+(m ﹣2)x﹣1向右平移3个单位长度,求平移后的解析式.24.(8分)(2009•宁德)如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.(1)求P点坐标及a的值;(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.25.(7分)(2013•湖北模拟)已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:_________;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)2011-2012学年北京市海淀区中考数学模拟试卷参考答案与试题解析一、选择题(本题共8个小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的.D2.(4分)(2010•平谷区一模)温家宝总理在2010年3月5日的十一届全国人大第三次会议的政府工作报告中指出,3.(4分)(2011•内江)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是()4.(4分)(2012•武鸣县一模)一个几何体的三视图如图所示,这个几何体是()5.(4分)(2013•武侯区一模)小明要给刚结识的朋友小林打电话,他只记住了电话号码的前5位的顺序,后3位.C D.=6.(4分)(2007•韶关)2007年5月份,某市市区一周空气质量报告中某项污染指数的数据是:31 35 31 34 30 32 31,7.(4分)(2010•福州)已知反比例函数y=(k≠0)的图象经过点(1,3),则此反比例函数的图象在()y=y=中8.(4分)(2008•丽水)如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是()≤≤.所以≤OP=≤二、填空题(本题共16分,每小题4分)9.(4分)(2013•普洱)函数y=中,自变量x的取值范围是x≠2.10.(4分)(2008•无锡)如图,CD⊥AB于E,若∠B=60°,则∠A=30度.11.(4分)(2011•石景山区二模)分解因式:8a3﹣8a2+2a=2a(2a﹣1)2.12.(4分)(2012•宿迁模拟)如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11…的点作OA 的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4…则第一个黑色梯形的面积S1= 4;观察图中的规律,第n(n为正整数)个黑色梯形的面积S n=8n﹣4.(×三、解答题(本题共25分,每小题5分)13.(5分)(2009•黄石)求值:|﹣2|+20090﹣(﹣)﹣1+3tan30°.==6﹣14.(5分)(2013•湖北模拟)解分式方程:.15.(5分)(2013•东城区二模)已知:如图,点E、F分别为▱ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.16.(5分)(2010•平谷区一模)已知x2﹣4x+3=0,求(x﹣1)2﹣2(1+x)的值.17.(5分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)求b的值;(2)不解关于x,y的方程组,,请你直接写出它的解;(3)直线l3:y=nx+m是否也经过点P?请说明理由.经过.的坐标即为方程组的解;,所以四、解答题(本题共10分,每小题5分)18.(5分)(2009•金华)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.(1)求梯形ABCD面积;(2)求图中阴影部分的面积.=5=(×π=CD=25π25π)19.(5分)(2013•兰州)已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.五、解答题(本题共6分)20.(6分)(2009•本溪)初中生对待学习的态度一直是教育工作者关注的问题之一.为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了名学生;(2)将图①补充完整;(3)求出图②中C级所占的圆心角的度数;(4)根据抽样调查结果,请你估计该市近20 000名初中生中大约有多少名学生学习态度达标?(达标包括A级和B级)六、解答题(本题共9分,21小题5分,22小题4分)21.(5分)(2012•合浦县模拟)某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?,;,22.(4分)如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α,且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.(1)在图(2)正方形ABCD内画一个半等角点P,且满足α≠β;(2)在图(3)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法).七、解答题(共22分,其中23题7分、24题8分,25题7分)23.(7分)(2013•密云县二模)已知:关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0(m为实数)(1)若方程有两个不相等的实数根,求m的取值范围;(2)在(1)的条件下,求证:无论m取何值,抛物线y=(m﹣1)x2+(m﹣2)x﹣1总过x轴上的一个固定点;(3)关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0有两个不相等的整数根,把抛物线y=(m﹣1)x2+(m ﹣2)x﹣1向右平移3个单位长度,求平移后的解析式.,再根据两根之积等于﹣解方程,得是整数.24.(8分)(2009•宁德)如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.(1)求P点坐标及a的值;(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.y=m=点坐标为(,点坐标为(,)或(;y=,点坐标为(,点坐标为(,)或(,25.(7分)(2013•湖北模拟)已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:AH=AB;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)中,中,参与本试卷答题和审题的老师有:ln_86;zhjh;Linaliu;nhx600;zcx;kuaile;HLing;zhangCF;蓝月梦;心若在;lf2-9;shuiyu;张超。

2012 年中考数学压轴题100题优选(11-20题)答案【011】解:(1)证明:在Rt△FCD中,∵G为D F 的中点,∴CG= FD.⋯⋯⋯ 1分同理,在Rt△DEF 中,EG= FD .⋯⋯⋯⋯ 2分∴CG=EG.⋯⋯⋯⋯⋯⋯⋯ 3分(2 )(1 )中结论仍然成立,即EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯4证法一:连结AG,过G点作MN⊥AD 于M ,与EF 的延伸线交于N 点.在△DAG 与△DCG 中,∵AD=CD,∠ADG=∠CDG ,DG=DG ,∴△DAG≌△DCG .∴AG=CG.⋯⋯⋯⋯⋯⋯⋯⋯分⋯5在△DMG 与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴MG=NG 在矩形AENM 中,AM=EN.⋯⋯⋯⋯⋯分6在R t△AMG 与Rt△ENG 中,∵AM=EN,MG=NG ,∴△AMG≌△ENG .∴AG=EG .∴EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯证8法二:延伸CG至M,使MG=CG,连结MF,ME,E C,⋯⋯⋯⋯⋯⋯⋯⋯分4在△DCG 与△FMG 中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.∴MF∥CD∥AB.⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴5在Rt△MFE与Rt△CBE 中,∵MF=CB,EF=BE,∴△MFE ≌△CBE.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.∴△MEC为直角三角形.∵MG = CG,∴EG= MC.⋯⋯⋯ 8分(3)(1)中的结论仍旧建立,即EG=CG.其余的结论还有:EG⊥CG.⋯⋯10分OO【012】解:(1)圆心在座标原点,圆的半径为1,A、B、C、D0)B(0,1、) C(1,、0)D(0,1)A( 1,、点的坐标分别为AM、NMA、NCOC y 抛x 物线与直线交于点,且分别与圆相切于点和点,、DM 、N 1、) N(11),D(01),、M( 1,1、) N(11),M( 1 ,.点在抛物线上,将的坐标代入c 1a 1 2 1 a b cb 1,y 得:ax b解x之,c得:1 a b cc 12 y x x1·············:.·····································4 分抛物线的分析式为215 2y x x 1 x( 2 )24 1x 抛物线的对称轴为, 2115 OE ,DE 1.······················6 分242 yBF ,BFD 90连°结, D NDEOD △BFD∽△EOD,,DBFD E A O x C5 F DE ,OD ,1DB 2又,P M 2 B45 FD , 545535 EF FD DE .···············································································8 分5210P(3)点在抛物线上.·············································································b过点的直································9 分D、Cy kx设线为:,k ,1b ,1、0)D(01),y kx bC的(1坐标代入,得:,将点DCy x 1·························································10 分直线为:.·xBBPPOy过1点作圆的切线与轴平行,点的纵坐标为,x 2y 1y x将代1 入,得:.22 Px 2y x x 1 2 2 1 1 (2,,当时,,点的坐标为2Py x x 因此1 ,点在抛物线上.·············································································0该抛物线·12 分 2 y ax bx 2 ,,2)可C(设的分析式为.【013】解:(1)该抛物线过点0)B(1,0)A(4,,代入,将1 a ,16a 4b2 ,0 2得解得5a b 2.0 b .2152y x x 2 ······························(3 分)此抛物线的分析式为.·22(2)存在.··························································································································(4 分)m P 如图,设点的横坐标为,152 m m则2P点的纵坐标为,22 y1 m 4 当时,P D152PM m m 2AM ,4.m A B 22 M 1 xO 4 COA PMA 又9,0 ° E AMAO2 2时,①当 C PMOC1(第26题图)△APM∽△ACO ,15 24 m 2 m m 2 即.22 m ,2m 41) P (,2.·解得,····································································(6 分)(舍去)12AMOC1152 2(4 m) m △mA PM2∽△CAO②当时,,即.PMOA222m 4m 解5 得,(均不合题意,舍去)12 1 m 41),P.(2 ······················································,·······································(7 分)当时m 4 2)P(5,.·近似地可求出当时,·········································································(8 分)m 1 14)P( ,.3 当时,P1) 14)( ,3(2,(5,2)或.·或综上所述,符合条件的点为·································(9 分)152t t 2 DDt(0 t.(4) 3)如图,设点的横坐标为,则点的纵坐标为221y x 2DEACAC过y作轴的平行线交于.由题意可求得直线的分析式为.(10 分)215111 22 Et ,t 2 DE t t 2 t 2 点t 的2 t坐标为..·(11 分)2222211 222 S t 2t 4 t 4t .(t 2) 422 t 2△DAC1) D(2,···············································△DAC,面积最大.045AOAy x【014】(1)···········(13 分).·当时解:∵点第一次落在直线上时停止旋转,∴旋转了.2 45 2O A. ⋯⋯⋯⋯⋯分4∴在旋转过程中所扫过的面积为3602MNAC BMN BAC 45 BNM B C(A 2 4)5解:∵∥,∴,. BMN BNMBM BNBA BCAM∴.∴又∵,∴.OAOC OAM OCN OAM A O O C M N CON 又∵,,∴.∴.∴1 AOM (90 45 OABC. MNAC 过程中,当和平行时,正方形旋转的度∴旋转245 数为.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯0⋯ 8AOE 45 AOMBAEpy(3 )答:值无变化.证明:延伸交轴于点,则,000 AOE CON 90 45 AOM 45 AO M ,∴. 又∵,000 OAE 180 90 90 OCN OAE OCNOE ON,AE CN.∴.∴. 0OM OM OME OMN MOE MO y N又45 ∵,, ∴. y x E MN ME AM AEMN AM ∴.∴C N, AM p MN BN BM AM CN BN BM AB∴. B C B 4 OABCp∴在旋转正方形的过程中,值无变化. ⋯⋯⋯⋯⋯分12 xN O C (第26题)72【015】⑴设二次函数的分析式为:y=a(x-h)+k∵极点C 的横坐标为4 ,且过点(0 ,)3972∴y=a(x-4)+k ⋯⋯⋯⋯⋯3⋯①16a k又9 ∵对称轴为直线x=4,图象在x轴上截得的线段长为6 ∴A(1,0),B(7,0)332 ∴0=9a+k ⋯⋯⋯⋯⋯⋯②由①②解得a=,k=∴二次函数的分析式为:y=(x-4)--33 99⑵∵点A、B 对于直线x=4对称∴PA=PB∴PA+PD=PB+PD≥ D B∴当点P 在线段DB上时P A+PD获得最小值∴DB与对称轴的交点即为所求点P设直线x=4 与x轴交于点M∵PM∥OD ,∴∠BPM=∠BDO ,又∠PBM=∠DBO 73 3 PMBM339∴点P 的坐标为(4 ,)∴△BPM∽△BDO∴∴PM DOBO373 3 ⑶由⑴知点C(4,) ,又∵AM=3 ,∴在Rt△AMC 中,cot∠ACM= , 3 3oo∴∠ACM=60 ,∵AC=BC,Q作QN⊥x,过∴∠ACB=120 ①当点Q 在x轴上方时轴于N 假如AB=BQ,由△ABC∽△ABQ有oo BQ=6,∠QBN=60∴QN=3,BN=3,ON=10,此∠ABQ=120,则时点Q(10,),333 假如AB=AQ,由对称性知Q(-2,)33 ②当点Q 在x轴下方时,△QAB就是△ACB,此时点Q 的坐标是( 4,),3经查验,点(10,)与(-2,)都在抛物线上3333综上所述,存在这样的点Q,使为(10,)或(-2,)或△QAB∽△ABC 点Q 的坐标(4,).3333 3 y kx(k 【0)016】解:(1)设正比例函数的分析式为,11k 1y kx3 3k3),A,(3因此,解得.由于的图象过点111y x这个正比率函数的分析式为.·················································································(1 分)kk22y (k 0)y ,A(3)设反比率函数的分析式为.由于的图象过点,因此2xxk923 y k ,解9得.这个反比例函数的解析式为.········································(2 分)23x9933 y m ,B m(6)B6,(2 )由于点在的图象上,所以,则点.········(3 分)x622 y kx b(k 0)y kx设b一y次函x数分析式为.因为的图象是由平移获得的,3333 k 1y x by x,因此bB,6即.又由于的图象过点,所以32 399 6 bb y ,x 解得,一次函数的解析式为.·································(4 分)22299 y x ,DD0 (y3)由于的图象交轴于点,所以的坐标为.22 2y ax bx c(a设二0)次函数的解析式为.39 2Dy ax bx ,c 3B)6A,(3 0 ,、、和由于的图象过点,22 1 9a 3b,a c3, 2 3 b ,436a 6b c ,所以·····················(5 分)解得 2 99 c. c .2 2192y x这4x个二次函数的分析式为.····························································(6 分)2299 x y x CC,0(4)交轴于点,点的坐标是,22 151131 y6 6 6 3 3 如图3所S示,22222 A 99 3 45 18 B E4281 .O 6 3 C x 4281227 S S ,E y()x假定存在点,使.1003432 Dy x0 ECDOE,四边形的极点只能在轴上方,019919819 y y .S S001S△OCD△OCE2222284819273 y y E(x ,y) ,.在二次函数的图象上,000084221932 x 4x x .2解x 得或6.00002223 x 6x 6BCD,O E当E时6,点与点重合,这时不是四边形,故舍去,002 3 ,点E的2坐标为.(8 分)2 2y b x x c,,0)B(0 ,2)A(1 ,【017 】解:(1 )已知抛物线经过0 1 b cb 3 解得2 0 0 cc 2 2 y x 3x2··················分··所····2·······求抛物线的分析式为.·OA ,1OB 2,0)B(0,2) A(1,,(2)C(31),可得旋转后点的坐标为·································································································3 分·2x 3y x 3x 2y 2当时,由得,2y x 3x 22,)(3 可知抛物线过点Cy将原抛物线沿轴向下平移 1 个单位后过点. 2 y x 3x 1·····················分·5·平·移·后·的·抛·物·线·解·析·式············为:.·22 NNy x3x 1(x,x 3x 1() 3 )点在上,可设点坐标为0002335 2x y x 3x 1y将配x方得,其对称轴为.··································6 分224 3 y 0 x ①当时,如图①,02 S 2S △NBB△NDD B11113 1 x 2 1 00 A 222 1 O x D N D 1图①x 1 02x 3x 1 此时1 00 N(1,1) 点的坐标为·········································································································8 分.·y 3x ②当时,如图②02113 B 1 x 2 同理x 可得00222 N B C 1 A x 3 O x D 0D12x 3x 1 此1时00图②N,(31).点的坐标为N,1)(1(31) ,或综上,点的坐标为 (10)分.·2 y ax bx ,40a)C(0,4)A( 1,两点,【018】解:(1)抛物线经过a b 4a ,0a,1解得4a 3. 2 y x 3x 抛物线的分析式为. 2 m 1 m 3m 4,D(mm 1)( 2 )点在抛物线上,,y2 m 1m 3m 2m 即3,或0. D CDD 4)(,3 .点在第一象限,点的坐标为CBA 45°O A,.O B由(1)知 E DEBC设点对于直线的对称点为点. A B x C∥D ABCD 3 C,(04) O ,,且,ECB DCB,45°ECE CD 3y点在轴上,且.OE 1 ,E(10),.DBC即点对于直线对称的点的坐标为(0,1).PF⊥ABFEDE⊥BC(3 )方法一:作于,于.y OBC 4 5°OB OC,,4由(1)有:DBP 45,°CBD P.BA D C∥D OBCD 3 C,(,0 4)D(3,4) C ,且.P EDCE CBO,4 53°2 A B DE CE.xF O 2 52 BC 42 OB OC 4 C B E C E B,,,2DE3 tan PBF tan C.BD BE5PF 3tBF 5tOF 5t设4,则,,P( 5t ,43t).P点在抛物线上, 2 3t ( 5t 4) 3( 5t ,4) 4 22266 t t 0 ,(P 舍去)或,.25525 DBDPBD⊥D HxHQG⊥DHQQ 方法二:过点作的垂线交直线于点,过点作轴于.过点作G 于.yPBD ,45°QD D.B 90°QDG ,BDHD C Q G P DQG QDG 90°DQG BDH 又,. A BDG BH 1△QDG≌△DBH QG DH ,,4.x OH 4) Q( 1,3)D(3 ,,.由( 2 )知312y x BP ,0B)(,4直线的分析式为.552 2 x ,y x 3x ,4 x 4,2 5解1方程组得312y;606y x,1y 55. 2 25 266 P ,点的坐标为.525 【019】(1)EO>EC,原因以下:由折叠知,EO=EF,在Rt△EFC中,EF为斜边,∴EF>EC,故EO>EC ⋯ 2 分(2 )m为定值22222∵S=CF=EF -EC=EO -EC=(EO+EC)(EO―EC)=CO·(EO―E C C F)G H四边形S=CM·CO=|CE―EO|·CO=(EO―E·C C)O C M N O四边形S四边形CFGHm ∴1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯⋯ 4 S 四边形CMNO12121 QFC,E QF∴EF=EO= ( 3 )∵CO=1 ,33331∴cos∠FEC=∴∠FEC=60°, 2180 60 60 ,O E E A A O30 FEA三角等边∴22EQ ∴△EFQ为形,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯5 31133EQ EQ 作QI⊥EO 于I,EI=,IQ= 2323 21131 ∴(,)IO=∴Q 点坐标为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯336333 312(,)∵抛物线y=mx+bx+c过点C(0,1),Q,m=1 33b ∴3可求得,c=1 2y x 3x ∴抛1 物线分析式为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯ 7 2 AO 3EO 3 (4)由(3),3 2221 2x 3y (3) 3 3 当1时,<AB 3333231(,)∴P 点坐标为⋯⋯⋯⋯⋯⋯⋯分833121 ∴BP=AO 33 方法1:若△PBK 与△AEF相像,而△AEF≌△AEO,则分状况以下: 2 234383 B K BK (,1)(,1)时①,∴K点坐标为或 3 999 223 332 2343BK (,1)(0,1) BK②时,∴K 点坐标为或⋯⋯⋯⋯1分0 333 223 3 3 故直线K P 与y轴交点T 的坐标为571(0, 或) (0,)或(0, 或)(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯333 12 方法2:若△BPK与△AEF相像,由(3)得:P作PR⊥y轴于R,则∠RTP=60°或30°23 RT 3 2当①∠RTP=30°∠BPK=3°0或60°,过时, 3 232 3 RT 当②∠RTP=60°时,33 175T(0,),T(0, ,) T(0, ,)T(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴112234333【020】解:(1)①CF⊥BD,CF=BD ②建立,理由以下:∵∠FAD=∠BAC=9°0∴∠BAD=∠CAF又BA=CA ,AD=AF ∴△BAD≌△CAF∴CF=BD∠ACF=∠ACB=4°5∴∠BCF=90°∴CF⊥BD (1 分)(⋯2⋯)当∠ACB=4°5时可得CF⊥BC,原因以下:如图:过点 A 作AC 的垂线与CB 所在直线交于G则∵∠ACB=4°5∴AG=AC ∠AGC=∠ACG=4°5 ∵AG=AC AD=AF ⋯(⋯1⋯分)∴△GAD≌△CAF(SAS)∴∠ACF=∠AGD=4°5 ∴∠GCF=∠GCA+∠ACF=90°∴CF⊥BC ⋯(⋯⋯2分⋯)(3)如图:作AQBC 于Q ∵∠ACB=4°5AC=4 ∴CQ=AQ=4 2∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°∴△ADQ∽△DPC ⋯(1 分)PCCD∴= DQAQ 设CD为x(0 <x < 3 )则D Q=CQ -CD=4 -x 则xPC= ⋯⋯⋯⋯(1 分)44 x1212∴PC=(-x+4x)=-(x-2)+1≥1 44 当x=2时,PC最长,此时P C=1 ⋯⋯⋯(1 分)。
1、如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 1、解:(1)抛物线2(1)0)y a x a =-+≠经过点(20)A -,09a a ∴=+= ∴二次函数的解析式为:2y x x =++ (2)D为抛物线的顶点(1D ∴过D 作DN OB ⊥于N,则DN =,3660AN AD DAO =∴==∴∠=,°OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形66(s)OP t ∴=∴=②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH = (如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求AH 55(s)OP DH t ∴===③当PD OA =时,四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. · 7分 (3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则3PE =113633(62)222BCPQS t t ∴=⨯⨯⨯-⨯23363328t ⎫-⎪⎝⎭当32t =时,BCPQ S 6338∴此时3339333324444OQ OP OE QE PE ==∴=-==,=, 22223393344PQ PE QE ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭2、如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值2、解.(1)点A 的坐标为(4,8) 将A (4,8)、C (8,0)两点坐标分别代入y=ax2+bx 8=16a+4b得0=64a+8b得a=-12,b=4解∴抛物线的解析式为:y=-12x2+4x …………………3分 (2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE=PE AP =BC AB ,即PE AP =48 ∴PE=12AP=12t .PB=8-t .(第4题)∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t2+8. ∴EG=-18t2+8-(8-t) =-18t2+t.∵-18<0,∴当t=4时,线段EG 最长为2.②共有三个时刻.t1=163, t2=4013,t3= .3、如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移, 设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关t 的函数关系式,并写出相应的t 的取值范围.3、(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ∴111263622ABC C S AB y ==⨯⨯=△·.(2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,.又∵点E 在2l上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,.∴8448OE EF =-==,.(3)①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =.Rt Rt AFH AMC △∽△, ∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.4、如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
2012年北京市中考数学模拟试卷(六)2012年北京市中考数学模拟试卷(六)一、单项选择题(每小题4分,共20分,请将所选选项的字母写在题目后的括号内)2.(4分)(2013•桂林模拟)函数的自变量x的取值范围是()3.(4分)为了了解某校300名初三学生的睡眠时间,从中抽取30名学生进行调查,在这个问题中,下列说法正确4.(4分)(2009•吴江市模拟)如图,△ABC和△GAF是两个全等的等腰直角三角形,图中相似三角形(不包括全等)共有()5.(4分)(2012•藤县一模)一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这二、填空题(每小题4分,共20分,请把下列各题的正确答案填写在横线上)6.(4分)计算:﹣2﹣1+(π﹣3.142)0+2cos230°=_________.7.(4分)若x2﹣4x﹣1=(x+a)2﹣b,则|a﹣b|=_________.8.(4分)若相交两圆的半径长分别是方程x2﹣3x+2=0的两个根,则它们的圆心距d的取值范围是_________9.(4分)(2009•太原)有两把不同的锁和三把钥匙,其中两把钥匙分别能打开其中一把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率为_________.10.(4分)(2001•绍兴)如图,菱形ABCD中,对角线AC、BD交于O点,分别以A、C为圆心,AO、CO为半径画圆弧,交菱形各边于点E、F、G、H,若AC=,BD=2,则图中阴影部分的面积是_________.三、解答下列各题(每小题6分,共30分)11.(6分)解不等式组(要求利用数轴求出解集):.12.(6分)(2006•自贡)已知x=+1,求的值.13.(6分)观察下面的几个算式:13×17=221可写成100×1×(1+1)+21;23×27=621可写成100×2×(2+1)+21;33×37=1221可写成100×3×(3+1)+21;43×47=2021可写成100×4×(4+1)+21;…根据上面规律填空:(1)83×87可写成_________.(2)(10n+3)(10n+7)可写成_________.(3)计算:1993×1997=_________.14.(6分)如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B为(﹣1,﹣1).(1)把△ABC向左平移8格后得到△A1B1C1,则点B1的坐标为_________;(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,则点B2的坐标为_________;(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,则B3的坐标为_________.15.(6分)如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,∠BAD与∠CDE满足什么条件时AD=AE?写出你的推理过程.四、解答下列各题(每小题9分,共28分)16.(9分)初三年级一位学生对本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:(1)该班共有多少名学生?(2)在图①中将表示“骑车”的部分补充完整;(3)在扇形统计图中,“步行”部分对应的圆心角的度数是多少?(4)如果全年级共有300名学生,请你估算全年级骑车上学的学生人数.17.(7分)(2001•苏州)已知如图,一次函数y=kx+b的图象与反比例函数的图象相交于A、B两点.(1)利用图中条件,求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.18.(7分)某班同学到离校24千米的农场参观,一部分骑自行车的同学先走,1小时后,没有自行车的同学乘汽车出发,结果他们同时到达农场,已知汽车速度是自行车速度的3倍,求两种车的速度.19.(7分)一条船在海面上自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上.(1)请根据以上描述,画出图形.(2)已知以航标C为圆心,120米为半径的圆形区域内有浅滩,若这条船继续前进,是否有被浅滩阻碍的危险?为什么?五、解答下列各题(每小题12分,共27分)20.(12分)如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.(1)求证:DE是⊙O的切线;(2)求直径AB的长.21.(12分)(2006•兰州)如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.(1)在如图的坐标系中求抛物线的解析式;(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?22.(12分)如图所示,△OAB是边长为的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.(1)设OB′的长为x,△OB′E的周长为c,求c关于x的函数关系式;(2)当B′E∥y轴时,求点B′和点E的坐标;(3)当B′在OA上运动但不与O、A重合时,能否使△EB′F成为直角三角形?若能,请求出点B′的坐标;若不能,请说明理由.2012年北京市中考数学模拟试卷(六)参考答案与试题解析一、单项选择题(每小题4分,共20分,请将所选选项的字母写在题目后的括号内)2.(4分)(2013•桂林模拟)函数的自变量x的取值范围是()3.(4分)为了了解某校300名初三学生的睡眠时间,从中抽取30名学生进行调查,在这个问题中,下列说法正确4.(4分)(2009•吴江市模拟)如图,△ABC和△GAF是两个全等的等腰直角三角形,图中相似三角形(不包括全等)共有()5.(4分)(2012•藤县一模)一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这二、填空题(每小题4分,共20分,请把下列各题的正确答案填写在横线上)6.(4分)计算:﹣2﹣1+(π﹣3.142)0+2cos230°=2.+1+2(7.(4分)若x2﹣4x﹣1=(x+a)2﹣b,则|a﹣b|=7.8.(4分)若相交两圆的半径长分别是方程x2﹣3x+2=0的两个根,则它们的圆心距d的取值范围是1<d<39.(4分)(2009•太原)有两把不同的锁和三把钥匙,其中两把钥匙分别能打开其中一把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率为..=10.(4分)(2001•绍兴)如图,菱形ABCD中,对角线AC、BD交于O点,分别以A、C为圆心,AO、CO为半径画圆弧,交菱形各边于点E、F、G、H,若AC=,BD=2,则图中阴影部分的面积是.××AC=×==,×=2三、解答下列各题(每小题6分,共30分)11.(6分)解不等式组(要求利用数轴求出解集):.12.(6分)(2006•自贡)已知x=+1,求的值.+1=.13.(6分)观察下面的几个算式:13×17=221可写成100×1×(1+1)+21;23×27=621可写成100×2×(2+1)+21;33×37=1221可写成100×3×(3+1)+21;43×47=2021可写成100×4×(4+1)+21;…根据上面规律填空:(1)83×87可写成100×8×(8+1)+21.(2)(10n+3)(10n+7)可写成100n(n+1)+21.(3)计算:1993×1997=3980021.14.(6分)如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B为(﹣1,﹣1).(1)把△ABC向左平移8格后得到△A1B1C1,则点B1的坐标为(﹣9,﹣1);(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,则点B2的坐标为(5,5);(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,则B3的坐标为(﹣5,﹣5)或(7,7).15.(6分)如图,△ABC中,AB=AC,D、E分别是BC、AC上的点,∠BAD与∠CDE满足什么条件时AD=AE?写出你的推理过程.四、解答下列各题(每小题9分,共28分)16.(9分)初三年级一位学生对本班同学的上学方式进行了一次调查统计,图①和图②是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:(1)该班共有多少名学生?(2)在图①中将表示“骑车”的部分补充完整;(3)在扇形统计图中,“步行”部分对应的圆心角的度数是多少?(4)如果全年级共有300名学生,请你估算全年级骑车上学的学生人数.17.(7分)(2001•苏州)已知如图,一次函数y=kx+b的图象与反比例函数的图象相交于A、B两点.(1)利用图中条件,求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.)据题意,反比例函数﹣,,18.(7分)某班同学到离校24千米的农场参观,一部分骑自行车的同学先走,1小时后,没有自行车的同学乘汽车出发,结果他们同时到达农场,已知汽车速度是自行车速度的3倍,求两种车的速度.依题意得19.(7分)一条船在海面上自西向东沿直线航行,在A处测得航标C在北偏东60°方向上,前进100米到达B处,又测得航标C在北偏东45°方向上.(1)请根据以上描述,画出图形.(2)已知以航标C为圆心,120米为半径的圆形区域内有浅滩,若这条船继续前进,是否有被浅滩阻碍的危险?为什么?CAD=,五、解答下列各题(每小题12分,共27分)20.(12分)如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.(1)求证:DE是⊙O的切线;(2)求直径AB的长.21.(12分)(2006•兰州)如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.(1)在如图的坐标系中求抛物线的解析式;(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?22.(12分)如图所示,△OAB是边长为的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.(1)设OB′的长为x,△OB′E的周长为c,求c关于x的函数关系式;(2)当B′E∥y轴时,求点B′和点E的坐标;(3)当B′在OA上运动但不与O、A重合时,能否使△EB′F成为直角三角形?若能,请求出点B′的坐标;若不能,请说明理由.,而我们还可以通过∠+BE+OE=x+OB==,;E+OE=BE+OE=2+,参与本试卷答题和审题的老师有:feng;心若在;lf2-9;lanchong;sd2011;gbl210;csiya;ln_86;kuaile;zcx;hnaylzhyk;zzz;zhehe;CJX;Joyce;wdxwzk;lanyan;bjf;MMCH;Liuzhx;wdxwwzy;蓝月梦;星期八;zxw;zhjh;自由人(排名不分先后)菁优网2014年2月27日。
中考数学模拟题汇总《几何综合压轴题》练习(含答案解析)一、倍长八字共5小题1.在△ABC中,D是BC的中点,且∠BAD≠90°,将线段AB沿AD所在直线翻折,得到线段AB′,作CE//AB交直线AB′于点E.(1)如图,若AB>AC,①依题意补全图形;②用等式表示线段AB,AE,CE之间的数量关系,并证明;(2)若AB<AC,上述结论是否仍然成立?若成立,简述理由;若不成立,直接用等式表示线段AB,AE,CE 之间新的数量关系(不需证明).2.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,EF垂直平分CD,分别交AC,BC于点E,F,连接DE,DF.(1)求∠EDF的度数;(2)用等式表示线段AE,BF,EF之间的数量关系,并证明.3.如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点(不与点A,B重合),作射线C D,过点A作AE⊥CD于E,在线段AE上截取EF=EC,连接BF交CD于G.(1)依题意补全图形;(2)求证:∠CAE=∠BCD(3)判断线段BG与GF之间的数量关系,并证明.4.如图,在△ABC中,∠BAC=α,点D在边BC上(不与B,C重合),连接AD,以点A为中心,将线段AD逆时针旋转180°-α得到线段AE,连接BE.(1)∠BAC+∠DAE= °(2)取CD的中点F,连接AF,用等式表示线段AF与BE的数量关系,并证明。
5.如图,△ACB中,AC=BC,∠ACB=90°,D为边BC上一点(不与点C重合),CD<BD,点E在AD的延长线上,且ED=AD,连接BE,过点B作BE的垂线,交边AC于点F.(1)依题意补全图形;(2)求证:BE=BF;(3)用等式表示线段AF与CD的数量关系,并证明.二、一线三垂直共1小题 6.如图,在Rt △ACB 中, ∠ACB =90°,AC =BC .点D 是BC 延长线上一点,连接AD .将线段AD 绕点A 逆时针旋转90°,得到线段AE .过点E 作EF //BD ,交AB 于点F .(1)①直接写出∠AFE 的度数是____________;②求证:∠DAC =∠E ;(2)用等式表示线段AF 与DC 的数量关系,并证明.三、三线合一共1小题 7.已知:如图,OB =BA ,∠OBA =150°,线段BA 绕点A 逆时针旋转90°得到线段AC .连接BC ,OA ,OC ,过点O 作OD ⊥AC 于点D .(1)依题意补全图形;(2)求∠DOC 的度数.A B C D A B C D四、手拉手共5小题8.如图,在三角形ABC 中,AB =AC ,∠BAC <60°,AD 是BC 边的高线,将线段AC 绕点A 逆时针旋转60°得到线段AE ,连接BE 交AD 于点F .(1)依题意补全图形,写出∠CAE= °(2)求∠BAF+∠ABF 和∠FBC 的度数;(3)用等式表示线段AF ,BF ,EF 之间的数量关系,并证明.9.如图,在等边△ABC 中,将线段AC 绕点A 顺时针旋转α(0∘<α<60∘),得到线段AD ,连接CD ,作∠BAD 的平分线AE ,交BC 于E .(1)① 根据题意,补全图形;② 请用等式写出∠BAD 与∠BCD 的数量关系,并证明.(2)分别延长CD 和AE 交于点F ,用等式表示线段AF ,CF ,DF 的数量关系,并证明.10.已知:等边△ABC ,过点B 作AC 的平行线l .点P 为射线AB 上一个动点(不与点A,B 重合),将射线PC 绕点P 顺时针旋转60°交直线l 于点D .(1)如图1,点P 在线段AB 上时,依题意补全图形;①求证:∠BDP =∠PCB ;②用等式表示线段BC,BD,BP 之间的数量关系,并证明;(2)点P 在线段AB 的延长线上,直接写出线段BC,BD,BP 之间的数量关系.A B C A B C AB C11.在Rt△ABC中,∠ABC=90°,∠BAC=30°,D为边BC上一动点,点E在边AC上,CE=CD.点D关于点B 的对称点为点F,连接AD,P为AD的中点,连接PE,PF,EF.(1)如图1,当点D与点B重合时,写出线段PE与PF之间的位置关系与数量关系;(2)如图2,当点D与点B,C不重合时,判断(1)中所得的结论是否仍然成立?若成立,请给出证明,若不成立,请举出反例。
2012年全国中考数学压轴题分类解析汇编专题9:几何综合问题(答案部分)24. (2012湖北恩施12分)【答案】解:(1)证明:连接OB ,∵OB=OA,CE=CB ,∴∠A=∠OBA,∠CEB=∠ABC。
又∵CD⊥OA,∴∠A+∠AED=∠A+∠CEB=90°。
∴∠OBA+∠ABC=90°。
∴OB⊥BC。
∴BC 是⊙O 的切线。
(2)连接OF ,AF ,BF ,∵DA=DO,CD⊥OA,∴△OAF 是等边三角形。
∴∠AOF=60°。
∴∠ABF=12∠AOF=30°。
(3)过点C 作CG⊥B E 于点G ,由CE=CB , ∴EG=12BE=5。
易证Rt△ADE∽Rt△CGE, ∴sin∠ECG=sin∠A=513, ∴EG 5CE ==13sin ECG 13=∠。
∴CG 12===。
又∵CD=15,CE=13,∴DE=2,由Rt△ADE∽Rt△CGE 得AD DE CG GE =,即AD 2125=,解得24AD 5=。
∴⊙O 的半径为2AD=485。
【考点】等腰(边)三角形的性质,直角三角形两锐角的关系,切线的判定,圆周角定理,勾股定理,相似三角形的判定和性质,锐角三角函数定义。
【分析】(1)连接OB ,有圆的半径相等和已知条件证明∠OBC=90°即可证明BC 是⊙O 的切线。
(2)连接OF ,AF ,BF ,首先证明△OAF 是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF 的度数。
(3)过点C 作CG⊥BE 于点G ,由CE=CB ,可求出EG=12BE=5,由Rt△ADE∽Rt△CGE 和勾股定理求出DE=2,由Rt △ADE∽Rt△CGE 求出AD 的长,从而求出⊙O 的半径。
25. (2012黑龙江哈尔滨10分)【答案】解:(1)证明:∵BA⊥AM,MN⊥AP,∴∠BAM=ANM=90°。