2014年全国大学生数学建模竞赛深圳杯C题

日期时间SPD十分钟平均风速(m/s)风向12011/4/13 8:00 2.5西22011/4/14 8:00 1.4西32011/4/15 8:000.1西北42011/4/16 8:00 2.7东北52011/4/17 8:00 1.2东北62011/4/18 8:00 2.9南72011/4/19 8:00 2.4西82011/4/20 8:00 4.9西92011/4/21 8:00 3.7西102011/4/22 8:000.7北112011/4/23 8:00 2.2西南122011/4/24 8:00 1.2西南132011/4/25 8:000.2西142011/4/26 8:000.4北152011/4/27 8:00 1.4东南162011/4/28 8:000.9西北172011/4/29 8:00 1.6西182011/4/30 8:00 1.7北192011/5/1 8:001北202011/5/2 8:001西北212011/5/3 8:00 1.9北222011/5/4 8:00 1.8东南232011/5/5 8:002西242011/5/6 8:000.8北252011/5/7 8:00 2.5西北262011/5/8 8:00 2.8西北272011/5/9 8:00 1.7西北282011/5/10 8:00 2.3西北292011/5/11 8:00 1.1东北302011/5/12 8:001东北312011/5/13 8:00 1.6西南322011/5/14 8:00 4.2西332011/5/15 8:00 2.9西342011/5/16 8:000.3西南352011/5/17 8:00 2.1西南362011/5/18 8:00 2.5西南372011/5/19 8:00 1.8西382011/5/20 8:00 1.7西392011/5/21 8:002西402011/5/22 8:00 3.5西北412011/5/23 8:003东南422011/5/24 8:00 2.7西南432011/5/25 8:00 1.7西南442011/5/26 8:00 2.4南452011/5/27 8:00 1.9南472011/5/29 8:00 2.4西南482011/5/30 8:00 3.3西492011/5/31 8:00 1.4南502011/6/1 8:00 1.4东512011/6/2 8:000.8西522011/6/3 8:00 1.8东北532011/6/4 8:00 2.6北542011/6/5 8:00 3.2北552011/6/6 8:002东北562011/6/7 8:00 2.1东北572011/6/8 8:00 1.7东北582011/6/9 8:00 1.8北592011/6/10 8:000.9西北602011/6/11 8:00 2.3东北612011/6/12 8:00 1.6东622011/6/13 8:00 2.6北632011/6/14 8:002北642011/6/15 8:00 4.1北652011/6/16 8:00 3.3西北662011/6/17 8:003北672011/6/18 8:00 2.8西北682011/6/19 8:002西692011/6/20 8:00 1.3西南702011/6/21 8:00 3.6西南712011/6/22 8:007.2西722011/6/23 8:009.7西北732011/6/24 8:00 4.1西北742011/6/25 8:00 2.6东752011/6/26 8:00 1.4东762011/6/27 8:00 1.4东772011/6/28 8:00 1.8东北782011/6/29 8:00 5.6北792011/6/30 8:00 4.6西北802011/7/1 8:00 3.6西北812011/7/2 8:00 2.7北822011/7/3 8:00 1.9北832011/7/4 8:00 1.3东北842011/7/5 8:00 2.1东北852011/7/11 8:000.7东南862011/7/12 8:000.8西872011/7/13 8:00 2.9西882011/7/14 8:000.8西892011/7/15 8:000西902011/7/16 8:00 4.5东北912011/7/17 8:00 3.3东北922011/7/18 8:00 3.5东942011/7/20 8:00 2.9东北952011/7/21 8:00 1.1北962011/7/22 8:002北972011/7/23 8:00 1.1西北982011/7/24 8:000.8东南992011/7/25 8:00 1.7东1002011/7/26 8:00 1.3北1012011/7/27 8:00 1.7西南1022011/7/28 8:00 2.1南1032011/7/29 8:00 4.4西1042011/7/30 8:00 4.2西1052011/7/31 8:00 1.5西1062011/8/1 8:00 1.4东南1072011/8/2 8:000.5东1082011/8/3 8:00 1.6东1092011/8/4 8:00 3.6东北1102011/8/5 8:000.7东南1112011/8/6 8:000.4东北1122011/8/7 8:000.5东1132011/8/8 8:000.2东南1142011/8/9 8:000.6北1152011/8/10 8:00 2.3西北1162011/8/11 8:00 1.4西北1172011/8/12 8:00 1.7西北1182011/8/13 8:000.9北1192011/8/14 8:001东北1202011/8/15 8:00 1.3东北1212011/8/16 8:001东北1222011/8/17 8:00 2.1西1232011/8/18 8:00 2.6西北1242011/8/19 8:00 1.5西1252011/8/20 8:00 1.4西1262011/8/21 8:001南1272011/8/22 8:000.2东南1282011/8/23 8:00 1.4东北1292011/8/24 8:00 1.7东北1302011/8/25 8:00 1.1南1312011/8/26 8:00 2.1西南1322011/8/27 8:00 2.9西南1332011/8/28 8:00 1.9南1342011/8/29 8:00 3.5东南1352011/8/30 8:00 2.8东南1362011/8/31 8:00 3.4东南1372011/9/1 8:00 2.6东南1382011/9/2 8:000.4东1392011/9/3 8:00 1.1西北1412011/9/5 8:000.1东南1422011/9/6 8:00 1.1西北1432011/9/7 8:00 2.2西1442011/9/8 8:00 1.8西南1452011/9/9 8:00 2.2西1462011/9/10 8:00 2.7西1472011/9/11 8:00 3.6西南1482011/9/12 8:00 3.2西1492011/9/13 8:00 2.2西南1502011/9/14 8:00 1.8西1512011/9/15 8:00 2.5西1522011/9/16 8:00 1.9西南1532011/9/17 8:00 2.1南1542011/9/18 8:00 2.4西1552011/9/19 8:00 1.9西南1562011/9/20 8:003西南1572011/9/21 8:00 4.1西南1582011/9/22 8:00 4.2西南1592011/9/23 8:00 2.8西南1602011/9/24 8:00 4.2西南1612011/9/25 8:00 3.5西南1622011/9/26 8:00 4.2西1632011/9/27 8:000.7西南1642011/9/28 8:00 3.3西南1652011/9/29 8:008西1662011/9/30 8:00 4.9西1672011/10/1 8:00 5.9西1682011/10/2 8:00 3.6西南1692011/10/3 8:00 6.4西南1702011/10/4 8:00 3.3西南1712011/10/5 8:00 3.8西南1722011/10/6 8:00 2.8西南1732011/10/7 8:00 2.2西南1742011/10/8 8:00 2.5西南1752011/10/9 8:00 1.6西南1762011/10/10 8:00 2.4西南1772011/10/11 8:00 2.9西南1782011/10/12 8:00 3.9西1792011/10/13 8:00 3.5西1802011/10/14 8:00 2.9西南1812011/10/15 8:00 3.8西南1822011/10/16 8:00 2.6西南1832011/10/17 8:00 2.1西南1842011/10/18 8:00 2.5西南1852011/10/19 8:00 3.6西1862011/10/20 8:00 2.8西南1882011/10/22 8:00 1.8西南1892011/10/25 8:00 3.4西南1902011/10/26 8:00 3.6西南1912011/10/27 8:00 4.4西1922011/10/28 8:00 2.4西南1932011/10/29 8:00 1.7西南1942011/10/30 8:00 2.9西南1952011/10/31 8:00 4.5西1962011/11/1 8:00 2.7西南1972011/11/2 8:002西南1982011/11/3 8:00 1.6南1992011/11/4 8:00 2.6西2002011/11/5 8:00 1.5西南2012011/11/6 8:00 2.3西南2022011/11/7 8:00 2.7西南2032011/11/8 8:00 3.4西南2042011/11/12 8:000北2052011/11/13 8:00 2.2西南2062011/11/14 8:00 2.5西南2072011/11/15 8:00 2.6西南2082011/11/16 8:00 2.1西南2092011/11/17 8:00 2.1西南2102011/11/18 8:000.8西2112011/11/19 8:002南2122011/11/20 8:00 3.1西南2132011/11/21 8:00 3.6西南2142011/11/22 8:00 2.8西南2152011/11/23 8:00 4.5西南2162011/11/24 8:00 3.8西南2172011/11/25 8:00 2.8西南2182011/11/26 8:00 3.7西南2192011/11/27 8:00 1.1西南2202011/11/28 8:00 2.4西2212011/11/29 8:00 2.4西2222011/11/30 8:00 1.5西南2232011/12/1 8:00 4.4南2242011/12/2 8:00 4.7南2252011/12/3 8:00 2.5南2262011/12/4 8:00 3.3西南2272011/12/5 8:00 2.9西2282011/12/6 8:00 2.2西2292011/12/7 8:00 2.9西南2302011/12/8 8:00 5.8南2312011/12/9 8:00 5.5南2322011/12/10 8:00 5.4南2332011/12/11 8:004南2352011/12/13 8:00 2.1西南2362011/12/14 8:00 1.7南2372011/12/15 8:003西南2382011/12/16 8:005西南2392011/12/17 8:00 3.3西南2402011/12/18 8:00 3.6西南2412011/12/19 8:00 2.8西南2422011/12/20 8:00 2.5西南2432011/12/21 8:00 3.2西南2442011/12/22 8:004南2452011/12/23 8:003西南2462011/12/24 8:00 5.6西南2472011/12/25 8:004西南2482011/12/26 8:00 3.4西南2492011/12/27 8:00 2.8西2502011/12/28 8:00 1.4南2512011/12/29 8:004西2522011/12/30 8:00 3.2西南2532012/1/1 8:00 2.6西南2542012/1/4 8:00 5.5西南2552012/1/18 8:00 3.1西2562012/1/19 8:00 2.1西2572012/1/20 8:00 4.5西2582012/1/21 8:00 4.4西2592012/1/22 8:00 4.6西南2602012/1/23 8:00 3.9西南2612012/1/24 8:00 4.3西南2622012/1/25 8:00 4.3南2632012/1/26 8:00 3.9西南2642012/1/27 8:00 2.8西南2652012/1/28 8:00 2.3西南2662012/1/29 8:002西南2672012/1/30 8:00 3.3西南2682012/1/31 8:00 3.6西南2692012/2/1 8:00 3.1西2702012/2/2 8:00 3.9西南2712012/2/3 8:00 3.3西南2722012/2/4 8:00 3.5西2732012/2/5 8:003西2742012/2/6 8:00 3.2西2752012/2/7 8:00 4.4南2762012/2/8 8:004西南2772012/2/9 8:004西2782012/2/10 8:00 2.7西南2792012/2/11 8:00 3.5西南2802012/2/12 8:00 2.4西南2822012/2/14 8:00 2.1西2832012/2/15 8:00 1.5西南2842012/2/16 8:00 3.2西南2852012/2/17 8:00 4.1西南2862012/2/18 8:00 4.1西南2872012/2/19 8:00 4.4西南2882012/2/20 8:00 1.5西南2892012/2/21 8:003西2902012/2/22 8:00 3.1西2912012/2/23 8:00 2.1西北2922012/2/24 8:00 3.6西北2932012/2/25 8:00 3.3西南2942012/2/26 8:00 4.7西南2952012/2/27 8:00 4.4西南2962012/2/28 8:00 2.3西南2972012/2/29 8:00 5.8西南2982012/3/1 8:00 2.5西南2992012/3/2 8:00 2.7西3002012/3/3 8:00 4.9西3012012/3/4 8:004西3022012/3/5 8:003西北3032012/3/6 8:00 3.7西北3042012/3/7 8:00 3.7西北3052012/3/8 8:00 4.9西3062012/3/9 8:00 3.7西南3072012/3/10 8:00 3.7西南3082012/3/11 8:003西南3092012/3/12 8:00 3.8西南3102012/3/13 8:00 2.7西南3112012/3/14 8:00 2.7西南3122012/3/15 8:00 5.9西3132012/3/16 8:00 2.1西3142012/3/17 8:00 1.5西3152012/3/18 8:000.4西南3162012/3/19 8:00 4.7西3172012/3/20 8:003西3182012/3/21 8:00 3.9西3192012/3/22 8:00 2.4西3202012/3/23 8:000.8西南3212012/3/24 8:00 5.1西南3222012/3/25 8:00 2.5西南3232012/3/26 8:00 3.1西南3242012/3/27 8:00 4.9西3252012/3/28 8:00 3.4西3262012/3/29 8:003西3272012/3/30 8:00 2.6西。

答卷编号（参赛学校填写）：答卷编号（竞赛组委会填写）：论文题目：（同时标明A、B、C、D、E、F）C组别：(填写本科生、专科生)本科生参赛学校：(必填)北华大学报名序号：（可以不填）参赛队员信息(必填)：答卷编号（竞赛组委会填写）：评阅情况（省赛评阅专家填写）：省赛评阅1：省赛评阅2：省赛评阅3：省赛评阅4：省赛评阅5：题目垃圾焚烧厂的经济补偿问题：（1）根据焚烧炉的排放符合国家新的污染物排放标准和垃圾焚烧厂周边环境，设计一种环境指标监测方法，实现对垃圾焚烧厂烟气排放及相关环境影响状况的动态监控。

以环境动态监控体系实际监控结果为依据，设计合理的周围居民风险承担经济补偿方案。

（2）由于各种因素焚烧炉的除尘装置损坏或出现其他故障导致污染物的排放增加，致使相关各项指标将严重超标属等排放超标，请在考虑故障发生概率的情况下修正你设计的监测方法和补偿方案。

摘要本问题针对“垃圾围城”问题，首先我们对垃圾的分布状况进行分析，明确垃圾在地方的产生量，根据实际情况对垃圾进行分类处理剔除可回收垃圾和有害垃圾后将剩余垃圾在焚烧炉中焚烧处理，既可避免垃圾填埋侵占大量的土地，又可利用垃圾焚烧产生的能量进行发电等获得可观的经济效益。

然而，由于监管不力，致使运营过程中产生大量环境污染物，引起一些地区的群众对此项工程产生怀疑和不支持，因此我们准本设计一个建立垃圾焚烧厂对周围居民承担风险的经济补偿方案。

针对问题（1）我们首先利用EXCEL和SPSS统计软件对各种污染物进行统计处理，再用MATLAB软件绘制出烟气排放统计图，依据HJ--2.2，高斯烟雨，偏微分，利用求得相应权重，给予经济补偿，评价范围以焚烧垃圾厂烟筒底部中心坐标为中心点，建立监测系统，分别以100m,200m,300m…为半径建立污染物监控站点，对垃圾焚烧厂周围的空气进行24小时实时监控。

将监测结果与所给附件1中的标准进行对比。

若该环境动态监测结果符合国家新的污染物排放标准，则不用补偿；若超标，则在经过以下综合分析后，得出合理的周围居民风险承担经济补偿方案计采样频率:1.依浓度分布的时间特性2.依气象条件变化的特征，按高中低浓度，提高监测数据要求的精确程度例如：日平均浓度，每隔2－4h采样一次采样时间和采样频率表监测项目采样时间和频率二氧化硫隔日采样，每天24±0.5小时，每年12个月氮氧化物同二氧化硫总悬浮颗粒物隔双日采样，每天连续24±0.5小时，每月5－6天，每年12个月灰尘自然降尘量每月采样30±2天，每年12个月硫速盐化速率每月采样30±2天，每年12个月根据所得数据实施垃圾焚烧厂周围的环境监测，进而评估对周围居民承担的经济风险针对问题（2）由于各种因素焚烧炉的除尘装置（如袋式除尘器）损坏或出现其他故障导致污染物的排放增加，致使相关各项指标将严重超标（如：烟尘浓度、二氧化硫、氮氧化物、一氧化碳、二恶英类及重金属等排放超标，层次分析，建立了双层规划法的模型，要计算迭代次数，和最优解，根据故障发生概率和上问中解决的问题，及相应数据，附件2给出了一台可处理垃圾350吨/天的焚烧炉正常运作时的在线排放监测记录和监控情况增加一定补偿金额关键词：EXCEL SPSS MATLAB 统计图HJ--2.2 坐标系样方法高斯烟雨偏微分双层规划法层次分析模型一、问题重述垃圾焚烧是现在垃圾处理的主要方式，不仅可以有效减少垃圾存放量，而且可以再生能源发电，但是获得这些好处的同时，也会带来一些不利影响，就是对于居住在垃圾焚烧厂周围的居民产生一定的安全隐患，一些有害物质会影响他们的身体健康，因此我们做个课题研究在进行科学定量分析的基础上，确立一套可行的垃圾焚烧厂环境影响动态监控评估方法，并针对潜在环境风险制定出合理的经济补偿方案，具体要解决的问题有：（1）假定焚烧炉的排放符合国家新的污染物排放标准，根据对周围环境各种有害物质的监测，及地理天气，建筑对染污物扩散的影响设计一种环境指标监测方法，实现对垃圾焚烧厂烟气排放及相关环境影响状况的动态监控（2）根据上面设计的环境动态监控体系实际监控结果为依据，设计合理的周围居民风险承担经济补偿方案。

2014年厦门理工学院数学建模竞赛2014年4月26日－5月26日题目：垃圾焚烧厂的经济补偿问题厦门理工学院创新创业园厦门理工学院应用数学学院垃圾焚烧厂的经济补偿问题摘要本文针对深圳市某地点拟建一个垃圾焚烧厂，要求制定一套环境动态评估体系，并设计合理的周围居民潜在环境风险承担经济赔偿方案这一问题，根据题目提供的位置坐标及相关监测数据，通过多方面搜集关于空气质量监测、环境影响评估及预测和社会赔偿体制的资料，综合考虑地理环境、人口分布、经济状况等各方面因素并运用数理统计知识分析相关数据后，得到后文所述的数学模型，该模型很好的结合了该地自然及人文的实际情况，对相关部门制定相关政策具有很强的参考意义，因此具有很强的实用性和合理性，可以很好的运用到实际生活中。

针对问题一“根据垃圾焚烧厂周边环境设计一种环境指标监测方法，实现对垃圾焚烧厂烟气排放及相关环境影响状况的动态监控”，我们根据题目提供的坐标（焚烧厂地点为Google地图经纬度22.686033，114.097586）用“谷歌地球”经行定位确定其位置为中国广东省深圳市宝安区白鸽湖路67号。

鉴于该地地形较为平整，但功能分区较为复杂，而污染源较为单一集中，因此采用同心圆布点法和功能分区布点法相结合的布点方法选取了周围10km范围内13个重要居民区和水源地作为监测点，以SO2、NOx、二恶英等六种大气污染物进行监测。

先参考国家相关标准制定了一套评价标准，再结合多种因素综合作用的结果，运用加权函数给出了各个区域环境影响分指数的计算方法，从而建立了模型一。

根据题目要求“以你设计的环境动态监控体系实际监控结果为依据，设计合理的周围居民风险承担经济补偿方案”，我们结合各区域环境影响情况和垃圾焚烧厂的收益情况，参照当地政府的财政预算，以不同百分比从现金补偿、公共设施建设等五个方面做出了具体的总体赔偿方案，然后再结合不同区域居民承担的潜在风险不同将现金补偿部分做出更加细致的分配方案，从而建立了模型二。

精品资料全国大学生数学建模大赛c题........................................输油管的布置模型摘要建造炼油厂时要综合各方面的情况，对输油管线作周密的布置，因为输油管线的不同布置将直接影响总费用的多少。

某油田计划在铁路线一侧建造两家炼油厂，为了方便运送成品油，需在铁路线上增建一个车站。

此种模式具有一定的普遍性，油田设计院希望建立管线建设费用最省的一般数学模型与方法。

对于问题1,综合考虑铺设时，不同生产能力造成的输油管线标准不同和是否有共用管线以及共用管线与非共用管线费用同异等问题，建立模型：n y p y b a x m y b a x Z ⨯+⨯-+-+⨯-+-=21222121)()()()(min结合模型建立过程的流程图，用图形结合法和比较分析法来确定可能出现的各种情形，通过赋值，得出不同情况下的最优化模型。

对于问题2,考虑到城区必须的拆迁和工程补偿等附加费用，建立优化模型：my k m y b c l m y y c x y a x Z ⨯++⨯-+-+⨯-+-+-+=)()(()())()()((min 20220222用Lingo 软件求解，得出：车站应建在离炼油厂A 所在线5.45km ，且共用管线1.85km 时费用最少，最少费用为=min Z 282.70（万元）。

对于问题3,是在问题2 的基础上，做进一步改进，将问题2中的特殊模型一般化，建立优化模型：322022202122)()()()()()(min m y k m y b c l m y y c x m y a x Z ⨯++⨯-+-+⨯-+-+⨯-+=用Lingo 软件求解，得出：车站应建在离A 炼油厂所在线6.73km ，且共用管线0.14km 时费用最少，最少费用为：=min Z 252.00（万元）。

关键词:数形结合 Lingo 程序 优化方案 最小费用1、问题的提出1.1基本情况某油田计划在铁路线一侧建造两家炼油厂同时在铁路线上增建一个车站，用来运送成品油。

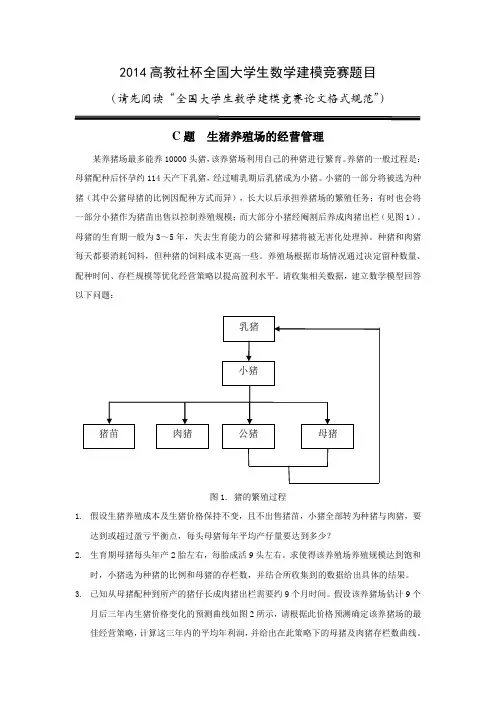
2014高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）
C题生猪养殖场的经营管理
某养猪场最多能养10000头猪，该养猪场利用自己的种猪进行繁育。

养猪的一般过程是：母猪配种后怀孕约114天产下乳猪，经过哺乳期后乳猪成为小猪。

小猪的一部分将被选为种猪（其中公猪母猪的比例因配种方式而异），长大以后承担养猪场的繁殖任务；有时也会将一部分小猪作为猪苗出售以控制养殖规模；而大部分小猪经阉割后养成肉猪出栏（见图1）。

母猪的生育期一般为3～5年，失去生育能力的公猪和母猪将被无害化处理掉。

种猪和肉猪每天都要消耗饲料，但种猪的饲料成本更高一些。

养殖场根据市场情况通过决定留种数量、配种时间、存栏规模等优化经营策略以提高盈利水平。

请收集相关数据，建立数学模型回答以下问题：
图1. 猪的繁殖过程
1.假设生猪养殖成本及生猪价格保持不变，且不出售猪苗，小猪全部转为种猪与肉猪，要
达到或超过盈亏平衡点，每头母猪每年平均产仔量要达到多少？
2.生育期母猪每头年产2胎左右，每胎成活9头左右。

求使得该养殖场养殖规模达到饱和
时，小猪选为种猪的比例和母猪的存栏数，并结合所收集到的数据给出具体的结果。

3.已知从母猪配种到所产的猪仔长成肉猪出栏需要约9个月时间。

假设该养猪场估计9个
月后三年内生猪价格变化的预测曲线如图2所示，请根据此价格预测确定该养猪场的最佳经营策略，计算这三年内的平均年利润，并给出在此策略下的母猪及肉猪存栏数曲线。

横坐标说明：以开始预测时为第一年，D2表示第二年，依次类推。

2014年深圳杯数学建模A题D目录一、问题重述..................................................... １二、问题分析..................................................... １2.1............................................................ １2.2............................................................ ２三、模型假设..................................................... ２四、符号说明..................................................... ３五、模型的建立与求解............................................. ４5.1人口发展总量的中长期预测模型................................ ４5.1.1模型的建立.............................................. ４5.1.2模型的求解.............................................. ５5.2吉林省人口城镇化的研究与分析................................ ８5.2.1吉林省人口城镇化时空路径................................ ８5.2.2吉林省人口结构分析...................................... ９5.2.3吉林省人口城镇化发展特点.............................. １１5.2.4吉林省人口城镇化发展中人口就业结构与产业结构比例不适应１４5.3城镇化进程中的劳动力供给及就业竞争........................ １４5.4城镇化进程中的教育发展.................................... １５六、结果分析................................................... １５七、模型检验与评价............................................. １６7.1对多区域离散型人口发展模型(方案一)的检验.................. １６7.2对基于1.8总和生育率的方案二的检验........................ １６7.3模型优点................................................. １６7.4模型不足................................................. １６7.5改进方向................................................. １６参考文献....................................................... １７一、问题重述人口数量的多少不仅影响国民经济发展，也影响社会稳定、生产安排、劳动力就业以及资源的可持续利用等重要方面因素。

2014高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题嫦娥三号软着陆轨道设计与控制策略嫦娥三号于2013年12月2日1时30分成功发射，12月6日抵达月球轨道。

嫦娥三号在着陆准备轨道上的运行质量为2.4t，其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力，其比冲（即单位质量的推进剂产生的推力）为2940m/s，可以满足调整速度的控制要求。

在四周安装有姿态调整发动机，在给定主减速发动机的推力方向后，能够自动通过多个发动机的脉冲组合实现各种姿态的调整控制。

嫦娥三号的预定着陆点为19.51W，44.12N，海拔为-2641m。

嫦娥三号在高速飞行的情况下，要保证准确地在月球预定区域内实现软着陆，关键问题是着陆轨道与控制策略的设计。

其着陆轨道设计的基本要求：着陆准备轨道为近月点15km，远月点100km的椭圆形轨道；着陆轨道为从近月点至着陆点，其软着陆过程共分为6个阶段，要求满足每个阶段在关键点所处的状态；尽量减少软着陆过程的燃料消耗。

根据上述的基本要求，请你们建立数学模型解决下面的问题：（1）确定着陆准备轨道近月点和远月点的位置，以及嫦娥三号相应速度的大小与方向。

（2）确定嫦娥三号的着陆轨道和在6个阶段的最优控制策略。

（3）对于你们设计的着陆轨道和控制策略做相应的误差分析和敏感性分析。

根据计划，嫦娥三号将在北京时间12月14号在月球表面实施软着陆。

嫦娥三号如何实现软着陆以及能否成功成为外界关注焦点。

目前，全球仅有美国、前苏联成功实施了13次无人月球表面软着陆。

北京时间12月10日晚，嫦娥三号已经成功降轨进入预定的月面着陆准备轨道，这是嫦娥三号“落月”前最后一次轨道调整。

在实施软着陆之前，嫦娥三号还将在这条近月点高度约15公里、远月点高度约100公里的椭圆轨道上继续飞行。

期间，将稳定飞行姿态，对着陆敏感器、着陆数据等再次确认，并对软着陆的起始高度、速度、时间点做最后准备。

A 最优行驶轨迹
设一艘轮船经一强水流区域。

水流方向是已知的位置函数
(,),V u u x y y h
==- (,)0,v v x y ==
式中x 和y 为直角坐标；
u 和v 分别是水流在x 和y 方向的速度分量；V 是轮船相对水的速度，为一常数；h 为恒值。

1. 试建立数学模型，讨论如何驾驶轮船，使得船以最短时间从起点（003.66, 1.86x y h h ==-）驾驶到（0,0f f x y h h ==）
； 2. 模拟出船行驶的相应轨迹。

B题：“大球时代”乒乓球直径与赛事观赏性2000年，国际乒乓球联合会（简称国际乒联）将国际乒乓球职业赛事中的官方用球直径由38mm增加至40mm。

其宗旨在于进一步增加球在空中运行中的空气阻力，减缓比赛中球运行的速度，从而达到进一步增加和丰富乒乓球职业运动员击球技术和技巧的目的，最终增加乒乓球赛事的整体观赏性。

然而自乒乓球“大球时代”到来迄今为止，关于用球直径的争议始终未有停止。

国内外各界教练和运动员褒贬不一。

值得注意的事，由于职业运动员身高，打球习惯，握拍习惯的不同，其对球直径变化的敏感度也颇有差异。

请通过建模分析当前的比赛用球直径是否较之“小球时代”提升了运动员的体验质量和观众的观赏质量？请通过建模进一步分析您认为的最佳乒乓球直径的长度？。

2013年“认证杯”数学中国数学建模网络挑战赛
第一阶段
C题公路运输业对于国内生产总值的影响分析
交通运输作为国民经济的载体，沟通生产和消费，在经济发展中扮演着极其重要的角色。

纵观几百年来交通运输与经济发展的相互关系，生产水平越高，就越要求基础结构超前发展。

工业化时期的基础结构，已经不允许交通运输滞后。

进入现代化社会，经济社会对交通运输的要求本质上就是超前的，交通运输是国民经济的先行官，发展经济，交通先行，是经济发展的内在规律。

公路运输是在公路上运送旅客和货物的运输方式，是交通运输系统的组成部分之一，主要承担中短途客货运输。

发展公路运输对国内生产总值（GDP）增长的贡献产生于交通建设和客货运输两个阶段，表现为公路运输对国民经济的直接贡献、波及效果、对于相关行业的直接消费以及创造就业机会等几个方面。

某省的统计部门想通过调查研究的方法估计公路运输业对于GDP的影响，通过随机发放问卷，获得了附件1中所示的数据，该数据为真实调查得到的原始数据。

请参照该数据完成如下问题：
问题1请你建立合理的数学模型，估计该省公路运输业对于GDP的影响。

问题2考虑所获得数据的情况，如果由你来设计调查项目，为了能够提高问题1中模型的精度，需要对现有的调查项目做哪些调整，并请陈述理由。

1。

2021高教社杯全国大学生数学建模比赛C题评阅要点[说明]本要点仅供参考, 各赛区评阅组应根据对题目的理解及学生的解答, 自主地进行评阅。

本题要求根据生猪预测价格, 建立大型生猪养殖场的经营管理模型, 从而求出较合理的经营管理策略。

本题目主要考察学生对一个涉及因素较多且随时间动态变化的实际问题的建模功底, 以及根据这个模型作出合理决策的功底。

问题1. 最小平均产仔量问题本问题关键是建立收支平衡方程, 然后根据此方程求出每头母猪每年平均产仔量与各种成本参数以及生猪价格参数之间的关系, 有明确的最终关系表达式为佳。

评阅时需注意有无遗漏收入或成本因素的情形。

本问不要求给出具体数值结果。

问题2. 最大规模平衡态问题本问题主要是根据养殖场规模, 计算小猪转化为母猪的比例, 使达到最大养殖规模且保持动态平衡。

在求数值结果时, 需要对母猪生育年限作出具体约定, 从而结果有一定的变化范围, 小猪转化为母猪的比例应当在0. 8%~2%之间较为合理, 母猪存栏数在1000头左右问题3. 经营管理模型及策略问题本问题要求在已知9个月后预测价格条件下, 寻求养殖场较合理的经营管理策略, 这是本题的核心问题。

应有明确的优化策略。

母猪存栏数以及育龄母猪配种率直接影响大约9个月后的生猪存栏数, 从而影响利润率, 所以这是本问题要考虑的关键因素。

在利用题目所给的生猪价格预测曲线时, 预测区间取为9个月较为切合实际。

并且, 预测价格与实际价格之间肯定存在一定的偏差, 加入在建模时能够将这种偏差纳入策略挑选考虑, 则更佳。

评阅时应考察各种成本参数取值是否在合理范围内, 以及猪苗出售价格是否合理。

在参数合理取值的条件下, 平均年利润的合理范围大约为: 400万~700万, 过低则优化不足, 过高应检查假定及参数取值是否过于脱离实际。

解决本问题的方法之一是: 建立分时段的母猪、小猪及肉猪数量之间的递推关系式, 然后通过仿真比较不同策略下的利润率, 寻求较合理的经营管理策略。

相关程序代码●污染物浓度分布clear all;[x,y]=meshgrid(0:20:5000,-2000:20:2000); %设定网格%Q=4943.7*3;%SO2的源强%Q=6448*3; %NOx的源强Q=3008.6*3; %烟尘的源强sigy=0.08*x.*(1+0.0001*x).^(-0.5);%y方向烟气扩散系数sigz=0.06*x.*(1+0.0015*x).^(0.5);%z方向烟气扩散系数H=80+[ 255.763 255.763 323.966 303.718 156.758 161.983 323.966 211.282];%泄漏源有效高度u=1./[1.9 1.8 1.5 1.6 3.1 2.9 3 2.6];%各个方向的速度f=[ 0.384146341 0.082317073 0.042682927 0.070121951 0.067073171 0.0792682930.240853659 0.033536585];%风频s=size(u);%计算u的元素个数，以便设置循环次数for i=1:s(2)Qpi=3*Q./(pi*u(i)*sigy.*sigz+eps);%计算公式第一部分ex1=exp(-0.5*(y./(sigy+eps)).^2);%计算公式第二部分ex2=exp(-0.5*((H(i)+80)./(sigz+eps).^2));%计算公式第三部分X1(:,:,i)=Qpi.*ex1.*ex2*f(i);%计算扩散气体浓度高维数组endX=X1;for j=2:s(2)X(:,:,j)=X(:,:,(j-1))+X(:,:,j);%计算扩散气体浓度高维数组各二维数组之和endX2=1000000*X(:,:,s(2));%计算求和后最终扩散气体浓度mesh(x,y,X2);xlabel('x轴向距离(m)'),ylabel('y轴向距离(m)'),zlabel('烟尘气体扩散浓度（mg/m3）'),title('焚烧炉污染物浓度分布图');●修正高斯模型后污染物分布和扩散function eformat short eQ1=9; Q2=14.8; Q3=19.3; Q4=1.358*10^(-5); %污染物源强x=0:1:2000;y=-350:1:350;[x,y]=meshgrid(x,y);arfa1=0.929; arfa2=0.931; gama1=0.111; gama2=0.126;sigmay=gama1*x.^arfa1; %垂直于主导风方向的横向扩散系数sigmaz=gama2*x.^arfa2; %铅直扩散系数height1=43; height2=123; %气象台测风仪所在的高度、烟囱出口处高度(与height1有相同高度基准)H=80; windspeed=3; %排气筒距地面几何高度、邻近气象台(站)height1高度五年平均风速envirmentspeed=windspeed*(height2/height1)^0.15; %烟囱出口处环境平均风速u=15; D=4; %烟气出口风速、烟囱直径smokeT=365.5; environmentT=296.15; %烟气出口温度、环境大气温度pressure=1005.6; emissionrate=188.5; %大气压力、实际排烟率ditaT=smokeT-environmentT;Qh=0.35*pressure*emissionrate*ditaT/smokeT; %烟气热释放率if windspeed<1.5 ; %烟气抬升高度ditaH=5.5*Qh^0.25*0.0198^(-3/8);elseif Qh<1700 || ditaT<35;ditaH=2*(1.5*u*D+0.01*Qh)/envirmentspeed;elseif Qh<2100;ditaH1=2*(1.5*u*D+0.01*Qh)/envirmentspeed-0.048*(Qh-1700)/envirmentspeed;ditaH2=0.332*Qh^(3/5)*H^(2/5)/envirmentspeed;ditaH=ditaH1+(ditaH2-ditaH1)*(Qh-1700)/400;elseif Qh<21000;ditaH=0.332*Qh^(3/5)*H^(2/5)/envirmentspeed;elseditaH=1.427*Qh^(1/3)*H^(2/3)/envirmentspeed;endHe=H+ditaH;sigmay ;sigmaz;ans0=exp((-y.^2)./(2*(sigmay.^2)))./(2*pi*u*sigmay.*sigmaz); %为便于计算而引入a=1.2*10^(-5); b=0.5; impulse=0.22; %a,b 为经验系数、impulse为雨强A=a*impulse^b; %冲洗系数Rain=exp(-A*x/u); %雨洗作用下的源强修正量ans1=exp(-He^2./(2*sigmaz.^2));concentration1=Q1*Rain.*ans0*2.*ans1; %固体颗粒在地面上的浓度concentration2=Q2*Rain.*ans0*2.*ans1; %SOx 在地面上的浓度concentration3=Q3*Rain.*ans0*2.*ans1; %NOx 在地面上的浓度Thalf=717120; %二恶英的半衰期Radiation=exp(-0.693*x/(Thalf*u)); %含有放射物质时的源强修正量rou=1.35; g=9.8; diameter=0.00002; niu=1.8*10^(-5); %粒子密度、重力加速度、粒子直径、空气的动力粘性系数dripspeed=rou*g*diameter^2/(18*niu); %沉降速度ans2=exp(-(-He+dripspeed*x/u).^2./(2*sigmaz.^2));ans3=exp(-(He-dripspeed*x/u).^2./(2*sigmaz.^2));concentration4=0.8*Q4*Rain.*Radiation.*ans0.*(ans2+0.5*ans3)+0.2*Q4*Rain.*Radiation.*ans0 *1.5.*ans1; %二恶英在地面的浓度figure(1);mesh(x,y,concentration1);title('烟尘浓度变化曲线');xlabel('风向上的距离(m)'); %增加x轴ylabel('风向上的距离(m)');zlabel('烟尘浓度(g/m^3)');figure(2);mesh(x,y,concentration2);title('SO2浓度变化曲线');xlabel('风向上的距离(m)'); %增加x轴ylabel('风向上的距离(m)');zlabel('SO2浓度(g/m^3)');figure(3);mesh(x,y,concentration3);title('NOx变化曲线');xlabel('风向上的距离(m)'); %增加x轴ylabel('风向上的距离(m)');zlabel('NOx(g/m^3)');figure(4);hold on;title('二恶英浓度变化曲线');xlabel('风向上的距离(m)'); %增加x轴ylabel('风向上的距离(m)');zlabel('二恶英浓度(g/m^3)');mesh(x,y,concentration4);●.太阳高度角的计算d=input('一年中序数'); e=114.097586;%纬度f=22.686033;%经度t=input('北京时间,h');m=360*d/365;a=0.006918-0.399912*cos(m)+0.070257*sin(m)-0.006758*cos(2*m)+0.000907*sin(2*m)-0.0026 97*cos(3*m)+0.001480*sin(3*m);p=a*180/pi;%太阳倾角h0=asin(sin(e)*sin(p)+cos(e)*cos(p)*cos(15*t+f-300));%太阳高度角h0●污染物扩散距离a=xlsread('E:\数学建模\模拟\垃圾处理\污染源1_点源计算结果.xlsx');%数据详细见附件6 a(:,2)=[]x=a(:,3);y1=a(:,4);y2=a(:,5);y3=a(:,6);plot(x,y1);figureplot(x,y2);figureplot(x,y3);。

垃圾焚烧厂的补偿问题——2014“深圳杯”数学建模夏令营
C题评述
边馥萍
【期刊名称】《数学建模及其应用》
【年(卷),期】2014(003)003
【摘要】垃圾焚烧厂造成污染物的补偿问题是由深圳环保部门提出的.参加2014年“深圳杯”的同学们在研究此问题时,给出了不同的模型,分析了对污染物实行动态监控、选择最优监控点等问题,设计了周围居民的经济补偿方案.本文仅对参加夏令营C组讨论的学生代表队所提交的论文给出简单评述.
【总页数】3页(P67-69)
【作者】边馥萍
【作者单位】天津大学理学院,天津300072
【正文语种】中文
【中图分类】O29
【相关文献】
1.计划生育政策调整对人口数量的影响——2014“深圳杯”数学建模夏令营A题评述 [J], 周义仓
2.计划生育政策调整对人口数量的影响—2014“深圳杯”数学建模夏令营A题评述 [J], 周义仓;
3.基因组组装问题建模——2014“深圳杯”数学建模夏令营B题评述 [J], 邓明华;
4.垃圾焚烧厂的补偿问题——2014“深圳杯”数学建模夏令营C题评述 [J], 边馥萍;
5.基因组组装问题建模——2014“深圳杯”数学建模夏令营B题评述 [J], 邓明华因版权原因，仅展示原文概要，查看原文内容请购买。

2014“深圳杯”数学建模夏令营题目
全国大学生数学建模竞赛组委会
【期刊名称】《数学建模及其应用》
【年(卷),期】2014(003)003
【摘要】A题:计划生育政策调整对人口数量、结构及其影响的研究人口的数量和结构是影响经济社会发展的重要因素。

20世纪70年代后期以来,我国鼓励晚婚晚育,提倡一对夫妻生育一个孩子。

该政策实施30多年来,有效地控制了我国人口的过快增长,对经济发展和人民生活的改善做出了积极的贡献。

但另一方面,其负面影响也开始显现。

如小学招生人数(1995年以来)、高校报名人数(2009年以来)逐年下降,劳动人口绝对数量开始步入下降通道,人口抚养比的相变时刻即将到来。

这些对经济社会健康、可持续发展将产生一系列影响。

【总页数】3页(P57-58,63)
【作者】全国大学生数学建模竞赛组委会
【作者单位】
【正文语种】中文
【相关文献】
1.2015“深圳杯”数学建模夏令营题目简述 [J], ;
2.2015“深圳杯”数学建模夏令营题目简述 [J],
3.2014年“深圳杯”数学建模夏令营将在深圳举行 [J], 本刊编辑部;
4.2014“深圳杯”数学建模夏令营题目 [J], ;
5.2012年'深圳杯”全国大学生数学建模夏令营竞赛题目 [J], ;
因版权原因，仅展示原文概要，查看原文内容请购买。