eviews 联立方程模型
- 格式:ppt
- 大小:502.50 KB
- 文档页数:105

联立方程模型_Eviews 案例操作1.下面建立一个包含3个方程的中国宏观经济模型,已经判断消费方程式恰好识别的,投资方程是过度识别的。
对模型进行估计。
样本观测值见表6.101211012t t t t t t t t t t t C Y C u I Y u Y I C G αααββ−=+++⎧⎪=++⎨⎪=++⎩表6.1中国宏观经济数据单位:亿元年份Y I C G 年份Y I C G 197836061378175946919912128075171031634471979407414742005595199225864963 612460376819804551159023176441993345011499815682382119814901158126047161 994466911926120810662019825489176028688611995585112387726945768919836076 200531838881996683302686732152931119847164246936751020199774894284583485 511581198587923386458981719987900329546369211253619861013338465175111219 998267330702393341263719871178443225961150120008934132500428961394519881 47045495763315762001985933746145898152341989164666095852418472001107514423554853516624199018320644491132763(1用狭义的工具变量法估计消费方程选取方程中未包含的先决变量G 作为内生解释变量Y 的工具变量,过程如下:结果如下:所以,得到结构参数的工具变量法估计量为: 012ˆˆˆ582.27610.2748560.432124ααα===,,(2用间接最小二乘法估计消费方程消费方程中包含的内生变量的简化式方程为: 1011112120211222t t t t t t t tC C G Y C G πππεπππε−−=+++⎧⎨=+++⎩参数关系体系为:11121210012012122000παπαπααππαπ−−=⎧⎪−−=⎨⎪−=⎩用普通最小二乘法估计,结果如下:所以参数估计量为:101112ˆˆˆ1135.937,0.619782, 1.239898πππ===202122ˆˆˆ2014.368,0.682750, 4.511084πππ===所以,得到间接最小二乘估计值为: 12122ˆˆ0.274856ˆπαπ==211121ˆˆˆˆ0.432124απαπ=−=010120ˆˆˆˆ582.2758απαπ=−=(3用两阶段最小二乘法估计消费方程第一阶段使用普通最小二乘法估计内生解释变量的简化方程,得到1ˆ2014.3680.68275 4.511084t t tY C G −=++用Y 的预测值替换消费方程中的Y ,过程如下:得到预测值,然后使用工具变量法进行估计。



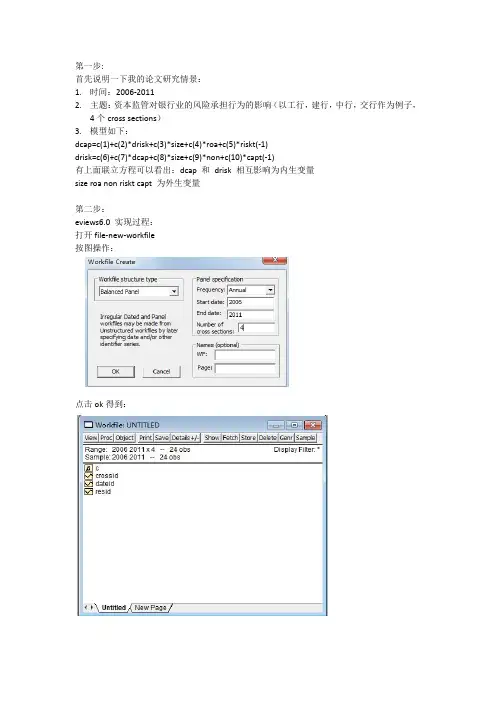
第一步:首先说明一下我的论文研究情景:1.时间:2006-20112.主题:资本监管对银行业的风险承担行为的影响(以工行,建行,中行,交行作为例子,4个cross sections)3.模型如下:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)有上面联立方程可以看出:dcap 和drisk 相互影响为内生变量size roa non riskt capt 为外生变量第二步:eviews6.0 实现过程:打开file-new-workfile按图操作:点击ok得到:点击object-new objectType选pool,ok:跳出的横框:Cross Section Identifiers 填入数据变量名称:(这是纵轴的)GSYHJSYHZGYHJTYH(前面提及的四大银行)然后点view-spreadsheet(stacked data)series list小框输入(这是横轴的变量名称)dcap drisk size roa non riskt capt点击edit+/- 手动输入数据或用import导入数据或粘贴复制进去也行:此时点object-new object,这次type选择system 用以联立方程分析:在system框内输入联立方程和工具变量:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)inst dcap drisk size roa non riskt(-1) capt(-1)点右上方的estimate,method选择TSLS(两阶段最小二乘估计):整个过程就是先建立workfile再建立panel data最后建立联立方程systemTSLS估计即可。


第一步:首先说明一下我的论文研究情景:1.时间:2006-20112.主题:资本监管对银行业的风险承担行为的影响(以工行,建行,中行,交行作为例子,4个cross sections)3.模型如下:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)有上面联立方程可以看出:dcap 和drisk 相互影响为内生变量size roa non riskt capt 为外生变量第二步:eviews6.0 实现过程:打开file-new-workfile按图操作:点击ok得到:点击object-new objectType选pool,ok:跳出的横框:Cross Section Identifiers 填入数据变量名称:(这是纵轴的)GSYHJSYHZGYHJTYH(前面提及的四大银行)然后点view-spreadsheet(stacked data)series list小框输入(这是横轴的变量名称)dcap drisk size roa non riskt capt点击edit+/- 手动输入数据或用import导入数据或粘贴复制进去也行:此时点object-new object,这次type选择system 用以联立方程分析:在system框内输入联立方程和工具变量:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)inst dcap drisk size roa non riskt(-1) capt(-1)点右上方的estimate,method选择TSLS(两阶段最小二乘估计):整个过程就是先建立workfile再建立panel data最后建立联立方程systemTSLS估计即可。
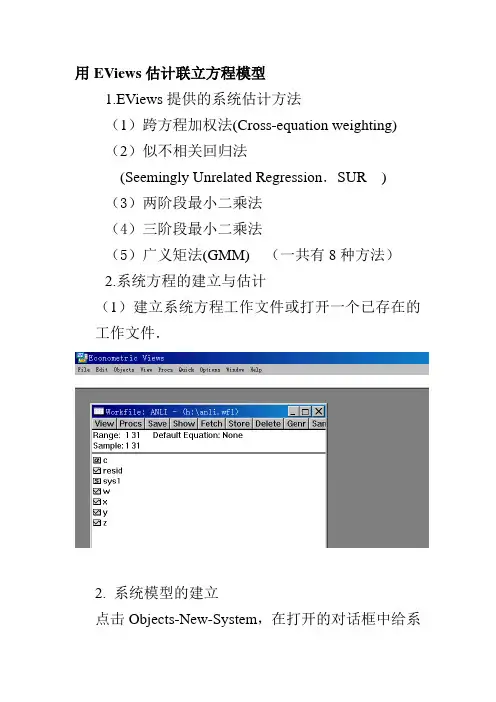
用EViews估计联立方程模型1.EViews提供的系统估计方法(1)跨方程加权法(Cross-equation weighting)(2)似不相关回归法(Seemingly Unrelated Regression.SUR ) (3)两阶段最小二乘法(4)三阶段最小二乘法(5)广义矩法(GMM) (一共有8种方法)2.系统方程的建立与估计(1)建立系统方程工作文件或打开一个已存在的工作文件.2. 系统模型的建立点击Objects-New-System,在打开的对话框中给系统方程命名.点击OK出现如图所视的对话框,然后可以将系统方程直接键入窗口.系统方程中的方程应当是行为方程式(需要估计参数的方程).例如包含两个方程的系统方程,可以在对话框中输入如下的方程3. 估计方程点击系统窗口工具栏中Estimate功能键,出现如下对话框如果选择两阶段最小二乘法,应在方程对话框中在键入工具变量y=c(1)+c(2)*x+c(3)*y(-1)+c(4)*zx=c(5)+c(6)*y+c(7)*z(-1)INST Y Y(-1) X Z对话框提供了8种估计方法,选择两阶段最小二乘法,点击OK.得到如下的输出结果System: UNTITLEDEstimation Method: Two-Stage Least Squares Date: 11/23/05 Time: 19:47 Sample: 2 248Included observations: 247Total system (balanced) observations 494 C(1) -860.3344 293.0996 -2.935297 0.0035 C(2) 0.155681 0.034374 4.529044 0.0000 C(3) 0.832925 0.020329 40.97300 0.0000 C(4) 1941557. 690610.1 2.811365 0.0051 C(5) 7569.148 219.1231 34.54290 0.0000 C(6) 0.532777 0.057813 9.215462 0.0000 Equation: Y=C(1)+C(2)*X+C(3)*Y(-1)+C(4)*Z Observations: 247 R-squared0.990558 Mean dependent var 1942.944 Adjusted R-squared 0.990441 S.D. dependent var 226.2892 S.E. of regression 22.12439 Sum squared resid 118945.8 Equation: X=C(5)+C(6)*Y+C(7)*Z(-1)Observations: 247 R-squared0.981143 Mean dependent var 5197.016 Adjusted R-squared 0.980989 S.D. dependent var 523.0837 S.E. of regression 72.12362 Sum squared resid 1269243. 根据输出结果中的数据对模型进行检验 联立模型系统的练习1 简述联立模型的识别条件;估计方法及方法所适用的条件。



实验2:联立方程模型的估计1实验目的1)通过实验加深对课堂讲授知识的理解,化解繁杂的计算过程。
2)熟练使用计算机和Eviews软件进行计量分析,了解联立方程模型的识别和估计的原理,掌握常用的估计、检验方法。
3)独立地建立和应用计量经济学模型及方法来研究实际的经济问题。
2实验软件EViews 53实验数据下表是1978年—2003年我国宏观经济历史数据,表中给出了国民生产总值GDP,消费C,投资I,政府支出G(单位:亿元)。
年份Y C I G19783605.62239.11377.9480197940742619.41474.261419804551.32976.1159065919814901.43309.1158170519825489.23637.91760.277019836076.34020.5200583819847164.44694.52468.6102019858792.1577333861184198610132.8654238461367198711784.77451.2432214901988147049360.15495172719891646610556.560952033199018319.511365.264442252199121280.413145.975172830199225863.715952.196363492.3199334500.720182149984499.7199446690.72679619260.65986.2199558510.533635238776690.5199668330.440003.926867.27851.6199774894.243579.428457.68724.8199879003.346405.929545.99484.8199982673.149722.730701.610388.3200089340.954600.932499.811705.3200198592.958927.437460.813029.32002107897.662798.542304.913916.92003121511.467422.551382.7147644实验内容及其步骤1、设定模型为:消费方程:C t = 0 + 1Y t + 2 C t-1+ u1t投资方程:I t = 0 + 1 Y t+ 2 I t-1 + u2t收入方程;Y t = C t + I t + G t2、判断消费方程、投资方程均为过度识别,用两阶段最小二乘法进行估计未知参数。
联立方程模型(simultaneous-equations model )13.1 联立方程模型的概念有时由于两个变量之间存在双向因果关系,用单一方程模型就不能完整的描述这两个变量之间的关系。
有时为全面描述一项经济活动只用单一方程模型是不够的。
这时应该用多个方程的组合来描述整个经济活动。
从而引出联立方程模型的概念。
联立方程模型:对于实际经济问题,描述变量间联立依存性的方程体系。
联立方程模型的最大问题是E(X 'u ) ≠ 0,当用OLS 法估计模型中的方程参数时会产生联立方程偏倚,即所得参数的OLS 估计量βˆ是有偏的、不一致的。
给出三个定义:内生变量(endogenous variable ):由模型内变量所决定的变量。
外生变量(exogenous variable ):由模型外变量所决定的变量。
前定变量(predetermined variable ):包括外生变量、外生滞后变量、内生滞后变量。
例如:y t = α0 + α1 y t -1 + β0 x t + β1 x t -1 + u ty t 为内生变量;x t 为外生变量;y t -1, x t , x t -1为前定变量。
联立方程模型必须是完整的。
所谓完整即“方程个数 ≥ 内生变量个数”。
否则联立方程模型是无法估计的。
13.2 联立方程模型的分类(结构模型,简化型模型,递归模型) ⑴结构模型(structural model ):把内生变量表述为其他内生变量、前定变量与随机误差项的方程体系。
例:如下凯恩斯模型(为简化问题,对数据进行中心化处理,从而不出现截距项) c t = α1 y t + u t 1 消费函数, 行为方程(behavior equation ) I t = β1 y t + β2 y t-1 + u t 2 投资函数, 行为方程 y t = c t + I t + G t国民收入等式,定义方程(definitional equation ) (1)其中,c t 消费;y t 国民收入;I t 投资;G t 政府支出。