杨氏弹性模量测量-HainanUniversity
- 格式:doc
- 大小:156.50 KB
- 文档页数:10

杨氏模量的测量【实验目的】1.1.掌握螺旋测微器的使用方法。
2.学会用光杠杆测量微小伸长量。
3.学会用拉伸法金属丝的杨氏模量的方法。
【实验仪器】杨氏模量测定仪(包括:拉伸仪、光杠杆、望远镜、标尺),水准器,钢卷尺,螺旋测微器,钢直尺。
1、金属丝与支架(装置见图1):金属丝长约0.5米,上端被加紧在支架的上梁上,被夹于一个圆形夹头。
这圆形夹头可以在支架的下梁的圆孔内自由移动。
支架下方有三个可调支脚。
这圆形的气泡水准。
使用时应调节支脚。
由气泡水准判断支架是否处于垂直状态。
这样才能使圆柱形夹头在下梁平台的圆孔转移动时不受摩擦。
2、光杠杆(结构见图2):使用时两前支脚放在支架的下梁平台三角形凹槽内,后支脚放在圆柱形夹头上端平面上。
当钢丝受到拉伸时,随着圆柱夹头下降,光杠杆的后支脚也下降,时平面镜以两前支脚为轴旋转。
图1 图2 图33、望远镜与标尺(装置见图3):望远镜由物镜、目镜、十字分划板组成。
使用实现调节目镜,使看清十字分划板,在调节物镜使看清标尺。
这是表明标尺通过物镜成像在分划板平面上。
由于标尺像与分划板处于同一平面,所以可以消除读书时的视差(即消除眼睛上下移动时标尺像与十字线之间的相对位移)。
标尺是一般的米尺,但中间刻度为0。
【实验原理】1、胡克定律和杨氏弹性模量固体在外力作用下将发生形变,如果外力撤去后相应的形变消失,这种形变称为弹性形变。
如果外力后仍有残余形变,这种形变称为塑性形变。
应力:单位面积上所受到的力(F/S )。
应变:是指在外力作用下的相对形变(相对伸长∆L/L )它反映了物体形变的大小。
用公式表达为:24F L FL Y S L d L π=⋅=∆∆ (1)2、光杠杆镜尺法测量微小长度的变化在(1)式中,在外力的F 的拉伸下,钢丝的伸长量∆L 是很小的量。
用一般的长度测量仪器无法测量。
在本实验中采用光杠杆镜尺法。
初始时,平面镜处于垂直状态。
标尺通过平面镜反射后,在望远镜中呈像。
实验4-2 金属杨氏弹性模量的测量(刘白鸽)【实验目的】1. 掌握不同长度测量器具的选择和使用方法; 2. 掌握用光杠杆测长度微小变化量的原理和方法; 3. 学会用逐差法和作图法处理数据。
【关键词】杨氏弹性摸量 光杠杆放大法 望远镜 逐差法 作图法 【实验原理】设金属丝的原长L ,横截面积为S ,在轴向拉力F 的作用下伸长了L ∆,定义单位长度的伸长量L L ∆称为应变,单位横截面积所受的力SF则称为应力。
根据胡克定律,在弹性限度内,应变与应力成正比关系,即LLES F ∆= (1) 式中比例常数E 称为杨氏弹性模量,简称杨氏摸量,常用单位为2N/m 。
杨氏模量仅与材料的性质有关,其大小表征金属抗形变能力的强弱,数值上等于产生单位应变的应力。
若实验测出在外力F 作用下钢丝的伸长量L ∆,则就能算出钢丝的杨氏模量LS FLE ∆=(2) 式中F 、L 和S 都比较容易测定,而长度的微小变化量L ∆则很难用通常测长仪器准确地度量。
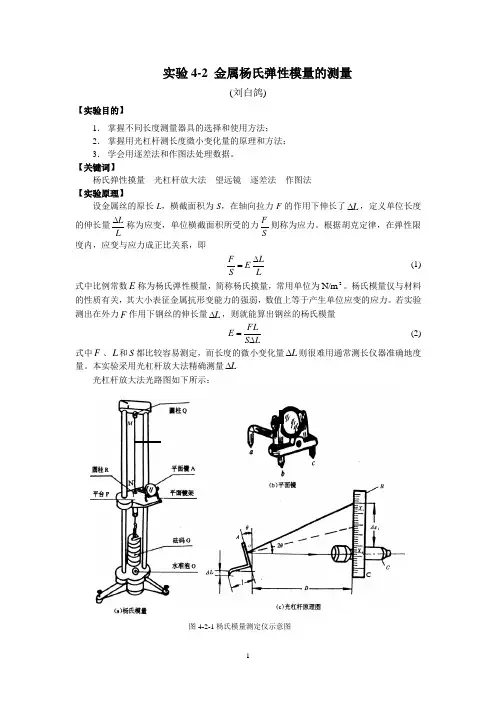
本实验采用光杠杆放大法精确测量L ∆光杠杆放大法光路图如下所示:图4-2-1杨氏模量测定仪示意图C当钢丝下端加上砝码使其伸长L ∆时,平面镜后足尖a 随之下降,平面镜绕bc 轴转过一微小角度θ,这时从标尺i x 处发出的光线经反射镜反射后进入望远镜,从望远镜中观测到的读数变为i x 。
由图4-2-1(c)可知,入射光和反射光的夹角为θ2。
由于θ角很小,所以l L ∆=≈θθtg Dx x i |2tg 20-=≈θθ于是有02x x DlL i -=∆ (3) 式中D 为镜面到标尺的距离。
可见利用光杠杆装置测量长度微小变化量的原理是:将长度微小变化量L ∆经平面镜转变为微小角度变化θ,再经尺读望远镜转变为刻度尺上较大范围的读数变化量||0x x i -,通过测量||0x x i -实现对长度微小变化量L ∆的测量。
lD2=β放大倍数 数据处理公式: 逐差法:mx l d Dm gL E 28π=作图法 :m lE d DgLx x i 208π=- 【实验仪器】杨氏模量测定仪、砝码、螺旋测微器、米尺、钢板尺等【实验内容】 (略)【数据处理】[]2222100.4)15.212.2()14.212.2()06.212.2(151-⨯=-++-+--=m X S (cm ) 因5=n 95.0=p 查表24.1)1(=-nn t p ()mm 2.02⨯=∆仪故 22222104.6)04.0(24.1)1(-⨯=+=∆+⎥⎦⎤⎢⎣⎡-=)(仪m m mx x p x S S n n t U (cm)()cm U x x m x m m 07.012.2±=±=螺旋测微器测量钢丝直径(6次)(mm)005.00-=d 单位:mmmm 606.06161==∑=i iddcm 50.65=L cm 80.7=l cm 20.31=A cm 15.62=Acm 14850)20.315.6(210021=⨯-=-=A A D 21162N/m 1099.10212.00780.0)103676.0(1415.36550.0794.9548.188⨯=⨯⨯⨯⨯⨯⨯⨯⨯==-m x l d DmgL E π不确定度E U 的计算[](mm)1029.2108.4)606.0607.0()606.0607.0()610.0606.0(51)(16136222612--⨯=⨯=-+-+-=--=∑ d dS id(mm)106.4004.0108.432622--⨯=+⨯=∆+=仪d d S U cm 2=D U cm 2.0=L U cm 05.0=l U222222⎪⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=mx d l D L E x U d U l U D U L U E U m 其中:622103.950.652.0-⨯=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛L U L 422108.11482-⨯=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛D U D522101.480.705.0-⨯=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛l U l 42104.22-⨯=⎪⎭⎫ ⎝⎛d U d422100.912.2064.0-⨯=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛m xx U m将上式不确定各分项代入E U E式中:2107.3-⨯=EU E 2111111N/m 1008.010073.0037.01099.1⨯≈⨯=⨯⨯=⨯=EU E U EE 测量结果的最终表达式:()211N/m 1008.099.1⨯±=E 根据(5)公式: m lEd DgLx x i 208π=- 作图m x i ~(图略) 作图比例:cm/cm20.0:cm 17kg/cm 500.0:cm 25)轴()轴(i x m kg cm 417.082==lEd DgLk π斜率 代入公式 2112N/m 1002.28⨯==lkd DgLE π 由讲义P272附表7可知:碳钢211N/m 1010.2~00.220⨯=︒)(时的杨氏摸量标E c实验结果与其基本吻合。

学生姓名: 学号: 专业班级: 班级编号:试验时间: 时 分 第 周 星期 座位号: 教师编号: 成绩:杨氏模量的测定【实验目的】1. 掌握用光杠杆测量微小长度变化的原理和方法,了解其应用。
2. 掌握各种长度测量工具的选择和使用。
3. 学习用逐差法和作图法处理实验数据。
【实验仪器】MYC-1型金属丝杨氏模量测定仪(一套)、钢卷尺、米尺、螺旋测微计、重垂、砝码等。
【实验原理】 一、杨氏弹性模量设金属丝的原长L ,横截面积为S ,沿长度方向施力F 后,其长度改变ΔL ,则金属丝单位面积上受到的垂直作用力F/S 称为正应力,金属丝的相对伸长量ΔL/L 称为线应变。
实验结果指出,在弹性范围内,由胡克定律可知物体的正应力与线应变成正比,即LL Y S F ∆= (1)则LL SF Y ∆=(2) 比例系数Y 即为杨氏弹性模量。
在它表征材料本身的性质,Y 越大的材料,要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。
Y 的国际单位制单位为帕斯卡,记为Pa (1Pa =12m N ;1GPa =910Pa )。
本实验测量的是钢丝的杨氏弹性模量,如果钢丝直径为d ,则可得钢丝横截面积S42d S π=则(2)式可变为L d FLY ∆=24π (3)可见,只要测出式(3)中右边各量,就可计算出杨氏弹性模量。
式中L (金属丝原长)可由米尺测量,d (钢丝直径),可用螺旋测微仪测量,F (外力)可由实验中钢丝下面悬挂的砝码的重力F=mg 求出,而ΔL 是一个微小长度变化(在此实验中 ,当L ≈1m时,F 每变化1kg 相应的ΔL 约为0.3mm)。
因此,本实验利用光杠杆的光学放大作用实现对钢丝微小伸长量ΔL 的间接测量。
二、光杠杆测微小长度变化尺读望远镜和光杠杆组成如图2所示的测量系统。
光杠杆系统是由光杠杆镜架与尺读望远镜组成的。
光杠杆结构见图2(b )所示,它实际上是附有三个尖足的平面镜。
三个尖足的边线为一等腰三角形。

应用干涉法测量杨氏弹性模量
花世群;骆英;花世荣;牛险峰
【期刊名称】《半导体光电》
【年(卷),期】2007(28)6
【摘要】将空气劈尖的等厚干涉原理与CCD图像处理技术相结合,提出了一种对材料杨氏弹性模量进行高精度自动测量的新方法。
该方法利用待测试件受力产生的形变改变空气劈尖顶角,并用一元线性回归方法对CCD的像元序号与所接收到的干涉条纹光强极大值序号之间线性关系进行拟合,进而确定出空气劈尖顶角大小。
由导出的杨氏弹性模量与空气劈尖顶角变化量之间的关系,对待测试件的杨氏弹性模量进行了计算。
测量结果表明,新的测量方法是可行的,测量相对误差为1.5%,而且测量系统具有高精度、高灵敏度的特点,可广泛应用于各种微小形变的测量。
【总页数】4页(P897-900)
【关键词】光学测量;杨氏弹性模量;干涉;图像处理
【作者】花世群;骆英;花世荣;牛险峰
【作者单位】江苏大学理学院;海安百协锻锤有限公司
【正文语种】中文
【中图分类】TG113.25
【相关文献】
1.用拉仲法测量金属丝杨氏弹性模量实验误差分析及改进 [J], 李颖
2.数字激光散斑法测量杨氏弹性模量的实验设计 [J], 汪涛;蔡小龙;李远;梁欢
3.用读数显微镜法测量发丝的杨氏弹性模量 [J], 赵莹; 罗旺; 李奇楠
4.基于SPSS的拉伸法测量金属丝杨氏弹性模量实验数据处理 [J], 张燕
5.用拉伸法测量金属丝杨氏弹性模量实验误差分析及改进 [J], 李颖
因版权原因,仅展示原文概要,查看原文内容请购买。


实验二 动力学共振法测定材料的杨氏弹性模量杨氏弹性模量(杨氏模量)是固体材料的重要力学参量,它标志者材料抵抗力产生拉伸(或压缩)形变的能力,是选择机械构件材料的依据之一。
测定杨氏模量的方法有静态拉伸法和动力学共振法。
前者常用于大形变、常温下的测量。
但由于静态拉伸法载荷大,加载速度慢,有驰豫过程,而不能真实地反应材料内部结构的变化,它既不适用于对脆性材料的测量,也不能测量材料在不同温度时的杨氏模量。
动力学共振法不仅克服了前者的缺陷,而且更具有实用价值,它也是国家GB/T2105-91所推荐使用的测量方法。
本实验采用当前工程技术常用的“动力学共振法”测量杨氏弹性模量。
其基本方法是:将一根截面均匀的试样(棒)悬挂在两只传感器(一只激振,一只拾振)下面,在两端自由的条件下,使之作自由振动,测出试样的固有基频,并根据试样的几何尺寸、密度参数,测得材料的杨氏弹性模量。
【实验目的与要求】1.学会用动力学法测定材料的杨氏模量;2.学习用内插法测量、处理实验数据;3.了解压电陶瓷换能器的功能,熟悉信号源和示波器的使用;4.培养学生综合运用知识和使用常用实验仪器的能力。
【实验原理】杨氏弹性模量是固体材料在弹性形变范围内正应力与相应正应变的比值,其数值大小与材料的结构、化学成分和加工制造方法有关。
如图2-1所示,一细长棒的横振动满足下述动力学方程:02244=∂∂+∂∂tEJ S xξρξ棒两端是自由端时,端部既不受正应力也不受切向力,棒的轴线沿x 方向,ξ为棒上距左端x 处截面的z 方向位移。
求解上述方程,对圆形棒(162Sd J =)得2436067.1f dm L E = (1)式中E ——杨氏弹性模量,单位牛顿/米2(N·m -2);S ——棒的横截面积,J ——某一截面的惯性矩;L ——棒的长度;d ——棒的横截面直径;m ——棒的质量;f ——棒基频共振频率。
如果在实验中测得(1)式右边的各量,即可由(1)式计算出试样的杨氏弹性模量E 。

实验1 拉伸法测量杨氏模量杨氏弹性模量(以下简称杨氏模量)是表征固体材料性质的重要的力学参量,它反映材料弹性形变的难易程度,在机械设计及材料性能研究中有着广泛的应用。
其测量方法有静态拉伸法、悬臂梁法、简支梁法、共振法、脉冲波传输法,后两种方法测量精度较高;本实验采用静态拉伸法测量金属丝的杨氏模量,因涉及多个长度量的测量,需要研究不同测量对象如何选择不同的测量仪器。
【实验目的】1. 学习用静态拉伸法测量金属丝的杨氏模量。
2. 掌握钢卷尺、螺旋测微计和读数显微镜的使用。
3. 学习用逐差法和作图法处理数据。
4.掌握不确定度的评定方法。
【仪器用具】杨氏模量测量仪(包括砝码、待测金属丝)、螺旋测微计、钢卷尺、读数显微镜【实验原理】1. 杨氏模量的定义本实验讨论最简单的形变——拉伸形变,即棒状物体(或金属丝)仅受轴向外力作用后的伸长或缩短。
按照胡克定律:在弹性限度内,弹性体的应力S F 与应变LL δ成正比。
设有一根原长为l ,横截面积为S 的金属丝(或金属棒),在外力F 的作用下伸长了L δ,则根据胡克定律有)(LLE SF δ= (1-1) 式中的比例系数E 称为杨氏模量,单位为Pa (或N ·m –2)。
实验证明,杨氏模量E 与外力F 、金属丝的长度L 、横截面积S 的大小无关,它只与制成金属丝的材料有关。
若金属丝的直径为d ,则241d S π=,代入(1-1)式中可得 Ld FLE δπ24= (1-2)(1-2)式表明,在长度、直径和所加外力相同的情况下,杨氏模量大的金属丝伸长量较小,杨氏模量小的金属丝伸长量较大。
因此,杨氏模量反映了材料抵抗外力引起的拉伸(或压缩)形变的能力。
实验中,测量出L d L F δ、、、值就可以计算出金属丝的杨氏模量E 。
2. 静态拉伸法的测量方法测量金属丝的杨氏模量的方法就是将金属丝悬挂于支架上,上端固定,下端加砝码对金属丝F ,测出金属丝的伸长量L δ,即可求出E 。



![大学物理实验-杨氏模量[精编文档]](https://uimg.taocdn.com/f037092aff4733687e21af45b307e87101f6f8df.webp)
206 第八章 选做与设计性实验本章为选做与设计性实验,是对第六、七章的补充和扩展。
实验一 杨氏弹性模量的测定物体在外力作用下都要或多或少地发生形变。
当形变不超过某一限度时,撤走外力之后,形变随之消失,这种形变称之为弹性形变。
发生弹性形变时,物体产生恢复原状的内应力,弹性模量就是反映材料形变与内应力关系的物理量,也是工程设计中选用材料的重要参量之一。
由于此定义最初由英国人Thomas young 提出,故也称杨氏模量。
本实验将综合运用多种测量长度的方法,并采用逐差法处理数据。
一、实验目的:(1)学习一种测量杨氏弹性模量的方法; (2)掌握用光杠杆测量微小长度变化的方法; (3)学会用逐差法处理数据。
二、实验仪器与器件:测量杨氏模量专用装置一套(包括光杠杆,砝码,镜尺组),钢卷尺、钢板尺、外径千分尺各一把。
三、实验原理:1.测定杨氏弹性模量的原理本实验讨论最简单的形变,即棒状物体(金属丝)仅受轴向外力作用而发生伸长的形变(称拉伸形变)。
设有一长度为L ,截面积为S 的均匀金属丝或棒,沿长度方向受一外力F 的作用后金属丝伸长∆L 。
单位横截面上垂直作用力F /S 称为正应力,金属丝的相对伸长△L /L 称为线应变。
根据胡克(Robert Hooke )定律有: 金属丝在弹性限度内,线应变L L ∆与正应力SF成正比,即 L L YS F ∆= 或 LS FLY ∆= (1) 式中Y 称为该金属材料的杨氏弹性模量,它的大小仅与材料有关。
在SI 制中,Y 的单位是2N/m 。
式中F 、S 、L 都比较容易测量,而∆L 必须采用光放大的办法测量。
2072.装置简介及光杠杆测量原理 (1)金属丝及支架。
如图8-1-1所示,三角底座上装有两根平行立柱组成支架,待测金属丝上端固定于支架顶部A ,下端连接一个金属框架C 。
框架较重,使金属丝维持伸直,其下端有一个砝码钩,可以载荷不同数值的砝码。
G 是一个可以升降的水平平台,中间开有一个圆形孔,金属框架C 可在孔中上下自由运动。
金属丝杨氏弹性模量的测定本实验是根据胡克定律测定固体材料的一个力学常量——杨氏弹性模量。
实验中采用光杠杆放大原理测量金属丝的微小伸长量,并用不同准确度的测长仪器测量不同的长度量;在数据处理中运用了两种基本而常用的方法——逐差法和作图法。
[一]. 实验目的1.掌握不同长度测量器具的选择和使用,掌握光杠杆测微原理和调节。
2.学习误差分析和误差均分原理思想。
3.学习使用逐差法处理数据及最终测量结果的表达。
4.测定钢丝的杨氏弹性模量E 值。
[二]. 实验原理固体材料在外力作用下产生各部分间相对位置的变化,称之为形变。
如果外力较小时,一旦外力停止作用,形变将随之消失,这种形变称为弹性形变;如果外力足够大,当停止作用时,形变却不能完全消失,这叫剩余形变。
当剩余形变开始出现时,就表明材料达到了弹性限度。
在许多种不同的形变中,伸长(或缩短)形变是最简单、最普遍的形变之一。
本实验是针对连续、均匀、各向同性的材料做成的丝,进行拉伸试验。
设细丝的原长为l ,横截面积为A ,在外加力P 的作用下,伸长了l ∆的长度,单位长度的伸长量l l /∆称为应变,单位横截面所受的力则称为应力。
根据虎克定律,在弹性限度内,应变与应力成正比关系,即llE A P ∆= (1) 式中比例常数E 称为杨氏弹性模量,它仅与材料性质有关。
若实验测出在外加力P 作用下细丝的伸长量l ∆,则就能算出钢丝的杨氏弹性模量E :lA l P E ⋅∆⋅=工程中E 的常用单位为(N/m 2)或(Pa)。
几种常用材料的杨氏模量E 值见下表:应当指出,(1)式只适合于材料弹性形变的情况。
如果超出弹性限度,应变与应力的关系将是非线性的。
右图表示合金钢和硬铝等材料的应力-应变曲线。
为了测定杨氏弹性模量值,在(2)式中的P 、l 和A 都比较容易测定,而长度微小变化量l 则很难用通常测长仪器准确地度量。
本实验将采用光杠杆放大法 进行精确测量。
[三]. 实验装置实验装置原理如右图所示。
欢迎阅读用拉伸法测金属丝的杨氏弹性模量一、实验目的1.学会用光杠杆法测量杨氏弹性模量;2.掌握光杠杆法测量微小伸长量的原理;3.学会用逐差法处理实验数据;4.学会不确定的计算方法,结果的正确表达;5.学会实验报告的正确书写。
二、实验仪器、钢三、的伸长∆∆∆DnxL四、<一>然后继<二>测量7.计下无挂物时刻度尺的读数0n;8.依次挂上kg1的砝码,七次,计下7654321,,,,,,nnnnnnn;9.依次取下kg1的砝码,七次,计下'7'65'4'3'2'1,,,,,,'nnnnnnn;10.用米尺测量出金属丝的长度L(两卡口之间的金属丝)、镜面到尺子的距离D;11.用游标卡尺测量出光杠杆x、用螺旋测微器测量出金属丝直径d。
<三>数据处理方法——逐差法1. 实验测量时,多次测量的算术平均值最接近于真值。
但是简单的求一下平均还是不能达到最好的效果,我们多采用逐差法来处理这些数据。
2. 逐差法采用隔项逐差:3. 注:上式中的n ∆为增重kg 4的金属丝的伸长量。
五、 实验数据记录处理金属丝伸长量:cm A A A A A A A A A 82.14)()()()(37261504=-+-+-+-=金属丝直径:mm d d d d d d d 600.0654321=+++++=1110⨯值:100.2~002/m差分析分请同自己实勿抄一>注光杠杆、望远镜和标尺所构成的光学系统一经调节好后,在实验过程中就不可在移动,否则,所测的数据将不标准,实验又要重新开始;2.不准用手触摸目镜、物镜、平面反射镜等光学镜表面,更不准用手、布块或任意纸片擦拭镜面;<二> 误差分析:3.实验测数据前没有事先放上去一个kg2砝码,将金属丝拉直,作为一个基准点;4.用游标卡尺在纸上测量x值和螺旋测微器测量读数时易产生误差;5.测量金属丝长度时没有找准卡口;6.米尺使用时常常没有拉直,且应该注意水平测量D,铅垂测量L;7.在加减砝码是应该注意轻放,避免摇晃。
杨氏弹性模量的测定实验报告一、实验目的1、学会用拉伸法测量金属丝的杨氏弹性模量。
2、掌握用光杠杆放大法测量微小长度变化的原理和方法。
3、学会使用游标卡尺、螺旋测微器等长度测量仪器。
4、学习数据处理和误差分析的方法。
二、实验原理杨氏弹性模量是描述材料在弹性限度内抵抗形变能力的物理量。
对于一根长度为 L、横截面积为 S 的金属丝,在受到沿长度方向的拉力 F 作用时,伸长量为ΔL。
根据胡克定律,在弹性限度内,应力(F/S)与应变(ΔL/L)成正比,比例系数即为杨氏弹性模量E,其表达式为:\E =\frac{FL}{S\Delta L}\由于伸长量ΔL 很小,难以直接测量,本实验采用光杠杆放大法来测量。
光杠杆原理:光杠杆是一个带有三个尖足的平面镜,前两尖足放在一个固定的平台上,后尖足放在金属丝的测量端。
当金属丝发生微小伸长时,光杠杆的后尖足会随之移动,从而带动平面镜转动一个微小角度θ。
通过望远镜和标尺可以测量出平面镜转动前后反射光线在标尺上的读数差 n。
根据几何关系,有:\(\Delta L =\frac{nD}{2d}\)其中,D 为望远镜到光杠杆平面镜的距离,d 为光杠杆后足到两前足连线的垂直距离。
将上式代入杨氏弹性模量的表达式,可得:\E =\frac{8FLD}{S\pi d^2 n}\三、实验仪器杨氏模量测定仪、光杠杆、望远镜、标尺、螺旋测微器、游标卡尺、砝码、待测金属丝等。
四、实验步骤1、调整杨氏模量测定仪调节底座螺丝,使立柱铅直。
调节光杠杆平面镜,使其与平台垂直。
调节望远镜,使其与光杠杆平面镜等高,并能清晰看到标尺的像。
2、测量金属丝的长度 L使用米尺测量金属丝的有效长度,重复测量三次,取平均值。
3、测量金属丝的直径 d用螺旋测微器在金属丝的不同部位测量直径,共测量六次,取平均值。
4、测量光杠杆常数 d用游标卡尺测量光杠杆后足到两前足连线的垂直距离,重复测量三次,取平均值。
5、测量望远镜到平面镜的距离 D用米尺测量望远镜到平面镜的距离,重复测量三次,取平均值。
杨氏弹性模量测量
【实验目的】
1、学习光杠杆原理及使用光杠杆测量微小长度变化时的调节方法及测量方法。
2、学习使用逐差法处理数据
3、用拉伸法测定钢丝的杨氏弹性模量。
【实验原理】
1.胡克定律和杨氏弹性模量
固体在外力作用下将发生形变,如果外力撤去后相应的形变消失,这种形变称为弹性形变。
如果外力后仍有残余形变,这种形变称为范性形变。
协强:单位面积上所受到的力(F/S)。
协变是指在外力作用下的相对形变(相对伸长 L/L)它反映了物体形变的大小。
胡克定律:在物体的弹性限度内,胁强于胁变成正比,其比例系数称为杨氏模量(记为Y)。
用公式表达为:
(1)
Y在数值上等于产生单位胁变时的胁强。
它的单位是与胁强的单位相同。
杨氏弹性模量是材料的属性,与外力及物体的形状无关。
本试验主要测量的是钢丝的杨氏弹性模量。
2.光杠杆镜尺法测量微小长度的变化
在(1)式中,在外力的F 的拉伸下,钢丝的伸长量∆L 是很小的量。
用一般的的长度测量仪器无法测量。
在本实验中采用光杠杆镜尺法。
图
光杠杆是一块平面镜直立的装在一个三足底板上。
三个足尖f 1,f 2,f 3构成一个等腰三角形。
f 1,f 2为等腰三角形的底边。
f 3到这底边的垂直距离(即距离三角形底边上的高)为光杠杆常数,记为b 。
如果f 1,f 2在一个平台上,而f 3下降∆L ,那么平面镜将绕f 1,f 2转动θ。
初始时,平面镜处于垂直状态。
标尺通过平面镜反射后,在望远镜中呈像。
则望远镜可以通过平面镜观察到标尺的像。
望远镜中十字线处在标尺上刻度为r 0。
当f 3 下降∆L 时,平面镜将绕f 1,f 2转θ角。
则望远镜中标尺的像也发生移动,十字线降落在标尺的刻度为r 处。
由于平面镜转动θ角,进入望远镜的光线旋转2θ角。
从图中看出望远镜中标尺刻度的变化a 1 = r 1 – r 0。
又
由此可得到
即
(2)
……
由于
所以望远镜中标尺读数的变化a
比钢丝伸长量 L大得多,放大了2D/b倍。
1
2D/b就称为光杠杆常数。
钢丝的截面积
d为钢丝的直径)。
将(2)代入(1)中,最后得到:
(3)
……
【实验仪器】
1金属丝与支架、装置见图。
金属丝长约1米,上端被加紧在支架的上梁上,被夹于一个圆形夹头。
这圆形夹头可以在支架的下梁的圆孔内自由移动。
支架下方有三个可调支脚。
这圆形的气泡水准。
使用时应调节支脚。
由气泡水准判断支架是否处于垂直状态。
这样才能使圆柱形夹头在下梁平台的圆孔转移动时不受摩
擦。
2. 光杠杆:结构见图。
使用时支脚
f
1,f
2
放在支架的下梁平台三角形凹
槽内,f
3
放在圆柱形夹头上端平面上。
当钢丝受到拉伸时,随着圆柱夹头下
降,光杠杆的f
3
脚也下降,时平面镜
绕f
1f 2
为轴旋
转。
3. 望远
镜与标
尺
望远镜由物镜、目镜、十字分划板组成。
使用实现调节目镜,使看清十字分划板,在调节物镜使看清标尺。
这是表明标尺通过物镜成像在分划板平面上。
由于标尺像与分划板处于同一平面,所以可以消除读书时的视差(即消除眼睛上下移动时标尺像与十字线之间的相对位移)。
标尺是一般的米尺,但中间刻度为0。
4卷尺、螺旋测微器。
【实验步骤】
1.调整支架呈竖直状态(钢丝先已夹好)
2.放上光杠杆。
f
1,f
2
置于平台的V型凹槽内。
F3置于圆柱夹头的上
平面,平面镜竖直。
3.调节望远镜,使之处与平面镜同一高度。
调节目镜看清十字叉丝。
观察望远镜中的标尺像。
如果望远镜中哦尼顾客看到标尺的像,就调节物镜调焦手轮,使看清标尺像,并无视差。
如无标尺的像,则可在望远镜外观察,移动望远镜,使准星A,B与平面镜中标尺像在一直线上,这是在望远镜中就可以看到标尺的像。
4.记录望远镜中标尺的初始读数r
(不一定要零),再在钢丝下端及
阿0.5公斤砝码,记录望远镜中标尺读数r
1
,以后依次加0.5公斤,并分别记录望远镜中标尺读数,直到4公斤为止。
这是增量过程中的读数。
然后再每次减少0.5公斤,并记下减重时望远镜中标尺的读数。
数据记录表格见后面数据记录部分。
5.取下所有砝码,用卷尺测量平面镜与标尺之间的距离,钢丝长度,
测量光杠杆常数b(把光杠杆在纸上按一下,留下f
1,f
2
,f
3
三点的痕迹,
连成一个等腰三角形。
作其底边上的高,即可测出(b)
6.用螺旋测微器测量钢丝直径6次。
可以在钢丝的不同部位和不同的
经向测量。
因为钢丝直径不均匀,截面积也不是理想的圆。
7.整理仪器
注意事项:
1.光杠杆的支脚z
1, z
2
的尖端必须放在V形槽的最深处,时光杠杆最
平衡。
z
3
支脚应放在圆柱夹头的圆平面处,而不能放在圆柱形夹头的顶部
夹住钢丝的孔或缝里。
2.望远镜调整要消除视差
3.有刻度尺中间刻度为零。
因此在逐次加砝码时,如果望远镜中标尺读数由零的一侧变化到另一侧时,应在读数上加负号。
4.在读数时应随时注意读数是否有误。
这可以由二点来判断。
(1)在相同的F下,增重与减重时标尺上的读数应大致相同。
(2)由于胁变与胁强成正比,因此每次加0.5公斤时引起的伸长量(即相邻二个读数误差)应大致相同。
如果离开这二点要求偏差过大,应检验仪器是否正常,钢丝
本身是否直,光杠杆主杆尖脚z
3
不要与金属丝相碰,钢丝夹头是否夹紧(特别是光杠杆的支脚的位置及平面镜是否松动,读数是否正确。
5.在整个测量过程中,光杠杆、望远镜、标尺一经调好,不可再变动。
增减砝码时要防止砝码晃动。
6.测量D时应该是标尺到平面的垂直距离。
测量时卷尺应该放水平。
7.L的测量应是指钢丝上夹头的下平面到下夹头的上平面。
【数据记录】
1。
钢丝伸长记录(读到0.1mm )
2.钢丝直径 (读数到0.001mm ) 初读数d 0
3. 其它数据
L =( ) (mm) D = ( )(mm) b = ( )(mm)
【数据处理】 (1) 逐差法处理数据
选取连续的2n 个数据,分成二组,r 0, r 1,….r n ; r n+1, r n+2, ….,r 2n-1
在本实验中 n = 4
但要注意,这样求出的 a是指在2公斤(0.5公斤的4倍)砝码拉力下钢丝的伸长。
因此用公式(3)计算Y时,F应使2公斤砝码的重力。
(2)图解法
由(3)式可知
在毫米方格纸上作 a ~ F图线(直线),其斜率
所以
1.实验结果的不确定计算
较方便。
其关系为:由(3)式可知,先求出Y的相对不确定E
Y
其中F,L,D,b只测量了一次,因此它们的不确定度中只有B类分量而无A 类分量。
即
,,,
其中∆L = ∆D = 1mm。
∆b = 0.5 mm。
它们都是仪器误差。
∆F是由四个砝码的仪器误差合成。
根据误差的“方和根”合成原则,
u
F
是一个砝码(0.5公斤)的仪器误差。
为d的不确定完全包括了A类分量与
B类分量,S
d 与u
d
u
d
= 0.004 mm
⎺a也是多次测量,它的不确定度也包括A类分量S a与B类分量u a
u
a
= 0.5 mm
这里
a 1 = r
4
–r
, a
2
= r
5
- r
1
, a
3
= r
6
– r
2
, a
4
= r
7
– r
3
2.实验结果:
【预习思考题】
1.从光杠杆的放大倍数考虑,增大D与减小b都可以增加放大倍数,那么它们有何不同?
2.是否可以增大D无限制地增大放大倍数。
光杠杆放大倍数增大有无限制?
3.为什么在测量中,望远镜中标尺的读数应尽可能在望远镜所在处标尺位置的上下附近?【复习思考题】
1. 拉伸法测量钢丝的杨氏弹性模量中需要测量那些物理量?分别用什么仪
器测?应估读到哪一位?
2. 什么是逐差法?什么情况下应用逐差?逐差法有何优点?。