北师大版高中数学必修一课后训练2.2.3映射

[A基础达标]1．下列各个对应关系中，能构成映射的是()解析：选D.A、B中原像集合中的元素2无像；C中原像集合中元素1有两个元素与之对应，所以A、B、C均不符合映射的定义，故选D.2．若A为含三个元素的数集，B＝{－1，3，5}，使得f：x→2x－1是从A到B的映射，则A等于()A．{－1，2，3}B．{－1，0，2}C．{0，2，3} D．{0，1，2}解析：选C.由映射的概念，A中的元素在关系x→2x－1下，成为－1，3，5，则A＝{0，2，3}．3．下列对应是集合M到集合N的一一映射的是()A．M＝N＝R，f：x→y＝－1x，x∈M，y∈NB．M＝N＝R，f：x→y＝x2，x∈M，y∈NC．M＝N＝R，f：x→y＝1|x|＋x，x∈M，y∈ND．M＝N＝R，f：x→y＝x3，x∈M，y∈N解析：选D.A中集合M的元素0，在N中没有元素与之对应，所以这个对应不是映射；B中集合M的元素±1，在f下的像都是1，故这个对应不是一一映射；C中，负实数及0在f下没有元素和它对应，故这个对应不是映射，故选D.4．设集合A＝{a，b}，B＝{0，1}，则从A到B的映射共有()A．2个B．3个C．4个D．5个解析：选C.如图．5．已知a ，b 为实数，集合M ＝⎩⎨⎧⎭⎬⎫b a ，1，N ＝{a ，0}，f ：x →x 表示把集合M 中的元素x 映射到集合N 中仍为x ，则a ＋b 的值为( )A ．－1B ．0C ．1D ．±1解析：选C.因为f ：x →x ，所以M ＝N .所以⎩⎪⎨⎪⎧a ＝1，b a ＝0，解得⎩⎪⎨⎪⎧a ＝1，b ＝0.所以a ＋b ＝1. 6．在映射f ：A →B 中，集合A ＝B ＝{(x ，y )|x ，y ∈R }，且f ：(x ，y )→(x －y ，x ＋y )，则B 中的元素(－1，3)在集合A 中的原像为________．解析：由题意得⎩⎪⎨⎪⎧x －y ＝－1，x ＋y ＝3，所以⎩⎪⎨⎪⎧x ＝1，y ＝2，即原像为()1，2. 答案：()1，27．已知从A 到B 的映射是x →2x ＋1，从B 到C 的映射是y →y 2－1，其中A ，B ，C ⊆R ，则从A 到C 的映射是________．解析：设x ∈A ，y ∈B ，z ∈C ，则y ＝2x ＋1，z ＝y 2－1， 所以z ＝12(2x ＋1)－1＝x －12.所以从A 到C 的映射是x →x －12. 答案：x →x －128．设M ＝{a ，b }，N ＝{－2，0，2}，则从M 到N 的映射中满足f (a )≥f (b )的映射f 的个数为________．解析：当f (a )＞f (b )时有三种：f (a )＝0，f (b )＝－2；f (a )＝2，f (b )＝0；f (a )＝2，f (b )＝－2.当f (a )＝f (b )时，有f (a )＝f (b )＝0，2，－2，共3种可能．综上所述，满足条件f (a )≥f (b )的映射有6个．答案：69．设集合P ＝Q ＝{(x ，y )|x ，y ∈R }，从集合P 到集合Q 的映射为f ：(x ，y )→(x ＋y ，xy )．求(1)集合Q 中与集合P 中元素(3，2)对应的元素；(2)集合P 中与集合Q 中元素(3，2)对应的元素．解：(1)由3＋2＝5，3×2＝6可得到集合Q 中与集合P 中元素(3，2)对应的元素为(5，6)．(2)设集合P 中与集合Q 中元素(3，2)对应的元素为(x ，y )，则⎩⎪⎨⎪⎧x ＋y ＝3，xy ＝2，解得⎩⎪⎨⎪⎧x ＝2，y ＝1或⎩⎪⎨⎪⎧x ＝1，y ＝2. 所以集合P 中与集合Q 中元素(3，2)对应的元素为(2，1)或(1，2)．10．(1)若A ＝{a ， b ，c }，B ＝{1，2}，从集合A 到集合B 可以建立多少个不同的映射？从集合B 到集合A 呢？(2)已知集合A ＝{1，2，3，4，5}，B ＝{－1，－2}，设映射f ：A →B ，如果B 中的元素都是A 中的元素在f 下的像，这样的映射有几个？解：(1)A ＝{a ，b ，c }，B ＝{1，2}，则从A 到B 的映射共有：23＝8个．反过来从B 到A 的映射共有：32＝9个．(2)由题意知，从集合A 到集合B 的映射总个数是25＝32个，因为B 中的元素都是A 中的元素在f 下的像，所以要除去A 中1，2，3，4，5都对应－1和1，2，3，4，5都对应－2这两个，故满足题意的映射共有32－2＝30个．[B 能力提升]1．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y ＝2x 2＋1，值域为{5，1，19}的“孪生函数”共有( )A ．4个B ．6个C ． 8个D ．9个解析：选D.当2x 2＋1＝5时，x ＝±2，当2x 2＋1＝1时，x ＝0，当2x 2＋1＝19时，x ＝±3，定义域中含3个元素时有4种，定义域中含4个元素时有4种，定义域中含5个元素时有1种．综上，“孪生函数”共有4＋4＋1＝9个．2．若A ＝{a ，b ，c }，B ＝{1，2}，从A 到B 建立映射，使f (a )＋f (b )＋f (c )＝4，则满足条件的映射个数是________．解析：由题意知a 、b 、c 中有两个像为1，一个像为2，所以这样的映射有3个． 答案：33．已知：集合A ＝{x |－2≤x ≤2}，B ＝{x |－1≤x ≤1}．对应关系f ：x →y ＝ax .若在f 的作用下能够建立从A 到B 的映射f ：A →B ，求实数a 的取值范围．解：①当a ≥0时，由－2≤x ≤2得－2a ≤ax ≤2a .若能够建立从A 到B 的映射，则[－2a ，2a ]⊆[－1，1]，即⎩⎪⎨⎪⎧－2a ≥－1，2a ≤1，所以0≤a ≤12. ②当a ＜0时，集合A 中元素的像满足2a ≤ax ≤－2a .若能建立从A 到B 的映射，则[2a ，－2a ]⊆[－1，1]，即⎩⎪⎨⎪⎧2a ≥－1，－2a ≤1，所以－12≤a ＜0.综合①②可知－12≤a ≤12. 4．(选做题)已知A ＝{1，2，3，4}，B ＝{5，6}，取适当的对应关系．(1)以集合A 为定义域、B 为值域(注意：值域为B ，而不是B 的子集，即B 中元素都有原像)的函数有多少个？(2)在所有以集合A 为定义域、B 为值域的函数中，满足条件f (1)≤f (2)≤f (3)≤f (4)的函数有多少个？解：(1)根据映射与函数的定义，集合A 中的元素均可与B 中的两个元素对应，故从A 到B 可建立24＝16个函数，但在1，2，3，4都对应5或都对应6这两种情况下，值域不是B ，应予以排除，所以以集合A 为定义域、B 为值域的函数有14个．(2)在上述14个函数中，满足条件f (1)≤f (2)≤f (3)≤f (4)的函数具体为：f (1)＝5，f (2)＝f (3)＝f (4)＝6；f (1)＝f (2)＝5，f (3)＝f (4)＝6；f (1)＝f (2)＝f (3)＝5，f (4)＝6.所以满足条件的函数共有3个．。

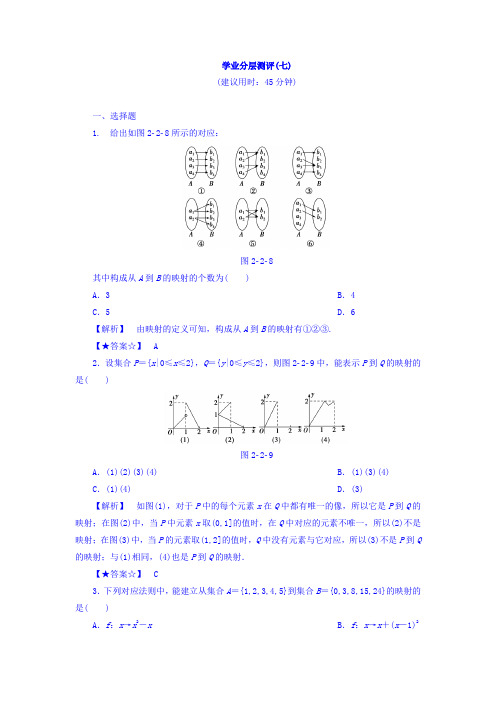
学业分层测评(七)(建议用时：45分钟)一、选择题1. 给出如图2­2­8所示的对应：图2­2­8其中构成从A到B的映射的个数为( )A．3 B．4C．5 D．6【解析】由映射的定义可知，构成从A到B的映射有①②③.【★答案☆】 A2．设集合P＝{x|0≤x≤2}，Q＝{y|0≤y≤2}，则图2­2­9中，能表示P到Q的映射的是( )图2­2­9A．(1)(2)(3)(4) B．(1)(3)(4)C．(1)(4) D．(3)【解析】如图(1)，对于P中的每个元素x在Q中都有唯一的像，所以它是P到Q的映射；在图(2)中，当P中元素x取(0,1]的值时，在Q中对应的元素不唯一，所以(2)不是映射；在图(3)中，当P的元素取(1,2]的值时，Q中没有元素与它对应，所以(3)不是P到Q 的映射；与(1)相同，(4)也是P到Q的映射．【★答案☆】 C3．下列对应法则中，能建立从集合A＝{1,2,3,4,5}到集合B＝{0,3,8,15,24}的映射的是( )A．f：x→x2－x B．f：x→x＋(x－1)2C ．f ：x →x 2＋1D ．f ：x →x 2－1【解析】 因为12－1＝0,22－1＝3,32－1＝8,42－1＝15,52－1＝24. 故从集合A 到集合B 的映射的对应关系为f ：x →x 2－1. 【★答案☆】 D4. 已知A ＝B ＝R ，x ∈A ，y ∈B ，f ：x →y ＝ax ＋b 是从A 到B 的映射，若1和8的原像分别是3和10，则5在f 下的像是( )A ．3B ．4C ．5D ．6【解析】 由题意⎩⎪⎨⎪⎧3a ＋b ＝1，10a ＋b ＝8，解得⎩⎪⎨⎪⎧a ＝1，b ＝－2.∴f ：x →y ＝x －2， ∴5在f 下的像是5－2＝3. 【★答案☆】 A5. 已知映射f ：A →B ，其中集合A ＝{－3，－2，－1,1,2,3,4}，集合B 中的元素都是A 中的元素在映射f 下的像，且对任意的a ∈A ，在B 中和它对应的元素是|a |，则集合B 中的元素的个数是( )A ．4B ．5C ．6D ．7【解析】 对应关系是f ：a →|a |.因此，3和－3对应的像是3；－2和2对应的像是2；1和－1对应的像是1；4对应的像是4.所以B ＝{1,2,3,4}．故选A.【★答案☆】 A 二、填空题6. 设M ＝N ＝R ，f ：x →－x 2＋2x 是M 到N 的映射，若对于N 中元素p ，在M 中恰有一个原像，则p 的值为________．【解析】 由题意知，关于x 的方程－x 2＋2x ＝p 有两相等实根，∴Δ＝4－4p ＝0，p ＝1.【★答案☆】 17. 下列对应f 是从集合A 到集合B 的函数的是________． ①A ＝{1,2,3}，B ＝{7,8,9}，f (1)＝f (2)＝7，f (3)＝8；②A ＝Z ，B ＝{－1,1}，n 为奇数时，f (n )＝－1；n 为偶数时，f (n )＝1；③A ＝{高一一班的男生}，B ＝{男生的身高}，对应关系f ：每个男生对应自己的身高． 【解析】 对于①，集合A 中的元素没有剩余，即A 中的任何一个元素在B 中都有唯一确定的像，同时集合A 和B 都是数集，可知对应f 是集合A 到集合B 的函数．同理，对于②，对应f 也是集合A 到集合B 的函数． 对于③，集合A ，B 不是数集，不是函数关系．【★答案☆】 ①②8. 已知集合A ＝B ＝R ，映射f ：x →x 2＋2x －4，若a 在B 中且在A 中没有原像，则a 的取值范围是________．【解析】 x 2＋2x －4＝(x ＋1)2－5≥－5， ∵a 在B 中且在A 中没有原像， ∴a <－5.【★答案☆】 (－∞，－5) 三、解答题9. 设集合P ＝Q ＝{(x ，y )|x ，y ∈R }，从集合P 到集合Q 的映射为f ：(x ，y )→(x ＋y ，xy )，求：(1)集合Q 中与集合P 中元素(3,2)对应的元素； (2)集合P 中与集合Q 中元素(3,2)对应的元素． 【解】 (1)由3＋2＝5,3×2＝6， 故与集合P 中元素对应的元素为(5,6)．(2)由⎩⎪⎨⎪⎧x ＋y ＝3，xy ＝2，解得⎩⎪⎨⎪⎧x ＝1，y ＝2或⎩⎪⎨⎪⎧x ＝2，y ＝1.故与集合Q 中元素(3,2)对应的元素为(1,2)或(2,1)． 10. 下列对应是否是从A 到B 的映射，能否构成函数？ (1)A ＝R ，B ＝R ，f ：x →y ＝1x ＋1； (2)A ＝{0,1,2,9}，B ＝{0,1,4,9,64}，f ：a →b ＝(a －1)2；(3)A ＝1. 设集合A 与集合B 都是自然数集N ，映射f ：A →B 把集合A 中的元素n 映射到集合B 中为元素n 2＋n ，则在映射f 下，像20的原像是( )A ．2B ．3C ．4D ．4或－5【解析】 令n 2＋n ＝20，即n 2＋n －20＝0， 解得n ＝－5或4. ∵n ∈N ，∴n ＝4. 【★答案☆】 C2. 集合A ＝{a ，b }，B ＝{－1,0,1}，从A 到B 的映射f ：A →B 满足f (a )＋f (b )＝0，那么这样的映射f ：A →B 的个数有( )A ．2个B ．3个C ．5个D ．8个【解析】 由f (a )，f (b )∈{－1,0,1}，且f (a )＋f (b )＝0知，这样的映射有：共3个．【★答案☆】 B3．给定映射f (x ，y )→(x ，x ＋y )，在对应关系f 下像(2,3)的原像是(a ，b )，则函数y ＝ax 2＋bx 的顶点坐标是________．【解析】 由题意a ＝4，b ＝－1，则y ＝4x 2－x 的顶点坐标为⎝ ⎛⎭⎪⎫18，－116.【★答案☆】 ⎝ ⎛⎭⎪⎫18，－1164．设集合A ＝B ＝{(x ，y )|x ，y ∈R }，f 是A 到B 的一个映射，并满足f ：(x ，y )→(－xy ，x －y )．(1)求B 中元素(3，－4)在A 中的原像； (2)试探索B 中哪些元素在A 中存在原像；(3) 求B 中元素(a ，b )在A 中有且只有一个原像时，a ，b 所满足的关系式. 【导学号：04100023】【解】 (1)设(x ，y )是B 中元素(3，－4)在A中的原像，于是⎩⎪⎨⎪⎧－xy ＝3，x －y ＝－4，解得⎩⎪⎨⎪⎧x ＝－1，y ＝3或⎩⎪⎨⎪⎧x ＝－3，y ＝1.所以(3，－4)在A 中的原像有两个，即(－1,3)和(－3,1)．(2)设任意(a ，b )∈B ，则它在A 中的原像(x ，y )应满足，⎩⎪⎨⎪⎧ －xy ＝a ，x －y ＝b ，①②由②式得y ＝x －b ，将它代入①式，并化简得x 2－bx ＋a ＝0.③当且仅当Δ＝b 2－4a ≥0时，方程③有实数根，因此只有当B 中元素(a ，b )满足b 2－4a ≥0时，在A 中才有原像．(3)由以上(2)的解题过程可知，当B 中元素(a ，b )满足b 2＝4a 时，它在A 中有且只有一个原像．。

课后训练基础巩固1．下列图形是函数y ＝－|x |(x ∈[－2,2])的图像的是( )．2．函数f (x )＝21,1,2,1,x x x x⎧+≤⎪⎨>⎪⎩则f (f (3))＝( )．A ．15B ．3C ．23D ．1393．已知f (x 3－1)＝x ＋1，则f (7)的值为( )． A1 B1 C ．3 D ．24．已知f (x )＝21,0,(2,)0,x x f x x ⎧-≤⎨->⎩则f [f (1)]的值为( )．A ．－1B ．0C ．1D ．25．若11x f x x ⎛⎫=⎪-⎝⎭，则当x ≠0且x ≠1时，f (x )＝( )． A ．1x B ．11x -C ．11x -D ．11x-6．已知函数f (x )＝2x ＋1(1≤x ≤3)，则( )． A ．f (x －1)＝2x ＋2(0≤x ≤2) B ．f (x －1)＝2x －1(2≤x ≤4) C ．f (x －1)＝2x －2(0≤x ≤2) D ．f (x －1)＝－2x ＋1(2≤x ≤4) 能力提升7．已知f (x )＝kx ＋b (k ＜0)，且f [f (x )]＝4x ＋1，则f (x )＝( )． A ．－2x －1 B ．－2x ＋1 C ．－x ＋1 D ．122x --8．对a ，b ∈R ，记max{a ，b }＝,,,.a ab b a b ≥⎧⎨<⎩函数f (x )＝max{|x ＋1|，|x －2|}(x ∈R )的最小值是()．A．0B．12C．32D．39．已知函数f(x)＝2,0,1,0.x xx x>⎧⎨+<⎩若f(a)＋f(1)＝0，则实数a的值等于()．A．－3 B．－1 C．1 D．310．已知函数f(x)＝21,0,2,0.x xx x⎧+≤⎨->⎩若f(x)＝10，则x＝______.11．设函数f(x)＝2,0,2,0,x bx c xx⎧++≤⎨>⎩若f(－4)＝f(0)，f(－2)＝－2，则关于x的方程f(x)＝x的解的个数为________．12．已知函数f(x)在[－1,2]________．13．若定义运算a b＝,,,b aa a b⎧⎨<⎩则函数f(x)＝x(2－x)的值域是______．14．已知函数f(x)满足2f(x)＋f(－x)＝3x＋2，则f(x)＝________.15．设f(x)＝11,0,21,0x xxx⎧-≥⎪⎪⎨⎪<⎪⎩若f(x)＞－1，则实数x的取值范围为________．16．当m为怎样的实数时，方程x2－4|x|＋5＝m有四个互不相等的实数根？17．已知函数f(x)对任意的实数x，y，都有f(x＋y)＝f(x)＋2y(x＋y)，且f(1)＝1，求f(x)的解析式．参考答案1．B点拨：y＝－|x|＝,02,,20,x xx x-≤≤⎧⎨-≤<⎩注意端点的取舍．2．D点拨：f(3)＝23，f(f(3))＝24131399f⎛⎫=+=⎪⎝⎭.3．C点拨：令x3－1＝7，得x3＝8，∴x＝2，∴f(7)＝2＋1＝3.4．A点拨：∵f(1)＝f(－1)＝(－1)2－1＝0，∴f[f(1)]＝f(0)＝02－1＝－1.5．B点拨：令1x＝t，则1xt=，∴f(t)＝1111 1ttt=--.∴f(x)＝11 x-.6．B点拨：∵f(x)＝2x＋1的定义域为[1,3]，∴f(x－1)＝2(x－1)＋1＝2x－1，且其定义域为[2,4]．7．A点拨：∵f[f(x)]＝k(kx＋b)＋b＝k2x＋kb＋b＝4x＋1，∴24,1,0.kkb bk⎧=⎪+=⎨⎪<⎩∴2,1.kb=-⎧⎨=-⎩8．C点拨：函数f(x)＝max{|x＋1|，|x－2|}(x∈R)的图像如图所示(实线部分)，由图像可得，其最小值为32.因此选C.9．A点拨：f(a)＋f(1)＝f(a)＋2＝0，∴f(a)＝－2.结合函数表达式可知a＜0，∴f(a)＝a ＋1＝－2，∴a＝－3.10．－3点拨：分两种情况：当x≤0时，由f(x)＝x2＋1＝10得x＝－3或x＝3(舍去)；当x＞0时，由f(x)＝－2x＝10得x＝－5(舍去)，综上可知x＝－3.11．3点拨：由函数解析式可得f(－4)＝(－4)2＋b×(－4)＋c＝16－4b＋c，f(0)＝02＋b ×0＋c＝c，f(－2)＝(－2)2＋b×(－2)＋c＝4－2b＋c.∵f(－4)＝f(0)，f(－2)＝－2，∴16－4b＋c＝c，且4－2b＋c＝－2，即b＝4，c＝2.∴f(x)＝242,0, 2,0.x x xx⎧++≤⎨>⎩当x≤0时，由f(x)＝x得x2＋4x＋2＝x，即x2＋3x＋2＝0，∴x＝－1，或x＝－2. 当x＞0时，由f(x)＝x得，x＝2.综上可知，关于x 的方程f (x )＝x 的解的个数为3.12．f (x )＝1,10,1,022x x x x +-≤≤⎧⎪⎨-<≤⎪⎩点拨：设y 轴左侧函数的解析式为y ＝kx ＋b (k ＞0，－1≤x ≤0)，把点(－1,0)，(0,1)的坐标代入上式得0,1,k b b -+=⎧⎨=⎩∴1,1.k b =⎧⎨=⎩∴y ＝x ＋1(－1≤x ≤0)． 同理可得y 轴右侧函数的解析式为y ＝－12x (0＜x ≤2)． 13．(－∞，1] 点拨：由题意，得f (x )＝,1,2, 1.x x x x <⎧⎨-≥⎩画函数f (x )的图像，如图所示．由图像得函数f (x )的值域是(－∞，1]． 14．233x +点拨：∵2f (x )＋f (－x )＝3x ＋2①，用－x 替代关系式中的x ， 得2f (－x )＋f (x )＝3(－x )＋2②， ∴①×2－②得f (x )＝233x +. 15．(－∞，－1)∪(0，＋∞) 点拨：画出函数f (x )的图像，如图中实线部分所示，再作出直线y ＝－1.若f (x )＞－1，则x ＜－1，或x ＞0.16．解：先作出y ＝x 2－4|x |＋5＝2245,0,45,0x x x x x x ⎧-+≥⎨++<⎩的图像(如图所示)．再作出直线y＝m，从图中可以直接看出，当1＜m＜5时，方程有四个互不相等的实根．17．解：∵f(x＋y)＝f(x)＋2y(x＋y)对任意x，y∈R都成立，可令x＝0，y＝1，得f(1)＝f(0)＋2×1×(0＋1)，又f(1)＝1，解得f(0)＝－1，再令x＝0，y＝x，得f(x)＝f(0)＋2x(0＋x)＝－1＋2x2，即f(x)＝2x2－1.。

高中数学北师大版必修一：2.2.3《映射》双基达标+综合提高1．已知集合M ＝{x |0≤x ≤6}，P ＝{y |0≤y ≤3}，则下列对应关系中不能看作从M 到P 的映射的是( )．A ．f ：x →y ＝12xB ．f ：x →y ＝13xC ．f ：x →y ＝xD ．f ：x →y ＝16x解析 选项C 中，集合M 中元素6没有像，不是映射． 答案 C2．已知集合A ＝N ＋，B ＝{a |a ＝2n －1，n ∈Z }，映射f ：A →B ，使A 中任一元素a 与B 中元素2a －1对应，则与B 中元素17对应的A 中元素是( )． A ．3 B ．5 C ．17 D ．9解析 利用对应法则转化为解方程．由题意，得2a －1＝17，解得a ＝9. 答案 D3．定义在R 上的函数y ＝f (x )的值域为[a ，b ]，则y ＝f (x ＋1)的值域为( )． A ．[a ，b ]B ．[a ＋1，b ＋1]C ．[a －1，b －1]D ．无法确定解析 将函数y ＝f (x )的图像向左平移一个单位得函数y ＝f (x ＋1)的图像，由于定义域均是R ，则这两个函数图像上点的纵坐标的取值范围相同，所以y ＝f (x ＋1)的值域也是[a ，b ]．故选择A. 答案 A4．设集合A 和B 都是自然数集，映射f ：A →B 把A 中的元素n 映射到B 中的元素2n＋n ，则在映射f 下，A 中的元素________对应B 中的元素3.解析 对应法则为f ：n →2n ＋n ，根据题意2n＋n ＝3，可得n ＝1. 答案 15．已知：A ＝{a ，b ，c }，B ＝{1,2}，从A 到B 建立映射f ，使f (a )＋f (b )＋f (c )＝4，则满足条件的映射共有________个．解析 ∵B ＝{1,2}，f (a )＋f (b )＋f (c )＝4， ∴f (a )，f (b )，f (c )当中有一个取2，另两个取1. ∴只有3种对应方法． 答案 36．A ＝R ，B ＝{(x ，y )|x 、y ∈R }，f ：A →B ，f ：x →(x ＋1，x 2＋1)． (1)求A 中元素2的像；(2)B 中元素⎝ ⎛⎭⎪⎫32，54的原像． 解 (1)x ＝2时，x ＋1＝2＋1，x 2＋1＝3， ∴2的像是(2＋1,3)．(2)设B 中元素⎝ ⎛⎭⎪⎫32，54的原像为x ， 则⎩⎪⎨⎪⎧32＝x ＋1，54＝x 2＋1，得x ＝12.∴B 中元素⎝ ⎛⎭⎪⎫32，54的原像为12. 综合提高限时25分钟7．下列对应是从集合S 到T 的映射的是( )． A ．S ＝N ，T ＝{－1,1}，对应法则是(－1)n，n ∈SB ．S ＝{0,1,4,9}，T ＝{－3，－2，－1,0,1,2,3}，对应法则是开平方C ．S ＝{0,1,2,5}，T ＝{1，12，15}，对应法则是取倒数D ．S ＝{x |x ∈R }，T ＝{y |y ∈R }，对应法则是x →y ＝1＋x1－x解析 判断映射方法简单地说应考虑A 中的元素是否都可以受f 作用，作用的结果是否一定在B 中，作用的结果是否唯一这三个方面．很明显A 符合定义；B 是一对多的对应；C 命题中的元素0没有像；D 命题集合S 中的元素1也无像． 答案 A8．设f ，g 都是由A 到A 的映射，其对应法则如下表(从上到下)： 表1 映射f 的对应法则原像 1 2 3 4 像3421表2 映射g 的对应法则原像 1 2 3 4 像4312则与f [g (1)]相同的是( )A ．g [f (1)] B ．g [f (2)] C ．g [f (3)] D ．g [f (4)]解析 f (a )表示在对应法则f 下a 对应的像，g (a )表示在对应法则g 下a 对应的像． 由表1和表2，得f [g (1)]＝f (4)＝1，g [f (1)]＝g (3)＝1，g [f (2)]＝g (4)＝2，g [f (3)]＝g (2)＝3，g [f (4)]＝g (1)＝4，则有f [g (1)]＝g [f (1)]＝1.答案 A9．已知集合M ＝{a ，b ，c ，d }，P ＝{x ，y ，z }，则从M 到P 能建立不同映射的个数是________． 解析 集合M 中有4个元素，集合P 中有3个元素，则从M 到P 能建立34＝81个不同的映射． 答案 8110．已知(x ，y )在映射f 作用下的像是(x ＋y ，xy )，则(3,4)的像为________，(1，－6)的原像为________．解析 根据条件可知x ＝3，y ＝4，则x ＋y ＝3＋4＝7，xy ＝3×4＝12，所以(3,4)的像为(7,12)；设(1，－6)的原像为(x ，y )，则有⎩⎪⎨⎪⎧x ＋y ＝1，xy ＝－6，解得⎩⎪⎨⎪⎧x ＝－2，y ＝3，或⎩⎪⎨⎪⎧x ＝3，y ＝－2.所以(1，－6)的原像为(－2,3)或(3，－2)． 答案 (7,12) (－2,3)或(3，－2)11．已知集合A ＝{1,2,3，k}，B ＝{4,7，a 4，a 2＋3a }，且a ∈N ，k ∈N ，x ∈A ，y ∈B ，映射f ：A →B ，使B 中元素y ＝3x ＋1和A 中元素x 对应，求a 及k 的值．解 ∵B 中元素y ＝3x ＋1和A 中元素x 对应，∴A 中元素1的像是4；2的像是7；3的像是10，即a 4＝10或a 2＋3a ＝10. ∵a ∈N ，∴由a 2＋3a ＝10，得a ＝2. ∵k 的像是a 4，∴3k ＋1＝16，得k ＝5.∴a ＝2，k ＝5.12．(创新拓展)已知集合A ＝{x |(x －1)(x 2＋3x －4)＝0}，集合B ＝{a ，a ＋5，a 2－2a －5}，映射f ：A →B 是“加2”，求实数a 的值，并判断映射f ：A →B 是不是一一映射？ 解 ∵(x －1)(x 2＋3x －4)＝0，∴x 1＝x 2＝1，x 3＝－4， ∴集合A ＝{1，－4}，∵映射f ：A →B 是“加2”， ∴1＋2＝3∈B ，－4＋2＝－2∈B .①当a ＝3时，a ＋5＝8，a 2－2a －5＝－2， ∴B ＝{3，－2,8}．此时8无原像，∴f ：A →B 不是一一映射． ②当a ＝－2时，a ＋5＝3，a 2－2a －5＝3. ∴B ＝{－2,3}，与B 有三个元素矛盾，∴a ≠－2. ③当a ＋5＝－2时，a ＝－7，a 2－2a －5＝58， ∴B ＝{7，－2,58}，与3∈B 矛盾，∴a ≠－7. ④当a 2－2a －5＝－2时，a 1＝3，a 2＝－1.当a＝3时，B＝{3，－2,8}；当a＝－1时，a＋5＝4，B＝{－2，－1,4}，与3∈B矛盾，则a≠－1. ∴a＝3，B＝{－2,3,8}，映射f：A→B不是一一映射．。

1．下列对应法则f 中，能构成从A 到B 的函数的有( )①A ＝{0,2}，B ＝{0,1}，f ：x →y ＝x 2；②A ＝{－2,0,2}，B ＝{4}，f ：x →y ＝x 2；③A ＝R ，B ＝{y |y >0}，f ：x →y ＝1x 2；④A ＝R ，B ＝R ，f ：x →y ＝2x ＋1. A ．1个 B ．2个C ．3个 D ．4个解析：选B.②中A 的元素0在B 中无像，不能构成映射，也就不能构成函数；③中A 的元素0在B 中无像，不能构成映射，也就不能构成函数．①④都能构成A 到B 的函数．2．下列对应关系是从集合M 到集合N 的一一映射的是( )A ．M ＝N ＝R ，f ：x →y ＝－1x，x ∈M ，y ∈N B ．M ＝N ＝R ，f ：x →y ＝x 2，x ∈M ，y ∈NC ．M ＝N ＝R ，f ：x →y ＝1|x |＋x，x ∈M ，y ∈N D ．M ＝N ＝R ，f ：x →y ＝x 3，x ∈M ，y ∈N解析：选 D.判断一个对应关系是否为一一映射，要从基本概念入手，看是否满足一一映射的条件，A 选项M 中元素0在N 中没有像与之对应，所以A 不是映射；B 选项M 中元素±1在N 中对应相同的像1，虽然B 是映射，但不是一一映射；C 选项M 中元素0及负实数在N 中没有元素与之对应，所以C 不是映射；D 选项M 中的每一个元素在N 中都有唯一元素与之对应，M 中的不同元素在N 中的像也不同，且N 中的元素在M 中都有原像，所以D 是一一映射．3．设集合A 和B 都是坐标平面上的点集{(x ，y )|x ∈R ，y ∈R}，映射f ：A →B 把集合A 中的元素(x ，y )映射成集合B 中的元素(x ＋y ，x －y )，则在映射f 下，像(2,1)的原像是________．解析：本题即为求方程组⎩⎪⎨⎪⎧x ＋y ＝2，x －y ＝1的解． 答案：⎝⎛⎭⎫32，124．已知映射f ：A →B ，其中，集合A ＝{－3，－2，－1,1,2,3,4}，集合B 中的元素都是A 中元素在映射f 下的像，且对任意的a ∈A ，在集合B 中和它对应的元素是|a |，则集合B 中元素的个数最少是________．解析：本题题意叙述虽长，但转换成图表语言则非常简洁．如图，即可知个数最少应为4. 答案：4[A 级 基础达标]1．(2012·九江检测)在从集合A 到集合B 的映射中，下列说法正确的是( )A ．集合B 中的某一个元素b 的原像可能不止一个B．集合A中的某一个元素a的像可能不止一个C．集合A中的两个不同元素所对应的像必不相同D．集合B中的两个不同元素的原像可能相同解析：选A.由映射的概念可知，A中的每个元素都有像，且像唯一，B中未必每个元素都有原像且不一定唯一，故选A.2．下列对应关系f中，不是从集合A到集合B的映射的是()A．A＝{x|1<x<4}，B＝[1,3)，f：求算术平方根B．A＝R，B＝R，f：取绝对值C．A＝{正实数}，B＝R，f：求平方D．A＝R，B＝R，f：取倒数解析：选D.因为D中0取倒数无意义，故选D.3．设集合A和B都是自然数集合N，映射f：A→B，把集合A中的元素n映射到集合B中的元素2n＋n，则在映射f下，像20的原像是()A．2 B．3C．4 D．5解析：选C.∵20＝2n＋n，分别将选择项代入检验，知当n＝4时成立．4．(2012·淮北质检)已知A＝{x|0≤x≤4}，B＝{y|0≤y≤2}，从A到B的对应法则分别是：(1)f：x→y＝12x，(2)f：x→y＝x－2，(3)f：x→y＝x，(4)f：x→y＝|x－2|其中能构成一一映射的是________．解析：(1)y＝12x.x∈[0,4]．y∈[0,2]＝B(2)y＝x－2∈[－2,2]≠B.(3)y＝x∈[0,2]＝B.(4)y＝|x－2|∈[0,2]，但如y＝1.∴x＝3或x＝1. 答案：(1)(3)5．已知从A到B的映射是x→2x＋1，从B到C的映射是y→y2－1，其中A，B，C⊆R，则从A到C的映射是________．解析：x∈A.y∈B.z∈C.∴y＝2x＋1.z＝y2－1∴z＝12(2x＋1)－1＝x－12.∴x→x－12答案：x→x－1 26．设A＝B＝{a，b，c，d，e，…，x，y，z}(元素为26个英文字母)，作映射A→B为：并称A中字母拼成的文字为明文，相应B中对应字母拼成的文字为密文，则：(1)“mathematics”的密文是什么？(2)试破译密文“ju jt gvooz”．解：由明文与密文的关系可知：(1)“mathematics”对应的密文是“nbuifnbujdt”．(2)“ju jt gvooz”对应的明文是“it is funny”．[B级能力提升]7．下列对应法则是从集合A到集合B的映射的是()A．A＝R，B＝{x|x>0}，f：x→y＝|x|B．A＝{x|x≥0}，B＝{y|y>0}，f：x→y＝xC．A＝N，B＝N＋，f：x→y＝|x－1|D．A＝R，B＝{y|y≥0}，f：x→y＝x2－2x＋2解析：选D.x＝0，y＝0∉B，A错．同理B错．C中：当x＝1时，y＝0∉B.C错.8．已知集合A＝{1,2,3}，B＝{4,5,6}，f：A→B为集合A到集合B的一个函数，那么该函数的值域C的不同情况有()A．6种B．7种C ．8种D ．27种解析：选B.该函数的值域C 的不同情况有{4}，{5}，{6}，{4,5}，{4,6}，{5,6}，{4,5,6}7种．9．已知(x ，y )在映射f 作用下的像是(x ＋y ，xy )，则(3,4)的像为________，(1，－6)的原像为________．解析：根据条件可知x ＝3，y ＝4，则x ＋y ＝3＋4＝7，xy ＝3×4＝12，所以(3,4)的像为(7,12)；设(1，－6)的原像为(x ，y )，则有⎩⎪⎨⎪⎧ x ＋y ＝1，xy ＝－6，解得⎩⎪⎨⎪⎧ x ＝－2，y ＝3，或⎩⎪⎨⎪⎧x ＝3，y ＝－2. 所以(1，－6)的原像为(－2,3)或(3，－2)．答案：(7,12) (－2,3)或(3，－2)10．(创新题)已知集合A ＝{1,2,3，k }，B ＝{4,7，a 4，a 2＋3a }，a ∈N ＋，k ∈N ＋，x ∈A ，y ∈B ，f ：x →y ＝3x ＋1是从定义域A 到值域B 的一个函数，求a ，k ，A ，B .解：根据对应法则f ，有：f ：1→4；2→7；3→10；k →3k ＋1.若a 4＝10，则a ∉N ＋，不符合题意，舍去；若a 2＋3a ＝10，则a ＝2(a ＝－5不符合题意，舍去)．故3k ＋1＝a 4＝16，得k ＝5.综上可知，a ＝2，k ＝5, 集合A ＝{1,2,3,5}，B ＝{4,7,10,16}．11．已知集合A 到集合B ＝⎩⎨⎧⎭⎬⎫0，1，12，13的映射f ：x →1|x |－1，那么集合A 中的元素最多有几个？并写出元素个数最多时的集合A .解：∵f 是映射，∴A 中的每一个元素都应在B 中有唯一的元素对应．∵1|x |－1≠0，∴0在A 中不存在原像； 由1|x |－1＝1，得x ＝±2，∴±2可取作1的对应元素； 由1|x |－1＝12，得x ＝±3，∴±3可取作12的对应元素； 由1|x |－1＝13，得x ＝±4，∴±4可取作13的对应元素； ∴A 中元素最多只能是6个，即A ＝{－4，－3，－2,2,3,4}．。

2.3 映射整体设计教学分析课本将映射作为函数的一种推广，这与传统的处理方式有了逻辑顺序上的变化．这样处理，主要是想较好地衔接初中的学习，让学生将更多的精力集中理解函数的概念，同时，也体现了从特殊到一般的思维过程．三维目标了解映射的概念及表示方法，会利用映射的概念来判断“对应关系”是否是映射，感受对应关系在刻画函数和映射概念中的作用，提高对数学高度抽象性和广泛应用性的认识．重点难点映射的概念．课时安排1课时教学过程导入新课思路1.复习初中常见的对应关系1．对于任何一个实数a，数轴上都有唯一的点P和它对应．2．对于坐标平面内任何一个点A，都有唯一的有序实数对(x，y)和它对应．3．对于任意一个三角形，都有唯一确定的面积和它对应．4．某影院的某场电影的每一张电影票有唯一确定的座位与它对应．5．函数的概念．我们已经知道，函数是建立在两个非空数集间的一种对应，若将其中的条件“非空数集”弱化为“任意两个非空集合”，按照某种法则可以建立起更为普通的元素之间的对应关系，这种对应就叫映射(板书课题)．思路2.前面学习了函数的概念是：一般地，设A，B是两个非空数集，如果按照某种对应法则f，对于集合A中的每个元素x，在集合B中都有唯一的元素y和它对应．(1)对于任意一个实数，在数轴上都有唯一的点与之对应．(2)班级里的每一位同学在教室内都有唯一的坐位与之对应．(3)对于任意的三角形，都有唯一确定的面积与之对应．那么这些对应又有什么特点呢？这种对应称为映射．引出课题．推进新课新知探究提出问题①给出以下对应关系：图1这三个对应关系有什么共同特点？②像问题①中的对应我们称为映射，请给出映射的定义．③“都有唯一”是什么意思？④函数与映射有什么关系？讨论结果：①集合A，B均为非空集合，并且集合A中的元素在集合B中都有唯一的元素与之对应．②一般地，设A ，B 是两个非空的集合，如果按某一个确定的对应法则f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应f ：A →B 为从集合A 到集合B 的一个映射．记作“f ：A →B ”．如果集合A 中的元素x 对应集合B 中元素y ，那么集合A 中的元素x 叫集合B 中元素y 的原像，集合B 中元素y 叫集合A 中的元素x 的像．③包含两层意思：一是必有一个；二是只有一个，也就是说有且只有一个的意思，即是一对一或多对一．④函数是特殊的映射，映射是函数的推广．应用示例思路1例1 下列哪些对应是从集合A 到集合B 的映射？(1)A ＝{P |P 是数轴上的点}，B ＝R ，对应关系f ：数轴上的点与它所代表的实数对应；(2)A ＝{P |P 是平面直角坐标系中的点}，B ＝{(x ，y )|x ∈R ，y ∈R }，对应关系f ：平面直角坐标系中的点与它的坐标对应；(3)A ＝{三角形}，B ＝{x |x 是圆}，对应关系f ：每一个三角形都对应它的内切圆；(4)A ＝{x |x 是新华中学的班级}，B ＝{x |x 是新华中学的学生}，对应关系f ：每一个班级都对应班里的学生．活动：学生思考映射的定义．判断一个对应是否是映射，要紧扣映射的定义．(1)中数轴上的点对应着唯一的实数；(2)中平面直角坐标系中的点对应着唯一的有序实数对；(3)中每一个三角形都有唯一的内切圆；(4)中新华中学的每个班级对应其班内的多个学生．解：(1)是映射；(2)是映射；(3)是映射；(4)不是映射．新华中学的每个班级对应其班内的多个学生，是一对多，不符合映射的定义.变式训练1．图2(1)，(2)，(3)，(4)用箭头所标明的A 中元素与B 中元素的对应法则，是不是映射？图2答案：(1)不是；(2)是；(3)是；(4)是．2．在图3中的映射中，A 中元素60°的对应的元素是什么？在A 中的什么元素与B 中元素22对应？图3答案：A 中元素60°的对应的元素是32，在A 中的元素45°与B 中元素22对应. 思路2例1 下列对应是不是从集合A 到集合B 的映射，为什么？(1)A ＝R ，B ＝{x ∈R |x ≥0}，对应法则是“求平方”；(2)A ＝R ，B ＝{x ∈R |x ＞0}，对应法则是“求平方”；(3)A ＝{x ∈R |x ＞0}，B ＝R ，对应法则是“求平方根”；(4)A ＝{平面内的圆}，B ＝{平面内的矩形}，对应法则是“作圆的内接矩形”． 活动：学生回顾映射的概念，教师适时点拨或提示．判断一个对应是否是映射，关键是确定是否是“一对一”或“多对一”的对应，即集合A 中的任意一个元素，在集合B 中都有唯一确定的元素与之对应．解：(1)是映射，因为A 中的任何一个元素，在B 中都能找到唯一的元素与之对应．(2)不是从集合A 到集合B 的映射，因为A 中的元素0，在集合B 中没有对应的元素．(3)不是从集合A 到集合B 的映射，因为任何正数的平方根都有两个值，即集合A 中的任何元素，在集合B 中都有两个元素与之对应．(4)不是从集合A 到集合B 的映射．因为一个圆有无穷多个内接矩形，即集合A 中任何一个元素在集合B 中有无穷多个元素与之对应．点评：本题主要考查映射的概念．给定两集合A ，B 及对应法则f ，判断是否是从集合A 到集合B 的映射，主要利用映射的定义．用通俗的语言讲：A →B 的对应有“多对一”，“一对一”，“一对多”，前两种对应是A 到B 的映射，而后一种不是A 到B 的映射. 变式训练1．设集合A ＝{a ，b ，c }，集合B ＝R ，以下对应关系中，一定能建立集合A 到集合B 的映射的是( )．A ．对集合A 中的数开平方B ．对集合A 中的数取倒数C ．对集合A 中的数取算术平方根D ．对集合A 中的数立方分析：当a ＜0时，对a 开平方或取算术平方根均无意义，则A ，C 错；当a ＝0时，对a 取倒数无意义，则B 错；由于对任何实数都能立方，并且其立方仅有一个，所以对集合A 中的数立方能建立映射，故选D.答案：D2．设f ：A →B 是A 到B 的一个映射，其中A ＝B ＝{(x ，y )|x ，y ∈R }，f ：(x ，y )→(x －y ，x ＋y )，求：(1)A 中元素(－1,2)在B 中对应的元素；(2)在A 中什么元素与B 中元素(－1,2)对应？分析：这是一个映射的问题，由于A 中元素(x ，y )对应B 中元素为(x －y ，x ＋y )，确定了对应法则，转化为解方程组．解：(1)A 中元素(－1,2)在B 中对应的元素为(－1－2，－1＋2)，即(－3,1)．(2)设A 中元素(x ，y )与B 中元素(－1,2)对应，则⎩⎪⎨⎪⎧x －y ＝－1，x ＋y ＝2， 解得⎩⎪⎨⎪⎧ x ＝12，y ＝32.所以A 中元素⎝ ⎛⎭⎪⎫12，32与B 中元素(－1,2)对应. 例2 设映射f ：x →－x 2＋2x 是实数集R ＝M 到实数集R ＝N 的映射，若对于实数p ∈N ，在M 中不存在原像，则实数p 的取值范围是( )．A ．(1，＋∞)B ．[1，＋∞)C ．(－∞，1)D ．(－∞，1]活动：让学生思考：若对于实数p ∈N ，在M 中不存在原像，与函数f (x )＝－x 2＋2x 有什么关系？若对于实数p ∈N ，在M 中不存在原像是指实数p 表示函数f (x )＝－x 2＋2x 值域中的元素，转化为求函数f (x )＝－x 2＋2x ，x ∈R 的值域．集合M 是函数f (x )＝－x 2＋2x 的定义域，集合N 是函数f (x )＝－x 2＋2x 的值域．解：(方法一)由于集合M ，N 都是数集，则映射f ：x →－x 2＋2x 就是函数f (x )＝－x 2＋2x ，其定义域是M ＝R ，则有值域Q ＝{y |y ≤1}⊆N ＝R .对于实数p ∈N ，在M 中不存在原像，则实数p 的取值范围是∁N Q ＝∁R Q ＝{y |y ＞1}，即p 的取值范围是(1，＋∞)；(方法二)当p ＝0时，方程－x 2＋2x ＝0有解x ＝0,2，即在M 中存在原像0和2，则p ＝0不合题意，排除C ，D ；当p ＝1时，方程－x 2＋2x ＝1有解x ＝1，即在M 中存在原像1，则p ＝1不合题意，排除B.答案：A点评：本题主要考查映射的概念和函数的值域，以及综合应用知识解决问题的能力．解决本题的关键是转化思想的应用．把映射问题转化为函数的值域问题，进一步转化为求函数的值域在实数集中的补集．其转化的依据是对映射概念的理解以及对函数与映射关系的把握程度.变式训练设f ，g 都是由A 到A 的映射，其对应法则如下表(从上到下)：则与f [g (1)]相同的是( )．A ．g [f (1)]B ．g [f (2)]C ．g [f (3)]D ．g [f (4)]分析：f (a )表示在对应法则f 下a 对应的像，g (a )表示在对应法则g 下a 对应的像． 由表1和表2，得f [g (1)]＝f (4)＝1，g [f (1)]＝g (3)＝1，g [f (2)]＝g (4)＝2，g [f (3)]＝g (2)＝3，g [f (4)]＝g (1)＝4，则有f [g (1)]＝g [f (1)]＝1.答案：A 知能训练 1．下列对应是从集合S 到T 的映射的是( )．A ．S ＝N ，T ＝{－1,1}，对应法则是(－1)n ，n ∈SB ．S ＝{0,1,4,9}，T ＝{－3，－2，－1,0,1,2,3}，对应法则是开平方C ．S ＝{0,1,2,5}，T ＝⎩⎨⎧⎭⎬⎫1，12，15，对应法则是取倒数 D ．S ＝{x |x ∈R }，T ＝{y |y ∈R }，对应法则是x →y ＝1＋x 1－x分析：判断映射方法简单地说应考虑A 中的元素是否都可以受f 作用，作用的结果是否一定在B 中，作用的结果是否唯一这三个方面．很明显A 符合定义；B 是一对多的对应；C 命题中的元素0没有像；D 命题集合S 中的元素1也无像．答案：A2．已知集合M ＝{x |0≤x ≤6}，P ＝{y |0≤y ≤3}，则下列对应关系中不能看作从M 到P 的映射的是( )．A ．f ：x →y ＝12xB ．f ：x →y ＝13x C ．f ：x →y ＝x D ．f ：x →y ＝16x 分析：选项C 中，集合M 中元素6没有像，其他均是映射．答案：C3．已知集合A ＝N ＋，B ＝{a |a ＝2n －1，n ∈Z }，映射f ：A →B ，使A 中任一元素a 与B 中元素2a －1对应，则与B 中元素17对应的A 中元素是( )．A ．3B ．5C ．17D ．9分析：利用对应法则转化为解方程．由题意得2a －1＝17，解得a ＝9.答案：D4．若映射f ：A →B 的像的集合是Y ，原像的集合是X ，则X 与A 的关系是________；Y 与B 的关系是________．分析：根据映射的定义，可知集合A 中的元素必有像且唯一；集合B 中的元素在集合A 中不一定有原像．故像的集合是B 的子集．所以X ＝A ，Y ⊆B .答案：X ＝A Y ⊆B5．已知集合M ＝{a ，b ，c ，d }，P ＝{x ，y ，z }，则从M 到P 能建立不同映射的个数是________．分析：集合M 中有4个元素，集合P 中有3个元素，则从M 到P 能建立34＝81个不同的映射．答案：816．下列对应哪个是集合M 到集合N 的映射？哪个不是映射？为什么？(1)设M ＝{矩形}，N ＝{实数}，对应法则f 为矩形到它的面积的对应．(2)设M ＝{实数}，N ＝{正实数}，对应法则f 为x →1|x |. (3)设M ＝{x |0≤x ≤100}，N ＝{x |0≤x ≤100}，对应法则f 为开方再乘10.解：(1)是M 到N 的映射，因为它是一对一的对应．(2)不是映射，因为当x ＝0时，集合M 中没有元素与之对应．(3)是映射，因为它是一对一的对应．7．设集合A 和B 都是自然数集，映射f ：A →B 把A 中的元素n 映射到B 中的元素2n ＋n ，则在映射f 下，A 中的元素________对应B 中的元素3.( )．A ．1B ．3C ．9D ．11分析：对应法则为f ：n →2n ＋n ，根据选项验证2n ＋n ＝3，可得n ＝1.答案：A8．已知集合A ＝{1,2,3，k }，B ＝{4,7，a 4，a 2＋3a }，且a ∈N ，k ∈N ，x ∈A ，y ∈B ，映射f ：A →B ，使B 中元素y ＝3x ＋1和A 中元素x 对应，求a 及k 的值．分析：先从集合A 和对应法则f 入手，同时考虑集合中元素的互异性．可以分析出此映射必为一一映射，再由3→10，求得a 值，进而求得k 值．解：∵B 中元素y ＝3x ＋1和A 中元素x 对应，∴A 中元素1的像是4；2的像是7；3的像是10，即a 4＝10或a 2＋3a ＝10.∵a∈N，∴由a2＋3a＝10，得a＝2.∵k的像是a4，∴3k＋1＝16，得k＝5.∴a＝2，k＝5.9．A＝{(x，y)|x＋y＜3，x∈N，y∈N}，B＝{0,1,2}，f：(x，y)→x＋y，这个对应是否为映射？是否为函数？说明理由．解：是映射，不是函数．由题意得A＝{(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(2,0)}，显然对于A中的每一个有序实数对，它们的和是0或1或2，则在B中都有唯一一个数与它对应，所以是映射，因为集合A不是数集而是点集，所以不是函数．拓展提升问题：集合M中有m个元素，集合N中有n个元素，则从M到N能建立多少个不同的映射？探究：当m＝1，n＝1时，从M到N能建立1＝11个不同的映射；当m＝2，n＝1时，从M到N能建立1＝12个不同的映射；当m＝3，n＝1时，从M到N能建立1＝13个不同的映射；当m＝2，n＝2时，从M到N能建立4＝22个不同的映射；当m＝2，n＝3时，从M到N能建立9＝32个不同的映射．集合M中有m个元素，集合N中有n个元素，则从M到N能建立n m个不同的映射．课堂小结本节课学习了：(1)映射是一种特殊的对应，元素之间的对应必须满足“一对一或多对一”．(2)映射由三个部分组成：集合A，集合B及对应法则f，称为映射的三要素．(3)映射中集合A，B中的元素可以为任意的．作业练习1.设计感想本节教学设计的内容拓展较深，在实际教学中根据学生实际选取例题和练习．本节重点设计了映射的概念，对于映射来说，只需要掌握概念即可，不要求拓展其内容，以免加重学生的负担，也偏离了课标要求和高考的方向．备课资料[备选例题]区间[0，m]在映射f：x→2x＋m所得的像集区间为[a，b]，若区间[a，b]的长度比区间[0，m]的长度大5，则m等于( )．A．5 B．10C．2.5 D．1分析：函数f(x)＝2x＋m在区间[0，m]上的值域是[m,3m]，则有[m,3m]＝[a，b]，则a＝m，b＝3m，又区间[a，b]的长度比区间[0，m]的长度大5，则有b－a＝(m－0)＋5，即b－a＝m＋5，所以3m－m＝m＋5，解得m＝5.答案：A[知识总结]1．函数与映射的知识记忆口诀：函数新概念，记准要素三；定义域值域，解析式相连；函数表示法，记住也不难；图像和列表，解析最常见；对应变映射，只是变唯一；映射变函数，集合变数集．2．映射到底是什么？怎样理解映射的概念？剖析：对于映射这个概念，可以从以下几点来理解：(1)映射中的两个集合A和B可以是数集、点集或由图形组成的集合等；(2)映射是有方向的，A到B的映射与B到A的映射往往是不一样的；(3)映射要求对集合A中的每一个元素在集合B中都有元素与之对应，而这个与之对应的元素是唯一的，这样集合A中元素的任意性和在集合B中对应的元素的唯一性构成了映射的核心；(4)映射允许集合B中存在元素在A中没有元素与其对应；(5)映射允许集合A中不同的元素在集合B中有相同的对应元素，即映射只能是“多对一”或“一对一”，不能是“一对多”；(6)映射是特殊的对应，函数是特殊的映射．3．函数与映射的关系函数是特殊的映射，对于映射f：A→B，当两个集合A，B均为非空数集时，则从A到B 的映射就是函数，所以函数一定是映射，而映射不一定是函数．(设计者：林大华)。

课后训练基础巩固下列四个函数中，在区间(0，＋∞)上单调递增的函数是()．A．f(x)＝－x＋3B．f(x)＝(x＋1)2C．f(x)＝－|x－1| D．f(x)＝1 x2．若函数y＝f(x)定义在[－1,2]上，且满足12f⎛⎫- ⎪⎝⎭＜f(1)，则f(x)在区间[－1,2]上的单调性是()．A．增函数B．减函数C．先减后增D．无法判断其单调性3．已知函数y＝ax和byx=-在(0，＋∞)上都是减函数，则函数f(x)＝bx＋a在R上是()．A．减函数且f(0)＞0 B．增函数且f(0)＞0 C．减函数且f(0)＜0 D．增函数且f(0)＜04．函数f(x)＝2210x xx x⎧+≥⎪⎨-<⎪⎩，，，的单调性为()．A．在(0，＋∞)上为减函数B．在(－∞，0)上为增函数，在(0，＋∞)上为减函数C．不能判断单调性D．在(－∞，＋∞)上是增函数5．若函数f(x)＝x2＋(a－1)x＋a在区间[2，＋∞)上是增函数，则a的取值范围是__________．6．已知函数f(x)＝11a x-(a＞0，x＞0)．(1)求证：f(x)在(0，＋∞)上是单调递增函数；(2)若f(x)在1,22⎡⎤⎢⎥⎣⎦上的值域是1,22⎡⎤⎢⎥⎣⎦，求a的值．能力提升7．定义在R上的函数f(x)对任意两个不等实数a，b，总有()()f a f bb a--＞0成立，则必有()．A．函数f(x)是先增后减B．函数f(x)是先减后增C．f(x)在R上是增函数D．f(x)在R上是减函数8．设函数f(x)是(－∞，＋∞)上的减函数，又若a∈R，则()．A．f(a)＞f(2a) B．f(a2)＜f(a)C．f(a2＋a)＜f(a) D．f(a2＋1)＜f(a)9．已知函数f(x)在(－∞，＋∞)上是增函数，若a，b∈R且a＋b＞0，则有()．A．f(a)＋f(b)＞－f(a)－f(b)B．f(a)＋f(b)＜－f(a)－f(b)C．f(a)＋f(b)＞f(－a)＋f(－b)D．f(a)＋f(b)＜f(－a)＋f(－b)10．函数f(x)在其定义域M上是增函数，且f(x)＞0，那么在M上为减函数的是()．A．y＝4＋3f(x) B．y＝[f(x)]2C ．y ＝3＋1f x () D ．y ＝2－1f x ()11．若f (x )＝－x 2＋2ax 与g (x )＝1ax +在区间[1,2]上都是减函数，则a 的取值范围是( )．A ．(－1,0)∪(0,1)B ．(－1,0)∪(0,1]C ．(0,1)D ．(0,1]12．函数f (x )＝x |x －1|的单调增区间为__________．13．已知函数f (x )＝22x -(x ∈[3,6])， (1)讨论函数f (x )在[3,6]上的单调性，并证明你的结论； (2)求函数f (x )的最大值与最小值；(3)若函数g (x )＝m 的图像恒在f (x )的图像的上方，求m 的取值范围．14．定义域在(0，＋∞)上的函数f (x )满足(1)f (2)＝1；(2)f (xy )＝f (x )＋f (y )；(3)当x ＞y 时，有f (x )＞f (y )．若f (x )＋f (x －3)≤2，求x 的取值范围．15．建造一个容积为8 m 3，深为2 m 的长方体形无盖水池，如果池底和池壁的造价分别为120元/m 2和80元/m 2.(1)求总造价关于一边长的函数解析式，并指出该函数的定义域；(2)判断(1)中函数在(0,2)和[2，＋∞)上的单调性并用定义法加以证明； (3)如何设计水池尺寸，才能使总造价最低？参考答案1．B 点拨：画出各个函数的图像，由单调函数图像特征可知，选项B 正确．2．D 点拨：增、减函数的定义中的x 1，x 2具有任意性，仅由两个特殊自变量12-和1的函数值的大小关系无法判断函数f (x )的单调性．3．C 点拨：由题意，知a ＜0，b ＜0.∴f (x )＝bx ＋a 在R 上是减函数，且f (0)＝a ＜0.4．D 点拨：画出分段函数f (x )的图像可知，f (x )在(－∞，＋∞)上是增函数．5．a ≥－3 点拨：12a-≤2⇒a ≥－3. 6．解：(1)证明：设x 2＞x 1＞0，则x 2－x 1＞0，x 1x 2＞0， ∵f (x 2)－f (x 1)＝21211212111111x x a x a x x x x x ⎛⎫⎛⎫----=-=⎪ ⎪⎝⎭⎝⎭＞0， ∴f (x 2)＞f (x 1)，∴f (x )在(0，＋∞)上是单调递增的．(2)∵f (x )在1,22⎡⎤⎢⎥⎣⎦上单调递增，∴1122f ⎛⎫= ⎪⎝⎭，f (2)＝2，易得25a =.7．D 点拨：由()()0f a f b b a->-，知a －b 与f (a )－f (b )永远异号，由单调函数的定义知，f (x )在R 上是减函数．8．D 点拨：当a ∈R 时，a 与2a ，a 2与a ，a 2＋a 与a 的大小关系不确定，所以不能由函数的单调性比较相应的两个函数值的大小，而a 2＋1－a ＝21324a ⎛⎫-+ ⎪⎝⎭＞0，∴a 2＋1＞a .∵f (x )是(－∞，＋∞)上的减函数，∴f (a 2＋1)＜f (a )．9．C 点拨：∵a ＋b ＞0，∴a ＞－b ，b ＞－a .由函数的单调性可知，f (a )＞f (－b )，f (b )＞f (－a )，两式相加得选项C 正确．10．C 点拨：(特例法)取f (x )＝x (x ＞0)，很容易可以判断y ＝3＋1()f x 在定义域内为减函数．11．D 点拨：函数g (x )＝1ax +在区间[1,2]上是减函数，则a ＞0，f (x )＝－x 2＋2ax 在区间[1,2]上是减函数，则a ≤1，故0＜a ≤1.12．1,2⎛⎤-∞ ⎥⎝⎦和[1，＋∞) 点拨：f (x )＝x |x －1|＝22,1,,1,x x x x x x ⎧-≥⎨-+<⎩当x ≥1时，f (x )＝x 2－x 在[1，＋∞)上单调递增；当x ＜1时，f (x )＝x －x 2在1,2⎛⎤-∞ ⎥⎝⎦上单调递增；所以单调增区间为1,2⎛⎤-∞ ⎥⎝⎦和[1，＋∞)．13．解：(1)函数f (x )在[3,6]上是减函数，下面进行证明：任取x 1，x 2∈[3,6]，且x 1＜x 2，则x 2－x 1＞0. ∴f (x 1)－f (x 2)＝2112122()2222(2)(2)x x x x x x --=----＞0， 即f (x 1)＞f (x 2)．由单调函数的定义可知，函数f (x )＝22x -在[3,6]上是减函数． (2)由(1)知，f (x )max ＝f (3)＝2， f (x )min ＝f (6)＝12. (3)若函数g (x )＝m 的图像恒在f (x )的图像的上方，则m 应不小于函数f (x )的最大值2，∴m 的取值范围是m ≥2.14．解：∵当x ＞y 时，有f (x )＞f (y )，∴函数f (x )在(0，＋∞)上是增函数． ∵f (xy )＝f (x )＋f (y )，f (2)＝1，∴若f (x )＋f (x －3)≤2，即f (x )＋f (x －3)≤f (2)＋f (2)，则f [x (x －3)]≤f (4)．∴0,30,(3)4,x x x x >⎧⎪->⎨⎪-≤⎩解得3＜x ≤4. ∴x 的取值范围是(3,4]．15．解：(1)设长方体无盖水池的池底一边长为x m ，则另一边长为4xm ，又设总造价为y 元，由题意得8412080222y x x ⎡⎤⎛⎫=⨯+⨯+⨯⨯ ⎪⎢⎥⎝⎭⎣⎦，即y ＝480＋3204x x ⎛⎫+⎪⎝⎭，x ∈(0，＋∞)． (2)函数在(0,2)上是减少的，在[2，＋∞)上是增加的，下面进行证明： 任取x 1，x 2∈(0,2)，且x 1＜x 2，则x 1－x 2＜0. ∴f (x 1)－f (x 2) ＝121244480320480320x x x x ⎡⎤⎡⎤⎛⎫⎛⎫++-++⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦＝121244320x x x x ⎛⎫+-- ⎪⎝⎭ ＝121212320()(4)x x x x x x --＞0，即f (x 1)＞f (x 2)．∴函数f (x )在(0,2)上是减少的． 同理可证，f (x )在[2，＋∞)上是增加的．(3)由(2)中函数的单调性可知，当x ＝2，即池底是正方形时，总造价最低，最低为1 760元．。

§2 双曲线2．1 双曲线及其标准方程必备知识基础练知识点一 双曲线的定义1.动点P 到点M (1，0)及点N (5，0)的距离之差为2a ，则当a ＝1和a ＝2时，点P 的轨迹分别是( )A ．双曲线和一条直线B ．双曲线和一条射线C ．双曲线的一支和一条射线D ．双曲线的一支和一条直线 2．一动圆与两圆：x 2＋y 2＝1和x 2＋y 2－8x ＋12＝0都外切，则动圆圆心的轨迹为( ) A ．抛物线 B ．圆 C ．双曲线的一支 D ．椭圆 知识点二 双曲线的标准方程3.“m >1且m ≠2”是“方程x 22－m －y 2m －1＝1表示双曲线”的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 4．求适合下列条件的双曲线的标准方程：(1)焦点分别为(－2，0)，(2，0)，且经过点(2，3)； (2)焦点在y 轴上，且经过点(2，－5)，a ＝25 ；(3)以椭圆x 28＋y 25＝1的长轴端点为焦点，且经过点(3，10 )；(4)经过点A (2，233)，B (3，－22 )；(5)与双曲线x 216－y 24＝1有公共焦点，且经过点(32 ，2).知识点三 双曲线的定义及方程的应用5.若双曲线E ：x 29 －y 2160＝1的左、右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝15，则|PF 2|＝( )A ．9B ．21C ．9或21D ．186．已知双曲线x 2m －y 27＝1，直线l 过其左焦点F 1，交双曲线左支于A ，B 两点，且|AB |＝4，F 2为双曲线的右焦点，△ABF 2的周长为20，则m 的值为( )A ．8B ．9C ．16D ．207．已知F 1，F 2为双曲线C ：x 2－y 2＝2的左、右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝________.关键能力综合练一、选择题1．已知M (－2，0)，N (2，0)，|PM |－|PN |＝4，则动点P 的轨迹是( )A ．双曲线B ．双曲线左支C ．一条射线D ．双曲线右支2．双曲线x 225 －y 29＝1上的点到一个焦点的距离为12，则到另一个焦点的距离为( )A ．22或2B ．7C ．22D ．23．已知双曲线的一个焦点为F 1(－5 ，0)，点P 在该双曲线上，线段PF 1的中点坐标为(0，2)，则该双曲线的标准方程是( )A ．x 24 －y 2＝1B ．x 2－y 24＝1C ．x22－y23＝1 D ．x23－y 22＝1 4．已知双曲线的中心在原点，两个焦点F 1，F 2分别为(5 ，0)和(－5 ，0)，点P 在双曲线上，且PF 1⊥PF 2，△PF 1F 2的面积为1，则双曲线的方程为( )A ．x 22－y 23＝1 B ．x 23－y 22＝1C ．x24 －y 2＝1 D ．x 2－y24＝15．[易错题]已知O 为坐标原点，设F 1，F 2分别是双曲线x 2－y 2＝1的左、右焦点，P 为双曲线上任一点，过点F 1作∠F 1PF 2的平分线的垂线，垂足为H ，则|OH |＝( )A ．1B ．2C ．4D ．12二、填空题6．[双空题]若方程y 24 －x 2m ＋1＝1表示双曲线，则实数m 的取值范围是____________；若表示椭圆，则m 的取值范围是____________．7．已知双曲线与椭圆x 227 ＋y 236＝1有相同的焦点，且与椭圆的一个交点的纵坐标为4，则双曲线的方程为________.8．[探究题]已知双曲线C ：x 2－y 23＝1的左焦点为F 1，点Q (0，23 )，P 是双曲线C右支上的动点，则|PF 1|＋|PQ |的最小值为________.三、解答题9．在①m >0，且C 的右支上任意一点到左焦点的距离的最小值为3＋23 ；②C 的焦距为43 ；③C 上一点到两焦点距离之差的绝对值为6，这三个条件中任选一个，补充在下面的问题中并解答．问题：已知双曲线C ：x 23m －y 2m＝1，________，求C 的方程．注：如果选择多个条件分别解答，则按第一个解答计分．学科素养升级练1.[多选题]已知点P 在双曲线C ：x 216 －y 29＝1上，F 1，F 2是双曲线C 的左、右焦点，若△PF 1F 2的面积为20，则下列说法正确的有( )A ．点P 到x 轴的距离为203B ．|PF 1|＋|PF 2|＝503C ．△PF 1F 2为钝角三角形D ．∠F 1PF 2＝π32.[情境命题——生活情境]某地发生地震，为了援救灾民，救援员在如图所示的P 处收到一批救灾药品，现要把这批药品沿道路PA ，PB 运送到矩形灾民区ABCD 中去，已知PA ＝100 km ，PB ＝150 km ，BC ＝60 km ，∠APB ＝60°，试在灾民区中确定一条界线，使位于界线一侧的点沿道路PA 送药较近，而另一侧的点沿道路PB 送药较近，请说明这一界线是一条什么曲线，并求出其方程．2．1 双曲线及其标准方程必备知识基础练1．解析：由题意，知|MN |＝4，当a ＝1时，|PM |－|PN |＝2a ＝2<4，此时点P 的轨迹是双曲线的一支；当a ＝2时，|PM |－|PN |＝2a ＝4＝|MN |，点P 的轨迹为以N 为端点沿x 轴向右的一条射线．答案：C2．解析：由题意两定圆的圆心坐标分别为O 1(0，0)，O 2(4，0)，半径分别为1，2.设动圆圆心为C ，动圆半径为r ，则|CO 1|＝r ＋1，|CO 2|＝r ＋2，∴|CO 2|－|CO 1|＝1<|O 1O 2|＝4，故动圆圆心的轨迹为双曲线的一支．答案：C3．解析：若方程x 22－m －y 2m －1 ＝1表示双曲线，则(2－m )·(m －1)>0，解得1<m <2.当1<m <2时，可推出“方程x 22－m－y 2m －1 ＝1表示双曲线”，故“m >1且m ≠2”是“方程x 22－m－y 2m －1＝1表示双曲线”的必要不充分条件．答案：B4．解析：(1)∵双曲线的焦点在x 轴上，∴设双曲线的标准方程为x 2a 2 －y 2b2 ＝1(a >0，b >0).由题知c ＝2，∴a 2＋b 2＝4 ①.又∵点(2，3)在双曲线上， ∴22a 2 －32b2 ＝1 ②. 由①②解得a 2＝1，b 2＝3，所求双曲线的标准方程为x 2－y 23＝1.(2)因为双曲线的焦点在y 轴上，所以可设双曲线的标准方程为y 2a 2 －x 2b2 ＝1(a >0，b >0).由a ＝25 ，点(2，－5)在双曲线上，可得⎩⎪⎨⎪⎧a ＝25，25a 2－4b2＝1， 解得b 2＝16.故所求双曲线的标准方程为y 220 －x 216＝1.(3)由题意得，双曲线的焦点在x 轴上，且c ＝22 .设双曲线的标准方程为x 2a 2 －y 2b2 ＝1(a >0，b >0)，由点(3，10 )在双曲线上，可得⎩⎪⎨⎪⎧a 2＋b 2＝c 2＝8，9a 2－10b2＝1， 解得⎩⎪⎨⎪⎧a 2＝3，b 2＝5， 故所求双曲线的标准方程为x 23－y 25＝1.(4)可设双曲线的方程为mx 2＋ny 2＝1(mn <0).因为点A ⎝⎛⎭⎪⎫2，233 ，B (3，－22 )在双曲线上，所以⎩⎪⎨⎪⎧4m ＋43n ＝1，9m ＋8n ＝1， 解得⎩⎪⎨⎪⎧m ＝13，n ＝－14，故所求双曲线的标准方程为x 23－y 24＝1.(5)易知双曲线x 216 －y 24＝1的焦点在x 轴上，且c 21 ＝16＋4＝20，则待求双曲线的焦点也在x 轴上，且c 22＝c 21＝20.设其标准方程为x 2a 22 －y 220－a 22＝1(a 22 <20) ①，因为点(32 ，2)在双曲线上，所以将(32 ，2)代入①中，得18a 22 －420－a 22＝1，得a 2＝12或a 2＝30(舍去)，故所求双曲线的标准方程为x 212 －y 28＝1.5．解析：由于|PF 1|＝15<c ＋a ＝13＋3＝16，所以点P 在双曲线E 的左支上，所以由双曲线的定义，得|PF 2|－|PF 1|＝2a ＝6，即|PF 2|－15＝6，故|PF 2|＝21.答案：B6．解析：由已知，得|AB |＋|AF 2|＋|BF 2|＝20.因为|AB |＝4，所以|AF 2|＋|BF 2|＝16.根据双曲线的定义，知2a ＝|AF 2|－|AF 1|＝|BF 2|－|BF 1|，所以4a ＝|AF 2|＋|BF 2|－(|AF 1|＋|BF 1|)＝16－4＝12，即a ＝3，所以m ＝a 2＝9.答案：B 7．解析：由双曲线定义，知|PF 1|－|PF 2|＝22 ，a ＝b ＝2 .∵|PF 1|＝2|PF 2|，∴|PF 2|＝22 ，|PF 1|＝42 ，|F 1F 2|＝2c ＝2a 2＋b 2＝4，∴cos∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1||PF 2| ＝32＋8－162×42×22＝34 .答案：34关键能力综合练1．解析：因为|PM |－|PN |＝4＝|MN |，所以动点P 的轨迹是一条射线．故选C. 答案：C2．解析：因为a 2＝25，所以a ＝5.设双曲线的左、右焦点分别为F 1，F 2，双曲线上一点为P . 由双曲线的定义可得||PF 1|－|PF 2||＝10， 不妨设|PF 1|＝12，所以|PF 1|－|PF 2|＝±10， 所以|PF 2|＝22或2.故选A. 答案：A3．解析：设双曲线的标准方程为x 2a 2 －y 2b 2 ＝1(a >0，b >0)，因为c ＝5 ，c 2＝a 2＋b 2，所以b 2＝5－a 2，所以x 2a 2 －y 25－a2 ＝1，因为线段PF 1的中点坐标为(0，2)，所以点P 的坐标为(5 ，4)，将P (5 ，4)代入双曲线方程，得5a 2 －165－a2 ＝1，解得a 2＝1或a 2＝25(舍去)，所以双曲线的标准方程为x 2－y 24＝1.故选B.答案：B4．解析：由题可得⎩⎨⎧|PF 1|·|PF 2|＝2，|PF 1|2＋|PF 2|2＝（25）2，得(|PF 1|－|PF 2|)2＝16，即2a ＝4，解得a ＝2，又因为c ＝5 ，所以b ＝1，所以双曲线的方程为x 24－y 2＝1，故选C.答案：C5．解析：不妨在双曲线右支上取点P ，延长PF 2，F 1H ，交于点Q ，由角平分线性质可知|PF 1|＝|PQ |，根据双曲线的定义得，|PF 1|－|PF 2|＝2，从而|QF 2|＝2，在△F 1QF 2中，OH 为其中位线，故|OH |＝1.故选A.答案：A6．解析：若表示双曲线，则应有m ＋1>0，即m >－1；若表示椭圆，则有⎩⎪⎨⎪⎧m ＋1<0，m ＋1≠－4，解得m <－1且m ≠－5.答案：(－1，＋∞) (－∞，－5)∪(－5，－1)7．解析：椭圆的焦点为F 1(0，－3)，F 2(0，3)，故可设双曲线方程为y 2a 2 －x 2b 2 ＝1(a >0，b >0)，其中a 2＋b 2＝9，因为双曲线与椭圆的一个交点的纵坐标为4，所以该点的坐标为(15 ，4)或(－15 ，4)，故16a 2 －15b2 ＝1.解方程组⎩⎪⎨⎪⎧a 2＋b 2＝9，16a 2－15b 2＝1， 得⎩⎪⎨⎪⎧a 2＝4，b 2＝5，所以所求双曲线的方程为y 24－x 25＝1.答案：y 24－x 25＝18．解析：设双曲线的右焦点为F 2，如图，连接PF 2，QF 2.根据双曲线的定义可知|PF 1|－|PF 2|＝2a ＝2，所以|PF 1|＝|PF 2|＋2，所以|PF 1|＋|PQ |＝|PF 2|＋|PQ |＋2≥|QF 2|＋2，而Q (0，23 )，F 2(2，0)，所以|QF 2|＝22＋（23）2 ＝4，所以|PF 1|＋|PQ |的最小值为6.9．解析：选①：因为m >0，所以a 2＝3m ，b 2＝m ，c 2＝a 2＋b 2＝4m ， 则a ＝3m ，c ＝2m ，因为C 的右支上任意一点到左焦点的距离的最小值为3＋23 ，所以3m ＋2m ＝(3 ＋2)m ＝3＋23 ，解得m ＝3，C 的方程为x 29－y 23＝1.选②：若m >0，则a 2＝3m ，b 2＝m ，c 2＝a 2＋b 2＝4m ，c ＝2m ，因为C 的焦距为43 ，所以2c ＝4m ＝43 ，m ＝3，C 的方程为x 29－y 23＝1；若m <0，则a 2＝－m ，b 2＝－3m ，c 2＝a 2＋b 2＝－4m ，c ＝2－m ，因为C 的焦距为43 ，所以2c ＝4－m ＝43 ，m ＝－3，C 的方程为y 23－x 29＝1，综上所述，C 的方程为x 29－y 23＝1或y 23－x 29＝1.选③：若m >0，则a 2＝3m ，a ＝3m ，因为C 上一点到两焦点距离之差的绝对值为6，所以2a ＝23m ＝6，m ＝3，C 的方程为x 29－y 23＝1；若m <0，则a 2＝－m ，a ＝－m ，因为C 上一点到两焦点距离之差的绝对值为6，所以2a ＝2－m ＝6，m ＝－9，C 的方程为y 29－x 227＝1，综上所述，C 的方程为x 29－y 23＝1或y 29－x 227＝1.学科素养升级练1．解析：因为在双曲线x 216－y 29＝1中，a ＝4，b ＝3，所以c ＝16＋9 ＝5，因为S △PF 1F 2＝12·2c ·|y P |＝5|y P |＝20，所以|y P |＝4，所以P 到x 轴的距离为4，故A 错误；不妨取P (203 ，4)，又因为F 1(－5，0)，F 2(5，0)，则|PF 1|＝（203＋5）2＋16 ＝373，|PF 2|＝ （203－5）2＋16 ＝133 ，所以|PF 1|＋|PF 2|＝503 ，故B 正确；因为kPF 2＝4－0203－5 ＝125>0，所以∠PF 2F 1为钝角，所以△PF 1F 2为钝角三角形，故C 正确；因为S △SS 1S 2＝12|PF 1|·|PF 2|sin ∠F 1PF 2，即12 ×133 ×373 sin ∠F 1PF 2＝20，则sin ∠F 1PF 2＝360481 ，所以∠F 1PF 2≠π3，故D 错误．2．解析：灾民区ABCD中的点可分为三类，第一类沿道路PA送药较近，第二类沿道路PB送药较近，第三类沿道路PA和PB送药一样近．依题意，知界线是第三类点的轨迹．设M为界线上的任一点，则|PA|＋|MA|＝|PB|＋|MB|，即|MA|－|MB|＝|PB|－|PA|＝50，因为|AB|＝1002＋1502－2×100×150×cos 60°＝507>50，所以界线是以A，B为焦点的双曲线的右支的一部分．如图所示，以AB所在直线为x轴，线段AB的垂直平分线为y轴，建立平面直角坐标系．设所求双曲线的标准方程为x2a2－y2b2＝1(a>0，b>0)，易知a＝25，c＝257，所以b2＝c2－a2＝3 750.故双曲线的标准方程为x2625－y23 750＝1.注意到点C的坐标为(257，60)，故y的最大值为60，此时x＝35，故界线的曲线方程为x2625－y23 750＝1(25≤x≤35，0≤y≤60).。