当前位置：文档之家 › 第六章偏心受力构件-2(cb)详解

第六章偏心受力构件-2(cb)详解

  • 格式：pdf
  • 大小：1.14 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

同济大学混凝土结构基本原理第6章答案

同济大学混凝土结构基本原理第6章答案

其中 当 当
为混凝土极限压应变。 时，截面属于大偏心受压； 时，截面属于小偏心受压。
6-6.长细比对偏心受压构件的承载力有直接影响， 请说明基本计算公式中是如何来考虑这一 问题的。 答：当 ，即短柱情况下，取弯矩增大系数 ；否则，取
28
其中，
。
6-7 请根据 N cu − M u 相关曲线说明大偏心受压及小偏心受压时轴向力与弯矩的关系，偏压 构件在什么情况下的抗弯承载力最大？ 答：在小偏心受压破坏时候，随着轴向力 N c 的增大，构件的抗弯能力 M 逐渐减少；在大偏 心受压构件破坏的时候，随着轴向力 N c 的增大,会提高构件的抗弯承载力。在偏心构件的破 坏处于破坏时,构件的抗弯承载力达到最大值。 6-8 N cu − M u 相关曲线有哪些用途？ 答：Ncu-Mu 相关曲线是由具有相同的截面尺寸,相同高度,相同配筋,相同材料强度但偏心距 e0 不同的构件进行系列偏心受压实验得到破坏时每个构件所承受的不同轴力 Ncu 和弯矩 Mu 所 绘制而成的,在此曲线中,我们可以轻松查阅到此构件在小偏心受压或者大偏心受压时候构 件的破坏荷载,了解构件性能.
思考题
6-1.偏心受力构件截面上同时作用有轴向力和弯矩， 除教材上列出的外， 再举出实际工程中 的偏心受压构件和偏心受拉构件各五种。 答：偏心受压构件有屋架的上弦杆、框架结构柱，砖墙及砖垛等。偏心受拉构件有矩形水池 的池壁、矩形剖面料仓或煤斗的壁板、受地震作用的框架边柱，以及双肢柱的受拉肢等。 6-2.对比偏心受压构件与受弯构件正截面的应力及应变分布，说明其相同之处与不同之处。 答： 受弯构件在混凝土出现裂缝前， 混凝土分为受压区和受拉区， 分别承受压应力和拉应力， 受拉区混凝土开裂后， 退出工作， 钢筋单独承担拉应力， 受压区混凝土受压区高度逐渐变小， 压应力不断增大，最终压碎破坏。应变一开始钢筋与混凝土应变相同，慢慢达到混凝土开裂 应变，钢筋屈服应变。而偏心受压构件则因偏心距不同其应力分布亦有不同。当 较大 中时，出现大偏心受压破坏，形式接近受弯。而当 较大 较大或 较小 适

第6章钢结构偏心受力构件

第6章钢结构偏心受力构件

min 63.9 116.0 52.1N/mm2
max min 179 .9 52 .1 0 max 179 .9
平面外稳定公式
tx M x N f y A bW1x
y—弯矩作用平面外轴心受压构件稳定系数 —截面影响系数：箱形截面0.7, 其他截面1.0 b—均匀弯曲的受弯构件整体稳定系数(附录3) tx—弯矩作用平面外的等效弯矩系数
1）弯矩作用平面外有支承，由支点弯矩定 无横向荷载作用时 0.65 0.35 M 2
178.5N/mm2
f 215N/mm2
满足强度条件
2017/10/20 21
《钢结构》— 原理与设计
3. 弯矩作用平面内的稳定验算 x 55.3 b类截面 x 0.831
无端弯矩，有横向荷载：mx=1.0 2 EA 2 2.06105 14080 5 N Ex 85 . 1 10 N 2 2 1.1x 1.1 55.3 N mx M x x A xW1x 1 0.8 N / N Ex
《钢结构》— 原理与设计
第6章 拉弯和压弯构件
6.1 6.2 6.3 6.4 拉弯和压弯构件概述 拉(压)弯构件的强度和刚度 压弯构件的稳定 框架柱的设计要点
2017/10/20
1
《钢结构》— 原理与设计
6.1 拉弯和压弯构件概述
基本概念
外力因素
• 轴向拉力或轴向压力 • 弯矩：轴向力偏心、端弯矩、横向荷载
6
《钢结构》— 原理与设计
单偏心
N Mx f An xWnx
双偏心
My N Mx f An xWnx yWny
不考虑塑性发展的情况

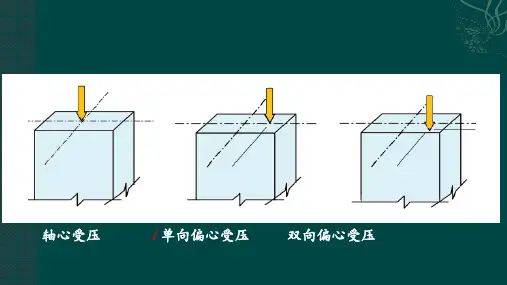
偏心受压构件受力分析ppt课件

偏心受压构件受力分析ppt课件

量有很大关系
压
弯
构
件
As
h
e0
N
N, M=Ne0
b
8.1.1 破坏形态
受拉破坏(大偏心受压破坏)
As
当相对偏心距e0 / h0较大，且As配置的
不过多时会出现受拉破坏。受拉破坏也
称为大偏心受压破坏。
应力应变的分布 破坏特点
受拉钢筋首先屈服， 而后受压区混凝土被 压坏。
受拉和受压钢筋均可
N Nu a1 fcbh0 fyAs fy As
Ne Nue a1 fcasbh02 fyAs h0 as As minbh
截面设计
大偏心受压构件
As和A’s均未知，求As和A’s
以As＋A’s最小为补充条件
取 = b
As
Ne
a1 fcb (1 0.5b )bh02
fy(h0 as)
As
a1 fcbh0b fy
fyAs N
minbh
取 As minbh
已知A’s，求As
as
Ne
fyAs(h0 a1 fcbh02
as)
2as / h0 1 1 2as b
As a1 fcbh0
fyAs N fy
minbh
截面设计
小偏心受压构件
As和A’s均未知，求As和A’s
x
ei N
N
l0
考虑构件挠曲二阶效应的条件
弯矩作用平面内截面对称的偏心受压构件，
当同一主轴方向的杆端弯矩M1/M2 不大于0.9
且设计轴压比不大于0.9 时，
若满足:
lc / i 34 -12( M1 / M 2 )
可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响；

偏心受力构件承载力

偏心受力构件承载力

承载力分析的方法
解析法
基于力学原理和数学公式，通过计算得出构件的承载力。 解析法适用于简单结构和规则截面。
有限元法
利用数值计算方法，将构件离散化为有限个单元，通过求 解单元的应力分布来得到构件的承载力。有限元法适用于 复杂结构和不规则截面。
试验法
通过试验手段对实际构件进行加载测试，直接测得其承载 力。试验法具有较高的精度和可靠性，但成本较高。
ABCD
数值分析
利用数值计算方法，如有限元分析、有限差分法 等，对构件进行受力分析和性能评估。
人工智能
利用人工智能算法，如遗传算法、模拟退火算法 等，对设计方案进行智能优化。
优化设计的实施步骤
需求分析
明确设计需求和目标，分析构件的工作环境 和受力特点。
建立模型
根据需求分析结果，建立描述构件性能的数学 模型。
偏心受力构件
指在承受外力时，外力作用点与构件 重心不重合的构件。
承载力的计算方法
01
02
03
解析法
通过数学公式和物理原理， 计算出结构或构件的承载 力。
试验法
通过实际试验，测量出结 构或构件的承载力。
经验法
根据工程经验，估算结构 或构件的承载力。
承载力的影响因素
材料性能
材料的弹性模量、泊松比、抗拉压强度等性能参数对承载力有直接影 响。
根据计算结果，评估构件的承 载能力和稳定性，对不满足要
求的构件进行优化设计。
04 偏心受力构件的优化设计
优化设计的目标
提高构件承载能力
通过优化设计，使构件在承受偏心荷 载时具有更高的承载能力，减少因荷 载过大而导致的破坏。
降低成本
在满足承载力要求的前提下，通过优 化设计降低材料消耗和制造成本，提 高经济效益。

偏心受压构件课件

偏心受压构件课件

si
cu
Es
(
x
/ h0i
1)
得一元三次方程
Ax3 Bx2 Cx D 0
7-20
1.当 h / h0 z b 时,取 x / h0
由7-10可钢筋应力 s
s
cu
E
s
(
h0
x
1)
求得钢
筋中的应力 。s 再将钢筋面积 、As 钢筋应力 以及s 值代x
入式（7-4）中，
0 Nd fcdbx fsd As s As
即可得所需钢筋面积 As且应满足 。 As' m inbh
当 时h / h，0 取 则钢x 筋h面积 计算式为As ：
As'
Nes
)]
➢当 2as x 时bh，0
As
fcdbx
f
' sd
As'
0 Nd
f sd
➢当 x ，bh且0
时x ， 2as
令 x ,2则a可s 求得
As
0 Nd es
fsd (ho as )
2）当 e0 0时.3h0
已知：b h N d M d
f cd
f sd
f sd
l0
求： As 、As'
N
2．受压破坏——小偏心受压破坏
N
产生条件： （1）偏心距很小。 （2）偏心距 (e0 较/ h小) ，或偏心距较大而受拉钢
筋较多。 （3）偏心距 (e0很/ h小) ，但离纵向压力较远一侧
钢筋数量少，而靠近纵向力N一侧钢筋较多时。 破坏特征：
一般是靠近纵向力一侧的混凝土首先达到极限 压应变而压碎，该侧的钢筋达到屈服强度，远离 纵向力一侧的钢筋不论受拉还是受压，一般达不 到屈服强度。构件的承载力取决于受压区混凝土 强度和受压钢筋强度。 破坏性质：脆性破坏。

第六章 偏心受力构件

第六章 偏心受力构件

第六章 拉弯和压弯构件第一节 构件的应用和破坏形式 第二节 构件的强度和刚度 第三节 压弯柱的整体稳定性 第四节 格构式柱的整体稳定性 第五节 压弯柱的局部稳定性 第六节 压弯构件设计 第七节 压弯构件计算长度第六章 拉弯和压弯构件大纲要求:1、了解拉弯和压弯构件的应用和截面形式； 2、了解压弯构件整体稳定的基本原理；掌握其计算方法； 3、了解实腹式压弯构件局部稳定的基本原理；掌握其计 算方法； 4、掌握拉弯和压弯的强度和刚度计算; 5、掌握实腹式压弯构件设计方法及其主要的构造要求； 6、了解压弯构件的计算长度第六章 拉弯和压弯构件第一节 构件的应用和破坏形式一、应用一般工业厂房和多层房屋的框 架柱均为拉弯和压弯构件。

N e Ne NM Ne N N第六章 拉弯和压弯构件第一节 构件的应用和破坏形式二、类型实腹式—框架和刚架 格构式—工业厂房单向受弯—平面结构 双向受弯—空间结构第六章 拉弯和压弯构件第一节 构件的应用和破坏形式三、构件的截面a)b)弯矩小、轴力大：采用轴心受压构件截面形式； 当仅一个方向的弯矩较大：用单轴对称截面，较大翼缘位 于受压一侧第六章 拉弯和压弯构件第一节 构件的应用和破坏形式四、拉弯(压弯)构件的破坏形式1、强度破坏 截面的部分或全部应力都达到甚至超过钢材屈服 点的状况。

2、刚度破坏 指构件的挠度（或长细比）达到甚至超过规范的 限值。

3、平面内失稳（弯矩作用平面内弯曲失稳破坏） 弯矩作用平面内的弯曲变形，不存在分枝现象。

条件：侧向有足够支撑 。

第六章 拉弯和压弯构件第一节 构件的应用和破坏形式四、拉弯(压弯)构件的破坏形式4、平面外失稳（弯矩作用平面外失稳破坏、弯扭失稳） 弯矩作用方向存在弯曲变形，垂直于弯矩作用方向会突 然产生弯曲变形，同时截面会绕杆轴发生扭转。

条件：侧向缺乏足够支撑或承受双向弯矩的压弯构件。

5、局部失稳破坏 发生在腹板和受压翼缘。

条件：板件较薄第六章 拉弯和压弯构件第一节 构件的应用和破坏形式五、拉弯(压弯)构件的计算拉弯构件： 承载能力极限状态：强度 正常使用极限状态：刚度 拉弯构件没有稳定问题？ 当所属弯矩较大时，需要按照受弯构件进行整体稳定 和局部稳定验算。

钢结构-偏心受力构件学习讲义


为避免塑性区过大，导致变形过大，考虑截面部分
发展塑性，取用截面塑性发展系数，同时引入抗力分项
系数，得到： N
An f

γ
M W
x nx
f
1
当构件在两个主轴内承受弯矩时：
N An

Mx
γW
x
nx

My γ y W ny

f
6
说明：
① 受压翼缘的外伸宽度 b1与厚度 t 之比介于13 235 f y 和 15 235 f y 之间时，取γ x＝1.0；
«规范»借用了弹性压弯构件边缘纤维屈服时计算
公式的形式，提出一近似相关公式：
N
β mx M x
f
x A (1 0.8N NEx ) W1x
y
考虑塑性深入部分截面，采用γ x1W1x，并引入抗力
分项系数，得： N
βM mx x
f
x A γ x1W1x (1 0.8N NEx )
② 需要计算疲劳强度的压弯构件，宜取γ x＝γ y＝1.0；
③ 适用于拉弯构件，轴向荷载使变形减小，偏于安全；
④ 适用于单轴对称截面；
但需验算两点，若N大、M小，1点应力绝对值最大，
若N小、M大，2点应力绝对值最大， 1
x
验算不同点时， γ x 取值不同。 ⑤ 适用于格构式；
M 2
y M
当弯矩作用在与缀材面平行的主平面内时，γ x=1.0
y
当弯矩矢量作用在刚度最大平面内，即弯矩位于腹
板平面内时，构件绕强轴 x 轴弯曲，当荷载增大到某一
数值时，挠度迅速增大而破坏，因为挠曲线始终在弯矩
作用平面内，故称为平面内失稳。
若侧向抗弯刚度 EIy较小，且侧向又无足够的支撑， 可能在平面内失稳之前，突然产生侧向的，即绕 y 轴方

《偏心受力构》课件


抗震性能 评估：对 构件的抗 震性能进 行评估， 确保其满 足抗震要 求
抗震加固： 对不满足 抗震要求 的构件进 行加固， 提高其抗 震性能
抗震设计的实例分析
实例一：上海中心大厦
实例二：台北101大楼
实例三：广州塔
实例四：北京鸟巢
抗震设计的未来发展
智能抗震设计：利用人工智能和 大数据技术，提高抗震设计的准 确性和效率
偏心受力构件的承载能力计算
承载能力的计算方法
确定偏心受力构 件的受力状态
计算偏心受力构 件的应力分布
确定偏心受力构 件的承载能力极 限
计算偏心受力构 件的承载能力
承载能力的计算公式
偏心受力构件的承载能力计算公式为：F=M/L F表示承载能力，M表示偏心受力构件的力矩，L表示偏心受力构件的长度 偏心受力构件的承载能力与力矩和长度有关，力矩越大，承载能力越大 偏心受力构件的承载能力还与材料的强度和刚度有关，材料的强度和刚度越大，承载能力越大
偏心受力构件的分类
添加标题
按照受力方向分类：轴向偏心受力构件、径向偏心受力构件、切 向偏心受力构件
添加标题
按照受力位置分类：中心偏心受力构件、边缘偏心受力构件
添加标题
按照受力大小分类：大偏心受力构件、小偏心受力构件
添加标题
按照受力性质分类：静力偏心受力构件、动力偏心受力构件
添加标题
按照受力形式分类：单偏心受力构件、双偏心受力构件
基础的构造要求
偏心受力构件的 尺寸和形状应满 足设计要求
构件的材质和强 度应满足使用要 求
构件的连接方式 应满足受力要求
构件的防腐蚀和 防锈处理应满足 环境要求连接 Nhomakorabea构造要求
连接方式：采用螺栓、铆钉、焊 接等连接方式

钢筋混凝土偏心受力构件承载力计算

' Ne大
f y (h0 as' )
' 大
h 其中：e ei as' 2
③小偏心受压构件的配筋计算 I.受弯平面内的计算： 将б s的公式(6-14)代人式(6-12)及式(6-13)，并将x代换为 x=ξ h0，则小偏心受压的基本公式为
（6-22）
（6-23） （6-24） 式(6-22)及式(6-23)中有三个未知 数ξ ，As及As’故不能得出唯一的 解、一般情况下As’无论拉压其应力 都达不到强度设计值，故配置数量 很多的钢筋是无意义的。故可取As ＝0.002bh，但考虑到在N较大而e0 较小的全截面受压情况下如附加偏 心
如图6-7所示，ab段表示大偏心受压时的M-N相 关曲线，为二次抛物线、随着轴向压力N的增大 截面能承担的弯矩也相应提高。 b点为受拉钢筋与受压混凝土同时达到其强 度值的界限状态。此时偏心受压构件承受的弯矩 M最大。 bc段表示小偏心受压时的M-N曲线，是一条 接近于直线的二次函数曲线。由曲线趋向可以看 出，在小偏心受压情况下，随着轴向压力的增大 截面所能承担的弯矩反而降低。
第六章 计算
本章的重点是：
钢筋混凝土偏心受力构件承载力
了解偏心受压构件的受力工作特性，熟悉两 种不同的受压破坏特性及由此划分成的两类受压 构件 掌握两类偏心受压构件的判别方法； 掌握两类偏心受压构件正截面承载力的计算 方法；
掌握偏心受压构件斜截面受剪承载力计算方
法。
§6.1
概述
结构构件的截面上受到轴力和弯矩的共同作用或受 到偏心力的作用时该结构构件称为偏心受压构件。 分为偏心受压构件和偏心受拉构件。 偏心受压构件又分为：单向偏心受压构件(图6-1a) 及双向偏心受压构件(图6-1b)。 偏心受拉构件在偏心拉力的作用下 是一种介于轴 心受拉构件与受弯构件之间的受力构件。承受节间荷载 的悬臂式桁架上弦(图6-2a)一般建筑工程及桥梁工程中 的双肢柱的受拉肢属于偏心受拉构件(图6-2b)。此外， 如图6-2c所示的矩形水池的池壁 其竖向截面同时承受轴 心拉力及平面外弯矩的作用故也属于偏心受拉构件。

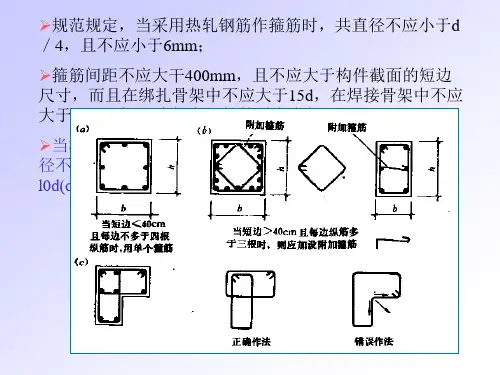
06-2偏心受压构件


适用条件：
对矩形截面受压构件，其截面应符合：
V Vu
1 . 75
1 .0
f t bh 0 0 . 07 N )
对矩形截面受压构件，截面剪力如果符合：
V 0 . 25 c f c bh 0
则可不进行承载力计算，直接按构造要求配箍。
偏心受压构件的构造要求
轴心受压柱的纵向受力钢筋、箍筋以及混凝土保护层的各项 构造措施均适用于偏心受压柱，此外，在值心受压拄中还应 满足下列构造要求： (一)截面形式及尺寸 偏心受压柱多采用矩形截面，且将长边布置在弯矩作用方 向。长短边的比值一般在1.0~2.0范围内变化，当偏心距较大 时，可适当加大，但最大不宜超过3.0。 正方形柱网无梁顶盖中的支柱，由于弯矩可能作用在两个 相互垂直方向中的任意一方，故可采用正方形截面，并在两 个相互垂直的方向均采用对称配筋。
规范规定，当采用热轧钢筋作箍筋时，共直径不应小于d ／4，且不应小于6mm； 箍筋间距不应大干400mm，且不应大于构件截面的短边 尺寸，而且在绑扎骨架中不应大于15d，在焊接骨架中不应 大于20d，此处d为纵向钢筋的最小直径。 当柱中全部纵向受力钢筋的配筋率超过3%时，则箍筋直 径不宜小于8mm，且应焊成封闭式环，其间距不应大干 l0d(d为纵向钢筋的最小直径)．且不应大于100mm。
二、大、小偏心受压构件的界限
受拉破坏，受拉侧钢筋先屈服，而后压区混凝土 压坏。 ☆界限破坏———受拉钢筋屈服的同时，受压区混 凝土刚好达到极限压应变εcu。 受压破坏，受压区混凝土先压坏，而另一侧钢筋 可能受拉，也可能受压，但未屈服。
界限破坏——当纵向受拉钢筋屈服的同时，受压 区边缘混凝土达到极限压应变。它与正截面界限破 坏的概念是相同的。
' ' '
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

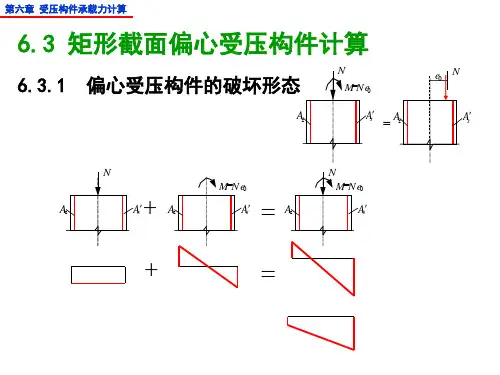
第三节压弯柱的整体稳定
(1)弯矩作用平面内失稳—轴压力和弯矩相互作用，弯矩作用平面内
弯曲变形增大
，弯曲失稳。

一、失稳模式
(2)弯矩作用平面外失稳—轴压力和侧向变形、扭转变形相互作用使变形增大，弯扭失稳第三节压弯柱的整体稳定
一、
失稳模式
二、平面内失稳
在N 和M 的同时作用下，构件在
弯矩作用平面内发生变形，当荷载增加到一定大小时则到达极限；超过此极限，要维持内外力平衡，只能减小N 和M ，即为压弯构件在弯矩作用平面内的稳定问题。

1、平面内稳定的概念:
第三节压弯柱的整体稳定
2、特征
压弯构件的曲线m y N 二、平面内失稳
第三节压弯柱的整体稳定
（1) 当构件在弯矩作用
平面外方向有足够的刚
度或侧向支承，则构件
在荷载作用开始时，会
沿弯矩作用方向弯曲，
直到压溃破坏，即构件
在弯矩作用平面内丧失
稳定，属于第二类稳定
问题。

2、特征
压弯构件的曲线m y N 二、平面内失稳
第三节压弯柱的整体稳定
(2) 弯矩随挠度加大而
增加，轴压力和挠度的
关系曲线呈非线性曲线
上升段OBA：稳定平衡状
态，荷载仍可增加。

曲
线下降段AC：不稳定平
衡状态，要保持平衡，
须迅速减小荷载。

2、特征
二、平面内失稳
第三节压弯柱的整体稳定
(3) 压弯构件达到临界状
态时所能承受的荷载Ncr，
与构件所受弯矩大小有
关。

弯矩影响用相对偏心
率来衡量,相对偏心率愈大
临界荷载愈低。

相对偏心率:截面核心距:ρ
εe A W e A N W M ===//A W =ρ
3、平面内整体稳定的计算
（1）按边缘纤维屈服准则方法计算；
（2）按极限承载能力准则的方法；
（3）实用计算公式（单项公式或相关公式的表达形式）
二、平面内失稳
第三节压弯柱的整体稳定
(1) 边缘纤维屈服准则的计算方法假设压弯构件为理想
弹
塑性材料，两端铰接并
承受压力N 和均匀弯矩
M x 作用时二、平面内失稳
第三节压弯柱的整体稳定
(1) 边缘纤维屈服准则的计算方法
则得最大弯矩则弯矩曲率方程:
设得
N EX 为平面内受压失稳的欧拉临界力
设失稳时构件变形曲线为:
第三节压弯柱的整体稳定
(1)
y
对于
实际杆件需考虑缺陷，如将杆件缺陷(变
形，弯曲)用等效附加偏心e o 考虑
则最大弯矩
临界方程为(1) 边缘纤维屈服准则的计算方法
第三节压弯柱的整体稳定
M
x =0时,退化成轴心受压柱，临界状态时轴力为
N cr = x f y A
临界方程变为
或
解方程得(1) 边缘纤维屈服准则的计算方法
第三节压弯柱的整体稳定
等效附加偏心
将
e o 代入边缘屈服相关方程，得(1) 边缘纤维屈服准则的计算方法
第三节压弯柱的整体稳定
对于
非均匀受弯，引进等效弯矩系数 mx ，
折算成均匀受弯
(最大弯矩相等)第三节压弯柱的整体稳定
(1) 边缘纤维屈服准则的计算方法
▲世界各国及我国规范，基本采用两项相关公式来计算压弯构件在弯矩作用平面内的整体稳定。

▲建立两项相关公式的主要根据是假定构件缺陷模式以及按边缘纤维屈服准则来近似求解压溃临界荷载。

二、平面内失稳
第三节压弯柱的整体稳定
（2）按极限承载能力准则的方法
第三节压弯柱的整体稳定
实腹式压弯构件
在边缘纤维屈服后
(a 点)，直到曲线的
顶点(b 点) 真正的
极限承载力N u ;
N u 的求解方法
很多，常用的为数
值法，可以考虑各
种缺陷，不同边界
条件，弹性和弹塑
性
（3）实用计算公式
对于
三、平面外失稳
式中第三节压弯柱的整体稳定
对侧向刚度较小的压弯构件，当N
和M 增加到一定程度，构件在弯矩作用
平面外不能保持平直，突然发生平面外
的弯曲变形，并伴随着绕纵向剪切中心
轴（扭转轴）的扭转。

这种现象称为压
弯构件丧失弯矩作用平面外的整体稳定
，或在弯矩作用平面外的整体屈曲。

三、平面外失稳
1、双轴对称工形截面压弯构件平面外弯扭失稳轴力+纯弯，弹性失稳相关方程
式中
纯弯梁临界弯矩第三节压弯柱的整体稳定
1、双轴对称工形截面压弯构件平面外弯扭失稳
相关方程的另一表达式：
一般情况N ω>N Ey ，可偏安全
取N ω= N Ey ，得
或三、平面外失稳
第三节压弯柱的整体稳定
考虑
弹塑性失稳，N Ey 用ϕy Af y 代替，M cr 用ϕb W 1x f y 代替相关方程对于非均匀弯曲，引入等效弯矩系数
ϕb 为纯弯梁失稳的稳定系数试验证明第三节压弯柱的整体稳定
三
双轴对称工形截面柱，当
3、等效弯矩系数
(1)弯矩作用平面外是悬臂构件：βtx =1.0
(2)弯矩作用平面外两相临侧向支承点之间构件段：
有端弯矩无横向荷载作用时，
βtx =0.65+0.35M 2/M 1，|M 1|≥|M 2|
横向荷载和端弯矩同时作用时，构件全长弯矩同号βtx =1.0，有正负弯矩βtx =0.85
有横向荷载、无端弯矩作用时，βtx =1.0
三、平面外失稳
第三节压弯柱的整体稳定
课前问题
•压弯构件存在哪些破坏形式？
•压弯构件的整体失稳包括哪几种类型？各自有什么特征？
•压弯构件平面内稳定，有哪几种计算准则？哪些情况不能考虑部分塑性发展？
•单轴对称截面压弯构件的强度验算公式？。